A Class of Hybrid Multistep Block Methods with A–Stability for the Numerical Solution of Stiff Ordinary Differential Equations

Abstract

Recently, block backward differentiation formulas (BBDFs) are used successfully for solving stiff differential equations. In this article, a class of hybrid block backward differentiation formulas (HBBDFs) methods that possessed $A$–stability are constructed by reformulating the BBDFs for the numerical solution of stiff ordinary differential equations (ODEs). The stability and convergence of the new method are investigated. The methods are found to be zero-stable and consistent, hence the method is convergent. Comparisons between the proposed method with exact solutions and existing methods of similar type show that the new extension of the BBDFs improved the stability with acceptable degree of accuracy.

1. Introduction

The aim of this paper is to develop a class hybrid multistep block method based on block backward differentiation formulas (BBDFs) for the numerical solution of first order ordinary differential equations (ODEs) of the form:

$$y^{\prime }\left(x\right)=f\left(x,y\left(x\right)\right), y\left(x_0\right)=y_0, x\in \left[a,b\right]$$

(1)

where $f$ is continuous and second variable Lipschitzian over its existence domain, so that the existence of Solution (1) is guaranteed.

Equation (1) frequently arise in many applications in science and engineering. Many of these applications often results to stiff ODEs. Stiff systems are found in description of atmospheric phenomena, chemical reactions occurring in living species, chemical kinetics (e.g., explosions), engineering control systems, electronic circuits, lasers, mechanics, and molecular dynamics [1,2,3]. Several other examples are given in [4]. There is no unique definition of stiffness. Various definition describing stiffness are given in the literature [4,5,6]. The first identification of stiff equations as a special class of problems is due to a chemist [5]. He states that stiff equations are equations where certain implicit methods, in particular BDF, perform better, usually tremendously better, than explicit ones [6] and systems containing very fast components as well as very slow components while [4] states that “stiff problems are problems for which explicit methods don’t work”.

In many practical applications, the difficulty associated with stiff ODEs is in choosing an efficient integration scheme since the choice of numerical methods is imposed by numerical stability. Besides numerical stability, the efficiency of numerical methods also depends on whether the method is explicit or implicit. Explicit schemes require the least amount of computation per time step but the allowable time step is severely restricted by the stability requirements, see [7]. Furthermore, the implementation of implicit method can be very costly in terms of computer time since solvers for stiff equations require the evaluation of the Jacobian, $J=\partial f/\partial y$.

The most widely used method to numerically solve (1) which is stiff are the backward differentiation formulas (BDFs) which is popularly known as the Gear method, see [8,9]. Recently, a great deal of effort has been proposed in the literature in the development of block methods for solving (1). The block methods are extensively discussed by [10,11,12,13,14,15] and are proven to be efficient in improving the accuracy and reduced the number of function evaluation. This approach is extended to various type by increasing the order, varies the step size and orders with extended stability region. All the methods, mentioned above, produced solutions at multiple points simultaneously at single iteration. Independent solution at selected grid points was generated using block method without overlapping. Despite the success of the block approach, there has been no guidance or recommendation on the choice of the most suitable numbers of interpolation points or the suitable order in improving the accuracy with lesser computational time when solving a very stiff problem. In deriving a good numerical method, the challenge is to increase the stability region while maintaining or even improving efficiency. Therefore, our objective is to construct a new class of hybrid methods by extending the existing block methods by [10] to address the setbacks associated with solving stiff ODEs. The improvement is obtained by considering [10] with a suitable hybrid points to find numerical solutions of (1).

The paper is organized as follows: in Section 2, we present the formulation of the hybrid method by presenting a review of classical block methods and hybrid block methods from the literature; Section 3 includes the analysis of the new method in terms of order, zero stability, and region of stability. Implementation of the method is discussed in Section 4. In Section 5 numerical tests are performed on first-order differential equation problems possessing stiffness and comparisons with MATLAB solvers are applied in providing numerical solutions for initial value problems of ordinary differential equations. Finally, conclusions are presented in Section 6.

2. Derivation of the Method

Various attempts have been proposed for solving (1) using block methods ranging from constant step size to variable step size, fully implicit and then to diagonally implicit methods, see [10,12,13]. We will illustrate the idea of computation in block by reviewing the theory of block methods available in the literature as follows.

2.1. Review of Block Methods

The idea of using block methods for solving ODEs was initially developed by [14,15] followed by [16]. Later, [17] proposed block methods in the form of predictor-corrector for solving special second-order ODEs of type non-stiff while [18] proposed parallel solution of solving (1). Adopting the definition by [17], the general form of a block method can be expressed as follows:

Definition 1.

A$k$—block,$r$—point block method is a matrix of finite difference equation of the form

$$Y_m={\displaystyle \sum }_{j=1}^k{A}_i{Y}_{m-i}+h{\displaystyle \sum }_{i=0}^k{B}_i{F}_{m-i}$$

(2)

where$Y_m$and$F_m$are defined by$Y_m={\left(y_n,y_{n+1},\dots ,y_{n+r-1}\right)}^T,$$F_{m }={\left(f_n,f_{n+1},\dots ,f_{n+r-1}\right)}^T$. All the$A_i\prime s$and$B_i\prime s$are properly chosen$r\times r$matrix coefficients and$m=0,1,2,\dots$represent the block number, and$n=mr$is the first step number of the$m$th block and$r$is the block size.

The method derived in the form of (2) has the advantage of producing $r$—point solutions simultaneously at each application. Lagrange Interpolation was adopted by some authors to generate continuous linear multistep method, among them are [11,12,13].

2.2. Hybrid Block Method

Recently many authors have extended existing block method by adding hybrid points which is also referred as off-step points to find numerical solutions for (1). Some of the works on hybrid methods when solving (1) has been developed by see [19,20,21,22]. From [21], the focus is on the construction of explicit hybrid methods with nonnegative coefficients, which are a class of multistep methods incorporating a function evaluation at an off-step point. In [22], researchers derived a two-step hybrid methods for $y\prime \prime =f\left(x,y\right)$, with oscillatory or periodic solutions, through the usage of the exponential fitting technique. Recently, [23] proposed a method by considering two intermediate points and the approximation of the true solution by an adequate polynomial and imposing collocation conditions. However, there are some drawbacks ranging from choosing the suitable order of the method and the number of off-step points to be included as hybrid methods.

2.3. Formulation of Hybrid Block

The method derived in this section is a hybrid block multistep method. The formulation is based on the existing BBDFs by adding off-step points in the formula that possessed $A$–stability property can be generated. The formulas are commonly derived by using an integrated form of the ODEs and replacing the integrals with interpolating polynomial. We consider the grid points,$\left(x_n,y_n\right),$ $\left(x_{n+1},y_{n+1}\right)$ and $\left(x_{n+2},y_{n+2}\right)$ with $h=x_{n+1}-x_n$ and three off-step-points $\left(x_{n-1/2},y_{n-1/2}\right),$ $\left(x_{n+1/2},y_{n+1/2}\right),$ and $\left(x_{n+3/2},y_{n+3/2}\right)$ as illustrated in Figure 1.

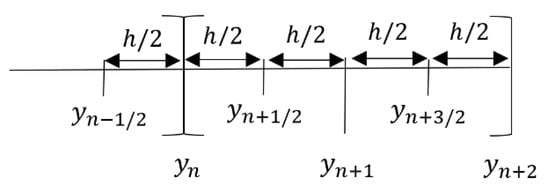
Figure 1. Hybrid block method with three off-step points.

The basic idea to formulate hybrid block backward differentiation formulas (HBBDF) is to replace $f\left(x,y\left(x\right)\right)$ in (1) by an interpolating polynomial $P_k\left(x\right)$ of degree $k.$ Assume the solution $y\left(x\right)$ to (1) is approximated by the polynomial $P_k\left(x\right)$:

$$y\left(x\right)\cong P_k\left(x\right)$$

(3)

The polynomial associated with interpolating points $\left(x_{n-1/2},y_{n-1/2}\right)$, $\left(x_n,y_n\right),\left(x_{n+1/2},y_{n+1/2}\right)$, $\left(x_{n+1},y_{n+1}\right)$, $\left(x_{n+3/2},y_{n+3/2}\right)$ and $\left(x_{n+2},y_{n+2}\right)$ is given by:

$$\begin{array}{ll}P\left(x\right)& =\frac{\left(x-x_n\right)\left(x-x_{n+1/2}\right)\left(x-x_{n+1}\right)\left(x-x_{n+3/2}\right)\left(x-x_{n+2}\right)}{\left(x_{n-1/2}-x_n\right)\left(x_{n-1/2}-x_{n+1/2}\right)\left(x_{n-1/2}-x_{n+1}\right)\left(x_{n-1/2}-x_{n+3/2}\right)\left(x_{n-1/2}-x_{n+2}\right)}{y}_{n-1/2}\\ & +\frac{\left(x-x_{n-1/2}\right)\left(x-x_{n+1/2}\right)\left(x-x_{n+1}\right)\left(x-x_{n+3/2}\right)\left(x-x_{n+2}\right)}{\left(x_n-x_{n-1/2}\right)\left(x_n-x_{n+1/2}\right)\left(x_n-x_{n+1}\right)\left(x_n-x_{n+3/2}\right)\left(x_n-x_{n+2}\right)}{y}_n\\ & +\frac{\left(x-x_{n-1/2}\right)\left(x-x_n\right)\left(x-x_{n+1}\right)\left(x-x_{n+3/2}\right)\left(x-x_{n+2}\right)}{\left(x_{n+1/2}-x_{n-1/2}\right)\left(x_{n+1/2}-x_n\right)\left(x_{n+1/2}-x_{n+1}\right)\left(x_{n+1/2}-x_{n+3/2}\right)\left(x_{n+1/2}-x_{n+2}\right)}{y}_{n+1/2}\\ & +\frac{\left(x-x_{n-1/2}\right)\left(x-x_n\right)\left(x-x_{n+1/2}\right)\left(x-x_{n+3/2}\right)\left(x-x_{n+2}\right)}{\left(x_{n+1}-x_{n-1/2}\right)\left(x_{n+1}-x_n\right)\left(x_{n+1}-x_{n+1/2}\right)\left(x_{n+2}-x_{n+3/2}\right)\left(x_{n+1}-x_{n+2}\right)}{y}_{n+1}\\ & +\frac{\left(x-x_{n-1/2}\right)\left(x-x_n\right)\left(x-x_{n+1/2}\right)\left(x-x_{n+1}\right)\left(x-x_{n+2}\right)}{\left(x_{n+3/2}-x_{n-1/2}\right)\left(x_{n+3/2}-x_n\right)\left(x_{n+3/2}-x_{n+1/2}\right)\left(x_{n+3/2}-x_{n+1}\right)\left(x_{n+3/2}-x_{n+2}\right)}{y}_{n+3/2}\\ & +\frac{\left(x-x_{n-1/2}\right)\left(x-x_n\right)\left(x-x_{n+1/2}\right)\left(x-x_{n+1}\right)\left(x-x_{n+3/2}\right)}{\left(x_{n+2}-x_{n-1/2}\right)\left(x_{n+2}-x_n\right)\left(x_{n+2}-x_{n+1/2}\right)\left(x_{n+2}-x_{n+1}\right)\left(x_{n+2}-x_{n+3/2}\right)}{y}_{n+2}\end{array}$$

(4)

Substituting $x=x_{n+1}+sh$ in (4), we obtain:

$$\begin{array}{ll}P\left(x_{n+1}+sh\right)=& \frac{\left(s+1\right)\left(s+1/2\right)\left(s\right)\left(s-1/2\right)\left(s-1\right)}{\left(-15/4\right)}{y}_{n-1/2}\\ & +\frac{\left(s+3/2\right)\left(s+1/2\right)\left(s\right)\left(s-1/2\right)\left(s-1\right)}{\left(3/2\right)}{y}_n\\ & +\frac{\left(s+3/2\right)\left(s+1\right)\left(s\right)\left(s-1/2\right)\left(s-1\right)}{\left(-3/2\right)}{y}_{n+1/2}\\ & +\frac{\left(s+3/2\right)\left(s+1\right)\left(s+1/2\right)\left(s-1/2\right)\left(s-1\right)}{\left(3/8\right)}{y}_{n+1}\\ & +\frac{\left(s+3/2\right)\left(s+1\right)\left(s+1/2\right)\left(s\right)\left(s-1\right)}{\left(-3/2\right)} y_{n+3/2}\\ & +\frac{\left(s+3/2\right)\left(s+1\right)\left(s+1/2\right)\left(s\right)\left(s-1/2\right)}{\left(15/4\right)}{y}_{n+2}\end{array}$$

(5)

Generally, if we differentiate (3), yields the following:

$$y^{\prime }\left(x\right)=f\left(x,y\left(x\right)\right)=P_k\prime \left(x\right)$$

(6)

In our case, we differentiate (5) once with respect to $s$ at the point $x=x_{n+1 },$ gives the following:

$$\begin{array}{ll}{P}^{\prime \left(x_{n+1}+sh\right)}=& h{f}_{n+1}\\ & =\left(-\frac{4}{3}{s}^4+s^2-\frac{1}{15}\right)y_{n-1/2}+\left(\frac{20}{3}{s}^4+\frac{8}{3}{s}^3-7s^2-\frac{1}{3}s+\frac{1}{2}\right)y_n\\ & +\left(-\frac{40}{3}{s}^4-\frac{32}{3}{s}^3+14s^2+\frac{16}{3}s-2\right)y_{n+1/2}+\left(\frac{40}{3}{s}^4-10s^3+16s^2-10s+\frac{2}{3}\right)y_{n+1}\\ & +\left(-\frac{20}{3}{s}^4-\frac{32}{3}{s}^3+s^2+\frac{16}{3}s+1\right)y_{n+3/2}+\left(\frac{4}{3}{s}^4+\frac{8}{3}{s}^3+s^2-\frac{1}{3}s-\frac{1}{10}\right)y_{n+2}\end{array}$$

(7)

Upon substituting $s=-1/2, 0,1/2, 1$ respectively into (7) we obtained the coefficients for the HBBDF method as follows:

$$\begin{array}{c} y_{n+1/2}=\frac{3}{20}{y}_{n-1/2}-\frac{3}{2}{y}_n+3y_{n+1}-\frac{3}{4}{y}_{n+3/2}+\frac{1}{10}{y}_{n+2}-\frac{3}{2}h{f}_{n+1/2}\\ y_{n+1}=\frac{1}{10}{y}_{n-1/2}-\frac{3}{4}{y}_n+3y_{n+1/2}-\frac{3}{2}{y}_{n+3/2}+\frac{3}{20}{y}_{n+2}+\frac{3}{2}h{f}_{n+1}\\ y_{n+3/2}=-\frac{3}{65}{y}_{n-1/2}+\frac{4}{13}{y}_n-\frac{12}{13}{y}_{n+1/2}+\frac{24}{13}{y}_{n+1}-\frac{12}{65}{y}_{n+2}+\frac{6}{13}h{f}_{n+3/2}\\ y_{n+2}=\frac{12}{137}{y}_{n-1/2}-\frac{75}{137}{y}_n+\frac{200}{137}{y}_{n+1/2}-\frac{300}{137}{y}_{n+1}+\frac{300}{137}{y}_{n+3/2}+\frac{30}{137}h{f}_{n+2}\end{array}\}$$

(8)

3. Analysis of the Proposed Method

In this section our objective is directed towards the discussion of the properties of the HBBDF method which includes order of the new method, zero stability and consistency which are the necessary conditions for convergence of the method. Region of absolute stability of the HBBDF will also be studied to determine its suitability of solving stiff ODEs.

3.1. Order

We start by defining the order and error constant as given in [24].

Definition 2.

(Order)

The linear multistep method associated with the linear difference operator are said to be of order $p$ if $C_0=C_1=\dots =C_{p+1}=0$ and $C_{p+1}\ne 0$.

Definition 3.

(Error constant)

The term$C_{p+1}$is called the error constant and it implies that the local truncation error is given by:

$$t_{n+k}=C_{p+2}{h}^{p+2}{y}^{\left(p+2\right)}\left(x_n\right)+O\left(h^{p+3}\right)$$

In order to check the consistency of the method, first, we will determine the order of the method. By rearranging the equation in (8), we get the following equation:

$$\begin{array}{c}-\frac{3}{20}{y}_{n-1/2}+\frac{3}{2}{y}_n+y_{n+1/2}-3y_{n+1}+\frac{3}{4}{y}_{n+3/2}-\frac{1}{10}{y}_{n+2}=-\frac{3}{2}h{f}_{n+1/2}\\ -\frac{1}{10}{y}_{n-1/2}+\frac{3}{4}{y}_n-3y_{n+1/2}+y_{n+1}+\frac{3}{2}{y}_{n+3/2}-\frac{3}{20}{y}_{n+2}=\frac{3}{2}h{f}_{n+1}\\ \frac{3}{65}{y}_{n-1/2}-\frac{4}{13}{y}_n+\frac{12}{13}{y}_{n+1/2}-\frac{24}{13}{y}_{n+1}+y_{n+3/2}+\frac{12}{65}{y}_{n+2}=\frac{6}{13}h{f}_{n+3/2}\\ -\frac{12}{137}{y}_{n-1/2}+\frac{75}{137}{y}_n-\frac{200}{137}{y}_{n+1/2}+\frac{300}{137}{y}_{n+1}-\frac{300}{137}{y}_{n+3/2}+y_{n+2}=\frac{30}{137}h{f}_{n+2}\end{array}\}$$

(9)

Based on the matrix form of Equation (2), Equation (9) can be written as follows:

$$\begin{array}{l}\left[\begin{array}{cccc}0& 0& -3/20& 3/2\\ 0& 0& -1/10& 3/4\\ 0& 0& 3/65& -4/13\\ 0& 0& -12/137& 75/137\end{array}\right]\left[\begin{array}{c}{y}_{n-3/2}\\ y_{n-1}\\ y_{n-1/2}\\ y_n\end{array}\right]\\ +\left[\begin{array}{cccc}1& -3& 3/4& -1/10\\ -3& 1& 3/2& -3/20\\ 12/13& -24/13& 1& 12/65\\ -200/137& 300/137& -300/137& 1\end{array}\right]\left[\begin{array}{c}{y}_{n+1/2}\\ y_{n+1}\\ y_{n+3/2}\\ y_{n+2}\end{array}\right]\\ \begin{array}{ccc}& =h\left[\begin{array}{cccc}-3/2& 0& 0& 0\\ 0& 3/2& 0& 0\\ 0& 0& 6/13& 0\\ 0& 0& 0& 30/137\end{array}\right]\left[\begin{array}{c}{f}_{n+1/2}\\ f_{n+1}\\ f_{n+3/2}\\ f_{n+2}\end{array}\right].& \end{array}\end{array}$$

with

$$\begin{array}{l}\begin{array}{cc}& A_0=A_1=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right],A_2=\left[\begin{array}{c}-3/20\\ -1/10\\ 3/65\\ -12/137\end{array}\right],A_3=\left[\begin{array}{c}3/2\\ 3/4\\ -4/13\\ 75/137\end{array}\right],A_4=\left[\begin{array}{c}1\\ -3\\ 12/13\\ -200/137\end{array}\right],A_5=\left[\begin{array}{c}-3\\ 1\\ -24/13\\ 300/137\end{array}\right],\end{array}\\ \begin{array}{cc}& A_6=\left[\begin{array}{c}3/4\\ 3/2\\ 1\\ -300/137\end{array}\right],A_7=\left[\begin{array}{c}-1/10\\ -3/20\\ 12/65\\ 1\end{array}\right], \end{array}\\ B_0=B_1=B_2=B_3=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right], B_4=\left[\begin{array}{c}-3/2\\ 0\\ 0\\ 0\end{array}\right],B_5=\left[\begin{array}{c}0\\ 3/2\\ 0\\ 0\end{array}\right],B_6=\left[\begin{array}{c}0\\ 0\\ 6/13\\ 0\end{array}\right],B_7=\left[\begin{array}{c}0\\ 0\\ 0\\ 30/137\end{array}\right]\end{array}$$

We defined the linear difference operator $L$ associated with the hybrid BBDFs method in Equation (2) which is given by [20] as:

$$L\left[y\left(x\right), h\right]={\displaystyle \sum }_{j=0}^7\left[A_{j}y\left(x+jh/2\right)-h{B}_j{y}^{\prime }\left(x+jh/2\right)\right]$$

(10)

where $A_j$ and $B_j$ are constants. Expanding $y\left(x+jh/2\right)$ and $y\prime \left(x+jh/2\right)$ in Equation (10) using Taylor series at $x,$ and collecting the coefficients of $h$, we obtained:

$$\begin{array}{ll}L\left[y\left(x\right),h\right]& ={\displaystyle {\displaystyle \sum }_{j=0}^7}{A}_j\left[y\left(x\right)+\frac{\left(jh/2\right)}{1!}{y}^{\prime }\left(x\right)+\frac{{(jh/2)}^2}{2!}{y}^{\left(2\right)}\left(x\right)+\frac{{(jh/2)}^3}{3!}{y}^{\left(3\right)}\left(x\right)+\cdots \right] \\ & -{\displaystyle {\displaystyle \sum }_{j=0}^7}h{B}_j\left[y^{\prime }\left(x\right)+\frac{\left(jh/2\right)}{1!}{y}^{\left(2\right)}\left(x\right)+\frac{{(jh/2)}^2}{2!}{y}^{\left(3\right)}\left(x\right)+\frac{{(jh/2)}^3}{3!}{y}^{\left(4\right)}\left(x\right)+\cdots \right] \\ & ={\displaystyle {\displaystyle \sum }_{j=0}^7}\left[A_j\right]y\left(x\right)+\frac{1}{2}{\displaystyle {\displaystyle \sum }_{j=0}^7}\left[j{A}_j-2B_j\right]hy\prime \left(x\right)+\frac{1}{4}{\displaystyle {\displaystyle \sum }_{j=0}^7}\left[\frac{1}{2!}{j}^2{A}_j-2\frac{1}{1!}j{B}_j\right]h^2{y}^{\left(2\right)}\left(x\right)\\ & +\frac{1}{8}{\displaystyle {\displaystyle \sum }_{j=0}^7}\left[\frac{1}{3!}{j}^3{A}_j-2\frac{1}{2!}{j}^2{B}_j\right]h^3{y}^{\left(3\right)}\left(x\right)+\dots \end{array}$$

(11)

By letting the collected terms of $y\left(x\right), y^{\prime }\left(x\right),y\prime \prime \left(x\right)$ in (11) as $C_{p }$ where $p=0,1,2\dots ,$ we can determine the order of the method and the error constant of the method:

$$\begin{array}{c}\begin{array}{ll}{C}_0={\displaystyle {\displaystyle \sum }_{j=0}^7}{A}_j=& A_0+A_1+A_3+\dots +A_7=0\\ & =\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]+\left[\begin{array}{c}-3/20\\ -1/10\\ 3/65\\ -12/137\end{array}\right]+\left[\begin{array}{c}3/2\\ 3/4\\ -4/13\\ 75/137\end{array}\right]+\left[\begin{array}{c}1\\ -3\\ 12/13\\ -200/137\end{array}\right]+\left[\begin{array}{c}-3\\ 1\\ -24/13\\ 300/137\end{array}\right]\\ & +\left[\begin{array}{c}3/4\\ 3/2\\ 1\\ -300/137\end{array}\right]+\left[\begin{array}{c}-1/10\\ -3/20\\ 12/65\\ 1\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]\end{array}\\ \begin{array}{ll}{C}_1={\displaystyle {\displaystyle \sum }_{j=0}^7}\left(j{A}_j\right)& -2{\displaystyle {\displaystyle \sum }_{j=0}^7}{B}_j=0\\ & =\left(0.A_0+1.A_1+2A_2+3A_3+4A_4+5A_5+6A_6+7A_7\right)-2(B_0+B_1+B_2+B_3\\ & +B_4+B_5+B_6+B_7)\\ & =2\left[\begin{array}{c}-3/20\\ -1/10\\ 3/65\\ -12/137\end{array}\right]+3\left[\begin{array}{c}3/2\\ 3/4\\ -4/13\\ 75/137\end{array}\right]+4\left[\begin{array}{c}1\\ -3\\ 12/13\\ -200/137\end{array}\right]+5\left[\begin{array}{c}-3\\ 1\\ -24/13\\ 300/137\end{array}\right]+6\left[\begin{array}{c}3/4\\ 3/2\\ 1\\ -300/137\end{array}\right]\\ & +7\left[\begin{array}{c}-1/10\\ -3/20\\ 12/65\\ 1\end{array}\right]-2\left( \left[\begin{array}{c}-3/2\\ 0\\ 0\\ 0\end{array}\right]+\left[\begin{array}{c}0\\ 3/2\\ 0\\ 0\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ 6/13\\ 0\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ 0\\ 30/137\end{array}\right] \right)=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]\end{array}\\ \begin{array}{ll}{C}_2={\displaystyle {\displaystyle \sum }_{j=0}^7}\frac{\left(j^2{A}_j\right)}{2!}& -2{\displaystyle {\displaystyle \sum }_{j=0}^7}\left(j{B}_j\right)=0\\ & =\frac{1}{2!}\left(0^2{A}_0+1^2{A}_1+2^2{A}_2+3^2{A}_3+4^2{A}_4+5^2{A}_5+6^2{A}_6+7^2{A}_7\right)-2(0.B_0\\ & +1.B_1+2B_2+2B_3+4B_4+5B_5+6B_6+7B_7)\\ & =\frac{1}{2}(\begin{array}{c}4\left[\begin{array}{c}-3/20\\ -1/10\\ 3/65\\ -12/137\end{array}\right]+9\left[\begin{array}{c}3/2\\ 3/4\\ -4/13\\ 75/137\end{array}\right]+16\left[\begin{array}{c}1\\ -3\\ 12/13\\ -200/137\end{array}\right]+25\left[\begin{array}{c}-3\\ 1\\ -24/13\\ 300/137\end{array}\right]\\ \end{array}\\ & +36\left[\begin{array}{c}3/4\\ 3/2\\ 1\\ -300/137\end{array}\right]+49\left[\begin{array}{c}-1/10\\ -3/20\\ 12/65\\ 1\end{array}\right])\\ & -2\left(4 \left[\begin{array}{c}-3/2\\ 0\\ 0\\ 0\end{array}\right]+5\left[\begin{array}{c}0\\ 3/2\\ 0\\ 0\end{array}\right]+6\left[\begin{array}{c}0\\ 0\\ 6/13\\ 0\end{array}\right]+7\left[\begin{array}{c}0\\ 0\\ 0\\ 30/137\end{array}\right] \right)=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]\end{array}\\ \begin{array}{c}{C}_3={\displaystyle {\displaystyle \sum }_{j=0}^7}\frac{\left(j^3{A}_j\right)}{3!}-2{\displaystyle {\displaystyle \sum }_{j=0}^7}\left(\frac{j^2{B}_j}{2!}\right)=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]\\ C_4={\displaystyle {\displaystyle \sum }_{j=0}^7}\frac{\left(j^4{A}_j\right)}{4!}-2{\displaystyle {\displaystyle \sum }_{j=0}^7}\left(\frac{j^3{B}_j}{3!}\right)=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]\\ C_5={\displaystyle {\displaystyle \sum }_{j=0}^7}\frac{\left(j^5{A}_j\right)}{5!}-2{\displaystyle {\displaystyle \sum }_{j=0}^7}\frac{\left(j^4{B}_j\right)}{4!}=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]\\ C_6={\displaystyle {\displaystyle \sum }_{j=0}^7}\frac{\left(j^6{A}_j\right)}{6!}-2{\displaystyle {\displaystyle \sum }_{j=0}^7}\frac{\left(j^5{B}_j\right)}{5!}=\left[\begin{array}{c}-1/20\\ -1/20\\ 2/65\\ -10/137\end{array}\right]\end{array}\end{array}$$

(12)

We obtained $C_6\ne 0$, hence the HBBDF is of order 5. Since the HBBDF method is of order $p=5\ge 1,$ it is consistent by definition. The error constant is just $C_6$ above.

3.2. Convergence of the Derived Method

In this section we investigate the convergence of the HBBDFs. The convergence of a numerical method is generally determined by analysing consistency and zero stability given in the following theorem.

Theorem 1.

(Convergence):

The necessary and sufficient conditions for the linear multistep method to be convergent are that it be both consistent and zero-stable.

Proof of Theorem 1.

See [24].

In order to check the consistency of the method, we use the following definition given by [24]. □

Definition 4.

(Consistent)

The linear multistep method is said to be consistent if it has the order of$p\ge 1$.

Hence, HBBDF in (8) is consistent. Next, we discuss the zero stability associated with HBBDFs.

Definition 5.

(Zero stable)

The block method is zero stable provided the roots$R_j, j=1\left(1\right)k$of the first characteristics polynomial$\rho \left(R\right)$specified as:

$$\rho \left(R\right)=\det \left[{\displaystyle \sum }_{i=0}^k{A}^{\left(i\right)}{R}^{\left(k-i\right)}\right]=0, A^{\left(0\right)}=-I$$

This satisfies$\left|R_j\right|\le 1,$and for those roots with$\left|R_j\right|=1,$the multiplicity must not exceed two.

We find the stability polynomial of HBBDF by applying linear test problem

$$\begin{array}{ccc}& y\prime =f=\lambda y, \lambda <0,& \end{array}$$

(13)

into Equation (8) yields,

$$\begin{array}{c}{y}_{n+1/2}=\frac{3}{20}{y}_{n-1/2}-\frac{3}{2}{y}_n+3y_{n+1}-\frac{3}{4}{y}_{n+3/2}+\frac{1}{10}{y}_{n+2}-\frac{3}{2}h{\lambda }_{n+1/2}\\ y_{n+1}=\frac{1}{10}{y}_{n-1/2}-\frac{3}{4}{y}_n+3y_{n+1/2}-\frac{3}{2}{y}_{n+3/2}+\frac{3}{20}{y}_{n+2}+\frac{3}{2}h{\lambda }_{n+1}\\ y_{n+3/2}=-\frac{3}{65}{y}_{n-1/2}+\frac{4}{13}{y}_n-\frac{12}{13}{y}_{n+1/2}+\frac{24}{13}{y}_{n+1}-\frac{12}{65}{y}_{n+2}+\frac{6}{13}h{\lambda }_{n+3/2}\\ y_{n+2}=\frac{12}{137}{y}_{n-1/2}-\frac{75}{137}{y}_n+\frac{200}{137}{y}_{n+1/2}-\frac{300}{137}{y}_{n+1}+\frac{300}{137}{y}_{n+3/2}+\frac{30}{137}h{\lambda }_{n+2}\end{array}\}$$

(14)

Next, we transformed Equation (14) into matrix form as below:

$$\begin{array}{c}\left[\begin{array}{cccc}1+\frac{3}{2}h\lambda & -3& 3/4& -1/10\\ -3& 1-\frac{3}{2}h\lambda & 3/2& -3/20\\ 12/13& -24/13& 1-\frac{6}{13}h\lambda & 12/65\\ -200/137& 300/137& -300/137& 1-\frac{30}{137}h\lambda \end{array}\right] \left[\begin{array}{c}{y}_{n+1/2}\\ \\ y_{n+1}\\ \\ y_{n+3/2}\\ \\ y_{n+2}\end{array}\right] \\ =\left[\begin{array}{cccc}0& 0& \frac{3}{20}& -\frac{3}{2}\\ 0& 0& \frac{1}{10}& -\frac{3}{4}\\ 0& 0& -\frac{3}{65}& \frac{4}{13}\\ 0& 0& \frac{12}{137}& -\frac{75}{137}\end{array}\right] \left[\begin{array}{c}{y}_{n-3/2}\\ \\ y_{n-1}\\ \\ y_{n-1/2}\\ \\ y_n\end{array}\right]\end{array}$$

with

$$\begin{array}{c}A=\left[\begin{array}{cccc}1+\frac{3}{2}h\lambda & -3& 3/4& -1/10\\ -3& 1-\frac{3}{2}h\lambda & 3/2& -3/20\\ 12/13& -24/13& 1-\frac{6}{13}h\lambda & 12/65\\ -200/137& 300/137& -300/137& 1-\frac{30}{137}h\lambda \end{array}\right],\\ B=\left[\begin{array}{cccc}0& 0& \frac{3}{20}& -\frac{3}{2}\\ 0& 0& \frac{1}{10}& -\frac{3}{4}\\ 0& 0& -\frac{3}{65}& \frac{4}{13}\\ 0& 0& \frac{12}{137}& -\frac{75}{137}\end{array}\right], \\ Y_{m-1}=\left[\begin{array}{c}{y}_{n-3/2}\\ \\ y_{n-1}\\ \\ y_{n-1/2}\\ \\ y_n\end{array}\right]\end{array}$$

and $Y_m=\left[\begin{array}{c}{y}_{n+1/2}\\ \\ y_{n+1}\\ \\ y_{n+3/2}\\ \\ y_{n+2}\end{array}\right]$ which is equivalent to $A{Y}_m=B{Y}_{m-1}$.

Denote $\widehat{h}=h\lambda ,$ the associated stability polynomial, $\rho \left(R, \widehat{h}\right)$ of the HBBDF method is obtained by computing $\det \left(AR-B\right)$,

$$\begin{array}{ll}\rho \left(R,\widehat{h}\right)=& -\frac{17109}{1781}{R}^4+\frac{16938}{1781}{R}^3+\frac{19251}{1781}{R}^4\widehat{h}-\frac{38709}{7124}{R}^4{\widehat{h}}^2+\frac{2727}{1781}{R}^4{\widehat{h}}^3-\frac{405}{1781}{R}^4{\widehat{h}}^4\\ & +\frac{171}{1781}{R}^2+\frac{63}{1781}{R}^2\widehat{h}+\frac{27}{7124}{R}^2{\widehat{h}}^2+\frac{15246}{1781}{R}^3\widehat{h}+\frac{10341}{3562}{R}^3{\widehat{h}}^2+\frac{81}{137}{R}^3{\widehat{h}}^3\end{array}$$

(15)

Substitute $\widehat{h}=0$ into (15) to find the roots of the stability polynomial,

$$\rho \left(R,0\right)=-\frac{17109}{1781}{R}^4+\frac{16938}{1781}{R}^3+\frac{171}{1781}{R}^2$$

Next, we solve for $R$ as follows:

$$\begin{array}{ccc}& -\frac{17109}{1781}{R}^4+\frac{16938}{1781}{R}^3+\frac{171}{1781}{R}^2=0.& \end{array}$$

This yields the roots $0,0, 1,$ and $-0.00999$. All of the roots have modulus less than one which satisfied the zero stable conditions given in definition 5. Thus, we conclude that HBBDF is zero stable. We have shown that the HBBDF method is consistent and zero stable. From Theorem 1, we conclude the HBBDF converged.

3.3. Stability of Mathematical Components

Before we construct the region of absolute stability of the HBBDF method derived in Section 2, we give some definitions adopt from [25].

Definition 6.

($A$–stable)

A numerical method is said to be $A$–stable if the left-hand half-plane with $\mathrm{Re}\left(\widehat{h}\right)<0$, $\widehat{h}=h\lambda$, is contained by the absolute stability regions of the method used. This means that the stability region covers the entire negative left half plane.

Definition 7.

$(A\left(\alpha \right)-$stable)

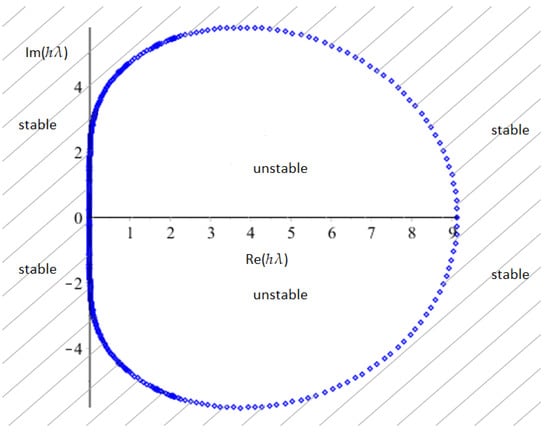
A method is said to be $A\left(\alpha \right)-$stable if it is stable for all $\lambda$ such that $\pi -\alpha \le \arg \left(\lambda \right)\le \pi +\alpha .$ The boundary of the stability region is given by the set of points determined by $R=e^{i\theta }, 0\le \theta \le 2\pi$ for which $\left|R\right|\le 1$. Note that the set of values of $\lambda$ for which the method is stable is called the stability domain. Below we present the stability region which corresponds to the HBBDF method drawn in the $h\lambda$ plane. The region of absolute stability is shown in Figure 2.

Figure 2. The region of absolute stability for the fifth order hybrid block backward differentiation formulas (HBBDF).

The shaded region represents the set of points for which $\left|R\right|<1$. Evidently, from Figure 2, this region of stability includes all the negative real axis which corresponds to an $A$–stable method. Next, we make comparison of stability region of HBBDF with the existing BBDF of the same order. The region for both methods are presented in Figure 3.

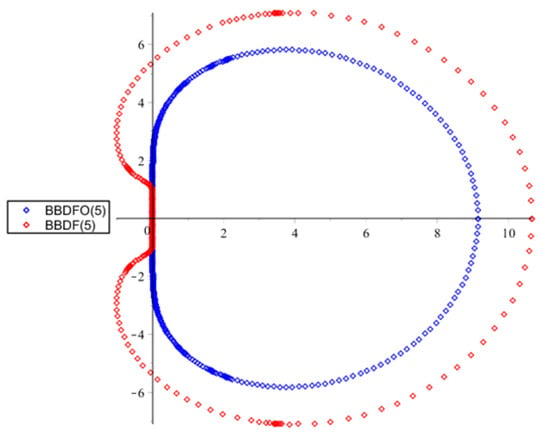
Figure 3. Comparison of stability regions between HBBDF and block backward differentiation formulas (BBDF, 5).

Looking at the stability regions in Figure 3, we see that the HBBDF is $A$–stable while the BBDF(5) is $A\left(\alpha \right)$ stable. The absolute instability interval of both methods is tabulated in Table 1.

Table 1. Instability boundaries for HBBDF versus BBDF (5).

Method	Interval of Instability
HBBDF	(0, 9.14)
BBDF(5)	(0, 10.80)

From Table 1, the interval of instability for HBBDF is smaller than BBDF (5).

4. Implementation of HBBDF Method

In this section, we discussed the application of Newton’s method in the implementation of the HBBDF method for integrating stiff ODEs. Let $i$ denote the iteration, $y_{n+j}^{\left[i+1\right]}$ denote the ${\left(i+1\right)}^{th}$ iterative value of $y_{n+j}$ and $e_{n+j}^{\left[i+1\right]}$ denote as the differences between ${\left[i\right]}^{th}$ and ${\left[i+1\right]}^{th}$ iteration values of $y_{n+j}$ as follows:

$$e_{n+j}^{\left[i+1\right]}=y_{n+j}^{\left[i+1\right]}-y_{n+j}^{\left[i\right]}, j=1/2, 1, 3/2, 2$$

(16)

Newton’s iteration for the HBBDF takes the following form,

$$\begin{array}{ccc}& y_{n+j}^{\left[i+1\right]}=y_{n+j}^{\left[i\right]}-\left[F_j\left(y_{n+j}^{\left[i\right]}\right)\right]{\left[F_j^{\prime }\left(y_{n+j}^{\left[i\right]}\right)\right]}^{-1},& \end{array}j=1/2, 1, 3/2, 2$$

where

$$\begin{array}{l}{F}_{\frac{1}{2}}=y_{n+\frac{1}{2}}-3y_{n+1}+\frac{3}{4}{y}_{n+\frac{3}{2}}-\frac{1}{10}{y}_{n+2}+\frac{3}{2}h{f}_{n+\frac{1}{2}}^p-{\eta }_{\frac{1}{2}}\\ F_1=-3y_{n+\frac{1}{2}}+y_{n+1}+\frac{3}{2}{y}_{n+\frac{3}{2}}-\frac{3}{20}{y}_{n+2}-\frac{3}{2}h{f}_{n+1}^p-{\eta }_1\\ F_{\frac{3}{2}}=\frac{12}{13}{y}_{n+\frac{1}{2}}-\frac{24}{13}{y}_{n+1}+y_{n+\frac{3}{2}}+\frac{12}{65}{y}_{n+2}-\frac{6}{13}h{f}_{n+\frac{3}{2}}^p-{\eta }_{\frac{3}{2}}\\ F_2=-\frac{200}{137}{y}_{n+1/2}+\frac{300}{137}{y}_{n+1}-\frac{300}{137}{y}_{n+3/2}+y_{n+2}-\frac{30}{137}h{f}_{n+2}^p-{\eta }_2\end{array}$$

${\eta }_{1/2}$, ${\eta }_1,{\eta }_{3/2}$ and ${\eta }_2$ are the back-values as follows,

$${\eta }_{1/2}=\frac{3}{20}{y}_{n-1/2}-\frac{3}{2}{y}_n , {\eta }_1=\frac{1}{10}{y}_{n-1/2}-\frac{3}{4}{y}_n, {\eta }_{3/2}=-\frac{3}{65}{y}_{n-1/2}+\frac{4}{13}{y}_n, {\eta }_2=\frac{12}{137}{y}_{n-1/2}-\frac{75}{137}{y}_n.$$

(17)

Therefore, from Equations (16) and (17), we get the following equation to calculate the approximation,

$$\left[F_j^{\prime }\left(y_{n+j}^{\left[i\right]}\right)\right]e_{n+j}^{\left[i+1\right]}=-\left[F_j\left(y_{n+j}^{\left[i\right]}\right)\right], j=1/2, 1, 3/2, 2$$

(18)

and the matrix form of Equation (19) becomes,

$$\begin{array}{ll}\left[\begin{array}{cccc}1+\frac{3}{2}h\frac{\partial f_{1/2}^{\left[i\right]}}{\partial y_{1/2}^{\left[i\right]}}& -3& 3/4& -1/10\\ -3& 1-\frac{3}{2}h\frac{\partial f_1^{\left[i\right]}}{\partial y_1^{\left[i\right]}}& 3/2& -3/20\\ 12/13& -24/13& 1-\frac{6}{13}h\frac{\partial f_{3/2}^{\left[i\right]}}{\partial y_{3/2}^{\left[i\right]}}& 12/65\\ -200/137& 300/137& -300/137& 1-\frac{30}{137}h\frac{\partial f_2^{\left[i\right]}}{\partial y_2^{\left[i\right]}}\end{array}\right]& \left[\begin{array}{c}\\ e_{n+1/2}^{\left[i+1\right]}\\ \\ e_{n+1}^{\left[i+1\right]}\\ \\ e_{n+3/2}^{\left[i+1\right]}\\ \\ e_{n+2}^{\left[i+1\right]}\\ \end{array}\right]\\ =\left[\begin{array}{cccc}-1& 3& -3/4& 1/10\\ 3& -1& -3/2& 3/20\\ -12/13& 24/13& -1& -12/65\\ 200/137& -300/137& 300/137& -1\end{array}\right]\left[\begin{array}{c}{y}_{n+1/2}^{\left[i\right]}\\ y_{n+1}^{\left[i\right]}\\ y_{n+3/2}^{\left[i\right]}\\ y_{n+2}^{\left[i\right]}\end{array}\right]\\ +h\left[\begin{array}{cccc}-3/2& 0& 0& 0\\ 0& 3/2& 0& 0\\ 0& 0& 6/13& 0\\ 0& 0& 0& 30/137\end{array}\right]\left[\begin{array}{c}{f}_{n+1/2}^{\left[i\right]}\\ f_{n+1}^{\left[i\right]}\\ f_{n+3/2}^{\left[i\right]}\\ f_{n+2}^{\left[i\right]}\end{array}\right]+\left[\begin{array}{c}\begin{array}{c}{\eta }_{1/2}\\ {\eta }_1\\ {\eta }_{3/2}\end{array}\\ {\eta }_2\end{array}\right]\end{array}$$

(19)

The code developed will be using the PECE (predict–evaluate–correct–evaluate) mode. $f_{n+j}^p$ denote the predicted value of $f_{n+j}.$ For example, to approximate point $y_{n+1}$ using PECE mode, a predictor equation for $y_{n+1}$ is denoted as $y_{n+1}^{\left[0\right]}$ which can be expressed as follows,

$$\begin{gathered} \begin{array}{cc}\mathrm{Predict}& y_{n+1}^{\left[0\right]}=y_{n-2}-5y_{n-3/2}+10y_{n-1}-10y_{n-1/2}+5y_n\hfill \\ \left(\mathrm{P}\right)& y_{n+2}^{\left[0\right]}=35y_{n-2}-160y_{n-3/2}+280y_{n-1}-224y_{n-1/2}+70y_n\hfill \\ \mathrm{Evaluate} \left(\mathrm{E}\right)& y_{n+1}^{\left[1\right]}=\frac{1}{10}{y}_{n-1/2}-\frac{3}{4}{y}_n+3y_{n+1/2}-\frac{3}{2}{y}_{n+3/2}+\frac{3}{20}f\left(x_{n+2},y_{n+2}^{\left[0\right]}\right)+\frac{3}{2}hf\left(x_{n+1},y_{n+1}^{\left[0\right]}\right)\hfill \\ \mathrm{Correct} \left(\mathrm{C}\right)& \\ {y}_{n+1}^{\left[2\right]}=\frac{1}{10}{y}_{n-1/2}-\frac{3}{4}{y}_n+3y_{n+1/2}-\frac{3}{2}{y}_{n+3/2}+\frac{3}{20}f\left(x_{n+2},y_{n+2}^{\left[1\right]}\right)+\frac{3}{2}hf\left(x_{n+1},y_{n+1}^{\left[1\right]}\right)\hfill \\ \mathrm{Evaluate} \left(\mathrm{E}\right)& y_{n+1}^{\left[3\right]}=\frac{1}{10}{y}_{n-1/2}-\frac{3}{4}{y}_n+3y_{n+1/2}-\frac{3}{2}{y}_{n+3/2}+\frac{3}{20}f\left(x_{n+2},y_{n+2}^{\left[2\right]}\right)+\frac{3}{2}hf\left(x_{n+1},y_{n+1}^{\left[2\right]}\right)\hfill \end{array} \end{gathered}$$

5. Numerical Results and Discussion

In this section, we present some numerical results in order to illustrate the performance of the new method in solving stiff ODEs. Three sets of stiff problems are tested under various step sizes ${10}^{-2}, {10}^{-4},$ and ${10}^{-6}.$ The numerical results will be compared with stiff solver ode15s in MATLAB and with the existing BBDF by [26] of the same order. For error calculations, the error formula is given by:

$$E\left(x_n\right)=y_n-y\left(x_n\right)$$

(20)

In (20),$y\left(x_n\right)$ is the exact solution for the problem considered and $y_n$ is the computed solution.

Problem 1.

Source [9]

$$y^{\prime }=-100\left(y-x\right)+1, y\left(0\right)=1, 0\le x\le 10,\lambda =-100$$

Exact Solution:$y\left(x\right)=e^{-100x}+x$.

Problem 2.

Source [27]

$$y^{\prime }=-20y+20\sin x+\cos x, y\left(0\right)=1, 0\le x\le 2,\lambda =-20$$

Exact Solution:$y\left(x\right)=\sin x+e^{-20x}$.

Problem 3.

Source [28]

$$\begin{array}{c}{y}_1^{\prime }=42y_2-43y_1, y_1\left(0\right)=8, 0\le x\le 1,\\ y_2^{\prime }=-8y_2+7y_1 , y_2\left(0\right)=1, \\ {\lambda }_1=-1, {\lambda }_2=-50\end{array}$$

Exact Solution:

$$\begin{array}{c}{y}_1\left(x\right)=2e^{-x}+6e^{-50x},\\ y_2\left(x\right)=2e^{-x}-e^{-50x}.\end{array}$$

The evaluation of maximum error, MAXE is computed as follows,

$$\mathrm{MAXE}=\underset{1\le x\le TS}{\max }\left(\underset{1\le i\le N}{\max } E\left(x_i\right)\right)$$

with $N$ is the number of equations, and $TS$ is the total number of step. The results obtained by HBBDF are summarized in the following Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7 and Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10.

Table 2. Numerical results for Problem 1.

h	Method	MAXE
${10}^{-2}$	BBDFO(5)	3.17747 × 10−2
	BBDF(5)	2.47875 × 10−2
	ode15s	8.36936 × 10−3
${10}^{-4}$	BBDFO(5)	6.24695 × 10−5
	BBDF(5)	2.56073 × 10−4
	ode15s	1.66333 × 10−4
${10}^{-6}$	BBDFO(5)	6.41334 × 10−9
	BBDF(5)	2.69869 × 10−8
	ode15s	2.75058 × 10−6

Table 3. Solutions for Problem 1.

$\mathit{x}$	Exact Solution	New HBBDF	BBDF(5)	ode15s
0.0	1.0000000000	1.0000000000	1.0000000000	1.0000000000
0.1	0.1000453999	0.1000478886	0.1000503772	0.0994412895
0.2	0.2000000021	0.2000025021	0.2000050021	0.2054339092
0.3	0.3000000000	0.3000025000	0.3000050000	0.2978049816
0.4	0.4000000000	0.4000025000	0.4000050000	0.4000000064
0.5	0.5000000000	0.5000025000	0.5000050000	0.4999999998
0.6	0.6000000000	0.6000025000	0.6000050000	0.5841506756
0.7	0.7000000000	0.7000025000	0.7000050000	0.7000000008
0.8	0.8000000000	0.8000025000	0.8000050000	0.8000000000
0.9	0.9000000000	0.9000025000	0.9000050000	0.8999999998
1.0	1.0000000000	1.0000025000	1.0000050000	0.9775502641

Table 4. Numerical results for Problem 2.

h	Method	MAXE
${10}^{-2}$	HBBDF	1.49360$\times {10}^{-2}$
	BBDF(5)	3.56801$\times {10}^{-2}$
	ode15s	8.36909$\times {10}^{-3}$
${10}^{-4}$	HBBDF	2.55244$\times {10}^{-6}$
	BBDF(5)	1.06868$\times {10}^{-5}$
	ode15s	1.66322$\times {10}^{-4}$
${10}^{-6}$	HBBDF	2.56588$\times {10}^{-10}$
	BBDF(5)	1.07993$\times {10}^{-9}$
	ode15s	2.75074$\times {10}^{-6}$

Table 5. Approximated solutions for Problem 2.

$\mathit{x}$	Exact	HBBDF	BBDF(5)	ode15s
0.0	1.0000000000	1.0000000000	1.0000000000	1.0000000000
0.1	0.2351686998	0.2351644208	0.2351601419	0.2333555364
0.2	0.2169849697	0.2169865041	0.2169880385	0.2147135216
0.3	0.2979989589	0.2980012232	0.2980034877	0.2974433131
0.4	0.3897538049	0.3897560908	0.3897583767	0.3847970907
0.5	0.4794709385	0.4794731302	0.4794753219	0.4768615143
0.6	0.5646486176	0.5646506806	0.5646527437	0.5590250294
0.7	0.6442185187	0.6442204308	0.6442223429	0.6493777179
0.8	0.7173562034	0.7173579452	0.7173596869	0.7100931674
0.9	0.7833269248	0.7833284789	0.7833300329	0.7919088442
1.0	0.8414709869	0.8414723376	0.8414736884	0.8405372397

Table 6. Numerical results for Problem 3.

h.	Method	MAXE
${10}^{-2}$	HBBDF	2.37429$\times {10}^{-1}$
	BBDF(5)	1.97128$\times {10}^{-1}$
	ode15s	5.02584$\times {10}^{-2}$
${10}^{-4}$	HBBDF	9.49700$\times {10}^{-5}$
	BBDF(5)	3.94490$\times {10}^{-4}$
	ode15s	9.96987$\times {10}^{-4}$
${10}^{-6}$	HBBDF	9.62257$\times {10}^{-9}$
	BBDF(5)	4.04965$\times {10}^{-8}$
	ode15s	1.81196$\times {10}^{-5}$

Table 7. Approximated solutions for Problem 3.

$\mathit{x}$	Exact	HBBDF	BBDF(5)	ode15s
$y_1\left(x\right)$
0.0	8.0000000000	8.0000000000	8.0000000000	8.0000000000
0.1	1.8501025180	1.8500929407	1.8500833638	1.8545518680
0.2	1.6377339060	1.6377297781	1.6377256504	1.6351481569
0.3	1.4816382760	1.4816345725	1.4816308682	1.4734657183
0.4	1.3406401040	1.3406367529	1.3406334013	1.3406398807
0.5	1.2130613190	1.2130582869	1.2130552542	1.2092413617
0.6	1.0976232720	1.0976205282	1.0976177841	1.0707188433
0.7	0.9931706076	0.9931681247	0.9931656418	1.0240545524
0.8	0.8986579282	0.8986556817	0.8986534350	0.8959146678
0.9	0.8131393194	0.8131372867	0.8131352538	0.8195251399
1.0	0.7357588824	0.7357570430	0.7357552036	0.7357585308
$y_2\left(x\right)$
0.0	1.0000000000	1.0000000000	1.0000000000	1.0000000000
0.1	1.8029368890	1.8029332071	1.8029295250	1.8046095992
0.2	1.6374161060	1.6374120183	1.6374079303	1.6348536019
0.3	1.4816361350	1.4816324314	1.4816287274	1.4734642088
0.4	1.3406400900	1.3406367384	1.3406333868	1.3406401219
0.5	1.2130613190	1.2130582868	1.2130552541	1.2092413372
0.6	1.0976232720	1.0976205282	1.0976177841	1.0976231642
0.7	0.9931706076	0.9931681247	0.9931656418	0.9931705121
0.8	0.8986579282	0.8986556816	0.8986534350	0.8959145584
0.9	0.8131393194	0.8131372867	0.8131352538	0.8195251888
1.0	0.7357588824	0.7357570430	0.7357552036	0.7357585295

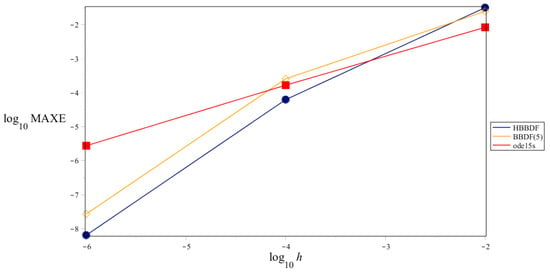
Figure 4. Accuracy curves for Problem 1.

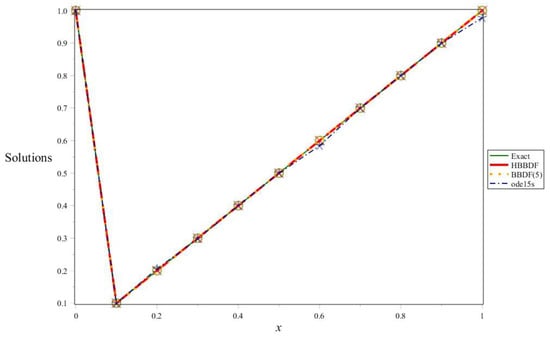
Figure 5. The graph of exact and approximated solutions for Problem 1.

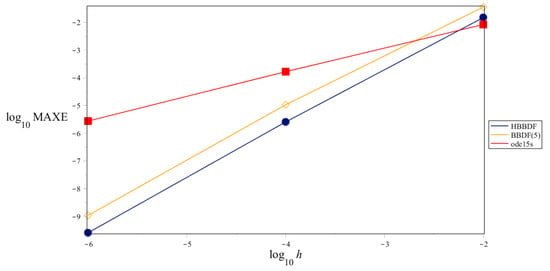
Figure 6. Accuracy curves for Problem 2.

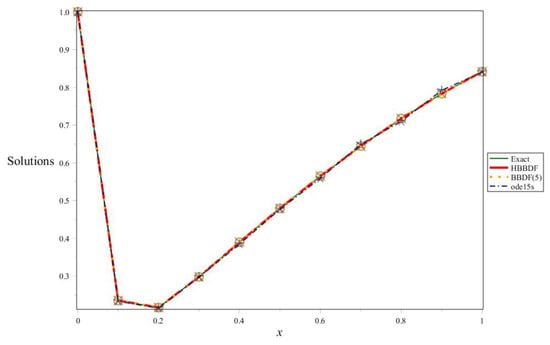
Figure 7. The graph of exact and approximated solutions for Problem 2.

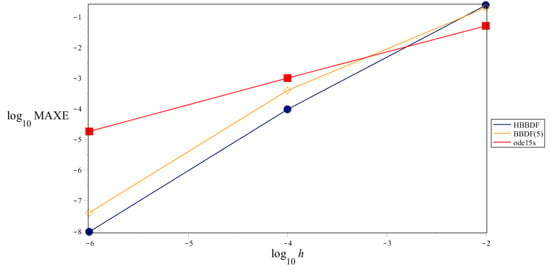
Figure 8. Accuracy curves for Problem 3.

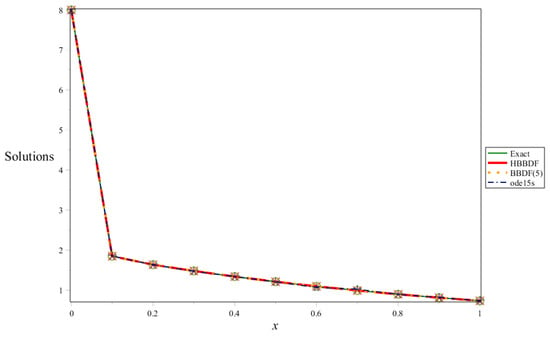
Figure 9. The graph of exact and approximated solutions for Problem 3 of $y_1\left(x\right)$.

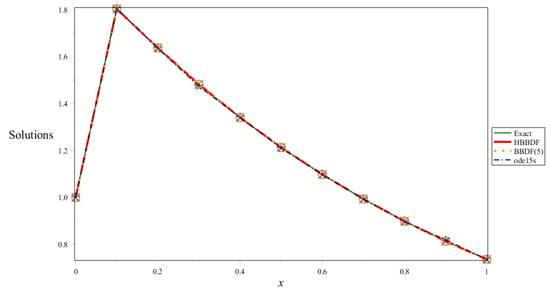
Figure 10. The graph of exact and approximated solutions for Problem 3 of $y_2\left(x\right)$.

Table 3, Table 5 and Table 7 gives the comparison of numerical solution at ten points equally spaced in the interval of integration to exact solution when $h={10}^{-6}$.

Here we observe that the graph of the approximated solution and the graph of the exact solution coincide with each other.

6. Conclusions

In this paper we have derived a class of hybrid BBDF for the numerical integration of stiff ordinary differential equations. By restricting the method to three off-step points, the results presented in show that the stability region for the HBBDF with three off-step points are larger than the stability of the BBDF method without the off-step points even though both methods are of the same order. We also establish the convergence of the new method by investigate the zero-stability and consistency which are the necessary conditions for convergence. Our numerical experiments support the conclusion that HBBDF solve the problem with acceptable efficiency when compared to MATLAB solver, ode15s, especially when we are integrating at smaller step sizes. It is recommended to extend the HBBDF to a variable step size variable order, VSVO code.