Abstract
This paper discusses the torque data during Parachute Landing Fall (PLF) activity on the sagittal plane by applying Kane’s method. The value of torque is determined in order to identify the movement of extension and flexion at every joint-segment on the parachutist during landing. Data were obtained from three professional and eighteen amateur parachutists, each with three consecutive landings. Quintic Biomechanics Software v26 was selected to capture motion analysis. The mathematical model for the PLF technique was presented based on a two-link kinematics open chain in a two-dimensional space using Kane’s method. The t-test result showed the p-value of torque at each joint between professionals and amateurs (p ≤ 0.05). According to the torque result, the professional parachutists extended their arm then flexion their elbow, shoulder, hip, knee and the ankle plantar flexion during the foot strike phase. The professional demonstrated a perfect PLF technique by identifying the flexion and extension on each joint segment that was involved during landing activity. The value of torque at each joint segment from professional parachutists may be used as a guideline for amateurs to perform optimal landing and minimise the injury.
1. Introduction
The Malaysian Armed Forces (MAF) is the fortress of national defence that is responsible to ensure Malaysia prevent from all external threats coming from the land, ocean and air as well as assisting the public authority by handling internal threat issues in the country. Mostly, all military activities and training are robust and may cause serious injuries. According to [1], parachute landing is the second-highest activity with a high risk of injury in the military. There are various factors that can cause injury while doing parachute landing which are: applying the wrong technique during landing, landing on uneven terrain, problems when opening a parachute and the wind factor. Niu et al. [2] show a study on the impact of the floor surface which has an effect when landing parachutes, especially on the ankle.
There are two types of technique for parachute landing activity which is named as Parachute Landing Fall (PLF) and Half-Squat Parachute Landing (HSPL). The MAF has used the PLF technique as a parachute landing activity. The difference between the PLF and HSPL techniques is that the PLF has 2 phases where the first phase happens when knees and hips are bent immediately upon feet touching the ground (foot strike) and the second phase is by rolling [3], whereas the HSPL technique has only one phase which is by hugging the knees, ankles and forefeet while the plantar foot is parallel to the ground [4]. By comparing both techniques, PLF is considered as a more effective and favourable technique considering less impact is asserted to the body segment during the rolling process.
Anterior cruciate ligament (ACL) injuries often occur especially on the ankle and knee during landing activity [5,6,7,8]. In biomechanics explanation, the ankle is the first joint on the body segment to gain impact towards the body when it touches the ground and thus has a high tendency to be injured [9]. According to [10], a collection of data for parachute injuries has been made on 110,000 sport jumps: 59.7% of injuries are involved on the lower extremities and 17% was the upper extremities. The highest part of injury at lower extremities was the ankle fracture with 44%, meanwhile the upper extremities were wrist fracture with 9.1%. In addition, [11] also did a research about the collection of data for the injuries during parachute landing for the military. The result also showed that the lower extremity was the highest with 65% followed by 22% of neck or back injuries and 22% of head injuries.
Numerous studies have found that the ankle and knee have the highest inclination towards injury during the parachute landing activity. Therefore, [12] made a study about the use of ankle braces to avoid the injuries which will also reduce the budget cost of hospitalisation. In addition, ACL injury at the knee joint regularly happened when parachutists bent over during landing, hence [13] suggested the use of semi-rigid knee brace to reduce knee injuries. A good technique during landing is called “prepare to land attitude” where the flexion of ankles and knees must be less than 45° and the knee flexion must not exceed 130° to avoid ACL injury [10]. My previous study was about the comparison of the kinematic data between professional and the amateur parachutist [14] and also found that there are significant differences among the professional parachutists where they demonstrated body bending at a greater angle, especially at the lower extremity part, which utilised minimal velocity, acceleration and angle-joint values in the midst of landing.
Biomechanical analysis is a 2-dimensional motion analysis that involves a study of the mechanics of different segments of the body, especially the force acting by the muscle and the gravitational force on the body segment. Mathematical models were developed to represent each segment of the body and enable an introduction to a set of movement variables during task function. Some researchers also studied the kinematic data on the upper limb but most of them focused more on the daily routine movement and for stroke patients [15,16,17,18]. In addition, there are many researchers who did their research on kinematic and kinetic data, especially in jump activity [2,5,19,20,21,22,23,24]. However, there are still no studies using Kane’s method of mathematical modelling for parachute landing activities.
Kane’s method is a simpler and more effective method than Newton–Euler or Lagrange’s method since it exerted its influence and eliminated interactive power and constraints on the bodies involved in model construction. Dynamic equations for multi-body systems can be built more elegantly and effectively through Kane’s technique where they are used for automatic numerical calculations [25]. A number of researchers have used Kane’s method including [26] by developing dynamic motion equations for space robotics. Moreover, [27] solved the problem of shooting with a rifle for the army. Furthermore, [28] applied Kane’s method in the field of badminton. In addition, Kane’s method has also been used to solve the problem of shoulder injury when planting palm oil [29]. Additionally, [30,31] have applied Kane’s method for the construction of mathematical models for lifting activities as well as the effects of heavy lifting towards the spine. This shows that many activities have been improved to prevent injuries through mathematical modelling by using Kane’s method.
In contrast with the past literature, this research emphasises on the comparison of kinetics data between professional and amateur parachutists focusing on Malaysian Military Army located at Kem Sungai Udang Melaka by developing a full-body mathematical model by Kane’s method in parachute landing activity. Thus, this research is claimed to be original and new. In this study, a model formulation of the human body will be developed. The body parts involved were arms, elbows, shoulders, hips, knees and ankles. The inverse modelling approach will be used to estimate the value of torque force at each joint and the force acting on each segment of the body involved. A 2-dimensional motion recording of the sagittal plane was taken when the subject performs a parachute landing activity. The findings of this study are expected to give a torque value to each of the joint segments that involved the arms, elbows, shoulders, hips, knees and ankles. In addition, it can also be a guide and reference for amateur parachutists to land properly to avoid injury in the future.
2. Materials and Methods
2.1. Experimental
Three professional parachutists (age, 28 ± 1.73 yr; height, 1.67 ± 0.02 m; weight, 65.3 ± 7.6 kg) and eighteen amateur parachutists (age, 23.8 ± 2.1 yr; height, 1.69 ± 0.05 m; weight, 62.9 ± 5.9 kg) from the Malaysian armies were involved in the parachute course. The experiment was conducted at Commando Training Based Camp which is located at Kem Sg Udang, Melaka. According to the parachute trainer, a parachutist will be classified as professional if he can successfully land more than 50 times without injury. In this research, static line parachutists were selected having at least fifty-three with 1000-foot jumps without any injuries and classified them as professional parachutists. On the other hand, the armies who took the static parachute jump course without any experience in parachute landing were selected as amateur parachutists. University Kebangsaan Malaysia has approved a written consent for all subjects in accordance with the Hospital Canselor Tuanku Muhriz guidelines.
The attire for all subjects were camouflage military uniforms, used for testing and exercise, as well as helmet and boots specifically made for the purpose of parasol jump. In front of the body, they carried a 10kg-weight bag during the landing activity. The experiment was initiated with one subject clinging onto an iron swing and was pushed by a fellow participant until he swings like a pendulum. Upon reaching the pendulum-like swinging mode, the subject then releases the iron swing to land on a 1-cm thick mattress by implementing the PLF technique. All subjects will repeat this procedure for three consecutive rounds to obtain better results.
The 2-dimensional motion is recorded using two GO-Pro Hero 4 cameras with 60 frames per second (FPS) at 1080 pixels of high-quality resolution. All the cameras were synchronised and connected with Bluetooth so that they can start and stop simultaneously. Figure 1 represents the top view of each camera’s position over the landing location. Camera 1 was set on the right side to capture the position on the sagittal plane, meanwhile camera 2 was set at the back of the subject to capture the coronal plane. Figure 2 illustrates the position of the subject on the sagittal plane during parachute landing. Data regarding the angular displacement and angular acceleration has been generated by the digitising process using Quintic Biomechanic Software v26, and substituted into the inverse dynamic equation to generate the torque exerted on the joint. A 1-m ruler is placed as a benchmark for the calibration process and the line was created based on the position of the ruler with a 59.4 speed of the video.
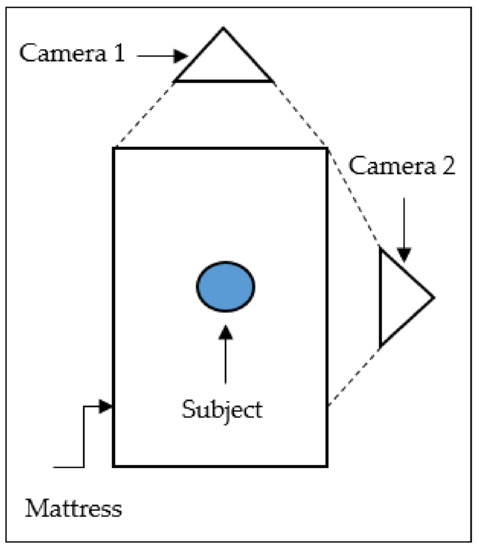
Figure 1.
Position of cameras and subject from the top view.

Figure 2.
Position of the subject on the sagittal plane.
2.2. Data Analysis
In order to do the analyses, the generation of dynamic curve patterns and the flexion and extension of the torque generated at each joint segment during the movement of parachute landing activity, the joint movement direction of the phases are listed in Table 1. The phase started from the preparation to land until the foot strike.

Table 1.
Movement of each joint segment during a parachute landing.
Figure 3 illustrates the movement of flexion and extension joints involved in parachute landing activity. The flexion and extension at each joint are important to be identified since it also affect the reading of torque. In the present study, in order to analyse the dynamic pattern, functional data analysis (FDA) was utilised by referring to the procedure by [32,33,34]. The data were smoothed by setting up an order six spline basis with knots at the frame of observation, along with roughness penalty on their fourth derivatives and smoothing parameter of . Then, the dynamic pattern was aligned via landmark registration with the extreme points as the locations of the landmark. Paired and t-test was applied to evaluate the difference of data value of torque at each joint between professional and amateur parachutists. The data were analysed using Welch’s t-test with p-value set at less than 0.05, (p ≤ 0.05), and 95% confidence interval was calculated where appropriate. Welch’s t-test was chosen due to the different number of professional and amateur parachutists.
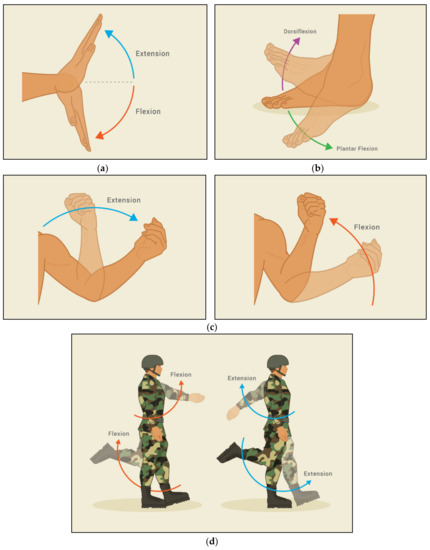
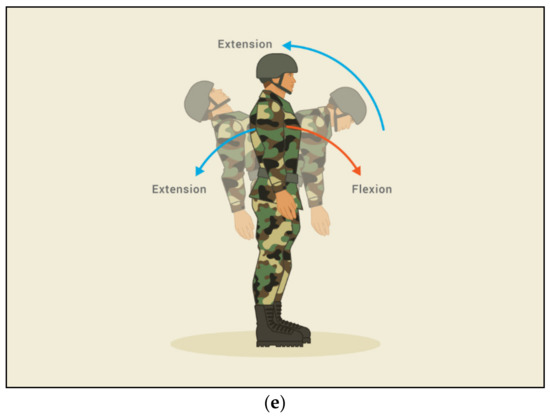
Figure 3.
Extension and flexion joint of (a) arm, (b) ankle, (c) elbow, (d) shoulder and knee, (e) hip.
2.3. Mathematical Modelling (Sagittal Plane)
In this study, a mathematical model was developed in a two-dimensional space to illustrate the inclination angles of the whole body which is the arm, elbow, shoulder, hip, knee and ankle joint flexion during the parachute landing activity. Figure 4a represents a skeletal model of the upper extremity and lower extremity of the human body in the sagittal plane. Figure 4b illustrates a free body diagram that shows the force acting at each body segment. By using Kane’s dynamic equation of motion with six degrees of the freedom of the human body was developed. There were six rigids for this model: rigid link A represented the forearm, rigid link B represented the arm, rigid link C represented the trunk, rigid link D represented the thigh, rigid link E represented the leg and rigid link G represented the foot. There are also six joint flexions, starting with the arm then elbow, shoulder, hip, knee and ankle joint. The movement of the body was described in terms of six generalised coordinates namely and , representing the arm, elbow, shoulder, hip, knee and ankle inclination angle, respectively.
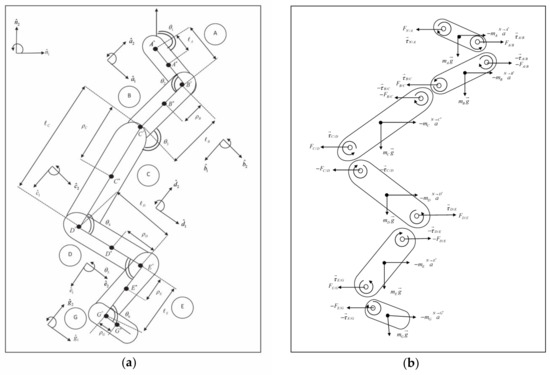
Figure 4.
(a) Two-link kinematics open-chain representing the whole body in the sagittal plane. (b) A free-body diagram that shows force acting at every body segment.
The symbols used in this model are:
- = centre of mass segments A, B, C, D, E and G, respectively
- = length of segments
- = distances of centre of mass from their proximal ends
- = mutually orthogonal unit
- = torque of each joints
The directional Cosine Table provides guidance on solving the frame of reference. It also includes the dot product operation between unit vectors for different reference frame positions. The unit vectors perpendicular to each segment and the angles of each joint can determine quantities such as angular velocity, angular acceleration, the linear velocity at points of each segment and linear acceleration at each centre of mass. According to Figure 4a, the angular velocity of each segments A, B, C, D, E and G with respect to the reference frame N are obtained as follows,
Furthermore, the angular acceleration of bodies A, B, C, D, E and G with respect to the reference frame N are given by,
Linear velocity will only apply to points and H°. Meanwhile, at point , the linear velocity point is zero because the joint position is tightly coupled to a reference frame that is considered to be a non-moving joint. The linear velocity at points, and H° to the reference frame are developed as,
Linear acceleration equation was published and it only applies to the centre of mass at points and G*. The linear accelerations at the centre of mass and G* referring to the reference frame N are given as follows,
The formulation of generalised active force for segments A, B, C, D, E and G was combined with the calculation and addition vector dot product between partial velocity and active force, respectively. Then, the dot product between partial angular velocity and torque force are combined. The generalised active force Fi is obtained as,
where FiR with i = 1, 2, 3, 4, 5, 6 represents first, second, third, fourth, fifth and sixth value of generalised active force. Meanwhile the values of and are the mass of each segment of the body A, B, C, D, E and G. Value is the action force and g is the value of gravity. Meanwhile, the generalised inertial forces are obtained as,
where with i = 1, 2, 3, 4, 5, 6 represents first, second, third, fourth, fifth and sixth value of generalised inertia forces. The value of I represents the inertia acting at each body segments involved.
Subsequently, the dynamic equation for movement is obtained by adding the generalised active forces and generalized inertia forces, where the equation is summarised as follows.
Since there are six body segments involved, there will be six dynamic equations. This can be written in a single matrix form to identified the value of torque as follows,
where
| : | Vector of applied torque |
| M: | Mass matrix |
| : | Angular acceleration vector |
| : | Vector of moments from gravitational forces |
| : | Vector of moments from external forces |
3. Results
Table 2 summarises the mean, standard deviation, maximum and minimum values of torque at each joint segment involved during the event of landing, namely the arm, elbow, shoulder, hip, knee and ankle. The data only focused on the value of torque during foot strike. Based on the results, the value of mean, maximum and minimum of each body segments between professional parachutists and amateur parachutists was a contrast. The comparison of value by using t-test showed that the p-value of arm, elbow, shoulder, hip, knee and ankle was less than 0.05 (p ≤ 0.05) and it can be concluded that the value of torque at every joint between professionals and amateurs has a significant difference. Consequently, the maximum value for the amateurs at each joint is higher than the professionals, hence the reading of minimum value for the amateurs is lower than professionals.

Table 2.
The meanSD, maximum and minimum value of professional and amateur parachutists at the event of foot strike.
Figure 5 shows a graph that illustrates the value of torque for arm, elbow, shoulder, hip, knee and ankle joint for professionals and amateurs. Based on the graph, the data were collected from the beginning when parachutists left the iron swing (to prepare for the landing event) until foot strike. Based on the observation, the graphs (a–f) show the value of torque between professionals and amateurs are slightly different during the preparation of landing phase. However, during the foot strike phase, the graphs of torque are significantly different. Based on the graphs, the amateurs generate more movement (flexion and extension) resulting in the fluctuation of the graphs.
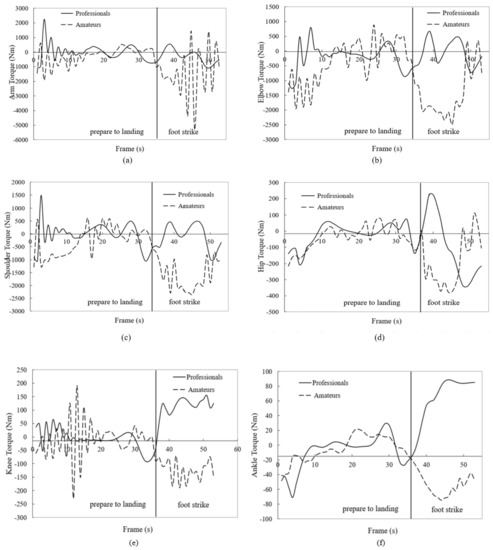
Figure 5.
Graph of Torque at (a) arm, (b) elbow, (c) shoulder, (d) hip, (e) knee and (f) ankle.
Table 3 shows the data collection is then validated with the numerical method technique by employing the Runge-Kutta analysis. The value of angle at knee joint θ5 (rad) from professional parachutist data has been chosen to identify the percentage error. The error value percentage is calculated, and we found that the experimental data are acceptable and reliable to be used in this study since the percentage error are relatively small.

Table 3.
Estimation percentage relative error εr on knee angle for the professional parachutist between Runge-Kutta analysis r and experimental result s.
4. Discussion
Torque is a twist or turn that tends to produce rotation. The value of torque can be negative (clockwise) or positive (counterclockwise) rotation for each segment of the body. The development of the model by using Kane’s method is to determine the value of torque for each joint which is the arm, elbow, shoulder, hip, knee and ankle during parachute landing activity. Table 2 shows the value of torque only when the feet touched the ground since that is the moment of highest percentage for the parachutist to get injured. The results showed a significant difference in data of torque between professional and amateur parachutists at every joint segment. As can been seen, each joint has its own value of torque whether it is positive or negative. During the foot strike, the force made the movement generated by the upper body to the downward vertical component of force. Therefore, the value of torque at the arm, elbow and shoulder was greater than at the lower limb. Furthermore, the force transfer increased from the upper body sequentially towards the trunk, hip, knee and ankle joint.
The motions of flexion and extension occur within the sagittal plane and this engages the anterior or posterior gestures of the limbs or body. In parachute landing, the flexion and extension movement at each joint segment is important to identify to avoid any injury. Table 1 represents excellent movement at each joint segment based on the PLF technique. The movement of the arm joint needed an extension. Meanwhile, the elbows, shoulders, hips and knees require in flexion position and finally, the ankles should be in plantar flexion during forefoot strike (landing the toes first). Figure 5 shows the value of torque at each joint involved during a parachute landing activity. Based on graph (a), the values of arm joint for amateurs during the foot strike phase fluctuates and can be concluded that there are numerous movements of flexion and extension compared to the professionals. Graph (b) shows that the amateurs extend their elbows starting from the beginning and produced a negative value of torque as compared to professionals. This behaviour continued during the foot strike phase, where the professionals flexed their elbows while the amateurs extend theirs. Furthermore, based on graph (c), the professional flexion their shoulder while amateur extension their shoulder joint during the foot strike event.
The lower extremity is the body part with higher percentage to get injured during parachute landing activity [10]. Referring to graph (d) in Figure 5, it is obvious that during the foot strike phase, the professionals flex their hip while the amateurs extend their hip joint. The hip flexion during landing activity is to reduce the impulse force to the knees and the ankles but it also can potentially cause risks for ACL rupture if the flexion was too large [35]. The rapid flexion of the hip was related to the higher knee abduction torque in the land. The value of maximum torque at the hips for professional parachutists only reached 65.23 Nm, meanwhile the amateurs reached until 710.43 Nm. It can be concluded that the amateurs demonstrated high value of torque and will get a higher risk of ACL rupture injury.
This study was continued by a glance at the reading value of torque at the knee joint. Based on Table 2, the maximum and minimum value of knee flexion torque for the professionals are 93.99 Nm and 61.08 Nm, while the amateurs are 123.57 Nm and −187.37 Nm during foot strike. According to graph (e) in Figure 5, at the starting from preparation to the landing phase, the amateurs did a lot of movement (flexion and extension) until it produced an oscillation graph. Then, at foot strike phase, the amateurs extend their knee joint in contrast with the professionals where they flexed their knee joint. The flexion of knee can add the time of landing and also reduce the impact force to the ankle joint. Finally, graph (f) shows that the professional’s ankle joint torque was negative (plantar flexion) before and positive (dorsiflexion) after the foot strike phase. Hence it can be concluded that the professionals landed with their toes first (forefoot strike). On the contrary, the amateurs’ value of torque decreases before and after foot strike phase, hence the dorsiflexion of the ankle occurs. Based on this movement, it can be concluded that amateurs’ landing was with heels first (heel strike). Landing with a flat-footed or heel strike has a potential risk to ACL rupture since it generated a higher value of ground reaction forces [35]. Meanwhile, landing with the toes first will extend the knee and the feet movement are more plantar flexed at the initial ground contact and may lead to a reduction in quadriceps activation and also reduce the injury [36].
The armies must wear their standard military uniforms with heavy protective equipment along with their weapons and other equipment for combat, even for paratroopers. The heavy load will potentially increase the risk of having musculoskeletal injuries. Carrying tandem load may also affect the landing kinematics and ground reaction forces. It can also initiate compensatory kinetic response at the knees, elevate the forces applied on the upper and the lower back and finally cause thoracic and lumbar spine curvature [37]. By applying the proper landing technique, this will avoid injuries. However, it can control the knee flexion torque since the greater the internal knee extension torque, the greater the proximal tibia anterior shear force will be. This will simultaneously increase the ACL strain.
This study analysed the difference of torque value which investigated the movement of flexion and extension at each joint segment from professional and amateur parachutists during foot strike phase on the sagittal plane. From the results, it is obvious that the professionals demonstrate a perfect PLF technique by identifying the flexion and extension of each joint that involved during landing activity, see Table 1. Data from the professionals can anticipate as a relevant guideline for the amateur parachutists to perform optimal landing and minimise the injury.
5. Conclusions
This study examined the comparison of torque value at the arm, elbow, shoulder, hip, knee and ankle joint between professional and amateur parachutists during foot strike phase. It is concluded that the professionals demonstrated the correct technique of flexion and extension at each joint segment during the parachute landing activity. This is attained when the hips are bent, leading to more knee and ankle flexion. The limitation of this study is that all subjects wore camouflage military uniforms and boots during the experiment so that it was performed using marker less motion capture for video recording. Furthermore, wearing heavy boots also affects the reading of kinematics data. However, this study design can produce data that are similar to the real training of parachute landing since all the subjects wore the same outfit. The results from professional’s data can be used as a reference for amateur parachutists who have never experienced a parachute landing in order to improve his performance and avoid potential injuries. Future research is needed to scrutinise the rolling phase, which is another event in the PLF technique. There are other parts of the body with a high tendency of injury during landing activity, such as the spine and pelvic area.
Author Contributions
S.A. and A.S.R. conceptualised the study; S.A. and A.S.R. developed the methodology; S.A. conducted the experiment; S.A. performed data analysis and wrote the article; A.S.R., K.B.G. and W.R.W.D. supervised and reviewed the article; and S.A. edited and revised the article. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by Short Term Grant Scheme (UPNM/2019/GPJP/SG/3) and GUP-2017-112.
Acknowledgments
The author would like to thank the cooperation given by the parachutist from Kem Komando, Sg Udang, Melaka.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Chervak, M.C.; Hooper, T.; Brennan, F.H.; Craigh, S.C.; Girasek, D.C.; Schaefer, R.A.; Barbour, G.; Ywe, K.S.; Jones, B.H. A systematic process to prioritise prevention activities sustaining progress toward the reduction of military injuries. Am. J. Prev. Med. 2010, 38, 11–18. [Google Scholar] [CrossRef] [PubMed]
- Niu, W.; Fan, Y. Terrain stiffness and ankle biomechanics during simulated half-squat parachute landing. Aviat. Space Environ. Med. 2013, 84, 1262–1267. [Google Scholar] [CrossRef] [PubMed]
- Whitting, J.; Steele, J.R.; Jaffrey, M.A.; Munro, B. Parachute landing fall characteristics at three realistic vertical descent velocities. Aviat. Space Environ. Med. 2007, 78, 1135–1142. [Google Scholar] [CrossRef] [PubMed]
- Niu, W.; Wang, Y.; He, Y.; Fan, Y.; Zhao, Q. Biomechanical gender differences of the ankle joint during simulated half-squat parachute landing. Aviat. Space Environ Med. 2010, 81, 761–767. [Google Scholar] [CrossRef]
- Taylor, K.A.; Terry, M.E.; Uttukar, G.M.; Spritzer, C.E.; Queen, R.M.; Irribarra, L.A.; Garrett, W.E.; DeFrate, L.E. Measurement of in vivo anterior cruciate ligament strain during dynamic jump landing. J. Biomech. 2011, 44, 365–371. [Google Scholar] [CrossRef]
- Malinzak, R.A.; Colby, S.M.; Kirkendall, D.T.; Yu, B.; Garrett, W.E. Comparison of knee joint motion patterns between men and women in selected athletic tasks. Clin. Biomech. 2011, 16, 438–445. [Google Scholar] [CrossRef]
- Colby, S.; Francisco, A.; Yu, B.; Kirkendall, D.; Finch, M.J.; Garret, W. Electromyographic and kinematic analysis of cutting maneuvers implications for anterior cruciate ligament injury. Am. J. Sport Med. 2000, 28, 234–240. [Google Scholar] [CrossRef]
- Patel, S.A.; Hageman, J.; Quatman, C.E.; Wordeman, S.C.; Hewett, T.E. Prevalence and Location of Bone Bruises Associated with Anterior Cruciate Ligament Injury and Implications for Mechanism of Injury: A Systematic Review. Sports Med. 2014, 44, 281–293. [Google Scholar] [CrossRef]
- Neves, E.; Souza, M.; Almeida, R. Military parachuting injuries in Brazil. Injury 2009, 40, 897–900. [Google Scholar] [CrossRef]
- Ellitsgaard, N. Parachuting injuries: A study of 110,000 sports jumps. Injury 1987, 21, 13–17. [Google Scholar] [CrossRef]
- Ball, V.L.; Sutton, J.A.; Aicha Hull, A.; Sinnott, B.A. Traumatic injury patterns associated with static line parachuting. Wilderness Environ. Med. 2014, 25, 89–93. [Google Scholar] [CrossRef] [PubMed]
- Knapik, J.J.; Spiess, A.; Swedler, D.I.; Grier, T.L.; Darakjy, S.; Jones, B. Systematic review of the parachute ankle brace injury risk reduction and cost effectiveness. Am. J. Prev. Med. 2010, 38, 182–188. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Zheng, C.; Wu, J.; Wang, L.; Wei, X.; Wang, L. Protective knee braces and the biomechanics of the half-squat parachute landing. Aerosp. Med. Hum. Perform. 2018, 89, 26–31. [Google Scholar] [CrossRef] [PubMed]
- Aziz, S.; Rambely, A.S.; Rauf, U.F.A. Kinematics study on PLF technique by comparing professional and amateur Malaysian army parachutists based on event during landing. J. Phys. Conf. Ser. 2019, 1366, 012054. [Google Scholar] [CrossRef]
- Abidin, S.B.Z.; Jusoh, W.N.I.W.; Beng, G.K. Kinematic analysis on reaching activity for hemiparetic stroke subjects using simplified video processing method. Malays. J. Fundam. Appl. Sci. 2018, 14, 386–390. [Google Scholar] [CrossRef][Green Version]
- Ariffin, M.S.; Rambely, A.S. Optimization of upper extremity muscles using compound bow via lagrange multiplier method. AIP Conf. Proc. 2016, 1750, 030030. [Google Scholar]
- Ponvel, P.; Singh, D.K.A.; Beng, G.K.; Chai, S.C. Factors affecting upper extremity kinematics in healthy adults: A systematic review. Crit. Rev. Phys. Rehabil. Med. 2019, 31, 101–123. [Google Scholar] [CrossRef]
- Ramlee, M.H.; Gan, K.B. Function and biomechanics of upper limb in post-stroke patients—A systematic review. J. Mech. Med. Biol. 2017, 17, 1750099. [Google Scholar] [CrossRef]
- Kernozek, T.W.; Torry, M.R.; Van Hoof, H.; Cowley, H.; Tanner, S. Gender differences in frontal and sagittal plane biomechanics during drop landing. J. Am. Coll. Sports Med. 2005, 37, 1003–1012. [Google Scholar] [CrossRef]
- Huston, L.; Vibert, B.; Ashton-Miller, J.; Wojtys, E. Gender differences in knee angle when landing from a drop-jump. Am. J. Knee Surg. 2001, 14, 215–220. [Google Scholar]
- Chappell, J.; Limpisvasti, O. Effect of neuromuscular training program on the kinetics and kinematics of jumping tasks. Am. J. Sports Med. 2008, 36, 1081–1086. [Google Scholar]
- Chappell, J.; Herman, D.; Knight, B.; Kirkendall, D.; Garrett, W.; Yu, B. Effect of fatigue on knee kinetics and kinematics in stop-jump task. Am. Orthop. Soc. Sports Med. 2005, 33, 1022–1029. [Google Scholar] [CrossRef] [PubMed]
- Decker, M.J.; Torry, M.R.; Wyland, D.J.; Sterett, W.I.; Steadman, J.R. Gender differences in lower extremity kinematics, kinetics and energy absorption during landing. Clin. Biomech. 2003, 18, 662–669. [Google Scholar] [CrossRef]
- Protopapadaki, A.; Drechsler, W.I.; Cramp, M.C.; Coutts, F.J.; Scott, O.M. Hip, knee, ankle kinematics and kinetics during stair ascent and descent in healthy young individuals. Clin. Biomech. 2007, 22, 203–210. [Google Scholar] [CrossRef]
- Huston, R.L. Multibody Dynamics; Butterworth-Heinemann: Boston, MA, USA, 1990. [Google Scholar]
- Purushotham, A.; Anjeneyulu, J. Kane’s Method for Robotic Arm Dynamics: A Novel Approach. J. Mech. Civ. Eng. 2013, 6, 7–13. [Google Scholar] [CrossRef]
- Wan Din, W.R.; Rambely, A.S. Biomechanics of rifle shooting model: Effects of rifle dynamics in target accuracy. In Proceedings of the 2nd International Conference on Mathematical Sciences, Kuala Lumpur, Malaysia, 30 November–3 December 2010; pp. 136–141. [Google Scholar]
- Ariff, F.H.M.; Rambely, A.S.; Ghani, N.A.A. Shoulder’s modeling via Kane’s method: Determination of torques in smash activity. IFMBE Proc. 2011, 35, 207–209. [Google Scholar] [CrossRef]
- Tumit, N.P.; Rambely, A.S.; Shamsul, B.M.T.; Shahriman, A.B.; Ng, Y.G.; Deros, B.M.; Zailina, H.Y.; Goh, M.; Manohar, A.; Ismail, I.A.; et al. An Upper Limb Mathematical Model of an Oil Palm Harvester. AIP Conf. Prof. 2014, 1614, 973–979. [Google Scholar] [CrossRef]
- Ismail, K.N.S.K.; Basah, S.N.; Omar, N.H.; Murugappan, M.; Yaacob, S.B. Matematical modeling of human Body for lifting task. In Proceedings of the IEEE International Conference on Control System, Computing and Engineering, Penang, Malaysia, 23–25 November 2012. [Google Scholar]
- Sharifah, A.A.R.; Azmin, S.R.; Rokiah, R.A. A biomechanical model via Kane’s equation-solving trunk motion with load carriage. Am. J. Sci. Ind. Res. 2011, 2, 678–685. [Google Scholar] [CrossRef]
- Page, A.; Ayala, G.; Leon, M.T.; Peydro, M.F.; Prat, J.M. Normalizing temporal pattern to analyse sit-to-stand movement by using registration of functional data. J. Biomech. 2006, 39, 2526–2534. [Google Scholar] [CrossRef]
- Zin, M.A.M.; Rambely, A.S.; Ariff, N.M.; Ariffin, M.S. Smoothing and differentiation of kinematics data using functional data analysis approach: An application of automatic and subjective method. Appl. Sci. 2020, 10, 2493. [Google Scholar] [CrossRef]
- Din, W.R.W.; Rambely, A.S.; Jemain, A.A. Load carriage analysis for military using functional data analysis technique: Registration and permutation test. Int. J. Basic Appl. Sci. 2015, 4, 1–9. [Google Scholar] [CrossRef][Green Version]
- Boden, B.P.; Torg, J.S.; Knowles, S.B.; Hewett, T.E. Video analysis of anterior cruciate ligament injury: Abnormalities in hip and ankle kinematics. Am. J. Sport Med. 2009, 37, 252–259. [Google Scholar] [CrossRef]
- Sell, T.; Chu, Y.; Abt, J.P.; Nagai, T.; Deluzio, J.; McGrail, M.; Rowe, R.; Lephart, S. Minimal addition weight of combat equipment alters air assault soldiers landing biomechanics. Mil. Med. 2010, 17, 41–47. [Google Scholar] [CrossRef] [PubMed]
- Shimokochi, Y.; Yong Lee, S.; Shultz, S.J.; Schmitz, R.J. The relationships among sagittal-plane lower extremity moments: Implications for landing strategy in anterior cruciate ligament injury prevention. J. Athl. Train. 2009, 44, 33–38. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).