Models of Set Theory in which Nonconstructible Reals First Appear at a Given Projective Level

Abstract

Models of set theory are defined, in which nonconstructible reals first appear on a given level of the projective hierarchy. Our main results are as follows. Suppose that $n\ge 2$. Then: 1. If it holds in the constructible universe $\mathbf{L}$ that $a\subseteq \omega$ and $a\notin {\Sigma }_n^1\cup {\Pi }_n^1$, then there is a generic extension of $\mathbf{L}$ in which $a\in {\mathsf{\Delta }}_{n+1}^1$ but still $a\notin {\Sigma }_n^1\cup {\Pi }_n^1$, and moreover, any set $x\subseteq \omega$, $x\in {\Sigma }_n^1$, is constructible and ${\Sigma }_n^1$ in $\mathbf{L}$. 2. There exists a generic extension $\mathbf{L}$ in which it is true that there is a nonconstructible ${\mathsf{\Delta }}_{n+1}^1$ set $a\subseteq \omega$, but all ${\Sigma }_n^1$ sets $x\subseteq \omega$ are constructible and even ${\Sigma }_n^1$ in $\mathbf{L}$, and in addition, $\mathbf{V}=\mathbf{L}\left[a\right]$ in the extension. 3. There exists an generic extension of $\mathbf{L}$ in which there is a nonconstructible ${\Sigma }_{n+1}^1$ set $a\subseteq \omega$, but all ${\mathsf{\Delta }}_{n+1}^1$ sets $x\subseteq \omega$ are constructible and ${\mathsf{\Delta }}_{n+1}^1$ in $\mathbf{L}$. Thus, nonconstructible reals (here subsets of $\omega$) can first appear at a given lightface projective class strictly higher than ${\Sigma }_2^1$, in an appropriate generic extension of $\mathbf{L}$. The lower limit ${\Sigma }_2^1$ is motivated by the Shoenfield absoluteness theorem, which implies that all ${\Sigma }_2^1$ sets $a\subseteq \omega$ are constructible. Our methods are based on almost-disjoint forcing. We add a sufficient number of generic reals to $\mathbf{L}$, which are very similar at a given projective level n but discernible at the next level $n+1$.

1. Introduction

Problems of definability and effective construction of mathematical objects have always been in the focus of attention during the development of mathematical foundations. In particular, Hadamard, Borel, Baire, and Lebesgue, participants of the discussion published in [1], in spite of significant differences in their positions regarding problems of mathematical foundations, emphasized that a pure existence proof and a direct definition (or an effective construction) of a mathematical object required are different mathematical results, and the second one of them does not follow from the first. Problems of definability and effectivity are considered in such contemporary monographs on foundations as [2,3,4,5]. Moschovakis, one of founders of modern set theory, pointed in [6] (p. xiv), that

the central problem of descriptive set theory and definability theory in general [is] to find and study the characteristic properties of definable objects.

The general goal of the research line of this paper is to explore the existence of effectively definable structures in descriptive set theory on specific levels of the projective hierarchy. One of the directions here is the construction of set theoretic models, in which this or another problem is decided, at a predefined projective level n, differently than it is decided in $\mathbf{L}$, Gödel’s constructible universe, or, that is equivalent, by adding the axiom of constructibility, dubbed $\mathbf{V}=\mathbf{L}$.

Such set theoretic models are usually defined as generic extensions of $\mathbf{L}$ itself. Any such a generic extension leads to consistency and independence results in set theory, because if a sentence $\mathsf{\Phi }$ holds in $\mathbf{L}$ or in a generic extension of $\mathbf{L}$ then $\mathsf{\Phi }$ is consistent with the axioms of $\mathbf{ZFC}$, the Zermelo–Fraenkel set theory (with the axiom of choice $\mathbf{AC}$).

As a first, and perhaps most immediately interesting problem of this sort, in this paper, we consider the problem of the existence of effectively definable (that is, occurring in one of lightface classes ${\Sigma }_n^1$ of the projective hierarchy) but nonconstructible reals. It follows from Shoenfield’s absoluteness theorem [7] that every (lightface) ${\Sigma }_2^1$ set $x\subseteq \omega$ belongs to $\mathbf{L}$. Generic models, in which there exist nonconstructible reals on effective levels of the projective hierarchy higher than ${\Sigma }_2^1$, were defined in the early years of forcing; see a brief account in [8]. This culminated in two different generic extensions [9,10] containing a nonconstructible ${\Pi }_2^1$ singleton, hence, a ${\mathsf{\Delta }}_3^1$ set $a\subseteq \omega$. (We are concentrated on generic extensions of $\mathbf{L}$ in this paper, and therefore leave aside another research line, related to models with large cardinals, with many deep and fruitful results connected, in particular, with properties of ${\Pi }_2^1$ singletons, see e.g., [11,12,13]).

Then it was established in [14] that for any $n\ge 2$ there is a generic extension of $\mathbf{L}$ in which there exists a nonconstructible ${\mathsf{\Delta }}_{n+1}^1$ real $a\subseteq \omega$, but all ${\Sigma }_n^1$ sets $x\subseteq \omega$ are constructible. Our motivation here is to further extend this research line. The next three theorems are the main results in this paper.

Theorem 1.

If $𝕟\ge 2$ and $b\subseteq \omega ,b\notin {\Sigma }_{𝕟}^1\cup {\Pi }_{𝕟}^1$, then there is a generic extension of $\mathbf{L}$ in which $b\in {\mathsf{\Delta }}_{𝕟+1}^1$ but still $b\notin {\Sigma }_{𝕟}^1\cup {\Pi }_{𝕟}^1$, and moreover, any set $x\subseteq \omega ,x\in {\Sigma }_{𝕟}^1$, is constructible and ${\Sigma }_{𝕟}^1$ in $\mathbf{L}$.

Theorem 1 shows that being at a certain lightface projective level is hardly an intrinsic property of a constructible real, unless it is already at that level in $\mathbf{L}$. The theorem definitely fails for $𝕟=1$ since being ${\mathsf{\Delta }}_2^1$ is an ablosute property of a real by the Shoenfield absoluteness theorem.

Theorem 2.

If $𝕟\ge 2$, then there exists a generic extension of the universe $\mathbf{L}$ in which it is true that

(i)

there is a nonconstructible ${\mathsf{\Delta }}_{𝕟+1}^1$ set $a\subseteq \omega$, but all ${\Sigma }_{𝕟}^1$ sets $x\subseteq \omega$ are constructible and ${\Sigma }_{𝕟}^1$ in $\mathbf{L};$

(ii)

we can strengthen (i) by the requirement that $\mathbf{V}=\mathbf{L}\left[a\right]$ in the extension.

Theorem 3.

If $𝕟\ge 2$ then there exists an extension of $\mathbf{L}$ in which there is a nonconstructible ${\Sigma }_{𝕟+1}^1$ set $a\subseteq \omega$ but all ${\mathsf{\Delta }}_{𝕟+1}^1$ sets $x\subseteq \omega$ are constructible and ${\mathsf{\Delta }}_{𝕟+1}^1$ in $\mathbf{L}$.

The common denominator of Theorems 2 and 3 is that nonconstructible reals can first appear at a given lightface projective class strictly higher than ${\Sigma }_2^1$, in an appropriate generic extension of $\mathbf{L}$. The lower limit ${\Sigma }_2^1$ is motivated by the Shoenfield absoluteness theorem.

The generic models, which we define to prove the main theorems, make use of modifications of the almost-disjoint forcing by Jensen–Solovay [9].

Some other recent results can be mentioned here, which resemble Theorems 1–3 in that they give models in which a particular property of some kind holds at a certain pre-selected level of the projective hierarchy. Yet they are different in that they use modifications of Jensen’s minimal ${\Pi }_2^1$ singleton forcing [10] and its finite-support products first considered by Enayat [15], as well as its collapse-style modification by Abraham [16], rather than the almost-disjoint forcing.

• A model defined in [17], in which, for a given $n\ge 2$, there is a (lightface) ${\Pi }_n^1$ Vitali equivalence class in the real line $\mathbb{R}$ (that is, a set of the form $x+\mathbb{Q}$ in $\mathbb{R}$), containing no OD (ordinal definable) elements, and in the same time every countable ${\Sigma }_n^1$ set consists of OD elements.
• A model in [18], in which, for a given $n\ge 2$, there is a ${\Pi }_n^1$ singleton $\left\{a\right\}$, such that a codes a collapse of ${\omega }_1^{\mathbf{L}}$, and in the same time every ${\Sigma }_n^1$ set $a\subseteq \omega$ is still constructible.
• A model defined in [19], in which, for a given $n\ge 2$, there is a ${\Pi }_n^1$ non-OD-uniformizable planar set with countable cross-sections, and at the same time, every ${\Sigma }_n^1$ set with countable cross-sections is OD-uniformizable.

Organization of the Paper

Our plan of the proofs of the main results will be to construct, in $\mathbf{L}$, a sequence of forcing notions $\mathbb{P}\left(\nu \right)$, $\nu <{\omega }_1$, satisfying the following three key conditions.

• $\mathbb{P}\left(\nu \right)$ are sufficiently homogeneous and independent of each other in the sense that, for any ${\nu }_0$, there are no $\mathbb{P}\left({\nu }_0\right)$-generic reals in a $\left({\prod }_{\nu \ne {\nu }_0}\mathbb{P}\left(\nu \right)\right)$-generic extensions of $\mathbf{L}$.
• The property of a real x being $\mathbb{P}\left(\nu \right)$-generic over $\mathbf{L}$ is ${\Pi }_{𝕟}^1$ as a binary relation, where $𝕟\ge 2$ is a number chosen in Theorems 1–3.
• A condition which makes $\mathbb{P}\left(\nu \right)$-generic reals for different values $\nu <{\omega }_1$ undistinguishable from each other below the ${\Pi }_{𝕟}^1$ definability level (at which they are distinguishable by condition 2).

Each $\mathbb{P}\left(\nu \right)$ will be a forcing notion of almost-disjoint type, determined by a set $\mathbb{U}\left(\nu \right)\subseteq {\omega }^{\omega }$. To make the exposition self-contained, we review some basic details related to almost-disjoint forcing, finite-support products, and related generic extensions, taken mainly from [9], in Section 2 and Section 3.

Having the construction of $\mathbb{P}\left(\nu \right),\nu <{\omega }_1$, accomplished in Section 4, the proof of, e.g., Theorem 1 (Section 7.1) is performed as follows. Let $b\in \mathbf{L},b\subseteq \omega$ be chosen as in Theorem 1 for a given $𝕟\ge 2$. We consider a $\mathbb{P}$-generic extension $\mathbf{L}\left[G\right]$ of $\mathbf{L}$, where $\mathbb{P}={\prod }_{i<\omega }\mathbb{P}\left(i\right)$. Let $a_i\subseteq \omega$ be the $\mathbb{P}\left(i\right)$-generic real generated by the ith projection $G_i$ of G; these reals are nonconstructible and $\mathbf{L}\left[G\right]=\mathbf{L}\left[{\left\{a_i\right\}}_{i<\omega }\right]$. Let $z=\left\{0\right\}\cup \{2k:k\in b\}\cup \{2k+1:k\notin b\}$ Consider the subextension $\mathbf{L}\left[{\left\{a_i\right\}}_{i\in z}\right]$. Then it is true in $\mathbf{L}\left[{\left\{a_i\right\}}_{i\in z}\right]$ by condition 1, that

$$\begin{array}{ccc}\hfill b& =& \left\{k<\omega :\mathrm{there}\mathrm{exist}\mathbb{P}\left(2k\right)-\mathrm{generic}\mathrm{reals}\right\}\hfill \\ \hfill & =& \left\{k<\omega :\mathrm{there}\mathrm{are}\mathrm{no}\mathbb{P}(2k+1)-\mathrm{generic}\mathrm{reals}\right\},\hfill \end{array}$$

so using condition 2, we easily get $b\in {\mathsf{\Delta }}_{𝕟+1}^1$ in $\mathbf{L}\left[{\left\{a_i\right\}}_{i\in z}\right]$. A similar construction (but with b being generic over $\mathbf{L}$) was carried out in the early years of forcing in [9] for $𝕟=2$, which is the least possible value. In the case $𝕟=2$, the fact, that all ${\Sigma }_2^1$ sets $x\subseteq \omega$ in the extension belong to $\mathbf{L}$ and are ${\Sigma }_2^1$ in $\mathbf{L}$, is guaranteed by the Shoenfield absoluteness theorem.

If $𝕟\ge 3$, then the Shoenfield absoluteness argument does not work, of course. Still we can argue that any lightface ${\Sigma }_{𝕟}^1$ set $x\subseteq \omega$ in $\mathbf{L}\left[{\left\{a_i\right\}}_{i\in z}\right]$ belongs to $\mathbf{L}$ by the general forcing theory, because the product forcing ${\mathbb{P}}_z={\prod }_{i\in z}\mathbb{P}\left(i\right)\in \mathbf{L}$ is homogeneous by condition 1. However this does not immediately imply the lightface definability of b in $\mathbf{L}$, as ${\mathbb{P}}_z$ is defined via z, hence via b. To solve this difficulty, we make use of condition 3 to prove another absoluteness property: ${\Sigma }_{𝕟}^1$ formulas turn out to be absolute between $\mathbf{L}\left[{\left\{a_i\right\}}_{i\in z}\right]$ and the entire extension $\mathbf{L}\left[G\right]=\mathbf{L}\left[{\left\{a_i\right\}}_{i<\omega }\right]$, which is an $\mathbb{P}$-generic extension of $\mathbf{L}$. Here $\mathbb{P}={\prod }_{i<\omega }\mathbb{P}\left(i\right)$ is a parameter-free definable forcing in $\mathbf{L}$, leading to the parameter-free definability of b in $\mathbf{L}$. There are two issues here that need to be explained.

First, how to secure condition 3 in a sufficiently effective form. To explain the main technical device, we recall that by [9] the system of forcing notions $\mathbb{P}\left(\nu \right)$ is the result of certain transfinite ${\omega }_1$-long construction of assembling it from countable fragments in $\mathbf{L}$. The construction can be viewed as a maximal branch in a certain “mega-tree”, say $\mathcal{T}$, whose nodes are such countable fragments, and each of them is chosen to be the Gödel-least appropriate one over the previous one. The complexity of this construction is ${\mathsf{\Delta }}_2^1$ in the codes, leading in [9] to the ${\Pi }_2^1$ definability of the property of being generic, as in condition 2, in case $𝕟=2$.

To adapt this construction for the case $𝕟\ge 3$, our method requires us to define a maximal branch in $\mathcal{T}$ that intersects all dense sets in $\mathcal{T}$ of class ${\Sigma }_{𝕟-1}^1$. Such a construction is carried out in Section 4. This genericity-like condition of meeting all dense ${\Sigma }_{𝕟-1}^1$ sets, results in the ${\Pi }_{𝕟}^1$ definability of the property of being generic in condition 2, and also yields condition 3, since the abundance of order automorphisms of the “mega-tree” $\mathcal{T}$ (including those related to index permutations) allows to establish some homogeneity properties of a certain auxiliary forcing-style relation.

This auxiliary forcing-style relation, defined and studied in Section 5 and Section 6. The auxiliary relation approximates the truth in ${\mathbb{P}}^{\prime }$-generic extensions, as $\mathbf{L}\left[{\left\{a_i\right\}}_{i\in z}\right]$ above, up to ${\Sigma }_{𝕟}^1$ formulas, but, unlike the ordinary ${\mathbb{P}}^{\prime }$-forcing relation, is sufficiently homogeneous. In particular, it helps to obtain the mentioned absoluteness property. This will allow us to accomplish the proof of the main results, Theorem 1 together with part (i) of Theorem 2 in Section 7, part (ii) of Theorem 2 in Section 8, Theorem 3 in Section 9. The flowchart can be seen in Figure 1.

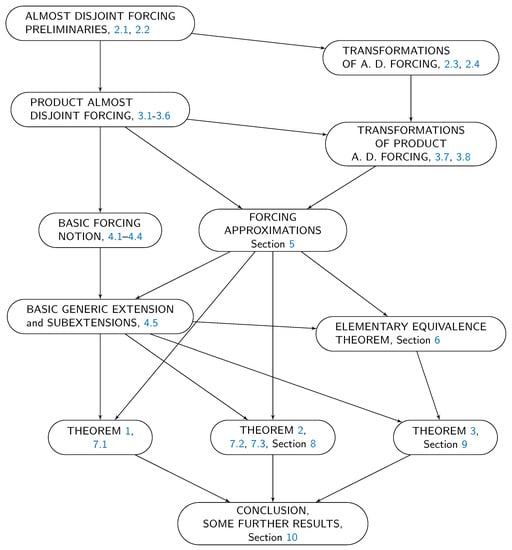
Figure 1. Flowchart.

The flowchart can be seen in Figure 1. And we added the index and contents as Supplementary Materials for easy reading.

General Set-Theoretic Notation Used in This Paper

• $\omega =\{0,1,2,\dots \}:$ natural numbers; ${\omega }^2=\omega \times \omega$.
• $X\subseteq Y$ iff $\forall x(x\in X⟹x\in Y):$ the inclusion.
• $X⫋Y$ means that $X\subseteq Y$ but $Y⊈X:$ strict inclusion.
• $\mathtt{card}X$ is the cardinality of a set $X,$ equal to the number of elements of X in case X is finite.
• $\mathtt{dom}P$ = $\left\{x:\exists y\right(⟨x,y⟩\in P\left)\right\}$ and $\mathtt{ran}P$ = $\left\{y:\exists x\right(⟨x,y⟩\in P\left)\right\}$ — thedomain and range of any set P that consists of pairs.
• In particular if $P=f$ is a function then $\mathtt{dom}f$ and $\mathtt{ran}f$ are the domain and the range of f.
• Functions are identified with their graphs: if $P=f$ is a function then $f=\{⟨x,f\left(x\right)⟩:x\in \mathtt{dom}f\},$ so that $y=f\left(x\right)$ is equivalent to $⟨x,y⟩\in f$.
• $f\left[X\right]=\{f\left(x\right):x\in X\cap \mathtt{dom}f\}$, the $f$-image of X.
• $f^{-1}\left[Y\right]=\{x\in \mathtt{dom}f:f\left(x\right)\in Y\}$, the $f$-pre-image of a set Y.
• $f^{-1}\left(y\right)=\{x\in \mathtt{dom}f:f\left(x\right)=y\}$, the $f$- pre-image of an element y.
• $\mathsf{\Delta }$ is the symmetric difference.
• ${\left\{x_a\right\}}_{a\in A}$ is the map f defined on A by $f\left(a\right)=x_a,\forall a$.
• $\mathcal{P}\left(X\right)=\{x:x\subseteq X\}$, the power set.
• $X^{<\omega }$ is the set of all strings (finite sequences) of elements of a set $X.$
• In particular ${\omega }^{<\omega }$ is the set of strings of natural numbers.
• $\mathtt{lh}s<\omega$ is the length of a string s.
• $s^x$ is the string obtained by adjoining x as the rightmost term to a given string $s.$
• $s\subset t$ means that the string t is a proper extension of s.
• $⌀=\mathsf{\Lambda }$ is resp. the empty set and the empty string.
• ${\omega }^{\omega }$ is the Baire space.

2. Almost Disjoint Forcing

In this section, we review basic definitions and results related to almost disjoint forcing, as well as some rarely used results related, for instance, to symmetries of almost disjoint forcing notions.

Assumption 1.

In this paper, we assume that $\mathbf{L}$ is the ground universe. Thus all forcing notions are defined in $\mathbf{L}$ while all generic extensions are those of $\mathbf{L}$. (In fact many intermediate results remain true w.r.t. any ground universe.)

2.1. Almost Disjoint Forcing

We present this forcing in a form based on the fact that the set $\mathbf{Fun}$ of all functions $f:\omega \to \omega$ is almost disjoint in the sense that if $f\ne g$ belong to $\mathbf{Fun}$ then the infinite sets $\{f\upharpoonright m:m\in \omega \}$ and $\{g\upharpoonright m:m\in \omega \}$ of finite strings have a finite intersection.

Definition 1.

$\mathbf{Seq}={\omega }^{<\omega }\setminus \left\{\mathsf{\Lambda }\right\}$ = all finite non-empty strings of natural numbers. A recursive enumeration ${\omega }^{<\omega }=\{{\mathrm{s}}_k:k\in \omega \}$ is fixed, such that ${\mathrm{s}}_0=\mathsf{\Lambda }$, the empty string, and ${\mathrm{s}}_k\subseteq {\mathrm{s}}_{\ell }⟹k⩽\ell$. Thus $\mathbf{Seq}={\omega }^{<\omega }\setminus \left\{\mathsf{\Lambda }\right\}=\{{\mathrm{s}}_k:k\ge 1\}$. For any $s={\mathrm{s}}_k$, we let $\mathtt{num}s=k$; in particular $\mathtt{num}\mathsf{\Lambda }=0$.

$\mathbf{Fun}={\omega }^{\omega }$ = all infinite sequences of natural numbers. A set $X\subseteq \mathbf{Fun}$ is dense iff for any $s\in \mathbf{Seq}$ there is $f\in X$ such that $s\subset f$.

Let $S\subseteq \mathbf{Seq},f\in \mathbf{Fun}$. If the set $S/f=\{n:f\upharpoonright n\in S\}$ is infinite then we say that S covers f, otherwise S does not cover f.

We underline that $\mathsf{\Lambda }$, the empty string, does not belong to $\mathbf{Seq}$.

Given a set $u\subseteq \mathbf{Fun}$ in the ground universe, the general goal of almost disjoint forcing is to find a generic set $S\subseteq \mathbf{Seq}$ such that the equivalence

$$f\in u⟺S\mathrm{does}\mathrm{not}\mathrm{cover}f$$

(1)

holds for each $f\in \mathbf{Fun}$ in the ground universe. This goal will be achieved by a forcing $P\left[u\right]$ introduced in Definition 4. In fact $P\left[u\right]$ will be a part, determined by u, of a common reservoir $P^{*}$.

Definition 2.

$P^{*}$ is the set of all pairs $p=⟨S_p;F_p⟩$ of finite sets $F_p\subseteq \mathbf{Fun}$, $S_p\subseteq \mathbf{Seq}$. Elements of $P^{*}$ will sometimes be called (forcing) conditions. If $p\in P^{*}$ then put $F_p^{\vee }=\{f\upharpoonright n:f\in F_p\wedge n\ge 1\}$. The set $F_p^{\vee }$ is an infinite (or else $F_p^{\vee }=F_p=⌀$) tree in $\mathbf{Seq}$, without terminal nodes.

Definition 3 (order).

Let $p,q\in P^{*}$. We define $q\le p$ (q is stronger) iff $S_p\subseteq S_q,F_p\subseteq F_q$, and the difference $S_q\setminus S_p$ does not intersect $F_p^{\vee }$, that is, $S_q\cap F_p^{\vee }=S_p\cap F_p^{\vee }$.

Thus any condition $p\in P^{*}$ is a pair that consists of a “finite” component $S_p$ and an “infinite” component $F_p$. Either of the components is a finite set (possibly, empty), but $S_p$ consists of finite strings of integers while $F_p$ consists of infinite sequences of integers that will be called functions (from $\omega$ to $\omega$). Both components of a stronger condition q, naturally, increase, but strings $t\in S_q\setminus S_p$ must satisfy $t\notin F_p^{\vee }$—in other words, t is not a substring of any function (infinite sequence) $f\in F_p$.

If $p\in P^{*}$ then both $⟨⌀;F_p⟩$ and $⟨S_p;⌀⟩$ belong to $P^{*}$ and $p\le ⟨S_p;⌀⟩$, but $p\le ⟨⌀;F_p⟩$ may fail. In fact $p\le ⟨⌀;F_p⟩$ iff $S_p\cap F_p^{\vee }=⌀$.

Lemma 1.

Conditions $p,q\in P^{*}$ are compatible in $P^{*}$ iff $\left(1\right)$ $S_q\setminus S_p$ does not intersect $F_p^{\vee }$, and $\left(2\right)$ $S_p\setminus S_q$ does not intersect $F_q^{\vee }$. Therefore, any $p,q\in P^{*}$ are compatible in $P^{*}$ iff $p\wedge q\le p$ and $p\wedge q\le q$.

Proof. 

The pair $p\wedge q=⟨S_p\cup S_q;F_p\cup F_q⟩$ isa condition in $P^{*}$. Moreover if (1) and (2) hold then we have $p\wedge q\le p$ and $p\wedge q\le q$, thus $p,q$ are compatible. □

Now let us introduce a relativized version of $P^{*}$. The parameter of relativization will be an arbitrary set $u\subseteq \mathbf{Fun}$ served as a reservoir of functions allowed to occur in sets $F_p$.

Definition 4.

If $u\subseteq \mathbf{Fun}$ then put $P\left[u\right]=\{p\in P^{*}:F_p\subseteq u\}$.

Note that if $p,q\in P\left[u\right]$ then $p\wedge q\in P\left[u\right]$. Thus in this case if conditions $p,q$ are compatible in $P^{*}$ then they are compatible in $P\left[u\right]$, too. Therefore, we will say that conditions $p,q\in P^{*}$ are compatible (or incompatible) without an indication which set $P\left[u\right]$ containing both conditions is considered.

Lemma 2.

If $u\subseteq \mathbf{Fun}$ then $P\left[u\right]$ is a ccc forcing.

Proof. 

If $S_p=S_q$ then p and q are compatible by Lemma 1. However there are only countably many sets of the form $S_p$. □

2.2. Almost-Disjoint Generic Extensions

Fix, in $\mathbf{L}$, a set $u\subseteq \mathbf{Fun}$ and consider a $P\left[u\right]$-generic extension $\mathbf{L}\left[G\right]$ of the ground (constructible by Assumption 1) set universe $\mathbf{L}$, obtained by adjoining a $P\left[u\right]$-generic set $G\subseteq P\left[u\right]$. Put $S_G={\bigcup }_{p\in G}{S}_p$; thus $S_G\subseteq \mathbf{Seq}$. The next lemma reflects the idea of almost-disjoint forcing: elements of u are distinguished by the property of $S_G$ not covering f in the sense of Definition 1.

Lemma 3.

Suppose that $u\subseteq \mathbf{Fun}$ in the universe $\mathbf{L}$, and $G\subseteq P\left[u\right]$ is a set $P\left[u\right]$-generic over $\mathbf{L}$. Then

(i)

G belongs to $\mathbf{L}\left[S_G\right];$

(ii)

if $f\in \mathbf{Fun}\cap \mathbf{L}$ then $f\in u$ iff $S_G$ does not cover $f;$

(iii)

if $p\in P\left[u\right]$ then $p\in G$ iff $s_p\subseteq S_G\wedge (S_G\setminus s_p)\cap (F_p^{\vee }\cup S_p^{\vee })=⌀$.

Proof. 

(ii) Let $f\in u$. The set $D_f=\{p\in P\left[u\right]:f\in F_p\}$ is dense in $P\left[u\right]$. (Let $q\in P\left[u\right]$. Define $p\in P\left[u\right]$ so that $S_p=S_q$ and $F_p=F_q\cup \left\{f\right\}$. Then $p\in D_f$ and $p⩽q$.) Therefore $D_f\cap G\ne ⌀$. Pick any $p\in D_f\cap G$. Then $f\in F_p$. Now every $r\in G$ is compatible with p, and hence $S_r/f\subseteq S_p/f$ by Lemma 1. Thus $S_G/f=S_p/f$ is finite.

Let $f\notin u$. The sets $D_{fl}=\{p\in P\left[u\right]:\mathtt{sup}\left(S_p/f\right)>l\}$ are dense in $P\left[u\right]$. (If $q\in P\left[u\right]$ then $F_q$ is finite. As $f\notin u$, there is $m>l$ with $f\upharpoonright m\notin F_q^{\vee }$. Define p so that $F_p=F_q$ and $S_p=S_q\cup \left\{f\upharpoonright m\right\}$. Then $p\in D_{fl}$ and $p⩽q$.) Let $p\in D_{fl}\cap G$. Then $\mathtt{sup}\left(S_G/f\right)>l$. As l is arbitrary, $S_G/f$ is infinite.

(iii) Consider any $p\in P\left[u\right]$. Suppose that $p\in G$. Then obviously $s_p\subseteq S_G$. If there exists $s\in (S_G\setminus S_p)\cap F_p^{\vee }$ then by definition we have $s\in S_q$ for some $q\in G$. However, then $p,q$ are incompatible by Lemma 1, a contradiction.

Now suppose that $p\notin G$. Then there exists $q\in G$ incompatible with p. By Lemma 1, there are two cases. First, there exists $s\in (S_q\setminus S_p)\cap F_p^{\vee }$. Then $s\in S_G\setminus S_p$, so p is not compatible with $S_G$. Second, there exists $s\in (S_p\setminus S_q)\cap F_q^{\vee }$. Then any condition $r\le q$ satisfies $s\notin S_r$. Therefore $s\notin S_G$, so $S_p⊈S_G$, and p is not compatible with $S_G$.

(i) $G=\{p\in P\left[u\right]:s_p\subseteq S_G\wedge (S_G\setminus s_p)\cap F_p^{\vee }=⌀\}$ by (iii). □

2.3. Lipschitz Transformations

Let $\mathbf{Lip}$ be the group of all $\subseteq$-automorphisms of $\mathbf{Seq}$; these transformations may be called Lipschitz by obvious association. Any $\mathit{\lambda }\in \mathbf{Lip}$ preserves the length $\mathtt{lh}$ of finite strings, that is, $\mathtt{lh}s=\mathtt{lh}\left(\mathit{\lambda }·s\right)$ for all $s\in \mathbf{Seq}$. Define the action of any transformation $\mathit{\lambda }\in \mathbf{Lip}$ on:

–

finite strings $s\in \mathbf{Seq}$ by: $\mathit{\lambda }·s=\mathit{\lambda }\left(s\right)$;

–

functions $f\in \mathbf{Fun}$: $\mathit{\lambda }·f\in \mathbf{Fun}$ is defined so that $\left(\mathit{\lambda }·f\right)\upharpoonright m=\mathit{\lambda }·\left(f\upharpoonright m\right)$;

–

sets $S\subseteq \mathbf{Seq},F\subseteq \mathbf{Fun}$ by: $\mathit{\lambda }·S=\{\mathit{\lambda }·s:s\in S\}$, $\mathit{\lambda }·F=\{\mathit{\lambda }·f:f\in F\}$;

–

conditions $p\in P^{*}$, by: $\mathit{\lambda }·p=⟨\mathit{\lambda }·S_p;\mathit{\lambda }·F_p⟩$.

Lemma 4 (routine).

The action of any $\mathit{\lambda }\in \mathbf{Lip}$ is an order-preserving automorphism of $P^{*}.$ If $u\subseteq \mathbf{Fun}$ and $p\in P\left[u\right]$ then $\mathit{\lambda }·p\in P\left[\mathit{\lambda }·u\right]$.

Lemma 5.

Suppose that $u,v\subseteq \mathbf{Fun}$ are countable sets topologically dense in $\mathbf{Fun}$, and $p\in P\left[u\right],q\in P\left[v\right]$. Then there is $\mathit{\lambda }\in \mathbf{Lip}$ and conditions $p^{\prime }\in P\left[u\right],p^{\prime }\le p$ and $q^{\prime }\in P\left[v\right],q^{\prime }\le q$, such that $\mathit{\lambda }·u=v$, and $\mathit{\lambda }·p^{\prime }=q^{\prime }$ — therefore conditions $\mathit{\lambda }·p$ and q are compatible in $P\left[v\right]$.

Proof. 

Put $\mathtt{bas}r=\{s\left(0\right):s\in S_r\}\cup \{f\left(0\right):f\in F_r\}$ for any $r\in P^{*}$; $\mathtt{bas}r\subseteq \omega$ is finite. Let $M<\omega$ satisfy $\mathtt{bas}p\cup \mathtt{bas}q\subseteq M$. Because of density, for any $i<M$ there exist $f_i\in u$ and $g_i\in u^{\prime }$ such that $f_i\left(0\right)=i$ and $g_i\left(0\right)=M+i$.

For any $f\ne g\in \mathbf{Fun}$, let $\mathrm{N}(f,g)$ be the largest n with $f\upharpoonright n=g\upharpoonright n$.

We will define enumerations $u=\{f_k:k<\omega \}$ and $u^{\prime }=\{g_k:k<\omega \}$, without repetitions, which agree with the above definition for $k<M$ and satisfy $\mathrm{N}(f_k,f_l)=\mathrm{N}(g_k,g_l)$ for all $k,l$, and $g_k\left(0\right)=f_k\left(0\right)$ for all $k\ge M$. As soon as this is accomplished, define $\mathit{\lambda }\in \mathbf{Lip}$ as follows. Consider any $s\in \mathbf{Seq}$ of length $m=\mathtt{lh}s$. As u is dense, $s=f_k\upharpoonright m$ for some k. Put $\mathit{\lambda }\left(s\right)=g_k\upharpoonright m$. Clearly $\mathit{\lambda }·u=u^{\prime }$, and in particular $\mathit{\lambda }·f_k=g_k$ for all k, and hence

(∗)

if $k<M$ then $\mathit{\lambda }(⟨k⟩)=⟨M+k⟩$ and $\mathit{\lambda }(⟨M+k⟩)=⟨k⟩$, but if $k\ge 2M$ then $\mathit{\lambda }(⟨k⟩)=⟨k⟩$.

Now to define $q^{\prime }$ put $r^{\prime }=\mathit{\lambda }·p$. Then $r^{\prime }\in P\left[v\right]$, and $\mathtt{bas}{r}^{\prime }=\mathit{\beta }·\mathtt{bas}p\subseteq \omega \setminus M$ by (∗), since $\mathtt{bas}p\subseteq M$. Therefore, $\mathtt{bas}{r}^{\prime }\cap \mathtt{bas}q=⌀$ because $\mathtt{bas}q\subseteq M$ as well. It follows that conditions $r^{\prime }$ and q are compatible in $P\left[v\right]$, and hence condition $q^{\prime }=r^{\prime }\wedge q$ (that is, $S_{q^{\prime }}=S_{r^{\prime }}\cup S_q$ and $X_{q^{\prime }}=X_{r^{\prime }}\cup X_q$) belongs to $P\left[v\right]$, and obviously $q^{\prime }\le q$. Pretty similarly, to define q, we put $r={\mathit{\lambda }}^{-1}·q\in P\left[u\right]$, thus $\mathtt{bas}r\subseteq \omega \setminus M$, $\mathtt{bas}r\cap \mathtt{bas}p=⌀$, conditions r, p are compatible, condition $p^{\prime }=p\wedge r$ (that is, $S_{p^{\prime }}=S_p\cup S_r$ and $X_{p^{\prime }}=X_p\cup X_r$) belongs to $P\left[u\right]$, and $p^{\prime }\le p$. Note that $q=\mathit{\lambda }·r$ and $r^{\prime }=\mathit{\lambda }·p$ by construction. It follows that $q^{\prime }=r^{\prime }\wedge q=\mathit{\lambda }·(p\wedge r)=\mathit{\lambda }·p^{\prime }$, as required.

To define $f_k$ and $g_k$ by induction, suppose that $k\ge M$, $f_0,\dots ,f_{k-1}$ and $g_0,\dots ,g_{k-1}$ are defined, and $\mathrm{N}(f_i,f_j)=\mathrm{N}(g_i,g_j)$ holds in this domain. Consider any next function $f\in u\setminus \{f_0,\dots ,f_{k-1}\}$, and let it be $f_k$. There are functions $g\in \mathbf{Fun}$ satisfying $\mathrm{N}(f_j,f_k)=\mathrm{N}(g_j,g)$ for all $j<k$. This property of g is determined by a certain finite part $g\upharpoonright m$. By the density the set v contains a function g of this type. Let $g_k$ be any of them. In the special case when $\mathrm{N}(f_j,f_k)=0$ for all $j<k$ (then $k\ge 2M$), we take any $g_k\in v$ satisfying $\mathrm{N}(f_j,f_k)=0$ for all $j<k$ and $g_k\left(0\right)=f_k\left(0\right)$. □

2.4. Substitution Transformations

The next lemma (Lemma 6) will help to prove that the forcing notions considered are sufficiently homogeneous. Assume that $p,q\in P^{*}$ satisfy the following requirement:

$$F_p=F_q\mathrm{and}{S}_p\cup S_q\subseteq F_p^{\vee }=F_q^{\vee }.$$

(2)

We define a transformation $H_q^p$ acting as follows. Let $p^{\prime }\in P^{*}$, $p^{\prime }\le p$. Then by definition $S_p\subseteq S_{p^{\prime }}$, $F_p\subseteq F_{p^{\prime }}$, and $S_{p^{\prime }}\cap F_p^{\vee }=S_p$ (by (2)). We put $H_q^p\left(p^{\prime }\right)=q^{\prime }:=⟨S_{q^{\prime }},F_{q^{\prime }}⟩$, where $F_{q^{\prime }}=F_{p^{\prime }}$ and $S_{q^{\prime }}=(S_{p^{\prime }}\setminus S_p)\cup S_q$. Thus the difference between $S_{q^{\prime }}$ and $S_{p^{\prime }}$ lies entirely within the set $F_p^{\vee }=F_q^{\vee }$, and in particular $S_{q^{\prime }}$ has $S_q$ there while $S_{p^{\prime }}$ has $S_p$ there.

Lemma 6 (routine).

If $p,q\in P^{*}$, $F_p=F_q$, and $S_p\cup S_q\subseteq F_p^{\vee }=F_q^{\vee }$, then

$$H_q^p:P=\{p^{\prime }\in P^{*}:p^{\prime }\le p\}\stackrel{\mathrm{onto}}{⟶}Q=\{q^{\prime }\in P^{*}:q^{\prime }\le q\}$$

is an order isomorphism, and $H_q^p={\left(H_p^q\right)}^{-1}.$ If moreover $u\subseteq \mathbf{Fun}$ and $p,q\in P\left[u\right]$ then $H_q^p$ maps the set $\{p^{\prime }\in P\left[u\right]:p^{\prime }\le p\}$ onto $\{q^{\prime }\in P\left[u\right]:q^{\prime }\le q\}$ order-preservingly.

3. Almost Disjoint Product Forcing

Here we review the structure and basic properties of product almost-disjoint forcing over $\mathbf{L}$ and corresponding generic extensions of $\mathbf{L}$. In order to support various applications, we make use of ${\omega }_1$-many independent forcing notions.

3.1. Product Forcing, Systems, Restrictions

We begin with ${\omega }_1$-products of $P^{*}$ after which we consider more complicated forcing notions.

Definition 5.

Let $\mathcal{I}={\omega }_1$. This is the index set for the forcing products considered below. Let ${\mathbf{P}}^{*}$ be the product of $\mathcal{I}$ copies of the set $P^{*}$ (Definition 2), with finite support. That is, ${\mathbf{P}}^{*}$ consists of all functions $p:\left|p\right|\to P^{*}$ such that the set $\left|p\right|=\mathtt{dom}p\subseteq \mathcal{I}$ is finite.

If $p\in {\mathbf{P}}^{*}$ then put $F_p\left(\nu \right)=F_{p\left(\nu \right)}$ and $S_p\left(\nu \right)=S_{p\left(\nu \right)}$ for all $\nu \in \left|p\right|$, so that $p\left(\nu \right)=⟨S_p\left(\nu \right);F_p\left(\nu \right)⟩$. We order ${\mathbf{P}}^{*}$ componentwise: $p\le q$ iff $\left|q\right|\subseteq \left|p\right|$ and $p\left(\nu \right)\le q\left(\nu \right)$ for all $\nu \in \left|q\right|$. Put

$$F_p^{\vee }\left(\nu \right)=F_{p\left(\nu \right)}^{\vee }=\{f\upharpoonright m:f\in F_p\left(\nu \right)\wedge m\ge 1\}.$$

If $p,q\in {\mathbf{P}}^{*}$ then define a condition $r=p\wedge q\in {\mathbf{P}}^{*}$ so that $\left|p\wedge q\right|=\left|p\right|\cup \left|q\right|$, $(p\wedge q)\left(\nu \right)=p\left(\nu \right)\wedge q\left(\nu \right)$ whenever $\nu \in \left|p\right|\cap \left|q\right|$, and if $\nu \in \left|p\right|\setminus \left|q\right|$ or $\nu \in \left|q\right|\setminus \left|p\right|$, then $(p\wedge q)\left(\nu \right)=p\left(\nu \right)$, resp., $(p\wedge q)\left(\nu \right)=q\left(\nu \right)$. Then Conditions $p,q$ are compatible iff $p\wedge q\le p$ and $p\wedge q\le q$.

We consider certain subforcings of the total product almost disjoint forcing notion ${\mathbf{P}}^{*}$. This involves the following notion of a system.

Definition 6.

A system is any map $U:\left|U\right|\to \mathcal{P}\left(\mathbf{Fun}\right)$ such that $\left|U\right|\subseteq \mathcal{I}$ and each set $U\left(\nu \right)$ ($\nu \in \left|U\right|$) is topologically dense in $\mathbf{Fun}$. A system U is:

• disjoint, if its components $U\left(\nu \right)\subseteq \mathbf{Fun}(\nu \in \mathcal{I})$ are pairwise disjoint;
• countable, if the set $\left|U\right|$ and each $U\left(\nu \right)(\nu \in |U\left|\right)$ are at most countable.
• If $U,V$ are systems, $\left|U\right|\subseteq \left|V\right|$, and $U\left(\nu \right)\subseteq V\left(\nu \right)$ for all $\nu \in \left|U\right|$ then we write that V extends U, in symbol $U\preccurlyeq V$.
• If ${\left\{U_{\xi }\right\}}_{\xi <\mathit{\lambda }}$ is a sequence of systems then define a system $U={\bigvee }_{\xi <\mathit{\lambda }}{U}_{\xi }$ by $\left|U\right|={\bigcup }_{\xi <\mathit{\lambda }}\left|U_{\xi }\right|$ and $U\left(\nu \right)={\bigcup }_{\xi <\mathit{\lambda },\nu \in |U_{\xi }|}{U}_{\xi }\left(\nu \right)$ for all $\nu \in \left|U\right|$.
• If U is a system then let $\mathbf{P}\left[U\right]$ be the finite support product of sets $P\left[U\left(\nu \right)\right],\nu \in \left|U\right|$, that is, $\mathbf{P}\left[U\right]=\left\{p\in {\mathbf{P}}^{*}:\right|p|\subseteq |U|\wedge \forall \nu (F_p\left(\nu \right)\subseteq U\left(\nu \right))\}.$

Definition 7 (restrictions).

Suppose that $c\subseteq \mathcal{I}$.

If $p\in {\mathbf{P}}^{*}$ then define $p^{\prime }=p\upharpoonright c\in {\mathbf{P}}^{*}$ so that $|p^{\prime }|=c\cap |p|$ and $p^{\prime }\left(\nu \right)=p\left(\nu \right)$ whenever $\nu \in |p^{\prime }|$. Accordingly if U is a system then define a system $U\upharpoonright c$ so that $\left|U\upharpoonright c\right|=c\cap \left|U\right|$ and $\left(U\upharpoonright c\right)\left(\nu \right)=U\left(\nu \right)$ for $\nu \in \left|U\upharpoonright c\right|$. A special case: if $\nu \in \mathcal{I}$ then let $p{\upharpoonright }_{\ne \nu }=p\upharpoonright \left(\right|p|\setminus \{\nu \left\}\right)$ and $U{\upharpoonright }_{\ne \nu }=U\upharpoonright \left(\right|U|\setminus \{\nu \left\}\right)$.

Note that writing $p\upharpoonright c$ or $U\upharpoonright c$, it is not assumed that $c\subseteq \left|p\right|$, resp., $c\subseteq \left|U\right|$.

3.2. Regular Forcing Notions

Unfortunately, product forcing notions of the form $\mathbf{P}\left[U\right]$ (U being a system in $\mathbf{L}$) do not provide us with all the definability effects we need. We will make use of certain more complicated forcing notions $K\subseteq {\mathbf{P}}^{*}$ in $\mathbf{L}$. To explain the idea, let a system $U\in \mathbf{L}$ satyisfy $\left|U\right|=\omega$. Let $G\subseteq \mathbf{P}\left[U\right]$ be generic over $\mathbf{L}$. The sets $S_G\left(\nu \right)=S_{G\left(\nu \right)}={\bigcup }_{p\in G}{S}_p\left(\nu \right)\subseteq \mathbf{Seq}$ then belong to $\mathbf{L}\left[G\right]$, and in fact $\mathbf{L}\left[G\right]=\mathbf{L}\left[{\left\{S_G\left(\nu \right)\right\}}_{\nu <\omega }\right]$. As $\mathbf{Seq}=\{s_k:k\ge 1\}$ (a fixed recursive enumeration, Definition 1), let $a_0\left[G\right]=\{k\ge 1:{\mathrm{s}}_k\in S_0\left[G\right]\}$ and $c=\left\{0\right\}\cup a_G\left(0\right)$. Consider the model $\mathbf{L}\left[{\left\{S_G\left(\nu \right)\right\}}_{\nu \in c}\right]$. The first idea is to make use of $U\upharpoonright c$, but oops, clearly $c\notin \mathbf{L}$, and consequently $U\upharpoonright c\notin \mathbf{L}$ and $\mathbf{P}\left[U\upharpoonright c\right]\notin \mathbf{L}$, so that many typical product forcing results do not apply in this case. The next definition attempts to view the problem from another angle.

Definition 8 (in L).

A set $K\subseteq {\mathbf{P}}^{*}$ is called a regular subforcing if:

(1) 

if conditions $p,q\in K$ are compatible then $p\wedge q\in K$;

(2) 

if $p,q\in K$ then $p\upharpoonright \left|q\right|\in K$ — but it is not assumed that $p\in K$ necessarily implies $p\upharpoonright c\in K$ for an arbitrary $c\subseteq \left|p\right|$;

(3) 

if $p,q\in {\mathbf{P}}^{*}$, $q\le p$, and $\left|q\right|=\left|p\right|$ exactly, then $p\in K$ implies $q\in K$;

(4) 

for any condition $p\in {\mathbf{P}}^{*}$, there exist: a condition $p^{*}\in {\mathbf{P}}^{*}$ and a set $d\subseteq |p^{*}|$ such that $p^{*}\le p$, $F_{p^{*}}\left(\nu \right)=F_p\left(\nu \right)$ for all $\nu \in \left|p\right|$, $F_{p^{*}}\left(\nu \right)=⌀$ for all $\nu \in |p^{*}|\setminus |p|$, $p^{*}\upharpoonright d\in K$, and every condition $q\in K,q\le p^{*}\upharpoonright d$, satisfies $\left|q\right|\cap |p^{*}|=d$, and hence q is compatible with $p^{*}$ and with p.

In this case, if U is a system then define $K\left[U\right]=K\cap \mathbf{P}\left[U\right]$. In particular, if simply $K={\mathbf{P}}^{*}$ then ${\mathbf{P}}^{*}\left[U\right]={\mathbf{P}}^{*}\cap \mathbf{P}\left[U\right]=\mathbf{P}\left[U\right]$.

Example 1 (trivial).

If $c\subseteq \mathcal{I}$ in the ground universe $\mathbf{L}$, then ${\mathbf{P}}^{*}\upharpoonright c$ is a regular forcing. To prove (4) of Definition 8 let $p^{*}=p$ and $d=\left|p\right|\cap c$.

Example 2 (less trivial).

Consider the set K of all conditions $p\in {\mathbf{P}}^{*}$ such that $\left|p\right|\subseteq \omega$ and if $\nu \in \left|p\right|$, $\nu \ge 1$, then ${\mathrm{s}}_{\nu }\in S_p\left(0\right)$. We claim that K is a regular subforcing.

To verify 8(2), note that if $q\in K$ then either $0\in \left|q\right|$ or $\left|q\right|=⌀$.

To verify 8(4), let $p\in {\mathbf{P}}^{*}$. If $\left|p\right|\subseteq \left\{0\right\}$, then setting $p^{*}=p$ and $d=\left|p\right|$ works, so we assume that $\left|p\right|⊈\left\{0\right\}$. Define $p^{*}\in {\mathbf{P}}^{*}$ so that $p^{*}\left(\nu \right)=p\left(\nu \right)$ for all $\nu \ge 1$, $F_{p^{*}}\left(0\right)=F_p\left(0\right)$, and $S_{p^{*}}\left(0\right)=S_p\left(0\right)\cup \{{\mathrm{s}}_{\nu }:\nu \in I^{\prime }\}$, where $I^{\prime }$ consists of all $\nu \in \left|p\right|,\nu \ge 1$, such that ${\mathrm{s}}_{\nu }\notin S_p\left(0\right)\cup F_p^{\vee }\left(0\right)$. Then $|p^{*}|=|p|\cup |0|$, $p^{*}\le p$, and we have ${\mathrm{s}}_{\nu }\in S_{p^{*}}\left(0\right)\cup F_{p^{*}}^{\vee }\left(0\right)$ (not necessarily $s_{\nu }\in S_{p^{*}}\left(0\right)$) for all $\nu \in \left|p\right|,\nu \ge 1$. Let $d\subseteq |p^{*}|$ contain 0 and all $\nu \in \left|p\right|,\nu \ge 1$ with ${\mathrm{s}}_{\nu }\in S_{p^{*}}\left(0\right)$; easily $p^{*}\upharpoonright d\in K.$

Now let $q\in K,q\le r=p^{*}\upharpoonright d$. Consider any index $\nu \in |p^{*}|\setminus d$. Then ${\mathrm{s}}_{\nu }\notin S_{p^{*}}\left(0\right)=S_r\left(0\right)$, hence ${\mathrm{s}}_{\nu }\in F_{p^{*}}^{\vee }\left(0\right)=F_r^{\vee }\left(0\right)$. We claim that $\nu \notin \left|q\right|$. Indeed otherwise ${\mathrm{s}}_{\nu }\in S_q\left(0\right)$ as $q\in K$. However ${\mathrm{s}}_{\nu }\in F_r^{\vee }\left(0\right)\setminus S_r\left(0\right)$ (see above). However, this contradicts ${\mathrm{s}}_{\nu }\in S_q\left(0\right)$, because $q\le r$.

Theorem 4 (in L).

The partially ordered set ${\mathbf{P}}^{*}$, and hence each $\mathbf{P}\left[U\right]$, and generally each regular subforcing of $\mathbf{P}\left[U\right]$ (for any system U) satisfies CCC (countable antichain condition).

Proof. 

Suppose towards the contrary that $A\subseteq {\mathbf{P}}^{*}$ is an uncountable antichain. We may assume that there is $m\in \omega$ such that $\left|p\right|=m$ for all $p\in A$. Applying the $\mathsf{\Delta }$-lemma argument, we obtain an uncountable set $A^{\prime }\subseteq A$ and a finite set $w\subseteq \mathcal{I}$ with $\mathtt{card}w<m$ strictly, such that $\left|p\right|\cap \left|q\right|=w$ for all $p\ne q$ in $A^{\prime }$. Then $A^{\prime \prime }=\{p\upharpoonright w:p\in A^{\prime }\}$ is still an uncountable antichain, with $\left|p\right|=w$ for all $p\in A^{\prime }$, easily leading to a contradiction (see the proof of Lemma 2). □

Lemma 7 (in L).

If $K\subseteq {\mathbf{P}}^{*}$ is a regular forcing and U is a system then $K\left[U\right]=K\cap \mathbf{P}\left[U\right]$ is a regular subforcing of $\mathbf{P}\left[U\right]$.

To show how (4) of Definition 8 works, we prove

Lemma 8 (in L).

If U is a system and $K\subseteq \mathbf{P}\left[U\right]$ is a regular subforcing of $\mathbf{P}\left[U\right]$ then any set $D\subseteq K$ pre-dense in K remains pre-dense in $\mathbf{P}\left[U\right]$.

Proof. 

Consider any $p\in \mathbf{P}\left[U\right]$. Let $p^{*}\in \mathbf{P}\left[U\right]$ and $d\subseteq |p^{*}|$ satisfy (4) of Definition 8. In particular, $p^{*}\le p$ and $p^{*}\upharpoonright d\in K$. By the pre-density, there is a condition $q\in D$ compatible with $p^{*}\upharpoonright d$. Then by (1) of Definition 8 there is a condition $r=q\wedge \left(p^{*}\upharpoonright d\right)\in K$ such that $r\le q$ and $r\le p^{*}\upharpoonright d$. Then r is compatible with p by the choice of $p^{*}$ and d. □

3.3. Outline of Product and Regular Extensions

We consider sets of the form $\mathbf{P}\left[U\right]$, U being a system in $\mathbf{L}$, as well as regular subforcings $K\subseteq \mathbf{P}\left[U\right]$, as forcing notions over $\mathbf{L}$. Accordingly, we will study $\mathbf{P}\left[U\right]$-generic and $K$-generic extensions $\mathbf{L}\left[G\right]$ of the ground universe $\mathbf{L}$. Define some elements of these extensions.

Definition 9.

Suppose that $G\subseteq {\mathbf{P}}^{*}$. Put $\left|G\right|={\bigcup }_{p\in G}\left|p\right|$; $\left|G\right|\subseteq \mathcal{I}$. Let

$$S_G\left(\nu \right)=S_{G\left(\nu \right)}={\bigcup }_{p\in G}{S}_p\left(\nu \right)and{a}_{G\left(\nu \right)}=a_G\left(\nu \right)=\{k\ge 1:{\mathrm{s}}_k\in S_G\left(\nu \right)\},$$

for any $\nu \in \mathcal{I}$, where $G\left(\nu \right)=\{p\left(\nu \right):p\in G\}\subseteq P^{*}$, and $\mathbf{Seq}=\{{\mathrm{s}}_k:k\ge 1\}$ is a fixed recursive enumeration (see Definition 1).

Thus $S_G\left(\nu \right)\subseteq \mathbf{Seq},a_G\left(\nu \right)\subseteq \omega \setminus \left\{0\right\}$, and $S_G\left(\nu \right)=a_G\left(\nu \right)=⌀$ for any $\nu \notin \left|G\right|$.

By the way, this defines a sequence ${\overrightarrow{S}}_G={\left\{S_G\left(\nu \right)\right\}}_{\nu \in \mathcal{I}}$ of subsets of $\mathbf{Seq}$.

If $c\subseteq \mathcal{I}$ then let $G\upharpoonright c=\left\{p\in G:\right|p|\subseteq c\}$. It will typically happen that $G\upharpoonright c=\{p\upharpoonright c:p\in G\}$. Put $G{\upharpoonright }_{\ne \nu }=\{p\in G:\nu \notin |p\left|\right\}=G\upharpoonright (\mathcal{I}\setminus \{\nu \left\}\right)$.

If U is a system in $\mathbf{L}$, the ground universe, then any $\mathbf{P}\left[U\right]$-generic set $G\subseteq \mathbf{P}\left[U\right]$ splits into the family of sets $G\left(\nu \right),\nu \in \mathcal{I}$, and each $G\left(\nu \right)$ is $P\left[U\left(\nu \right)\right]$-generic.

Lemma 9.

Let U be a system and $K\subseteq \mathbf{P}\left[U\right]$ be a regular subforcing in the ground universe $\mathbf{L}$. Let $G\subseteq \mathbf{P}\left[U\right]$ be a set $\mathbf{P}\left[U\right]$-generic over $\mathbf{L}$. Then:

(i)

$G\in \mathbf{L}\left[S_G\right];$

(ii)

the set $G\cap K$ is $K$-generic over $\mathbf{L};$

(iii)

$\mathbf{L}[G\cap K]=\mathbf{L}\left[G\upharpoonright c\right]$, where $c=\left|G\cap K\right|$ (it is not necessary that $c\in \mathbf{L}$!);

(iv)

if $\nu \notin \left|G\cap K\right|$ then $\mathbf{L}[G\cap K]\subseteq \mathbf{L}\left[G{\upharpoonright }_{\ne \nu }\right];$

(v)

if $\nu \in \mathcal{I}$ then $S_G\left(\nu \right)\notin \mathbf{L}\left[G{\upharpoonright }_{\ne \nu }\right];$

(vi)

if $\nu \in \left|G\right|$ then the set $G\left(\nu \right)=\{p\left(\nu \right):p\in G\}\in \mathbf{L}\left[G\right]$ is $P\left[U\left(\nu \right)\right]$-generic over $\mathbf{L}$, hence if $f\in \mathbf{Fun}\cap \mathbf{L}$ then $f\in U\left(\nu \right)⟺S_G\left(\nu \right)/f\mathrm{is}\mathrm{finite}$.

Proof. 

(ii) This follows from Lemma 8.

(iii) Let us show that $G\upharpoonright c=\{q\in {\mathbf{P}}^{*}:\exists p\in G\cap K(p\le q)\}$; this proves $G\upharpoonright c\in \mathbf{L}[G\cap K]$. Suppose that $q\in G\upharpoonright c$, so that $q\in G$ and $\left|q\right|\subseteq c$, in other words, $\left|q\right|\subseteq |p_1|\cup \cdots \cup |p_n|$ for a finite set of conditions $p_1,\dots ,p_n\in G\cap K$. Note that $p=p_1\wedge \cdots \wedge p_n\in K$ by Definition 8(1). Thus $p\in G\cap K$, and $\left|q\right|\subseteq \left|p\right|$. Yet $q\in G$ as well, therefore, $p^{\prime }=p\wedge q\in G$, and $|p^{\prime }|=|p|$. It follows that $p^{\prime }\in K$, by Definition 8(3), so that $p^{\prime }\in G\cap K$. Finally $p^{\prime }\le q$.

Now suppose that $p\in G\cap K$ and $p\le q\in {\mathbf{P}}^{*}$. Then obviously q belongs to $\mathbf{P}\left[U\right]$ (since so does p), hence $q\in G$ (since G is generic). Finally $\left|q\right|\subseteq \left|p\right|\subseteq c$.

Let us show that $G\cap K=\left(G\upharpoonright c\right)\cap K$; this proves $G\cap K\in \mathbf{L}\left[G\upharpoonright c\right]$. Indeed if $p\in G\cap K$ then by definition $\left|p\right|\subseteq c=\left|G\cap K\right|$, therefore $p\in G\upharpoonright c$, as required.

(iv) This is clear since we have $G\cap K=G{\upharpoonright }_{\ne \nu }\cap K$ in the case considered.

(v) The set $\mathbf{P}\left[U\right]$ can be identified with the product $\mathbf{P}\left[U\right]{\upharpoonright }_{\ne \nu }\times P\left[U\left(\nu \right)\right]$. Thus $G\left(\nu \right)$ and $S_G\left(\nu \right)$ are $P\left[U\left(\nu \right)\right]$-generic over $\mathbf{L}\left[\mathbf{P}\left[U\right]{\upharpoonright }_{\ne \nu }\right]$.

(vi) The genericity easily follows from Definition 8(3). Then use Lemma 3.

(i) First of all, $G={\prod }_{\nu }G\left(\nu \right)$ by the product-forcing theorem. Then, each $G\left(\nu \right)$ is recovered from the associated $S_G\left(\nu \right)$ by means of a simple uniform formula, see the proof of Lemma 3(i). □

3.4. Names for Sets in Product and Regular Extensions

For any set X we let ${\mathbf{N}}_X$ be the set of all ${\mathbf{P}}^{*}$-names for subsets of X. Thus ${\mathbf{N}}_X$ consists of all sets $\tau \subseteq {\mathbf{P}}^{*}\times X$. Let ${\mathbf{SN}}_X$ (small names) consist of all at most countable names $\tau \in {\mathbf{N}}_X$.

We define $\mathtt{dom}\tau =\left\{p:\exists x\right(⟨p,x⟩\in \tau \left)\right\}$, $\left|\tau \right|=\bigcup \{\left|p\right|:p\in \mathtt{dom}\tau \}$ for any name $\tau$.

Say that a name $\tau$ is below a given $p\in {\mathbf{P}}^{*}$ if all $p^{\prime }\in \mathtt{dom}\tau$ satisfy $p^{\prime }\le p$.

For any set $K\subseteq {\mathbf{P}}^{*}$, we let ${\mathbf{N}}_X\left(K\right)$ be the set of all names $\tau \in {\mathbf{N}}_X$ such that $\mathtt{dom}\tau \subseteq K$, and accordingly ${\mathbf{SN}}_X\left(K\right)={\mathbf{N}}_X\left(K\right)\cap {\mathbf{SN}}_X$ (small names). In particular, we’ll consider such sets of names as ${\mathbf{SN}}_X\left(\mathbf{P}\left[U\right]\right)$ and ${\mathbf{SN}}_X\left(\mathbf{P}\left[U\right]\upharpoonright c\right)$. Names in ${\mathbf{N}}_X\left(K\right)$ for different sets X will be called $K$-names. Accordingly, names in ${\mathbf{SN}}_X\left(K\right)$ for different sets X will be called small $K$-names.

Definition 10 (valuations).

If $\tau \in {\mathbf{N}}_X$ and $G\subseteq {\mathbf{P}}^{*}$ then define $\tau \left[G\right]=\{x:\exists p\in G(⟨p,x⟩\in \tau \left)\right\}$, the $G$-valuation of τ; $\tau \left[G\right]$ is a subset of X.

Example 3 (some names).

Let $\odot \in {\mathbf{P}}^{*}$ be the empty condition, that is, $|\odot |=⌀$. This is the weakest condition in any $\mathbf{P}\left[U\right]$. If X is a set in the ground universe then $\breve{X}=\{⟨\odot ,x⟩:x\in X\}$ is a $K$-namefor any regular forcing $K\subseteq {\mathbf{P}}^{*}$, and $\breve{X}\left[G\right]=X$ for any set G containing ⊙.

We will typically use breve-names like $\breve{X}$ for sets in the ground universe, and dot-names (like $\stackrel{.}{x}$) for setsin generic extensions.

Suppose that $K\subseteq {\mathbf{P}}^{*}$. Let $\underline{G}=\{⟨p,p⟩:p\in K\}$. (In principle, $\underline{G}$ depends on K but this dependence will usually be suppressed.) Clearly $\underline{G}\in {\mathbf{N}}_K\left(K\right)$ (but $\underline{G}\notin {\mathbf{SN}}_K\left(K\right)$ unless K is countable), and in addition $\underline{G}\left[G\right]=G$ for any $⌀\ne G\subseteq K$. Thus $\underline{G}$ is a name for the generic set $G\subseteq K$.

Similarly, $\underline{G}\upharpoonright c=\{⟨p,p⟩:p\in K\upharpoonright c\}$ ($c\subseteq \mathcal{I}$) is a name for $G\upharpoonright c$ (see Definition 9).

3.5. Names for Functions

For any sets $X,Y$ let ${\mathbf{N}}_Y^X$ be the set of all ${\mathbf{P}}^{*}$-names for functions $X\to Y$; it consists of all $\tau \subseteq {\mathbf{P}}^{*}\times (X\times Y)$ such that the sets $\tau ″⟨x,y⟩=\{p:⟨p,⟨x,y⟩⟩\in \tau \}$ satisfy the followingrequirement:

$$\mathrm{if}y\ne y^{\prime },p\in \tau ″⟨x,y⟩,p^{\prime }\in \tau ″⟨x,y^{\prime }⟩,\mathrm{then}p,p^{\prime }\mathrm{are}\mathrm{incompatible}.$$

Let $\mathtt{dom}\tau ={\bigcup }_{x,y}\tau ″⟨x,y⟩$ and $\left|\tau \right|=\bigcup \{\left|p\right|:p\in \mathtt{dom}\tau \}$.

As above, ${\mathbf{SN}}_Y^X$ consists of all at most countablenames $\tau \in {\mathbf{N}}_Y^X$.

For any set $K\subseteq {\mathbf{P}}^{*}$, we let ${\mathbf{N}}_Y^X\left(K\right)$ be the set of all names $\tau \in {\mathbf{N}}_Y^X$ such that $\mathtt{dom}\tau \subseteq K$, and accordingly ${\mathbf{SN}}_Y^X\left(K\right)={\mathbf{N}}_Y^X\left(K\right)\cap {\mathbf{SN}}_Y^X$ (small names).

A name $\tau \in {\mathbf{N}}_Y^X\left(K\right)$ is $K$-full iff the union $\tau ″x={\bigcup }_y\tau ″⟨x,y⟩$ is pre-dense in K for any $x\in X$. A name $\tau \in {\mathbf{N}}_Y^X\left(K\right)$ is $K$-full below some $p_0\in K$, iff all sets $\tau ″x$ are pre-dense in K below $p_0$, that is, any condition $q\in K,q\le p_0$, is compatible with some $r\in {\tau }_x$ (and this holds for all $x\in X$).

Note that ${\mathbf{N}}_Y^X\left(K\right)\subseteq {\mathbf{N}}_{X\times Y}\left(K\right)$, and accordingly ${\mathbf{SN}}_Y^X\left(K\right)\subseteq {\mathbf{SN}}_{X\times Y}\left(K\right)$. Thus all names in ${\mathbf{N}}_Y^X\left(K\right)$ and in ${\mathbf{SN}}_Y^X\left(K\right)$ are still $K$-names in the sense above.

Corollary 1 (of Lemma 8, (in L).

If U is a system, $K\subseteq \mathbf{P}\left[U\right]$ is a regular subforcing, $X,Y$ any sets, and τ is a name in ${\mathbf{N}}_Y^X\left(K\right)$, then τ is $K$-full (resp., $K$-full below $p\in K$) iff τ is $\mathbf{P}\left[U\right]$-full (resp., $\mathbf{P}\left[U\right]$-full below p).

Suppose that $\tau \in {\mathbf{N}}_Y^X$. Call a set $G\subseteq {\mathbf{P}}^{*}$ minimally $\tau$-generic iffit is compatible in itself (if $p,q\in G$ then there is $r\in G$ with $r\le p,r\le q$), and intersects each set of the form $\tau ″x,x\in X$. In this case put

$$\tau \left[G\right]=\left\{⟨x,y⟩\in X\times Y:\right(\tau ″⟨x,y⟩)\cap G\ne ⌀\},$$

so that $\tau \left[G\right]\in Y^X$ and $\tau \left[G\right]\left(x\right)=y⟺\tau ″⟨x,y⟩\cap G\ne ⌀$. If $\phi$ is a formula in which some names $\tau \in {\mathbf{N}}_Y^X$ occur (for various sets $X,Y$), and a set $G\subseteq {\mathbf{P}}^{*}$ is minimally $\tau$-generic for any name $\tau$ in $\phi$, then accordingly $\phi \left[G\right]$ is theresult of substitution of $\tau \left[G\right]$ for each name $\tau$ in $\phi$.

Claim 1 (obvious).

Suppose that, in $\mathbf{L}$, $X,Y$ are any sets, $p\in K\subseteq {\mathbf{P}}^{*}$ and $\tau \in {\mathbf{N}}_Y^X\left(K\right)$ is $K$-full (resp., $K$-full below p). Then, any set $G\subseteq K$, $K$-generic over $\mathbf{L}$ (resp., $K$-generic over $\mathbf{L}$ and containing p), is minimally $\tau$-generic.

Definition 11 (equivalent names).

Names $\tau ,\mu \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbf{P}}^{*}\right)$ are called equivalent iff conditions $q,r$ are incompatiblewhenever $q\in \tau ″⟨m,j⟩$ and $r\in \mu ″⟨m,k⟩$ for some m and $j\ne k$. (Recall that $\tau ″⟨m,k⟩=\{p:⟨p,⟨m,k⟩⟩\in \tau \}$.) Similarly, names $\tau ,\mu$ are equivalent below some $p\in {\mathbf{P}}^{*}$ iff the triple ofconditions $p,q,r$ is incompatible (that is, $p\wedge q\wedge r$ is not ≤ than at least one of $p,q,r$) whenever $q\in \tau ″⟨m,j⟩$ and $r\in \mu ″⟨m,k⟩$ for some m and $j\ne k$.

Claim 2 (obvious).

Suppose that, in $\mathbf{L}$, $p\in K\subseteq {\mathbf{P}}^{*}$, and names $\mu ,\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(K\right)$ are equivalent (resp., equivalent below p). Then, for any $G\subseteq K$ both minimally $\mu$-generic and minimally $\tau$-generic (resp., and containing p), $\mu \left[G\right]=\tau \left[G\right]$.

Lemma 10.

Suppose that, in $\mathbf{L}$, U is a system, $K\subseteq \mathbf{P}\left[U\right]$ is a regular subforcing, $p_0\in K$, $A\subseteq P=\{p\in K:p\le p_0\}$ is a countable antichain, and, for any $p\in A$, ${\tau }_p\in {\mathbf{SN}}_{\omega }^{\omega }\left(K\right)$ is a name $K$-full below $p_0$. Then there is a $K$-full name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(K\right)$, equivalent to ${\tau }_p$ below p for any $p\in A$.

Proof. 

Let B be a maximal (countable) antichain in the set of all conditions $q\in K$ incompatible with $p_0$. Then $A\cup B$ is a countable maximal antichain in K. We let $\tau$ consist of: (1) all triples $⟨r\wedge q,⟨k,m⟩⟩$, such that $q\in A$ and $⟨r,⟨k,m⟩⟩\in {\tau }_q$, and (2) all triples $⟨q,⟨k,0⟩⟩$, such that $q\in B$ and $m\in \omega$. □

3.6. Names and Sets in Generic Extensions

For any forcing P, let ${\left|\right|--}_P$ denote the $P$-forcing relation over $\mathbf{L}$ as the ground model.

Theorem 5.

Suppose that U is a system and $K\subseteq \mathbf{P}\left[U\right]$ a regular subforcing in $\mathbf{L}$. Let $G\subseteq K$ be a set $K$-generic over $\mathbf{L}$. Then:

(i)

if $p\in K$ and φ is a closed formula with $K$-names as parameters, then

$$p{\left|\right|--}_K\phi iffp{\left|\right|--}_{\mathbf{P}\left[U\right]}“\mathbf{L}[\underline{G}\cap \breve{K}]\vDash \phi \left[\underline{G}\right]”;$$

(ii)

if $X,Y$ are countable sets in $\mathbf{L}$, and $f\in \mathbf{L}\left[G\right],f:X\to Y$, then there is a $K$-full name $\tau \in {\mathbf{SN}}_Y^X\left(K\right)$ in $\mathbf{L}$ such that $f=\tau \left[G\right]$.

(iii)

if $X\in \mathbf{L},y\in \mathbf{L}\left[G\right],y\subseteq X$, then there is a name $\tau \in {\mathbf{N}}_X\left(K\right)$ in $\mathbf{L}$ such that $y=\tau \left[G\right]$, and in addition if X is countable in $\mathbf{L}$ then $\tau \in {\mathbf{SN}}_X\left(K\right)$.

(iv)

if $X,Y$ are countable sets in $\mathbf{L}$, $p\in K$, $\phi \left(f\right)$ is a formula with $K$-names as parameters, and $p{\left|\right|--}_K\exists f\in Y^X\phi \left(f\right)$, then there is a $K$-full name $\tau \in {\mathbf{SN}}_Y^X\left(K\right)$ in $\mathbf{L}$ such that $p{\left|\right|--}_K\phi \left(\tau \right)$.

Proof. 

(i) Suppose $p{\left|\right|--}_K\phi$. To prove $p{\left|\right|--}_{\mathbf{P}\left[U\right]}“\mathbf{L}[\underline{G}\cap \breve{K}]\vDash \phi \left[\underline{G}\right]”$, consider a set $G\subseteq \mathbf{P}\left[U\right]$, $\mathbf{P}\left[U\right]$-generic over $\mathbf{L}$. Then $G\cap K$ is $K$-generic over $\mathbf{L}$ by Lemma 8, hence $\phi \left[G\right]$ is true in $\mathbf{L}[G\cap K]$, as required. Conversely assume $\neg p{\left|\right|--}_K\phi$. There is a condition $q\in K,q\le p$, $q{\left|\right|--}_k\neg \phi$. Then $q{\left|\right|--}_{\mathbf{P}\left[U\right]}“\mathbf{L}[\underline{G}\cap \breve{K}]\vDash \neg \phi \left[\underline{G}\right]”$ by the above, thus $p{\left|\right|--}_{\mathbf{P}\left[U\right]}“\mathbf{L}[\underline{G}\cap K]\vDash \phi \left[\underline{G}\right]”$ fails.

(ii) It follows from general forcing theory that there is a $K$-full name $\sigma \in {\mathbf{N}}_Y^X\left(K\right)$, not necessarily countable, such that $f=\sigma \left[G\right]$. Then all sets $Q_x=\sigma ″x,x\in X$, are pre-dense in K. Put $\tau =\{⟨p,⟨x,y⟩⟩\in \sigma :x\in X\wedge y\in Y\wedge p\in A_x\},$ where $A_x\subseteq Q_x$ is a maximal (countable, by Theorem 4) antichain for any x.

(iv) We conclude from (ii) that the set Q of all conditions $q\in K,q\le p$, such that $q{\left|\right|--}_K\phi \left(\tau \right)$ for some name $\tau ={\tau }_q\in {\mathbf{SN}}_Y^X\left(K\right)$, is dense in K below p. Let $A\subseteq Q$ be a maximal antichain in Q; A is countable and pre-dense in K below p. Apply Lemma 10 to get a name $\tau$ as required. □

Example 4.

Consider the regular forcing $K=\mathbf{P}\left[U\upharpoonright c\right]$, where U is a system and $c\subseteq \mathcal{I}$ in $\mathbf{L}$. If $G\subseteq \mathbf{P}\left[U\right]$ is $\mathbf{P}\left[U\right]$-generic over $\mathbf{L}$ then the restricted set $G\upharpoonright c=G\cap \left(\mathbf{P}\right[U\upharpoonright c\left]\right)$ is $\mathbf{P}\left[U\upharpoonright c\right]$-generic over $\mathbf{L}$, by Lemma 9 (with $K=\mathbf{P}\left[U\upharpoonright c\right]$). Furthermore, it follows from Lemma 9 and Theorem 5 that if $\nu \in \mathcal{I}$ then $S_G\left(\nu \right)\in \mathbf{L}\left[G\upharpoonright c\right]$ iff $\nu \in c$, so that $\mathbf{L}\left[G\upharpoonright c\right]=\mathbf{L}\left[{\left\{S_G\left(\nu \right)\right\}}_{\nu \in c}\right]$.

Example 5.

Consider the regular forcing K defined in Example 2 in Section 3.2. Suppose that U is a system in $\mathbf{L}$ and $G\subseteq \mathbf{P}\left[U\right]$ is a set $\mathbf{P}\left[U\right]$-generic over $\mathbf{L}$. Then $K\left[U\right]=K\cap \mathbf{P}\left[U\right]$ is a regular subforcing of $\mathbf{P}\left[U\right]$ by Lemma 7. We conclude that $G^{\prime }=G\cap K$ is a set $K\left[U\right]$-generic over $\mathbf{L}$, by Lemma 9.

It follows by the definition of K that the set $|G^{\prime }|={\bigcup }_{p\in G^{\prime }}\left|p\right|$ satisfies $|G^{\prime }|\subseteq \omega$, contains 0, and if $\nu \ge 1$ then $\nu \in |G^{\prime }|$ iff ${\mathrm{s}}_{\nu }\in S_G\left(0\right)$. Therefore, by Lemma 9 and Theorem 5, the sets $G\left(0\right)$ and $S_G\left(0\right)$ belong to $\mathbf{L}\left[G^{\prime }\right]$, and if $1\le \nu <\omega$ then $S_G\left(\nu \right)\in \mathbf{L}\left[G^{\prime }\right]$ iff ${\mathrm{s}}_{\nu }\in S_G\left(0\right)$. Thus

$$\mathbf{L}\left[G^{\prime }\right]=\mathbf{L}[S_G\left(0\right),{\left\{S_G\left(\nu \right)\right\}}_{{\mathrm{s}}_{\nu }\in S_G\left(0\right)}]=\mathbf{L}\left[G^{\prime }\right]=\mathbf{L}\left[G\upharpoonright c\right],$$

where $c=|G^{\prime }|=\left\{0\right\}\cup \{\nu <\omega :{\mathrm{s}}_{\nu }\in S_G\left(0\right)\}\notin \mathbf{L}$.

3.7. Transformations Related to Product Forcing

There are three important families of transformations of the whole system of objects related to product forcing. Two of them are considered in this Subsection.

Family 1: permutations. If $c,c^{\prime }\subseteq \mathcal{I}$ are sets of equal cardinality then let ${\mathrm{BIJ}}_{c^{\prime }}^c$ be the set of all bijections $\pi :c\stackrel{\mathrm{onto}}{⟶}{c}^{\prime }$. Let $\left|\pi \right|=\{\nu \in c:\pi \left(\nu \right)\ne \nu \}\cup \{\nu \in c^{\prime }:{\pi }^{-1}\left(\nu \right)\ne \nu \}$, so that $\pi$ is essentially a bijection $c\cap \left|\pi \right|\stackrel{\mathrm{onto}}{⟶}{c}^{\prime }\cap \left|\pi \right|$, equal to the identity on $c\setminus \left|\pi \right|=c^{\prime }\setminus \left|\pi \right|$. Define the action of any $\pi \in {\mathrm{BIJ}}_{c^{\prime }}^c$ onto:

–

sets $e\subseteq c$: $\pi ·e:=\{\pi \left(\nu \right):\nu \in e\}$ — then $\pi ·e\subseteq c^{\prime }$ and $\pi ·c=c^{\prime }$;

–

systems U with $\left|U\right|\subseteq c$: $\left(\pi ·U\right)\left(\pi \right(\nu \left)\right):=U\left(\nu \right)$ for all $\nu \in \left|U\right|$ — then $\left|\pi ·U\right|=\pi ·\left|U\right|\subseteq c^{\prime }$;

–

conditions $p\in {\mathbf{P}}^{*}$ with $\left|p\right|\subseteq c$: $\left(\pi ·p\right)\left(\pi \right(\nu \left)\right):=p\left(\nu \right)$ for all $\nu \in \left|p\right|$;

–

sets $G\subseteq {\mathbf{P}}^{*}\upharpoonright c$: $\pi ·G:=\{\pi ·p:p\in G\}$ — then $\pi ·G\subseteq {\mathbf{P}}^{*}\upharpoonright c^{\prime }$, in particular, $\pi ·K=\{\pi ·p:p\in K\}\subseteq {\mathbf{P}}^{*}\upharpoonright c^{\prime }$ for any regular subforcing $K\subseteq {\mathbf{P}}^{*}\upharpoonright c$;

–

names $\tau \in {\mathbf{N}}_Y^X\left({\mathbf{P}}^{*}\upharpoonright c\right)$: $\pi ·\tau :=\{⟨\pi ·p,⟨\ell ,k⟩⟩:⟨p,⟨\ell ,k⟩⟩\in \tau \}$ — then $\pi ·\tau \in {\mathbf{N}}_Y^X\left({\mathbf{P}}^{*}\upharpoonright c^{\prime }\right);$

Lemma 11.

If $c,c^{\prime }\subseteq \mathcal{I}$ are sets of equal cardinality and $\pi \in {\mathrm{BIJ}}_{c^{\prime }}^c$ then $p⟼\pi ·p$ is an order preserving bijection of ${\mathbf{P}}^{*}\upharpoonright c$ onto ${\mathbf{P}}^{*}\upharpoonright c^{\prime }$, and if U is a system and $\left|U\right|\subseteq c$ then $\left|\pi ·U\right|\subseteq c^{\prime }$, and we have $p\in \mathbf{P}\left[U\right]⟺\pi ·p\in \mathbf{P}\left[\pi ·U\right]$.

Family 2: Lipschitz transformations. Let ${\mathbf{Lip}}^{\mathcal{I}}$ be the $\mathcal{I}$-product of the group $\mathbf{Lip}$ (see Section 2.3), with countable support; this will be our second family of transformations. Thus a typical element $\mathit{\alpha }\in {\mathbf{Lip}}^{\mathcal{I}}$ is $\mathit{\alpha }={\left\{{\alpha }_{\nu }\right\}}_{\nu \in \left|\mathit{\alpha }\right|}$, where $\left|\mathit{\alpha }\right|=\mathtt{dom}\mathit{\alpha }\subseteq \mathcal{I}$ is at most countable, and ${\alpha }_{\nu }\in \mathbf{Lip},\forall \nu$. We will routinely identify each $\mathit{\alpha }\in {\mathbf{Lip}}^{\mathcal{I}}$ with its extension on $\mathcal{I}$ defined so that ${\alpha }_{\nu }$ is the identity map (on $\mathbf{Seq}$) for all $\nu \in \mathcal{I}\setminus \left|\mathit{\alpha }\right|$. Keeping this identification in mind, define the action of any $\mathit{\alpha }\in {\mathbf{Lip}}^{\mathcal{I}}$ on:

–

systems U: $\left|\mathit{\alpha }·U\right|:=\left|U\right|$ and $\left(\mathit{\alpha }·U\right)\left(\nu \right):={\alpha }_{\nu }·U\left(\nu \right)$;

–

conditions $p\in {\mathbf{P}}^{*}$, by $\left|\mathit{\alpha }·p\right|=\left|p\right|$ and $\left(\mathit{\alpha }·p\right)\left(\nu \right)={\alpha }_{\nu }·p\left(\nu \right)$;

–

sets $G\subseteq {\mathbf{P}}^{*}$: $\mathit{\alpha }·G:=\{\mathit{\alpha }·p:p\in G\}$, in particular, $\mathit{\alpha }·K=\{\mathit{\alpha }·p:p\in K\}$ for any regular subforcing $K\subseteq {\mathbf{P}}^{*}$;

–

names $\tau \in {\mathbf{N}}_Y^X$: $\mathit{\alpha }·\tau :=\{⟨\mathit{\alpha }·p,⟨n,k⟩⟩:⟨p,⟨n,k⟩⟩\in \tau \}$;

In the first two lines, we refer to the action of ${\alpha }_{\nu }\in \mathbf{Lip}$ on sets $u\subseteq \mathbf{Fun}$ and on forcing conditions, as defined in Section 2.3.

Lemma 12.

If $\mathit{\alpha }\in {\mathbf{Lip}}^{\mathcal{I}}$ then $p⟼\pi ·p$ is an order preserving bijection of ${\mathbf{P}}^{*}$ onto ${\mathbf{P}}^{*}$, and if U is a system then we have $p\in \mathbf{P}\left[U\right]⟺\mathit{\alpha }·p\in \mathbf{P}\left[\mathit{\alpha }·U\right]$.

Corollary 2 (of Lemma 5).

Suppose that $U,V$ are countable systems, $\left|U\right|=\left|V\right|$, and $p\in \mathbf{P}\left[U\right],q\in \mathbf{P}\left[V\right]$. Then there is a transformation $\mathit{\alpha }\in {\mathbf{Lip}}^{\mathcal{I}}$ such that

(i)

$\left|\mathit{\alpha }\right|=\left|U\right|=\left|V\right|$, $\mathit{\alpha }·U=V$, and

(ii)

there are conditions $p^{\prime }\in \mathbf{P}\left[U\right],p^{\prime }\le p$ and $q^{\prime }\in \mathbf{P}\left[V\right],q^{\prime }\le q$ such that $\alpha ·p^{\prime }=q^{\prime }$—in particular, conditions $\mathit{\alpha }·p$ and q are compatible in $\mathbf{P}\left[V\right]$.

Proof. 

Apply Lemma 5 componentwise for every $\nu \in \left|U\right|=|U^{\prime }|$. □

3.8. Substitutions and Homogeneous Extensions

Assume that conditions $p,q\in {\mathbf{P}}^{*}$ satisfy (2) of Section 2.4 for all $\nu$, that is:

$$\left|p\right|=\left|q\right|,\mathrm{and}{S}_p\left(\nu \right)\cup S_q\left(\nu \right)\subseteq F_p^{\vee }\left(\nu \right)=F_q^{\vee }\left(\nu \right)\mathrm{for}\mathrm{all}\nu \in \left|p\right|=\left|q\right|.$$

(3)

Definition 12.

If (3) holds and $p^{\prime }\in {\mathbf{P}}^{*}$, $p^{\prime }\le p$, then define $q^{\prime }=H_q^p\left(p^{\prime }\right)$ so that $|q^{\prime }|=|p^{\prime }|$, $q^{\prime }\left(\nu \right)=p^{\prime }\left(\nu \right)$ whenever $\nu \in |p^{\prime }|\setminus |p|$, but $q^{\prime }\left(\nu \right)=H_{q\left(\nu \right)}^{p\left(\nu \right)}\left(p^{\prime }\left(\nu \right)\right)$ for all $\nu \in \left|p\right|$, where $H_{q\left(\nu \right)}^{p\left(\nu \right)}$ is defined as in Section 2.4. This is Family 3 of transformations, called substitutions.

Theorem 6.

If U is a system, and conditions $p,q\in \mathbf{P}\left[U\right]$ satisfy (3) above, then

$$H_q^p:P=\{p^{\prime }\in \mathbf{P}\left[U\right]:p^{\prime }\le p\}\stackrel{\mathrm{onto}}{⟶}Q=\{q^{\prime }\in \mathbf{P}\left[U\right]:q^{\prime }\le q\}$$

is an order isomorphism.

Proof. 

Apply Lemma 6 componentwise. □

Suppose that $U,p,q\in \mathbf{P}\left[U\right],H_q^p$ are as in Theorem 6. Extend the action of $H_q^p$ onto names and formulas. Recall that a name $\tau \in {\mathbf{N}}_Y^X$ is below p iff $p^{\prime }\le p$ holds for any triple $⟨p^{\prime },⟨n,k⟩⟩\in \tau$.

• If $X,Y$ are any sets and $\tau \in {\mathbf{N}}_Y^X$ is a name below p then put $H_q^p\left(\tau \right)=\{⟨H_q^p\left(p^{\prime }\right),⟨n,k⟩⟩:⟨p^{\prime },⟨n,k⟩⟩\in \tau \}$, so $H_q^p\left(\tau \right)\in {\mathbf{N}}_Y^X$ is a name below q.
• If $\phi$ is a formula with names below p as parameters then $H_q^p\left(\phi \right)$ denotes the result of substitution of $H_q^p\left(\tau \right)$ for any name $\tau$ in $\phi$.

Forcing notions of the form $\mathbf{P}\left[U\right]$ are quite homogeneous by Theorem 6. The next result is a usual product forcing application of such a homogeneity.

Theorem 7.

Suppose that, in $\mathbf{L}$, U is a system, $d\subseteq c\subseteq \mathcal{I}$, K is a regular subforcing of $\mathbf{P}\left[U\upharpoonright d\right]$, and $Q=\{p\in \mathbf{P}\left[U\upharpoonright c\right]:p\upharpoonright d\in K\}=K\times \mathbf{P}\left[U\upharpoonright \right(c\setminus d\left)\right]$. Let φ be a formula which contains as parameters: $(*)$ $K$-names, and $(†)$ names of the form $\underline{G}\upharpoonright e$, where $e\in \mathbf{L}$, $e\subseteq c$, and $\underline{G}\upharpoonright e$ enters φ only via $\mathbf{L}\left[\underline{G}\upharpoonright e\right]$. Then:

(i)

if $p\in Q$ and $p{\left|\right|--}_Q\phi$ then $p\upharpoonright d{\left|\right|--}_Q\phi ;$

(ii)

in particular, for $d=⌀$ (and $Q=\mathbf{P}\left[U\upharpoonright c\right]$), Q decides any formula Φ which contains only names for sets in $\mathbf{L}$ and names $\underline{G}\upharpoonright e$ via $\mathbf{L}\left[\underline{G}\upharpoonright e\right]$ of the form $(†)$ with $e\subseteq c$, as parameters;

(iii)

if $p\in Q$ and $p{\left|\right|--}_Q\exists x\in \mathbf{L}\left[\underline{G}\upharpoonright c\right]\phi \left(x\right)$ then $p\upharpoonright d{\left|\right|--}_Q\exists x\in \mathbf{L}\left[\underline{G}\upharpoonright c\right]\phi \left(x\right)$.

Proof. 

(i) Otherwise there are conditions $p,q\in Q$ with $p\upharpoonright d=q\upharpoonright d$, $p{\left|\right|--}_Q\phi$, but $q{\left|\right|--}_Q\neg \phi$. We can w.l.o.g. assume that $p,q$ satisfy (3) above (otherwise extend $p,q$ appropriately). Define $P,Q,H_q^p$ as in Definition 12 and Theorem 6.

Let $G\subseteq Q$ be a generic set containing p. Assuming w.l.o.g. that $G\subseteq P$, the set $H=\{H_q^p\left(p^{\prime }\right):p^{\prime }\in G\}\subseteq Q$ will be generic as well by Theorem 6, and $q\in H$. Therefore $\phi \left[G\right]$ is true in $\mathbf{L}\left[G\right]$ but $\phi \left[H\right]$ is false in $\mathbf{L}\left[H\right]$. Yet $\mathbf{L}\left[G\right]=\mathbf{L}\left[H\right]$ since $H_q^p\in \mathbf{L}$. Moreover $\phi \left[G\right]$ coincides with $\phi \left[H\right]$ since (1) $H_q^p$ is the identity on d (indeed $p\upharpoonright d=q\upharpoonright d$), and (2) if $e\in \mathbf{L},e\subseteq c$, then $\mathbf{L}\left[G\upharpoonright e\right]=\mathbf{L}\left[H\upharpoonright e\right]$ since $G\upharpoonright e,H\upharpoonright e$ can be obtained from each other via maps coded in $\mathbf{L}$. This is a contradiction.

(iii) This is a particular case. □

Corollary 3.

Under the assumptions of Theorem 7, suppose that $X,Y$ are arbitrary sets in $\mathbf{L}$, $p\in Q$, and $p{\left|\right|--}_Q\exists f\in \mathbf{L}[\underline{G}\cap K](f\in Y^X\wedge \phi \left(f\right))$. Then there is a $K$-full name $\tau \in {\mathbf{SN}}_Y^X\left(K\right)$ such that $p\upharpoonright d{\left|\right|--}_Q\phi \left(\tau \right)$.

Proof. 

We can assume that $\left|p\right|\subseteq d$ by Theorem 7(iii), thus $p=p\upharpoonright d\in K$. It follows from Theorems 5(ii) and 7(i) that there exist: a (countable) antichain $A\subseteq K$ maximal below p, and, for any $q\in A$, a $K$-full name ${\tau }_q\in {\mathbf{SN}}_Y^X\left(K\right)$ such that $q{\left|\right|--}_Q\phi \left({\tau }_q\right)$. Now compose a $K$-full name $\tau \in {\mathbf{SN}}_Y^X\left(K\right)$, such that every $q\in A$ forces $\tau ={\tau }_q$, as in the proof of Theorem 5(iv). □

4. Basic Forcing Notion and Basic Generic Extension

The proofs of Theorems 1–3, that follow in Section 7, Section 8 and Section 9, will have something in common. Namely the generic extensions we employ to get the results required will be parts of a basic extension, introduced and studied in this section. To define the extension, we’ll define (in $\mathbf{L}$ as the ground universe) an increasing sequence ${\left\{⟨M_{\xi },U_{\xi }⟩\right\}}_{\xi <{\omega }_1}$ of pairs of certain type—a Jensen–Solovay sequence, since this construction goes back to [9]—and make use of a forcing notion of the form $\mathbf{P}\left[U\right]$, where $U={\bigvee }_{\xi <{\omega }_1}{U}_{\xi }$. It turns out that if such a sequence is $n$-complete, in sense that it meets all sets of n-complexity within the whole tree of possible constructions, then the truth of analytic formulas up to level n in corresponding generic extensions has a remarkable connection with the forcing approximations studied in Section 5. This will allow us to convert the homogeneity of the construction of Jensen–Solovay sequences into a uniformity of the corresponding generic extensions, expressed by Theorem 13.

Recall that $\mathbf{V}=\mathbf{L}$ assumed in the ground universe by Assumption 1.

4.1. Jensen–Solovay Sequences

If $U\preccurlyeq V$ are systems then by definition $\mathbf{P}\left[U\right]\subseteq \mathbf{P}\left[V\right]$ holds. However this is not necessarily a suitably good notion. For instance a dense set $X\subseteq \mathbf{P}\left[U\right]$ may not be pre-dense in $\mathbf{P}\left[V\right]$, thus if $G\subseteq \mathbf{P}\left[V\right]$ is a generic set then the “projection” $G\cap \mathbf{P}\left[U\right]$ is not necessarily $\mathbf{P}\left[U\right]$-generic. Yet there is a special type of extension of systems, introduced by Jensen and Solovay [9], which preserves the density. This method is based on the requirement that the functions in $\mathbf{Fun}$ that occur in V but not in U must be generic over a certain model that contains U.

Recall that ${\mathbf{ZFC}}^{-}$ is $\mathbf{ZFC}$ minus the Power Set axiom, see Section 5.1 below. Let ${\mathbf{ZFC}}_1^{-}$ be ${\mathbf{ZFC}}^{-}$ plus the axioms $\mathbf{V}=\mathbf{L}$ and “every set is at most countable”.

Definition 13.

Let $U,U^{\prime }$ be a pair of systems. Suppose that M is any transitive model of ${\mathbf{ZFC}}^{-}$. Define $U{\preccurlyeq }_M{U}^{\prime }$ iff $U\preccurlyeq U^{\prime }$ and we have:

(a) 

the set $\mathsf{\Delta }(U,U^{\prime })={\bigcup }_{\nu \in \left|U\right|}(U^{\prime }\left(\nu \right)\setminus U\left(\nu \right))$ (note the union over $\left|U\right|$ rather than $|U^{\prime }|$!) is multiply Cohen generic over M, in the sense that every string $⟨f_1,\dots f_m⟩$ of pairwise different functions $f_{\ell }\in \mathsf{\Delta }(U,U^{\prime })$ is Cohen generic over M, and

(b) 

if $\nu \in \left|U\right|$ and $U^{\prime }\left(\nu \right)\setminus U\left(\nu \right)\ne ⌀$ then $U^{\prime }\left(\nu \right)\setminus U\left(\nu \right)$ is dense in $\mathbf{Fun}={\omega }^{\omega }$.

Let $\mathbf{JS}$, Jensen–Solovay pairs, be the set of all pairs $⟨M,U⟩$ of a transitive model $M\vDash {\mathbf{ZFC}}^{-}$ and a disjoint ($\nu \ne {\nu }^{\prime }⟹U\left(\nu \right)\cap U\left({\nu }^{\prime }\right)=⌀$) system $U\in M$. Let $\mathbf{sJS}$, small pairs, consist of all $⟨M,U⟩\in \mathbf{JS}$ such that $M\vDash {\mathbf{ZFC}}_1^{-}$ and M (then U as well) is countable. Define the extension relations:

$⟨M,U⟩\preccurlyeq ⟨M^{\prime },U^{\prime }⟩$ 

iff $M\subseteq M^{\prime }$ and $U{\preccurlyeq }_M{U}^{\prime }$;

$⟨M,U⟩\prec ⟨M^{\prime },U^{\prime }⟩$ 

iff $⟨M,U⟩\preccurlyeq ⟨M^{\prime },U^{\prime }⟩$ and $\forall \nu \in \left|U\right|(U\left(\nu \right)⫋U^{\prime }\left(\nu \right))$.

It would be a vital simplification to get rid of M as an explicit element of the construction, e.g., by setting $U{\preccurlyeq }^{*}{U}^{\prime }$ iff $U\preccurlyeq U^{\prime }$ and there is a CTM M containing U and such that $U{\preccurlyeq }_M{U}^{\prime }$.

Lemma 13.

Suppose that pairs $⟨M,U⟩\preccurlyeq ⟨M^{\prime },U^{\prime }⟩\preccurlyeq ⟨M^{″},U^{″}⟩$ belong to $\mathbf{JS}$. Then $⟨M,U⟩\preccurlyeq ⟨M^{″},U^{″}⟩$. Thus ≼ is a partial order on $\mathbf{JS}$.

Proof. 

Prove that the set $F={\bigcup }_{\nu \in \left|U\right|}(U^{″}\left(\nu \right)\setminus U\left(\nu \right))$ is multiply Cohen generic over M. Consider a simple case when $f\in U^{\prime }\left(\nu \right)\setminus U\left(\nu \right)$ and $g\in U^{″}\left(\mu \right)\setminus U^{\prime }\left(\mu \right)$, where $\nu ,\mu \in \left|U\right|$, and prove that $⟨f,g⟩$ is Cohen generic over M. (The general case does not differ much.) By definition, f is Cohen generic over M and g is Cohen generic over $M^{\prime }$. Therefore, g is Cohen generic over $M\left[f\right]$, which satisfies $M\left[f\right]\subseteq M^{\prime }$ since $f\in M^{\prime }$. It remains to apply the product forcing theorem. □

Remark 1.

We routinely have $⟨M,U⟩\preccurlyeq ⟨M^{\prime },U⟩$ (the same U) provided $M\subseteq M^{\prime }$. On the other hand, $⟨M,U⟩\preccurlyeq ⟨M,U^{\prime }⟩$ (with the same M) is possible only in the case when $\mathsf{\Delta }(U,U^{\prime })=⌀$, that is, $U\left(\nu \right)=U^{\prime }\left(\nu \right)$ for all $\nu \in \left|U\right|$. In particular, if $⟨M,U⟩\in \mathbf{JS},c\in M,c\subseteq \left|U\right|$, then $⟨M,U\upharpoonright c⟩\preccurlyeq ⟨M,U⟩$.

Lemma 14 (extension).

If $⟨M,U⟩\in \mathbf{sJS}$ and $z\subseteq \mathcal{I}$ is countable, then there is a pair $⟨M^{\prime },U^{\prime }⟩\in \mathbf{sJS}$ such that $⟨M,U⟩\prec ⟨M^{\prime },U^{\prime }⟩$ and $z\subseteq |U^{\prime }|$.

Proof. 

Let $d=\left|U\right|\cup z$, and let $\overrightarrow{f}={\left\{f_{\nu k}\right\}}_{\nu \in d,k<\omega }\in {\left(\mathbf{Fun}\right)}^{d\times \omega }$ be Cohen generic over M. Now define $U^{\prime }\left(\nu \right)=U\left(\nu \right)\cup \{f_{\nu k}:k\in \omega \}$ for each $\nu \in d$, and let $M^{\prime }\vDash {\mathbf{ZFC}}_1^{-}$ be any CTM satisfying $M\subseteq M^{\prime }$ and containing $U^{\prime }$. □

Definition 14.

A Jensen–Solovay sequence of length $\lambda \le {\omega }_1$ is any strictly $\prec$-increasing $\lambda$-sequence ${\left\{⟨M_{\xi },U_{\xi }⟩\right\}}_{\xi <\lambda }$ of pairs $⟨M_{\xi },U_{\xi }⟩\in \mathbf{sJS}$, which satisfies $U_{\eta }={\bigvee }_{\xi <\eta }{U}_{\xi }$ on limit steps. Let ${\overrightarrow{\mathbf{JS}}}_{\lambda }$ be the set of all such sequences.

Lemma 15.

Suppose that $\lambda \le {\omega }_1$ is a limit ordinal, and ${\left\{⟨M_{\xi },U_{\xi }⟩\right\}}_{\xi <\mathit{\lambda }}$ belongs to ${\overrightarrow{\mathbf{JS}}}_{\lambda }$. Put $U={\bigvee }_{\xi <\lambda }{U}_{\xi }$, that is, $U\left(\nu \right)={\bigcup }_{\xi <\lambda }{U}_{\xi }\left(\nu \right)$ for all $\nu \in \mathcal{I}$.

Then $U_{\xi }{\preccurlyeq }_{M_{\xi }}U$ for every ξ.

If, moreover, $\lambda <{\omega }_1$ and M is a CTM of ${\mathbf{ZFC}}_1^{-}$ containing ${\left\{⟨M_{\xi },U_{\xi }⟩\right\}}_{\xi <\lambda }$ then $⟨M,U⟩\in \mathbf{sJS}$ and $⟨M_{\xi },U_{\xi }⟩\prec ⟨M,U⟩$ for every ξ.

Proof. 

The same idea as in the proof of Lemma 13. □

4.2. Stability of Dense Sets

Assume that $⟨M,U⟩\in \mathbf{sJS}$ and D is a pre-dense subset of $\mathbf{P}\left[U\right]$ (say, a maximal antichain). If $U^{\prime }$ is another system satisfying $U{\preccurlyeq }_{}{U}^{\prime }$, then it may well happen that D is not maximal in $\mathbf{P}\left[U^{\prime }\right]$. The role of the multiple genericity requirement (a) in Definition 13, first discovered in [9], is to somehow seal the property of pre-density of sets already in M for any further extensions. This is the content of the following key theorem. The product forcing arguments allow us to extend the stability result to pre-dense sets not necessarily in M, as in items (ii), (iii) of the following theorem.

Theorem 8.

Assume that, in $\mathbf{L}$, $⟨M,U⟩\in \mathbf{sJS}$, $U^{\prime }$ is a disjoint system, and $U{\preccurlyeq }_M{U}^{\prime }$. If D is a pre-dense subset of $\mathbf{P}\left[U\right]$ (resp., pre-dense below some $p\in \mathbf{P}\left[U\right]$) then D remains pre-dense in $\mathbf{P}\left[U^{\prime }\right]$ (resp., pre-dense in $\mathbf{P}\left[U^{\prime }\right]$ below p) in each of the following three cases:

(i)

$D\in M;$

(ii)

$D\in M\left[G\right]$, where $G\subseteq Q$ is $Q$-generic over $\mathbf{L}$ and $Q\in M$ is a PO set;

(iii)

$D\in M\left[H\right]$, where $H\subseteq U^{\prime }\left({\nu }_0\right)$ is finite, ${\nu }_0\in \left|U\right|$ is fixed, and $D\subseteq \mathbf{P}\left[U{\upharpoonright }_{\ne {\nu }_0}\right]$.

Proof. 

We consider only the case of sets D pre-dense in $\mathbf{P}\left[U\right]$ itself; the case of pre-density below some $p\in \mathbf{P}\left[U\right]$ is treated similarly.

(i) Suppose, towards the contrary, that a condition $p\in \mathbf{P}\left[U^{\prime }\right]$ is incompatible with each $q\in D$. As $D\subseteq \mathbf{P}\left[U\right]$, we can w.l.o.g. assume that $\left|p\right|\subseteq \left|U\right|$.

Our plan is to define a condition $p^{\prime }\in \mathbf{P}\left[U\right]$, also incompatible with each $q\in D$, contrary to the pre-density. To maintain such a construction, consider the finite string $\overrightarrow{f}=⟨f_1,\dots ,f_m⟩$ of all elements $f\in \mathbf{Fun}$ occurring in ${\bigcup }_{\nu \in \left|p\right|}{F}_p\left(\nu \right)$ but not in U. It follows from $U{\preccurlyeq }_M{U}^{\prime }$ that $\overrightarrow{f}$ is Cohen-generic over M. Further analysis shows that p being incompatible with D is implied by the fact that $\overrightarrow{f}$ meets a certain M-countable family of Cohen-dense sets. Therefore, we can simulate this in M, getting a string $\overrightarrow{g}\in M$ which meets the same Cohen-dense sets, and hence yields a condition $p^{\prime }\in \mathbf{P}\left[U\right]$, also incompatible with each $q\in D$.

This argument was first carried out in [9] in full generality, where we address the reader. However, to present the key idea in sufficient detail in a somewhat simplified subcase, we assume that (1) $\left|p\right|=\left\{\nu \right\}$ is a singleton; $\nu \in \left|U\right|$. Then $p\left(\nu \right)=⟨S_p\left(\nu \right);F_p\left(\nu \right)⟩\in P\left[U^{\prime }\left(\nu \right)\right]$, where $S_p\left(\nu \right)\subseteq \mathbf{Seq}$ and $F_p\left(\nu \right)\subseteq U^{\prime }\left(\nu \right)$ are finite sets. The (finite) set $X=F_p\left(\nu \right)\setminus U\left(\nu \right)$ is multiply Cohen generic over M since $U{\preccurlyeq }_M{U}^{\prime }$. To make the argument even more transparent, we suppose that (2) $X=\{f,g\}$, where $f\ne g$ and the pair $⟨f,g⟩$ is Cohen generic over M. (The general case follows the same idea and can be found in [9]; we leave it to the reader.)

Thus $F_p\left(\nu \right)=F\cup \{f,g\}$, where $F=F_p\left(\nu \right)\cap U\left(\nu \right)\in M$ is by definition a finite set.

The plan is to replace the functions $f,g$ by some functions $f^{\prime },g^{\prime }\in U\left(\nu \right)$ so that the incompatibility of p with conditions in D will be preserved.

It holds by the choice of p and Lemma 1 that $D=D_1(f,g)\cup D_2$, where

$$\begin{array}{ccc}\hfill D_1(f,g)& =& \{q\in D:A_q\cap F_p^{\vee }\left(\nu \right)\ne ⌀\},\mathrm{where}{A}_q=S_q\left(\nu \right)\setminus S_p\left(\nu \right)\subseteq \mathbf{Seq};\hfill \\ \hfill D_2& =& \{q\in D:(S_p\left(\nu \right)\setminus S_q\left(\nu \right))\cap F_q^{\vee }\left(\nu \right)\ne ⌀\}\in M;\hfill \end{array}$$

and $D_1$ depends on $f,g$ via $F_p\left(\nu \right).$ (See Section 3.1 on notation.) The equality $D=D_1(f,g)\cup D_2\cup D_3$ can be rewritten as $\mathsf{\Delta }\subseteq D_1(f,g)$, where $\mathsf{\Delta }=D\setminus D_2\in M$. Further, $\mathsf{\Delta }\subseteq D_1(f,g)$ is equivalent to

(∗)

$\forall A\in \mathcal{A}(A\cap F_p^{\vee }\left(\nu \right)\ne ⌀)$, where $\mathcal{A}=\{A_q:q\in D\}\in M$,

and each $A_q=S_q\left(\nu \right)\setminus S_p\left(\nu \right)\subseteq \mathbf{Seq}$ is finite. Recall that $F_p\left(\nu \right)=F\cup \{f,g\}$, therefore $F_p^{\vee }\left(\nu \right)=Z\cup S(f,g)$, where $Z=\{h\upharpoonright m:m\ge 1\wedge h\in F\}\in M$ and $S(f,g)={\bigcup }_{m\ge 1}\{f\upharpoonright m,g\upharpoonright m\}$. Thus (∗) is equivalent to

(†)

$\forall A^{\prime }\in {\mathcal{A}}^{\prime }(A^{\prime }\cap S(f,g)\ne ⌀)$, where ${\mathcal{A}}^{\prime }=\{A_q\setminus Z:q\in D\}\in M$.

Note that each $A^{\prime }\in {\mathcal{A}}^{\prime }$ is a finite subset of $\mathbf{Seq}$, so we can reenumerate ${\mathcal{A}}^{\prime }=\{A_k^{\prime }:k<\omega \}$ in M and rewrite (†) as follows:

(‡)

$\forall k(A_k^{\prime }\cap S(f,g)\ne ⌀)$, where each $A_k^{\prime }\subseteq \mathbf{Seq}$ is finite.

As the pair $⟨f,g⟩$ is Cohen-generic, there is a number $m_0$ such that (‡) is forced over M by $⟨{\sigma }_0,{\tau }_0⟩$, where ${\sigma }_0=f\upharpoonright m_0$ and ${\tau }_0=g\upharpoonright m_0$. In other words, $A_k^{\prime }\cap S(f^{\prime },g^{\prime })\ne ⌀$ holds for all k whenever $⟨f^{\prime },g^{\prime }⟩$ is Cohen-generic over M and ${\sigma }_0\subset f^{\prime }$, ${\tau }_0\subset g^{\prime }$. It follows that for any k and strings $\sigma ,\tau \in \mathbf{Seq}$ extending resp. ${\sigma }_0,{\tau }_0$ there are strings ${\sigma }^{\prime },{\tau }^{\prime }\in \mathbf{Seq}$ extending resp. $\sigma ,\tau$, at least one of which extends one of $w\in A_k^{\prime }$. This allows us to define, in M, a pair of $f^{\prime },g^{\prime }\in \mathbf{Fun}$ such that ${\sigma }_0\subset f^{\prime }$, ${\tau }_0\subset g^{\prime }$, and for any k at least one of $f^{\prime },g^{\prime }$ extends one of $w\in A_k^{\prime }$. In other words, we have

$$\forall k(A_k^{\prime }\cap S(f^{\prime },g^{\prime })\ne ⌀)\mathrm{and}\forall A^{\prime }\in {\mathcal{A}}^{\prime }(A^{\prime }\cap S(f^{\prime },g^{\prime })\ne ⌀).$$

It follows that the condition $p^{\prime }$ defined by $|p^{\prime }|=\left\{\nu \right\}$, $S_{p^{\prime }}\left(\nu \right)=S_p\left(\nu \right)$, $F_{p^{\prime }}\left(\nu \right)=F\cup \{f^{\prime },g^{\prime }\}$, still satisfies $\forall A\in \mathcal{A}(A\cap F_{p^{\prime }}^{\vee }\left(\nu \right)\ne ⌀)$ (compare with (∗)), and further $D=D_1(f^{\prime },g^{\prime })\cup D_2\cup D_3$, therefore, $p^{\prime }$ is incompatible with each $q\in D$. Yet $p^{\prime }\in M$ since $f^{\prime },g^{\prime }\in M$, which contradicts the pre-density of D.

(ii) The above proof works with $M\left[G\right]$ instead of M since the set X as in the proof is multiple Cohen generic over $M\left[G\right]$ by the product forcing theorem.

(iii) Assuming w.l.o.g. that $H\subseteq U^{\prime }\left({\nu }_0\right)\setminus U\left({\nu }_0\right)$, we conclude that $M\left[H\right]$ is a Cohen generic extension of M. Following the above, let $\nu \in \left|U\right|,\nu \ne {\nu }_0$. By the definition of ≼ the set $F=F_p\left(\nu \right)\setminus U\left(\nu \right)$ is multiply Cohen generic not only over M but also over $M\left[H\right]$. This allows to carry out the same argument as above. □

Corollary 4.

(i) Assume that, in $\mathbf{L}$, $⟨M,U⟩\in \mathbf{sJS}$, and $⟨M,U⟩\preccurlyeq ⟨M^{\prime },U^{\prime }⟩\in \mathbf{JS}$. Let a set $G\subseteq \mathbf{P}\left[U^{\prime }\right]$ be $\mathbf{P}\left[U^{\prime }\right]$-generic over $M^{\prime }$. Then $G\cap \mathbf{P}\left[U\right]$ is $\mathbf{P}\left[U\right]$-generic over M.

(ii) If moreover, $K\in M$, $K\subseteq \mathbf{P}\left[U\right]$ is a regular subforcing, then $G\cap K$ is $K$-generic over M.

Proof. 

To prove (i), note that if a set $D\in M$, $D\subseteq \mathbf{Q}\left(U\right)$, is pre-dense in $\mathbf{Q}\left(U\right)$, then it is pre-dense in $\mathbf{Q}\left(U^{\prime }\right)$ by Theorem 8, and hence $G\cap D\ne ⌀$ by the genericity. To prove (ii), apply Lemma 8. □

The next corollary returns us to names, the material of Section 3.4 and Section 3.5.

Corollary 5 (of Theorem 8(i)).

In $\mathbf{L}$, suppose that $⟨M,U⟩\in \mathbf{sJS}$, $⟨M,U⟩\preccurlyeq ⟨M^{\prime },U^{\prime }⟩\in \mathbf{JS}$, and $X,Y$ belong to M. Assume that $\tau \in M\cap {\mathbf{SN}}_Y^X\left(\mathbf{P}\left[U\right]\right)$ is a $\mathbf{P}\left[U\right]$-full name. Then τ remains $\mathbf{P}\left[U^{\prime }\right]$-full. If moreover $p\in \mathbf{P}\left[U\right]$ and τ is $\mathbf{P}\left[U\right]$-full below p, then τ remains $\mathbf{P}\left[U^{\prime }\right]$-full below p.

4.3. Digression: Definability in $\mathrm{HC}$

The next subsection will contain a transfinite construction of a key forcing notion in $\mathbf{L}$ relativized to $\mathrm{HC}$. Recall that $\mathrm{HC}$ is the collection of all hereditarily countable sets. In particular, $\mathrm{HC}={\mathbf{L}}_{{\omega }_1}$ in $\mathbf{L}$. In matters of related definability classes, we refer to e.g., Part B, Chapter 5, Section 4 in [20], or Chapter 13 in [21], on the Lévy hierarchy of ∈-formulas and definability classes ${\Sigma }_n^X,{\Pi }_n^X,{\mathsf{\Delta }}_n^X$ for any set X, and especially on ${\Sigma }_n^{\mathrm{HC}},{\Pi }_n^{\mathrm{HC}},{\mathsf{\Delta }}_n^{\mathrm{HC}}$ for $X=\mathrm{HC}$ in Sections 8 and 9 in [22], or elsewhere. In particular,

• ${\Sigma }_n^{\mathrm{HC}}$ = all sets $X\subseteq \mathrm{HC}$, definable in $\mathrm{HC}$ by a parameter-free ${\Sigma }_n^{}$ formula.
• ${\Sigma }_n^{\mathrm{HC}}$ = all sets $X\subseteq \mathrm{HC}$ definable in $\mathrm{HC}$ by a ${\Sigma }_n^{}$ formula with sets in $\mathrm{HC}$ as parameters.

Something like ${\Sigma }_n^{\mathrm{HC}}\left(x\right),x\in \mathrm{HC}$, means that only x is admitted as a parameter, while ${\Sigma }_n^{\mathrm{HC}}\left(M\right)$, where $M\subseteq \mathrm{HC}$ is a transitive model, means that all $x\in M$ are admitted as parameters. Collections like ${\Pi }_n^{\mathrm{HC}},{\Pi }_n^{\mathrm{HC}}\left(x\right),{\Pi }_n^{\mathrm{HC}}\left(M\right)$ are defined similarly, and ${\mathsf{\Delta }}_n^{\mathrm{HC}}={\Sigma }_n^{\mathrm{HC}}\cap {\Pi }_n^{\mathrm{HC}}$, etc. The boldface classes are defined as follows: ${\Sigma }_n^{\mathrm{HC}}={\Sigma }_n^{\mathrm{HC}}\left(\mathrm{HC}\right),{\mathsf{\Pi }}_n^{\mathrm{HC}}={\Pi }_n^{\mathrm{HC}}\left(\mathrm{HC}\right),{\mathsf{\Delta }}_n^{\mathrm{HC}}={\mathsf{\Delta }}_n^{\mathrm{HC}}\left(\mathrm{HC}\right)$.

Remark 2.

It is known that the classes ${\Sigma }_n^{\mathrm{HC}},{\Pi }_n^{\mathrm{HC}},{\mathsf{\Delta }}_n^{\mathrm{HC}}$ are equal to resp. ${\Sigma }_{n+1}^1,{\Pi }_{n+1}^1,{\mathsf{\Delta }}_{n+1}^1$ for sets of reals, and the same for parameters and boldface classes. This well-known result was explicitly mentioned in [23] (Lemma on p. 281), a detailed proof see Lemma 25.25 in [21], or Theorem 9.1 in [22].

Remark 3.

Recall that ${<}_{\mathbf{L}}$ is the Gödel wellordering of $\mathbf{L}$, the constructible universe.

It is known that the restriction ${<}_{\mathbf{L}}\upharpoonright \mathrm{HC}$ is a ${\mathsf{\Delta }}_1^{\mathrm{HC}}$ relation, and if $n\ge 1$, $p\in {\omega }^{\omega }$ is any parameter, and $R(x,y,z,\dots )$ is a finitary ${\mathsf{\Delta }}_n^{\mathrm{HC}}\left(p\right)$ relation on $\mathrm{HC}$ then the relations $\exists x{<}_{\mathbf{L}}yR(x,y,z,\dots )$ and $\forall x{<}_{\mathbf{L}}yR(x,y,z,\dots )$ (with arguments $y,z,\dots$) are ${\mathsf{\Delta }}_n^{\mathrm{HC}}\left(p\right)$ as well.

4.4. Complete Sequences and the Basic Notion of Forcing

Say that a pair $⟨M,U⟩\in \mathbf{sJS}$ solves a set $D\subseteq \mathbf{sJS}$ iff either $⟨M,U⟩\in D$, or there is no pair $⟨M^{\prime },U^{\prime }⟩\in D$ extending $⟨M,U⟩$. Let $D^{\mathrm{solv}}$ be the set of all pairs $⟨M,U⟩\in \mathbf{sJS}$ which solve D.

Definition 15.

Let $n\ge 3$. A sequence ${\left\{⟨M_{\xi },U_{\xi }⟩\right\}}_{\xi <{\omega }_1}\in {\overrightarrow{\mathbf{JS}}}_{{\omega }_1}$ is $n$- complete iff itintersects every set of the form $D^{\mathrm{solv}}$, where $D\subseteq \mathbf{sJS}$ is ${\Sigma }_{n-2}^{\mathrm{HC}}$. (See Section 4.3 on definability classes in $\mathrm{HC}$.)

Let us prove the existence of complete sequences.

Theorem 9 (in L).

Let $n\ge 2$. There is a sequence ${\left\{⟨M_{\xi },U_{\xi }⟩\right\}}_{\xi <{\omega }_1}\in {\overrightarrow{\mathbf{JS}}}_{{\omega }_1}$ of class ${\mathsf{\Delta }}_{n-1}^{\mathrm{HC}}$, $n$-complete in case $n\ge 3$, and such that $\xi \in |U_{\xi +1}|$ for all ξ — hence the limit system $U={\bigvee }_{\xi <{\omega }_1}{U}_{\xi }$ satisfies $\left|U\right|=\mathcal{I}$.

Proof. 

Define pairs $⟨M_{\xi },U_{\xi }⟩,\xi <{\omega }_1$, by induction. Let $U_0$ be the null system with $|U_0|=⌀$, and $M_0$ be the least CTM of ${\mathbf{ZFC}}_1^{-}$. If $\lambda <{\omega }_1$ is limit then put $U_{\lambda }={\bigvee }_{\xi <\lambda }{U}_{\xi }$ and let $M_{\lambda }$ be the least CTM of ${\mathbf{ZFC}}_1^{-}$ containing the sequence ${\left\{⟨M_{\xi },U_{\xi }⟩\right\}}_{\xi <\lambda }$. If $⟨M_{\xi },U_{\xi }⟩\in \mathbf{sJS}$ is defined then by Lemma 14 there is a pair $⟨M^{\prime },U^{\prime }⟩\in \mathbf{sJS}$ with $⟨M_{\xi },U_{\xi }⟩\prec ⟨M^{\prime },U^{\prime }⟩$ and $\xi \in |U^{\prime }|$. Let $\mathsf{\Theta }\subseteq {\omega }_1\times \mathrm{HC}$ be a universal ${\Sigma }_{n-2}^{\mathrm{HC}}$ set, and $D_{\xi }=\{z\in \mathbf{sJS}:⟨\xi ,z⟩\in \mathsf{\Theta }\}$. Let $⟨M_{\xi +1},U_{\xi +1}⟩$ be the ${<}_{\mathbf{L}}$-least pair $⟨M,U⟩\in {D_{\xi }}^{\mathrm{solv}}$ satisfying $⟨M^{\prime },U^{\prime }⟩\preccurlyeq ⟨M,U⟩$. To check the definability property use the fact mentioned by Remark 3 in Section 4.3. □

Now define the basic forcing notion.

Definition 16 (in L).

Fix a number $𝕟\ge 2$. Let ${\left\{⟨{\mathbb{M}}_{\xi },{\mathbb{U}}_{\xi }⟩\right\}}_{\xi <{\omega }_1}\in {\overrightarrow{\mathbf{JS}}}_{{\omega }_1}$ be any $𝕟$-complete Jensen–Solovay sequenceof class ${\mathsf{\Delta }}_{𝕟-1}^{\mathrm{HC}}$ as in Theorem 9—in case $𝕟\ge 3$, or just any Jensen–Solovay sequence of class ${\mathsf{\Delta }}_1^{\mathrm{HC}}$—in case $𝕟=2$, and in both cases $\xi \in |{\mathbb{U}}_{\xi +1}|$ for every $\xi <{\omega }_1$, as in Theorem 9. Put $\mathbb{U}={\bigvee }_{\xi <{\omega }_1}{\mathbb{U}}_{\xi }$, so $\mathbb{U}$ is a system, $\left|\mathbb{U}\right|=\mathcal{I}={\omega }_1$, $\mathbb{U}\left(\nu \right)={\bigcup }_{\xi <{\omega }_1,\nu \in \left|{\mathbb{U}}_{\xi }\right|}{\mathbb{U}}_{\xi }\left(\nu \right)$ for all $\nu \in \mathcal{I}$. We finally define $\mathbb{P}=\mathbf{P}\left[\mathbb{U}\right]$ and ${\mathbb{P}}_{\gamma }=\mathbf{P}\left[{\mathbb{U}}_{\gamma }\right]$ for $\gamma <{\omega }_1$.

Thus $\mathbb{P}$ is the product of sets $\mathbb{P}\left(\nu \right)=P\left[\mathbb{U}\left(\nu \right)\right],\nu \in \mathcal{I}$, with finite support.

We proceed with a couple of simple lemmas.

Corollary 6.

Suppose that, in $\mathbf{L}$, M is a transitive model of ${\mathbf{ZFC}}^{-}$ containing the sequence ${\left\{⟨{\mathbb{M}}_{\xi },{\mathbb{U}}_{\xi }⟩\right\}}_{\xi <{\omega }_1}\in {\overrightarrow{\mathbf{JS}}}_{{\omega }_1}$ of Definition 16. Then, for every $\xi <{\omega }_1:$

(i)

$⟨M,\mathbb{U}⟩\in \mathbf{JS}$ and $⟨{\mathbb{M}}_{\xi },{\mathbb{U}}_{\xi }⟩\prec ⟨M,\mathbb{U}⟩;$

(ii)

if $\nu \in \mathcal{I}$ then $\mathbb{U}\left(\nu \right)$ is uncountable and topologically dense in ${\omega }^{\omega }$, and if $\nu \ne \mu$ belong to $\mathcal{I}$ then $\mathbb{U}\left(\nu \right)\cap \mathbb{U}\left(\mu \right)$ is empty;

(iii)

any set $D\in {\mathbb{M}}_{\xi },D\subseteq {\mathbb{P}}_{\xi }$, pre-dense in ${\mathbb{P}}_{\xi }$ (resp., pre-dense in ${\mathbb{P}}_{\xi }$ below some $p\in {\mathbb{P}}_{\xi }$), is pre-dense in $\mathbb{P}$ (resp., pre-dense in $\mathbb{P}$ below p);

(iv)

any name $\tau \in {\mathbb{M}}_{\xi }\cap {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbb{P}}_{\xi }\right)$, ${\mathbb{P}}_{\xi }$-full (resp., ${\mathbb{P}}_{\xi }$-full below some $p\in {\mathbb{P}}_{\xi }$), is $\mathbb{P}$-full (resp., $\mathbb{P}$-full below p);

(v)

if $G\subseteq \mathbb{P}$ is a set $\mathbb{P}$-generic over the ground universe $\mathbf{L}$ then the set $G^{\xi }=G\cap {\mathbb{P}}_{\xi }$ is ${\mathbb{P}}_{\xi }$-generic over ${\mathbb{M}}_{\xi }$.

Proof. 

To prove (i) use Lemma 15. Both claims of (ii) hold by Definition 13. To prove (iii) and (iv) use Corollary 5. Finally, (v) follows from (iii). □

Now let us address definability issues.

Lemma 16 (in L).

The binary relation $f\in \mathbb{U}\left(\nu \right)$ is ${\mathsf{\Delta }}_{𝕟-1}^{\mathrm{HC}}$.

The sets $\mathbb{P}$ and ${\mathbf{SN}}_{\omega }^{\omega }\left(\mathbb{P}\right)$ ($\mathbb{P}$-names for functions in $\mathbf{Fun}$) are ${\mathsf{\Delta }}_{𝕟-1}^{\mathrm{HC}}$.

The set of all $\mathbb{P}$-full names in ${\mathbf{SN}}_{\omega }^{\omega }\left(\mathbb{P}\right)$ is ${\mathsf{\Delta }}_{𝕟-1}^{\mathrm{HC}}$.

Proof. 

The sequence ${\left\{⟨{\mathbb{M}}_{\xi },{\mathbb{U}}_{\xi }⟩\right\}}_{\xi <{\omega }_1}$ is ${\mathsf{\Delta }}_{𝕟-1}^{\mathrm{HC}}$ by definition, hence the relation $f\in \mathbb{U}\left(\nu \right)$ is ${\Sigma }_{𝕟-1}^{\mathrm{HC}}$. On the other hand, if $f\in \mathbf{Fun}$ belongs to some ${\mathbb{M}}_{\xi }$ then $f\in \mathbb{U}\left(\nu \right)$ obviously implies $f\in {\mathbb{U}}_{\xi }\left(\nu \right)$, leading to a ${\Pi }_{𝕟-1}^{\mathrm{HC}}$ definition of the relation $f\in \mathbb{U}\left(\nu \right)$. To prove the last claim, note that by Corollary 5 if a name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left({\mathbb{P}}_{\xi }\right)\cap {\mathbb{M}}_{\xi }$ is ${\mathbb{P}}_{\xi }$-full then it remains $\mathbb{P}$-full. □

4.5. Basic Generic Extension and Regular Subextensions

Recall that an integer $𝕟\ge 2$ and sets ${\mathbb{U}}_{\xi },{\mathbb{M}}_{\xi },\mathbb{U},{\mathbb{P}}_{\xi },\mathbb{P}$ are fixed in $\mathbf{L}$ by Definition 16. These sets are fixed for the remainder.

Suppose that, in $\mathbf{L}$, $K\subseteq \mathbb{P}$ is a regular subforcing. If $G\subseteq \mathbb{P}$ is a set $\mathbb{P}$-generic over $\mathbf{L}$ then $G\cap K$ is $K$-generic over $\mathbf{L}$ by Lemma 9(vi), and hence $\mathbf{L}[G\cap K]$ is a $K$-generic extension of $\mathbf{L}$. The following formulas ${ℾ}_i$ ($i\in \mathcal{I}$) will give us a useful coding tool in extensions of this form:

$${ℾ}_{\nu }\left(S\right):{=}_{\mathrm{def}}\nu \in \mathcal{I}\wedge S\subseteq \mathbf{Seq}\wedge \forall f\in \mathbf{Fun}\cap \mathbf{L}(f\in \mathbb{U}\left(\nu \right)⟺\mathtt{max}\left(S/f\right)<\omega ).$$

This is based on the next two results. Recall that $\left|G\cap K\right|={\bigcup }_{p\in G\cap K}\left|p\right|$.

Lemma 17.

${ℾ}_{\nu }\left(S\right)$ as a binary relation belongs to ${\Pi }_{𝕟-1}^{\mathrm{HC}}$ in any cardinal-preserving generic extension of $\mathbf{L}$.

Proof. 

The set $W=\{⟨\nu ,f⟩:\nu \in \mathcal{I}\wedge f\in \mathbb{U}(\nu \left)\right\}$ is ${\mathsf{\Delta }}_{𝕟-1}^{\mathrm{HC}}$ in $\mathbf{L}$, by Lemma 16, and hence so is $W^{\prime }=\{⟨\nu ,f⟩:\nu \in \mathcal{I}\wedge f\in \mathbf{Fun}\setminus \mathbb{U}\left(\nu \right)\}$. Let $\phi (\nu ,f)$ and ${\phi }^{\prime }(\nu ,f)$ be ${\Sigma }_{𝕟-1}^{}$ formulas that define resp. W, $W^{\prime }$ in $\mathrm{HC}$, in $\mathbf{L}$. Then, in any generic extension of $\mathbf{L}$, ${ℾ}_{\nu }\left(S\right)$ is equivalent to $\nu \in \mathcal{I}\wedge S\subseteq \mathbf{Seq}\wedge \forall f\in \mathbf{Fun}\cap \mathbf{L}\mathbf{\Psi }(\nu ,f)$, where $\mathbf{\Psi }(\nu ,f)$ is the ${\Pi }_{𝕟-1}^{}$ formula

$$\left((\mathbf{L}\vDash \phi (\nu ,f\left)\right)⟹\mathtt{max}\left(S/f\right)<\omega \right)\wedge \left((\mathbf{L}\vDash {\phi }^{\prime }(\nu ,f))⟹\mathtt{max}\left(S/f\right)=\omega \right).\square$$

Theorem 10.

Suppose that, in $\mathbf{L}$, $K\subseteq P$ is a regular subforcing. Let $G\subseteq \mathbb{P}$ be $\mathbb{P}$-generic over $\mathbf{L}$. Then:

(i)

if $\nu \in \left|G\cap K\right|$, then $S_G\left(\nu \right)\in \mathbf{L}[G\cap K]$ and ${ℾ}_{\nu }\left(S_G\left(\nu \right)\right)$ holds, but

(ii)

if $\nu \notin \left|G\cap K\right|$, then $S_G\left(\nu \right)\notin \mathbf{L}[G\cap K]$, and there is no sets $S\subseteq \mathbf{Seq}$ in $\mathbf{L}[G\cap K]$ satisfying ${ℾ}_{\nu }\left(S\right)$.

Proof. 

(i) This is a corollary of Lemma 9(vi).

(ii) Suppose towards the contrary that some $S\in \mathbf{L}[G\cap K]$ satisfies ${ℾ}_{\nu }\left(S\right)$. Note that $S\in \mathbf{L}\left[G{\upharpoonright }_{\ne \nu }\right]$ by Lemma 9(iv). Now we can forget about the given set K. It follows from Theorem 5(iii) (with $K=\mathbb{P}{\upharpoonright }_{\ne \nu }$), that there is a name $\tau \in {\mathbf{SN}}_{\mathbf{Seq}}\left(\mathbb{P}{\upharpoonright }_{\ne \nu }\right)$ such that $S=\tau \left[G{\upharpoonright }_{\ne \nu }\right]$. There is an ordinal $\xi <{\omega }_1$ satisfying $\tau \in {\mathbb{M}}_{\xi }$ and $\tau \in {\mathbf{SN}}_{\mathbf{Seq}}\left({\mathbb{P}}_{\xi }{\upharpoonright }_{\ne \nu }\right)$. Then $S=\tau \left[G^{\xi }{\upharpoonright }_{\ne \nu }\right]$, where $G^{\xi }=G\cap {\mathbb{P}}_{\xi }$ is ${\mathbb{P}}_{\xi }$-generic over ${\mathbb{M}}_{\xi }$ by Corollary 6, and hence S belongs to ${\mathbb{M}}_{\xi }\left[G^{\xi }{\upharpoonright }_{\ne \nu }\right]$.

Note that $\mathbb{U}\left(\nu \right)$ is uncountable by Corollary 6(ii), and hence $F=\mathbb{U}\left(\nu \right)\setminus {\mathbb{U}}_{\xi }\left(\nu \right)$ is uncountable. Let $f\in F$. Then f is Cohen generic over the model ${\mathbb{M}}_{\xi }$ by Corollary 6. On the other hand $G^{\xi }{\upharpoonright }_{\ne \nu }$ is ${\mathbb{P}}_{\xi }{\upharpoonright }_{\ne \nu }$-generic over ${\mathbb{M}}_{\xi }\left[f\right]$ by Theorem 8(iii). Therefore f is Cohen generic over ${\mathbb{M}}_{\xi }\left[G^{\xi }{\upharpoonright }_{\ne \nu }\right]$ as well.

Recall that $S\in {\mathbb{M}}_{\xi }\left[G^{\xi }{\upharpoonright }_{\ne \nu }\right]$ and ${ℾ}_{\nu }\left(S\right)$ holds, hence $\mathtt{max}\left(S/f\right)<\omega$. As f is Cohen generic over ${\mathbb{M}}_{\xi }\left[G^{\xi }{\upharpoonright }_{\ne \nu }\right]$, it follows that there is a string $s\in \mathbf{Seq},s\subset f$, such that S contains no strings extending s. Take any $\mu \in \mathcal{I},j\ne \nu$. By Corollary 6(ii), there exists a function $g\in \mathbb{U}\left(\mu \right)\setminus {\mathbb{U}}_{\xi }\left(\mu \right),g\notin \mathbb{U}\left(\nu \right)$, satisfying $s\subset g$. Then, $\mathtt{max}\left(S/g\right)=\omega$ by ${ℾ}_{\nu }\left(S\right)$. However, this is absurd by the choice of s. □

Corollary 7.

Suppose that, in $\mathbf{L}$, $K\subseteq \mathbb{P}$ is a regular forcing. Let $G\subseteq \mathbb{P}$ be a set $\mathbb{P}$-generic over $\mathbf{L}$. Then

(i)

$\left|G\cap K\right|$ is equal to the set $\{\nu \in \mathcal{I}:\mathbf{L}[G\cap K]\vDash \exists S{ℾ}_{\nu }\left(S\right)\};$

(ii)

it is true in $\mathbf{L}[G\cap K]$ that the set $\left\{⟨\nu ,S⟩:{ℾ}_{\nu }\left(S\right)\right\}$ is ${\Pi }_{𝕟-1}^{\mathrm{HC}};$

(iii)

therefore $\left|G\cap K\right|$ is ${\Sigma }_{𝕟}^{\mathrm{HC}}$ in $\mathbf{L}[G\cap K]$.

Proof. 

Claim (i) follows from the theorem, because by the regularity we have $G\cap K\in \mathbf{L}\left[G{\upharpoonright }_{\ne \nu }\right]$ for all $\nu \notin \left|G\cap K\right|$. Claim (ii) immediately follows from Lemma 17. To prove (iii) note that, by (i) and (ii), it holds in $\mathbf{L}[G\cap K]$ that the set $\left|G\cap K\right|$ is defined by a ${\Sigma }_{𝕟}^{\mathrm{HC}}$ formula $\exists S{ℾ}_{\nu }\left(S\right)$ in $\mathrm{HC}$. □

5. Forcing Approximations

Here we define and study here an important forcing-like relation $\mathbf{forc}$. It will give us control over various phenomena of analytic definability in the generic extensions considered.

We continue to assume $\mathbf{V}=\mathbf{L}$ in the ground universe by Assumption 1.

5.1. Models and Absolute Sets

To consider transitive models of weaker theories, we let ${\mathbf{ZFC}}^{-}$ be $\mathbf{ZFC}$ minus the Power Set axiom, with the schema of Collection instead of replacement, and AC in the form of well-orderability of every set. See [24] on ${\mathbf{ZFC}}^{-}$ in detail.

Let ${\mathbf{ZFC}}_1^{-}$ be ${\mathbf{ZFC}}^{-}$ plus the axioms $\mathbf{V}=\mathbf{L}$ and “every set is at most countable”.

Let $W\subseteq \mathrm{HC}$. By definition, a set $X\subseteq \mathrm{HC}$ is ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(W\right)$ iff there exist a ${\Sigma }_1^{}$ formula $\sigma \left(x\right)$ and a ${\Pi }_1^{}$ formula $\pi \left(x\right)$, with sets in W as parameters, such that

$$X=\left\{x\in \mathrm{HC}:{\sigma }^{\mathrm{HC}}\left(x\right)\right\}=\left\{x\in \mathrm{HC}:{\pi }^{\mathrm{HC}}\left(x\right)\right\},$$

(4)

in particular, we have ${\sigma }^{\mathrm{HC}}\left(x\right)⟺{\pi }^{\mathrm{HC}}\left(x\right)$ for all x. However, generally speaking, this does not imply that $X\cap M\in {\mathsf{\Delta }}_1^M\left(W\right)$, where $M\in \mathrm{HC}$ is a countable transitive model (CTM). The goal of the next two definitions is to distinguish and formalize this kind of absoluteness.

Definition 17.

If for a given ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(W\right)$ set X, there exists such a pair of formulas, containing only parameters in W and satisfying (4) and $\forall x\in M\left({\sigma }^M\left(x\right)⟺{\pi }^M\left(x\right)\right)$ for all countable transitive models $M\vDash {\mathbf{ZFC}}^{-}$ containing all parameters that occur in σ and/or in π, then we say that X is absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(W\right)$. In this case, if M is as indicated then the set $X\cap M$ is ${\mathsf{\Delta }}_1^M\left(W\right)$ via the same pair of formulas. In particular, any ${\mathsf{\Delta }}_0^{\mathrm{HC}}\left(W\right)$ set is absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(W\right)$ by obvious reasons.

Definition 18.

In continuation of the last definition, a function $f:D\to \mathrm{HC}$, defined on a set $D\subseteq \mathrm{HC}$, is absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(W\right)$ function, if f is absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(W\right)$ as a set of pairs in the sense of Definition 17, and inaddition, if $M\vDash {\mathbf{ZFC}}^{-}$ is a CTM and $x\in D\cap M$ then $f\left(x\right)\in M$.

5.2. Formulas

Here we introduce a language that will help us study analytic definability in $\mathbf{P}\left[U\right]$-generic extensions, for different systems U, and their submodels.

Definition 19.

Let $\mathcal{L}$ be the 2nd order Peano language, with variables of type 1 over ${\omega }^{\omega }$. If $K\subseteq {\mathbf{P}}^{*}$ then an $\mathcal{L}\left(K\right)$ formula is any formula of $\mathcal{L}$, with somefree variables of types $0,1$ replaced by resp. numbers in ω and names in ${\mathbf{SN}}_{\omega }^{\omega }\left(K\right)$, and some type 1 quantifiers are allowed to have bounding indicesB (i.e., ${\exists }^B,{\forall }^B$) such that $B\subseteq \mathcal{I}$ is finite or countable.

Typically K will be a regular forcing in Definition 19, in the sense of Definition 8, or a regular subforcing of the form $K\left[U\right]$, U being a system.

If $\phi$ is a $\mathcal{L}\left({\mathbf{P}}^{*}\right)$ formula then let

$$\begin{array}{ccc}\hfill \mathrm{NAM}\phi & =& \mathrm{the}\mathrm{set}\mathrm{of}\mathrm{all}\mathrm{names}\tau \mathrm{that}\mathrm{occur}\mathrm{in}\phi ;\hfill \\ \hfill \left|\phi \right|& =& \bigcup _{\tau \in \mathrm{NAM}\phi }\left|\tau \right|(\mathrm{at}\mathrm{most}\mathrm{countable});\hfill \\ \hfill \mathrm{IND}\phi & =& \mathrm{the}\mathrm{set}\mathrm{of}\mathrm{all}\mathrm{quantifier}\mathrm{indices}B\mathrm{which}\mathrm{occur}\mathrm{in}\phi ;\hfill \\ \hfill \left|\right|\phi \left|\right|& =& \left|\phi \right|\cup \left(\bigcup \mathrm{IND}\phi \right)(\mathrm{at}\mathrm{most}\mathrm{countable}).\hfill \end{array}$$

Note that $\left|\phi \right|\subseteq \left|\right|\phi \left|\right|\subseteq \mathcal{I}$ provided $\phi$ is an $\mathcal{L}\left({\mathbf{P}}^{*}\right)$ formula.

If a set $G\subseteq {\mathbf{P}}^{*}$ is minimally $\phi$-generic (i.e., minimally $\tau$-generic w.r.t. every name $\tau \in \mathrm{NAM}\phi$, in the sense of Section 3.5), then let the valuation $\phi \left[G\right]$ be the result of substitution of $\tau \left[G\right]$ for any name $\tau \in \mathrm{NAM}\phi$, and changing each quantifier ${\exists }^{B}x$, ${\forall }^{B}x$ to $\exists \left(\forall \right)x\in {\omega }^{\omega }\cap \mathbf{L}\left[G\upharpoonright B\right]$ respectively, while index-free type 1 quantifiers are relativized to ${\omega }^{\omega }$; $\phi \left[G\right]$ is a formula of $\mathcal{L}$ with real parameters, and with some quantifiers of type 1 explicitly relativized to certain submodels of $\mathbf{L}\left[G\right]$.

An arithmetic formula in $\mathcal{L}\left(K\right)$ is a formula with no quantifiers of type 1 (names in ${\mathbf{SN}}_{\omega }^{\omega }\left(K\right)$ as in Definition 19 are allowed). If $n<\omega$ then let a $\mathcal{L}{\Sigma }_n^1\left(K\right)$, resp., $\mathcal{L}{\Pi }_n^1\left(K\right)$ formulabe a formula of the form

$${\exists }^{\circ }{x}_1{\forall }^{\circ }{x}_2\dots {\forall }^{\circ }\left({\exists }^{\circ }\right)x_{n-1}\exists \left(\forall \right)x_n\psi ,{\forall }^{\circ }{x}_1{\exists }^{\circ }{x}_2\dots {\exists }^{\circ }\left({\forall }^{\circ }\right)x_{n-1}\forall \left(\exists \right)x_n\psi$$

respectively, where $\psi$ is an arithmetic formula in $\mathcal{L}\left(K\right)$, all variables $x_i$ are of type 1 (over ${\omega }^{\omega }$), the sign ${}^{\circ }$ means that this quantifier can have a bounding index as in Definition 19, and it is required that the rightmost (closest to the kernel $\psi$) quantifier doesn’t have a bounding index.

If in addition $M\vDash {\mathbf{ZFC}}^{-}$ is a transitive model and $U\in M$ a system then define

$\mathcal{L}{\Sigma }_n^1(K\left[U\right],M)=$ all $\mathcal{L}{\Sigma }_n^1\left(K\right)$ formulas $\phi$ such that $\mathrm{NAM}\phi \subseteq {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[U\right]\right)\cap M$ and all indices $B\in \mathrm{IND}\phi$ belong to M and satisfy $B\subseteq \left|U\right|$.

Define $\mathcal{L}{\Pi }_n^1(K\left[U\right],M)$ similarly. All formulas in $\mathcal{L}{\Sigma }_n^1(K\left[U\right],M)\cup \mathcal{L}{\Pi }_n^1(K\left[U\right],M)$ are by definition (finite) strings in M.

5.3. Forcing Approximation

The next definition invents a convenient forcing-type relation $\mathbf{forc}$ for pairs $⟨M,U⟩$ in $\mathbf{sJS}$ and formulas $\phi$ in $\mathcal{L}\left(K\right[U\left]\right)$, associated with the truth in $K\left[U\right]$-generic extensions of $\mathbf{L}$, where $K\subseteq {\mathbf{P}}^{*}$ is a regular forcing. Recall that $K\left[U\right]=K\cap \mathbf{P}\left[U\right]$ whenever $K\subseteq {\mathbf{P}}^{*}$ is a regular forcing and U is a system.

Definition 20 (in L).

We introduce a relation $p{}^K\mathbf{forc}{}_U^M\phi$. First of all,

(F1)

Writing $p{}^K\mathbf{forc}{}_U^M\phi$, it is assumed that:

(a) 

$⟨M,U⟩\in \mathbf{sJS}$,

(b) 

$K\subseteq {\mathbf{P}}^{*}$ is a regular forcing and an absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(M\right)$ set,

(c) 

p belongs to $K\left[U\right]$ (a regular subforcing of $\mathbf{P}\left[U\right]$ by Lemma 7),

(d) 

φ is a closed formula in $\mathcal{L}{\Pi }_k^1(K\left[U\right],M)\cup \mathcal{L}{\Sigma }_{k+1}^1(K\left[U\right],M)$ for some $k\ge 1$, and each name $\tau \in \mathrm{NAM}\phi$ is $K\left[U\right]$-full below p.

Under these assumptions, the sets $U,K\left[U\right],p,\mathrm{NAM}\phi ,\mathrm{IND}\phi$ belong to M. The property of $K\left[U\right]$-fullness in (F1)d is equivalent to just $\mathbf{P}\left[U\right]$-fullness, by Corollary 1, since $K\left[U\right]$ is a regular subforcing of $\mathbf{P}\left[U\right]$ by Lemma 7.

The definition of $\mathbf{forc}$ goes on by induction on the complexity of formulas.

(F2)

If $⟨M,U⟩\in \mathbf{sJS},p\in K\left[U\right]$, and φ is a closed formula in $\mathcal{L}{\Pi }_1^1(K\left[U\right],M)$ (then by definition it has no quantifier indices), then: $p{}^K\mathbf{forc}{}_U^M\phi$ iff (F1) holds and p $K\left[U\right]$-forces φ over M in the usual sense. Note that the forcing notion $K\left[U\right]$ belongs to M in this case by (F1)b.

(F3)

If $\phi \left(x\right)\in \mathcal{L}{\Pi }_k^1(K\left[U\right],M),k\ge 1$, then:

(a) 

$p{}^K\mathbf{forc}{}_U^M{\exists }^{B}x\phi \left(x\right)$ iff there is a name $\tau \in M\cap {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[U\right]\upharpoonright B\right)$, $K\left[U\right]$-full below p (by (F1)d) and such that $p{}^K\mathbf{forc}{}_U^M\phi \left(\tau \right)$.

(b) 

$p{}^K\mathbf{forc}{}_U^M\exists x\phi \left(x\right)$ iff there is a name $\tau \in M\cap {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[U\right]\right)$, $K\left[U\right]$-full below p (by (F1)d) and such that $p{}^K\mathbf{forc}{}_U^M\phi \left(\tau \right)$.

(F4)

If $k\ge 2$, φ is a closed $\mathcal{L}{\Pi }_k^1(K\left[U\right],M)$ formula, $p\in K\left[U\right]$, and (F1) holds, then $p{}^K\mathbf{forc}{}_U^M\phi$ iff we have $\neg q{}^K\mathbf{forc}{}_{U^{\prime }}^{M^{\prime }}\phi {\phantom{)}}^{\neg }$ for every pair $⟨M^{\prime },U^{\prime }⟩\in \mathbf{sJS}$ extending $⟨M,U⟩$, and every condition $q\in K\left[U^{\prime }\right],q\le p$, where $\phi {\phantom{)}}^{\neg }$ is the result of canonical conversion of $\neg \phi$ to $\mathcal{L}{\Sigma }_k^1(K\left[U\right],M)$.

Lemma 18 (in L).

Let $K,⟨M,U⟩,p,\phi$ satisfy (F1) of Definition 20. Then:

(i)

if $p{}^K\mathbf{forc}{}_U^M\phi$, $⟨M,U⟩\preccurlyeq ⟨M^{\prime },U^{\prime }⟩\in \mathbf{sJS}$ and $q\in K\left[U^{\prime }\right],q\le p$, then $q{}^K\mathbf{forc}{}_{U^{\prime }}^{M^{\prime }}\phi ;$

(ii)

if $k\ge 2$, φ is $\mathcal{L}{\Pi }_k^1(K\left[U\right],M)$, and $p{}^K\mathbf{forc}{}_U^M\phi$, then $p{}^K\mathbf{forc}{}_U^M\phi {\phantom{)}}^{\neg }$ fails.

Thus by the first claim of the lemma $\mathbf{forc}$ is monotone w.r.t. both the extension of pairs in $\mathbf{sJS}$ and the strengthening of forcing conditions.

Proof. 

(i) Let $\phi =\phi ({\tau }_1,\dots ,{\tau }_m)$ be a closed formula in $\mathcal{L}{\Pi }_1^1(K\left[U\right],M)$, where all names ${\tau }_j\in {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[U\right]\right)\cap M$ are $K\left[U\right]$-full below the condition $p\in K\left[U\right]$ considered. Then all names ${\tau }_j$ remain $K\left[U^{\prime }\right]$-full below p, and below q as well since $q\le p$, by Corollary 5. Consider a set $G^{\prime }\subseteq K\left[U^{\prime }\right]$, $K\left[U^{\prime }\right]$-generic over $M^{\prime }$ and containing q. We have to prove that $\phi \left[G^{\prime }\right]$ is true in $M^{\prime }\left[G^{\prime }\right]$. Note that the set $G=G^{\prime }\cap K\left[U\right]$ is $K\left[U\right]$-generic over M by Corollary 4, and we have $p\in G$. Moreover the valuation $\phi \left[G^{\prime }\right]$ coincides with $\phi \left[G\right]$ since all names in $\phi$ belong to ${\mathbf{SN}}_{\omega }^{\omega }\left(K\left[U\right]\right)$. $\phi \left[G\right]$ is true in $M\left[G\right]$ as $p{}^K\mathbf{forc}{}_U^M\phi$. It remains to apply Mostowski’s absoluteness between the models $M\left[G\right]\subseteq M^{\prime }\left[G^{\prime }\right]$.

The inductive steps related to (F3), (F4) of Definition 20 are easy.

Claim (ii) immediately follows from (F4) of Definition 20. □

The next theorem classifies the complexity of $\mathbf{forc}$ in terms of projective hierarchy. Recall that all formulas in ${\bigcup }_n\left(\mathcal{L}{\Sigma }_n^1(K,M)\cup \mathcal{L}{\Pi }_n^1(K,M)\right)$ are by definition (finite) strings in M. This allows us to consider and analyze sets

$$\begin{array}{cccc}{\mathbf{Forc}}_w^K\left({\Sigma }_n^1\right)\hfill & =& \{\hfill & ⟨M,U,p,\phi ⟩:⟨M,U⟩\in \mathbf{sJS}\wedge w\in M\wedge p\in K\left[U\right]\wedge \hfill \\ \hfill & & \hfill & \phi \mathrm{is}\mathrm{a}\mathrm{closed}\mathcal{L}{\Sigma }_n^1(K\left[U\right],M)\mathrm{formula}\wedge p{}^K\mathbf{forc}{}_U^M\phi \};\hfill \end{array}$$

and similarly defined ${\mathbf{Forc}}_w^K\left({\Pi }_n^1\right)$, where it is assumed that $w\in {\omega }^{\omega }$ and $K\subseteq {\mathbf{P}}^{*}$ is a regular forcing and an absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(w\right)$ set.

Theorem 11 (in L).

Let $w\in {\omega }^{\omega }$ and $K\subseteq {\mathbf{P}}^{*}$ be a regular forcing and an absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(w\right)$ set. Then:

(i)

${\mathbf{Forc}}_w^K\left({\Pi }_1^1\right)$ and ${\mathbf{Forc}}_w^K\left({\Sigma }_2^1\right)$ are ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(w\right);$

(ii)

if $k\ge 2$ then ${\mathbf{Forc}}_w^K\left({\Pi }_k^1\right)$ and ${\mathbf{Forc}}_w^K\left({\Sigma }_{k+1}^1\right)$ are ${\Pi }_{k-1}^{\mathrm{HC}}\left(w\right)$.

Proof 

(sketch). Suppose that $\phi$ is $\mathcal{L}{\Pi }_1^1$. Under the assumptions of the theorem, items (F1)a, (F1)c, (F1)d of Definition 20(F1) are ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(w\right)$ relations, (F1)b is automatic, while (F2) is reducible to a forcing relation over M that we can relativize to M. The inductive step goes on straightforwardly using (F3), (F4) of Definition 20. Note that the quantifier over names in (F3) is a bounded quantifier (bounded by M), hence it does not add any extra complexity. □

5.4. Advanced Properties of Forcing Approximations

The following lemma works whenever the domain $K\subseteq {\mathbf{P}}^{*}$ (a regular forcing) of conditions p related to the definition of $p{}^K\mathbf{forc}{}_U^M\phi$ is bounded by a set $c\subseteq \mathcal{I}$. (Compare with Theorem 7.)

Lemma 19 (restriction lemma, in L).

Suppose that $K,⟨M,U⟩,p,\phi$ satisfy (F1) of Definition 20, a set $c\subseteq \mathcal{I}$ is absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(M\right)$, $K\subseteq {\mathbf{P}}^{*}\upharpoonright c$, and $p{}^K\mathbf{forc}{}_U^M\phi$. Then $p{}^K\mathbf{forc}{}_{U\upharpoonright c}^M\phi$.

Note that $\left|U\right|\subseteq c$ is not assumed in the lemma. On the other hand, we have $\left|p\right|\subseteq c$ by Definition 20(F1)c, because $p\in K\left[U\right]$ and $K\subseteq {\mathbf{P}}^{*}\upharpoonright c$, and $\left|\phi \right|\subseteq c$ holds because $\phi$ is an $\mathcal{L}\left(K\right[U\left]\right)$ formula. In addition, $U\upharpoonright c\in M$ by the choice of c.

Proof. 

The direction $⟸$ immediately follows from Lemma 18(i) since we have $⟨M,U\upharpoonright c⟩\preccurlyeq ⟨M,U⟩$ by Remark 1 in Section 4.1. Prove the opposite implication by induction.

Case of $\mathcal{L}{\Pi }_1^1$ formulas: $K\left[U\right]=K\left[U\upharpoonright c\right]$ under the assumptions of the lemma.

Step $\mathcal{L}{\Pi }_n^1\to \mathcal{L}{\Sigma }_{n+1}^1$. Let $\psi \left(x\right)$ be a $\mathcal{L}{\Pi }_n^1(K\left[U\right],M)$ formula, and $\phi$ be ${\exists }^{B}x\psi \left(x\right)$, $B\subseteq \mathcal{I}$, $B\in M$. If $p{}^K\mathbf{forc}{}_U^M\phi$ then there is a name $\tau \in M\cap {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[U\right]\upharpoonright B\right)$ such that $p{}^K\mathbf{forc}{}_U^M\psi \left(\tau \right)$. We conclude that $p{}^K\mathbf{forc}{}_{U\upharpoonright c}^M\psi \left(\tau \right)$ by the inductive hypothesis. However we have ${\mathbf{SN}}_{\omega }^{\omega }\left(K\left[U\right]\upharpoonright B\right)={\mathbf{SN}}_{\omega }^{\omega }\left(K\left[U\upharpoonright c\right]\upharpoonright B\right)$ since $\left|K\right|\subseteq c$. Thus $p{}^K\mathbf{forc}{}_{U\upharpoonright c}^M\phi$. The case $\phi$ being $\exists x\psi \left(x\right)$ is similar.

Step $\mathcal{L}{\Sigma }_n^1\to \mathcal{L}{\Pi }_n^1,n\ge 2$. Let $\phi$ be a $\mathcal{L}{\Pi }_n^1(K\left[U\right],M)$ formula. Suppose towards the contrary that $p{}^K\mathbf{forc}{}_U^M\phi$ holds, but $p{}^K\mathbf{forc}{}_{U\upharpoonright c}^M\phi$ fails, so that there exist a pair $⟨M^{\prime },V⟩\in \mathbf{sJS}$ and a condition $q\in K\left[V\right]$, such that $⟨M,U\upharpoonright c⟩\preccurlyeq ⟨M^{\prime },V⟩$, $q\le p$, and $q{}^K\mathbf{forc}{}_V^{M^{\prime }}\phi {\phantom{)}}^{\neg }$. Then $q{}^K\mathbf{forc}{}_{V\upharpoonright c}^{M^{\prime }}\phi {\phantom{)}}^{\neg }$ by the inductive hypothesis. Note that $\left|q\right|\subseteq c$ by the choice of K, but not necessarily $\left|V\right|\subseteq c$.

Define a system $W\in M^{\prime }$ such that $\left|W\right|=\left(\right|V|\cap c)\cup \left(\right|U|\setminus c)$, $W\upharpoonright \left(\right|V|\cap c)=V\upharpoonright \left(\right|V|\cap c)$, and $W\upharpoonright \left(\right|U|\setminus c)=U\upharpoonright \left(\right|U|\setminus c)$. Then $⟨M^{\prime },V\upharpoonright c⟩\preccurlyeq ⟨M^{\prime },W⟩$, therefore still $q{}^K\mathbf{forc}{}_W^{M^{\prime }}\phi {\phantom{)}}^{\neg }$ by Lemma 18(i).

Now we claim that $⟨M,U⟩\preccurlyeq ⟨M^{\prime },W⟩$. Indeed, suppose that $\nu \in \left|U\right|$. If $\nu \notin c$ then $W\left(\nu \right)=U\left(\nu \right)$. If $\nu \in c$ then $U\left(\nu \right)\subseteq V\left(\nu \right)=W\left(\nu \right)$ by construction. It follows that $\left|U\right|\subseteq \left|W\right|$, $U\preccurlyeq W$, and $\mathsf{\Delta }(U,W)\subseteq \mathsf{\Delta }(U\upharpoonright c,V)$—which implies $U{\preccurlyeq }_{M}W$, since $⟨M,U\upharpoonright c⟩\preccurlyeq ⟨M^{\prime },V⟩$. Thus $⟨M,U⟩\preccurlyeq ⟨M^{\prime },W⟩$.

We have $q\le p$ as well. This contradicts the assumption $p{}^K\mathbf{forc}{}_U^M\phi$ by Lemma 18(ii). □

Lemma 20 (in L).

Let $K,⟨M,U⟩,p,\phi ,k$ satisfy (F1) of Definition 20, $\mathrm{NAM}\phi =\{{\tau }_1,\dots ,{\tau }_m\}$, ${\mu }_1,\dots ,{\mu }_m$ be another list of names in ${\mathbf{SN}}_{\omega }^{\omega }\left(K\left[U\right]\right)\cap M$, $K\left[U\right]$-full below p and such that ${\tau }_{\ell }$ and ${\mu }_{\ell }$ are equivalent below p for each $\ell =1,\dots ,m$. Then $p{}^K\mathbf{forc}{}_U^M\phi ({\tau }_1,\dots ,{\tau }_m)$ iff $p{}^K\mathbf{forc}{}_U^M\phi ({\mu }_1,\dots ,{\mu }_m)$.

Proof. 

It suffices to consider the case of ${\Pi }_1^1$ formulas; the induction steps $\mathcal{L}{\Pi }_k^1\to \mathcal{L}{\Sigma }_{k+1}^1$ and $\mathcal{L}{\Sigma }_k^1\to \mathcal{L}{\Pi }_k^1$ are rather easy.

Suppose that $\phi$ is $\mathcal{L}{\Pi }_1^1$ and $p{}^K\mathbf{forc}{}_U^M\phi ({\tau }_1,\dots ,{\tau }_m)$. Suppose that $G\subseteq K\left[U\right]$ is a set $K\left[U\right]$-generic over M, and $p\in G$. We claim that ${\tau }_{\ell }\left[G\right]={\mu }_{\ell }\left[G\right]$ for all ℓ; this obviously implies the result required. Suppose that this is not the case. Then, by definition, there exist numbers m and $j\ne k$ and conditions $q\in G\cap (\tau ″⟨m,j⟩)$ and $r\in G\cap (\mu ″⟨m,k⟩)$. Then $p,q,r$ must be compatible (as elements of the same generic set), which is a contradiction. □

Lemma 21 (in L).

Suppose that $K,⟨M,U⟩,p,\phi ,k$ satisfy (F1) of Definition 20, φ is $\mathcal{L}{\Pi }_k^1(K\left[U\right],M)$, $P=\{q\in K\left[U\right]:q\le p\}$, a set $A\in M$, $A\subseteq P$ is a maximal antichain in P, and $q{}^K\mathbf{forc}{}_U^M\phi$ for all $q\in A$. Then $p{}^K\mathbf{forc}{}_U^M\phi$.

Proof. 

If $\phi$ is a $\mathcal{L}{\Pi }_1^1$ formula then the result follows from (F2) of Definition 20 and known properties of the ordinary forcing over M. Now let $\phi$ be ${\Pi }_k^1,k\ge 2$. Suppose towards the contrary that $p{}^K\mathbf{forc}{}_U^M\phi$ fails. Then there exist: a pair $⟨M^{\prime },U^{\prime }⟩\in \mathbf{sJS}$ extending $⟨M,U⟩$, and a condition $r\in K\left[U^{\prime }\right],r\le p$, such that $r{}^K\mathbf{forc}{}_{U^{\prime }}^{M^{\prime }}\phi {\phantom{)}}^{\neg }$. Note that A remains a maximal antichain in the set $Q=\{q\in \mathbf{P}\left[U\right]:q\le p\}$ (bigger than P above), by Lemma 8. Therefore, A is still a maximal antichain in $Q^{\prime }=\{q\in \mathbf{P}\left[U^{\prime }\right]:q\le p\}$, by Theorem 8(i), hence a maximal antichain in $P^{\prime }=\{q\in K\left[U^{\prime }\right]:q\le p\}$. It follows that r is compatible in $K\left[U^{\prime }\right]$ with at least one condition $q\in A$. However, $r{}^K\mathbf{forc}{}_{U^{\prime }}^{M^{\prime }}\phi {\phantom{)}}^{\neg }$ while $q{}^K\mathbf{forc}{}_U^M\phi$, easily leading to a contradiction with Lemma 19. □

5.5. Transformations and Invariance

Here we show that, under certain assumptions, the transformations of the first two groups defined in Section 3.7 preserve forcing approximations $\mathbf{forc}$. This is not an absolutely elementary thing: there is no way to reasonably apply transformations to transitive models M involved in the definition of $\mathbf{forc}$. What we can do is to require that the transformations involved belong to the models involved. This leads to certain complications of different sort.

Family 1: permutations. First of all we have to extend the definition of the action of $\pi$ in Section 3.7 to include formulas. Suppose that $c,c^{\prime }\subseteq \mathcal{I}$. Define the action of any $\pi \in {\mathrm{BIJ}}_{c^{\prime }}^c$ onto formulas $\phi$ of $\mathcal{L}\left({\mathbf{P}}^{*}\right)$ such that $\left|\right|\phi \left|\right|\subseteq c$:

–

to get $\pi \phi$ substitute $\pi ·\tau$ for any $\tau \in \mathrm{NAM}\phi$ and $\pi ·B$ for any $B\in \mathrm{IND}\phi$.

Lemma 22.

Suppose that $⟨M,U⟩,K,p,\phi$ satisfy (F1) of Definition 20, sets $c,c^{\prime }\subseteq \mathcal{I}$ have equal cardinality and are absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(M\right)$, $\pi \in {\mathrm{BIJ}}_{c^{\prime }}^c$ is an absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(M\right)$ function, and $\left|\right|\phi \left|\right|\subseteq c,\left|U\right|\subseteq c,K\subseteq {\mathbf{P}}^{*}\upharpoonright c$.

Then, $p{}^K\mathbf{forc}{}_U^M\phi$ iff $\left(\pi ·p\right){}^{\pi ·K}\mathbf{forc}{}_{\pi ·U}^M\pi \phi$.

Proof. 

Under the assumptions of the lemma, in particular, the requirement of $c,c^{\prime },\pi$ being absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(M\right)$, $\pi$ acts as an isomorphism on all relevant domains and preserves all relevant relations between the objects involved. Thus $⟨M,\pi ·U⟩,\pi ·K,\pi ·p,\pi \phi$ still satisfy Definition 20(F1), and $\left|\right|\pi \phi \left|\right|\subseteq c^{\prime },\left|\pi ·U\right|\subseteq c^{\prime },\pi ·K\subseteq {\mathbf{P}}^{*}\upharpoonright c^{\prime }$. (For instance, to show that $\pi ·U$ still belongs to M, note that the set $\left|U\right|\subseteq c$ belongs to M, thus $\pi \upharpoonright \left|U\right|\in M$, too, since $\pi$ is an absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(M\right)$ function.) This allows to prove the lemma by induction on the complexity of $\phi$.

Suppose that $\phi$ is a closed formula in $\mathcal{L}{\Pi }_1^1(K\left[U\right],M)$. Then $\pi \phi$ is a closed formula in $\mathcal{L}{\Pi }_1^1(\left(\pi ·K\right)\left[\pi ·U\right],M)$. Then easily $P^{\prime }=\left(\pi ·K\right)\left[\pi ·U\right]=\pi ·\left(K\left[U\right]\right)\subseteq {\mathbf{P}}^{*}$ is a set in M order isomorphic to $P=K\left[U\right]$ itself by means of the map $p⟼\pi ·p$. Moreover a set $G\subseteq P$ is $P$-generic over M iff $\pi ·G$ is, accordingly, $P^{\prime }$-generic over M and the valuated formulas $\phi \left[G\right]$ and $\left(\pi \phi \right)\left[\pi ·G\right]$ coincide. Now the result for ${\Pi }_1^1$ formulas follows from (F2) of Definition 20.

Step ${\Pi }_n^1\to {\Sigma }_{n+1}^1,n\ge 1$. Let $\psi \left(x\right)$ be a $\mathcal{L}{\Pi }_n^1(K\left[U\right],M)$ formula, and $\phi$ be $\exists x\psi \left(x\right)$. Assume $p{}^K\mathbf{forc}{}_U^M\phi$. By definition there is a name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[U\right]\right)\cap M$ such that $p{}^K\mathbf{forc}{}_U^M\psi \left(\tau \right)$. Then, by the inductive hypothesis, $\pi ·p{}^{\pi ·K}\mathbf{forc}{}_{\pi ·U}^M\left(\pi \psi \right)\left(\pi ·\tau \right)$, and hence by definition $\pi ·p{}^{\pi ·K}\mathbf{forc}{}_{\pi ·U}^M\pi \phi$.

The case of $\phi$ being ${\exists }^{B}x\psi \left(x\right)$ is similar.

Step ${\Sigma }_n^1\to {\Pi }_n^1,n\ge 2$. This is somewhat less trivial. Assume that $\phi$ is a closed $\mathcal{L}{\Pi }_n^1(K\left[U\right],M)$ formula; all names in $\phi$ belong to ${\mathbf{SN}}_{\omega }^{\omega }\left(K\left[U\right]\right)\cap M$ and are $K\left[U\right]$-full below a given $p\in K\left[U\right]$. Then, by rather obvious reasons, $\pi \phi$ is a closed $\mathcal{L}{\Pi }_n^1(\left(\pi ·K\right)\left[\pi ·U\right],M)$ formula, whose all names belong to ${\mathbf{SN}}_{\omega }^{\omega }\left(\left(\pi ·K\right)\left[\pi ·U\right]\right)\cap M$ and are $\left(\pi ·K\right)\left[\pi ·U\right]$-full below $\pi ·p$. Suppose that $p{}^K\mathbf{forc}{}_U^M\phi$ fails. By definition there exist a pair $⟨M_1,U_1⟩\in \mathbf{sJS}$ with $⟨M,U⟩\preccurlyeq ⟨M_1,U_1⟩$, and a condition $q\in K\left[U_1\right],q\le p$, such that $q{}^K\mathbf{forc}{}_{U_1}^{M_1}\phi {\phantom{)}}^{\neg }$. We can also assume by Lemma 19, that $|U_1|\subseteq c$. Then $\left(\pi ·q\right){}^{\pi ·K}\mathbf{forc}{}_{\pi ·U_1}^{M_1}\pi \phi {\phantom{)}}^{\neg }$ by the inductive hypothesis. Yet the pair $⟨M_1,\pi ·U_1⟩$ belongs to $\mathbf{sJS}$ and extends $⟨M,\pi ·U⟩$. (As $\pi$ is absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(M\right)$ and $U\in M$, the restriction $\pi \upharpoonright \left|U\right|$ belongs to M.) In addition, $\pi ·q\in \left(\pi ·K\right)\left[\pi ·U_1\right]$, and $\pi ·q\le \pi ·p$. Therefore the statement $\left(\pi ·p\right){}^K\mathbf{forc}{}_{\pi ·U}^M\pi \phi$ fails, as required. □

Family 2: Lipschitz transformations. We extend the action of $\mathit{\alpha }\in {\mathbf{Lip}}^{\mathcal{I}}$ to formulas of $\mathcal{L}\left({\mathbf{P}}^{*}\right)$:

–

to get $\pi \phi$ substitute $\pi ·\tau$ for any $\tau \in \mathrm{NAM}\phi$ but do not change the quantifier indices B.

Note that the action of any $\mathit{\alpha }\in {\mathbf{Lip}}^{\mathcal{I}}\cap M$ on systems, conditions, names, and formulas, as defined there, is absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(M\right)$. This allows to prove the next invariance lemma similarly to Lemma 22, which we leave for the reader.

Lemma 23.

Suppose that $⟨M,U⟩,K,p,\phi$ satisfy (F1) of Definition 20, and $\mathit{\alpha }\in {\mathbf{Lip}}^{\mathcal{I}}\cap M$. Then $p{}^K\mathbf{forc}{}_U^M\phi$ iff $\left(\mathit{\alpha }·p\right){}^{\mathit{\alpha }·K}\mathbf{forc}{}_{\mathit{\alpha }·U}^M\mathit{\alpha }\phi$.

6. Elementary Equivalence Theorem

This section presents further properties of $\mathbb{P}$-generic extensions of $\mathbf{L}$ and their subextensions, including Theorem 13 and its corollaties on the elementary equivalence of different subextensions.

Assumption 2.

We continue to assume $\mathbf{V}=\mathbf{L}$ in the ground universe. Below in this section, a number $𝕟\ge 2$ is fixed, and pairs $⟨{\mathbb{M}}_{\xi },{\mathbb{U}}_{\xi }⟩$, the system $\mathbb{U}={\bigvee }_{\xi <{\omega }_1}{\mathbb{U}}_{\xi }$, the forcing notions ${\mathbb{P}}_{\xi }=\mathbf{P}\left[{\mathbb{U}}_{\xi }\right]$ and $\mathbb{P}=\mathbf{P}\left[\mathbb{U}\right]={\bigcup }_{\xi <{\omega }_1}{\mathbb{P}}_{\xi }$ are as in Definition 16 for this$𝕟$.

6.1. Further Properties of Forcing Approximations

Coming back to the complete sequence of pairs $⟨{\mathbb{M}}_{\xi },{\mathbb{U}}_{\xi }⟩$ introduced by Definition 16, we consider the auxiliary forcing relation $\mathbf{forc}$ with respect to those pairs. We begin with the following definition.

Definition 21 (in L).

Let $K\subseteq {\mathbf{P}}^{*}$ be a regular forcing. Recall that

$$K\left[\mathbb{U}\right]=K\cap \mathbb{P}\mathrm{and}K\left[{\mathbb{U}}_{\xi }\right]=K\cap \mathbf{P}\left[{\mathbb{U}}_{\xi }\right]=K\cap {\mathbb{P}}_{\xi }$$

for any $\xi <{\omega }_1$. Let $p{}^K\mathbf{forc}{}_{\xi }^{}\phi$ mean $p{}^K\mathbf{forc}{}_{{\mathbb{U}}_{\xi }}^{{\mathbb{M}}_{\xi }}\phi$—then by definition K has to be an absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left({\mathbb{M}}_{\xi }\right)$ set, by the way. We let $p{}^K\mathbf{forc}{}_{\infty }^{}\phi$ mean: $\exists \xi <{\omega }_1\left(p{}^K\mathbf{forc}{}_{\xi }^{}\phi \right)$.

Thus, if $p{}^K\mathbf{forc}{}_{\xi }^{}\phi$ then definitely K is an absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left({\mathbb{M}}_{\xi }\right)$ set, $p\in K\left[{\mathbb{U}}_{\xi }\right]$, $\phi$ is a formula with names in ${\mathbb{M}}_{\xi }\cap {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[{\mathbb{U}}_{\xi }\right]\right)$ as parameters, all names $\tau \in \mathrm{NAM}\phi$ are $K\left[{\mathbb{U}}_{\xi }\right]$-full below p, all indices $B\in \mathrm{IND}\phi$ belong to ${\mathbb{M}}_{\xi }$. The following is an easy consequence of Lemma 18.

Lemma 24 (in L).

Let $K\subseteq {\mathbf{P}}^{*}$ be a regular forcing. Assume that φ is a closed formula in $\mathcal{L}{\Pi }_k^1\left(K\left[\mathbb{U}\right]\right)\cup \mathcal{L}{\Sigma }_{k+1}^1\left(K\left[\mathbb{U}\right]\right)$, $1\le k$, $p\in K\left[\mathbb{U}\right]$. Then:

(i)

if $p{}^K\mathbf{forc}{}_{\xi }^{}\phi$ and $\xi ⩽\zeta <{\omega }_1$, $q\in K\left[{\mathbb{U}}_{\zeta }\right],q⩽p$, then $q{}^K\mathbf{forc}{}_{\zeta }^{}\phi ;$

(ii)

$p{}^K\mathbf{forc}{}_{\infty }^{}\phi$ and $p{}^K\mathbf{forc}{}_{\infty }^{}\phi {\phantom{)}}^{\neg }$ contradict to each other;

(iii)

if φ is a $\mathcal{L}{\Pi }_k^1\left(K\left[\mathbb{U}\right]\right)$ formula, $A\subseteq Q=\{q\in K\left[\mathbb{U}\right]:q\le p\}$ is a maximal antichain in Q, and $q{}^K\mathbf{forc}{}_{\infty }^{}\phi$ for all $q\in A$, then $p{}^K\mathbf{forc}{}_{\infty }^{}\phi .$

Proof. 

(iii) As A is a countable set, there exists an ordinal $\xi <{\omega }_1$ such that $q{}^K\mathbf{forc}{}_{\xi }^{}\phi$ for all $q\in A$. Apply Lemma 21. □

Lemma 25 (in L).

Assume that $K\subseteq {\mathbf{P}}^{*}$ is a regular forcing, φ is a closed formula in $\mathcal{L}{\Pi }_k^1\left(K\left[\mathbb{U}\right]\right)\cup \mathcal{L}{\Sigma }_k^1\left(K\left[\mathbb{U}\right]\right),2\le k<𝕟$, $p\in K\left[\mathbb{U}\right]$, all names in φ are $K\left[\mathbb{U}\right]$-full below p, and finally $w\in {\omega }^{\omega }$ and K is absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(w\right)$. Then:

(i)

there is $q\in K\left[\mathbb{U}\right],q⩽p$, such that $q{}^K\mathbf{forc}{}_{\infty }^{}\phi$ or $q{}^K\mathbf{forc}{}_{\infty }^{}\phi {\phantom{)}}^{\neg };$

(ii)

if φ is $\mathcal{L}{\Pi }_k^1\left(K\left[\mathbb{U}\right]\right),2\le k<𝕟$, then $p{}^K\mathbf{forc}{}_{\infty }^{}\phi$ iff there is no condition $q\in K\left[\mathbb{U}\right],q\le p$, such that $q{}^K\mathbf{forc}{}_{\infty }^{}\phi {\phantom{)}}^{\neg }.$

Proof. 

(i) As any name is a countable object, there is an ordinal $\eta <{\omega }_1$ such that $p\in K\left[{\mathbb{U}}_{\eta }\right]$, $w\in {\mathbb{M}}_{\eta }$, and all names in $\phi$ belong to ${\mathbb{M}}_{\eta }\cap {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[{\mathbb{U}}_{\eta }\right]\right)$; then all names in $\phi$ are $K\left[{\mathbb{U}}_{\eta }\right]$-full below p, of course. As $k<𝕟$, the set D of all pairs $⟨M,U⟩\in \mathbf{sJS}$ that extend $⟨{\mathbb{M}}_{\eta },{\mathbb{U}}_{\eta }⟩$ and there is a condition $q\in K\left[U\right],q⩽p$, satisfying $q{}^K\mathbf{forc}{}_U^M\phi {\phantom{)}}^{\neg }$, belongs to ${\Sigma }_{n-2}^{\mathrm{HC}}$ by Theorem 11. Therefore, by the $n$-completeness of the sequence ${\left\{⟨{\mathbb{M}}_{\xi },{\mathbb{U}}_{\xi }⟩\right\}}_{\xi <{\omega }_1}$, there is an ordinal $\zeta ,\eta ⩽\zeta <{\omega }_1$, such that $⟨{\mathbb{M}}_{\zeta },{\mathbb{U}}_{\zeta }⟩\in D^{\mathrm{solv}}$. (By the way, this is the only use of the $𝕟$-completeness!)

We have two cases.

Case 1: $⟨{\mathbb{M}}_{\zeta },{\mathbb{U}}_{\zeta }⟩\in D$. Then there is a condition $q\in K\left[{\mathbb{U}}_{\zeta }\right],q\le p$, satisfying $q{}^K\mathbf{forc}{}_{\zeta }^{}\phi {\phantom{)}}^{\neg }$. However, obviously $q\in K\left[\mathbb{U}\right]$.

Case 2: there is no pair $⟨M,U⟩\in D$ extending $⟨{\mathbb{M}}_{\zeta },{\mathbb{U}}_{\zeta }⟩$. Prove $p{}^K\mathbf{forc}{}_{\zeta }^{}\phi$. Suppose otherwise. Then by the choice of $\eta$ and (F4) of Definition 20 there exist a pair $⟨M,U⟩\in \mathbf{sJS}$ extending $⟨{\mathbb{M}}_{\zeta },{\mathbb{U}}_{\zeta }⟩$, and a condition $q\in K\left[U\right],q\le p$, such that $q{}^K\mathbf{forc}{}_U^M\phi {\phantom{)}}^{\neg }$. Then $⟨M,U⟩\in D$, a contradiction.

(ii) Suppose that there is no condition $q\in K\left[\mathbb{U}\right],q\le p$, with $q{}^K\mathbf{forc}{}_{\infty }^{}\phi {\phantom{)}}^{\neg }$. Then by (i) the set $Q=\{q\in K\left[\mathbb{U}\right]:q\le p\wedge q{}^K\mathbf{forc}{}_{\infty }^{}\phi \}$ is dense in $K\left[\mathbb{U}\right]$ below p. Let $A\subseteq Q$ be a maximal antichain. It remains to apply Lemma 24(iii). □

6.2. Relations to the Truth in Generic Extensions

According to the next theorem, the truth in the generic extensions considered is connected in the usual way with the relation ${\displaystyle \mathrm{forc}{}_{\infty }}$ up to the $𝕟$-th level of analytic hierarchy. Recall that $\mathbf{V}=\mathbf{L}$ is assumed in the ground universe.

Theorem 12.

Assume that, in $\mathbf{L}$, $K\subseteq {\mathbf{P}}^{*}$ is a regular forcing, φ is a closed formula in $\mathcal{L}{\Pi }_k^1\left(K\left[\mathbb{U}\right]\right)\cup \mathcal{L}{\Sigma }_{k+1}^1\left(K\left[\mathbb{U}\right]\right),1\le k\le 𝕟$, all names in $\mathrm{NAM}\phi$ are $K\left[\mathbb{U}\right]$-full, $w\in {\omega }^{\omega },$ and K is an absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(w\right)$ set.

Let $G\subseteq \mathbb{P}$ be a $\mathbb{P}$-generic set over $\mathbf{L}$. Then:

(i)

if $p\in G$ and $p{}^K\mathbf{forc}{}_{\infty }^{}\phi$, then $\phi \left[G\right]$ is true in $\mathbf{L}[G\cap K[\mathbb{U}\left]\right];$

(ii)

conversely, if $\phi \left[G\right]$ is true in $\mathbf{L}[G\cap K[\mathbb{U}\left]\right]$ and strictly $k<𝕟$ holds, then $\exists p\in G\cap K\left(p{}^K\mathbf{forc}{}_{\infty }^{}\phi \right)$.

The formulas $\phi \left[G\right]$, $\phi [G\cap K]$ coincide under the assumptions of the theorem.

Proof. 

(ii) We argue by induction on the complexity of $\phi$.

The case of $\mathcal{L}{\Pi }_1^1$ formulas. Let $\phi$ be a closed formula in $\mathcal{L}{\Pi }_1^1\left(K\left[\mathbb{U}\right]\right)$. As names in the formulas considered are countable objects, there is an ordinal $\xi <{\omega }_1$ such that $w\in {\mathbb{M}}_{\xi }$ and $\phi$ is a $\mathcal{L}{\Pi }_1^1(K\left[{\mathbb{U}}_{\xi }\right],{\mathbb{M}}_{\xi })$ formula. As $G\subseteq \mathbb{P}$ is $\mathbb{P}$-generic over $\mathbf{L}$, the smaller set $G_{\xi }=G\cap K\left[{\mathbb{U}}_{\xi }\right]$ is $K\left[{\mathbb{U}}_{\xi }\right]$-generic over ${\mathbb{M}}_{\xi }$ by Corollary 4, and the formulas $\phi \left[G\right]$, $\phi \left[G_{\xi }\right]$ coincide by the choice of $\xi$. Therefore if $\phi \left[G\right]$ holds in $\mathbf{L}[G\cap K[\mathbb{U}\left]\right]$ then $\phi \left[G_{\xi }\right]$ holds in ${\mathbb{M}}_{\xi }\left[G_{\xi }\right]$, by Shoenfield’s absoluteness theorem, and hence there is a condition $p\in G_{\xi }$ which $K\left[{\mathbb{U}}_{\xi }\right]$-forces $\phi$ over ${\mathbb{M}}_{\xi }$, that is, $p{}^K\mathbf{forc}{}_{\xi }^{}\phi$ by (F2) of Definition 20, and finally $p{}^K\mathbf{forc}{}_{\infty }^{}\phi$, as required. If conversely, $p\in G\cap K\left[\mathbb{U}\right]$, $\zeta ,\xi \le \zeta <{\omega }_1$, and $p{}^K\mathbf{forc}{}_{\zeta }^{}\phi$, then by definition p$K\left[{\mathbb{U}}_{\zeta }\right]$-forces $\phi$ over ${\mathbb{M}}_{\xi }$. It follows that $\phi \left[G_{\xi }\right]$ holds in ${\mathbb{M}}_{\xi }\left[G_{\xi }\right]$, and hence $\phi \left[G\right]$ holds in $\mathbf{L}[G\cap K[\mathbb{U}\left]\right]$ as well by the Shoenfield absoluteness.

Step $\mathcal{L}{\Pi }_k^1\to \mathcal{L}{\Sigma }_{k+1}^1,k<𝕟$. Let $\phi \left(x\right)$ be a $\mathcal{L}{\Pi }_k^1\left(K\left[\mathbb{U}\right]\right)$ formula; let us prove the result for $\exists x\phi \left(x\right)$. If $p\in G$ and $p{}^K\mathbf{forc}{}_{\xi }^{}\exists x\phi \left(x\right)$ then by definition there is a name $\tau \in {\mathbb{M}}_{\xi }\cap {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[{\mathbb{U}}_{\xi }\right]\right)$, $K\left[{\mathbb{U}}_{\xi }\right]$-full below p, and such that $p{}^K\mathbf{forc}{}_{\xi }^{}\phi \left(\tau \right)$. By Lemma 10, there is a $K\left[{\mathbb{U}}_{\xi }\right]$-full name ${\tau }^{\prime }\in {\mathbb{M}}_{\xi }\cap {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[{\mathbb{U}}_{\xi }\right]\right)$, equivalent to $\tau$ below p. Then $p{}^K\mathbf{forc}{}_{\xi }^{}\phi \left({\tau }^{\prime }\right)$ by Lemma 20. Note that ${\tau }^{\prime }$ is ${\mathbb{P}}_{\xi }$-full by Corollary 1, hence $\mathbb{P}$-full by Corollary 6(iv), and $K\left[\mathbb{U}\right]$-full, too. It follows that $\phi \left({\tau }^{\prime }\right)\left[G\right]$ holds in $\mathbf{L}[G\cap K[\mathbb{U}\left]\right]$ by the inductive hypothesis, thus $\left(\exists x\phi \right(x\left)\right)\left[G\right]$ holds in $\mathbf{L}[G\cap K[\mathbb{U}\left]\right]$ because ${\tau }^{\prime }\left[G\right]=\tau \left[G\right]\in \mathbf{L}[G\cap K\left[\mathbb{U}\right]]$ by the choice of $\tau$.

If conversely $\left(\exists x\phi \right(x\left)\right)\left[G\right]$ is true in $\mathbf{L}[G\cap K[\mathbb{U}\left]\right]$ then by definition there is an element $x\in \mathbf{L}[G\cap K]=\mathbf{L}[G\cap K[\mathbb{U}\left]\right]$ such that $\phi \left[G\right]\left(x\right)$ is true in $\mathbf{L}[G\cap K[\mathbb{U}\left]\right]$. By Theorem 5(ii), there is a $K\left[\mathbb{U}\right]$-full name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[\mathbb{U}\right]\right)$ such that $x=\tau \left[G\right]$. Thus $\phi \left(\tau \right)\left[G\right]$ is true in $\mathbf{L}[G\cap K[\mathbb{U}\left]\right]$. Note that $\tau$ is $\mathbb{P}$-full as well, by Corollary 1, and hence $K\left[\mathbb{U}\right]$-full, too. By the inductive hypothesis, there is a condition $p\in G$ such that $p{}^K\mathbf{forc}{}_{\infty }^{}\phi \left(\tau \right)$. It follows that $p{}^K\mathbf{forc}{}_{\infty }^{}\exists x\phi \left(x\right)$.

Step $\mathcal{L}{\Sigma }_k^1\to \mathcal{L}{\Pi }_k^1$, $2\le k<𝕟$. Prove the theorem for a $\mathcal{L}{\Pi }_k^1\left(K\left[\mathbb{U}\right]\right)$ formula $\phi$, assuming that the result holds for ${\phi }^{\neg }$. If $\phi \left[G\right]$ is false in $\mathbf{L}\left[G\right]$ then $\phi {\phantom{)}}^{\neg }\left[G\right]$ is true. Thus by the inductive hypothesis, there is a condition $p\in G$ such that $p{}^K\mathbf{forc}{}_{\infty }^{}\phi {\phantom{)}}^{\neg }$. Then $q{}^K\mathbf{forc}{}_{\infty }^{}\phi$ for any $q\in G$ is impossible by Lemma 24(ii). Conversely, suppose that $p{}^K\mathbf{forc}{}_{\infty }^{}\phi$ fails for all $p\in G\cap K$. Then by Lemma 25(i) there is $q\in G\cap K\left[\mathbb{U}\right]$ such that $q{}^K\mathbf{forc}{}_{\infty }^{}\phi {\phantom{)}}^{\neg }$. It follows that $\phi {\phantom{)}}^{\neg }\left[G\right]$ is true in $\mathbf{L}[G\cap K[\mathbb{U}\left]\right]$ by the inductive hypothesis, therefore $\phi \left[G\right]$ is false.

(i) Let $\phi$ be a $\mathcal{L}{\Pi }_{}^1\left(K\left[\mathbb{U}\right]\right)$ formula, $p\in G\cap K\left[\mathbb{U}\right]$, $p{}^K\mathbf{forc}{}_{\infty }^{}\phi$. By Lemma 24(ii), there is no $q\in G\cap K\left[\mathbb{U}\right]$ such that $q{}^K\mathbf{forc}{}_{\infty }^{}\phi {\phantom{)}}^{\neg }$. However, $\phi {\phantom{)}}^{\neg }$ is $\mathcal{L}{\Sigma }_{𝕟}^1\left(K\left[\mathbb{U}\right]\right)$, thus $\neg \phi \left[G\right]$ in $\mathbf{L}[G\cap K]$ holds by (ii).

Finally prove (i) for a formula $\phi :=\exists x\psi \left(x\right)$, $\psi$ being $\mathcal{L}{\Pi }_{𝕟}^1\left(K\left[\mathbb{U}\right]\right)$. Suppose that $p\in G\cap K\left[\mathbb{U}\right]$ and $p{}^K\mathbf{forc}{}_{\infty }^{}\phi$. Then there is a name $\tau \in {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[\mathbb{U}\right]\right)$, $K\left[\mathbb{U}\right]$-full below p and such that $p{}^K\mathbf{forc}{}_{\infty }^{}\psi \left(\tau \right)$. We can w.l.o.g. assume that $\tau$ is totally $K\left[\mathbb{U}\right]$-full, by Lemmas 10 and 20. We have to prove that the formula $\psi \left(\tau \right)\left[G\right]$, that is, $\psi \left[G\right]\left(\tau \right[G\left]\right)$, holds in $\mathbf{L}[G\cap K]$—then $\phi \left[G\right]$ holds in $\mathbf{L}[G\cap K]$ as well. Suppose to the contrary that $\psi \left(\tau \right)\left[G\right]$ fails in $\mathbf{L}[G\cap K]$. However, $\psi \left(\tau \right){\phantom{)}}^{\neg }$ is a ${\Sigma }_n^1$ formula. Therefore, by the first claim of the lemma, there is a condition $q\in G\cap K$ such that $q{}^K\mathbf{forc}{}_{\infty }^{}\psi \left(\tau \right){\phantom{)}}^{\neg }$. However, $p{}^K\mathbf{forc}{}_{\infty }^{}\psi \left(\tau \right)$ and $p,q$ are compatible (as they belong to the same generic set). This contradicts Lemma 24(ii). □

6.3. Consequences for the Ordinary Forcing Relation

For any forcing $P\in \mathbf{L}$, we let ${\left|\right|--}_P$ be the ordinary $P$-forcing relation over $\mathbf{L}$ as the ground universe. In particular ${\left|\right|--}_{\mathbb{P}}$ is the $\mathbb{P}$-forcing relationover $\mathbf{L}$.

Corollary 8 (in L).

Under the assumptions of Theorem 12, let $p\in K\left[\mathbb{U}\right]$. Then:

(i)

if φ is $\mathcal{L}{\Pi }_k^1\left(K\left[\mathbb{U}\right]\right)$ or $\mathcal{L}{\Sigma }_{k+1}^1\left(K\left[\mathbb{U}\right]\right)$ and $p{}^K\mathbf{forc}{}_{\infty }^{}\phi$, then $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi ;$

(ii)

if φ is $\mathcal{L}{\Pi }_k^1\left(K\left[\mathbb{U}\right]\right)$, then $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi$ iff $\neg \exists q\in K\left[\mathbb{U}\right](q\le p\wedge q{}^K\mathbf{forc}{}_{\infty }^{}\phi {\phantom{)}}^{\neg });$

(iii)

if $k<𝕟$ strictly, φ belongs to $\mathcal{L}{\Pi }_k^1\left(K\left[\mathbb{U}\right]\right)$ or $\mathcal{L}{\Sigma }_{k+1}^1\left(K\left[\mathbb{U}\right]\right)$, and $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi$, then

$\phantom{.}$$\exists q\in K\left[\mathbb{U}\right](q\le p\wedge q{}^K\mathbf{forc}{}_{\infty }^{}\phi );$

(iv)

if $k<𝕟$ strictly, φ is $\mathcal{L}{\Pi }_k^1\left(K\left[\mathbb{U}\right]\right)$, and $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi$ then $p{}^K\mathbf{forc}{}_{\infty }^{}\phi .$

Proof. 

(i) follows from Theorem 12(i).

(iii) Let $G\subseteq \mathbb{P}$ be $\mathbb{P}$-generic over $\mathbf{L}$, and $p\in G$. If $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi$ then $\phi \left[G\right]$ is true in $\mathbf{L}[G\cap K[\mathbb{U}\left]\right]$, and hence there is $r\in G\cap K$ such that $r{}^K\mathbf{forc}{}_{\infty }^{}\phi$, by Theorem 12. However, then $p,r$ are compatible (as members of G), hence $q=p\wedge r$ still is a condition, and $q\in K\left[\mathbb{U}\right]$.

(iv) If $p{}^K\mathbf{forc}{}_{\infty }^{}\phi$ fails, then by Lemma 25(ii) there is a condition $q\in K\left[\mathbb{U}\right],q\le p$, such that $q{}^K\mathbf{forc}{}_{\infty }^{}\phi {\phantom{)}}^{\neg }$. Then $q{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi {\phantom{)}}^{\neg }$ by (i), thus $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi$ fails.

(ii) Suppose that $q\in K\left[\mathbb{U}\right],q\le p,q{}^K\mathbf{forc}{}_{\infty }^{}\phi {\phantom{)}}^{\neg }$. Then $q{\left|\right|--}_{K\left[\mathbb{U}\right]}\neg \phi$ by (i), and hence $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi$ fails. Now suppose that $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi$ fails. Then there is a condition $r\in K\left[\mathbb{U}\right],r\le p,r{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi {\phantom{)}}^{\neg }$. However, then, by (iii), there is a condition $q\in K\left[\mathbb{U}\right],q\le r,q{}^K\mathbf{forc}{}_{\infty }^{}\phi {\phantom{)}}^{\neg }$, as required. □

The next corollary evaluates the complexity of the ordinary forcing relations ${\left|\right|--}_{K\left[\mathbb{U}\right]}$. The result is related to formulas in classes $\mathcal{L}{\Pi }_{𝕟}^1$ and higher.

Corollary 9 (in L).

Let $\phi (x_1,\dots ,x_m)$ be an $\mathcal{L}(⌀)$ formula (that is, no names), and $K\subseteq {\mathbf{P}}^{*}$ be a regular forcing. Suppose that $w\in {\omega }^{\omega }$, and K is an absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(w\right)$ set. Then:

(i)

if φ belongs to $\mathcal{L}{\Pi }_k^1$, $k\ge 𝕟$, then the following set is ${\Pi }_{k-1}^{\mathrm{HC}}\left(w\right):$

$$\begin{array}{cccc}{\mathbf{FORC}}_K\left(\phi \right)\hfill & =& \{\hfill & ⟨p,{\tau }_1,\dots ,{\tau }_m⟩:p\in K\left[\mathbb{U}\right]\wedge \hfill \\ \hfill & & \hfill & {\tau }_1,\dots ,{\tau }_m\in {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[\mathbb{U}\right]\right)areK\left[\mathbb{U}\right]-fullnames\wedge \hfill \\ \hfill & & \hfill & p{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi ({\tau }_1,\dots ,{\tau }_m)\}\hfill \end{array}$$

(ii)

similarly, if φ is $\mathcal{L}{\Sigma }_k^1,k>𝕟$, then ${\mathbf{FORC}}_K\left(\phi \right)$ is ${\Sigma }_{k-1}^{\mathrm{HC}}\left(w\right)$.

Proof. 

We argue by induction on $k\ge 𝕟$. Suppose that $\phi$ is $\mathcal{L}{\Pi }_{𝕟}^1$ and ${\tau }_1,\dots ,{\tau }_m\in {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[\mathbb{U}\right]\right)$ are $K\left[\mathbb{U}\right]$-full names. It follows from Corollary 8(ii) that $⟨p,{\tau }_1,\dots ,{\tau }_m⟩\in {\mathbf{FORC}}_K\left(\phi \right)$ iff

$$\neg \exists \xi <{\omega }_1\exists q\in K\left[{\mathbb{U}}_{\xi }\right](q\le p\wedge q{}^K\mathbf{forc}{}_{{\mathbb{U}}_{\xi }}^{{\mathbb{M}}_{\xi }}\phi {\phantom{)}}^{\neg }({\tau }_1,\dots ,{\tau }_m)).$$

The formula $q{}^K\mathbf{forc}{}_{{\mathbb{U}}_{\xi }}^{{\mathbb{M}}_{\xi }}\phi {\phantom{)}}^{\neg }({\tau }_1,\dots ,{\tau }_m)$ can be replaced by

$$⟨{\mathbb{M}}_{\xi },{\mathbb{U}}_{\xi },q,\phi ({\tau }_1,\dots ,{\tau }_m)⟩\in {\mathbf{Forc}}_w^K\left({\Sigma }_{𝕟}^1\right)$$

(see a definition in Theorem 11). However, ${\mathbf{Forc}}_w^K\left({\Sigma }_{𝕟}^1\right)$ is ${\mathsf{\Delta }}_{𝕟-1}^{\mathrm{HC}}\left(w\right)$ by Theorem 11 (even ${\Pi }_{𝕟-2}^{\mathrm{HC}}\left(w\right)$ provided $𝕟\ge 3$). On the other hand, the maps $\xi ⟼{\mathbb{M}}_{\xi }$ and $\xi ⟼{\mathbb{U}}_{\xi }$ are ${\mathsf{\Delta }}_{𝕟-1}^{\mathrm{HC}}$ by construction (Definition 16). As K is ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(w\right)$, it easily follows that $\xi ⟼K\left[{\mathbb{U}}_{\xi }\right]$ is ${\mathsf{\Delta }}_{𝕟-1}^{\mathrm{HC}}\left(w\right)$. We conclude that ${\mathbf{FORC}}_K\left(\phi \right)$ is ${\Pi }_{𝕟-1}^{\mathrm{HC}}\left(w\right)$.

Step $\mathcal{L}{\Pi }_k^1\to \mathcal{L}{\Sigma }_{k+1}^1$. Suppose that $\phi \left(\overrightarrow{\tau }\right)$ is a $\mathcal{L}{\Sigma }_{k+1}^1$ formula of the form $\exists y\psi (y,\overrightarrow{\tau })$, where accordingly $\psi$ is $\mathcal{L}{\Pi }_k^1$. Let us show that simply

$$⟨p,\overrightarrow{\tau }⟩\in {\mathbf{FORC}}_K\left(\phi \right)⟺\exists \sigma \in {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[\mathbb{U}\right]\right)(⟨p,\sigma ,\overrightarrow{\tau }⟩\in {\mathbf{FORC}}_K\left(\psi \right)),$$

(5)

which obviously suffices to carry out the step $\mathcal{L}{\Pi }_k^1\to \mathcal{L}{\Sigma }_{k+1}^1$.

If $\sigma$ is a name as in the right-hand side then obviously any p forces $\sigma \left[G\right]\in \mathbf{L}[G\cap K[\mathbb{U}\left]\right]$, and on the other hand by definition $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\psi (\sigma ,\overrightarrow{\tau })$. Thus $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi \left(\overrightarrow{\tau }\right)$, hence, $⟨p,\overrightarrow{\tau }⟩\in {\mathbf{FORC}}_K\left(\phi \right)$, as required. Now suppose that $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi \left(\overrightarrow{\tau }\right)$. This means, by definition, that $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\exists y\psi (y,\overrightarrow{\tau })$. By Theorem 5(iv), there is a $K\left[\mathbb{U}\right]$-full name $\sigma \in {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[\mathbb{U}\right]\right)$ such that $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\psi (\sigma ,\overrightarrow{\tau })$, thus $⟨p,\sigma ,\overrightarrow{\tau }⟩\in {\mathbf{FORC}}_K\left(\psi \right)$.

Step $\mathcal{L}{\Sigma }_k^1\to \mathcal{L}{\Pi }_k^1$, $k>𝕟$. Suppose that $\phi$ is a $\mathcal{L}{\Pi }_k^1$ formula; accordingly, $\phi {\phantom{)}}^{\neg }$ is $\mathcal{L}{\Sigma }_k^1$. It is clear that, under the assumptions that $p\in K\left[\mathbb{U}\right]$ and ${\tau }_1,\dots ,{\tau }_m\in {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[\mathbb{U}\right]\right)$ are $K\left[\mathbb{U}\right]$-full names, the following holds:

$$⟨p,\overrightarrow{\tau }⟩\in {\mathbf{FORC}}_K\left(\phi \right)⟺\neg \exists q\in K\left[\mathbb{U}\right](q\le p\wedge ⟨p,\overrightarrow{\tau }⟩\in {\mathbf{FORC}}_K\left(\phi {\phantom{)}}^{\neg }\right)),$$

(6)

which is sufficient to accomplish the step $\mathcal{L}{\Sigma }_k^1\to \mathcal{L}{\Pi }_k^1$. □

6.4. Elementary Equivalence Theorem

According to Theorem 10, sets S satisfying ${ℾ}_i\left(S\right)$ are different for different indices $i\in \mathcal{I}$, and the difference can be determined, in the extensions of the form $\mathbf{L}\left[G\upharpoonright z\right]$, at the level ${\Pi }_{𝕟-1}^{\mathrm{HC}}$ by Corollary 7, that is, ${\Pi }_{𝕟}^1$ (see Remark 2 in Section 4.3). On the other hand, the extensions considered remain rather amorphous w.r.t. lower levels of definability, as witnessed by the following key theorem.

Theorem 13.

Suppose that, in $\mathbf{L}:$ $d\subseteq \mathcal{I}$, $w\in {\omega }^{\omega },$ sets $b,c\subseteq d^{\complement }=\mathcal{I}\setminus d$ have equal cardinality, $d^{\complement }$ is uncountable, $K\subseteq {\mathbf{P}}^{*}\upharpoonright d$ is a regular forcing, $\mathsf{\Psi }\left(y\right)$ is a ${\Pi }_{𝕟-1}^1$ formula with parameters in ${\omega }^{\omega }\cap \mathbf{L}[G\cap K]$, and $K,b,c,d$ are absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(w\right)$ sets. Let $G\subseteq \mathbb{P}$ be $\mathbb{P}$-generic over $\mathbf{L}$.

Then, if there is a real $y\in {\omega }^{\omega }\cap \mathbf{L}[G\cap K,G\upharpoonright b]$ such that $\mathsf{\Psi }\left(y\right)$ holds in $\mathbf{L}[G\cap K,G\upharpoonright d^{\complement }]$, then there exists $y^{\prime }\in \mathbf{L}[G\cap K,G\upharpoonright c]$ such that $\mathsf{\Psi }\left(y^{\prime }\right)$ holds in $\mathbf{L}[G\cap K,G\upharpoonright d^{\complement }].$

Recall that ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(w\right)$ means that w is admitted as the only parameter. The assumption that $d^{\complement }$ is uncountable, can be avoided at the cost of extra complications, but the case of $d^{\complement }$ countable is not considered below. The proof makes use of the transformations introduced in Section 3.7.

Proof. 

As all cardinals are preserved in $\mathbf{L}\left[G\right]$, we w.l.o.g. assume that $b,c$ are countably infinite (or finite of equal cardinality) in $\mathbf{L}$. Suppose towards the contrary that

(A) there is a real $y\in \mathbf{L}[G\cap K,G\upharpoonright b]$ such that $\mathsf{\Psi }\left(y\right)$ holds in $\mathbf{L}[G\cap K,G\upharpoonright d^{\complement }]$, but

(B) there is no $y^{\prime }\in \mathbf{L}[G\cap K,G\upharpoonright c]$ satisfying $\mathsf{\Psi }\left(y^{\prime }\right)$ in $\mathbf{L}[G\cap K,G\upharpoonright d^{\complement }]$.

By Theorem 5(ii), for every real parameter z in $\mathsf{\Psi }$ there is a $K\left[\mathbb{U}\right]$-full name ${\tau }_z\in {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[\mathbb{U}\right]\right)$ such that $z={\tau }_z\left[G\right]$. Replace each parameter z in $\mathsf{\Psi }\left(x\right)$ by such a name ${\tau }_z$ in $\mathbf{L}$, and let $\psi \left(x\right)$ be the $\mathcal{L}{\Pi }_{𝕟-1}^1\left(K\left[\mathbb{U}\right]\right)$ formula obtained. Then $\left|\psi \right|\subseteq d$. Further, the set

$$K^{\prime }=\{p\in {\mathbf{P}}^{*}\upharpoonright (d\cup b):p\upharpoonright d\in K\}=K\times \left({\mathbf{P}}^{*}\upharpoonright b\right)\subseteq {\mathbf{P}}^{*}\upharpoonright (d\cup b)$$

is a regular forcing, and $\mathbf{L}[G\cap K,G\upharpoonright b]=\mathbf{L}[G\cap K^{\prime }]$. Choose y by (A). Once again, Theorem 5(ii), yields a $K^{\prime }\left[\mathbb{U}\right]$-full name ${\tau }_y\in {\mathbf{SN}}_{\omega }^{\omega }\left(K^{\prime }\left[\mathbb{U}\right]\right)$ such that $y={\tau }_y\left[G\right]$. The name ${\tau }_y$ is small, hence the set $|{\tau }_y|\subseteq d\cup b$ is countable (in $\mathbf{L}$). We let $d_0=\left|{\tau }_y\right|\cap d$; the set $B=d_0\cup b$ is still countable and $|{\tau }_y|\subseteq B$. Thus the formula ${\exists }^{B}y\psi \left(y\right)\left[G\right]$ is true in $\mathbf{L}[G\cap K,G\upharpoonright d^{\complement }]$.

Now let $Q=\{p\in {\mathbf{P}}^{*}:p\upharpoonright d\in K\}=K\times \left({\mathbf{P}}^{*}\upharpoonright d^{\complement }\right)$. Thus Q is a regular forcing, and $\mathbf{L}[G\cap K,G\upharpoonright d^{\complement }]=\mathbf{L}[G\cap Q]=\mathbf{L}[G\cap Q\left[\mathbb{U}\right]]$. Therefore ${\exists }^{B}y\psi \left(y\right)\left[G\right]$ is true in $\mathbf{L}[G\cap Q[\mathbb{U}\left]\right]$ by the above. It follows by Theorem 12(ii) that there is a condition $p\in G\cap Q$ such that $p{}^Q\mathbf{forc}{}_{\infty }^{}{\exists }^{B}y\psi \left(y\right)$, and, by (B), we can also assume that p $Q\left[\mathbb{U}\right]$-forces $\neg {\exists }^{C}y\psi \left(y\right)$ over $\mathbf{L}$ where $C=d_0\cup c$. Further, in $\mathbf{L}$, there exists an ordinal $\xi <{\omega }_1$ such that

$$p{}^Q\mathbf{forc}{}_U^M{\exists }^{B}y\psi \left(y\right),$$

(7)

where $M={\mathbb{M}}_{\xi }$ and $U={\mathbb{U}}_{\xi }$, and in addition the countable sets $d_0,b,c$ belong to M, $w\in M$, $p\in Q\left[U\right]$, $d_0\cup b\cup c\subseteq A=\left|U\right|$, and all names in $\psi$ belong to $M\cap {\mathbf{SN}}_{\omega }^{\omega }\left(K\left[U\right]\right)$, so that $\psi \left(x\right)$ is a $\mathcal{L}{\Pi }_{𝕟-1}^1(K\left[U\right],M)$ formula.

Now we can assume that both sets $\left|U\right|\setminus (d\cup b)$ and $\left|U\right|\setminus (d\cup c)$ are infinite. (Otherwise take a suitably bigger $\xi$.) Then there is a bijection $f\in M,f:\left|U\right|\stackrel{\mathrm{onto}}{⟶}\left|U\right|$, such that $f\upharpoonright d$ is the identity and $f\left[b\right]=c$. Define a bijection $\pi \in {\mathrm{BIJ}}_{\mathcal{I}}^{\mathcal{I}}$ such that $\pi \upharpoonright \left|U\right|$ coincides with f and $\pi \upharpoonright (\mathcal{I}\setminus |U\left|\right)$ is the identity. Let $q=\pi ·p$ and $V=\pi ·U$. Acting by $\pi$ on (7), we obtain, by Lemma 22,

$$q{}^Q\mathbf{forc}{}_V^M{\exists }^{C}y\psi \left(y\right),$$

(8)

Comments: (1) $\pi ·Q=Q$ since $\pi \upharpoonright d$ is the identity by construction and $K\subseteq {\mathbf{P}}^{*}\upharpoonright d$; (2) $\pi ·B=\pi \left[B\right]=f\left[B\right]=C$ by construction; (3) $\pi ·\psi \left(x\right)$ is $\psi \left(x\right)$ because $\left|\psi \right|\subseteq d$ and $\pi \upharpoonright d$ is the identity.

Note that $V\in M$ is a system with $\left|V\right|=\pi ·\left|U\right|=\left|U\right|$, and $p\in U$, $q\in V$, $U\upharpoonright d=V\upharpoonright d$ and $q\upharpoonright d=p\upharpoonright d$ by the choice of $\pi$ and f. In addition, $U,V$ are countable systems in $M\vDash {\mathbf{ZFC}}_1^{-}$. Corollary 2 yields a transformation $\mathit{\alpha }\in {\mathbf{Lip}}^{\mathcal{I}}$ in M such that $\left|\mathit{\alpha }\right|=\left|U\right|=\left|V\right|$, $\mathit{\alpha }·V=U$, conditions $q^{\prime }=\mathit{\alpha }·q\in Q\left[U\right]$ and p are compatible, and $\mathit{\alpha }\upharpoonright d$ is the identity (as $U\upharpoonright d=V\upharpoonright d$ and $p\upharpoonright d=q\upharpoonright d$). However, then $\mathit{\alpha }·Q=Q$, and $\mathit{\alpha }\left({\exists }^{C}x\psi \left(x\right)\right)$ coincides with ${\exists }^{C}x\psi \left(x\right)$ since $\left|\psi \right|\subseteq d$. Therefore $q^{\prime }{}^Q\mathbf{forc}{}_U^M{\exists }^{C}y\psi \left(y\right)$ by (8) and Lemma 23. This implies $q^{\prime }{}^Q\mathbf{forc}{}_{\infty }^{}{\exists }^{C}y\psi \left(y\right)$. We conclude that $q^{\prime }$ $Q\left[\mathbb{U}\right]$-forces ${\exists }^{C}y\psi \left(y\right)$ over $\mathbf{L}$, by Corollary 8(i). However, $q^{\prime }$ is compatible with p and p forces the negation of this sentence. The contradiction completes the proof. □

Corollary 10.

Under the assumptions of Theorem 13, if c is uncountable in $\mathbf{L}$, then $\mathbf{L}[G\cap K,G\upharpoonright c]$ is an elementary submodel of $\mathbf{L}[G\cap K,G\upharpoonright d^{\complement }]$ w.r.t. all ${\Sigma }_{𝕟}^1$ formulas with parameters in ${\omega }^{\omega }\cap \mathbf{L}[G\cap K,G\upharpoonright c]$.

Proof. 

Prove by induction that if $k\le 𝕟$ then $\mathbf{L}[G\cap K,G\upharpoonright c]$ is an elementary submodel of $\mathbf{L}[G\cap K,G\upharpoonright d^{\complement }]$ w.r.t. all ${\Sigma }_k^1$ formulas with parameters in $\mathbf{L}[G\cap K,G\upharpoonright c]$. If $k=2$ then the result holds by the Shoenfield absoluteness theorem. It remains to carry out the step $k\to k+1$ ($k<𝕟$). Let $\phi \left(x\right)$ be a ${\Pi }_k^1$ formula with parameters in $\mathbf{L}[G\cap K,G\upharpoonright c]$; we have to prove the result for the ${\Sigma }_k^1$ formula $\exists x\phi \left(x\right)$, assuming $k<𝕟$. First of all, as the cardinals are preserved, there is a set $\delta \in \mathbf{L},\delta \subseteq d^{\complement }$, countable in $\mathbf{L}$ and such that all parameters of $\phi$ belong to $\mathbf{L}[G\cap K,G\upharpoonright \delta ]$. Let $d^{\prime }=d\cup \delta$ and $K^{\prime }=\{p\in {\mathbf{P}}^{*}\upharpoonright d^{\prime }:p\upharpoonright d\in K\}$; we can identify $K^{\prime }$ with $K\times \left({\mathbf{P}}^{*}\upharpoonright \delta \right)$, of course. Then, in $\mathbf{L}$, $K^{\prime }$ is a regular forcing, $K^{\prime }\subseteq {\mathbf{P}}^{*}\upharpoonright d^{\prime }$, and all parameters of $\phi$ belong to $\mathbf{L}[G\cap K^{\prime }]$.

Now suppose that $\exists x\phi \left(x\right)$ holds in $\mathbf{L}[G\cap K,G\upharpoonright d^{\complement }]$, the bigger of the two models of the lemma. Let this be witnessed by a real $x_0\in \mathbf{L}[G\cap K,G\upharpoonright d^{\complement }]=\mathbf{L}[G\cap K^{\prime },G\upharpoonright {\left(d^{\prime }\right)}^{\complement }]$, where ${\left(d^{\prime }\right)}^{\complement }=\mathcal{I}\setminus d^{\prime }=d^{\complement }\setminus \delta$, so that $\phi \left(x_0\right)$ holds in the model $\mathbf{L}[G\cap K,G\upharpoonright d^{\complement }]=\mathbf{L}[G\cap K^{\prime },G\upharpoonright {\left(d^{\prime }\right)}^{\complement }]$. As the cardinals are preserved, there is a set $b^{\prime }\in \mathbf{L},b^{\prime }\subseteq {\left(d^{\prime }\right)}^{\complement }$, countably infinite in $\mathbf{L}$ and such that $x_0$ belongs to $\mathbf{L}[G\cap K^{\prime },G\upharpoonright b^{\prime }]$. Since c is uncountable, there exists a set $c^{\prime }\in \mathbf{L},c^{\prime }\subseteq {\left(d^{\prime }\right)}^{\complement }\cap c$, countably infinite in $\mathbf{L}$. By the choice of $\delta$, there is a real $w^{\prime }\in {\omega }^{\omega }\cap \mathbf{L}$ such that the sets $K^{\prime },d^{\prime },c^{\prime },b^{\prime }$ are absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(w^{\prime }\right)$ in $\mathbf{L}$. By Theorem 13, there is a real $y_0\in \mathbf{L}[G\cap K^{\prime },G\upharpoonright c^{\prime }]$ such that $\phi \left(y_0\right)$ holds in $\mathbf{L}[G\cap K^{\prime },G\upharpoonright {\left(d^{\prime }\right)}^{\complement }]=\mathbf{L}[G\cap K,G\upharpoonright d^{\complement }]$, and then in $\mathbf{L}[G\cap K,G\upharpoonright c]$ by the inductive assumption. □

Note that if say c is uncountable but b countable, and d is countable, then Theorem 13 fails by means of the formula “there is a real x such that all reals belong to $\mathbf{L}[x,G\cap K]$”, and $G\cap K$ is equiconstructible with a real in this case.

Question 1.

It would be very interesting to figure out whether Theorem 13 and Corollary 10 hold also for sets $b,c$ not necessarily constructible.

The following corollary presents a partial positive result.

A set $z\subseteq \mathcal{I}={\omega }_1^{\mathbf{L}}$ is bounded iff there is $\alpha <{\omega }_1^{\mathbf{L}}$ such that $z\subseteq \alpha$.

Corollary 11.

Suppose that $G\subseteq \mathbb{P}$ is $\mathbb{P}$-generic over $\mathbf{L}$, and $z\subseteq \mathcal{I}$ is a set unbounded in $\mathcal{I}$, locally constructible in the sense that $z\cap \alpha \in \mathbf{L}$ for all $\alpha \in \mathcal{I}$, and all $\mathbf{L}$-cardinals are preserved in $\mathbf{L}\left[G\upharpoonright z\right]$. Then $\mathbf{L}\left[G\upharpoonright z\right]$ is elementarily equivalent to $\mathbf{L}\left[G\right]$ w.r.t. all ${\Sigma }_{𝕟}^1$ formulas with parameters in $\mathbf{L}\left[G\upharpoonright z\right]$.

Remark: under the assumptions of the corollary, it is not necessary that $\mathbf{L}\left[G\upharpoonright z\right]\subseteq \mathbf{L}\left[G\right]$, since the set z is not assumed to belong to $\mathbf{L}\left[G\right]$, but we necessarily have $\mathbf{L}\left[G\upharpoonright z\right]\cap {\omega }^{\omega }\subseteq \mathbf{L}\left[G\right]\cap {\omega }^{\omega }$ by rather obvious reasons.

Proof. 

Prove by induction that for any $k\le 𝕟$, $\mathbf{L}\left[G\upharpoonright z\right]$ is elementarily equivalent to $\mathbf{L}\left[G\right]$ w.r.t. all ${\Sigma }_k^1$ formulas with parameters in $\mathbf{L}\left[G\upharpoonright z\right]$. For $k=2$ use Shoenfield’s absoluteness. To carry out the step $k\to k+1$ ($k<𝕟$), let $\phi :=\exists y\psi \left(y\right)$ be a ${\Sigma }_{k+1}^1$ formula with parameters in $\mathbf{L}\left[G\upharpoonright z\right]$. Then, by the choice of z, (1) there is a set $d\in \mathbf{L},d\subseteq z$, countable in $\mathbf{L}$ and such that all parameters in $\phi$ belong to $\mathbf{L}\left[G\upharpoonright d\right]$, and (2) there is a set $e\in \mathbf{L},e\subseteq z\setminus d$, countably infinite in $\mathbf{L}$.

Now suppose that $\exists y\psi \left(y\right)$ is true in $\mathbf{L}\left[G\right]$. This is witnessed by a real $y^{\prime }\in \mathbf{L}\left[G\upharpoonright (d\cup e^{\prime })\right]$ for a set $e^{\prime }\in \mathbf{L},e^{\prime }\subseteq \mathcal{I}\setminus d$, countably infinite in $\mathbf{L}$. Then, by Theorem 13 with $K={\mathbf{P}}^{*}\upharpoonright d$, there is a real $y\in \mathbf{L}\left[G\upharpoonright (d\cup e)\right]$, hence, $y\in \mathbf{L}\left[G\upharpoonright z\right]$, such that $\psi \left(y\right)$ is true in $\mathbf{L}\left[G\right]$. However, then $\psi \left(y\right)$ is true in $\mathbf{L}\left[G\upharpoonright z\right]$ by the inductive hypothesis. Hence $\phi$ is true in $\mathbf{L}\left[G\upharpoonright z\right]$ as well, as required. □

7. Application 1: Nonconstructible ${\mathsf{\Delta }}_n^1$ Reals

In this section, we proveTheorems 1 and 2(i). Theorem 1 provides change of definability of reals situated in the ground set universe $\mathbf{L}$, in generic extensions of $\mathbf{L}$. Thus, any real $a\notin {\Sigma }_{𝕟}^1\cup {\Pi }_{𝕟}^1$ in $\mathbf{L}$ can be placed exactly at ${\mathsf{\Delta }}_{𝕟+1}^1$ in an appropriate (almost disjoint) extension of $\mathbf{L}$. Theorem 2 contains several results for nonconstructible reals. The proofs of these results will make use of various results in Section 5 and Section 6, in particular, a result (Theorem 11) related to definability of relevant forcing relations.

Assumption 3.

We continue to assume $\mathbf{V}=\mathbf{L}$ in the ground universe. We fix an integer $𝕟\ge 2$, for which Theorems 1 and 2 will be proved, and make use of a system $\mathbb{U}$ and the forcing notion $\mathbb{P}=\mathbf{P}\left[\mathbb{U}\right]$ as in Definition 16; both $\mathbb{U}$ and $\mathbb{P}$ belong to $\mathbf{L}$.

7.1. Changing Definability of an Old Real

Proof (Theorem 1).

Fix a set $b\subseteq \omega ,b\notin {\Sigma }_n^1\cup {\Pi }_n^1$, in $\mathbf{L}$, and define

$c=\{2k:k\in b\}\cup \{2k+1:k\notin b\}\mathrm{and}K={\mathbf{P}}^{*}\upharpoonright c=\{p\in {\mathbf{P}}^{*}:\left|p\right|\subseteq c\}$.

Thus $c\subseteq \omega \subseteq \mathcal{I}={\omega }_1$, $c\in \mathbf{L}$, $K\subseteq {\mathbf{P}}^{*}$ is a regular forcing. Let $G\subseteq \mathbb{P}$ be a $P$-generic set over $\mathbf{L}$. Then the set $G\cap K=G\upharpoonright c$ is $K\left[\mathbb{U}\right]$-generic over $\mathbf{L}$ by Lemma 9(ii), where $K\left[\mathbb{U}\right]=K\cap \mathbf{P}\left[\mathbb{U}\right]$, as usual.

Define $S\left(\nu \right)=S_G\left(\nu \right)\subseteq \mathbf{Seq}$ and $a_{\nu }=a_G\left(\nu \right)=\{k\ge 1:{\mathrm{s}}_k\in S_G\left(\nu \right)\}$ for every $\nu$, as in Definition 9. We assert that the submodel $\mathbf{L}\left[G\upharpoonright c\right]=\mathbf{L}[G\cap K]=\mathbf{L}\left[{\left\{a_m\right\}}_{m\in c}\right]$ of the whole generic extension $\mathbf{L}\left[G\right]$ witnesses Theorem 1. This amounts to the two following claims:

Claim 3.

It is true in $\mathbf{L}\left[G\upharpoonright c\right]$ that c is ${\Sigma }_{𝕟+1}^1$, therefore b is ${\mathsf{\Delta }}_{𝕟+1}^1$.

Proof. 

By definition we have $c=\left|K\right|=\left|K\cap G\right|$. Therefore c is ${\Sigma }_{𝕟}^{\mathrm{HC}}$ in $\mathbf{L}\left[G\upharpoonright c\right]$ by Corollary 7(iii), hence ${\Sigma }_{𝕟+1}^1$ (see Remark 2 in Section 4.3), and $b=\{k:2k\in c\}=\{k:2k+1\notin c\}\in {\mathsf{\Delta }}_{𝕟+1}^1$, as required. In more detail,

$$\begin{array}{ccccc}\hfill c& =& \{m:S_G\left(m\right)\in \mathbf{L}\left[G\upharpoonright c\right]\}\hfill & =& \{m:\mathbf{L}\left[G\upharpoonright c\right]\vDash \exists S{ℾ}_m\left(S\right)\},\mathrm{hence}\hfill \\ \hfill a& =& \{k:S_G\left(2k\right)\in \mathbf{L}\left[G\upharpoonright c\right]\}\hfill & =& \{k:\mathbf{L}\left[G\upharpoonright c\right]\vDash \exists S{ℾ}_{2k}\left(S\right)\}\hfill \\ \hfill & =& \{k:S_G(2k+1)\notin \mathbf{L}\left[G\upharpoonright c\right]\}\hfill & =& \{k:\mathbf{L}\left[G\upharpoonright c\right]\vDash \neg \exists S{ℾ}_{2k+1}\left(S\right)\}\hfill \end{array}$$

by Theorem 10, and it remains to apply Lemma 17. □

Claim 4.

In $\mathbf{L}\left[G\upharpoonright c\right]:$ if $x\subseteq \omega$ is ${\Sigma }_{𝕟}^1$ then $x\in \mathbf{L}$ and x is ${\Sigma }_{𝕟}^1$ in $\mathbf{L}$.

Proof. (Claim 4).

Let $x=\left\{m:\phi \right(m\left)\right\}$ in $\mathbf{L}\left[G\upharpoonright c\right]$, where $\phi \left(m\right)$ is a ${\Sigma }_{𝕟}^1$ formula. Define $c^{\prime }=\omega$, $K^{\prime }={\mathbf{P}}^{*}\upharpoonright \omega$, and $K^{\prime }\left[U\right]=K^{\prime }\cap \mathbf{P}\left[U\right]$, as usual. Prove that

$$m\in x⟺\exists ⟨M,U⟩\in \mathbf{sJS}\exists p\in K^{\prime }\left[U\right]\left(p{}^{K^{\prime }}\mathbf{forc}{}_U^M\phi \left(m\right)\right).$$

(9)

The right-hand side of (9) is relativized to $\mathbf{L}$ and is ${\Sigma }_n^1$ in $\mathbf{L}$ by Theorem 11. Thus (9) implies Claim 4.

To verify $⟹$ in (9), suppose that $m\in x$, that is, $\phi \left(m\right)$ holds in $\mathbf{L}\left[G\upharpoonright c\right]=\mathbf{L}[G\cap K]$. Then by Theorem 12(ii) there is a condition $p\in G\cap K$ such that $p{}^K\mathbf{forc}{}_{\infty }^{}\phi \left(m\right)$, that is, $p{}^K\mathbf{forc}{}_U^M\phi \left(m\right)$, where $M={\mathbb{M}}_{\xi }$, $U={\mathbb{U}}_{\xi }$ for some $\xi <{\omega }_1$. As ${\mathbb{M}}_{\xi }=M\vDash {\mathbf{ZFC}}_1^{-}$, M contains $c,c^{\prime }$, and the increasing bijection $\pi \in {\mathrm{BIJ}}_{c^{\prime }}^c$. It follows that $q{}^{K^{\prime }}\mathbf{forc}{}_{U^{\prime }}^M\phi \left(m\right)$, by Lemma 22, where $U^{\prime }=\pi ·U$ and $q=\pi ·p$, as obviously $\pi ·K=K^{\prime }$. This implies the right-hand side of (9).

To verify $⟸$, let $⟨M^{\prime },U^{\prime }⟩\in \mathbf{sJS}$, $p^{\prime }\in K^{\prime }\left[U^{\prime }\right]$, and $p^{\prime }{}^{K^{\prime }}\mathbf{forc}{}_{U^{\prime }}^{M^{\prime }}\phi \left(m\right)$. Suppose towards the contrary that $\phi \left(m\right)$ fails in $\mathbf{L}[G\cap K]$, so that there is a condition $q\in G\cap K$ such that $q{\left|\right|--}_{K\left[\mathbb{U}\right]}\neg \phi \left(m\right)$. Then $q\in K\left[\mathbb{U}\right]$ (since $G\subseteq \mathbb{P}$), and hence there is an ordinal $\xi <{\omega }_1$ such that $q\in K\left[{\mathbb{U}}_{\xi }\right]$, $\omega \cup |U^{\prime }|\subseteq |{\mathbb{U}}_{\xi }|$ and $M^{\prime }\subseteq {\mathbb{M}}_{\xi }$. Then still $p^{\prime }{}^{K^{\prime }}\mathbf{forc}{}_{U^{\prime }}^{{\mathbb{M}}_{\xi }}\phi \left(m\right)$ by Lemma 18, and Lemma 22 implies $p{}^K\mathbf{forc}{}_U^{{\mathbb{M}}_{\xi }}\phi \left(m\right)$, where $p={\pi }^{-1}·p^{\prime }$ and $U={\pi }^{-1}·U^{\prime }$. (By obvious reasons, $K={\pi }^{-1}·K^{\prime }$.) Note that $\left|U\right|\subseteq |{\mathbb{U}}_{\xi }|$ by the choice of $\xi$. Therefore, we can define a system $V\in {\mathbb{M}}_{\xi }$ such that $V\upharpoonright \left|U\right|=U$ and $V\left(\nu \right)={\mathbb{U}}_{\xi }\left(\nu \right)$ for all $\nu \notin \left|U\right|$. Then obviously $⟨{\mathbb{M}}_{\xi },U⟩\preccurlyeq ⟨{\mathbb{M}}_{\xi },V⟩$, therefore $p{}^K\mathbf{forc}{}_V^{{\mathbb{M}}_{\xi }}\phi \left(m\right)$.

Now, V and ${\mathbb{U}}_{\xi }$ are countable systems in ${\mathbb{M}}_{\xi }$ with $\left|V\right|=|{\mathbb{U}}_{\xi }|$ and $p\in K\left[V\right]$ but $q\in K\left[{\mathbb{U}}_{\xi }\right]$. Corollary 2 yields a transformation $\mathit{\alpha }\in {\mathit{Lip}}^{\mathcal{I}}$ in M such that $\left|\mathit{\alpha }\right|\subseteq c$, $\mathit{\alpha }·V={\mathbb{U}}_{\xi }$, and conditions $r=\mathit{\alpha }·p\in K\left[{\mathbb{U}}_{\xi }\right]$ and q are compatible. Then $r{}^K\mathbf{forc}{}_{{\mathbb{U}}_{\xi }}^{{\mathbb{M}}_{\xi }}\phi \left(m\right)$ by Lemma 23. (Comment: $\mathit{\alpha }\phi$ is $\phi$, and $\mathit{\alpha }·K=K$ because regular forcings of the form $K={\mathbf{P}}^{*}\upharpoonright c$ are invariant w.r.t. the transformations in ${\mathbf{Lip}}^{\mathcal{I}}$.) Thus $r{}^K\mathbf{forc}{}_{\infty }^{}\phi \left(m\right)$, and hence $r{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi \left(m\right)$ by Corollary 8(i). However, r is compatible with q, and q forces the opposite, a contradiction. This ends the proof of (9).    (Claim 4) □

                              (Theorem 1) □

7.2. Nonconstructible ${\mathsf{\Delta }}_{𝕟+1}^1$ Real, Part 1

Here we begin the proof of Theorem 2(i). Suppose that a set $G\subseteq \mathbb{P}$ is $\mathbb{P}$-generic over $\mathbf{L}$. Define $S\left(\nu \right)=S_G\left(\nu \right)\subseteq \mathbf{Seq}$ and $a_{\nu }=a_G\left(\nu \right)=\{k\ge 1:{\mathrm{s}}_k\in S_G\left(\nu \right)\}$ for every $\nu$ as in Definition 9. Emulating the construction in Section 7.1, put

$$z=z_G=\left\{0\right\}\cup \{2k+2:k\in a_0\}\cup \{2k+1:k\notin a_0\}.$$

(10)

The sets $S_G\left(\nu \right)$ and $a_{\nu }$ do not belong to $\mathbf{L}$, accordingly, $z=z_G\in \mathbf{L}\left[a_0\right]\setminus \mathbf{L}$—unlike c in Section 7.1. Nevertheless, we are going to prove that the extension $\mathbf{L}\left[G\upharpoonright z\right]=\mathbf{L}\left[{\left\{a_m\right\}}_{m\in z}\right]$ witnesses Theorem 2(i) with $a=a_0$.

Note that the setup here is not exactly the same as in the proof of Theorem 1 in Section 7.1 since the set z does not belong to $\mathbf{L}$, the ground universe. Therefore we cannot treat ${\mathbf{P}}^{*}\upharpoonright z$ as a forcing in $\mathbf{L}$. Instead of ${\mathbf{P}}^{*}\upharpoonright z$, we make use of the set K of all conditions $p\in {\mathbf{P}}^{*}\upharpoonright \omega$ such that for any $k\ge 1$:

(A)

if $2k\in \left|p\right|$ then ${\mathrm{s}}_k\in S_p\left(0\right);$

(B)

if $2k-1\in \left|p\right|$ then ${\mathrm{s}}_k\in F_p^{\vee }\left(0\right)\setminus S_p\left(0\right)$—and hence $2k\notin \left|p\right|$ by (A).

as well as the related set $K\left[\mathbb{U}\right]=K\cap \mathbb{P}=K\cap \mathbf{P}\left[\mathbb{U}\right]$.

Lemma 26.

K is a regular forcing in $\mathbf{L}$. If $G\subseteq \mathbb{P}$ is $\mathbb{P}$-generic over $\mathbf{L}$ then $G\cap K=G\cap K\left[\mathbb{U}\right]$ is a set $K\left[\mathbb{U}\right]$-generic over $\mathbf{L}$ and $\mathbf{L}[G\cap K]=\mathbf{L}\left[G\upharpoonright z_G\right].$

Proof. 

The nontrivial item of the regularity property here is (4) of Definition 8. If $p\in {\mathbf{P}}^{*}$ then define $p^{*}\in {\mathbf{P}}^{*}$ to be equal to p everywhere except for $S_{p^{*}}\left(0\right)=S_p\left(0\right)\cup S$, where S consists of all strings $s={\mathrm{s}}_k$ such that (1) $2k\in \left|p\right|$ or $2k-1\in \left|p\right|$, and (2) $s\notin F_p^{\vee }\left(0\right)$ (to make sure that $p^{*}\le p$). Now we let d contain 0, all numbers $2k\in |p^{*}|$ such that ${\mathrm{s}}_k\in S_{p^{*}}\left(0\right)$, and all numbers $2k-1\in |p^{*}|$ such that ${\mathrm{s}}_k\in F_p^{\vee }\left(0\right)\setminus S_{p^{*}}\left(0\right)$. (Compare to Example 2 in Section 3.2!)

The rest of the lemma follows from Lemma 9. □

Thus extensions of the form $\mathbf{L}\left[G\upharpoonright z_G\right]$ considered here are exactly $K\left[\mathbb{U}\right]$-generic extensions of $\mathbf{L}$. To check that those extensions satisfy Theorem 2(i), we prove the following Claims 5 and 6. The first of them is entirely similar to Claim 3, so the proof is omitted (left to the reader).

Claim 5.

It is true in $\mathbf{L}\left[G\upharpoonright z\right]$ that z is ${\Sigma }_{𝕟+1}^1$, therefore $a_0$ is ${\mathsf{\Delta }}_{𝕟+1}^1$.

Claim 6.

In $\mathbf{L}\left[G\upharpoonright z\right]$, if $x\subseteq \omega$ is ${\Sigma }_{𝕟}^1$, then $x\in \mathbf{L}$ and x is ${\Sigma }_{𝕟}^1$ in $\mathbf{L}$.

The proof of this claim involves the following lemma.

Lemma 27

(proved below in Section 7.3). Suppose that $⟨M,U⟩\in \mathbf{sJS}$, $p\in K\left[U\right]$, $q\in K\left[\mathbb{U}\right]$. Let Φ be any closed parameter-free ${\Sigma }_{𝕟}^1$ formula. Then it is impossible that simultaneously $q{\left|\right|--}_{K\left[\mathbb{U}\right]}\neg \mathsf{\Phi }$ and $p{}^K\mathbf{forc}{}_U^M\mathsf{\Phi }$.

Proof 

(Claim 6 from the lemma). Assume that $x=\left\{m:\phi \right(m\left)\right\}$ in $\mathbf{L}\left[G\upharpoonright c\right]=\mathbf{L}[G\cap K]$, where $\phi \left(m\right)$ is a ${\Sigma }_{𝕟}^1$ formula. We claim that then

$$m\in x⟺\exists ⟨M,U⟩\in \mathbf{sJS}\exists p\in K\left[U\right]\left(p{}^K\mathbf{forc}{}_U^M\phi \right(m\left)\right).$$

(11)

This proves Claim 6, of course, by Theorem 11. Now let us check (11) itself; this will be similar to the proof of (9) in Section 7.1.

Assume that $m\in x$, that is, $\phi \left(m\right)$ holds in $\mathbf{L}[G\cap K]$. By Theorem 12(ii) there is a condition $p\in G\cap K$ such that $p{}^K\mathbf{forc}{}_{\infty }^{}\phi \left(m\right)$, that is, $p{}^K\mathbf{forc}{}_U^M\phi \left(m\right)$, where $M={\mathbb{M}}_{\xi }$, $U={\mathbb{U}}_{\xi }$, $\xi <{\omega }_1$. However, this implies the right-hand side of (9).

Now assume that $⟨M,U⟩\in \mathbf{sJS}$, $p\in K\left[U\right]$, and $p{}^K\mathbf{forc}{}_U^M\phi \left(m\right)$. Suppose towards the contrary that $\phi \left(m\right)$ is false in $\mathbf{L}[G\cap K]$, so that there is a condition $q\in G\cap K$ such that $q{\left|\right|--}_{K\left[\mathbb{U}\right]}\neg \phi \left(m\right)$. However, this contradicts Lemma 27.    (Claim 6 and Theorem 2(i) modulo Lemma 27) □

7.3. Nonconstructible ${\mathsf{\Delta }}_{𝕟+1}^1$ Real, Part 2

We continue the proof of Theorem 2(i).

The proof of Lemma 27 that follows below makes use of transformations in ${\mathrm{BIJ}}_{\omega }^{\omega }$ (bijections of $\omega$) and those in the set ${\mathbf{Lip}}^{\omega }=\{\mathit{\alpha }\in {\mathbf{Lip}}^{\mathcal{I}}:\left|\mathit{\alpha }\right|\subseteq \omega \}$, essentially the $\omega$-product of $\mathbf{Lip}$. Yet this will be somewhat more complicated than the proof of Theorem 1 above, because in this case K is not preserved under the action of arbitrary transformations in ${\mathrm{BIJ}}_{\omega }^{\omega }$ and ${\mathbf{Lip}}^{\omega }$. This is why we have to consider certain combinations of those transformations.

Namely consider superpositions of the form $\sigma =\pi \circ \mathit{\alpha }$, where $\pi \in {\mathrm{BIJ}}_{\omega }^{\omega }$ and $\mathit{\alpha }\in {\mathbf{Lip}}^{\omega }$. (Such $\sigma$ acts so that $\sigma ·x=\pi ·\left(\mathit{\alpha }·x\right)$ for any applicable object x.)

Remark 4.

The set $\mathsf{\Sigma }$ of all $\sigma$ of this form is a group under the superposition, because the transformations of the two families considered commute so that $\mathit{\alpha }\circ \pi =\pi \circ {\mathit{\alpha }}^{\prime }$, where ${\mathit{\alpha }}^{\prime }=\pi ·\mathit{\alpha }$, that is, ${\alpha }_k^{\prime }={\alpha }_{\pi \left(k\right)}$ for all k.

Definition 22.

A transformation $\sigma =\pi \circ \mathit{\alpha }\in \mathsf{\Sigma }$ is $K$-preserving, if $p\in K⟺\sigma ·p\in K$ for all $p\in {\mathbf{P}}^{*}\upharpoonright \omega$.

Not all $\pi \in {\mathrm{BIJ}}_{\omega }^{\omega }$ are $K$-preserving, and neither is any $\mathit{\alpha }\in {\mathbf{Lip}}^{\omega }$ with ${\alpha }_0\ne$ the identity. Yet there are plenty of $K$-preserving transformations in $\mathsf{\Sigma }$.

Lemma 28.

Let $U,V$ be countable systems with $\left|U\right|=\left|V\right|=\omega$, and $p\in K\left[U\right],q\in K\left[V\right]$. There is a $K$-preserving transformation $\sigma =\pi \circ \mathit{\alpha }\in \mathsf{\Sigma }$ such that $\sigma ·U=V$, and the conditions $\sigma ·p$ and q are compatible.

Proof. 

First of all, Lemma 5 yields a transformation ${\alpha }_0\in \mathbf{Lip}$ such that ${\alpha }_0·U\left(0\right)=V\left(0\right)$ and the conditions ${\alpha }_0·p\left(0\right)$ and $q\left(0\right)$ (in $P^{*}$) are compatible. Define $\mathit{\alpha }={\left\{{\alpha }_i\right\}}_{i\in \omega }\in {\mathbf{Lip}}^{\omega }$ so that ${\alpha }_0$ has just been defined, and ${\alpha }_k=$ the identity for all $k>0$. Note that ${\alpha }_0$ is a $\subseteq$-preserving bijection of the set $\mathbf{Seq}$ of all non-empty strings of integers. Let $f:\omega \stackrel{\mathrm{onto}}{⟶}\omega$ be the associated permutation of integers, so that $f\left(k\right)=n$ iff ${\alpha }_0\left({\mathrm{s}}_k\right)={\mathrm{s}}_n$ (and $f\left(0\right)=0$). Define $\pi \in {\mathrm{BIJ}}_{\omega }^{\omega }$ so that $\pi \left(0\right)=0$ and then $\pi (2k+2)=2f\left(k\right)+2$ and $\pi (2k+1)=2f\left(k\right)+1$. It is quite obvious that $\mathit{\rho }=\pi \circ \mathit{\alpha }$ is $K$-preserving. Let $U^{\prime }=\mathit{\rho }·U$ and $p^{\prime }=\mathit{\rho }·p$. Thus $U^{\prime }$ is a countable system with $|U^{\prime }|=\omega$, $p^{\prime }\in K\left[U^{\prime }\right]$, and in addition $U^{\prime }\left(0\right)=V\left(0\right)$ and the conditions $p^{\prime }\left(0\right)={\alpha }_0·p\left(0\right)$ and $q\left(0\right)$ are compatible.

It follows from Lemma 5 that there is a transformation $\gamma ={\left\{{\gamma }_{\nu }\right\}}_{\nu <\omega }\in {\mathbf{Lip}}^{\omega }$ such that ${\gamma }_0$ is the identity (and hence $\gamma$ is $K$-preserving) and for any $k\ge 1$ we have ${\gamma }_k·U^{\prime }\left(k\right)=V\left(k\right)$ and $\gamma ·p^{\prime }\left(k\right)$ is compatible with $q\left(k\right)$. We conclude that the transformation $\sigma =\gamma \circ \mathit{\rho }=\gamma \circ \pi \circ \mathit{\alpha }$ is $K$-preserving, $V=\gamma ·U^{\prime }=\sigma ·U$, and the condition $\gamma ·p^{\prime }=(\gamma \circ \pi \circ \mathit{\alpha })·p$ is compatible with q. Then, we have $\sigma \in \mathsf{\Sigma }$ by Remark 4 in Section 7.3. □

Proof 

(Lemma 27). Suppose towards the contrary that both $q{\left|\right|--}_{K\left[\mathbb{U}\right]}\neg \mathsf{\Phi }$ and $p{}^K\mathbf{forc}{}_U^M\mathsf{\Phi }$. By the way we can w.l.o.g. assume that $\left|U\right|\subseteq \omega$, by Lemma 19, and moreover, that $\left|U\right|=\omega$ exactly. (Otherwise extend U by $U\left(\nu \right)=Q$ for all $\nu \in \omega \setminus \left|U\right|$, where Q = all eventually-0 functions $f\in \mathbf{Fun}$.)

There is an ordinal $\xi <{\omega }_1$ such that $q\in K\left[{\mathbb{U}}_{\xi }\right]$, $\omega \subseteq |{\mathbb{U}}_{\xi }|$, and $M\subseteq {\mathbb{M}}_{\xi }$. Let $V={\mathbb{U}}_{\xi }\upharpoonright \omega$. Note that $\left|q\right|\subseteq \omega$ since $K\subseteq {\mathbf{P}}^{*}\upharpoonright \omega$. Thus $q\in K\left[V\right]$. Apply Lemma 28 in ${\mathbb{M}}_{\xi }$. It gives a $K$-preserving transformation $\sigma =\mathit{\alpha }\circ \pi \in {\mathbb{M}}_{\xi }$ such that $\sigma ·U=V$ and the conditions $r=\sigma ·p$ and q (both in $K\left[V\right]$) are compatible. On the other hand, we have $r{}^K\mathbf{forc}{}_V^{{\mathbb{M}}_{\xi }}\mathsf{\Phi }$ by Lemmas 22 and 23, and hence $r{}^K\mathbf{forc}{}_{{\mathbb{U}}_{\xi }}^{{\mathbb{M}}_{\xi }}\mathsf{\Phi }$ by Lemma 18, that is, $r{}^K\mathbf{forc}{}_{\infty }^{}\mathsf{\Phi }$. Thus $r{\left|\right|--}_{K\left[\mathbb{U}\right]}\mathsf{\Phi }$ by Corollary 8(i). However, r is compatible with q, and q forces the opposite, a contradiction.   (Lemma 27) (Claim 6) (Theorem 2) □

8. Application 2: Nonconstructible Self-Definable ${\mathsf{\Delta }}_n^1$ Reals

Note that the set a as in Theorem 2(i) is definable in the generic extension of $\mathbf{L}$, considered in Section 7.2, by means of other reals in that extension, including those which do not necessarily belong to $\mathbf{L}\left[a\right]$. Claim (ii) of Theorem 2 achieves the same effect with the advantage that a is definable inside $\mathbf{L}\left[a\right]$.

The key idea (originally from [9] Section 4) can be explained as follows. Recall that a set of the form $a_0=a_G\left(0\right)$ was made definable in a generic extension of the form $\mathbf{L}\left[G\upharpoonright z_G\right]$ by means of the presence/absense of other sets of the form $S_G\left(\nu \right),\left[0\right]\nu <\omega$, in $\mathbf{L}\left[G\upharpoonright z\right]$, see Section 7.2 and Section 7.3. Our plan will now be to make each of the according sets $a_G\left(\nu \right)\in \mathbf{L}\left[G\upharpoonright z\right]$ (note that $a_G\left(\nu \right)\subseteq \omega \setminus \left\{0\right\}$, see Definition 9), as well as the whole sequence of them, ${\mathsf{\Delta }}_{𝕟+1}^1$-definable in $\mathbf{L}\left[G\upharpoonright z\right]$. In order to do this, we need to develop a suitable coding construction.

Assumption 4.

We continue to assume $\mathbf{V}=\mathbf{L}$ in the ground universe. We fix an integer $𝕟\ge 2$, for which Theorem 1(ii) will be proved, and make use of a system $\mathbb{U}$ and the forcing notion $\mathbb{P}=\mathbf{P}\left[\mathbb{U}\right]$ as in Definition 16; both $\mathbb{U}$ and $\mathbb{P}$ belong to $\mathbf{L}$.

8.1. Nonconstructible Self-Definable ${\mathsf{\Delta }}_{𝕟+1}^1$ Reals: The Model

Here we begin the proof of Theorem 2(ii). Recall that ${\omega }^{\omega }=\{{\mathrm{s}}_k:k<\omega \}$ is a fixed recursive enumeration of strings of natural numbers, such that ${\mathrm{s}}_0=\mathsf{\Lambda }$, the empty string, and ${\mathrm{s}}_k\subseteq {\mathrm{s}}_{k^{\prime }}⟹k\le k^{\prime }$. Let ${\ell }_i^k=\mathtt{num}({\mathrm{s}}_k^i)$, thus ${\mathrm{s}}_{{\ell }_i^k}={\mathrm{s}}_k^i$. Then we have:

• Each set $L\left(k\right)=\{{\ell }_i^k:i<\omega \}\subseteq \omega$ is countably infinite, $k<{\mathtt{min}}_i{\ell }_i^k$, $k\ne k^{\prime }⟹L\left(k\right)\cap L\left(k^{\prime }\right)=⌀$ and $i\ne j⟹{\ell }_i^k\ne {\ell }_j^k$, and finally each $m\ge 1$ is equal to ${\ell }_i^k$ for exactly one pair of indices of $i,k<\omega$.

Define a partial order ≪ on $\omega$ so that $i\ll k$ iff ${\mathrm{s}}_i\subset {\mathrm{s}}_k$. Obviously $k\ll {\ell }_i^k$ for all $i,k\in \omega$, and 0 is the $\ll$-least element.

For any sequence $\overrightarrow{a}={\left\{a_k\right\}}_{k<\omega }$ of sets $a_k\subseteq \omega$, we define a set ${\zeta }_{\overrightarrow{a}}\subseteq \omega$ so that:

(1)

$0\in {\zeta }_{\overrightarrow{a}}$;

(2)

if $k\in {\zeta }_{\overrightarrow{a}}$ then, for every i: if $i\in a_k$ then ${\ell }_{2i}^k\in {\zeta }_{\overrightarrow{a}}$ and ${\ell }_{2i+1}^k\notin {\zeta }_{\overrightarrow{a}}$, but

if $k\in {\zeta }_{\overrightarrow{a}}$ then, for every i: if $i\notin a_k$ then ${\ell }_{2i}^k\notin {\zeta }_{\overrightarrow{a}}$ and ${\ell }_{2i+1}^k\in {\zeta }_{\overrightarrow{a}}$;

(3)

if $k\notin {\zeta }_{\overrightarrow{a}}$ then ${\ell }_i^k\notin {\zeta }_{\overrightarrow{a}}$ for all i.

The next theorem obviously implies Theorem 2(ii).

Theorem 14.

Let $G\subseteq \mathbb{P}$ be $\mathbb{P}$-generic over $\mathbf{L}$. Define $\overrightarrow{a}\left[G\right]={\left\{a_G\left(i\right)\right\}}_{i<\omega }$ and $\zeta ={\zeta }_{\overrightarrow{a}\left[G\right]}\subseteq \omega$. Then $\mathbf{L}\left[\zeta \right]=\mathbf{L}\left[G\upharpoonright \zeta \right]$, and it holds in $\mathbf{L}\left[\zeta \right]$ that:

(i)

ζ is ${\mathsf{\Delta }}_{𝕟+1}^1;$

(ii)

if $x\subseteq \omega$ is ${\Sigma }_{𝕟}^1$, then $x\in \mathbf{L}$ and x is ${\Sigma }_{𝕟}^1$ in $\mathbf{L}$.

Proof 

(will continue towards the end of Section 7). Our arguments will be a more elaborate version of arguments in Section 7.2, Section 7.3. We’ll make use of the set K of all conditions $p\in {\mathbf{P}}^{*}\upharpoonright \omega$ such that for all i and k:

(A)

if ${\ell }_{2i}^k\in \left|p\right|$ then ${\mathrm{s}}_i\in S_p\left(k\right);$

(B)

if ${\ell }_{2i+1}^k\in \left|p\right|$ then ${\mathrm{s}}_i\in F_p^{\vee }\left(k\right)\setminus S_p\left(k\right)$—and hence ${\ell }_{2i}^k\notin \left|p\right|$ by (A).

(compare to (A), (B) in Section 7.2), and the related set $K\left[\mathbb{U}\right]=K\cap \mathbb{P}$.

Lemma 29.

K is a regular forcing in $\mathbf{L}$. If $G\subseteq \mathbb{P}$ is a set $\mathbb{P}$-generic over $\mathbf{L}$ then $G\cap K=G\cap K\left[\mathbb{U}\right]$ is $K\left[\mathbb{U}\right]$-generic over $\mathbf{L}$, $\left|G\cap K\right|={\zeta }_{\overrightarrow{a}\left[G\right]}$, and accordingly $\mathbf{L}[G\cap K]=\mathbf{L}\left[G\upharpoonright {\zeta }_{\overrightarrow{a}\left[G\right]}\right]=\mathbf{L}\left[{\zeta }_{\overrightarrow{a}\left[G\right]}\right]$.

Proof. 

As above, the nontrivial item of the regularity property is (4) of Definition 8. Suppose that $p\in {\mathbf{P}}^{*}$. Then $\left|p\right|\subseteq \omega$ is finite. Let $\delta$ be the least $\ll$-initial segment of $\omega$ satisfying $\left|p\right|\subseteq \delta$; $\delta$ is finite as well. Define $p^{*}\in {\mathbf{P}}^{*}$ so that $|p^{*}|=\delta$ and $F_{p^{*}}\left(k\right)=F_p\left(k\right)$ for all k, but the sets $S_{p^{*}}\left(k\right)$ may be strictly bigger than the corresponding sets $S_p\left(k\right)$. The definition of $S_{p^{*}}\left(k\right)$ goes on by $\ll$-inverse induction on $k\in \delta$. If $k\in \delta$ is $\ll$-maximal in $\delta$ then obviously $k\in \left|p\right|$, and we put $S_{p^{*}}\left(k\right)=S_p\left(k\right)$. Assume that $k\in \delta$ is not $\ll$-maximal in $\delta$, and the value of $p^{*}\left({\ell }_m^k\right)=⟨S_{p^{*}}\left({\ell }_m^k\right);F_p\left({\ell }_m^k\right)⟩$ is defined for all m such that ${\ell }_m^k\in \delta$. Put $S_{p^{*}}\left(k\right)=S_p\left(k\right)\cup S$, where S consists of all strings $s={\mathrm{s}}_i$ such that

(a)

${\ell }_{2i+1}^k\in \left|p^{*}\right|=\gamma$ or ${\ell }_{2i}^k\in \left|p^{*}\right|$, and

(b)

$s\notin F_p^{\vee }\left(k\right)$ (to make sure that $p^{*}\le p$).

By definition, $|p^{*}|=\delta$, and if $i,k\in \omega$ and at least one of the numbers ${\ell }_{2i+1}^k$, ${\ell }_{2i}^k$ belongs to $\delta$, then the string ${\mathrm{s}}_i$ belongs to $F_{p^{*}}^{\vee }\left(k\right)\cup S_{p^{*}}\left(k\right)$.

Now we define a set $d\subseteq \delta$ so that the decision whether a number $k\in \delta$ belongs to d is made by direct $\ll$-induction. We put $0\in d$. Suppose that some $k\in \delta$ already belongs to d. We define:

(1)

${\ell }_{2i}^k\in d$, if ${\ell }_{2i+1}^k\in \delta$ and ${\mathrm{s}}_i\in S_{p^{*}}\left(k\right)$;

(2)

${\ell }_{2i+1}^k\in d$, if ${\ell }_{2i}^k\in \delta$ and ${\mathrm{s}}_i\in F_{p^{*}}^{\vee }\left(k\right)\setminus S_{p^{*}}\left(k\right)$.

A simple verification that $p^{*}$ and d satisfy Definition 8(4) is left to the reader.

Further, the set $G\cap K=G\cap K\left[\mathbb{U}\right]$ is $K\left[\mathbb{U}\right]$-generic by Lemma 9(ii).

By definition if $k\in {\zeta }_{\overrightarrow{a}\left[G\right]}$ then $a_G\left(k\right)=\{i:{\ell }_{2i}^k\in {\zeta }_{\overrightarrow{a}\left[G\right]}\}=\{i:{\ell }_{2i+1}^k\notin {\zeta }_{\overrightarrow{a}\left[G\right]}\}\in \mathbf{L}\left[{\zeta }_{\overrightarrow{a}\left[G\right]}\right]$, therefore $G\upharpoonright {\zeta }_{\overrightarrow{a}\left[G\right]}\in \mathbf{L}\left[{\zeta }_{\overrightarrow{a}\left[G\right]}\right]$ and $\mathbf{L}\left[G\upharpoonright {\zeta }_{\overrightarrow{a}\left[G\right]}\right]=\mathbf{L}\left[{\zeta }_{\overrightarrow{a}\left[G\right]}\right]$.

Now to prove $\mathbf{L}[G\cap K\left[\mathbb{U}\right]]=\mathbf{L}\left[G\upharpoonright {\zeta }_{\overrightarrow{a}\left[G\right]}\right]$ it remains to show that $\left|G\cap K\right|={\zeta }_{\overrightarrow{a}\left[G\right]}$—then use Lemma 9(iii). Note that both $\left|p\right|$ for any $p\in K$ and ${\zeta }_{\overrightarrow{a}\left[G\right]}$ are $\ll$-initial segments. Thus it suffices to check that if $k\in \left|G\cap K\right|\cap {\zeta }_{\overrightarrow{a}\left[G\right]}$ then

$${\ell }_{2i+1}^k\in \left|G\cap K\right|⟺{\ell }_{2i+1}^k\in {\zeta }_{\overrightarrow{a}\left[G\right]}\mathrm{and}{\ell }_{2i}^k\in \left|G\cap K\right|⟺{\ell }_{2i}^k\in {\zeta }_{\overrightarrow{a}\left[G\right]}.$$

Prove, e.g., the first equivalence. Suppose that ${\ell }_{2i+1}^k\in \left|G\cap K\right|$. Then ${\ell }_{2i+1}^k\in \left|p\right|$ for some $p\in K$ in G, and we have ${\mathrm{s}}_i\in F_p^{\vee }\left(k\right)\setminus S_p\left(k\right)$ by (B), so that ${\mathrm{s}}_i\notin S_G\left(k\right)$ and accordingly $i\notin a_G\left(k\right)$, thus by definition ${\ell }_{2i+1}^k\in {\zeta }_{\overrightarrow{a}\left[G\right]}$. Suppose conversely that ${\ell }_{2i+1}^k\in {\zeta }_{\overrightarrow{a}\left[G\right]}$. Then by definition $i\notin a_G\left(k\right)$, hence ${\mathrm{s}}_i\notin G_G\left(k\right)$. This must be forced by some $p\in K\cap G$, and, as $k\in \left|G\cap K\right|$, we can assume that $k\in \left|p\right|$. However, in this case forcing ${\mathrm{s}}_i\notin G_G\left(k\right)$ means by necessity that just ${\mathrm{s}}_i\in F_p^{\vee }\left(k\right)\setminus S_p\left(k\right)$, so there exists a stronger condition $p^{\prime }\in K\cap G$ with ${\ell }_{2i+1}^k\in \left|p^{\prime }\right|$. We conclude that ${\ell }_{2i+1}^k\in \left|G\cap K\right|$. (Lemma) □

It follows that ${\zeta }_{\overrightarrow{a}\left[G\right]}$ is ${\Sigma }_{𝕟+1}^1$ in $\mathbf{L}\left[G\upharpoonright \zeta \right]$ by Corollary 7. On the other hand, by definition, if $k\in {\zeta }_{\overrightarrow{a}\left[G\right]}$, then, for any k, we have ${\ell }_{2i}^k\in {\zeta }_{\overrightarrow{a}\left[G\right]}$ iff ${\ell }_{2i+1}^k\notin {\zeta }_{\overrightarrow{a}\left[G\right]}$. This easily leads to a ${\Pi }_{n+1}^1$ definition of ${\zeta }_{\overrightarrow{a}\left[G\right]}$. Thus ${\zeta }_{\overrightarrow{a}\left[G\right]}$ is ${\mathsf{\Delta }}_{𝕟+1}^1$ in $\mathbf{L}\left[G\upharpoonright \zeta \right]$, and hence we have claim (i) of Theorem 14. The proof of claim (ii) follows in the next two subsections.

Remark 5.

A slightly more elaborate argument, like in the end of Section 4 in [9], shows that even more $\left\{{\zeta }_{\overrightarrow{a}\left[G\right]}\right\}$ is a ${\Pi }_{𝕟}^1$ singleton in $\mathbf{L}\left[{\zeta }_{\overrightarrow{a}\left[G\right]}\right]$ since ${\zeta }_{\overrightarrow{a}\left[G\right]}$ is equalto the only set $\zeta \subseteq \omega$ in $\mathbf{L}\left[{\zeta }_{\overrightarrow{a}\left[G\right]}\right]$ satisfyings the following requirements:

(a)

$0\in \zeta$, and if $k\notin \zeta$ then ${\ell }_{2i}^k\notin \zeta$ and ${\ell }_{2i}^k\notin \zeta$ for all i;

(b)

if $k\in \zeta$ then we have ${\ell }_{2i}^k\in \zeta$ iff ${\ell }_{2i+1}^k\notin \zeta$ for every i, and

(c)

if $k\in \zeta$ then the set $S_{\zeta k}=\{s_i:{\ell }_{2i}^k\in \zeta \}$ satisfies ${ℾ}_k\left(S_{\zeta k}\right)$.

The conjunction of them amounts to a ${\Pi }_{𝕟}^1$ definition of $\left\{\zeta \right\}$ in $\mathbf{L}\left[\zeta \right]$.

8.2. Key Lemma

As in Section 7.2, Claim (ii) of Theorem 14 is a consequence of the following lemma (the key lemma from the title), the proof of which will end the proof of theorems 14 and 2(ii).

Lemma 30 (in L).

Suppose that $⟨M,U⟩\in \mathbf{sJS}$, $p\in K\left[U\right]$, $q\in K\left[\mathbb{U}\right]$. Let Φ be any closed parameter-free ${\Sigma }_{𝕟}^1$ formula. Then it is impossible that simultaneously $q{\left|\right|--}_{K\left[\mathbb{U}\right]}\neg \mathsf{\Phi }$ and $p{}^K\mathbf{forc}{}_U^M\mathsf{\Phi }$.

Following Definition 22, a transformation $\sigma \in \mathsf{\Sigma }$ (see Remark 4 in Section 7.3 on $\mathsf{\Sigma }$) is called $K$-preserving, if $p\in K⟺\sigma ·p\in K$ for all $p\in {\mathbf{P}}^{*}\upharpoonright \omega$. Clearly the regular forcing K here is different (and way more complex in some aspects) than K in Section 7.3. The following lemma is analogous to Lemma 28.

Lemma 31 (in L).

Suppose that $U,V$ are countable systems with $\left|U\right|=\left|V\right|=\omega$, and $p\in K\left[U\right],q\in K\left[V\right]$. Then there is a $K$-preserving transformation $\sigma \in \mathsf{\Sigma }$ such that $\sigma ·U=V$, and the conditions $\sigma ·p$ and q are compatible.

Proof. 

The proof resembles the proof of Lemma 28, but is somewhat more complicated. Essentially, we’ll have a ramified $\omega$-long iteration in which the construction employed in Lemma 28 will be just one step. We define ≪-cones $C_k=\{i\in \omega :k\ll i\}$ and $C_k^{\prime }=C_k\cup \left\{k\right\}$ for any $k\in \omega$.

Claim 7.

If $\mathit{\alpha }={\left\{{\alpha }_k\right\}}_{k<\omega }\in {\mathbf{Lip}}^{\omega }$, $k_0\in \omega$, and ${\alpha }_k$ is the identity for each $k\ne k_0$ then there is a bijection $\pi =\pi \left[{\alpha }_{k_0}\right]\in {\mathrm{BIJ}}_{\omega }^{\omega }$, recursive in α, $\ll$-preserving, and such that $\pi \left(k\right)=k$ for all $k\notin C_{k_0}$ and $\pi \circ \mathit{\alpha }$ is $K$-preserving.

Proof. 

Note that ${\alpha }_{k_0}$ is a $\subseteq$-preserving bijection of the set $\mathbf{Seq}$ of all finite non-empty strings of integers. Let $f=f_{{\alpha }_{k_0}}:\omega \stackrel{\mathrm{onto}}{⟶}\omega$ be the associated permutation of integers, so that $f\left(i\right)=j$ iff ${\alpha }_0\left({\mathrm{s}}_i\right)={\mathrm{s}}_j$. Let the transformation $\pi =\pi \left[{\alpha }_{k_0}\right]$ be the identity outside of the strict $\ll$-cone $C_{k_0}$; in particular, $\pi \left(k_0\right)=k_0$. Beyond this, put $\pi \left({\ell }_{2i}^{k_0}\right)={\ell }_{2f\left(i\right)}^{k_0}$ and $\pi \left({\ell }_{2i+1}^{k_0}\right)={\ell }_{2f\left(i\right)+1}^{k_0}$ for all i. Now, if $k\in C_{k_0}$ and $\pi \left(k\right)=k^{\prime }$ is defined then put $\pi \left({\ell }_{2m}^k\right)={\ell }_{2m}^{k^{\prime }}$ for all m.   (Claim) □

8.3. Matching Permutation

Now, in continuation of the proof of Lemma 31, given any $\mathit{\alpha }\in {\mathbf{Lip}}^{\omega }$ we outline a construction of a permutation $\mathsf{\Pi }\in {\mathrm{BIJ}}_{\omega }^{\omega }$ such that the superposition $\mathit{\alpha }\circ \mathit{\Pi }$ is $K$-preserving. Suppose that $\mathit{\alpha }={\left\{{\alpha }_k\right\}}_{k<\omega }\in {\mathbf{Lip}}^{\omega }$. We define

(I)

a sequence of numbers $k_m,m<\omega$, such that $k_0=0$ and, for any m, $k_{m+1}$ is the least (in the usual order of $\omega$) $\ll$-minimal element of $\omega \setminus d_m$, where $d_m=\{k_i:i\le m\}$,—then ${\bigcup }_m{d}_m=\omega$ and each $d_m$ is a $\ll$-initial segment of $\omega$;

(II)

for every m, a transformation ${\mathit{\alpha }}^m={\left\{{\alpha }_k^m\right\}}_{k<\omega }\in {\mathbf{Lip}}^{\omega }$, such that ${\alpha }_k^m$ is the identity for all $k\ne k_m$ but ${\alpha }_{k_m}^m={\alpha }_{k_m}$, and a matching permutation ${\pi }^m=\pi \left[{\alpha }_{k_m}^m\right]\in {\mathrm{BIJ}}_{\omega }^{\omega }$ by Claim 7 — thus ${\pi }^m$ is the identity outside of the cone $C_{k_m}$;

(III)

a $K$-preserving superposition ${\mathit{\rho }}_m={\pi }^m\circ {\mathit{\alpha }}^m$, equal to the identity outside of the extended ≪-cone $C_{k_m}^{\prime }=C_{k_m}\cup \left\{k_m\right\}$, in the sense that if U is a system with $\left|U\right|=\omega$, or a condition $p\in {\mathbf{P}}^{*}$ satisfies $\left|p\right|\subseteq \omega$, then $\left({\mathit{\rho }}_m·U\right)\left(k\right)=U\left(k\right)$ and $\left({\mathit{\rho }}_m·p\right)\left(k\right)=p\left(k\right)$ for all $k\in \omega \setminus C_{k_m}^{\prime }$.

The whole sequence of transformations is thereby specified by the choice of the components ${\alpha }_{k_m}^m\in \mathbf{Lip},m\in \omega$; we address this issue below. Now put

$$T_m={\mathit{\rho }}_m\circ \cdots \circ {\mathit{\rho }}_2\circ {\mathit{\rho }}_1\circ {\mathit{\rho }}_0\in \mathsf{\Sigma },{\mathsf{\Pi }}_m={\pi }_m\circ \dots \circ {\pi }_2\circ {\pi }_1\circ {\pi }_0\in {\mathrm{BIJ}}_{\omega }^{\omega }.$$

(12)

Claim 8.

(i) the sets $D_m={\left({\mathsf{\Pi }}_m\right)}^{-1}\left(d_m\right)$ satisfy ${\bigcup }_m{D}_m=\omega ;$

(ii) If $m\le i$ and $k\in D_m$ then ${\mathsf{\Pi }}_i\left(k\right)={\mathsf{\Pi }}_m\left(k\right);$

(iii) there is a single permutation $\mathsf{\Pi }\in {\mathrm{BIJ}}_{\omega }^{\omega }$ such that $\mathsf{\Pi }\left(k\right)={\mathsf{\Pi }}_m\left(k\right)={\mathsf{\Pi }}_i\left(k\right)$ whenever $i\ge m$ and $k\in D_m$.

Proof. 

(i) Suppose that $k<\omega$ belongs to some $D_m$. Prove that any number $j={\ell }_{2i}^k$ or $j={\ell }_{2i+1}^k$, $i<\omega$, also belongs to some $D_{m^{\prime }}$. By definition $k^{\prime }={\mathsf{\Pi }}_m\left(k\right)\in d_m$. The number $j^{\prime }={\mathsf{\Pi }}_m\left(j\right)$ either belongs to $d_m$, QED, or is $\ll$-minimal in $\omega \setminus d_m$. In the latter case, we have $\neg k_{m^{\prime }}\ll j^{\prime }$ for all $m^{\prime }>m$, and hence ${\mathsf{\Pi }}_{m^{\prime }}\left(j\right)$ is equal to $j^{\prime }$ for every $m^{\prime }>m$. Take $m^{\prime }>m$ big enough for $j^{\prime }\in d_{m^{\prime }}$; then $j\in D_{m^{\prime }}$.

To prove (ii) apply assumption (II) above. Finally (iii) easily follows from items (i), (ii). □

The transformation $\mathsf{\Pi }$ as in item (iii) of the claim can be understood as the infinite superposition $\cdots \circ {\pi }_m\circ \cdots \circ {\pi }_2\circ {\pi }_1\circ {\pi }_0$.

Claim 9.

Suppose that $m\le i$, U is a system, $\left|U\right|=\omega$, and $p\in {\mathbf{P}}^{*}$, $\left|p\right|\subseteq \omega$. Then $\left(T_i·U\right)\left(k_m\right)=\left((\mathit{\alpha }\circ \mathsf{\Pi })·U\right)\left(k_m\right)$ and $\left(T_i·p\right)\left(k_m\right)=\left((\mathit{\alpha }\circ \mathsf{\Pi })·p\right)\left(k_m\right)$.

Proof. 

By Claim 8(ii), there is an index $j\in D_m$ such that $k_m=\mathsf{\Pi }\left(j\right)={\mathsf{\Pi }}_i\left(j\right)$ for all $i\ge m$. Thus $\left(T_i·U\right)\left(k_m\right)$ is equal to ${\alpha }_{k_m}^m·U\left(j\right)={\alpha }_{k_m}^m·\left(\left(T_i·U\right)\left(k_m\right)\right)$.

The argument for p is similar.    (Claim) □

It follows that the superposition $\mathit{\alpha }\circ \mathsf{\Pi }\in \mathsf{\Sigma }$ is $K$-preserving. Indeed, since sets $\left|p\right|$ are finite, if $p\in K$ then there is m such that $\left|p\right|\subseteq d_m\cap D_m$. However, then $(\mathit{\alpha }\circ \mathsf{\Pi })·p=T_i·p$ by Claim 9, and on the other hand $T_i$ is $K$-preserving as a finite superposition of $K$-preserving transformations ${\mathit{\rho }}^m$.

8.4. Final Argument

Now let $U,V,p,q$ be as in Lemma 31. To accomplish the proof of Lemma 31, we note that the construction of ${\mathit{\alpha }}^m,{\pi }^m,{\mathit{\rho }}_m$ depends on ${\alpha }_{k_m}$ rather than on $\mathit{\alpha }={\left\{{\alpha }_k\right\}}_{k<\omega }\in {\mathbf{Lip}}^{\omega }$ as a whole. This enables us to carry out the following definition of ${\alpha }_{k_m}\in \mathbf{Lip}$ ($m\in \omega$) by induction on m.

Definition 23.

Choose, using Lemma 5, a transformation ${\alpha }_{k_0}\in \mathbf{Lip}$ such that ${\alpha }_{k_0}·U\left(k_0\right)=V\left(k_0\right)$ and the conditions ${\alpha }_{k_0}·p\left(k_0\right)$ and $q\left(k_0\right)$ (in $P^{*}$) are compatible.

Now suppose that transformations ${\alpha }_{k_0},\dots ,{\alpha }_{k_m}\in \mathbf{Lip}$ have been defined, and define ${\alpha }_{k_{m+1}}\in \mathbf{Lip}$. Note that $k_{m+1}$ is a $\ll$-minimal element in $\omega \setminus d_m$, where $d_m=\{k_0,\dots ,k_m\}$, as above. First of all if $\mu \le m$ then define:

–

${\mathit{\alpha }}^{\mu }={\left\{{\alpha }_k^{\mu }\right\}}_{k<\omega }\in {\mathbf{Lip}}^{\omega }$ so that ${\alpha }_{k_{\mu }}^{\mu }={\alpha }_{k_{\mu }}$, but ${\alpha }_k^{\mu }$ is the identity, whenever $k\ne k_{\mu }$;

–

${\pi }^{\mu }=\pi \left[{\alpha }_{k_{\mu }}^{\mu }\right]\in {\mathrm{BIJ}}_{\omega }^{\omega }$ as in assumption (II) of Section 8.3 — thus ${\pi }^{\mu }$ is the identity outside of $C_{k_{\mu }}$;

–

a $K$-preserving superposition ${\mathit{\rho }}_{\mu }={\pi }^{\mu }\circ {\mathit{\alpha }}^{\mu }$, equal to the identity outside of the extended cone $C_{k_{\mu }}^{\prime }$, as in assumption (III) of Section 8.3.

Define ${\mathsf{\Pi }}_m$ and $T_m$ by (12) above. Put $U^m=T_m·U$ and $p^m=T_m·p$. By Lemma 5, there is a transformation ${\alpha }_{k_{m+1}}\in \mathbf{Lip}$ such that ${\alpha }_{k_{m+1}}·U^m\left(k_{m+1}\right)=V\left(k_{m+1}\right)$ and the conditions ${\alpha }_{k_{m+1}}·p^m\left(k_{m+1}\right)$ and $q\left(k_{m+1}\right)$ are compatible.

After we have defined ${\alpha }_{k_m}\in \mathbf{Lip}$ by induction on m, let’s take the transformation $\mathit{\alpha }={\left\{{\alpha }_k\right\}}_{k<\omega }\in {\mathbf{Lip}}^{\omega }$ as the input of the construction in Section 8.3. The latter gives us a permutation $\mathsf{\Pi }\in {\mathrm{BIJ}}_{\omega }^{\omega }$ of Claim 8, such that the superposition $\sigma =\mathit{\alpha }\circ \mathsf{\Pi }\in \mathsf{\Sigma }$ is $K$-preserving. It remains to check that (1) $\sigma ·U=V$ and that (2) $\sigma ·p$ and q are compatible conditions.

To prove (1), consider any $k=k_{m+1}\in \omega$. (The argument will also work for the case $m=-1$, that is, $k=0$.) By definition, we have

$$V\left(k_{m+1}\right)={\alpha }_{k_{m+1}}·U^m\left(k_{m+1}\right)=\left({\mathit{\alpha }}^{m+1}·U^m\right)\left(k_{m+1}\right),$$

and hence, as obviously ${\pi }^{m+1}\left(k_{m+1}\right)=k_{m+1}$,

$$V\left(k_{m+1}\right)=\left(({\pi }^{m+1}\circ {\mathit{\alpha }}^{m+1}\circ T_m)·U\right))\left(k_{m+1}\right)=\left(T_{m+1}·U\right))\left(k_{m+1}\right),$$

therefore $V\left(k_{m+1}\right)=\left((\mathit{\alpha }\circ \mathsf{\Pi })·U\right)\left(k_{m+1}\right)=\left(\sigma ·U\right)\left(k_{m+1}\right)$ by Claim 9, as required.   (Lemma 31) □

Proof (Lemma 30).

Similar to the proof of Lemma 27, but using Lemma 31 just proved. □

(Theorem 14) (Theorem 2(ii)) □

9. Application 3: Nonconstructible ${\Sigma }_n^1$ Reals

Here we prove Theorem 3.

Assumption 5.

We continue to assume $\mathbf{V}=\mathbf{L}$ in the ground universe. We fix an integer $𝕟\ge 2$, for which Theorem 3 will be proved, and make use of a system $\mathbb{U}$ and the forcing notion $\mathbb{P}=\mathbf{P}\left[\mathbb{U}\right]$ as in Definition 16; both $\mathbb{U}$ and $\mathbb{P}$ belong to $\mathbf{L}$.

9.1. Nonconstructible ${\Sigma }_{𝕟+1}^1$ Reals: The Model

The most obvious idea as of getting an extension required is to slightly modify the proof of Theorem 2(ii) in the following direction. Suppose that $G\subseteq \mathbb{P}$ be $\mathbb{P}$-generic over $\mathbf{L}$, and let $S_G\left(\nu \right)$ and $a_{\nu }=a_G\left(\nu \right)=\{k\ge 1:{\mathrm{s}}_k\in S\left(i\right)\}$ be defined as in Definition 9. We proved (see the proof of Theorem 2(i) above) that if

$$z=\left\{0\right\}\cup \{2k+2:k\in a_0\}\cup \{2k+1:k\notin a_0\}$$

by (10) of Section 7.2 then the set $a_0$ is ${\mathsf{\Delta }}_{𝕟+1}^1$ in $\mathbf{L}\left[G\upharpoonright z\right]$, and the part $\{2k+2:k\in a_0\}$ of z is responsible for $a_0$ being ${\Sigma }_{𝕟+1}^1$ in $\mathbf{L}\left[G\upharpoonright z\right]$ (by means of the equality $a_0=\left\{k:\exists S{ℾ}_{2k+2}\left(S\right)\right\}$) while the part $\{2k+1:k\notin a_0\}$ is responsible for $a_0$ being ${\Pi }_{n+1}^1$ in $\mathbf{L}\left[G\upharpoonright z\right]$ (by means of the equality $a_0=\{k:\neg \exists S{ℾ}_{2k+1}\left(S\right)\}$). As now the second part is not needed, one might hope that if y is defined by

$$y=y_G:=\left\{0\right\}\cup a_0=\left\{0\right\}\cup a_G\left(0\right)$$

(13)

then $\mathbf{L}\left[G\upharpoonright y\right]$ will be a model for Theorem 3. At least $a_0$ will be ${\Sigma }_{𝕟+1}^1$ in $\mathbf{L}\left[G\upharpoonright y\right]$ by exactly the same reasons. However we have not been able to prove the second part of the theorem, i.e., that all reals ${\mathsf{\Delta }}_{𝕟+1}^1$ in $\mathbf{L}\left[G\upharpoonright y\right]$ belong to $\mathbf{L}$. The point of difficulty is the following hypothesis:

Conjecture 1.

Under the assumptions above, if $m\notin y=y_G$ then any parameter-free ${\Sigma }_{𝕟+1}^1$ formula true in $\mathbf{L}\left[G\upharpoonright y\right]$ is true in $\mathbf{L}[G\upharpoonright y,a_m]$ as well.

We definitely cannot expect the conjecture to be true for formulas with parameters in $\mathbf{L}\left[G\upharpoonright y\right]$ (the smaller model) since if $p\in \mathbf{L}\left[G\upharpoonright y\right],p\subseteq \omega$ codes the sequence ${\left\{a_i\right\}}_{i\in y}$ then $\mathbf{Fun}\subseteq \mathbf{L}\left[p\right]$ is true in $\mathbf{L}\left[G\upharpoonright y\right]$ but false in $\mathbf{L}[G\upharpoonright y,a_m]$.

We have a near-counterexample to Conjecture 1: the formula $\exists x({ℾ}_0\left(x\right)\wedge \mathbf{Fun}\subseteq \mathbf{L}\left[x\right])$ of class ${\Sigma }_{𝕟+1}^1$ (assuming $𝕟\ge 3$) holds in $\mathbf{L}\left[a_0\right]$ and fails in $\mathbf{L}[a_0,a_1]$. The set $y=\left\{a_0\right\}$ is definitely not of the form (13), so this is not literally a counterexample, yet it casts doubts on the approach based on (13).

Now we describe the extension involved in the proof of Theorem 3.

The model we define will be a submodel of the whole extension $\mathbf{L}\left[G\right]$, where G is $\mathbb{P}$-generic over $\mathbf{L}$, and a set y of (13) is involved in the definition. We let

$$Y=Y_G=y_G\cup (\mathcal{I}\setminus \omega )=\left\{0\right\}\cup a_0\cup (\mathcal{I}\setminus \omega ),$$

(14)

where $a_0=a_G\left(0\right)$ (then $Y\in \mathbf{L}\left[a_0\right]\setminus \mathbf{L}$) and $y_G$ is defined by (13). The goal is to prove that $\mathbf{L}\left[G\upharpoonright Y\right]$ witnesses Theorem 3 with $a=a_0$. The task splits in two claims:

Claim 10.

In $\mathbf{L}\left[G\upharpoonright Y\right]$, y is ${\Sigma }_{𝕟+1}^1$, therefore $a_0$ is ${\Sigma }_{𝕟+1}^1$ as well.

Claim 11.

In $\mathbf{L}\left[G\upharpoonright Y\right]$, if $x\subseteq \omega$ is ${\mathsf{\Delta }}_{𝕟+1}^1$ then $x\in \mathbf{L}$ and x is ${\mathsf{\Delta }}_{𝕟+1}^1$ in $\mathbf{L}$.

Claim 10 is established just as similar claims above, so we leave it for the reader.

Let us concentrate on Claim 11. We make use of the set $K_0$ of all conditions $p\in {\mathbf{P}}^{*}\upharpoonright \omega$ such that

$$\mathrm{if}k\ge 1\mathrm{and}k\in \left|p\right|,\mathrm{then}{\mathrm{s}}_k\in S_p\left(0\right)(=\mathrm{Example}2\mathrm{in}\mathrm{Section}3.2);$$

(15)

as well as the related sets: $K=K_0\times \left({\mathbf{P}}^{*}\upharpoonright (\mathcal{I}\setminus \omega )\right)=\{p\in {\mathbf{P}}^{*}:p\upharpoonright \omega \in K_0\}$, $K_0\left[\mathbb{U}\right]=K_0\cap \mathbb{P}$, and accordingly $K\left[\mathbb{U}\right]=K\cap \mathbb{P}$.

Lemma 32.

It is true in $\mathbf{L}$ that: $K_0$ and K are regular forcings and absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}$ sets, and if $z\subseteq \mathcal{I}$ contains 0 then the restrictions $K\upharpoonright z$, $K_0\upharpoonright z$ are regular forcings, too.

If $G\subseteq \mathbb{P}$ is a set $\mathbb{P}$-generic over $\mathbf{L}$ then $G\cap K=G\cap K\left[\mathbb{U}\right]$ is a set $K\left[\mathbb{U}\right]$-generic over $\mathbf{L}$, $G\cap K_0=G\cap K_0\left[\mathbb{U}\right]$ is a set $K_0\left[\mathbb{U}\right]$-generic over $\mathbf{L}$, and

$$\mathbf{L}[G\cap K_0]=\mathbf{L}\left[G\upharpoonright y_G\right],\mathbf{L}[G\cap K]=\mathbf{L}\left[G\upharpoonright Y_G\right]=\mathbf{L}[G\upharpoonright y_G,G\upharpoonright (\mathcal{I}\setminus \omega )].$$

Proof.#

To check (4) of Definition 8 for $K_0$ see Example 2 in Section 3.2. To prove, that the set $K_0\upharpoonright z=\{p\in K_0:\left|p\right|\subseteq z\}$ ($z\in \mathbf{L},z\subseteq \omega$) is regular, argue as in Example 2 in Section 3.2. The rest of the lemma is easy: apply Lemma 9. □

9.2. Key Lemma

Here we establish the following key lemma. Recall that sets $y_G,Y_G$ are defined by (13) and (14).

Lemma 33.

Suppose that $G\subseteq \mathbb{P}$ is $\mathbb{P}$-generic over $\mathbf{L}$, and $y_G=\left\{0\right\}\cup a_G\left(0\right)$, $y\subseteq \omega$, the symmetric difference $\delta =y\mathsf{\Delta }{y}_G$ is finite, and $0\notin \delta$. Then the models $\mathbf{L}\left[G\upharpoonright Y_G\right]=\mathbf{L}[G\upharpoonright y_G,G\upharpoonright (\mathcal{I}\setminus \omega )]$ and $\mathbf{L}[G\upharpoonright y,G\upharpoonright (\mathcal{I}\setminus \omega \left)\right]$ are $K\left[\mathbb{U}\right]$-generic extensions of $\mathbf{L}$, elementarily equivalent w.r.t. all ${\Sigma }_{𝕟}^1$ formulas with parameters in the common part $\mathbf{L}[G\upharpoonright (y_G\cap y),G\upharpoonright (\mathcal{I}\setminus \omega )]$ of the two models.

Proof. 

That $\mathbf{L}[G\upharpoonright y_G,G\upharpoonright (\mathcal{I}\setminus \omega )]=\mathbf{L}[G\cap K\left[\mathbb{U}\right]]$ is a $K\left[\mathbb{U}\right]$-generic extension of $\mathbf{L}$ follows from Lemma 32. Consider $\mathbf{L}[G\upharpoonright y,G\upharpoonright (\mathcal{I}\setminus \omega \left)\right]$, the other model.

Let $u=y\setminus y_G$ and $v=y_G\setminus y$; thus $\delta =u\cup v$. Then $v\subseteq a_G\left(0\right)$ but $u\cap a_G\left(0\right)=⌀$ by the definition of $y_G$. In other words, the finite disjoint sets $S^u=\{{\mathrm{s}}_k:k\in u\}$ and $S^v=\{{\mathrm{s}}_k:k\in v\}$ satisfy $S^v\subseteq S_G\left(0\right)$ but $S^u\cap S_G\left(0\right)=⌀$. It follows that there is a condition $p\in G\cap K\left[\mathbb{U}\right]$ such that $\left|p\right|=\left\{0\right\}$, $S^v\subseteq S_p\left(0\right)$, and $S^u\subseteq F_p^{\vee }\left(0\right)\setminus S_p\left(0\right)$. We can increase $F_p\left(0\right)$ if necessary for $S_p\left(0\right)\subseteq F_p^{\vee }\left(0\right)$ (a technical requirement) to hold.

Now let q be a condition obtained by the following modification of p: still $\left|q\right|=\left\{0\right\}$ and $F_q\left(0\right)=F_p\left(0\right)$ (therefore, q belongs to $K\left[\mathbb{U}\right]$ together with p), and $S_q\left(0\right)=(S_p\left(0\right)\cup S^u)\setminus S^v$. It is clear that $S_q\left(0\right)\subseteq F_q^{\vee }\left(0\right)=F_p^{\vee }\left(0\right)$, so $p,q$ satisfy (3) in Section 3.7. Therefore the map (Definition 12)

$$H_q^p:P=\{p^{\prime }\in {\mathbf{P}}^{*}:p^{\prime }\le p\}\stackrel{\mathrm{onto}}{⟶}Q=\{q^{\prime }\in {\mathbf{P}}^{*}:q^{\prime }\le q\}$$

is an order isomorphism of P onto Q by Theorem 6, acting so that:

(∗)

if $p^{\prime }\in P$ then $q^{\prime }=H_q^p\left(p^{\prime }\right)$ satisfies $|p^{\prime }|=|q^{\prime }|$, $p^{\prime }\left(i\right)=q^{\prime }\left(i\right)$ for all $i\ne 0$, and even $F_{q^{\prime }}\left(0\right)=F_{p^{\prime }}\left(0\right)$, but $S_{q^{\prime }}\left(0\right)=(S_{p^{\prime }}\left(0\right)\cup S^u)\setminus S^v$.

We conclude that $H_q^p$ also is an order isomorphism of $P\cap \mathbb{P}$ onto $Q\cap \mathbb{P}$ by (∗), and hence the set $H=\{H_q^p\left(p^{\prime }\right):p^{\prime }\in G\}\subseteq Q$ is $\mathbb{P}$-generic over $\mathbf{L}$. Moreover it follows from (∗) that $S_H\left(i\right)=S_G\left(i\right)$ and $a_H\left(i\right)=a_G\left(i\right)$ for all $i>0$, but $S_H\left(0\right)=(S_G\left(0\right)\cup S^u)\setminus S^v$ and $a_H\left(0\right)=(a_G\left(0\right)\cup u)\setminus v$. Therefore $y_H=(y_G\cup u)\setminus v=y$, thus $\mathbf{L}[G\upharpoonright y,G\upharpoonright (\mathcal{I}\setminus \omega \left)\right]$ is a $K\left[\mathbb{U}\right]$-generic extension of $\mathbf{L}$.

As for the elementary equivalence claim, note first of all that the common part $\mathbf{L}[G\upharpoonright (y_G\cap y),G\upharpoonright (\mathcal{I}\setminus \omega )]$ of the two models also is a $K\left[\mathbb{U}\right]$-generic extension of $\mathbf{L}$ by the above. (Take $y_G\cap y$ as a new y.) Thus in fact it suffices to prove that under the assumptions of the theorem if $j\in \omega \setminus y_G$ then $\mathbf{L}[G\upharpoonright y_G,a_G\left(j\right),G\upharpoonright (\mathcal{I}\setminus \omega )]$ is an elementary extension of $\mathbf{L}[G\upharpoonright y_G,G\upharpoonright (\mathcal{I}\setminus \omega )]$ w.r.t. all ${\Sigma }_{𝕟}^1$ formulas.

Let $\mathsf{\Phi }$ be a closed ${\Sigma }_{𝕟}^1$ formula with parameters in $\mathbf{L}[G\upharpoonright y_G,G\upharpoonright (\mathcal{I}\setminus \omega )]$. It can be deduced, using either Theorem 5(ii) or directly the CCC property of $\mathbb{P}$ (Theorem 4) that there is an ordinal $\gamma ,\omega \le \gamma <{\omega }_1$, such that all parameters of $\mathsf{\Phi }$ belong to $\mathbf{L}[G\upharpoonright y_G,G\upharpoonright h]$, where $h=\gamma \setminus \omega$.

Put $d=\gamma \setminus \left\{j\right\}$; the sets $b=\mathcal{I}\setminus \gamma$, $c=b\cup \left\{j\right\}$ have cardinality ${\omega }_1$, and $Y=h\cup b$ while $Y\cup \left\{j\right\}=h\cup c$. It follows from Lemma 32 that $K^{\prime }=K\upharpoonright d$ is a regular forcing, and in fact $G\upharpoonright \gamma \subseteq K^{\prime }$ since $j\notin y_G$. Moreover, by definition all of $K_0,K,K^{\prime },d,b,c$ are absolute ${\mathsf{\Delta }}_1^{\mathrm{HC}}\left(w\right)$ sets in $\mathbf{L}$ for some $w\in {\omega }^{\omega }$. Therefore by Corollary 10 $\mathsf{\Phi }$ is simultaneously true in $\mathbf{L}[G\cap K^{\prime },G\upharpoonright b]$ and in $\mathbf{L}[G\cap K^{\prime },G\upharpoonright c]$. However,

$$\mathbf{L}[G\cap K^{\prime },G\upharpoonright b]=\mathbf{L}[G\cap K_0,G\upharpoonright (\gamma \setminus \omega ),G\upharpoonright (\mathcal{I}\setminus \gamma )]=\mathbf{L}[y_G,G\upharpoonright (\mathcal{I}\setminus \omega )],$$

and similarly $\mathbf{L}[G\cap K^{\prime },G\upharpoonright c]=\mathbf{L}[y_G,a_G\left(j\right),G\upharpoonright (\mathcal{I}\setminus \omega )]$, as required. □

9.3. Second Key Lemma

In continuation of the proof of Claim 11, we establish another key lemma (Lemma 35). Suppose that

(I)

$G\subseteq \mathbb{P}$ is $\mathbb{P}$-generic over $\mathbf{L}$, $x\subseteq \omega ,x\in \mathbf{L}\left[G\upharpoonright Y_G\right]$, and $\phi \left(m\right),\psi \left(m\right)$ are parameter-free ${\Sigma }_{𝕟+1}^1$ formulas that give a ${\mathsf{\Delta }}_{𝕟+1}^1$ definition for $x=\left\{m\in \omega :\phi \right(m\left)\right\}=\{m:\neg \psi (m\left)\right\}$ in $\mathbf{L}\left[G\upharpoonright Y_G\right]$.

Thus it is true in $\mathbf{L}\left[G\right]$ that “the equivalence $\forall m\left(\phi \right(m)⟺\neg \psi (m\left)\right)$ holds in the model $\mathbf{L}\left[G\upharpoonright Y_G\right]$”. It follows that there is a condition $p_0\in G$ with

(II)

$p_0{\left|\right|--}_{\mathbb{P}}“\mathbf{L}\left[\underline{G}\upharpoonright Y_{\underline{G}}\right]\vDash \forall m(\phi \left(m\right)⟺\neg \psi \left(m\right))”$.

Lemma 34.

If $p_0\in G$ satisfies (II) then so does $p_0\upharpoonright \left\{0\right\}$.

Proof. 

We assume w.l.o.g. that $0\in |p_0|$. Let $u=|p_0|\setminus \left\{0\right\}$. In the context of Theorem 7, put $d=\mathcal{I}$, $c=\omega \setminus u$, and $K^{\prime }=K_0\upharpoonright c$ (a regular forcing by Lemma 32). Then $Y_G=(\mathcal{I}\setminus \omega )\cup y_G=(\mathcal{I}\setminus \omega )\cup (y_G\cap c)\cup (y_G\cap u)$, hence

$$\mathbf{L}\left[G\upharpoonright Y_G\right]=\mathbf{L}\left[G\upharpoonright (\mathcal{I}\setminus \omega )\right]\cup \mathbf{L}\left[G\upharpoonright (y_G\cap c)\right]\cup \mathbf{L}\left[G\upharpoonright (y_G\cap u)\right].$$

Here $\mathcal{I}\setminus \omega \subseteq d\setminus c$ is constructible while $y_G\cap u\subseteq d\setminus c$ is finite and hence constructible as well. We conclude by Theorem 7(i) that $p_0\upharpoonright c$ $\mathbb{P}$-forces $“\mathbf{L}\left[\underline{G}\upharpoonright Y_{\underline{G}}\right]\vDash \forall m(\phi \left(m\right)⟺\neg \psi \left(m\right))”$. However, $c\cap |p_0|=\left\{0\right\}$, so we are done. □

Following the lemma, fix a condition $p_0\in G$ satisfying $|p_0|=\left\{0\right\}$ and (II).

Lemma 35.

Assume (I) and (II) above. Let $m<\omega$. Then the sentence $\phi \left(m\right)$ is $K\left[\mathbb{U}\right]$-decided by $p_0:$ either $p_0{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi \left(m\right)$ or $p_0{\left|\right|--}_{K\left[\mathbb{U}\right]}\neg \phi \left(m\right)$.

Proof. 

It will be technically easier to establish the result in the following form equivalent to the original form by Theorem 5(i):

(1°)

the sentence “$\mathbf{L}\left[\underline{G}\upharpoonright Y_{\underline{G}}\right]\vDash \phi \left(m\right)$” is $\mathbb{P}$-decided by $p_0$.

Assume that this fails; then there exist two conditions $p,q\in \mathbb{P}$ stronger than $p_0$ and satisfying:

(2°)

$q{\left|\right|--}_{\mathbb{P}}“\mathbf{L}\left[\underline{G}\upharpoonright Y_{\underline{G}}\right]\vDash \phi \left(m\right)”$ and $p{\left|\right|--}_{\mathbb{P}}“\mathbf{L}\left[\underline{G}\upharpoonright Y_{\underline{G}}\right]\vDash \neg \phi \left(m\right)”$.

We can assume that $\left|p\right|=\left|q\right|=\left\{0\right\}$; otherwise apply Lemma 34 to formulas $\phi$ and $\neg \phi$. Strengthening $p,q$, if necessary, we can w.l.o.g. assume that

(a)

$F_q\left(0\right)=F_p\left(0\right)$ and $S_p\left(0\right)\cup S_q\left(0\right)\subseteq F_p^{\vee }\left(0\right)=F_q^{\vee }\left(0\right)$. (= (3) in Section 3.8.)

Working towards a contradiction, we w.l.o.g. assume that, in addition to (a), the following holds:

(b)

the symmetric difference $S_p\left(0\right)\mathsf{\Delta }{S}_q\left(0\right)$ contains a single element $s\in \mathbf{Seq}$.

(Any pair of conditions $p,q\le p_0$ satisfying (a) can be connected by a finite chain of conditions in which any two neighbours satisfy (b) and are $\le p_0$.)

Thus suppose that $p,q\le p_0$, $\left|p\right|=\left|q\right|=\left\{0\right\}$, (a), (b), 2° hold; the goal is to infer a contradiction. The associated transformation $H_q^p$ (Definition 12) maps $P=\{p^{\prime }\in \mathbb{P}:p^{\prime }\le p\}$ onto $Q=\{q^{\prime }\in \mathbb{P}:q^{\prime }\le q\}$ order-preservingly by Theorem 6. Let $G\subseteq P$ be a set $\mathbb{P}$-generic over $\mathbf{L}$ and containing p. Then $H=\{H_q^p\left(p^{\prime }\right):p^{\prime }\in G\}\subseteq Q$ is $\mathbb{P}$-generic as well, $q\in H$, and hence $\mathbf{L}\left[H\upharpoonright Y_H\right]\vDash \phi \left(m\right)$, while $\mathbf{L}\left[H\upharpoonright Y_G\right]\vDash \neg \phi \left(m\right)$ by 2°.

Case 1: $S_p\left(0\right)=S_q\left(0\right)\cup \left\{s\right\}$, where $s={\mathrm{s}}_{\ell }\in \mathbf{Seq}\setminus S_q\left(0\right)$. Then the map $H_q^p$ acts so that $q^{\prime }=H_q^p\left(p^{\prime }\right)$ is defined by $|p^{\prime }|=|q^{\prime }|\supseteq |p|=|q|$, $p^{\prime }\left(\nu \right)=q^{\prime }\left(\nu \right)$ for all $\nu \in \mathcal{I},\nu \ne 0$, $F_{q^{\prime }}\left(0\right)=F_{p^{\prime }}\left(0\right)$, but $S_{p^{\prime }}\left(0\right)=S_{q^{\prime }}\left(0\right)\cup \left\{s\right\}$. It follows that $S_H\left(\nu \right)=S_G\left(\nu \right)$ for all $\nu \ne 0$ but $S_G\left(0\right)=S_H\left(0\right)\cup \left\{s\right\}$. Thus $a_G\left(\nu \right)=a_H\left(\nu \right)$ for $\nu \ne 0$ but $a_G\left(0\right)=a_H\left(0\right)\cup \{\ell \}$ since $s={\mathrm{s}}_{\ell }$. In other words, $a_G\left(0\right)=a_H\left(0\right)\cup \{\ell \}$, therefore $y_G=y_H\cup \{\ell \}$ and $\mathbf{L}\left[G\upharpoonright Y_G\right]=\mathbf{L}[H\upharpoonright Y_H,a_H(\ell )]$. It follows from Lemma 33 that any ${\Sigma }_{𝕟+1}^1$ formula true in $\mathbf{L}\left[H\upharpoonright Y_H\right]$ remains true in $\mathbf{L}\left[G\upharpoonright Y_G\right]$. In particular, $\mathbf{L}\left[G\upharpoonright Y_G\right]\vDash \phi \left(m\right)$, a contradiction.

Case 2: $S_q\left(0\right)=S_p\left(0\right)\cup \left\{s\right\}$, where $s={\mathrm{s}}_{\ell }\in \mathbf{Seq}\setminus S_p\left(0\right)$. Then, similarly to the above, $a_G\left(\nu \right)=a_H\left(\nu \right)$ for $\nu \ne 0$, but $a_H\left(0\right)=a_G\left(0\right)\cup \{\ell \}$. Therefore, $y_H=y_G\cup \{\ell \}$ and $\mathbf{L}\left[H\upharpoonright Y_H\right]=\mathbf{L}[G\upharpoonright Y_G,a_G(\ell )]$. Thus any ${\Pi }_{𝕟+1}^1$ formula true in $\mathbf{L}\left[H\upharpoonright Y_H\right]$ remains true in $\mathbf{L}\left[G\upharpoonright Y_G\right]$ by Lemma 33. Apply this to the formula $\neg \psi \left(m\right)$, equivalent to $\phi \left(m\right)$ in both models by (II) above. (Note that $p,q\le p_0$, hence $p_0\in G\cap H$.) We have $\mathbf{L}\left[G\upharpoonright Y_G\right]\vDash \phi \left(m\right)$, a contradiction.   (Lemma 35) □

9.4. Final Argument

Here we finish the proof of both Claim 11 in Section 9.1 and Theorem 3. Suppose that $G\subseteq \mathbb{P}$ is a set $\mathbb{P}$-generic over $\mathbf{L}$, $Y=Y_G$, and a set $x\subseteq \omega$ in $\mathbf{L}\left[G\upharpoonright Y\right]$, formulas $\phi ,\psi$, and a condition $p_0$ satisfy assumptions (I), (II) above. Then, by Lemma 35,

$$x=\left\{m<\omega :p_0{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi \left(m\right)\right\}=\left\{m:A(p_0,m)\right\},$$

(16)

where, in $\mathbf{L}$, $A\subseteq K\left[\mathbb{U}\right]\times \omega$ is a ${\Sigma }_{𝕟}^{\mathrm{HC}}$ set such that $A(p,m)⟺p{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi \left(m\right)$ for all $p\in K\left[\mathbb{U}\right]$ and m (Corollary 9). It follows that, in $\mathbf{L}$, x is ${\Sigma }_{𝕟}^{\mathrm{HC}}\left(p_0\right)$, hence ${\Sigma }_{𝕟+1}^1\left(w\right)$ (see Remark 2 in Section 4.3), where $w\in \mathbf{L}\cap {\omega }^{\omega }$ is a suitable code of $p_0$.

To eliminate $p_0$, consider the set Q of all conditions $p\in K\left[\mathbb{U}\right]$ such that $\left|p\right|=|p_0|$ and $S_p\left(\nu \right)=S_{p_0}\left(\nu \right)$ for all $\nu \in \left|p\right|=|p_0|$. Note that $K\left[\mathbb{U}\right]=K\cap \mathbb{P}$ is a set of the same complexity as $\mathbb{P}$, that is, ${\mathsf{\Delta }}_{𝕟-1}^{\mathrm{HC}}$, and hence so is Q because $|p_0|$ and all $S_{p_0}\left(\nu \right),\nu \in \left|p_0\right|$ are finite sets. It follows that Q is ${\mathsf{\Delta }}_{𝕟-1}^{\mathrm{HC}}$.

We now claim that, in $\mathbf{L}$, $x=\{m\in \omega :\exists p\in QA(p,m\left)\right\};$ this obviously yields x being lightface ${\Sigma }_{n+1}^1$ in $\mathbf{L}$. Indeed ⊆ follows by taking $p=p_0\in Q$ and applying (16). Now suppose that $p\in Q$ and $A(p,m)$, that is, $p{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi \left(m\right)$. Recall that $p_0$ decides $\phi \left(m\right)$ by Lemma 35. However, $p_0{\left|\right|--}_{K\left[\mathbb{U}\right]}\neg \phi \left(m\right)$ is impossible since any condition in Q is compatible with $p_0$. Therefore $p_0{\left|\right|--}_{K\left[\mathbb{U}\right]}\phi \left(m\right)$ as required. Thus $x\in {\Sigma }_{𝕟+1}^1$ in $\mathbf{L}$ is established.

That the complementary set $\omega \setminus x$ is ${\Sigma }_{𝕟+1}^1$ as well is verified the same way, using the formula $\psi$ instead of $\phi$. (Theorem 3)

10. Conclusions and Some Further Results

With proofs of the main theorems accomplished, in this final section some further results are briefly discussed, which we plan to achieve and publish elsewhere.

10.1. Separation

This is another application of submodels of the same basic model. Recall that given a class $\mathbb{K}$ of pointsets, the separation principle $\mathbb{K}$-Sep claims that any two disjoint $\mathbb{K}$-sets in the same space can be separated by a set in $\mathbb{K}\cap \mathbb{K}{}^{\complement }$, where $\mathbb{K}{}^{\complement }$ consists of all complements of $\mathbb{K}$-sets. The separation principle was introduced by N. Luzin. Luzin proved (see [25]) that ${\mathsf{\Sigma }}_1^1$-Sep holds, and then P.Novikov [26,27] demonstrated that ${\mathsf{\Pi }}_1^1$-Sep fails, while at the second projective level, the other way around, ${\mathsf{\Pi }}_2^1$-Sep holds but ${\mathsf{\Sigma }}_2^1$-Sep fails.

As for higher projective levels, the separation problem belongs to a considerable list of problems related to the projective hieharchy in Luzin’s book [25], Chapter V. Further development of set theory showed that Luzin’s problems are very hard to solve. Some of them are now known to be independent of the Zermelo–Fraenkel set theory $\mathbf{ZFC}$, while some others are still open in different aspects, but it is known that adding Gödel’s axiom of constructibility $\mathbf{V}=\mathbf{L}$ solves most of them. In particular, $\mathbf{V}=\mathbf{L}$ implies [28,29] that ${\mathsf{\Pi }}_n^1$-Sep holds but ${\mathsf{\Sigma }}_n^1$-Sep fails for all $n\ge 3$—similarly to the classical case $n=2$. It follows that the statement $\forall n\ge 3({\mathsf{\Pi }}_n^1-\mathbf{Seq}\wedge \neg {\mathsf{\Sigma }}_n^1-\mathbf{Seq})$ is consistent with $\mathbf{ZFC}$, and the problem is then to find a model in which we have ${\mathsf{\Sigma }}_n^1$-Sep and/or $\neg {\mathsf{\Pi }}_n^1$-Sep (opposite to the state of affairs in $\mathbf{L}$) for one or several or all indices $n\ge 3$. This was the content of problems P 3029 and 3030 in the survey [8] of early years of forcing.

This turns out a very difficult question, and still open in its general forms, especially w.r.t. ${\mathsf{\Sigma }}_n^1$-Sep. (Compare to Problem 9 in [30], Section 9.) As for the $\neg {\mathsf{\Pi }}_n^1$-Sep side, there are indications in the set-theoretic literature, that generic extensions, where both ${\mathsf{\Sigma }}_n^1$-Sep and ${\mathsf{\Pi }}_n^1$-Sep fail, are constructed by L. Harrington for $n=3$ (see 5B.3 in [6]) and for arbitrary $n\ge 3$ (see [8] and [31], p. 230). These results were indeed announced in Harrington’s handwritten notes (Addendum A in [32]), with brief outline of some key arguments related mainly to case $n=3$ and based on almost-disjoint forcing. There are no such results in Harrington’s published works, assumed methods in their principal part (arbitrary n) are not used even for any other results, and separability theorems in this context are not considered. An article by Harrington, entitled “Consistency and independence results in descriptive set theory”, which apparently might have contained these results, was announced in the References list in [31], to appear in Ann. of Math., 1978, but in fact it has never been published.

The following conjecture concludes Addendum A of Harrington’s note [32]:

In fact (we believe) there is a model of $\mathbf{ZFC}$ in which Separation fails for all of the following at once: ${\mathsf{\Sigma }}_n^1$, ${\mathsf{\Pi }}_n^1$, $3\le n<\omega$, ${\mathsf{\Sigma }}_n^m$, ${\mathsf{\Pi }}_n^m$, $1\le n<\omega$, $2\le m<\omega$. ( ${\mathsf{\Sigma }}_n^m$, ${\mathsf{\Pi }}_n^m$ are classes arising in the type-theoretic hierarchy).

The hypothesis is partially confirmed by the following our theorem (to appear elsewhere).

Theorem 15 

(originally Harrington [32]). If $𝕟\ge 2$ then there is a generic extension of $\mathbf{L}$ in which ${\mathsf{\Pi }}_{𝕟+1}^1$-Sep and ${\mathsf{\Sigma }}_{𝕟+1}^1$-Sep fail, and moreover

(i)

there exist disjoint ${\mathsf{\Pi }}_{𝕟+1}^1$ sets of reals unseparable by disjoint ${\mathsf{\Sigma }}_{𝕟+1}^1$ sets,

(ii)

there exist disjoint ${\mathsf{\Sigma }}_{𝕟+1}^1$ sets of reals unseparable by disjoint ${\mathsf{\Pi }}_{𝕟+1}^1$ sets.

Moreover there is a generic extension of $\mathbf{L}$ in which (i) and (i) simultaneously hold for all $𝕟\ge 2$.

Note that generic models are defined in [33] in which both ${\mathsf{\Sigma }}_3^1$-Sep and ${\mathsf{\Pi }}_3^1$-Sep fail. We used different technique in [33], mostly related to Jensen’s minimal ${\Pi }_2^1$ singleton forcing [10] and its iterated forms (see [34,35,36]) rather than the almost-disjoint forcing as in this paper.

10.2. Projections of Uniform Sets

In his monograph [25] (pp. 276–291) Nikolas Luzin formulated a number of problems about the structure of the projective classes ${\mathsf{\Sigma }}_n^1$, ${\mathsf{\Pi }}_n^1$, ${\mathsf{\Delta }}_n^1$ (or ${\mathbf{A}}_n,{\mathbf{CA}}_n,{\mathbf{B}}_n$ in the old notational system). Their general meaning was to extend the results obtained by Luzin himself and P. S. Novikov for classes ${\mathsf{\Sigma }}_1^1$, ${\mathsf{\Pi }}_1^1$, ${\mathsf{\Delta }}_1^1$ (level $n=1$ of the projective hierarchy) to higher levels. Among these problems, the following stands out, along with the separation problem discussed above:

Projection problem: 

given $n\ge 2$, find out the nature of projections of uniform (planar) ${\mathsf{\Pi }}_n^1$ sets in comparison with the class ${\mathsf{\Sigma }}_{n+1}^1$ of arbitrary projections of ${\mathsf{\Pi }}_n^1$ sets and with the narrower class ${\mathsf{\Delta }}_n^1$. (A planar set is uniform, if it intersects every vertical line at no more than one point.)

Further research has shown the key importance of structural theorems on projective classes for the development of descriptive set theory. For example, separation principles play essential role in research on subsystems of second-order arithmetic, in particular, in the context of reverse mathematics [5].

If $n=1$ then every ${\mathsf{\Sigma }}_2^1$ set is equal to the projection of a uniform ${\mathsf{\Pi }}_1^1$ set by the Novikov–Kondo–Addison uniformization theorem [6, 4E.4]. Under $\mathbf{V}=\mathbf{L}$, the uniformization theorem fails for classes ${\mathsf{\Pi }}_n^1,n\ge 2$, but nevertheless it is known that if $n\ge 2$ then every ${\mathsf{\Sigma }}_{n+1}^1$ set is equal to the projection of a uniform ${\mathsf{\Pi }}_n^1$ set [37]. The next theorem (to appear elsewhere) demonstrates that this property is violated in suitable generic models.

Theorem 16.

If $𝕟\ge 2$ then there is a generic extension of $\mathbf{L}$ in which:

(i)

there is a ${\mathsf{\Sigma }}_{𝕟+1}^1$ set not equal to the projection of a uniform ${\mathsf{\Pi }}_{𝕟+1}^1$ sets,

(ii)

there is a ${\mathsf{\Delta }}_{𝕟+1}^1$ set not equal to the projection of a uniform ${\mathsf{\Pi }}_{𝕟}^1$ set.

10.3. Harvey Friedman’s ${\mathsf{\Delta }}_n^1$ Problem

Problem 87 in [38] requires to prove that for each $n>2$ there is a model of

$$\mathbf{ZFC}+“\mathrm{the}\mathrm{constructible}\mathrm{reals}\mathrm{are}\mathrm{precisely}\mathrm{the}{\mathsf{\Delta }}_n^1\mathrm{reals}”.$$

(17)

It is noted in the very end of [38] that Harrington had solved this problem affirmatively. Indeed, a sketch is given in the same handwritten notes [32], of a generic extension of $\mathbf{L}$, in which it is true that ${\omega }^{\omega }\cap \mathbf{L}={\mathsf{\Delta }}_3^1$, as well as a few sentences added as how Harrington planned to get a model in which ${\omega }^{\omega }\cap \mathbf{L}={\mathsf{\Delta }}_n^1$ holds for a given (arbitrary) $n\ge 3$, and a model in which ${\omega }^{\omega }\cap \mathbf{L}={\mathsf{\Delta }}_{\infty }^1$, where ${\mathsf{\Delta }}_{\infty }^1={\bigcup }_n{\mathsf{\Delta }}_n^1$ (all analytically definable reals). This positively solves Problem 87, including the case $n=\infty$. Full proofs have never been published except for an independent proof of the consistency of ${\omega }^{\omega }\cap \mathbf{L}={\mathsf{\Delta }}_{\infty }^1$ in [39]. Our plan will be to restore Harrington’s proof of the next theorem elsewhere.

Theorem 17

(originally Harrington [32]) (i) If $𝕟\ge 2$ then there is a generic extension of $\mathbf{L}$ in which it is true that ${\omega }^{\omega }\cap \mathbf{L}={\mathsf{\Delta }}_{𝕟+1}^1$.

(ii) There is a generic extension of $\mathbf{L}$ in which it is true that ${\omega }^{\omega }\cap \mathbf{L}={\mathsf{\Delta }}_{\infty }^1$.

Friedman concludes [38] with a modified version of the above problem, given as Problem 87${}^{\prime }$: find a model of

$$\mathbf{ZFC}+“\mathrm{for}\mathrm{any}\mathrm{reals}x,y,\mathrm{we}\mathrm{have}:\mathrm{if}x\in \mathbf{L}\left[y\right]\mathrm{then}x\mathrm{is}{\mathsf{\Delta }}_3^1\mathrm{in}y”.$$

(18)

This was solved in the positive by David [40], yet so far it is unknown whether this result generalizes to higher classes ${\mathsf{\Delta }}_n^1$, $n\ge 4$, or ${\mathsf{\Delta }}_{\infty }^1$. We also note that problems (17) and (18) were known in the early years of forcing, see, e.g., problems P 3110, 3111, 3112 in [8].

10.4. Axiom Schemata in 2nd Order Arithmetic

Different axiomatic systems in second-order arithmetic ${\mathbf{Z}}_2$ is widely represented in modern research, in particular, in the context of reverse mathematics and other sections of proof theory. See e.g., Simpson [5] (Part B), and numerous articles, and from older sources—for example, Kreisel [41], where the choice of subsystems is called the central problem. These systems are obtained by joining a particular combination of comprehension schema $\mathbf{CA}$, countable choice $\mathbf{AC}$, dependent choice $\mathbf{DC}$, transfinite induction $\mathbf{TI}$ and recursion $\mathbf{TR}$, etc., to the basic theory, say ${\mathbf{ACA}}_0$. The schemata can be specifieded by the complexity of the core formula in the Kleene hierarchy, as well as by allowing or prohibiting parameters. (For the importance of parameters, see [41], section III.)

The relationships between the subsystems have been actively studied. In particular, it is known that ${\mathsf{\Sigma }}_{n+1}^1$-CA is strictly stronger, than ${\mathsf{\Sigma }}_n^1$-CA, and the same for AC and DC. Proofs of these results in e.g., ([5] Chapter VII) use the fact that the schema at a higher quantifier level allows to get strictly more countable ordinals, than the schema at a lower level, but in essence, it is utilized that the $(n+1)$th level schema proves the consistency of the nth level schema.

A few more complex results are known, where the compared systems are equiconsistent, despite the increase in quantifier complexity in the schemata, so the consistency argument doesn’t work. It such a case one has to resort to set theoretic methods. This is the old result of A. Levy [42] that ${\mathsf{\Sigma }}_3^1$-AC does not follow from $\mathbf{CA}$, as well as a recent theorem in [43] saying that ${\mathsf{\Sigma }}_3^1$-DC does not follow from $\mathbf{AC}$; both are obtained using complex generic models of $\mathbf{ZF}$ without the full axiom of choice. The task of our further research in this direction will be to prove consistency theorems that demonstrate the importance of both the quantifier complexity and the presence of parameters in the ${\mathrm{Z}}_2$ schemata.

Theorem 18 (to appear elsewhere).

If $𝕟\ge 2$, then the theory ${\mathbf{ACA}}_0+{\mathbf{CA}}^{*}+{\mathsf{\Sigma }}_{𝕟}^1-\mathbf{CA}$ does not imply ${\mathsf{\Sigma }}_{𝕟+1}^1$-CA(unless inconsistent, of course).

Here CA* is the parameter-free part of the comprehension schema CA. Thus, both the quantifier complexity and the presence of parameters are essential for the deductive power of the comprehension schema in second-order arithmetic.

Theorem 19 (to appear elsewhere).

If $𝕟\ge 2$, then the theory ${\mathbf{ACA}}_0+\mathbf{CA}+\mathbf{AC}+{\mathsf{\Sigma }}_{𝕟}^1-\mathbf{DC}$ does not imply ${\mathsf{\Sigma }}_{𝕟+1}^1$-DC (unless inconsistent).

Remark 6.

We are grateful to one of the reviewers for pointing out possible connections of our research with some questions of fuzzy set theory [44,45], yet this issue cannot be considered for a short time.