Mixed Convective Stagnation Point Flow towards a Vertical Riga Plate in Hybrid Cu-Al₂O₃/Water Nanofluid

Abstract

The present work highlights the stagnation point flow with mixed convection induced by a Riga plate using a Cu-Al${}_2$O${}_3$/water hybrid nanofluid. The electromagnetohydrodynamic (EMHD) force generated from the Riga plate was influential in the heat transfer performance and applicable to delay the boundary layer separation. Similarity transformation was used to reduce the complexity of the governing model. MATLAB software, through the bvp4c function, was used to compute the resulting nonlinear ODEs. Pure forced convective flow has a distinctive solution, whereas two similarity solutions were attainable for the buoyancy assisting and opposing flows. The first solution was validated as the physical solution through the analysis of flow stability. The accretion of copper volumetric concentration inflated the heat transfer rate for the aiding and opposing flows. The heat transfer rate increased approximately up to an average of 10.216% when the copper volumetric concentration increased from 0.005 $(0.5\%)$ to 0.03 $(3\%)$.

1. Introduction

A new procreation fluid with good thermal performance is beneficial to fulfill industrial and technological needs. Formerly, Choi and Eastman [1] originated nanofluids and discovered that the dispersion of nanoparticles could augment the thermal conductivity of regular fluids. Currently, nano-suspensions have become one of the most hotly-debated subjects for advanced thermal engineering due to their high performance and sub-phenomena involved in this type of working fluid. Graphene is one of the nanoparticles that has received special attention due to its superior thermal conductivity and good stability when dispersed in a conventional coolant with poor thermal performance, such as water or ethylene glycol.

Sarafraz et al. [2] experimentally studied the convective heat transfer of graphene-water-ethylene glycol nanofluids inside a micro-channel. The results showed that the adoption of nanoparticles (graphene nano-platelets) could augment the thermal conductivity up to 32.1% of the working fluid. Later, Sarafraz et al. [3] found that an increase in the mass concentrations of the graphene-methanol nanofluid led to the augmentation of the solar collector’s thermal efficiency. In addition, Sarafraz et al. [4] conducted an experimental study and analyzed the thermal efficiency of carbon-acetone nanofluid for solar collectors.

A hybrid nanofluid is a combination of a base fluid (i.e., water, ethylene glycol, a mixture of ethylene glycol and water) with two different types of nanoparticles (i.e., metal oxides, metals, and carbon materials). Esfe et al. [5] developed a model to forecast the thermal conductivity of hybrid nanofluids particularly in carbon nanotubes. The carbon nanotubes were preferable in the preparation of hybrid nanofluid due to their great impact in the thermophysical properties. The pair of alumina and copper are also widely used in the theoretical and experimental studies of hybrid nanofluids. Alumina has low thermal conductivity; however, the good chemical inaction in alumina could maintain the stability of the hybrid nanofluid (see Suresh et al. [6]).

Reviews on the applications, preparation, and thermophysical properties of the hybrid nanofluids have been conducted by these researchers: see Jana et al. [7], Sarkar et al. [8], Sidik et al. [9], Akilu et al. [10], Babu et al. [11], Sundar et al. [12], Leong et al. [13], Huminic and Huminic [14], and Sajid and Ali [15]). The modified thermophysical properties, as in Devi and Devi [16], had excellent agreement with the existing experimental data by Suresh et al. [6]. They applied these new thermophysical properties into the existing single phase nanofluid model by Tiwari and Das [17].

Devi and Devi [16] found that the Cu-Al${}_2$O${}_3$/water hybrid nanofluid had a higher heat transfer rate than the nanofluid (Cu/water) with the imposition of a magnetic field (magnetohydrodynamics (MHD)). Nadeem et al. [18] studied the three-dimensional stagnation point flow with thermal slip towards a circular cylinder using a Cu-Al${}_2$O${}_3$/water hybrid nanofluid. Yousefi et al. [19] compared the influences of a titania-copper/water hybrid nanofluid, titania/water nanofluid, and regular fluid (viscous) on the stagnation point flow past a wavy cylinder. Muhammad et al. [20] used hybrid nanoparticles (cupric oxide (CuO) and carbon nanotubes (CNTs)) with gasoline oil to study the stagnation point flow over a stretching sheet. The convective condition with the viscous dissipation effect were also contemplated in their study. Khashi’ie et al. [21] analyzed the hybrid nanofluid flow and heat transfer over a permeable stretching/shrinking disc with the presence of a magnetic field and Joule heating.

The mixed convection flow arises due to the variations of surface temperature. It is a combination of free convection (assisting and opposing) and forced convection flows. The free or forced convection heat transfer is also significant in many engineering applications, such as double-wall thermal insulation, solar-collectors, underground cable systems, electric machinery, and cooling systems of micro-electronic devices. Das et al. [22] numerically investigated the buoyancy induced flow and heat transfer characteristics of a Newtonian fluid inside a wavy walled enclosure while the numerical simulation of a Newtonian fluid flow around a square cylinder was conducted by Mahmud et al. [23].

Tasnim et al. [24] presented the thermal and hydrodynamic behavior of a viscous fluid over an isothermal circular cylinder inside a square cavity. Later, the mixed convective flow of an alumina-water nanofluid inside a square cavity was investigated by Cong et al. [25] and Ting et al. [26]. An assisting flow appears when the surface temperature is greater than the ambient (far field) temperature while there is an opposing flow for the cooled wall surface. Ramachandran et al. [27] studied the steady mixed convective stagnation point flow of a viscous fluid and considered both arbitrary surface heat flux and temperature variations. They found that the dual solutions were possible within a specific range of the buoyancy parameter and a reverse flow began to develop in the opposing flow region. Later, the study was continued by Devi et al. [28] to the unsteady case, and they also obtained two solutions for the opposing flow case.

Ridha and Curie [29] reconsidered the problem from previous studies on axisymmetric mixed convection flow and mixed convection flow over horizontal and vertical surfaces. They proved that both opposing and aiding (assisting) flow could produce two similar solutions. Merrill et al. [30] revised the results from Nazar et al. [31], and they found non-unique solutions were attainable for both flow cases. They revealed the unstableness of the lower branch solution through temporal flow stability. Based on the numerical studies by Ishak et al. [32] and Ishak et al. [33], the suction and magnetic parameters could increase the range of the solutions. In addition, the duality of solutions were also observed in the opposing and aiding flow regions while producing a unique solution for the forced convective flow.

Rostami et al. [34] obtained upper and lower branch solutions for both assisting and opposing flow cases when the silica-alumina/water hybrid nanofluid was considered, while Waini et al. [35] scrutinized the hybrid nanofluid flow towards a vertical thin needle using the Cu-Al${}_2$O${}_3$ hybrid nanoparticles. The non-unique solutions of mixed convection flow also can be found in Khashi’ie et al. [36,37,38] and Ali et al. [39].

The study of electro-magneto-hydrodynamics (EMHD) has had a significant impact in technological and industrial applications, such as thermal reactors, submarines, and micro-coolers. A Riga plate is an electromagnetic device built from magnets and electrodes on a plane surface. This device can activate a wall parallel Lorentz force also known as an electromagnetohydrodynamic (EMHD) force, and this concept has been proposed by Gailitis and Lielausis [40]. This innovative actuator is also beneficial in delaying the boundary layer separation and diminishing the turbulence effects.

The early investigation of Blasius flow over a Riga plate using the Grinberg [41] term of Lorentz force was conducted by Tsinober and Shtern [42]. They found that the wall parallel Lorentz force affected the stability of the Blasius flow. Pantokratoras [43] discussed the Sakiadis flow (moved with constant velocity) and Blasius flow (constant free stream) over a Riga plate. The mixed convective flow and heat transfer of nanofluid towards a vertical permeable Riga plate was studied by Ahmad et al. [44] using the perturbation method. Ahmad et al. [45] also discussed the buoyancy effects on the stagnation point flow of nanofluid past a convectively heated Riga plate using both the shooting method and bvp4c solver program.

Zaib et al. [46] scrutinized the mixed convective flow of a micropolar TiO${}_2$-kerosene/water nanoparticles over a Riga plate. They used the Keller-box method for the numerical computation and obtained two solutions for the opposing flow and a unique solution for the assisting flow. Ahmed et al. [47] analyzed the squeezing flow of hybrid Ag-Fe${}_3$O${}_4$/water nanofluid between stretchable parallel Riga plates. The effects of chemical reaction and nonlinear thermal radiation were also have included in their work. Other reported works on the boundary layer flow along the Riga plate were extensively conducted by other researchers [48,49,50,51,52].

The separation point is important and acts as a signal for the occurrence of the transition flow from laminar to turbulent (boundary layer separation). Hence, it is important to discover the location of the separation point and the relevant parameters that are beneficial in delaying the separation process. Dual solutions are also within the scope of the study to prevent misinterpretation of the fluid flow behaviour. Previous works have proved that multiple solutions were possible in the mixed convection problem; however, only few cases reported the dual solutions in the assisting flow region.

Inspired and motivated by the literature above, the novelty of the present work is to scrutinize the dual solutions in mixed convective stagnation point flow of hybrid Cu-Al${}_2$O${}_3$/water nanofluid towards a Riga plate. The solutions were explored in both the assisting and opposing flow regions. Following Devi and Devi [16], the combination of alumina (first) and copper (second) nanoparticles was considered in the nanofluid model. Due to its complexity, the partial differential equations (PDEs) was simplified into a set of ordinary differential equations (ODEs) using the existing similarity transformation while the competent bvp4c solver was used for the numerical computation. The temporal stability analysis was necessary to validate the reliability of the similarity solution(s). Hence, the authors are confident that the present work is new, has significant impact in the mathematical and engineering fields, and can attract other researchers.

2. Mathematical Formulation

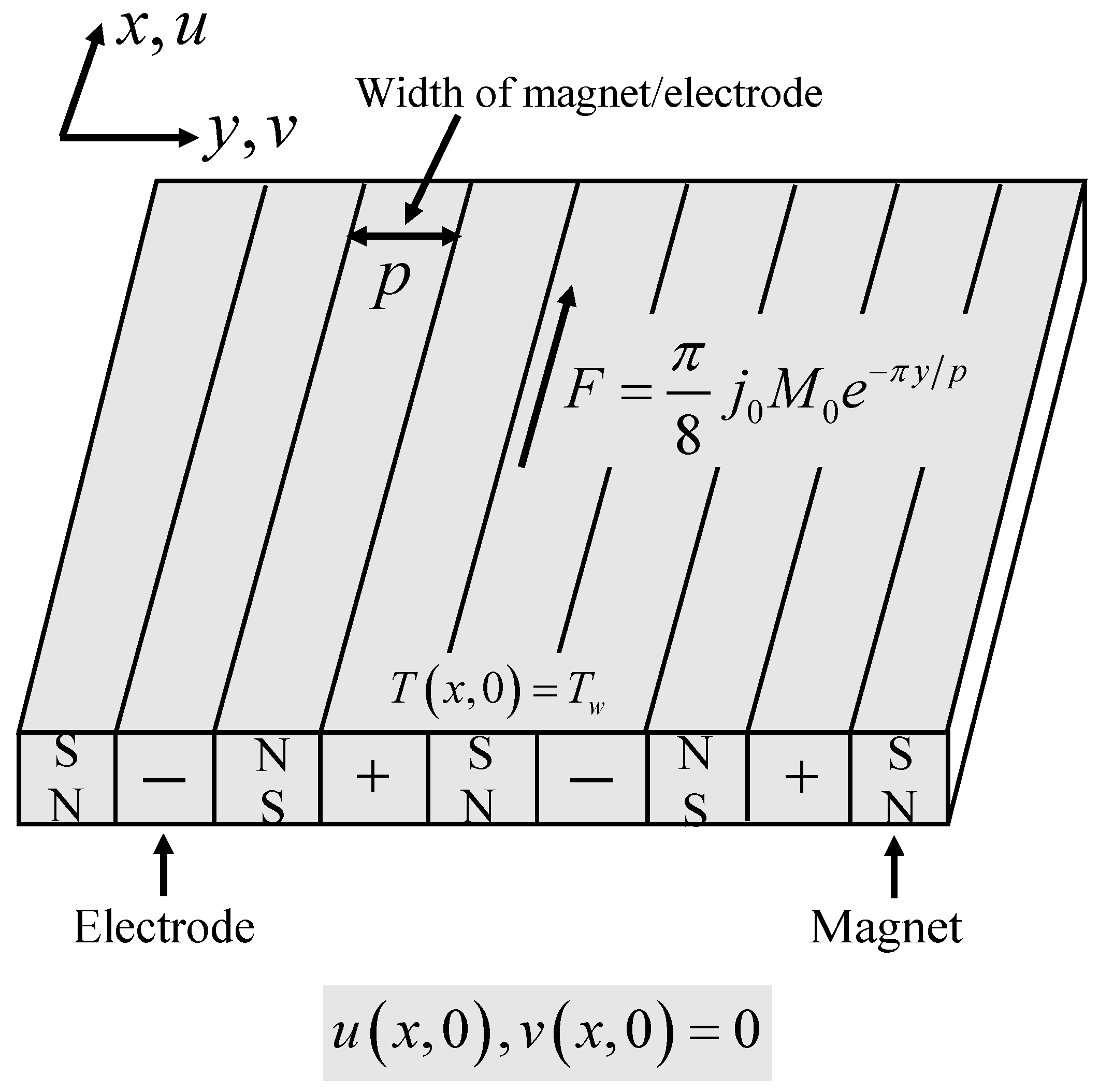
We considered a laminar, steady, and incompressible stagnation point flow towards a vertical Riga plate in a regular fluid (water) with Cu-Al${}_2$O${}_3$ hybrid nanoparticles. The Riga plate consisted of magnets and electrodes with the same width p as depicted in Figure 1. The polarity of the magnet is represented by N (north) and S (south) whereas the wall parallel Lorentz force is generated due to the electromagnetic field of the Riga plate (see Figure 1). The free stream velocity is assumed as ${\displaystyle u_e\left(x\right)=ax/\phantom{axL}L}$ with a as a positive constant and L as the characteristic length of the plate. The flow was assisted or opposed by the Lorentz force depending on the positive or negative x-direction. A few presumptions are also examined for the physical model:

• The base fluid and nanoparticles are maintained in a thermal equilibrium state.
• The nanofluid is assumed to be stable; hence, the effect of nanoparticle aggregation and sedimentation is omitted.
• The nanoparticles are uniform with a spherical shape.
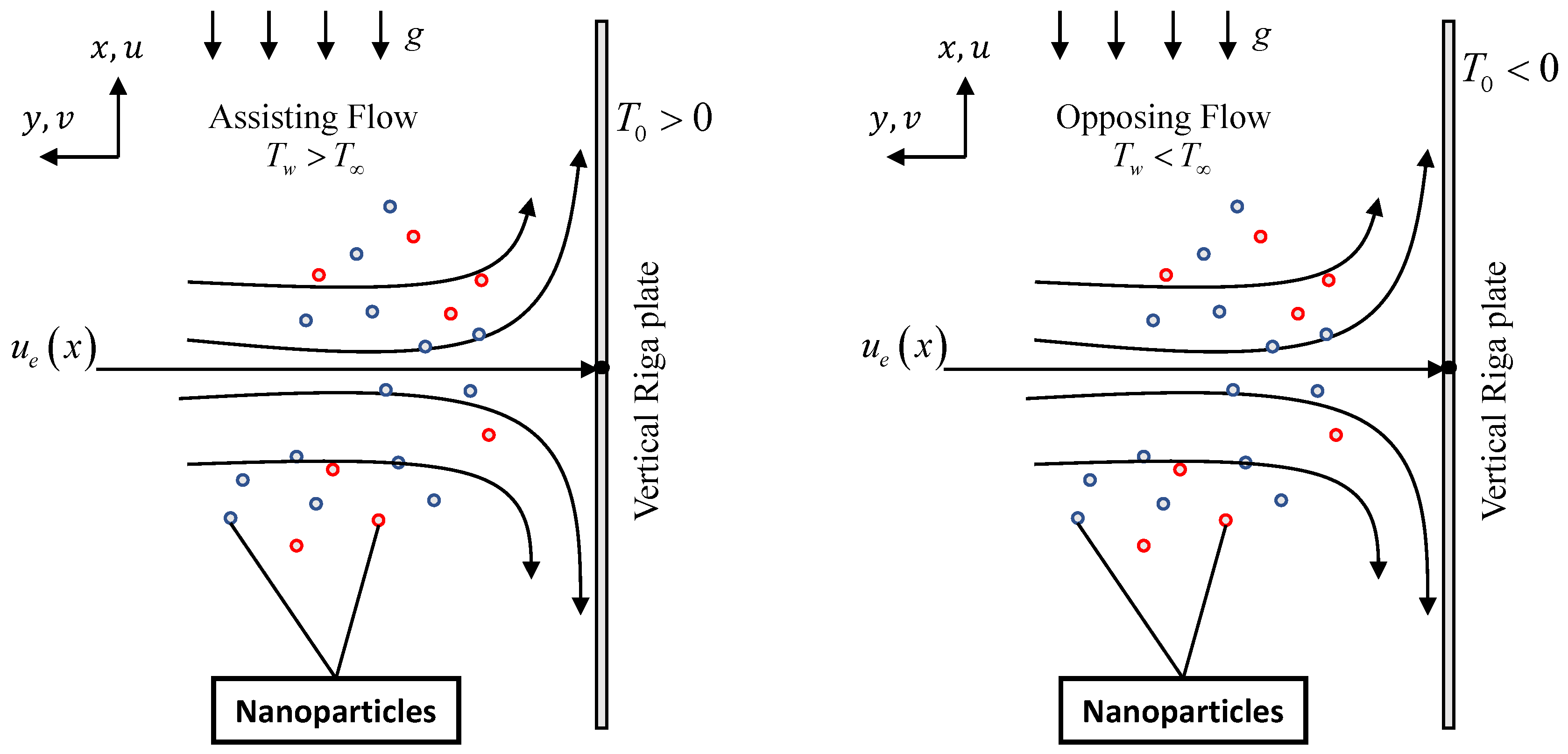
• The wall temperature is ${\displaystyle T_w\left(x\right)=T_{\infty }+T_0\left(x/\phantom{xL}L\right);}$${\displaystyle T_0>0\left(T_w>T_{\infty }\right)}$ specified for a heated sheet (assisting flow) while ${\displaystyle T_0<0\left(T_w<T_{\infty }\right)}$ for a cooled sheet (opposing flow) (see Figure 2).
• The constant ambient temperature $T_{\infty }$ is assumed for the case of unstratified fluid.
• The classical Hartmann term ${\displaystyle \left(\frac{{\sigma }_{hnf}{B_0}^{2}u}{{\rho }_{hnf}}\right)}$ is used to represent the magnetohydrodynamics (MHD) but the Grinberg term ${\displaystyle \left(\frac{\pi j_0{M}_0}{8{\rho }_{hnf}}{e}^{-\pi y/\phantom{-\pi yp}p}\right)}$ is used for the Riga plate in the momentum equation uncoupled with the flow velocity.

Under all these assumptions, by using the single phase nanofluid model by Tiwari and Das [17], the coupled boundary layer and energy equations are ([16,34,46])

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=u_e\frac{d{u}_e}{dx}+\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\frac{{\partial }^{2}u}{\partial y^2}+\frac{g{\left(\rho {\beta }_T\right)}_{hnf}\left(T-T_{\infty }\right)}{{\rho }_{hnf}}+\frac{\pi j_0{M}_0}{8{\rho }_{hnf}}{e}^{-\pi y/\phantom{-\pi yp}p},$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}={\left(\frac{k}{\rho C_p}\right)}_{hnf}\frac{{\partial }^{2}T}{\partial y^2},$$

(3)

with the compatible boundary conditions

$$\begin{array}{c}u\left(x,0\right)=0,v\left(x,0\right)=0,T\left(x,0\right)=T_w\left(x\right),\hfill \\ u\left(x,y\right)\to u_e\left(x\right),T\left(x,y\right)\to T_{\infty },y\to \infty .\hfill \end{array}$$

(4)

In the governing model, u and v represent the velocity components along the x- and y-directions, accordingly. The x-axis is measured along the plate whereas the y-axis is perpendicular to it. In addition, g is the gravitational acceleration, T is the fluid temperature, $M_0$ is the magnetization of the magnets while the magnets and electrodes width are symbolized as p. The current density applied in the electrodes is represented by $j_0$ (see Pantokratoras and Fang [53]).

Table 1. The thermophysical properties for hybrid nanofluids (see Devi and Devi [16], and Rostami et al. [34]).

Properties	Hybrid Nanofluid
Density	${\displaystyle {\rho }_{hnf}=\left(1-{\varphi }_2\right)\left[\left(1-{\varphi }_1\right){\rho }_f+{\varphi }_1{\rho }_{s1}\right]+{\varphi }_2{\rho }_{s2}}$
Heat Capacity	${\displaystyle {\left(\rho C_p\right)}_{hnf}=\left(1-{\varphi }_2\right)\left[\left(1-{\varphi }_1\right){\left(\rho C_p\right)}_f+{\varphi }_1{\left(\rho C_p\right)}_{s1}\right]+{\varphi }_2{\left(\rho C_p\right)}_{s2}}$
Dynamic Viscosity	${\displaystyle \frac{{\mu }_{hnf}}{{\mu }_f}=\frac{1}{{\left(1-{\varphi }_1\right)}^{2.5}{\left(1-{\varphi }_2\right)}^{2.5}}}$
Thermal Conductivity	$\begin{array}{c}{\displaystyle \frac{k_{hnf}}{k_{bf}}=\left[\frac{k_{s2}+2k_{bf}-2{\varphi }_2\left(k_{bf}-k_{s2}\right)}{k_{s2}+2k_{bf}+{\varphi }_2\left(k_{bf}-k_{s2}\right)}\right]}\hfill \\ \mathrm{where}\hfill \\ {\displaystyle \frac{k_{bf}}{k_f}=\left[\frac{k_{s1}+2k_f-2{\varphi }_1\left(k_f-k_{s1}\right)}{k_{s1}+2k_f+{\varphi }_1\left(k_f-k_{s1}\right)}\right]}\hfill \end{array}$
Thermal Expansion	${\left(\rho {\beta }_T\right)}_{hnf}=\left(1-{\varphi }_2\right)\left[\left(1-{\varphi }_1\right){\left(\rho {\beta }_T\right)}_f+{\varphi }_1{\left(\rho {\beta }_T\right)}_{s1}\right]+{\varphi }_2{\left(\rho {\beta }_T\right)}_{s2}$

and Table 2 summarize the thermophysical properties for both traditional and hybrid nanofluids, where $\rho$, $\rho C_p$, $\mu$, k, and ${\beta }_T$ describe the density, heat capacity, dynamic viscosity, thermal conductivity, and thermal expansion, respectively. The subscript terms f, $nf$, $hnf$, and s symbolize the base fluid, nanofluid, hybrid nanofluid, and nanoparticle while $s_1$ and $s_2$ represent the first and second type of nanoparticles. In addition, the nanoparticle solid volume fractions are represented by ${\varphi }_1$ (first nanoparticle) and ${\varphi }_2$ (second nanoparticle). In the present work, the first nanoparticle is alumina (Al${}_2$O${}_3$), copper (Cu) is the second nanoparticle, while water acts as the base fluid. The thermophysical properties for the selected nanoparticles and base fluid are displayed in Table 3.

There is also another practical model of hybrid nanofluids for future studies as discussed by Ghalambaz et al. [54,55]. In the model, the volume fraction of hybrid nanoparticles is represented by ${\varphi }_{hnf}={\varphi }_1+{\varphi }_2$ while the dynamic viscosity and density are ${\displaystyle \frac{{\mu }_{hnf}}{{\mu }_f}=\frac{1}{{\left(1-{\varphi }_1-{\varphi }_2\right)}^{2.5}}}$ and ${\displaystyle {\rho }_{hnf}=\left(1-{\varphi }_{hnf}\right){\rho }_f+{\rho }_{s1}{\varphi }_1+{\rho }_{s2}{\varphi }_2}$, respectively. Devi and Devi [16] successfully validated their proposed correlation of thermal conductivity in Table 1 with experimental data by Suresh et al. [6]. The thermal conductivity of hybrid nanofluid has a good correlation with the existing experimental data, hence, we are confident to use the thermophysical properties by Devi and Devi [16].

Table 2. The thermophysical properties for nanofluids (see Brinkman [56], Xuan and Li [57], Maxwell-Garnett [58], Das et al. [59], and Oztop and Abu-Nada [60]).

Properties	Nanofluid
Density	${\rho }_{nf}=\left(1-\varphi \right){\rho }_f+\varphi {\rho }_s$
Heat Capacity	${\left(\rho C_p\right)}_{nf}=\left(1-\varphi \right){\left(\rho C_p\right)}_f+\varphi {\left(\rho C_p\right)}_s$
Dynamic Viscosity	${\displaystyle \frac{{\mu }_{nf}}{{\mu }_f}=\frac{1}{{\left(1-\varphi \right)}^{2.5}}}$
Thermal Conductivity	${\displaystyle \frac{k_{nf}}{k_f}=\left[\frac{k_s+2k_f-2\varphi \left(k_f-k_s\right)}{k_s+2k_f+\varphi \left(k_f-k_s\right)}\right]}$
Thermal Expansion	${\left(\rho {\beta }_T\right)}_{nf}=\left(1-\varphi \right)\left(1-\varphi \right){\left(\rho {\beta }_T\right)}_f+\varphi {\left(\rho {\beta }_T\right)}_s$

Table 2. The thermophysical properties for nanofluids (see Brinkman [56], Xuan and Li [57], Maxwell-Garnett [58], Das et al. [59], and Oztop and Abu-Nada [60]).

Properties	Nanofluid
Density	${\rho }_{nf}=\left(1-\varphi \right){\rho }_f+\varphi {\rho }_s$
Heat Capacity	${\left(\rho C_p\right)}_{nf}=\left(1-\varphi \right){\left(\rho C_p\right)}_f+\varphi {\left(\rho C_p\right)}_s$
Dynamic Viscosity	${\displaystyle \frac{{\mu }_{nf}}{{\mu }_f}=\frac{1}{{\left(1-\varphi \right)}^{2.5}}}$
Thermal Conductivity	${\displaystyle \frac{k_{nf}}{k_f}=\left[\frac{k_s+2k_f-2\varphi \left(k_f-k_s\right)}{k_s+2k_f+\varphi \left(k_f-k_s\right)}\right]}$
Thermal Expansion	${\left(\rho {\beta }_T\right)}_{nf}=\left(1-\varphi \right)\left(1-\varphi \right){\left(\rho {\beta }_T\right)}_f+\varphi {\left(\rho {\beta }_T\right)}_s$

Table 3. Thermophysical properties for alumina, copper, and pure water (see Das et al. [61], Khanafer et al. [62] and Oztop and Abu-Nada [60], Cong et al. [25], and Ting et al. [26]).

Thermophysical Properties	Pure Water	Alumina	Copper
$\rho (\frac{kg}{m^3})$	997.1	3970	8933
$C_p(\frac{J}{kgK})$	4179	765	385
$k(\frac{W}{mK})$	0.6130	40	400
${\beta }_T(K^{-1})$	$21\times {10}^{-5}$	$0.85\times {10}^{-5}$	$1.67\times {10}^{-5}$

Table 3. Thermophysical properties for alumina, copper, and pure water (see Das et al. [61], Khanafer et al. [62] and Oztop and Abu-Nada [60], Cong et al. [25], and Ting et al. [26]).

Thermophysical Properties	Pure Water	Alumina	Copper
$\rho (\frac{kg}{m^3})$	997.1	3970	8933
$C_p(\frac{J}{kgK})$	4179	765	385
$k(\frac{W}{mK})$	0.6130	40	400
${\beta }_T(K^{-1})$	$21\times {10}^{-5}$	$0.85\times {10}^{-5}$	$1.67\times {10}^{-5}$

The similarity transformation in Equation (5) satisfied the continuity Equation (1) (see Rostami et al. [34] and Zaib et al. [46]),

$$u=u_e\left(x\right)f^{\prime }\left(\eta \right),v=-\sqrt{\frac{u_e\left(x\right){\nu }_f}{x}}f\left(\eta \right),\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w\left(x\right)-T_{\infty }},\eta =y\sqrt{\frac{u_e\left(x\right)}{x{\nu }_f}},$$

(5)

hence, by adopting (5) to Equations (2) and (3), the following nonlinear ODEs are attained (see Rostami et al. [34] and Zaib et al. [46]),

$$\left(\frac{{\mu }_{hnf}/\phantom{{\mu }_{hnf}{\mu }_f}{\mu }_f}{{\rho }_{hnf}/\phantom{{\rho }_{hnf}{\rho }_f}{\rho }_f}\right)f^{‴}+f{f}^{″}-{f\prime }^2+1+\left(\frac{{\left(\rho {\beta }_T\right)}_{hnf}/\phantom{{\left(\rho {\beta }_T\right)}_{hnf}{\left(\rho {\beta }_T\right)}_f}{\left(\rho {\beta }_T\right)}_f}{{\rho }_{hnf}/\phantom{{\rho }_{hnf}{\rho }_f}{\rho }_f}\right)\lambda \theta +\left(\frac{Z}{{\rho }_{hnf}/\phantom{{\rho }_{hnf}{\rho }_f}{\rho }_f}\right)e^{-d\eta }=0,$$

(6)

$${\theta }^{″}+Pr\frac{{\left(\rho C_p\right)}_{hnf}/\phantom{{\left(\rho C_p\right)}_{hnf}{\left(\rho C_p\right)}_f}{\left(\rho C_p\right)}_f}{k_{hnf}/\phantom{k_{hnf}{k}_f}{k}_f}\left(f{\theta }^{\prime }-f^{\prime }\theta \right)=0,$$

(7)

while Equation (8) is the simplified boundary condition

$$\begin{array}{c}{f}^{\prime }\left(0\right)=0,f\left(0\right)=0,\theta \left(0\right)=1,\hfill \\ f^{\prime }\left(\eta \right)\to 1,\theta \left(\eta \right)\to 0,as\eta \to \infty \hfill \end{array},$$

(8)

where ${\displaystyle \lambda ={Gr/\phantom{Gr{\mathrm{Re}}_x}{\mathrm{Re}}_x}^2}$ is the mixed convection or buoyancy parameter where $\lambda >0$ corresponds to the aiding or assisting flow, $\lambda <0$ corresponds to the opposing flow, and $\lambda =0$ denotes the pure forced convective flow. Further, $Gr=g{\left({\beta }_T\right)}_f\left(T_w\left(x\right)-T_{\infty }\right)x^3/\phantom{g{\left({\beta }_T\right)}_f\left(T_w\left(x\right)-T_{\infty }\right)x^3{{\nu }_f}^2}{{\nu }_f}^2$ is the Grashof number and ${\mathrm{Re}}_x=x{u}_e\left(x\right)/\phantom{x{u}_e\left(x\right){\nu }_f}{\nu }_f$ is the local Reynolds number. Additionally, $Z=\pi j_0{M}_0/\phantom{\pi j_0{M}_{0}8a^{2}x{\rho }_f}8a^{2}x{\rho }_f$ is the modified Hartmann number; $Z>0$ indicates that the Lorentz force is applied toward the positive (assisting) x-direction (refer to Ahmad et al. [45]). ${\displaystyle d=\frac{\pi }{p}\sqrt{\frac{{\nu }_f}{a}}}$ is the dimensionless parameter, which is associated to the magnets and electrode width and the Prandtl number is represented by ${\displaystyle Pr={\left(C_p\mu \right)}_f/\phantom{{\left(C_p\mu \right)}_f{k}_f}{k}_f}$. The skin friction coefficients $C_f$ and the local Nusselt number $N{u}_x$ are

$$C_f=\frac{{\tau }_w}{{\rho }_f{u}_e^2},N{u}_x=\frac{x{q}_w}{k_f(T_w\left(x\right)-T_{\infty })},$$

(9)

where ${\tau }_w$ indicates the surface shear stress while $q_w$ is the wall/surface heat flux, which are in the form of

$${\tau }_w={\mu }_{hnf}{\left(\frac{\partial u}{\partial y}\right)}_{y=0},q_w=-k_{hnf}{\left(\frac{\partial T}{\partial y}\right)}_{y=0}.$$

(10)

Using Equations (5), (9), and (10), the following reduced skin friction coefficient and local Nusselt number (heat transfer rate) are achieved

$$R{e}_x^{1/2}{C}_f=\frac{{\mu }_{hnf}}{{\mu }_f}{f}^{″}\left(0\right),R{e}_x^{-1/2}N{u}_x=-\frac{k_{hnf}}{k_f}{\theta }^{\prime }\left(0\right).$$

(11)

The present investigation is only decisive to the impermeable Riga plate in hybrid Cu-Al${}_2$O${}_3$/water nanofluids. More investigations are required to observe the flow and heat transfer characteristics due to the Riga plate. In future work, other researchers can consider the following conditions:

• Consider either a moving plate or stretching/shrinking plate $\left(u\left(x,0\right)=u_w\left(x\right)\right)$. In the present work, the Riga plate is static $\left(u\left(x,0\right)=0\right)$.
• Consider the permeable Riga plate $\left(v\left(x,0\right)=v_w\right)$ as studied by Ahmad et al. [44]. In the present work, the Riga plate is impermeable $\left(v\left(x,0\right)=0\right)$.
• Consider hybrid SiO${}_2$-Al${}_2$O${}_3$/water nanofluid as studied by Rostami et al. [34] and compare the heat transfer performance of both hybrid nanofluids. Equations (6)–(8) are reduced to Rostami et al. [34] when $Z=0$ and hybrid SiO${}_2$-Al${}_2$O${}_3$/water nanofluids are considered.

3. Temporal Flow Stability

The analysis of flow stability is decisive to test if either the first or second similarity solutions are physically stable and acceptable. The similarity solutions emerge from the Equations (6) and (7) subject to the Equation (8). The discussion on the stability analysis can be found in Salleh et al. [63,64,65], Anuar et al. [66,67], and Khashi’ie et al. [68,69,70] for nanofluids. Hence, following the work by Merkin [71] and the other literature on stability analysis, the unsteady problem is initially considered as follows:

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=u_e\frac{d{u}_e}{dx}+\frac{{\mu }_{hnf}}{{\rho }_{hnf}}\frac{{\partial }^{2}u}{\partial y^2}+\frac{g{\left(\rho {\beta }_T\right)}_{hnf}\left(T-T_{\infty }\right)}{{\rho }_{hnf}}+\frac{\pi j_0{M}_0}{8{\rho }_{hnf}}{e}^{-\pi y/\phantom{\pi yp}p},$$

(12)

$$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}}\frac{{\partial }^{2}T}{\partial y^2},$$

(13)

with a time variable transformation $\left(\tau =at/\phantom{atL}L\right)$, such that

$$u=\frac{ax}{L}\frac{\partial f\left(\eta ,\tau \right)}{\partial \eta },v=-\sqrt{\frac{a{\nu }_f}{L}}f\left(\eta ,\tau \right),\theta \left(\eta ,\tau \right)=\frac{T-T_{\infty }}{T_w\left(x\right)-T_{\infty }},\eta =y\sqrt{\frac{a}{{\nu }_{f}L}}.$$

(14)

Thus, the new transformed differential equations are attained

$$\left(\frac{{\mu }_{hnf}/\phantom{{\mu }_{hnf}{\mu }_f}{\mu }_f}{{\rho }_{hnf}/\phantom{{\rho }_{hnf}{\rho }_f}{\rho }_f}\right)\frac{{\partial }^{3}f}{\partial {\eta }^3}+f\frac{{\partial }^{2}f}{\partial {\eta }^2}-{\left(\frac{\partial f}{\partial \eta }\right)}^2+1+\left(\frac{{\left(\rho {\beta }_T\right)}_{hnf}/\phantom{{\left(\rho {\beta }_T\right)}_{hnf}{\left(\rho {\beta }_T\right)}_f}{\left(\rho {\beta }_T\right)}_f}{{\rho }_{hnf}/\phantom{{\rho }_{hnf}{\rho }_f}{\rho }_f}\right)\lambda \theta +\frac{Z}{{\rho }_{hnf}/\phantom{{\rho }_{hnf}{\rho }_f}{\rho }_f}{e}^{-d\eta }-\frac{{\partial }^{2}f}{\partial \eta \partial \tau }=0,$$

(15)

$$\frac{1}{Pr}\frac{k_{hnf}/\phantom{k_{hnf}{k}_f}{k}_f}{{\left(\rho C_p\right)}_{hnf}/\phantom{{\left(\rho C_p\right)}_{hnf}{\left(\rho C_p\right)}_f}{\left(\rho C_p\right)}_f}\frac{{\partial }^2\theta }{\partial {\eta }^2}+f\frac{\partial \theta }{\partial \eta }-\theta \frac{\partial f}{\partial \eta }-\frac{\partial \theta }{\partial \tau }=0,$$

(16)

subject to the new initial and boundary conditions

$$\begin{array}{c}{\displaystyle f\left(0,\tau \right)=0,\frac{\partial f}{\partial \eta }\left(0,\tau \right)=0,\theta \left(0,\tau \right)=1,}\hfill \\ {\displaystyle \frac{\partial f}{\partial \eta }\left(\eta ,\tau \right)\to 0,\theta \left(\eta ,\tau \right)\to 0,as\eta \to \infty .}\hfill \end{array}$$

(17)

Following Weidman et al. [72], the stability of the similarity solutions is tested by imposing Equation (18) into Equations (15)–(17) with $f\left(\eta \right)=f_0\left(\eta \right)$, $\theta \left(\eta \right)={\theta }_0\left(\eta \right)$ and $\gamma$ as an unknown eigenvalue. $F\left(\eta \right)$ and $G\left(\eta \right)$ are also assumed as small, relative to $f_0\left(\eta \right)$ and ${\theta }_0\left(\eta \right)$, correspondingly.

$$\left.\begin{array}{c}f(\eta ,\tau )=f_0\left(\eta \right)+e^{-\gamma \tau }F\left(\eta \right)\\ \theta (\eta ,\tau )={\theta }_0\left(\eta \right)+e^{-\gamma \tau }G\left(\eta \right)\end{array}\right\}.$$

(18)

The linearized eigenvalue equations relevant to the problem are

$$\frac{{\mu }_{hnf}/\phantom{{\mu }_{hnf}{\mu }_f}{\mu }_f}{{\rho }_{hnf}/\phantom{{\rho }_{hnf}{\rho }_f}{\rho }_f}{F}^{‴}+f_0{F}^{″}-\left(2{f_0}^{\prime }-\gamma \right)F^{\prime }+F{f_0}^{″}+\frac{{\left(\rho {\beta }_T\right)}_{hnf}/\phantom{{\left(\rho {\beta }_T\right)}_{hnf}{\left(\rho {\beta }_T\right)}_f}{\left(\rho {\beta }_T\right)}_f}{{\rho }_{hnf}/\phantom{{\rho }_{hnf}{\rho }_f}{\rho }_f}\lambda G=0,$$

(19)

$$\frac{1}{Pr}\frac{k_{hnf}/\phantom{k_{hnf}{k}_f}{k}_f}{{\left(\rho C_p\right)}_{hnf}/\phantom{{\left(\rho C_p\right)}_{hnf}{\left(\rho C_p\right)}_f}{\left(\rho C_p\right)}_f}{G}^{″}+F{{\theta }_0}^{\prime }+f_0{G}^{\prime }-F^{\prime }{\theta }_0-\left({f_0}^{\prime }-\gamma \right)G=0,$$

(20)

coupled with the linearized conditions

$$\begin{array}{c}{\displaystyle F\left(0\right)=0,F^{\prime }\left(0\right)=0,G\left(0\right)=0,}\hfill \\ {\displaystyle F^{\prime }\left(\eta \right)\to 0,G\left(\eta \right)\to 0,as\eta \to \infty .}\hfill \end{array}$$

(21)

Harris et al. [73] highlighted that it is required to relax one of the far field boundary conditions and substitute it with a new condition to prevent a trivial solution of $\gamma$. A new boundary condition $F^{″}\left(0\right)=1$ is adopted to replace $F^{\prime }(\infty )\to 0$ in Equation (21). The stability analysis in the present section was executed using the bvp4c solver. The resulting smallest eigenvalue ${\gamma }_1$ where ${\gamma }_1<{\gamma }_2<\dots <{\gamma }_n$ may determine the real (physical) solution between dual/multiple solutions.

4. Results and Discussion

Utilizing the MATLAB software with its excellent bvp4c solver, the similarity solutions were obtained through solving Equations (6)–(8). The solver is programmed with a collocation method with fourth order accuracy as discussed by Shampine et al. [74]. The bvp4c solver can efficiently work to predict the solutions by using a pair of arbitrary initial guesses; however, the average CPU time for calculating the results may differ depending on the usage of the initial guesses. The boundary layer thickness ${\eta }_{\infty }=15$, alumina solid volume fractions ${\varphi }_1=0.1$, and $Pr=6.2$ are fixed in the entire work, while the suitable initial guesses for the bvp4c code and the other parameters’ values must be chosen until the profiles (velocity and temperature) fulfill the boundary conditions (8) to justify the efficacy of the results. The relative tolerance error is set at ${10}^{-10}$. To solve Equations (6) and (7) inclusive with the condition (8), it is necessary to reduce these equations as follows:

$$\begin{array}{cc}\hfill f=& y\left(1\right),\hfill \\ \hfill f^{\prime }=& y\left(2\right),\hfill \\ \hfill f^{″}=& y\left(3\right),\hfill \\ \hfill \theta =& y\left(4\right),\hfill \\ \hfill {\theta }^{\prime }=& y\left(5\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill f^{‴}=& \frac{{\rho }_{hnf}/{\rho }_f}{{\mu }_{hnf}/{\mu }_f}\left({f\prime }^2-f{f}^{″}-\left(\frac{{\left(\rho {\beta }_T\right)}_{hnf}/{\left(\rho {\beta }_T\right)}_f}{{\rho }_{hnf}/{\rho }_f}\right)\lambda \theta -\left(\frac{Z}{{\rho }_{hnf}/{\rho }_f}\right)e^{-d\eta }-1\right),\hfill \\ \hfill =& \frac{{\rho }_{hnf}/{\rho }_f}{{\mu }_{hnf}/{\mu }_f}\left(y{\left(2\right)}^2-y\left(1\right)y\left(3\right)-\left(\frac{{\left(\rho {\beta }_T\right)}_{hnf}/{\left(\rho {\beta }_T\right)}_f}{{\rho }_{hnf}/{\rho }_f}\right)\lambda y\left(4\right)-\left(\frac{Z}{{\rho }_{hnf}/{\rho }_f}\right)e^{-d\eta }-1\right),\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\theta }^{″}=& -Pr\frac{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}{k_{hnf}/k_f}\left(f{\theta }^{\prime }-f^{\prime }\theta \right),\hfill \\ \hfill =& -Pr\frac{{\left(\rho C_p\right)}_{hnf}/{\left(\rho C_p\right)}_f}{k_{hnf}/k_f}\left(y\left(1\right)y\left(5\right)-y\left(2\right)y\left(4\right)\right),\hfill \end{array}$$

(23)

and

$$\begin{array}{c}ya\left(1\right),ya\left(2\right),ya\left(4\right)-1,yb\left(2\right)-1,yb\left(4\right)\end{array}$$

(24)

where $ya$ and $yb$ indicate the initial and far-field conditions, respectively. The detailed explanation for the bvp4c procedure can be found in Khashi’ie et al. [70] and Yahaya et al. [75].

Table 4. Numerical values of $f^{″}\left(0\right)$ for $\lambda ={\varphi }_1={\varphi }_2=0$, $Z=d=0.5$, $Pr=5$, and ${\eta }_{\infty }=20$.

	Present (bvp4c Solution)	Ahmad et al. [45] (bvp4c Solution)	Ahmad et al. [45] (Shooting Method)
$f^{″}\left(0\right)$	1.539473230	1.5394732	1.5394682
	(0.77 s)	(1.4 s)	(1.4 s)

() represents the average CPU computational time in seconds.

displays $f^{″}\left(0\right)$ when $\lambda ={\varphi }_1={\varphi }_2=0$, $Z=d=0.5$ and $Pr=5$ between the present study and Ahmad et al. [45]. Ahmad et al. [45] used a two-phase nanofluid model; hence, we only manage to compare the value of $f^{″}\left(0\right)$. In their work, two methods were used; the shooting method and collocation method using the bvp4c solver. It is clear from Table 4 that the results from the present bvp4c code are in good agreement with Ahmad et al. [45]. However, there are slight differences in the computational time due to the different usage of initial guesses, tolerance error, and total parameters between both studies and further investigation needed to be done in the future.

In addition to the validation part, $f^{″}\left(0\right)$ and $-{\theta }^{\prime }\left(0\right)$ between teh present model and those by Ishak et al. [33] and Rostami et al. [34] are explicated in

Table 5. $f^{″}\left(0\right)$ when ${\varphi }_1={\varphi }_2=Z=d=0$ and $\lambda =1$ for various values of Pr.

Pr	Present		Rostami et al. [34]		Ishak et al. [33]
	First Sol.	Second Sol.	First Sol.	Second Sol.	First Sol.	Second Sol.
$0.7$	1.7063	1.2387	1.7063	1.2344	1.7063	1.2387
1	1.6754	1.1332	1.6754	1.1296	1.6754	1.1332
7	1.5179	0.5824	1.5179	0.5815	1.5179	0.5824
10	1.4928	0.4958	1.4928	0.4956	1.4928	0.4958
20	1.4485	0.3436	1.4485	0.3436	1.4485	0.3436

and

Table 6. $-{\theta }^{\prime }\left(0\right)$ when ${\varphi }_1={\varphi }_2=Z=d=0$ and $\lambda =1$ for various values of Pr.

Pr	Present		Rostami et al. [34]		Ishak et al. [33]
	First Sol.	Second Sol.	First Sol.	Second Sol.	First Sol.	Second Sol.
$0.7$	0.7641	1.0226	0.7641	1.0235	0.7641	1.0226
1	0.8708	1.1691	0.8708	1.1706	0.8708	1.1691
7	1.7224	2.2192	1.7224	2.2203	1.7224	2.2192
10	1.9446	2.4940	1.9446	2.4943	1.9446	2.4940
20	2.4576	3.1647	2.4576	3.1647	2.4576	3.1646

, considering the case of $Z=d=0$ (flat plate without EMHD), ${\varphi }_1={\varphi }_2=0$ (pure water) and $\lambda =1$ (assisting buoyancy flow). Ishak et al. [33] used the Keller-box method for their computation whereas Rostami et al. [34] also employed the bvp4c solver. It is clear from Table 5 and Table 6 that the present results are agreeable with those results by Ishak et al. [33] and Rostami et al. [34]. Thus the authors are confident in the use of the present model and method.

All the numerical values in Table 4, Table 5 and Table 6 were obtained for the reduced case of a Newtonian fluid. In this section, we also compared the numerical values of $R{e}_x^{1/2}{C}_f$ for the Cu-water $\left({\varphi }_1=0,{\varphi }_2=\mathrm{varied}\right)$ and Al${}_2$O${}_3$-water $\left({\varphi }_1=\mathrm{varied},{\varphi }_2=0\right)$ nanofluids with those by Bachok et al. [76] and Yacob et al. [77] when $Z=d=\lambda =0$ as elucidated in

Table 7. $R{e}_x^{1/2}{C}_f$ when $\lambda =Z=d=0$, and $Pr=6.2$ for various nanofluids.

$\mathit{\varphi }$	Present		Bachok et al. [76]		Yacob et al. [77]
	Cu-Water	Al${}_2$O${}_3$-Water	Cu-Water	Al${}_2$O${}_3$-Water	Cu-Water	Al${}_2$O${}_3$-Water
$0.05$	1.5538	1.4088	-	-	-	-
$0.10$	1.8843	1.6020	1.8843	1.6019	1.8843	1.6019
$0.15$	2.2369	1.8168	-	-	-	-
$0.20$	2.6227	2.0583	2.6226	2.0584	2.6226	2.0584

. However, the values of $R{e}_x^{-1/2}N{u}_x$ in Bachok et al. [76] and Yacob et al. [77] cannot be compared with the present values as the present model considers a variable form of the wall temperature (mixed convection). For the future reference, the values of $R{e}_x^{-1/2}N{u}_x$ from the present model are displayed in

Table 8. $R{e}_x^{-1/2}N{u}_x$ when $\lambda =Z=d=0$, and $Pr=6.2$ for various nanofluids.

$\mathit{\varphi }$	Present		Bachok et al. [76]		Yacob et al. [77]
	Cu-Water	Al${}_2$O${}_3$-Water	Cu-Water	Al${}_2$O${}_3$-Water	Cu-Water	Al${}_2$O${}_3$-Water
$0.05$	1.7758	1.7169	-	-	-	-
$0.10$	1.9692	1.8603	-	-	-	-
$0.15$	2.1593	2.0045	-	-	-	-
$0.20$	2.3494	2.1502	-	-	-	-

.

Table 9. Critical values ${\lambda }_c$ for selected values of ${\varphi }_1$, ${\varphi }_2$, and Z when $Pr=6.2$ and $d=0.5$.

${\mathit{\varphi }}_1$	${\mathit{\varphi }}_2$	Z	${\mathit{\lambda }}_{\mathit{c}}$
0	0	0.5	−4.61663
0.1	0	0.5	−5.73469
0.1	0.005	0.5	−5.83576
0.1	0.005	0	−4.80459
0.1	0.005	−0.5	−3.81356

shows the critical values of ${\lambda }_c$ when $d=0.5$ and selected values of ${\varphi }_1$, ${\varphi }_2$ and Z. A critical value is the meeting point of the first (upper branch) and second (lower branch) solutions. The similarity solution is unique when $\lambda ={\lambda }_c$ and the dual solutions are feasible for $\lambda >{\lambda }_c$. Nevertheless, the boundary layer separation occurs when $\lambda <{\lambda }_c$ and no similarity solutions (unique/dual) are attainable beyond this critical value. From Table 9, the hybrid Cu-Al${}_2$O${}_3$/water nanofluid $\left({\varphi }_1=0.1,{\varphi }_2=0.005\right)$ has a larger absolute critical value than the alumina-water nanofluid $\left({\varphi }_1=0.1,{\varphi }_2=0\right)$ and viscous/regular fluid $\left({\varphi }_1=0,{\varphi }_2=0\right)$. Hence, the usage of the hybrid nanofluid can extend the range of the steady flow solution. Furthermore, the application of positive Z, which implies that the Lorentz force is assisted towards the positive x-direction of the Riga plate, can also induce a flow longer than $Z=-0.5$ (opposing positive x-direction) and $Z=0$ (no electromagnetohydrodynamic).

Table 10. The values of $R{e}_x^{-1/2}N{u}_x$ for the opposing and assisting flow cases when ${\varphi }_1=0.1$ and $Z=d=0.5$ ([] indicates the second solution).

$\mathit{\lambda }$	${\mathit{\varphi }}_2$
	0.005	0.01	0.03
−1	1.91254	1.93350	2.01692
	[−2.17399]	[−2.23545]	[−2.48587]
−0.5	1.94865	1.96932	2.05167
	[−4.34279]	[−4.47482]	[−5.02319]
0.5	2.01462	2.03486	2.11565
	[5.78122]	[5.95238]	[6.65825]
1	2.04501	2.06510	2.14530
	[3.54998]	[3.64189]	[4.02065]

presents the values of the reduced local Nusselt number $R{e}_x^{-1/2}N{u}_x$ for both opposing $(\lambda <0)$ and assisting flow $(\lambda >0)$ cases when ${\varphi }_1=0.1$ and $Z=d=0.5$ with various ${\varphi }_2$. As explicated in Table 10, two solutions are achievable for both flow cases where the first solution of assisting flow has a greater heat transfer rate than the opposing flow. In fact, the assisting flow (heated surface) has higher wall temperature than the fluid temperature, which signifies that the heat process occurs from the wall to the fluid while the opposing flow (cooled surface) acts adversely. Hence, the heat transfer process is always greater for an assisting flow than for an opposing flow.

The increment of heat transfer rate with an upsurge of ${\varphi }_2$ is found for both flow cases. The heat transfer rate approximately increases up to 10.438% $(\lambda =-1)$, 10.302% $(\lambda =-0.5)$, 10.103% $(\lambda =0.5)$, and 10.029% $(\lambda =1)$ when ${\varphi }_2$ increases from 0.005 to 0.03. This implies that the heat transfer rate in opposing flow has a higher increment than the assisting flow. This result is observable for the first solution only.

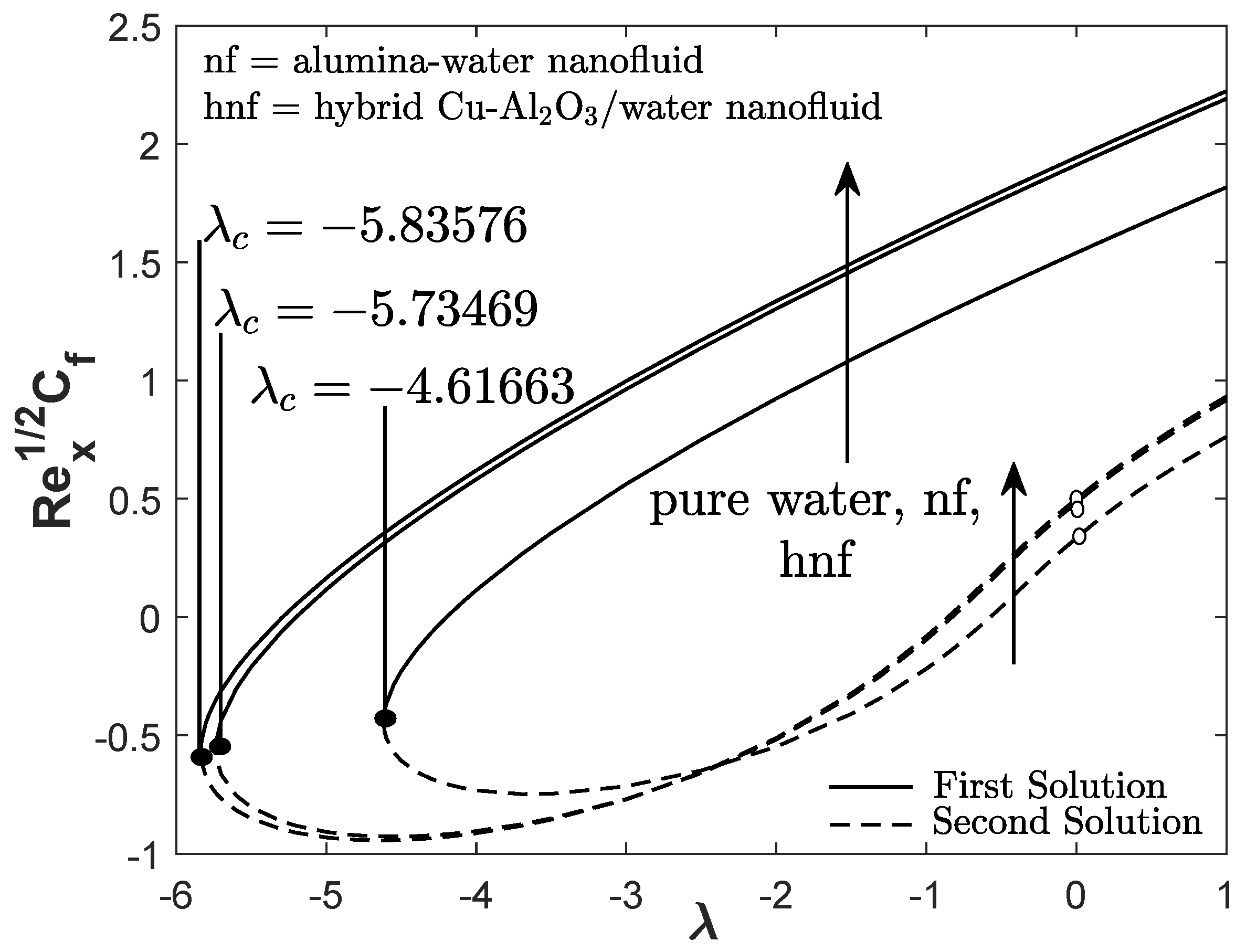
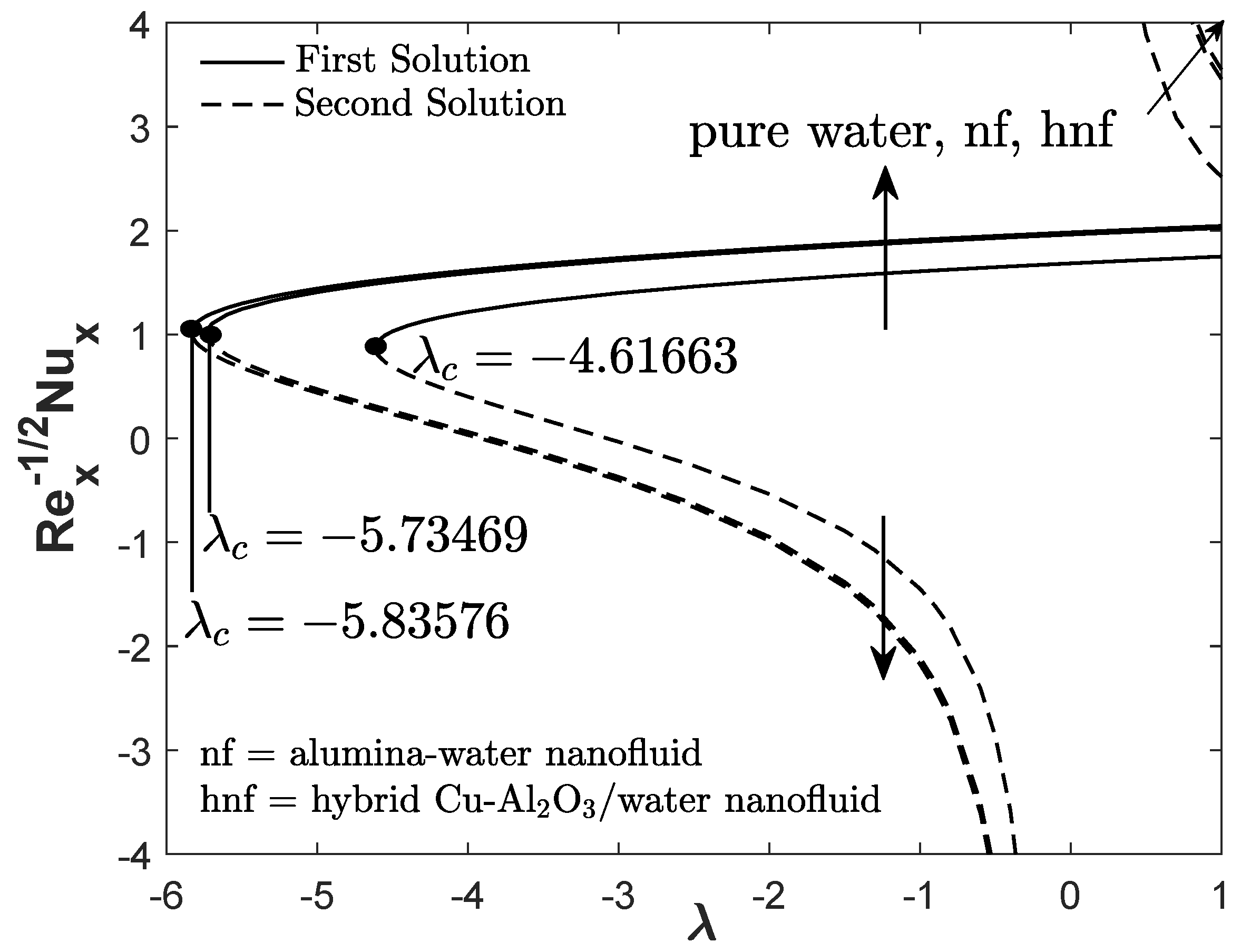
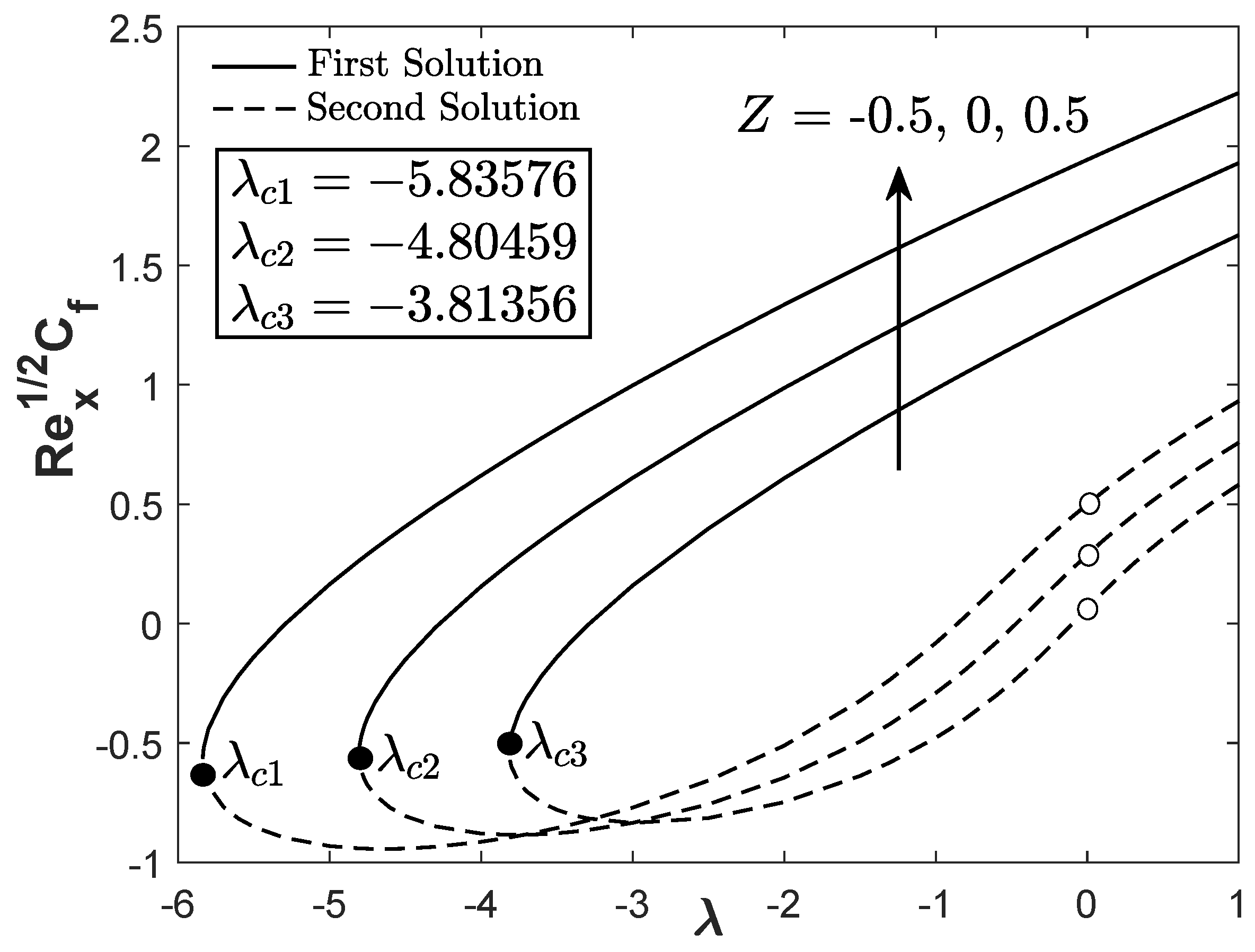
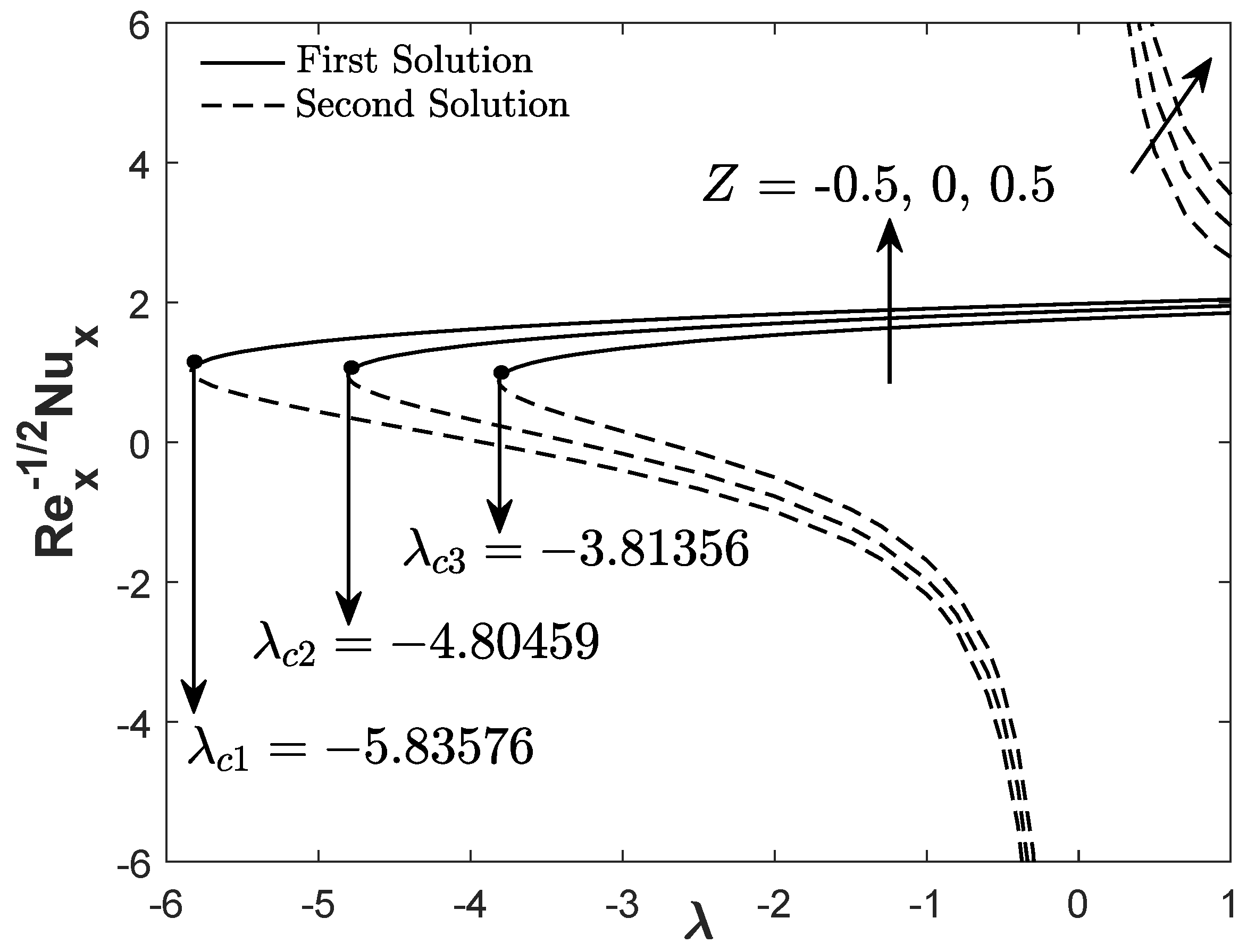
Figure 3 and Figure 4 demonstrate the reduced skin friction coefficient and heat transfer rate towards $\lambda$ for three types of fluids: hybrid Cu-Al${}_2$O${}_3$/water nanofluid, alumina-water nanofluid, and regular fluid. The first solution of hybrid Cu-Al${}_2$O${}_3$/water nanofluid has greater $R{e}_x^{1/2}{C}_f$ and $R{e}_x^{-1/2}N{u}_x$ than the alumina-water nanofluid and pure water. It is also apparent that two solutions are possible for $\lambda <0$ (opposing flow) and $\lambda >0$ (assisting flow) whereas, for the forced convective flow $(\lambda =0)$, only a unique solution is observable. Figure 5 and Figure 6 portray the graph of $R{e}_x^{1/2}{C}_f$ and $R{e}_x^{-1/2}N{u}_x$ towards $\lambda$ when ${\varphi }_2=0.005$ and $d=0.5$ with various values of Z. Both $R{e}_x^{1/2}{C}_f$ and $R{e}_x^{-1/2}N{u}_x$ intensify as the modified Hartmann number Z augments. This is in accordance with the results obtained by Ahmad et al. [45] that the magnitudes of $f^{″}\left(0\right)$ were augmented with the enhancement of $\lambda$ and Z. Further, Ahmad et al. [45] also showed that the values of $-{\theta }^{\prime }\left(0\right)$ were enhanced as the strength of the Lorentz force increased.

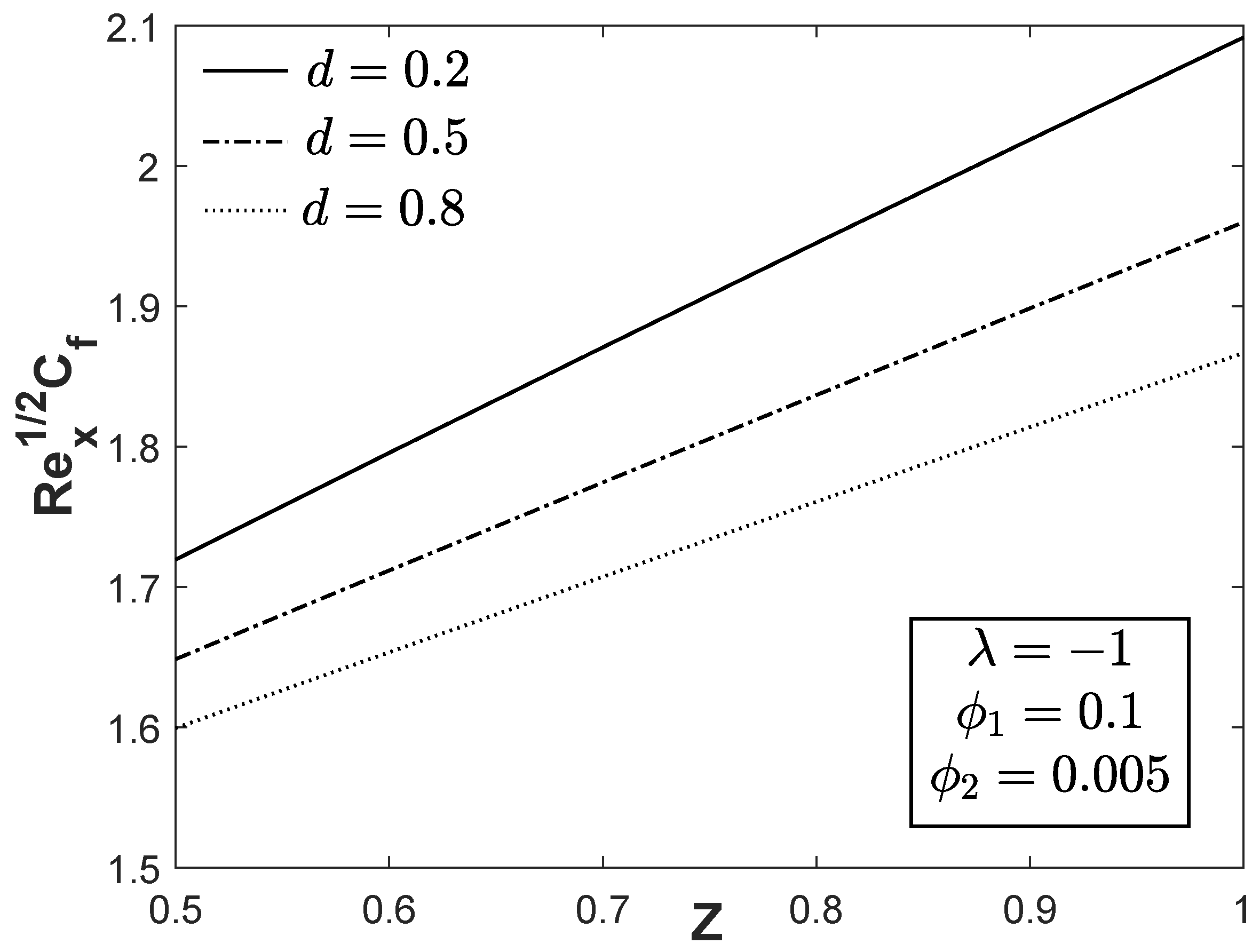
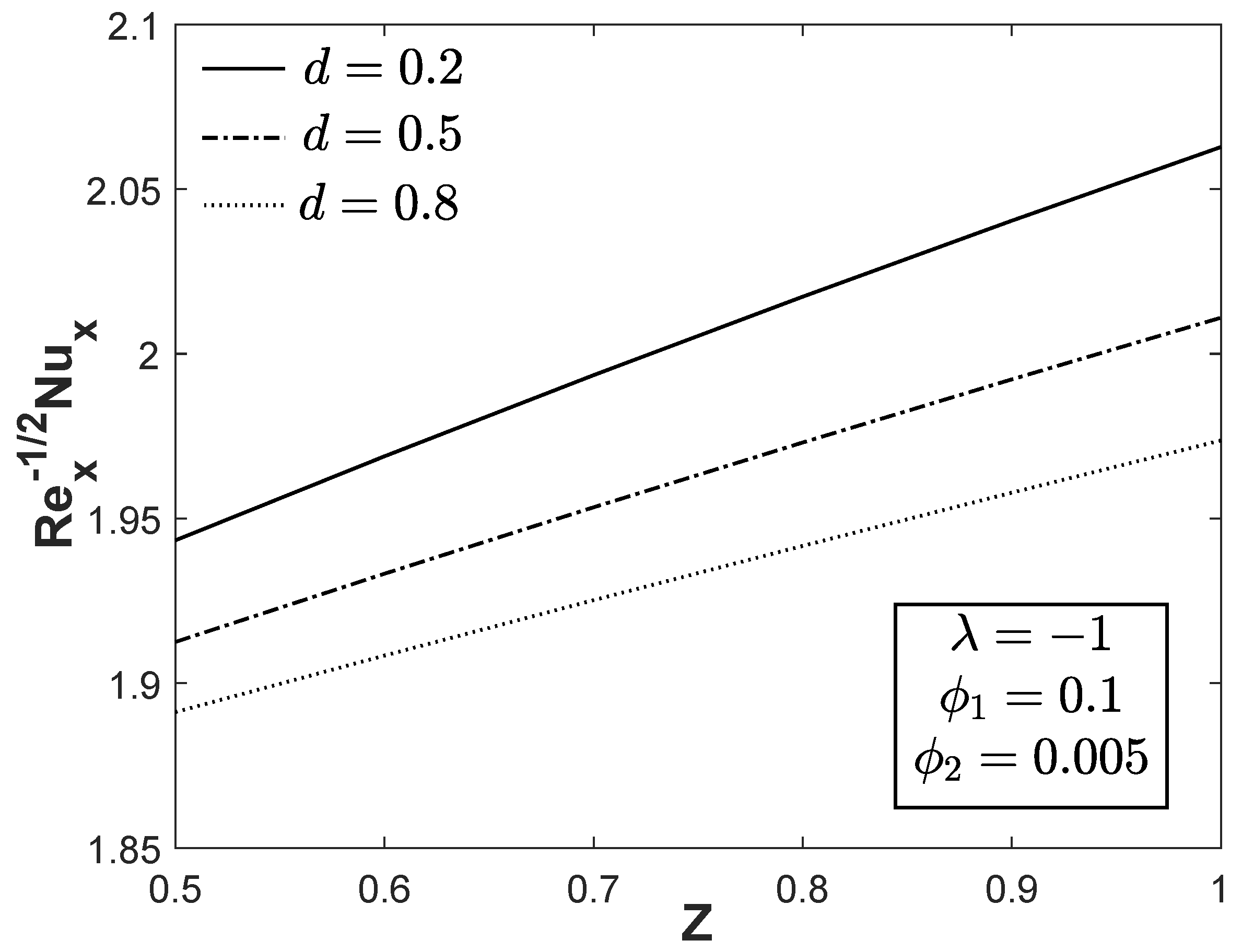
Figure 7 and Figure 8 illustrate the variations of $R{e}_x^{1/2}{C}_f$ and $R{e}_x^{-1/2}N{u}_x$ towards Z with various values of d. It is noticeable that a small value of d can produce a greater value of $R{e}_x^{1/2}{C}_f$ and $R{e}_x^{-1/2}N{u}_x$ for each value of positive Z. The heat transfer rate can also be controlled by decreasing the width of the magnets and electrodes d. 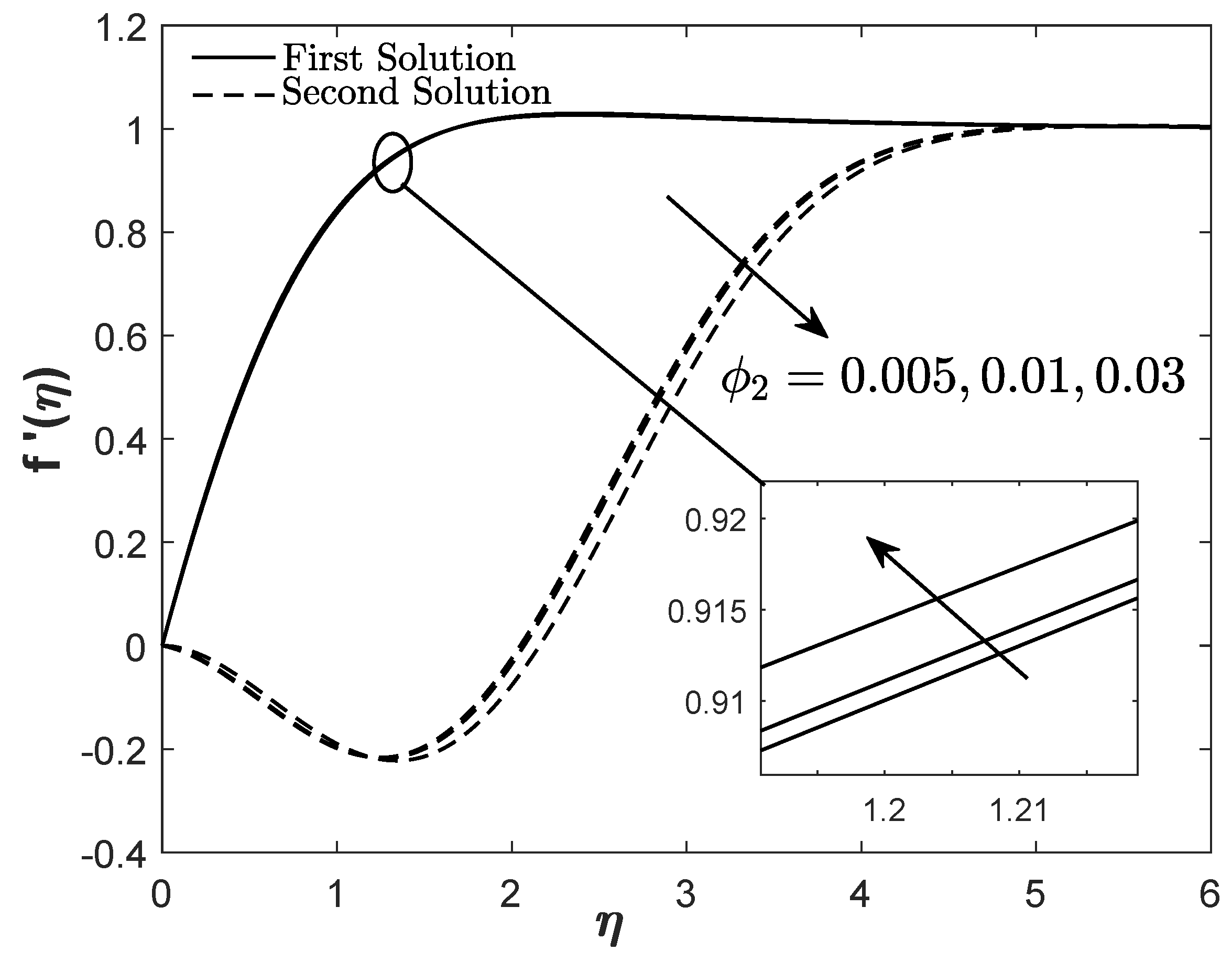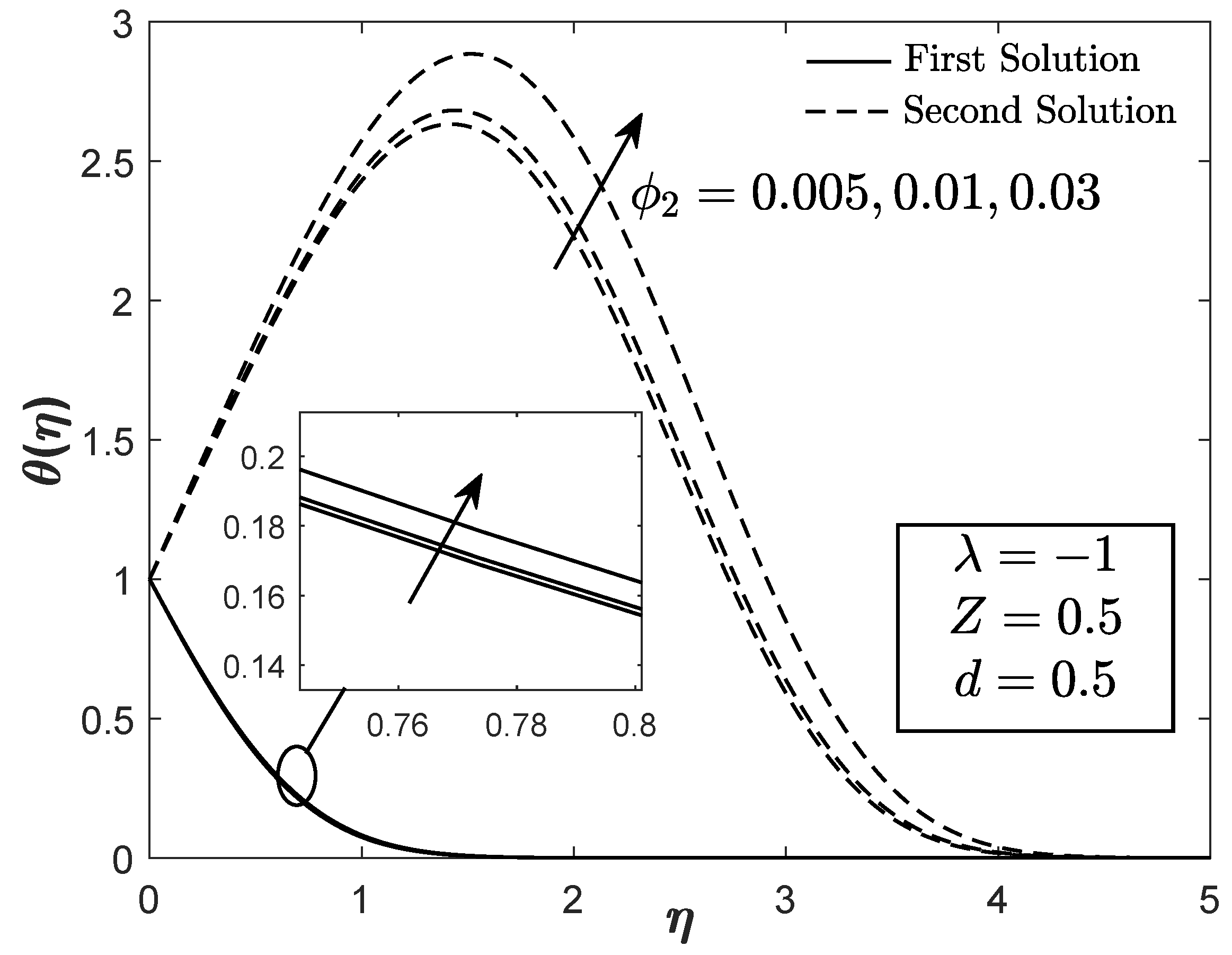Further, the velocity and temperature profiles for assorted values of ${\varphi }_2$ are elucidated in Figure 9 and Figure 10. Both profiles slightly escalate with the increasing values of the copper nanoparticle volume fraction. More energy is depleted with the accretion of nanoparticles volumetric concentration, which simultaneously increases both the velocity and temperature profiles. Since the paired solutions are attainable, the real solution is justified using the stability analysis.

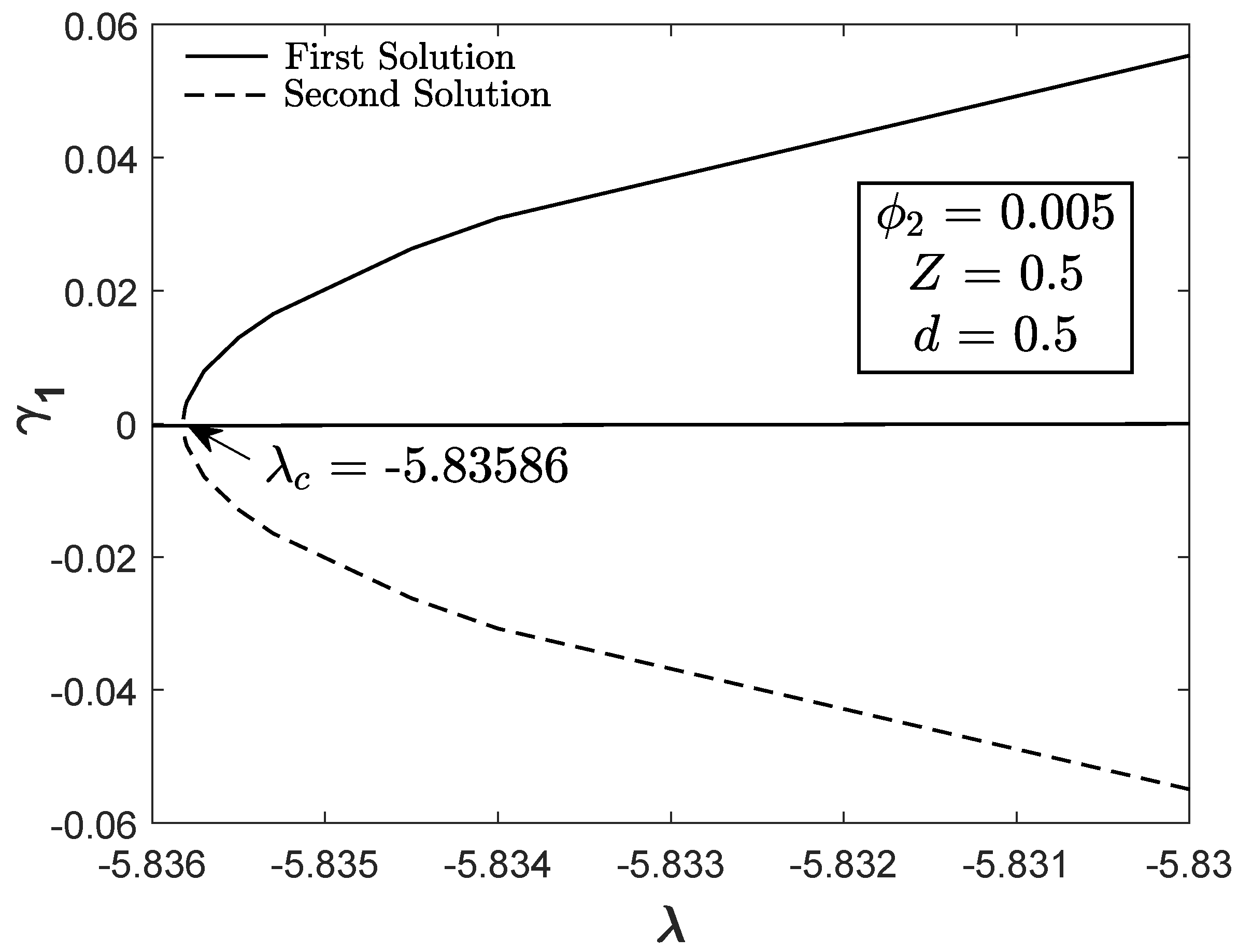
Hence, by employing the bvp4c solver, the linearized eigenvalue equations, as discussed in the previous section (see Equations (19) and (20)), are solved. However, the new relaxing condition is applied to Equation (21) so that the stability analysis can be successfully executed. Figure 11 exhibits ${\gamma }_1$ of both solutions towards $\lambda$ when ${\varphi }_1=0.1$, ${\varphi }_2=0.005$ and $Z=d=0.5$. The positive ${\gamma }_1$ indicates that the first solution is real while a contrary result is obtained for the second solution. In addition, the smallest eigenvalues for both solutions approach to 0 as $\lambda \to {\lambda }_c$ and ${\gamma }_1$ are approximately equal to 0 at $\lambda ={\lambda }_c$, which holds the validity of the stability formulation.

5. Conclusions

We studied the buoyancy driven flow of hybrid Cu-Al${}_2$O${}_3$/water nanofluids over a Riga plate. The reduced nonlinear ordinary differential equations (ODEs) coupled with the transformed boundary conditions were numerically solved and computed using the bvp4c function in Matlab software. Our conclusions for this problem are:

• Dual solutions were obtained for both assisting and opposing flow cases within a specific range of the buoyancy parameter. The separation point was located in the opposing flow region.
• The stability analysis proved that the upper branch/first solution were stable whereas the lower branch/second solution were not stable.
• Hybrid Cu-Al${}_2$O${}_3$/water nanofluid has a greater skin friction coefficient and heat transfer rate than the alumina-water nanofluid and pure water.
• The reduced skin friction coefficient and heat transfer rate was greater for the assisting flow case than for the opposing flow case.
• An upsurge of copper volumetric concentration and EMHD parameters can hold the boundary layer separation.
• An upsurge of the magnet and electrode width reduced the heat transfer rate, while the accretion of the copper volumetric concentration and EMHD parameters boosted the heat transfer rate for both the assisting and opposing buoyancy flows.
• The heat transfer rate approximately increased up to an average of 10.216% when the copper volumetric concentration increased from 0.005 $(0.5\%)$ to 0.03 $(3\%)$.
• Both the velocity and temperature profiles increased with the enhancement of the copper volumetric concentration ${\varphi }_2$.

Hence, it is beneficial to control the magnitude of relevant parameters to obtain the required result.