Admissible Perturbation of Demicontractive Operators within Ant Algorithms for Medical Images Edge Detection
Abstract
1. Introduction
2. Methodology
2.1. Theory of Admissible Perturbations
2.2. Ant Colony Optimization for Edge Detection Using Proposed Operators
- Initiate all K ants, the pheromone matrix, .
- For every solution construction step index
- Make the solution decision based on the final pheromone matrix .
- At first, ACO will build the transition probability matrix. .
- Secondly, ACO will update the pheromone matrix .
3. Case Study: ACO Algorithm for Edge Detection in Medical Images
- —
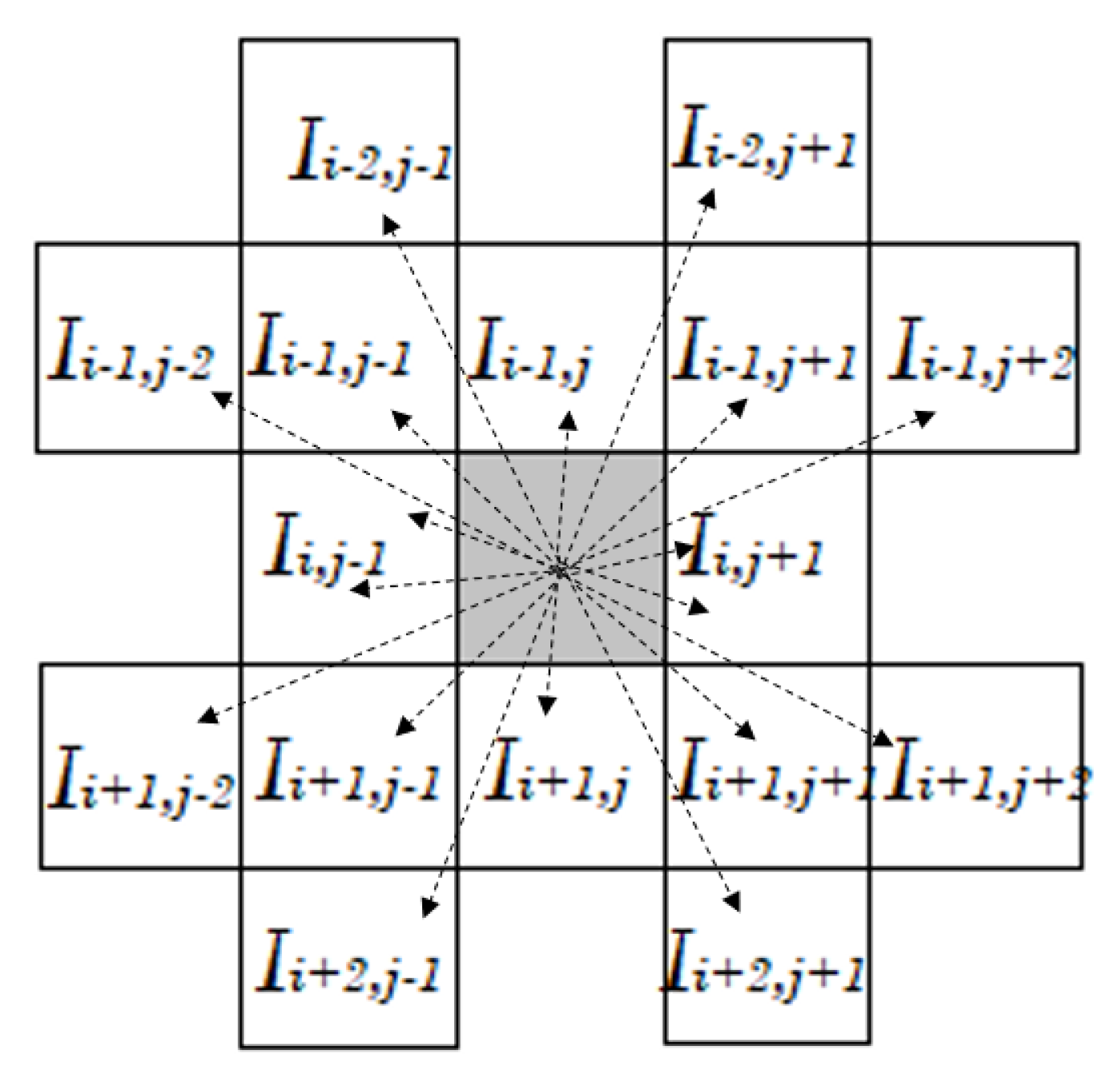
- Initialization process. In the initialization process, all the K ants are placed randomly on the image. Each pixel of the image is viewed as a node. Each value of the initial pheromone matrix is set to a constant . A constant value L used to define the number of movement steps in the construction process is defined.
- —
- Construction process. At the n-th construction step, one ant is randomly chosen from all K ants, this ant will be consecutively moving for L movement steps. The ant will move from node i to j based on the transition probability, Equation (9).
- First, it is the issue of establishing the heuristic from Equation (9).
- The second issue is to establish the domain in which one ant found in node can make moves, i.e., from Equation (9).
- —
- Update process. The algorithm uses two update operations for the pheromone matrix.
- —
- Decision process
4. Results and Discussion
4.1. Experimental Results
- A.
- Preliminary settings for Ant Colony Optimization:
- —
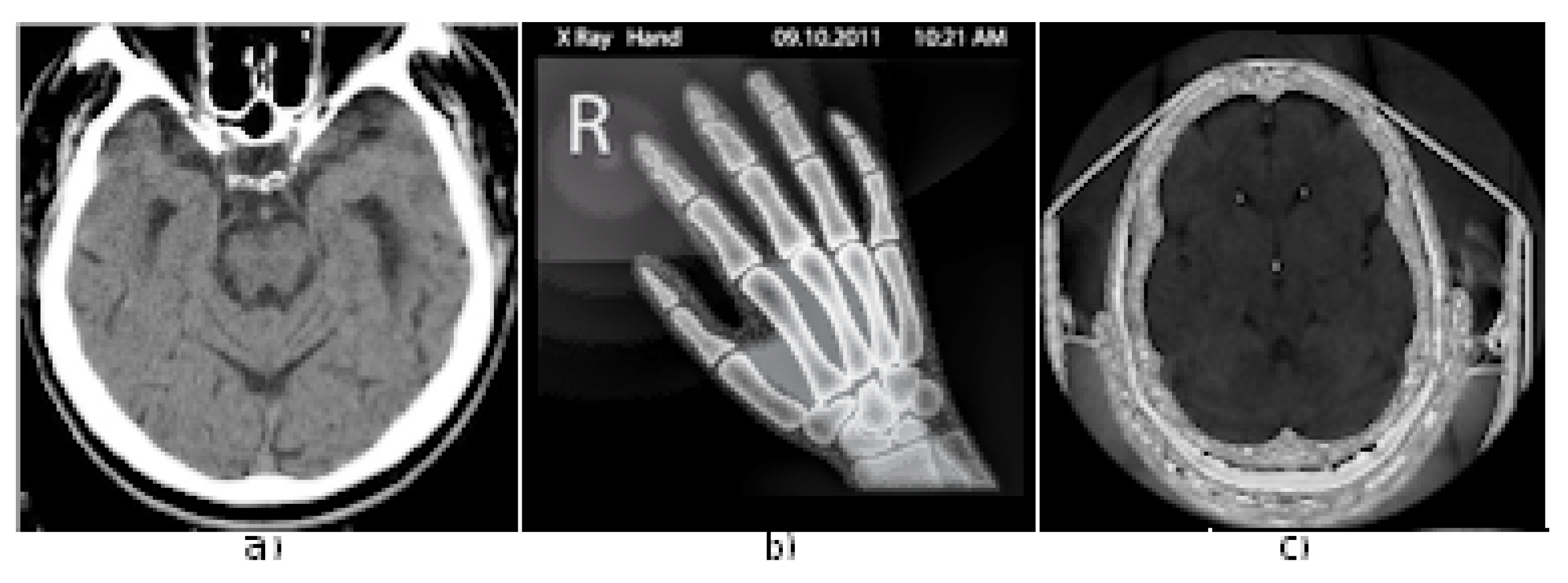
- Data-set. The experimental data set includes the medical images for the experiments as in Figure 3. The current study makes use of four medical images, as shows Figure 3. The medical image Brain CT with 128 × 128 resolution could be provided for free by request from authors for scientific reasons; Hand X-ray from [34] with original 225 × 225 resolution was reduced to 128 × 128 resolution to make a valid comparison with the other images, as Head CT from [35] has originally also 128 × 128 resolution; these two medical-images are available online for free.
- —
- Software used. The ACO-based edge detection approach was implemented using MatLab and run on a computer with an AMD Rysen 5 2500U, 2 GHz processor.
- —
- Parameter settings for Ant Colony Optimization.
- —
- Parameters considered for Ant Colony Optimization
- –
- the number of ants is based on the dimension of the image : where ⌊ and ⌋ are the left and right rounded values to the nearest integers less than or equal to x; for the particular case of the image resolution, 128 is the number of ants.
- –
- each ant makes 300 movements in each of the steps; therefore in the particular case of 128 ants, 38,400 movements are made during each of the L steps.
- –
- the connectivity neighborhood is based on the ant’s movement range in Equation (9);
- –
- the value of each component of the pheromone matrix, ;
- –
- weighting factors of the pheromone information, and heuristic information, , in Equation (9);
- –
- the evaporation rate, , Equation (10);
- –
- the pheromone decay coefficient, = 0.001, Equation (11);
- –
- –
- tolerance used in the decision process of the proposed method.
- –
- termination criteria is given by reaching the maximal number of steps L.
- B.
- Numerical results and running time:
- —
- ACO Numerical Results.Table 1 shows that more pixels are correctly identified on the edge of the image, more precise is the edge detection of an medical image. The results are decimal scaled, and are standard values of correctly identified edges with values in the unit interval for an accurate visibility.
- —
- ACO Running Time. Based on the computing characteristics, the average running time was 4500 seconds for each medical image. Furthermore, the running time increases as Denoise Convolutional Neural Network (DnCNN) to enhance each image as follows.
- C.
- Software:
- —
- We make use of the Tian et al. [32] software from the 2008 CEC conference, an image edge detection using Ant Colony Optimization MatLab software [36]. The existing software was at first modified for the use of the operators from [32] and described in Equation (16) (Sin-operator) and the proposed operators given in Equation (17) (KH-operator) and Equation (18) (Chi-operator).
- —
- Denoise Convolutional Neural Network (DnCNN) a pretrained network [37] is used to improve the quality of the resulting medical image. Image Processing Toolbox and Deep Learning Toolbox from Matlab are used.
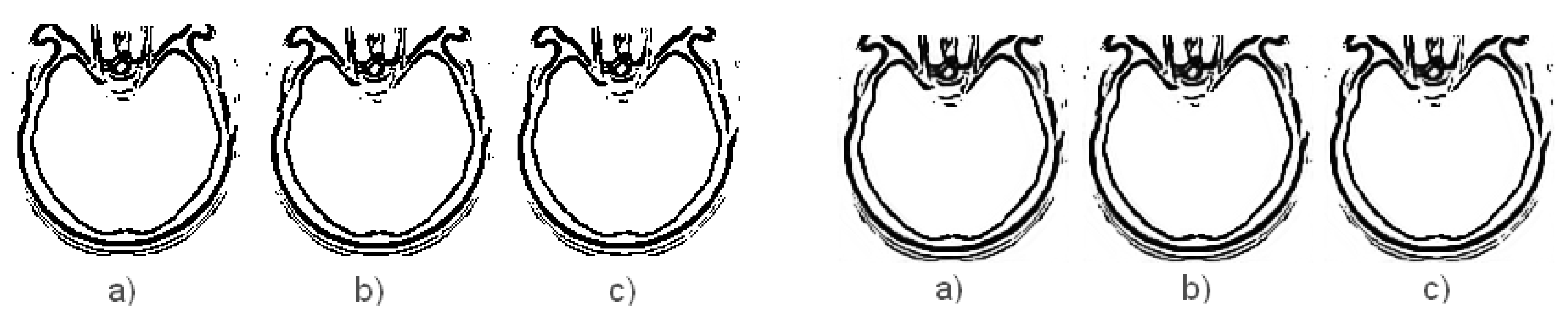
4.2. Representation of Results
4.3. Discussions
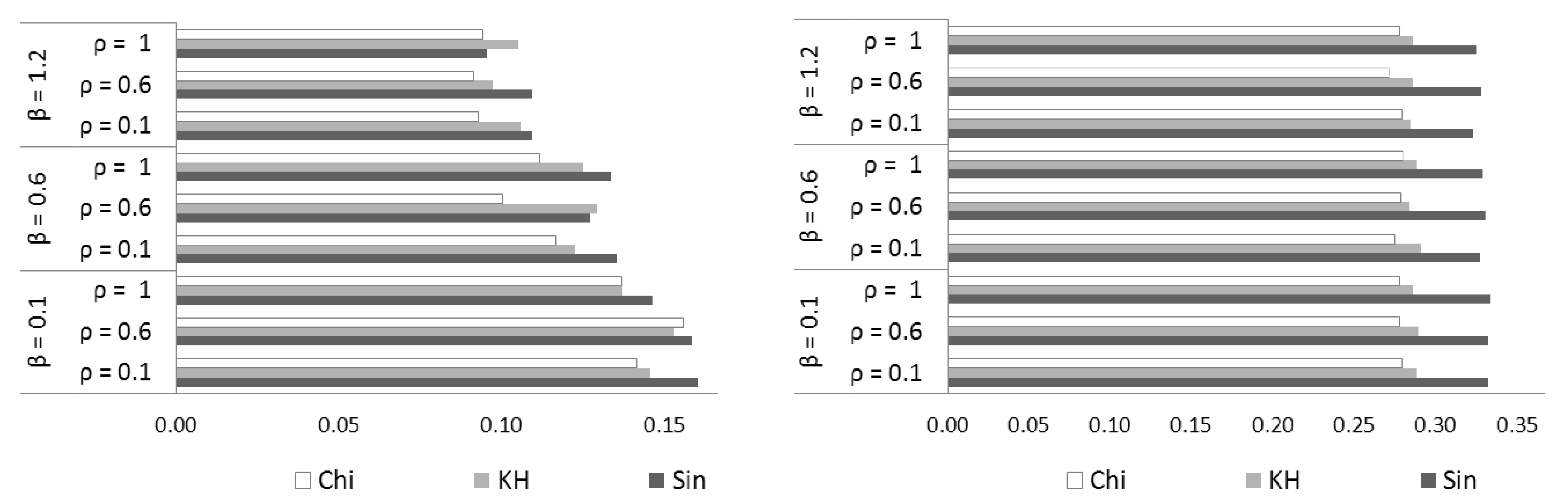
- The operator has the results similar with the operator, so between and , operator performs better for image edge detection with ACO (Table 5).
- The best paper results is that the newly introduced operators and preserve better the edges of the medical image during the image denoising process with DnCNN (Table 5).
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ACO | Ant Colony Optimization |
| DnCNN | Denoise Convolutional Neural Network |
References
- Rus, I.A. An abstract point of view on iterative approximation of fixed points. Fixed Point Theory 2012, 33, 179–192. [Google Scholar]
- Berinde, V. Convergence theorems for fixed point iterative methods defined as admissible perturbations of a nonlinear operator. Carpathian J. Math. 2013, 29, 9–18. [Google Scholar]
- Berinde, V.; Khan, A.R.; Fukhar-ud-din, H. Fixed point iterative methods defined as admissible perturbations of generalized pseudocontractive operators. J. Nonlinear Convex Anal. 2015, 16, 563–572. [Google Scholar]
- Kitkuan, D.; Kumam, P.; Berinde, V.; Padcharoen, A. Adaptive algorithm for solving the SCFPP of demicontractive operators without a priori knowledge of operator norms. Ann. Univ. Ovidius Math. Ser. 2019, 27, 153–175. [Google Scholar] [CrossRef]
- Padcharoen, A.; Kumam, P.; Cho, Y.J. Split common fixed point problems for demicontractive operators. Numer. Algorithms 2019, 82, 297–320. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, X.; Kim, T.W. Viscosity Methods and Split Common Fixed Point Problems for Demicontractive Mappings. Mathematics 2019, 7, 844. [Google Scholar] [CrossRef]
- Wang, F.; Xu, H.K. Weak and strong convergence of two algorithms for the split fixed point problem. Numer. Math. Theory Method Appl. 2018, 11, 770–781. [Google Scholar]
- Ticala, C. Approximating solutions of generalized pseudocontractive variational inequalities by admissible perturbation type iterative methods. Creat. Math. Inf. 2013, 22, 237–241. [Google Scholar]
- Ticala, C. A weak convergence theorem for a Krasnoselskij type fixed point iterative method in Hilbert spaces using an admissible perturbation. Sci. Stud. Res. 2015, 25, 243–252. [Google Scholar]
- Ticala, C. Approximating fixed points of demicontractive mappings by iterative methods defined as admissible perturbations. Creat. Math. Inf. 2016, 25, 121–126. [Google Scholar]
- Dorigo, M.; Stützle, T. Ant colony optimization: Overview and recent advances. In Handbook of Metaheuristics; Springer: Cham, Switzerland, 2019; pp. 311–351. [Google Scholar]
- Dorigo, M.; Stützle, T. Ant Colony Optimization; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Chira, C.; Pintea, C.M.; Dumitrescu, D. Learning sensitive stigmergic agents for solving complex problems. Comput. Inform. 2010, 29, 337–356. [Google Scholar]
- Pintea, C.-M.; Pop, P.C.; Chira, C.; Dumitrescu, D. A Hybrid Ant-Based System for Gate Assignment Problem. Lect. Notes Comp. Sci. 2008, 5271, 273–280. [Google Scholar]
- Crisan, G.C.; Nechita, E.; Palade, V. Ant-based system analysis on the traveling salesman problem under real-world settings. In Combinations of Intelligent Methods and Applications; Springer: Cham, Switzerland, 2016; pp. 39–59. [Google Scholar]
- Bella, J.E.; McMullen, P.R. Ant colony optimization techniques for the vehicle routing problem. Adv. Eng. Inf. 2004, 18, 41–48. [Google Scholar] [CrossRef]
- Pintea, C.M.; Pop, P.C.; Dumitrescu, D. An ant-based technique for the dynamic generalized travelling salesman problem. In Proceedings of the 7th International Conference on Systems Theory and Scientific Computation, Athens, Greece, 24–26 August 2007; pp. 255–259. [Google Scholar]
- Zhang, D.Y.; Zhao, H. Research of Generalized Ant Colony Algorithm for Logistics and Distribution. Appl. Mech. Mater. 2014, 513–517, 691–694. [Google Scholar] [CrossRef]
- Pintea, C.-M.; Pop, P.C.; Chira, C. The generalized traveling salesman problem solved with ant algorithms. Complex Adapt. Syst. Model. 2017, 5, 8. [Google Scholar] [CrossRef]
- Chowdhury, S.; Marufuzzaman, M.; Tunc, H.; Bian, L.; Bullington, W. A modified Ant Colony Optimization algorithm to solve a dynamic traveling salesman problem: A case study with drones for wildlife surveillance. J. Comput. Des. Eng. 2019, 6, 368–386. [Google Scholar] [CrossRef]
- Shi, Q.; An, J.; Gagnon, K.K.; Cao, R.; Xie, H. Image Edge Detection Based on the Canny Edge and the Ant Colony Optimization Algorithm. In Proceedings of the International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Suzhou, China, 19–21 October 2019; pp. 1–6. [Google Scholar]
- Mahalingam, T.; Subramoniam, M. ACO–MKFCM: An Optimized Object Detection and Tracking Using DNN and Gravitational Search Algorithm. Wirel. Pers. Commun. 2020, 110, 1567–1604. [Google Scholar] [CrossRef]
- Yu, Y.; Deng, Q.; Ren, L.; Tashi, N. Memristor Crossbar Array Based ACO for Image Edge Detection. Neural Process Lett. 2020, 51, 1891–1905. [Google Scholar] [CrossRef]
- Rundo, L.; Militello, C.; Vitabile, S.; Russo, G.; Sala, E.; Gilardi, M.C. A Survey on Nature-Inspired Medical Image Analysis: A Step Further in Biomedical Data Integration. Fundam. Inf. 2020, 171, 345–365. [Google Scholar] [CrossRef]
- Lahrichi, N.; Crainic, T.G.; Gendreau, M.; Rei, W.; Crişan, G.C.; Vidal, T. An integrative cooperative search framework for multi-decision-attribute combinatorial optimization: Application to the MDPVRP. Eur. J. Oper. Res. 2015, 246, 400–412. [Google Scholar] [CrossRef]
- Pintea, C.M.; Chira, C.; Dumitrescu, D.; Pop, P. A sensitive metaheuristic for solving a large optimization problem. Lect. Notes Comput. Sci. 2008, 4910, 551–559. [Google Scholar]
- Pintea, C.-M.; Chira, C.; Dumitrescu, D. Sensitive Ants: Inducing Diversity in the Colony. Stud. Comput. Intell. 2009, 236, 15–24. [Google Scholar]
- Pintea, C.-M.; Ticala, C. Medical image processing: A brief survey and a new theoretical hybrid ACO model. In Combinations of Intelligent Methods and Applications; Springer: Cham, Switzerland, 2016; pp. 117–134. [Google Scholar]
- Ticala, C.; Zelina, I. New ant colony optimization algorithm in medical images edge detection. Creat. Math. Inf. 2020, 29, 101–108. [Google Scholar]
- Hicks, T.L.; Kubicek, J.D. On the Mann iteration in a Hilbert space. J. Math. Anal. Appl. 1977, 59, 498–504. [Google Scholar] [CrossRef]
- Chidume, C.; Maruster, S. Iterative methods for the computation of fixed points of demicontractive mappings. J. Comput. Appl. Math. 2010, 234, 861–882. [Google Scholar] [CrossRef]
- Tian, J.; Yu, W.; Xie, S. An ant colony optimization algorithm for image edge detection. In Proceedings of the IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 751–756. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- X-ray Hand. Vista Medical Pack. License: Free for Non Commercial Use. id, 236487. Available online: https://www.iconspedia.com/ (accessed on 1 May 2020).
- Head CT. Online Medical Free Image. Available online: http://www.libpng.org/pub/png/pngvrml/ct2.9-128x128.png (accessed on 1 May 2020).
- Kanchi-Tian. Image Edge Detection Using Ant Colony Optimization. Version 1.2.0.0, Updated 24 January 2011. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/20997-image-edge-detection-using-ant-colony-optimization (accessed on 1 May 2020).
- Denoise Image Using Deep Neural Network. MATLAB Central File Exchange. Retrieved in 10 June. 2020. Available online: https://www.mathworks.com/help/images/ref/denoiseimage.html (accessed on 1 May 2020).




| Operator/Image | Brain_CT | Hand X-ray | Head_CT |
|---|---|---|---|
| Ant Colony Optimization | |||
| Sin | 0.2933 | 0.2942 | 0.3302 |
| KH | 0.2932 | 0.2539 | 0.2832 |
| Chi | 0.2782 | 0.2450 | 0.2788 |
| Mean | Std.Dev. | High | Low | Median | Ave.Dev. | ||
|---|---|---|---|---|---|---|---|
| ACO-Sin | 0.3059 | 0.0211 | 0.3302 | 0.2933 | 0.2942 | 0.0123 | |
| ACO-KH | 0.2768 | 0.0204 | 0.2932 | 0.2539 | 0.2832 | 0.0131 | |
| ACO-Chi | 0.2673 | 0.0193 | 0.2788 | 0.2450 | 0.2782 | 0.0113 |
| Operator/Image | Brain_CT | Hand X-ray | Head_CT |
|---|---|---|---|
| Ant Colony Optimization | |||
| 0.1047 | 0.0726 | 0.0900 | |
| 0.1090 | 0.1773 | 0.1774 | |
| 0.0867 | 0.1640 | 0.1745 |
| Operator/Image | Brain_CT | Hand X-ray | Head_CT |
|---|---|---|---|
| Ant Colony Optimization | |||
| 0.0670 | 0.0748 | 0.0808 | |
| 0.0668 | 0.0762 | 0.0719 | |
| 0.0612 | 0.0770 | 0.0712 |
| Similarities Rank | |||
|---|---|---|---|
| ACO | ACO with DnCNN | ||
| , | rank 1: most similar | rank 1: most similar | |
| , | rank 2 | rank 2 | |
| , | rank 3: less similar | rank 3: less similar | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ticala, C.; Zelina, I.; Pintea, C.-M. Admissible Perturbation of Demicontractive Operators within Ant Algorithms for Medical Images Edge Detection. Mathematics 2020, 8, 1040. https://doi.org/10.3390/math8061040
Ticala C, Zelina I, Pintea C-M. Admissible Perturbation of Demicontractive Operators within Ant Algorithms for Medical Images Edge Detection. Mathematics. 2020; 8(6):1040. https://doi.org/10.3390/math8061040
Chicago/Turabian StyleTicala, Cristina, Ioana Zelina, and Camelia-M. Pintea. 2020. "Admissible Perturbation of Demicontractive Operators within Ant Algorithms for Medical Images Edge Detection" Mathematics 8, no. 6: 1040. https://doi.org/10.3390/math8061040
APA StyleTicala, C., Zelina, I., & Pintea, C.-M. (2020). Admissible Perturbation of Demicontractive Operators within Ant Algorithms for Medical Images Edge Detection. Mathematics, 8(6), 1040. https://doi.org/10.3390/math8061040





