Hankel Determinants for New Subclasses of Analytic Functions Related to a Shell Shaped Region ^†

Abstract

Using the operator ${\mathcal{L}}_c^a$ defined by Carlson and Shaffer, we defined a new subclass of analytic functions ${\mathcal{ML}}_c^a(\lambda ;\psi )$ defined by a subordination relation to the shell shaped function$\psi \left(z\right)=z+\sqrt{1+z^2}$. We determined estimate bounds of the four coefficients of the power series expansions, we gave upper bound for the Fekete–SzegőSzegő functional and for the Hankel determinant of order two for $f\in {\mathcal{ML}}_c^a(\lambda ;\psi )$.

1. Introduction

Let $\mathcal{H}\left(\mathbb{D}\right)$ be the class of functions which are analytic in the open unit disk $\mathbb{D}:=\{z\in \mathbb{C}:|z|<1\}$, and also let $\mathcal{A}$ be the subset of $\mathcal{H}\left(\mathbb{D}\right)$ comprising of functions

$$f\left(z\right)=z+\sum _{n=2}^{\infty }{a}_n{z}^n,z\in \mathbb{D}.$$

(1)

Let $f_i\left(z\right)=\sum _{n=0}^{\infty }{a}_{n,i}{z}^n$$(i=1,2)$ which are analytic in $\mathbb{D}$, then the well-known Hadamard (or convolution) product of $f_1$ and $f_2$ is given by

$$(f_1*f_2)\left(z\right):=\sum _{n=0}^{\infty }{a}_{n,1}{a}_{n,2}{z}^n,z\in \mathbb{D}.$$

For two functions $f,g\in \mathcal{H}\left(\mathbb{D}\right)$, we say that f is subordinate to g, denoted by $f\prec g$, if there exists a Schwarz function $\vartheta \in \mathcal{H}\left(\mathbb{D}\right)$ with $\left|\vartheta \right(z\left)\right|<1$, $z\in \mathbb{D}$, and $\vartheta \left(0\right)=0$, such that $f\left(z\right)=g\left(\vartheta \right(z\left)\right)$ for all $z\in \mathbb{D}$. In particular, if g is univalent in $\mathbb{D}$, then the following equivalence relationship holds true:

$$f\left(z\right)\prec g\left(z\right)\iff f\left(0\right)=g\left(0\right)\mathrm{and}f\left(\mathbb{D}\right)\subset g\left(\mathbb{D}\right).$$

Let $\mathcal{P}$ be the well-known class of Carathéodory functions that is a set of functions $\varphi \in \mathcal{H}\left(\mathbb{D}\right)$ with the power series expansion

$$\varphi \left(z\right)=1+p_{1}z+p_2{z}^2+\cdots ,z\in \mathbb{D},$$

(2)

and such that $Re\varphi \left(z\right)>0$ for all $z\in \mathbb{D}$.

For the function $f\in \mathcal{A}$ of the form (1), Noonan and Thomas [1] defined q-th Hankel determinant as

$${\mathcal{H}}_{q,n}\left(f\right):=\left|\begin{array}{cccc}{a}_n& a_{n+1}& \cdots & a_{n+q-1}\\ a_{n+1}& a_{n+2}& \cdots & a_{n+q}\\ ⋮& ⋮& ⋮& ⋮\\ a_{n+q-1}& a_{n+q}& \cdots & a_{n+2q-2}\end{array}\right|\left(a_1=1,q,n\in \mathbb{N}:=\{1,2,3,\cdots \}\right).$$

In particular,

$${\mathcal{H}}_{2,1}\left(f\right)=\left|\begin{array}{cc}{a}_1& a_2\\ a_2& a_3\end{array}\right|=a_1{a}_3-a_2^2=a_3-a_2^2,\mathrm{and}{\mathcal{H}}_{2,2}\left(f\right)=\left|\begin{array}{cc}{a}_2& a_3\\ a_3& a_4\end{array}\right|=a_2{a}_4-a_3^2.$$

It is well-known (see Duren [2]) that, if f is given by (1) and is univalent in $\mathbb{D}$, then ${\mathcal{H}}_{2,1}\left(f\right)\le 1$ occurs, and this result is sharp. The determinant ${\mathcal{H}}_{q,n}$ has also been measured by many authors. For example, the rate of growth of ${\mathcal{H}}_{q,n}\left(f\right)$ as $n\to \infty$ for functions $f\in \mathcal{A}$ with bounded boundary was determined. In [3], it has been shown, a fraction of two bounded analytic functions with its Laurent series around the origin having integral coefficients, is rational. The Hankel determinant of meromorphic functions, (see [4]), and various properties of these determinants can be found in [5]). In 1966, the Hankel determinant of areally mean p-valent functions, univalent functions, and starlike functions were extensively studied by Pommerenke [6]. Lately, several authors have investigated ${\mathcal{H}}_{2,1}$ of innumerable subclasses of univalent and multivalent functions and, for more details on Hankel determinants, one may refer [1,6,7,8,9,10,11,12,13,14]. For $\mathcal{T}\subset \mathcal{A}$, a problem of finding a sharp (best possible) upper bound of $\left|a_3-\mu a_2^2\right|$ for the subclass $\mathcal{T}$ is generally called Fekete–Szegő problem for the subclass $\mathcal{T}$, where $\mu$ is a real or a complex number. There are some well known subclasses of univalent functions, such that the starlike functions, convex functions, and close-to-convex functions, for which the problem of finding sharp upper bounds for the functional $\left|a_3-\mu a_2^2\right|$ was completely solved (see [15,16,17,18]). For the family of analytic functions $\mathcal{R}:=\{f\in \mathcal{A}:Re{f}^{\prime }\left(z\right)>0,z\in \mathbb{D}\}$, Janteng et al. [19] have found the sharp upper bound to $\left|{\mathcal{H}}_{2,2}\left(f\right)\right|$. For initial work on the class $\mathcal{R}$, one may refer to the article of MacGregor [20].

The concept of shell-like domains gained importance in the recent times and it was introduced by Sokół and Paprocki [21]. Recently, for $\psi \left(z\right)=z+\sqrt{1+z^2}$, Raina and Sokół [22] have widely studied and found some coefficient inequalities for $f\in {\mathcal{S}}^{☆}\left(\psi \right)$ if it satisfies the subordination condition that $z{f}^{\prime }\left(z\right)/f\left(z\right)\prec \psi \left(z\right)$, and these results are further improved by Sokół and Thomas [23], the Fekete–Szegő inequality for $f\in \mathcal{C}\left(\psi \right)$ were obtained and, in view of the Alexander result between the class ${\mathcal{S}}^{*}\left(\psi \right)$ and $\mathcal{C}\left(\psi \right)$, the Fekete–Szegő inequality for functions in ${\mathcal{S}}^{*}\left(\psi \right)$ were also obtained. The function $\psi \left(z\right):=z+\sqrt{1+z^2}$ maps the unit disc $\mathbb{D}$ onto a shell shaped region on the right half plane, and it is analytic and univalent on $\mathbb{D}$. The range $\psi \left(\mathbb{D}\right)$ is symmetric respecting the real axis and $\psi \left(z\right)$ is a function with positive real part in $\mathbb{D}$, with $\psi \left(0\right)={\psi }^{\prime }\left(0\right)=1$. Moreover, it is a starlike domain with respect to the point $\psi \left(0\right)=1$ (see [24]), such as Figure 1 shows.

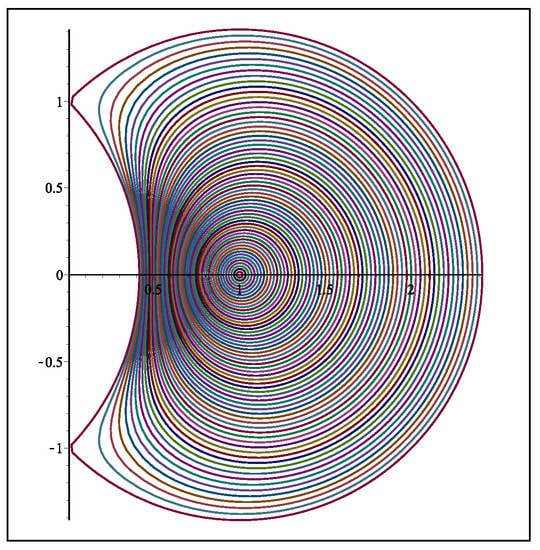
Figure 1. The image of $\mathbb{D}$ under $\psi \left(z\right)=\sqrt{1+z^2}+z$.

Definition 1.

[22] Let $f\in \mathcal{A}$ be normalized by $f\left(0\right)=f^{\prime }\left(0\right)-1=0$ in the unit disc $\mathbb{D}$. We denote by ${\mathcal{S}}^{*}\left(\psi \right)$ the class of analytic functions and satisfying the condition that

$$\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec z+\sqrt{1+z^2}=:\psi \left(z\right),$$

where the branch of the square root is chosen to be the principal one that is $\psi \left(0\right)=1$.

Now, we recall the Carlson–Shaffer operator [25] ${\mathcal{L}}_c^a:\mathcal{A}\to \mathcal{A}$ defined by

$${\mathcal{L}}_c^{a}f\left(z\right):=\Phi (a,c;z)*f\left(z\right),z\in \mathbb{D},$$

(3)

where

$$\begin{array}{c}\hfill \Phi (a,c;z):=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(a\right)}_n}{{\left(c\right)}_n}}{z}^{n+1}=\sum _{n=0}^{\infty }{\phi }_n{z}^{n+1},z\in \mathbb{D},\\ \hfill \left(a\in \mathbb{C},c\in \mathbb{C}\backslash {\mathbb{Z}}_0^{-},{\mathbb{Z}}_0^{-}:=\{\cdots ,-2,-1,0\}\right),\end{array}$$

is the incomplete beta function, and ${\left(t\right)}_n$ denotes the Pochhammer symbol (or the shifted factorial) defined in terms of the Gamma function by

$${\left(t\right)}_n:={\displaystyle \frac{\Gamma (t+n)}{\Gamma \left(t\right)}}=\left\{\begin{array}{ccc}t(t+1)(t+2)\cdots (t+n-1),\hfill & \mathrm{if}\hfill & n\in \mathbb{N},\hfill \\ 1,\hfill & \mathrm{if}\hfill & n=0.\hfill \end{array}\right.$$

For $f\in \mathcal{A}$ is given by (1) and by (3), one can get the Carlson and Shaffer operator

$${\mathcal{L}}_c^{a}f\left(z\right):=z+\sum _{n=1}^{\infty }{\displaystyle \frac{{\left(a\right)}_n}{{\left(c\right)}_n}}{a}_{n+1}{z}^{n+1}=z+\sum _{n=1}^{\infty }{\phi }_n{a}_{n+1}{z}^{n+1},z\in \mathbb{D}$$

(4)

where

$${\phi }_n={\displaystyle \frac{{\left(a\right)}_n}{{\left(c\right)}_n}},n\in \mathbb{N},$$

(5)

and

$$z{\left({\mathcal{L}}_c^{a}f\left(z\right)\right)}^{\prime }=a{\mathcal{L}}_c^{a+1}f\left(z\right)-(a-1){\mathcal{L}}_c^{a}f\left(z\right),z\in \mathbb{D}.$$

Remark 1.

Next, we will emphasize a few special cases of the operator $\mathcal{L}(a,c)$, as follows:

(i) ${\mathcal{L}}_a^{a}f\left(z\right)=f\left(z\right)$;

(ii) ${\mathcal{L}}_1^{2}f\left(z\right)=z{f}^{\prime }\left(z\right)$;

(iii) ${\mathcal{L}}_1^{3}f\left(z\right)=z{f}^{\prime }\left(z\right)+{\displaystyle \frac{1}{2}}{z}^2{f}^{\prime \prime }\left(z\right)$;

(iv)${\mathcal{L}}_1^{m+1}f\left(z\right)=:{\mathcal{D}}^{m}f\left(z\right)={\displaystyle \frac{z}{{(1-z)}^{m+1}}}*f\left(z\right)$, $m\in \mathbb{Z}$, $m>-1$is the well-known Ruscheweyh derivative of f [26];

(v)${\mathcal{L}}_{2-\delta }^{2}f\left(z\right)=:{\Omega }_z^{\delta }f\left(z\right)$, $0\le \delta <1$is the well-known Owa-Srivastava fractional differential operator of f [27].

Motivated by the articles of Raina and Sokół [22], Sokół and Thomas [23], Dziok and Raina [28], and Raina et al. [29], using the concept of subordination and the linear operator ${\mathcal{L}}_c^a$, we define a new subclass of $\mathcal{A}$ denoted by ${\mathcal{ML}}_c^a(\lambda ;\psi )$. For this subclass, we obtained coefficient inequalities, Fekete–Szegő inequality, and upper bound for the Hankel determinant $\left|H_2\left(2\right)\right|$.

We define a new subclass ${\mathcal{ML}}_c^a(\lambda ;\psi )$ of $\mathcal{A}$ as below:

Definition 2.

For $0\le \lambda \le 1$, let ${\mathcal{ML}}_c^a(\lambda ;\psi )$, with $a\in \mathbb{C}$ and $c\in \mathbb{C}\backslash {\mathbb{Z}}_0^{-}$, denote the subclass of functions $f\in \mathcal{A}$ that satisfies the subordination condition

$${\displaystyle \frac{z{\left({\mathcal{L}}_c^{a}f\left(z\right)\right)}^{\prime }}{(1-\lambda ){\mathcal{L}}_c^{a}f\left(z\right)+\lambda z}}\prec z+\sqrt{1+z^2}=\psi \left(z\right),$$

(6)

where the branch of the square root is chosen to be the principal one that is $\psi \left(0\right)=1$.

In the following remark, we prove that ${\mathcal{ML}}_c^a(\lambda ;\psi )$ is non-empty.

Remark 2.

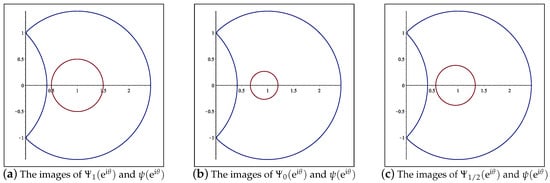
If we define the function $\tilde{f}:\mathbb{D}\to \mathbb{C}$ by $\tilde{f}\left(z\right)=z+\alpha z^2$, $\alpha \in \mathbb{C}$, a simple computation yields to

$${\displaystyle \frac{z{\left({\mathcal{L}}_c^a\tilde{f}\left(z\right)\right)}^{\prime }}{(1-\lambda ){\mathcal{L}}_c^a\tilde{f}\left(z\right)+\lambda z}}=\frac{1+2Az}{1+(1-\lambda )Az},\mathrm{where}A:=\frac{a\alpha }{c}.$$

Considering the circular transformation

$${\Psi }_{\lambda }\left(z\right):=\frac{1+2Az}{1+(1-\lambda )Az},z\in \mathbb{D},$$

with $0\le \lambda \le 1$, and assuming that $0\le A\le 1/2$, we obtain that ${\Psi }_{\lambda }$ maps the unit disc $\mathbb{D}$ onto the open disc that is symmetric respecting the real axes connecting the points ${\Psi }_{\lambda }(-1)$ and ${\Psi }_{\lambda }\left(1\right)$.

If $\alpha ={\displaystyle \frac{c}{4a}}$, then $A=1/4$, and for $\lambda =1$, $\lambda =0$, and $\lambda =1/2$, using the MAPLE™ software we get the next images of $\mathbb{D}$ by ${\Psi }_{\lambda }$ like in the Figure 2:

Figure 2. The images of ${\Psi }_{\lambda }\left({\mathrm{e}}^{\mathrm{i}\theta }\right)$ and $\psi \left({\mathrm{e}}^{\mathrm{i}\theta }\right),\theta \in [0,2\pi )$.

These show that ${\Psi }_{\lambda }\left(\mathbb{D}\right)\subset \psi \left(\mathbb{D}\right)$, which is ${\Psi }_{\lambda }\left(z\right)\prec \psi \left(z\right)$ for some values of $\lambda \in [0,1]$ that is $\tilde{f}\in {\mathcal{ML}}_c^a(\lambda ;\psi )$, whenever $\alpha ={\displaystyle \frac{c}{4a}}$, for $\lambda =1$, $\lambda =0$, and $\lambda =1/2$. It follows that there exist values of the parameters $a\in \mathbb{C}$, $c\in \mathbb{C}\backslash {\mathbb{Z}}_0^{-}$, and $\lambda \in [0,1]$, such that ${\mathcal{ML}}_c^a(\lambda ;\psi )\ne \varnothing$.

Now, by suitably specializing the parameter $\lambda$, we define the new subclasses of ${\mathcal{ML}}_c^a(\lambda ;\psi )$ as remarked below:

Remark 3.

(i) For $\lambda =0$, let ${\mathcal{ML}}_c^a(0,\psi )=:{\mathcal{SL}}_c^a\left(\psi \right)$ denote the subclass of $\mathcal{A}$, the members of which are given by (1) and satisfy the subordination condition

$${\displaystyle \frac{z{\left({\mathcal{L}}_c^{a}f\left(z\right)\right)}^{\prime }}{{\mathcal{L}}_c^{a}f\left(z\right)}}\prec z+\sqrt{1+z^2}.$$

(ii) For $\lambda =1$, let ${\mathcal{ML}}_c^a(1,\psi )=:{\mathcal{RL}}_c^a\left(\psi \right)$ denote the subclass of $\mathcal{A}$, members of which are of the form (1) and if it satisfy the condition

$${\left({\mathcal{L}}_c^{a}f\left(z\right)\right)}^{\prime }\prec z+\sqrt{1+z^2}.$$

(iii) For the special case for $a=c$, let $\mathcal{ML}(\lambda ;\psi ):={\mathcal{ML}}_c^c(\lambda ;\psi )$, members of which are given by (1) and satisfy the subordination

$${\displaystyle \frac{z{f}^{\prime }\left(z\right)}{(1-\lambda )f\left(z\right)+\lambda z}}\prec z+\sqrt{1+z^2}.$$

In the all of the above subordinations, and throughout the whole paper, the branch of the square root is chosen at the principal one, which is $\psi \left(0\right)=1$, and $a\in \mathbb{C}$, $c\in \mathbb{C}\backslash {\mathbb{Z}}_0^{-}$.

Using the techniques of Libera and Zlotkiewicz [11] and Koepf [17], combined with the help of MAPLE™ software, we find Fekete–Szegő inequality and Hankel determinant for the function of the class ${\mathcal{ML}}_c^a(\lambda ;\psi )$.

2. Preliminaries

To establish our main results, we recall the followings lemmas. The first lemma is the well-known Carathéodory’s lemma (see also [30] Corollary 2.3):

Lemma 1.

[31] If $p\in \mathcal{P}$ and given by (2), then $|p_k|\le 2$, for all $k\ge 1$, and the result is best possible for ${\varphi }_1\left(z\right)={\displaystyle \frac{1+\rho z}{1-\rho z}}$, $\left|\rho \right|=1$.

The next lemma gives us a majorant for the coefficients of the functions of the class $\mathcal{P}$, and more details may be found in [32] (Lemma 1):

Lemma 2.

[33] Let $\varphi \in \mathcal{P}$ be given by (2). Then,

$$\left|p_2-\nu p_1^2\right|\le 2max\left\{1;|2\nu -1|\right\},where\nu \in \mathbb{C}.$$

(7)

The result is sharp for the functions given by

$${\varphi }_1\left(z\right)={\displaystyle \frac{1+\rho z}{1-\rho z}},and{\varphi }_2\left(z\right)={\displaystyle \frac{1+{\rho }^2{z}^2}{1-{\rho }^2{z}^2}},with\left|\rho \right|=1.$$

Lemma 3.

[32] (Lemma 1 and Remark, pp. 162–163) If ϕ given by (2) is a member of the class $\mathcal{P}$, then

$$|p_2-\upsilon p_1^2|\le \left\{\begin{array}{ccc}-4\upsilon +2,\hfill & if\hfill & \upsilon \le 0,\hfill \\ 2,\hfill & if\hfill & 0\le v\le 1,\hfill \\ 4\upsilon -2,\hfill & if\hfill & \upsilon \ge 1.\hfill \end{array}\right.$$

(8)

When $\upsilon <0$ or $\upsilon >1$, the equality holds if and only if ϕ is ${\displaystyle \frac{1+z}{1-z}}$ or one of its rotations. If $0<v<1$, then equality holds if and only if ϕ is ${\displaystyle \frac{1+z^2}{1-z^2}}$ or one of its rotations. If $\upsilon =0$, the equality holds if and only if

$${\varphi }_3\left(z\right)=\left(\frac{1}{2}+\frac{\eta }{2}\right)\frac{1+z}{1-z}+\left(\frac{1}{2}-\frac{\eta }{2}\right)\frac{1-z}{1+z},0\le \eta \le 1,$$

or one of its rotations. If $\upsilon =1$, the equality holds if and only if ϕ is the reciprocal of one of the functions such that the equality holds in the case of $\upsilon =0$.

Although the above upper bound is sharp, when $0<\upsilon <1$, it can be improved as follows:

$$\left|p_2-\upsilon p_1^2\right|+\upsilon {\left|p_1\right|}^2\le 2,if0<\upsilon \le \frac{1}{2},$$

(9)

and

$$\left|p_2-\upsilon p_1^2\right|+(1-\upsilon ){\left|p_1\right|}^2\le 2,if\frac{1}{2}\le \upsilon <1.$$

(10)

We also need the following result:

Lemma 4.

[33] Let $\varphi \in \mathcal{P}$ given by (2). Then,

$$p_2={\displaystyle \frac{1}{2}}\left[p_1^2+\left(4-p_1^2\right)x\right],$$

(11)

and

$$p_3={\displaystyle \frac{1}{4}}\left[p_1^3+2\left(4-p_1^2\right)p_{1}x-\left(4-p_1^2\right)p_1{x}^2+2\left(4-p_1^2\right){(1-|x|}^2)z\right]$$

(12)

for some complex numbers x, z satisfying $\left|x\right|\le 1$ and $\left|z\right|\le 1$.

3. Coefficient Bounds and Fekete–Szegő Inequality

In our first result, we will determine coefficient bounds for $f\in {\mathcal{ML}}_c^a(\lambda ;\psi )$, and this tends to solve the Fekete–Szegő problem for the subclass ${\mathcal{ML}}_c^a(\lambda ;\psi )$.

Theorem 1.

If $f\in {\mathcal{ML}}_c^a(\lambda ;\psi )$ and is of the form (1), then

$$\begin{array}{c}|a_2|\le \left|{\displaystyle \frac{c}{a}}\right|{\displaystyle \frac{1}{1+\lambda }},\hfill \\ |a_3|\le \left|{\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right|\frac{1}{2+\lambda }max\left\{1;\left|{\displaystyle \frac{\lambda -3}{2(1+\lambda )}}\right|\right\},\hfill \\ |a_4|\le \left|{\displaystyle \frac{{\left(c\right)}_3}{{\left(a\right)}_3}}\right|{\displaystyle \frac{1}{2(3+\lambda )}}.\hfill \end{array}$$

Proof. 

If $f\in {\mathcal{ML}}_c^a(\lambda ;\psi )$, from (6), it follows that there exists a function $w\in \mathcal{H}\left(\mathbb{D}\right)$ with $w\left(0\right)=0$ and $\left|w\right(z\left)\right|<1$, $z\in \mathbb{D}$, such that

$${\displaystyle \frac{z{\left({\mathcal{L}}_c^{a}f\left(z\right)\right)}^{\prime }}{(1-\lambda ){\mathcal{L}}_c^{a}f\left(z\right)+\lambda z}}=\psi \left(w\left(z\right)\right)=w\left(z\right)+\sqrt{1+w^2\left(z\right)},z\in \mathbb{D}.$$

(13)

Define the function $\varphi$ by

$$\varphi \left(z\right)=\frac{1+w\left(z\right)}{1-w\left(z\right)}=1+p_{1}z+p_2{z}^2+p_3{z}^3+\cdots ,z\in \mathbb{D},$$

which is

$$w\left(z\right)=\frac{\varphi \left(z\right)-1}{\varphi \left(z\right)+1},z\in \mathbb{D},$$

(14)

and, since $w\in \mathcal{H}\left(\mathbb{D}\right)$ with $w\left(0\right)=0$ and $\left|w\right(z\left)\right|<1$, $z\in \mathbb{D}$, it follows that $\varphi \in \mathcal{P}$.

Substituting the function w from (14) on the right-hand side of (13) and simplifying, we get

$$\sqrt{1+{\left(\frac{\varphi \left(z\right)-1}{\varphi \left(z\right)+1}\right)}^2}+\frac{\varphi \left(z\right)-1}{\varphi \left(z\right)+1}=1+\frac{p_1}{2}z+\left(\frac{p_2}{2}-\frac{p_1^2}{8}\right)z^2+\left(\frac{p_3}{2}-\frac{p_1{p}_2}{4}\right)z^3+\cdots ,z\in \mathbb{D},$$

(15)

and, by using (4), the left-hand side of (13) will be

$$\begin{array}{c}\hfill {\displaystyle \frac{z{\left(\mathcal{L}(a,c)f\left(z\right)\right)}^{\prime }}{(1-\lambda )\mathcal{L}(a,c)f\left(z\right)+\lambda z}}=1+(1+\lambda ){\phi }_1{a}_{2}z+\left[(2+\lambda ){\phi }_2{a}_3+({\lambda }^2-1){\phi }_1^2{a}_2^2\right]z^2\\ \hfill +\left[(3+\lambda ){\phi }_3{a}_4+(2{\lambda }^2+\lambda -3){\phi }_1{\phi }_2{a}_2{a}_3+({\lambda }^3-{\lambda }^2-\lambda +1){\phi }_1^3{a}_2^3\right]z^3+\cdots ,z\in \mathbb{D},\end{array}$$

(16)

where ${\phi }_n$, $n\in \mathbb{N}$, is given by (5).

Hence, replacing (15) and (16) in (13) and comparing the coefficients of z, $z^2$ and $z^3$, we get

$$\begin{array}{c}{a}_2={\displaystyle \frac{c}{a}}{\displaystyle \frac{p_1}{2(1+\lambda )}},\hfill \end{array}$$

(17)

$$\begin{array}{c}{a}_3={\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}{\displaystyle \frac{1}{2(2+\lambda )}}\left[p_2-{\displaystyle \frac{3\lambda -1}{4(1+\lambda )}}{p}_1^2\right],\hfill \end{array}$$

(18)

$$\begin{array}{c}{a}_4={\displaystyle \frac{{\left(c\right)}_3}{{\left(a\right)}_3}}{\displaystyle \frac{1}{2(3+\lambda )}}\left[p_3-{\displaystyle \frac{3{\lambda }^2+4\lambda -1}{2(1+\lambda )(2+\lambda )}}{p}_1{p}_2+{\displaystyle \frac{4{\lambda }^2-3\lambda -1}{8(1+\lambda )(2+\lambda )}}{p}_1^3\right].\hfill \end{array}$$

(19)

Thus, from Lemma 1, we have

$$\begin{array}{c}|a_2|\le \left|{\displaystyle \frac{c}{a}}\right|{\displaystyle \frac{1}{1+\lambda }},\hfill \\ |a_3|\le \left|{\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right|{\displaystyle \frac{1}{2(2+\lambda )}}\left|p_2-{\displaystyle \frac{3\lambda -1}{4(1+\lambda )}}{p}_1^2\right|,\hfill \end{array}$$

and, according to Lemma 2, it follows that

$$|a_3|\le \left|{\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2(2+\lambda )}}\right|max\left\{1;\left|{\displaystyle \frac{\lambda -3}{2(1+\lambda )}}\right|\right\},$$

and

$$a_4={\displaystyle \frac{{\left(c\right)}_3}{{\left(a\right)}_3}}{\displaystyle \frac{1}{2(3+\lambda )}}\left[p_3-{\displaystyle \frac{3{\lambda }^2+4\lambda -1}{2(1+\lambda )(2+\lambda )}}{p}_1{p}_2+{\displaystyle \frac{4{\lambda }^2-3\lambda -1}{8(1+\lambda )(2+\lambda )}}{p}_1^3\right].$$

(20)

Replacing the values of $p_2$ and $p_3$ given by the relations (11) and (12) in (20), respectively, and, denoting $p:=p_1$, we get

$$\begin{array}{c}{a}_4={\displaystyle \frac{{\left(c\right)}_3}{{\left(a\right)}_3}}{\displaystyle \frac{1}{2(3+\lambda )}}\times \left[{\displaystyle \frac{3{\lambda }^2-\lambda +4}{8(1+\lambda )(2+\lambda )}}{p}^3-{\displaystyle \frac{2{\lambda }^2+\lambda +3}{2(1+\lambda )(2+\lambda )}}\left(4-p^2\right)px\right.\\ \left.-\frac{1}{4}\left(4-p^2\right)p{x}^2+\frac{1}{2}\left(4-p^2\right){(1-|x|}^2)z\right],\end{array}$$

for some complex numbers x and z, with $\left|x\right|<1$ and $\left|z\right|\le 1$. Using the triangle’s inequality and substituting $\left|x\right|=y$, we get

$$\begin{array}{c}|a_4|\le {\displaystyle \frac{{\left(c\right)}_3}{{\left(a\right)}_3}}{\displaystyle \frac{1}{4(3+\lambda )}}\times \left[{\displaystyle \frac{3{\lambda }^2-\lambda +4}{8(1+\lambda )(2+\lambda )}}{p}^3+{\displaystyle \frac{\left|2{\lambda }^2+\lambda +3\right|}{2(1+\lambda )(2+\lambda )}}\left(4-p^2\right)py\right.\\ \left.+\frac{1}{4}\left(4-p^2\right)p{y}^2+\frac{1}{2}\left(4-p^2\right)\left(1-y^2\right)\right]=:\mathcal{F}(p,y),(0\le p\le 2,0\le y\le 1).\end{array}$$

Now, we will find the maximum of the function $\mathcal{F}(p,y)$ on the closed rectangle $[0,2]\times [0,1]$. Denoting

$$\begin{array}{c}\mathcal{H}(p,y):={\displaystyle \frac{3{\lambda }^2-\lambda +4}{8(1+\lambda )(2+\lambda )}}{p}^3+{\displaystyle \frac{\left|2{\lambda }^2+\lambda +3\right|}{2(1+\lambda )(2+\lambda )}}\left(4-p^2\right)py+\frac{1}{4}\left(4-p^2\right)p{y}^2\\ +\frac{1}{2}\left(4-p^2\right)\left(1-y^2\right),\end{array}$$

and using the MAPLE™ software for the following code

[> H :=(3*l^2-l+4)*p^3/(8*(1+l)*(2+l))-

(2*l^2+l-3)*(-p^2+4)*p*y/(2*(1+l)*(2+l))

- 1/4*(-p^2+4)*p*y+1/2*(-p^2+4)*(-y^2+1);

[> maximize(H, p=0 .. 2, y=0 .. 1, location);

we get

max(2, (3*l^2-l+4)/((1+l)*(2+l))),

{[{p=2}, (3*l^2-l+4)/((1+l)*(2+l))],

[{p=0, y=0}, 2]}

that is

$$max\left\{\mathcal{H}(p,y):(p,y)\in [0,2]\times [0,1]\right\}=max\left\{2;{\displaystyle \frac{3{\lambda }^2-\lambda +4}{(1+\lambda )(2+\lambda )}}\right\},$$

and

$$2=\mathcal{H}(0,0),{\displaystyle \frac{3{\lambda }^2-\lambda +4}{(1+\lambda )(2+\lambda )}}=\mathcal{H}(2,y).$$

A simple computation shows that $2>{\displaystyle \frac{3{\lambda }^2-\lambda +4}{(1+\lambda )(2+\lambda )}}$ whenever $\lambda \ge 0$; therefore,

$$max\left\{\mathcal{H}(p,t):(p,t)\in [0,2]\times [0,1]\right\}=2=\mathcal{H}(0,0),$$

which implies that

$$max\left\{\mathcal{F}(p,y):(p,y)\in [0,2]\times [0,1]\right\}={\displaystyle \frac{{\left(c\right)}_3}{{\left(a\right)}_3}}{\displaystyle \frac{1}{2(3+\lambda )}}=\mathcal{F}(0,0),$$

and the proof of our theorem is complete.  □

Theorem 2.

If $f\in {\mathcal{ML}}_c^a(\lambda ;\psi )$ is of the form (1), then, for any $\mu \in \mathbb{C}$, we have

$$\left|a_3-\mu a_2^2\right|\le {\displaystyle \frac{{|\left(c\right)}_2|}{{|\left(a\right)}_2|}}{\displaystyle \frac{1}{2+\lambda }}max\left\{1;{\displaystyle \frac{\left|(\lambda -3)(1+\lambda )a(c+1)+2\mu (2+\lambda )c(a+1)\right|}{2{(1+\lambda )}^2\left|a(c+1)\right|}}\right\}.$$

Proof. 

If $f\in {\mathcal{ML}}_c^a(\lambda ;\psi )$ is of the form (1), from (17) and (18), we get

$$a_3-\mu a_2^2={\displaystyle \frac{1}{2(2+\lambda )}}{\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\left(p_2-\nu p_1^2\right),$$

where

$$\nu ={\displaystyle \frac{(3\lambda -1)(\lambda +1)a(c+1)+2\mu (2+\lambda )c(a+1)}{4{(1+\lambda )}^{2}a(c+1)}}.$$

Taking the modules for the both sides of the above relation, with the aid of the inequality (7) of Lemma 2, we easily get the required estimate.  □

For $a=c$, the above theorem reduces to the following special case:

Corollary 1.

If $f\in \mathcal{ML}(\lambda ;\psi )$ is given by (1) then, for any $\mu \in \mathbb{C}$, we have

$$\left|a_3-\mu a_2^2\right|\le {\displaystyle \frac{1}{2+\lambda }}max\left\{1;{\displaystyle \frac{\left|\right(\lambda -3\left)\right(1+\lambda )+2\mu (2+\lambda \left)\right|}{2{(1+\lambda )}^2}}\right\}.$$

Remark 4.

If $f\in \mathcal{ML}(\lambda ;\psi )$ is given by (1) then, for the special case $\mu =1$, we get

$$\left|a_3-a_2^2\right|\le {\displaystyle \frac{1}{2+\lambda }}max\left\{1;{\displaystyle \frac{{\lambda }^2+1}{2{(1+\lambda )}^2}}\right\}={\displaystyle \frac{1}{2+\lambda }}.$$

If we take $\mu \in \mathbb{R}$ in Theorem 2, we get the next special case:

Theorem 3.

1. If the function $f\in {\mathcal{ML}}_c^a(\lambda ;\psi )$ is given by (1), ${\displaystyle \frac{a(c+1)}{c(a+1)}}>0$ and $\mu \in \mathbb{R}$, then

$$\left|a_3-\mu a_2^2\right|\le \left\{\begin{array}{ccc}{\displaystyle \frac{a(c+1)(3-\lambda )(\lambda +1)-2\mu c(a+1)(2+\lambda )}{2a(c+1){(\lambda +1)}^2(2+\lambda )}}\left|{\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right|,\hfill & if\hfill & \mu \le {\delta }_1,\hfill \\ {\displaystyle \frac{1}{2+\lambda }}\left|{\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right|,\hfill & if\hfill & {\delta }_1\le \mu \le {\delta }_2,\hfill \\ {\displaystyle \frac{a(c+1)(\lambda -3)(\lambda +1)+2\mu c(a+1)(2+\lambda )}{2a(c+1){(\lambda +1)}^2(2+\lambda )}}\left|{\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right|,\hfill & if\hfill & \mu \ge {\delta }_2,\hfill \end{array}\right.$$

where

$${\delta }_1:=-{\displaystyle \frac{(3\lambda -1)(\lambda +1)}{2(2+\lambda )}}{\displaystyle \frac{a(c+1)}{c(a+1)}}\mathrm{and}{\delta }_2:={\displaystyle \frac{(\lambda +1)(\lambda +5)}{2(2+\lambda )}}{\displaystyle \frac{a(c+1)}{c(a+1)}}.$$

2. Furthermore, if ${\delta }_1<\mu \le {\delta }_3$, then

$$|a_3-\mu a_2^2|+{\displaystyle \frac{(3\lambda -1)(\lambda +1)a(c+1)+2\mu (2+\lambda )c(a+1)}{2(2+\lambda )c(a+1)}}{\left|a_2\right|}^2\le {\displaystyle \frac{{|\left(c\right)}_2|}{{|\left(a\right)}_2|}}\frac{1}{2+\lambda }.$$

(21)

If ${\delta }_3\le \mu <{\delta }_2$, then

$$|a_3-\mu a_2^2|+{\displaystyle \frac{(\lambda +1)(\lambda +5)a(c+1)-2\mu (2+\lambda )c(a+1)}{2(2+\lambda )c(a+1)}}{\left|a_2\right|}^2\le {\displaystyle \frac{{|\left(c\right)}_2|}{{|\left(a\right)}_2|}}\frac{1}{2+\lambda },$$

(22)

where

$${\delta }_3:={\displaystyle \frac{(\lambda +1)(3-\lambda )}{2(2+\lambda )}}{\displaystyle \frac{a(c+1)}{c(a+1)}}.$$

These results are sharp.

Proof. 

If $f\in {\mathcal{ML}}_c^a(\lambda ;\psi )$ is given by (1), from (17) and (18), we get

$$a_3-\mu a_2^2={\displaystyle \frac{1}{2(2+\lambda )}}{\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\left(p_2-\nu p_1^2\right),$$

(23)

where

$$\nu ={\displaystyle \frac{(3\lambda -1)(\lambda +1)a(c+1)+2\mu (2+\lambda )c(a+1)}{4{(1+\lambda )}^{2}a(c+1)}}=\frac{3\lambda -1}{4(1+\lambda )}+\mu \frac{2+\lambda }{2{(1+\lambda )}^2}\frac{c(a+1)}{a(c+1)}.$$

From the assumptions, using the second above equality, it follows that $\nu \in \mathbb{R}$. We have

$$4\nu -2={\displaystyle \frac{a(c+1)(\lambda -3)(\lambda +1)+2\mu c(a+1)(2+\lambda )}{a(c+1){(\lambda +1)}^2}},$$

$\nu \ge 1$ is equivalent to $\mu \ge {\delta }_2$, and $\nu \le 0$ is equivalent to $\mu \le {\delta }_1$.

Then, taking the modules for both sides of the above equality, with the aid of the inequality (8) of Lemma 3, we obtain the first estimates of Theorem 3.

For the proof of the second part, first we see that $0<\nu \le 1/2$ is equivalent to ${\delta }_1<\mu \le {\delta }_3$. Using the relations (23) and (17), and then applying the inequality (9) of Lemma 3, we get

$$\begin{array}{c}|a_3-\mu a_2^2|+(\mu -{\delta }_1)|a_2^2|=|a_3-\mu a_2^2|+|\mu -{\delta }_1\left|\right|a_2^2|=\\ \frac{1}{2(2+\lambda )}\left|{\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right|\left[|p_2-\nu a_1^2|+\nu |p_1^2|\right]\le \frac{1}{2+\lambda }\left|{\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right|,\end{array}$$

which represents the required inequality (21).

Furthermore, we easily check that $1/2\le \nu <1$ is equivalent to ${\delta }_3\le \mu <{\delta }_2$. From the relations (23) and (17), and then applying the inequality (10) of Lemma 3, we obtain

$$\begin{array}{c}|a_3-\mu a_2^2|+({\delta }_2-\mu )|a_2^2|=|a_3-\mu a_2^2|+|{\delta }_2-\mu \left|\right|a_2^2|=\\ \frac{1}{2(2+\lambda )}\left|{\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right|\left[|p_2-\nu a_1^2|+(1-\nu )|p_1^2|\right]\le \frac{1}{2+\lambda }\left|{\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right|,\end{array}$$

which is the inequality (21).

To prove that the bounds are sharp, we define the functions $F_{\eta }$ and $G_{\eta }$, $0\le \eta \le 1$, respectively, with $F_{\eta }\left(0\right)=0=F_{\eta }^{\prime }\left(0\right)-1$ and $G_{\eta }\left(0\right)=0=G_{\eta }^{\prime }\left(0\right)-1$ by

$$\frac{z{\left({\mathcal{L}}_c^a{F}_{\eta }\left(z\right)\right)}^{\prime }}{(1-\lambda ){\mathcal{L}}_c^a{F}_{\eta }\left(z\right)+\lambda z}=\psi \left(\frac{z(z+\eta )}{1+\eta z}\right),$$

and

$$\frac{z{\left({\mathcal{L}}_c^a{G}_{\eta }\left(z\right)\right)}^{\prime }}{(1-\lambda ){\mathcal{L}}_c^a{G}_{\eta }\left(z\right)+\lambda z}=\psi \left(-\frac{z(z+\eta )}{1+\eta z}\right),$$

respectively. Clearly, $K_{{\psi }_n}\left(z\right):=\psi \left(z^{n-1}\right),F_{\eta },G_{\eta }\in {\mathcal{ML}}_c^a(\lambda ;\psi )$. In addition, we write $K_{{\psi }_2}\left(z\right):=K_{\psi }\left(z\right)=z+\sqrt{1+z^2}$.

If $\mu <{\delta }_1$ or $\mu >{\delta }_2$, then the equality holds if and only if f is $K_{\psi }$ or one of its rotations. When ${\delta }_1<\mu <{\delta }_2$, then the equality holds if and only if f is $K_{{\psi }_3}\left(z\right)=z^2+\sqrt{1+z^4}$ or one of its rotations. If $\mu ={\delta }_1$, then the equality holds if and only if f is $F_{\eta }$ or one of its rotations. If $\mu ={\delta }_2$, then the equality holds if and only if f is $G_{\eta }$ or one of its rotations.  □

4. Hankel Determinant Result for $\mathit{f}\in {\mathcal{ML}}_{\mathbf{c}}^{\mathbf{a}}(\mathbf{\lambda };\mathbf{\psi })$

The next result deals with an upper bound of ${\mathcal{H}}_{2,2}\left(f\right)$ for the subclass ${\mathcal{ML}}_c^a(\lambda ;\psi )$:

Theorem 4.

If $f\in {\mathcal{ML}}_c^a(\lambda ;\psi )$ is given by (1) and

$$1\le \frac{{(c+1)}_2}{{(a+1)}_2}\le \frac{27}{20},$$

(24)

then

$$\left|a_2{a}_4-a_3^2\right|\le {\left({\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right)}^2{\displaystyle \frac{1}{2{(2+\lambda )}^2}}.$$

(25)

Proof. 

If $f\in {\mathcal{ML}}_c^a(\lambda ;\psi )$, using a similar proof like in the proof of Theorem 1, from (17), (18), and (19), we get

$$a_2{a}_4-a_3^2=k_1{p}_1^4+k_2{p}_1^2{p}_2+k_3{p}_1{p}_3+k_4{p}_2^2,$$

where

$$\begin{array}{c}{k}_1=\frac{c{\left(c\right)}_3}{a{\left(a\right)}_3}\frac{4{\lambda }^2-3\lambda -1}{32{(1+\lambda )}^2(3+\lambda )(2+\lambda )}-{\left({\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right)}^2\frac{1}{4{(2+\lambda )}^2}{\left(\frac{3\lambda -1}{4(1+\lambda )}\right)}^2,\hfill \\ k_2={\displaystyle \frac{3\lambda -1}{8{(2+\lambda )}^2(1+\lambda )}}{\left({\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right)}^2-{\displaystyle \frac{c}{a}}{\displaystyle \frac{{\left(c\right)}_3}{{\left(a\right)}_3}}{\displaystyle \frac{3{\lambda }^2+4\lambda -1}{4{(1+\lambda )}^2(2+\lambda )(3+\lambda )}},\hfill \\ k_3={\displaystyle \frac{c}{a}}{\displaystyle \frac{{\left(c\right)}_3}{{\left(a\right)}_3}}{\displaystyle \frac{1}{4(1+\lambda )(3+\lambda )}},\hfill \\ k_4=-\left[{\left({\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right)}^2{\displaystyle \frac{1}{4{(2+\lambda )}^2}}\right].\hfill \end{array}$$

Using the relations (11) and (12) of Lemma 4, we get

$$\begin{array}{cc}\hfill & \left|a_2{a}_4-a_3^2\right|=\hfill \\ \hfill & \left|A{p}_1^4+B\left(4-p_1^2\right)x{p}_1^2+\left[\frac{k_4}{4}\left(4-p_1^2\right)-\frac{k_3}{4}{p}_1^2\right]\left(4-p_1^2\right)x^2+\frac{k_3}{2}{p}_1\left(4-p_1^2\right)\left(1-{\left|x\right|}^2\right)z\right|,\hfill \end{array}$$

(26)

with $\left|x\right|\le 1$, $\left|z\right|\le 1$, and

$$\begin{array}{cc}\hfill & A:=\frac{1}{4}\left(4k_1+2k_2+k_3+k_4\right)={\displaystyle \frac{1}{64{(2+\lambda )}^2{(1+\lambda )}^2(3+\lambda )}}\times \hfill \\ \hfill & \left[2s(4{\lambda }^2-3\lambda -1)\left(2+\lambda \right){{\left(a\right)}_2}^2+\left(-20s{{\left(a\right)}_2}^2-{{\left(c\right)}_2}^2\right){\lambda }^3+\left(-60s{{\left(a\right)}_2}^2+3{{\left(a\right)}_2}^2\right){\lambda }^2\right.\hfill \\ \hfill & \left.+\left(-24s{{\left(a\right)}_2}^2+9{{\left(c\right)}_2}^2\right)\lambda +32s{\left(a\right)}_2^2-27{{\left(c\right)}_2}^2\right],\hfill \\ \hfill & B:=\frac{1}{2}\left(k_2+k_3+k_4\right)=\hfill \\ \hfill & \frac{\left(-4{{\left(a\right)}_2}^2+{{\left(c\right)}_2}^2\right){\lambda }^3+\left(-10s{{\left(a\right)}_2}^2+{{\left(c\right)}_2}^2\right){\lambda }^2+\left(2s{{\left(a\right)}_2}^2-9{{\left(c\right)}_2}^2\right)\lambda +12s{{\left(a\right)}_2}^2-9{{\left(c\right)}_2}^2}{16{\left(1+\lambda \right)}^2\left(3+\lambda \right){\left(2+\lambda \right)}^2{{\left(a\right)}_2}^2}\hfill \end{array}$$

where $s={\displaystyle \frac{c{\left(c\right)}_3}{a{\left(a\right)}_3}}$. Since $\varphi \in \mathcal{P}$, it follows that $\varphi \left(e^{-iarg{p}_1}z\right)\in \mathcal{P}$, hence we may assume without loss of generality that $p:=p_1\ge 0$, and, according to Lemma 1, it follows that $p\in [0,2]$. Now, using the triangle’s inequality in (26) and substituting $\left|x\right|=t$, we get

$$\begin{array}{c}\left|a_2{a}_4-a_3^2\right|\le \left|A\right|p^4+\left|B\right|\left(4-p^2\right)p^{2}t+\frac{|k_4|}{4}{\left(4-p^2\right)}^2{t}^2+\frac{|k_3|}{4}{p}^2\left(4-p^2\right)t^2\\ +\frac{|k_3|}{2}p\left(4-p^2\right)(1-t^2)=:\mathcal{G}(p,t),(0\le p\le 2,0\le t\le 1).\end{array}$$

Next, we will find maximum of $\mathcal{G}(p,t)$ on the closed rectangle $[0,2]\times [0,1]$. Using the MAPLE™ software for the following code, where we denoted $C:=k_4$ and $D1=E:=k_3$,

[>G :=abs(A)*p^4+abs(B)*(-p^2+4)*p^2*t+1/4*abs(C)*(-p^2+4)^2*t^2

+1/4*abs(D1)*p^2*(-p^2+4)*t^2+1/2*abs(E)*p*(-p^2+4)*(-t^2+1);

[> maximize(G, p=0 .. 2, t=0 .. 1, location);

max(16*abs(A), 4*abs(C)),

{[{p=2}, 16*abs(A)], [{p=0, t=1}, 4*abs(C)]}

or

max(16|A|, 4|C|), {[{p=2}, 16|A|], [{p=0, t=1}, 4|C|]},

which is

$$max\left\{\mathcal{G}(p,t):(p,t)\in [0,2]\times [0,1]\right\}=max\left\{16\right|A|;4|C\left|\right\},$$

and

$$16\left|A\right|=\mathcal{G}(2,t),4\left|C\right|=\mathcal{G}(0,1).$$

We will prove that, under our assumption we have $4\left|C\right|\ge 16\left|A\right|$, and therefore

$$max\left\{\mathcal{G}(p,t):(p,t)\in [0,2]\times [0,1]\right\}=4\left|C\right|=4\left|k_4\right|=\mathcal{G}(0,1).$$

(27)

Letting $\alpha :={\displaystyle \frac{c}{a}}{\displaystyle \frac{{\left(c\right)}_3}{{\left(a\right)}_3}}$ and $\beta :={\left({\displaystyle \frac{{\left(c\right)}_2}{{\left(a\right)}_2}}\right)}^2$, from (24), it follows that $\alpha \ge \beta >0$. A simple computation shows that

$$4A=4k_1+2k_2+k_3+k_4=\alpha M-\beta N,$$

where

$$M:=\frac{5(1-\lambda )}{8{(1+\lambda )}^2(2+\lambda )(3+\lambda )}\ge 0,\lambda \in [0,1],\mathrm{and}N:=\frac{{(\lambda -3)}^2}{16{\left[(1+\lambda )(2+\lambda )\right]}^2}.$$

Since

$$A=\frac{\alpha M-\beta N}{4}=\frac{10\alpha (1-\lambda )(2+\lambda )-\beta {(\lambda -3)}^2(3+\lambda )}{64{(1+\lambda )}^2{(2+\lambda )}^2(3+\lambda )},\lambda \in [0,1],$$

then $A\le 0$ if and only if the inequality $10\alpha (1-\lambda )(2+\lambda )-\beta {(\lambda -3)}^2(3+\lambda )\le 0$ holds for all $\lambda \in [0,1]$. This last inequality is equivalent to

$$\frac{\alpha }{\beta }=\frac{{(c+1)}_2}{{(a+1)}_2}\le \frac{{(\lambda -3)}^2(\lambda +3)}{10(\lambda +2)(1-\lambda )}=:t\left(\lambda \right),\lambda \in [0,1],$$

and a simple computation shows that $t\left(\lambda \right)\ge t\left(0\right)={\displaystyle \frac{27}{20}}$ for all $t\in [0,1]$. Therefore, the above inequality holds whenever the assumption (24) is satisfied, hence $A\le 0$. Since $C<0$, we have

$$\begin{array}{c}16\left|A\right|-4\left|C\right|=-16A+4C=-\alpha \frac{5(1-\lambda )}{2(3+\lambda ){(1+\lambda )}^2(2+\lambda )}\\ +\beta \frac{{(\lambda -3)}^2}{4{\left[(1+\lambda )(2+\lambda )\right]}^2}-\beta \frac{1}{{(2+\lambda )}^2}=\frac{\alpha U-\beta V}{4(3+\lambda ){\left[(1+\lambda )(2+\lambda )\right]}^2},\end{array}$$

with

$$U:=10(\lambda -1)(\lambda +2)\le 0,\lambda \in [0,1],\mathrm{and}V:=(3\lambda -1)(\lambda +3)(\lambda +5).$$

Since

$$U-V=-3{\lambda }^3-13{\lambda }^2-27\lambda -5<0,\lambda \in [0,1],$$

we have $U<V$.

If $\lambda \in \left[0,1/3\right]$, then $V\le 0$, and using the inequality $\alpha \ge \beta >0$, we get $\alpha U-\beta V<0$. If $\lambda \in \left[1/3,1\right]$, then $V\ge 0$, and, because $U\le 0$, $\alpha ,\beta >0$, it follows that $\alpha U-\beta V<0$.

Therefore, for all $\lambda \in [0,1]$, we have $16\left|A\right|<4\left|C\right|$. Since (27) was proved, the upper bound of $\mathcal{G}(p,t)$ on the closed rectangle $[0,2]\times [0,1]$ is attained at $p=0$ and $t=1$, which implies the inequality (25).  □

Remark 5.

By suitably specializing the parameter λ, one can deduce the above results for the subclasses of ${\mathcal{SL}}_c^a(\lambda ;\psi )$, and ${\mathcal{RL}}_c^a(\lambda ;\psi )$, which are defined, respectively, in Remark 3 (i) and (ii). Furthermore, by taking $a=c$, we can easily state the result for the function class $\mathcal{ML}(\lambda ,\psi )$ given in Remark 3 (iii). The details involved may be left as an exercise for the interested reader.