Stable Finite-Difference Methods for Elastic Wave Modeling with Characteristic Boundary Conditions
Abstract
1. Introduction
2. Related Work
3. Methodology and Formulation
3.1. First-Order Scheme
3.2. Second-Order Scheme
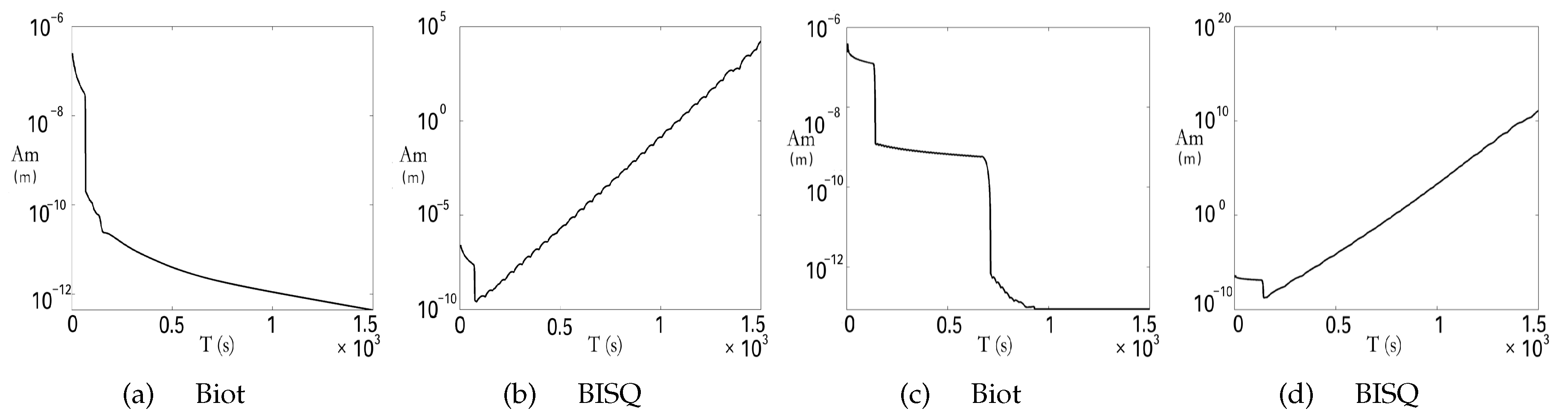
3.3. The Stability Criterion
4. Numerical Procedure and Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. The Truncation Errors of the Scheme (4)/(6)/(7)
Appendix A.2. The Truncation Errors of the Scheme (9)/(10)/(11)
Appendix B
Appendix B.1. The Proof of Theorem 2
Appendix B.2. The Proof of Theorem 3
Appendix C
| Symbol | Parameter | Symbol | Parameter |
|---|---|---|---|
| v | solid’s velocity | w | fluid’s velocity |
| the total stress of the bulk material | P | the total fluid pressure | |
| porosity | M | the uniaxial modulus of the skeleton | |
| poroelastic coefficient | viscosity | ||
| permeability | F | the Biot-flow coefficient | |
| S | the characteristic squirt-flow coefficient | solid’s density | |
| fluid’s density | the additional coupling density | ||
| f | frequency | the eigenvalue of the matrix | |
| the time-step size | the spatial increment |
| Acronym | Full-Form | Acronym | Full-Form |
|---|---|---|---|
| FD method | finite-difference method | BISQ model | Biot/squirt model |
| FE method | finite-element method | CFL condition | Courant–Friedrichs–Lewy condition |
| 3D | three-dimension |
References
- Burrascano, P.; Callegari, S.; Montisci, A.; Ricci, M.; Versaci, M. Ultrasonic Nondestructive Evaluation Systems: Industrial Application Issues; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Guo, Z.; Xue, G.; Liu, J.; Wu, X. Electromagnetic methods for mineral exploration in China: A review. Ore Geol. Rev. 2020, 118, 103357. [Google Scholar]
- Versaci, M. Fuzzy approach and Eddy currents NDT/NDE devices in industrial applications. Electron. Lett. 2016, 52, 943–945. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Dvorkin, J.; Nur, A. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms. Geophysics 1993, 58, 524–533. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T.; Dvorkin, J. The Rock Physics Handbook; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Pan, X.; Zhang, G.; Yin, X. Azimuthally anisotropic elastic impedance inversion for fluid indicator driven by rock physics. Geophysics 2017, 82, C211–C227. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, Z. Poroelastic wave equation including the Biot/squirt mechanism and the solid/fluid coupling anisotropy. Wave Motion 2002, 35, 223–245. [Google Scholar] [CrossRef]
- Carcione, J.M.; Gurevich, B. Differential form and numerical implementation of Biot’s poroelasticity equations with squirt dissipation. Geophysics 2011, 76, N55–N64. [Google Scholar] [CrossRef]
- Moczo, P.; Kristek, J.; Galis, M.; Pazak, P.; Balazovjech, M. The finite-difference and finite-element modeling of seismic wave propagation and earthquake motion. Acta Phys. Slovaca 2007, 57, 177–406. [Google Scholar] [CrossRef]
- Gauthier, O.; Virieux, J.; Tarantola, A. Two-dimensional nonlinear inversion of seismic waveforms: Numerical results. Geophysics 1986, 51, 1387–1403. [Google Scholar] [CrossRef]
- Virieux, J. P-SV wave propagation in heterogeneous media; velocity-stress finite-difference method. Geophysics 1986, 51, 889–901. [Google Scholar] [CrossRef]
- Igel, H.; Mora, P.; Riollet, B. Anisotropic wave propagation through finite-difference grids. Geophysics 1995, 60, 1203–1216. [Google Scholar] [CrossRef]
- Saenger, E.H.; Gold, N.; Shapiro, S.A. Modeling the propagation of elastic waves using a modified finite-difference grid. Wave Motion 2000, 31, 77–92. [Google Scholar] [CrossRef]
- Hustedt, B.; Operto, S.; Virieux, J. Mixed-grid and staggered-grid finite-difference methods for frequency-domain acoustic wave modelling. Geophys. J. Int. 2004, 157, 1269–1296. [Google Scholar] [CrossRef]
- Tian, X.F. Higher Order Time Difference Scheme and Stability Analysis for First-order Elastic Wave Staggered Grid; Coal geology of China, Taylor & Francis Online: Abingdon, UK, 2019; pp. 70–78. [Google Scholar]
- Yang, K.D.; Song, G.J.; Li, J.S. FCT compact difference simulation of wave propagation based on the Biot and the squirt-flow coupling interaction. Chin. J. Geophys. 2011, 54, 1348–1357. [Google Scholar]
- Liu, J.; Yong, W.A. Stability analysis of the Biot/squirt models for wave propagation in saturated porous media. Geophys. J. Int. 2016, 204, 535–543. [Google Scholar] [CrossRef]
- Yong, W.A. Boundary stabilization of hyperbolic balance laws with characteristic boundaries. Automatica 2019, 101, 252–257. [Google Scholar] [CrossRef]
- Zhu, Y.l.; Zhong, X.C.; Chen, B.M.; Zhang, Z.M. Difference Methods for Initial-Boundary-Value Problems and Flow Around Bodies; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 4. [Google Scholar]

| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| M (GPa) | 29 | (%) | 15 | 0.5702 | |
| (kg/m) | 2600 | (kg/m) | 1000 | (kg/m) | 450 |
| (kg/ms) | 100 | f (KHz) | 50 | R (m) | 0.001 |
| N | Order | Order | Order | |||
|---|---|---|---|---|---|---|
| 80 | 3.48 × | − | 1.36 | − | 7.08 × | − |
| 160 | 1.86 × | 0.90 | 7.93 × | 0.77 | 3.86 × | 0.88 |
| 320 | 9.71 × | 0.94 | 4.23 × | 0.91 | 2.16 × | 0.83 |
| 640 | 4.43 × | 1.13 | 2.08 × | 1.02 | 1.13 × | 0.93 |
| 1280 | 2.0 3× | 1.12 | 1.02 × | 1.03 | 5.80 × | 0.97 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yong, W.-A.; Liu, J.; Guo, Z. Stable Finite-Difference Methods for Elastic Wave Modeling with Characteristic Boundary Conditions. Mathematics 2020, 8, 1039. https://doi.org/10.3390/math8061039
Liu J, Yong W-A, Liu J, Guo Z. Stable Finite-Difference Methods for Elastic Wave Modeling with Characteristic Boundary Conditions. Mathematics. 2020; 8(6):1039. https://doi.org/10.3390/math8061039
Chicago/Turabian StyleLiu, Jiawei, Wen-An Yong, Jianxin Liu, and Zhenwei Guo. 2020. "Stable Finite-Difference Methods for Elastic Wave Modeling with Characteristic Boundary Conditions" Mathematics 8, no. 6: 1039. https://doi.org/10.3390/math8061039
APA StyleLiu, J., Yong, W.-A., Liu, J., & Guo, Z. (2020). Stable Finite-Difference Methods for Elastic Wave Modeling with Characteristic Boundary Conditions. Mathematics, 8(6), 1039. https://doi.org/10.3390/math8061039