Group Invariant Solutions and Conserved Quantities of a (3+1)-Dimensional Generalized Kadomtsev–Petviashvili Equation
Abstract
1. Introduction
2. Exact Solutions of the (3+1)-D gKPe
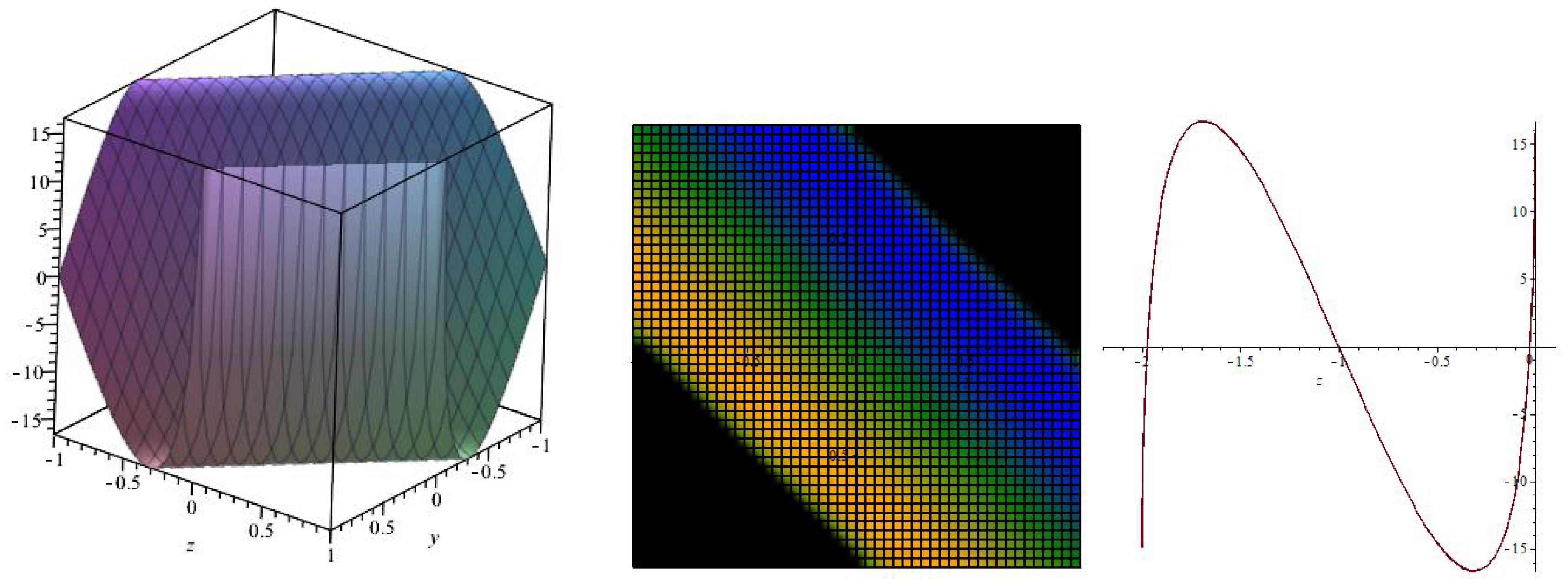
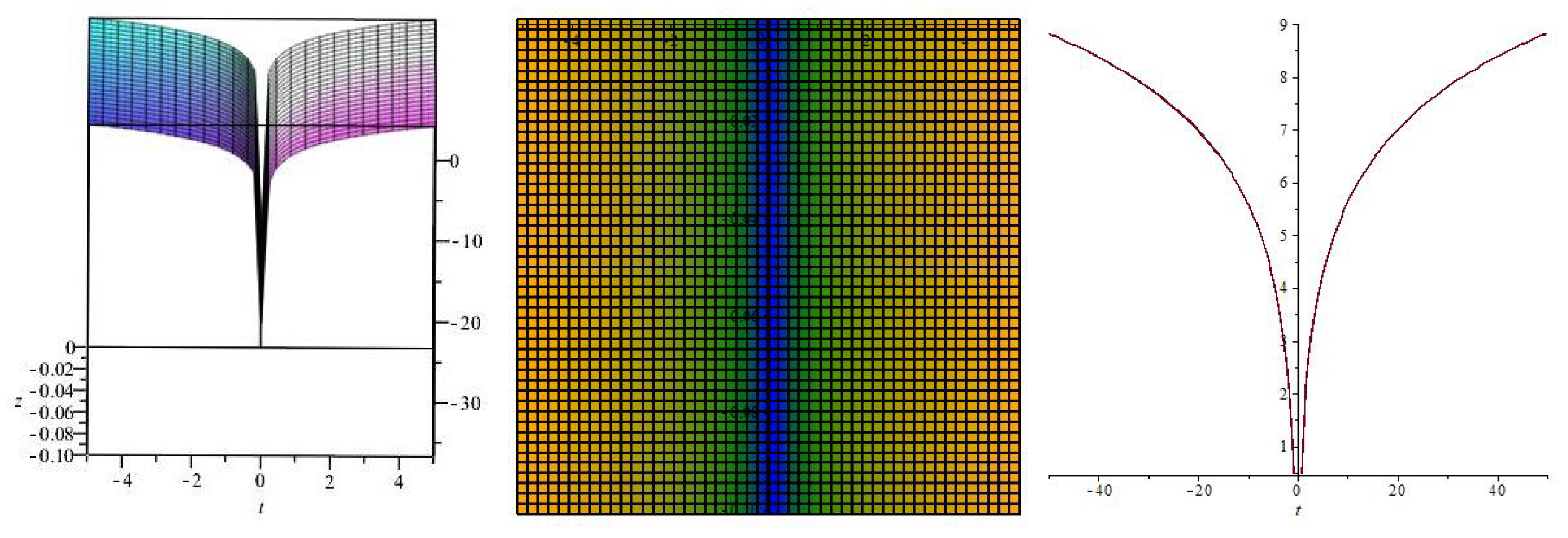
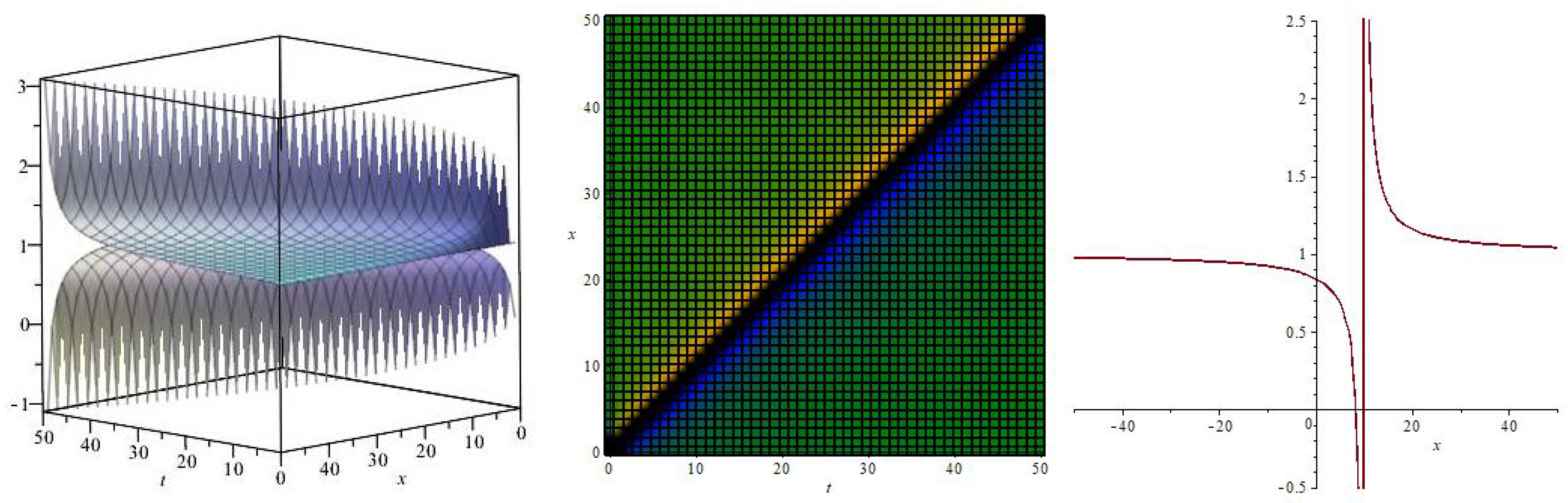
2.1. Invariant Solutions under the Symmetries , ⋯,
2.2. Invariant Solution under the Symmetry
2.3. Invariant Solution under the Symmetry
3. Conserved Quantities of the (3+1)-D gKPe
3.1. Multiplier Approach
3.1.1. Preliminaries
3.1.2. Application of the Method
3.2. Ibragimov’s Approach
3.2.1. Preliminaries
3.2.2. Application of the Method
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Prolongation Coefficients: Full Expansions
References
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Ibragimov, N.H. CRC Handbook of Lie Group Analysis of Differential Equations; CRC Press: Boca Raton, FL, USA, 1994; Volume 1. [Google Scholar]
- Stephani, H. Differential Equations: Their Solution Using Symmetries; Cambridge University Press: New York, NY, USA, 1989. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations, 2nd ed.; Springer: Berlin, Germany, 1993. [Google Scholar]
- Hydon, P.E. Symmetry Methods for Differential Equations; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Zhou, Y.; Wang, M.; Li, Z. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 1996, 216, 67–75. [Google Scholar]
- Hu, J.; Zhang, H. A new method for finding exact traveling wave solutions to nonlinear partial differential equations. Phys. Lett. A 2001, 286, 175–179. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Wang, M.; Li, X.; Zhang, J. The (G′/G)-expansion method and travelling wave solutions for linear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Khalique, C.M.; Moleleki, L.D. A (3+1)-dimensional generalized BKP-Boussinesq equation: Lie group approach. Results Phys. 2019, 13, 102239. [Google Scholar] [CrossRef]
- Kudryashov, N.A. One method for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2248–2253. [Google Scholar] [CrossRef]
- Motsepa, T.; Khalique, C.M. Closed-form solutions and conserved vectors of the (3+1)-dimensional negative-order KdV equation. Adv. Math. Model. Appl. 2020, 5, 7–18. [Google Scholar]
- Kudryashov, N.A. Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos Soliton Fract. 2005, 24, 1217–1231. [Google Scholar] [CrossRef]
- Simbanefayi, I.; Khalique, C.M. Travelling wave solutions and conservation laws for the Korteweg-de Vries-Benjamin-Bona-Mahony equation. Results Phys. 2018, 8, 57–63. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, M.; Wang, Y. Periodic wave solutions to a coupled KdV equations with variable coefficients. Phys. Lett. A 2003, 308, 31–36. [Google Scholar] [CrossRef]
- Zhang, L.; Khalique, C.M. Classification and bifurcation of a class of second-order ODEs and its application to nonlinear PDEs. Discret. Contin. Dynam. Syst. S 2018, 11, 777–790. [Google Scholar] [CrossRef]
- Ma, W.X. Comment on the (3+1)-dimensional Kadomtsev–Petviashvili equations. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2663–2666. [Google Scholar] [CrossRef]
- Kadomtsev, B.B.; Petviashvili, V.I. On the stability of solitary waves in weakly dispersing media. Sov. Phys. Dokl. 1970, 192, 753–756. [Google Scholar]
- You, F.; Xia, T.; Chen, D. Decomposition of the generalized KP, cKP and mKP and their exact solutions. Phys. Lett. A 2008, 372, 3184–3194. [Google Scholar] [CrossRef]
- Kuznetsov, E.A.; Turitsyn, S.K. Two- and three-dimensional solitons in weakly dispersive media. Zh. Ebp. Teor. Fa. 1982, 82, 1457–1463. [Google Scholar]
- Ablowitz, M.J.; Segur, H. On the evolution of packets of water waves. J. Fluid Mech. 1979, 92, 691–715. [Google Scholar] [CrossRef]
- Infeld, E.; Rowlands, G. Three-dimensional stability of Korteweg–de Vries waves and solitons II. Acta Phys. Pol. A 1979, 56, 329–332. [Google Scholar]
- Senatorski, A.; Infeld, E. Simulations of two-dimensional Kadomtsev–Petviashvili soliton dynamics in three-dimensional space. Phys. Rev. Lett. 1996, 77, 2855–2858. [Google Scholar] [CrossRef]
- Alagesan, T.; Uthayakumar, A.; Porsezian, K. Painlevé analysis and Bäcklund transformation for a three-dimensional Kadomtsev–Petviashvili equation. Chaos Soliton Fract. 1997, 8, 893–895. [Google Scholar] [CrossRef]
- Xu, G.; Li, Z. Symbolic computation of the Painlevé test for nonlinear partial differential equations using Maple. Comput. Phys. Commun. 2004, 161, 65–75. [Google Scholar] [CrossRef]
- Ma, W.X.; Fan, E. Linear superposition principle applying to Hirota bilinear equations. Comput. Math. Appl. 2011, 61, 950–959. [Google Scholar] [CrossRef]
- Ma, W.X.; Abdeljabbar, A.; Asaad, M.G. Wronskian and Grammian solutions to a (3+1)-dimensional generalized KP equation. Appl. Math. Comput. 2011, 217, 10016–10023. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Multiple-soliton solutions for a (3 +1)-dimensional generalized KP equation, Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 491–495. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; El-Tantawy, S.A. A new (3+1)-dimensional generalized Kadomtsev–Petviashvili equation. Nonlinear Dyn. 2016, 84, 1107–1112. [Google Scholar] [CrossRef]
- Liu, J.G.; Tian, Y.; Zeng, Z.F. New exact periodic solitary-wave solutions for the new (3+1)-dimensional generalized Kadomtsev–Petviashvili equation in multi-temperature electron plasmas. AIP Adv. 2017, 7, 2158–3226. [Google Scholar] [CrossRef]
- Noether, E. Invariante variationsprobleme. Nachr. VD Ges. D. Wiss. Göttingen 1918, 2, 235–257. [Google Scholar]
- Bessel-Hagen, E. Uber die Erhaltungsatze der Elektrodynamik. Math. Ann. 1921, 84, 258–276. [Google Scholar] [CrossRef]
- Bluman, G.W.; Cheviakov, A.F.; Anco, S.C. Applications of Symmetry Methods to Partial Differential Equations; Springer: New York, NY, USA, 2010. [Google Scholar]
- Leveque, R.J. Numerical Methods for Conservation Laws, 2nd ed.; Birkhäuser-Verlag: Basel, Switzerland, 1992. [Google Scholar]
- Sarlet, W. Comment on ‘Conservation laws of higher order nonlinear PDEs and the variational conservation laws in the class with mixed derivatives’. J. Phys. A Math. Theor. 2010, 43, 458001. [Google Scholar] [CrossRef]
- Anco, S.C. Generalization of Noether’s Theorem in Modern Form to Non-variational Partial Differential Equations. In Recent Progress and Modern Challenges in Applied Mathematics, Modeling and Computational Science; Melnik, R., Makarov, R., Belair, J., Eds.; Fields Institute Communications, Springer: New York, NY, USA, 2017; Volume 79. [Google Scholar]
- Johnpillai, A.G.; Khalique, C.M.; Mahomed, F.M. Travelling wave group-invariant solutions and conservation laws for θ-equation. Malays. J. Math. Sci. 2019, 13, 13–29. [Google Scholar]
- Motsepa, T.; Abudiab, M.; Khalique, C.M. A Study of an extended generalized (2+1)-dimensional Jaulent-Miodek equation. Int. J. Nonlin. Sci. Numer. Simul. 2018, 19, 391–395. [Google Scholar] [CrossRef]
- Khalique, C.M.; Abdallah, S.A. Coupled Burgers equations governing polydispersive sedimentation: A Lie symmetry approach. Results Phys. 2020, 16, 102967. [Google Scholar] [CrossRef]
- Bruzón, M.S.; Gandarias, M.L. Traveling wave solutions of the K(m, n) equation with generalized evolution. Math. Meth. Appl. Sci. 2018, 41, 5851–5857. [Google Scholar] [CrossRef]
- Khalique, C.M.; Adeyemo, O.D. A study of (3+1)-dimensional generalized Korteweg-de Vries-Zakharov- Kuznetsov equation via Lie symmetry approach. Results Phys. 2020, in press. [Google Scholar]
- Ibragimov, N.H. Integrating factors, adjoint equations and Lagrangians. J. Math. Anal. Appl. 2006, 318, 742–757. [Google Scholar] [CrossRef]
- Ibragimov, N.H. A new conservation theorem. J. Math. Anal. Appl. 2007, 333, 311–328. [Google Scholar] [CrossRef]
- Cheviakov, A.F. Computation of fluxes of conservation laws. J. Eng. Math. 2010, 66, 153–173. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Exact soliton and kink solutions for new (3+1)-dimensional nonlinear modified equations of wave propagation. Open Eng. 2017, 7, 169–174. [Google Scholar] [CrossRef]
- Baumann, G. Symmetry Analysis of Differential Equations with Mathematica®; Springer: New York, NY, USA, 2000. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Billingham, J.; King, A.C. Wave Motion; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Phil Mag. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Drazin, P.G.; Johnson, R.S. Soliton: An Introduction; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simbanefayi, I.; Khalique, C.M. Group Invariant Solutions and Conserved Quantities of a (3+1)-Dimensional Generalized Kadomtsev–Petviashvili Equation. Mathematics 2020, 8, 1012. https://doi.org/10.3390/math8061012
Simbanefayi I, Khalique CM. Group Invariant Solutions and Conserved Quantities of a (3+1)-Dimensional Generalized Kadomtsev–Petviashvili Equation. Mathematics. 2020; 8(6):1012. https://doi.org/10.3390/math8061012
Chicago/Turabian StyleSimbanefayi, Innocent, and Chaudry Masood Khalique. 2020. "Group Invariant Solutions and Conserved Quantities of a (3+1)-Dimensional Generalized Kadomtsev–Petviashvili Equation" Mathematics 8, no. 6: 1012. https://doi.org/10.3390/math8061012
APA StyleSimbanefayi, I., & Khalique, C. M. (2020). Group Invariant Solutions and Conserved Quantities of a (3+1)-Dimensional Generalized Kadomtsev–Petviashvili Equation. Mathematics, 8(6), 1012. https://doi.org/10.3390/math8061012





