Revealing Spectrum Features of Stochastic Neuron Spike Trains
Abstract
1. Introduction
2. Model and Methods
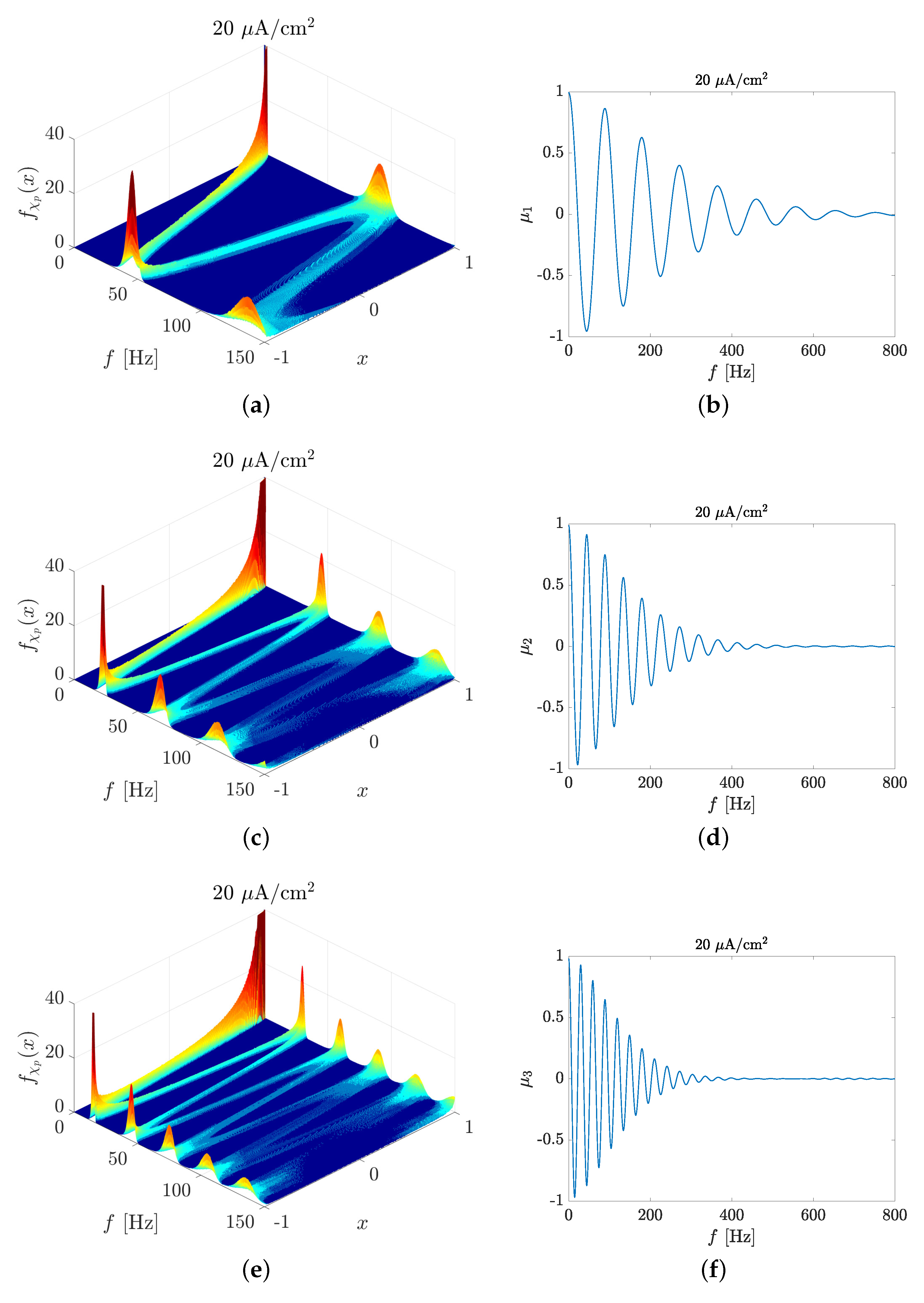
2.1. Spike Train PSD Model
2.2. Test Data
3. Results
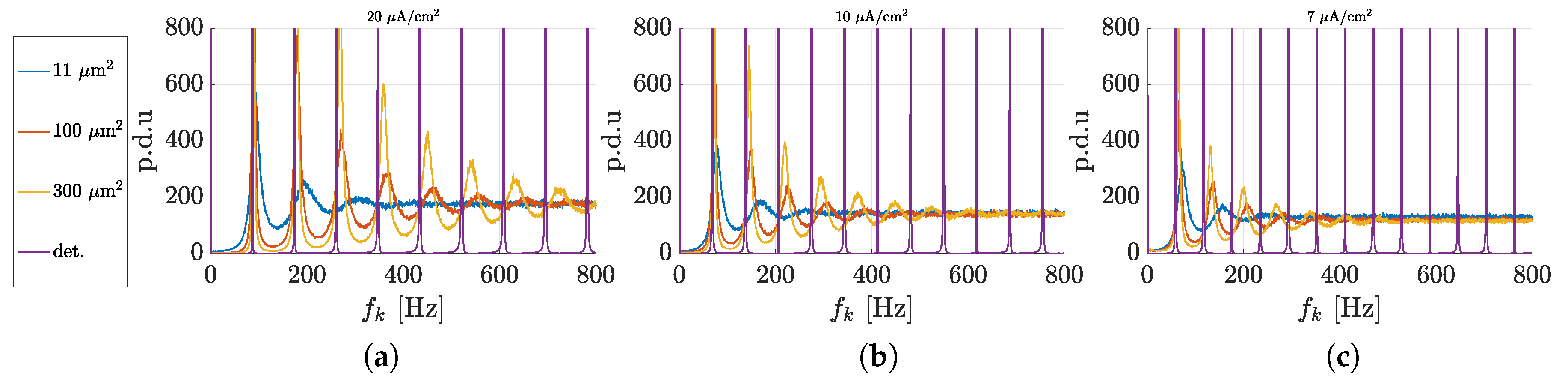
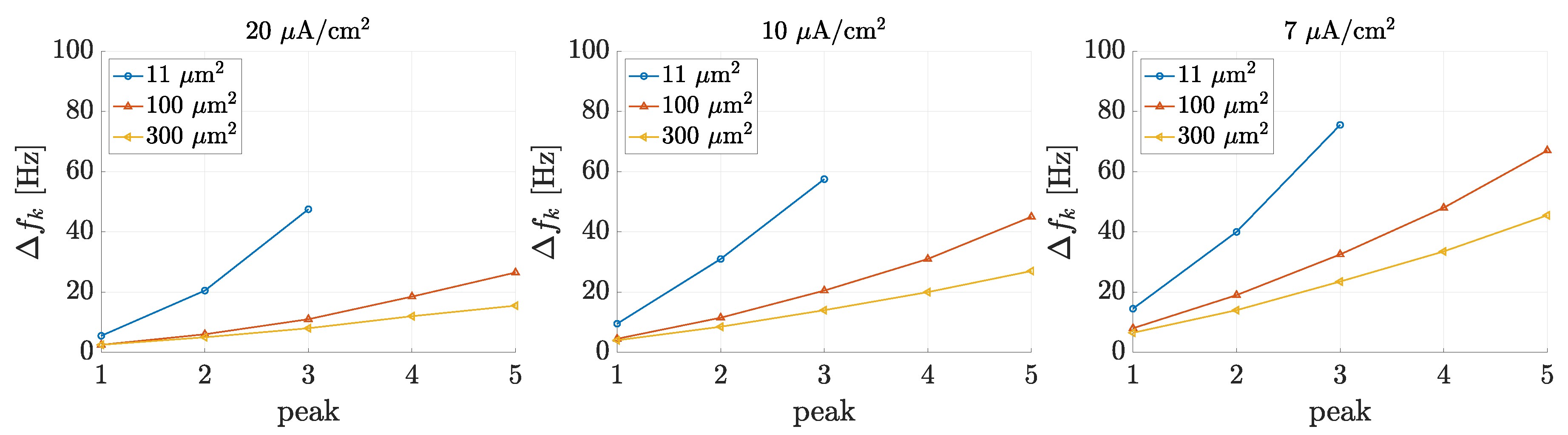
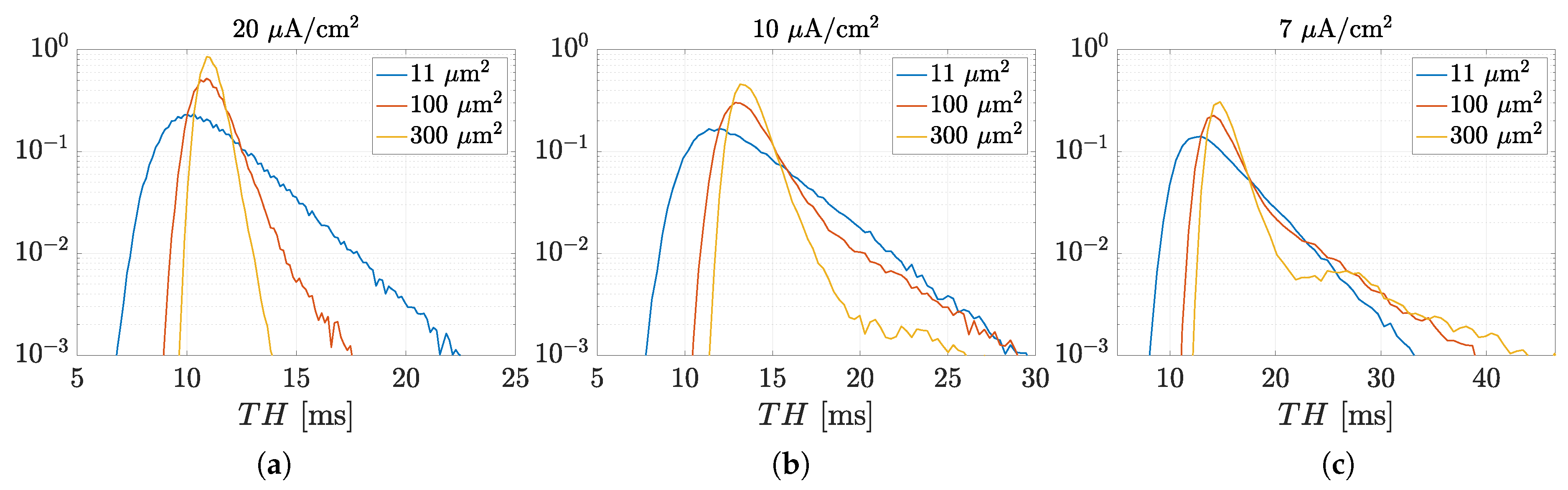
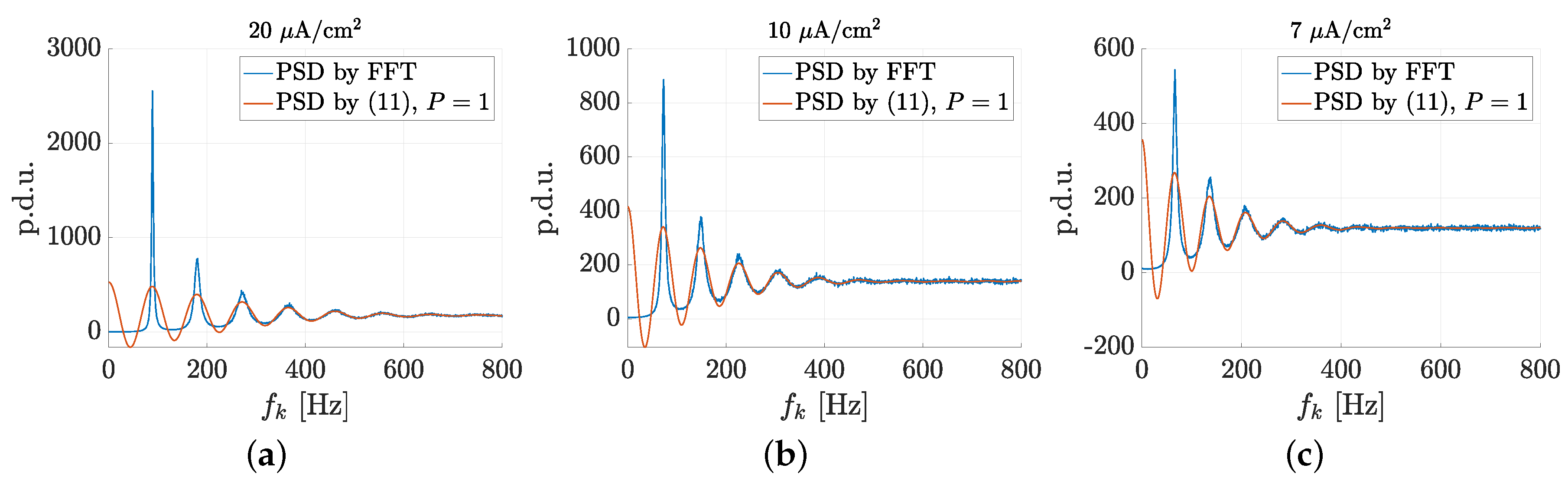
3.1. Spectral Features of Stochastic Neuron Spike Trains
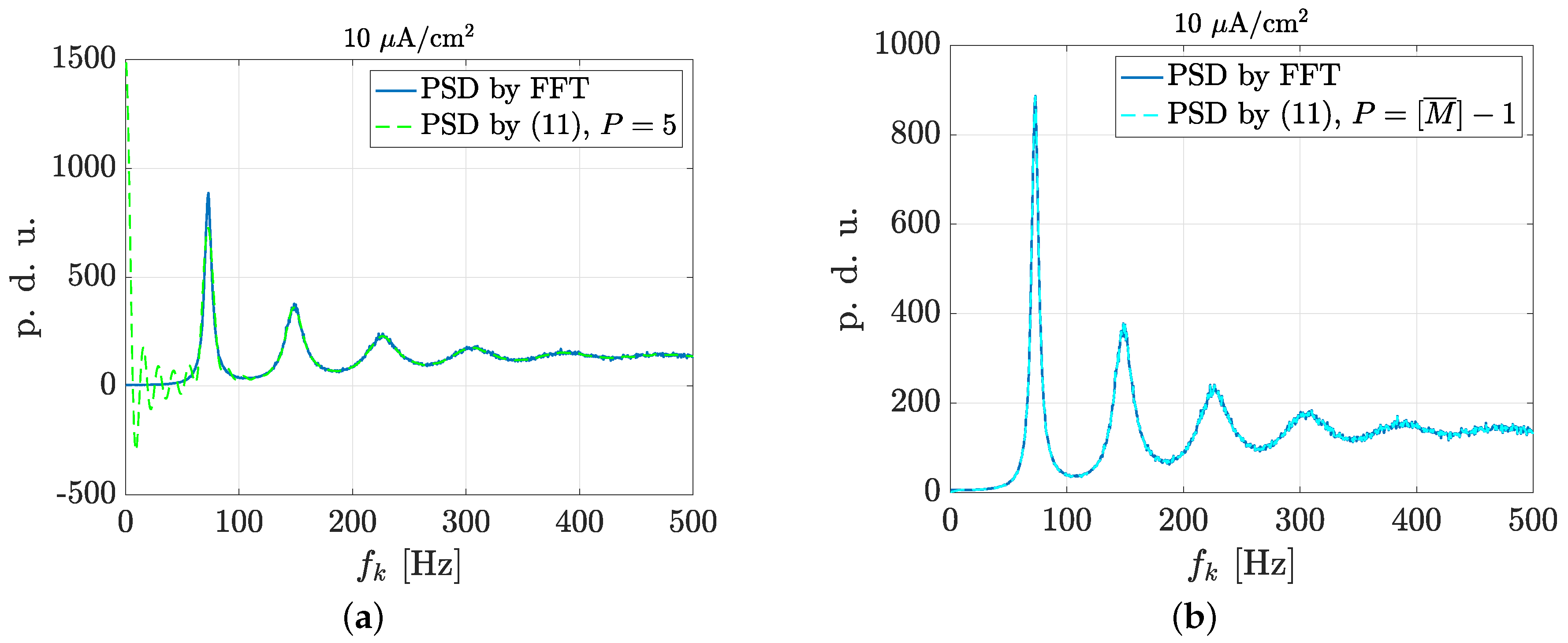
3.2. Estimation of Neuronal Spectral Features
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Johnson, D.H. Point process models of single-neuron discharges. J. Comput. Neurosci. 1996, 3, 275–299. [Google Scholar] [CrossRef]
- Mino, H. The Effects of Spontaneous Random Activity on Information Transmission in an Auditory Brain Stem Neuron Model. Entropy 2014, 16, 6654–6666. [Google Scholar] [CrossRef]
- Rinzel, J.; Ermentrout, B. Analysis of neural excitability and oscillations. In Methods in Neuronal Modeling: From Ions to Networks, 2nd ed.; Koch, C., Segev, I., Eds.; MIT Press: Cambridge, MA, USA, 1998; Chapter 7. [Google Scholar]
- Gammaitoni, L.; Hänggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 1998, 70, 223–287. [Google Scholar] [CrossRef]
- Moss, F. Stochastic resonance and sensory information processing: A tutorial and review of application. Clin. Neurophysiol. 2004, 115, 267–281. [Google Scholar] [CrossRef]
- Mino, H.; Durand, D.M. Enhancement of information transmission of sub-threshold signals applied to distal positions of dendritic trees in hippocampal CA1 neuron models with stochastic resonance. Biol. Cybern. 2010, 103, 227–236. [Google Scholar] [CrossRef] [PubMed]
- Bensaid, S.; Modolo, J.; Merlet, I.; Wendling, F.; Benquet, P. COALIA: A Computational Model of Human EEG for Consciousness Research. Front. Syst. Neurosci. 2019, 13. [Google Scholar] [CrossRef] [PubMed]
- Modolo, J.; Legros, A.; Beuter, A. The next move in neuromodulation therapy: A question of timing. Front. Comput. Neurosci. 2015, 8. [Google Scholar] [CrossRef]
- Modolo, J.; Legros, A.; Thomas, A.W.; Beuter, A. Model-driven therapeutic treatment of neurological disorders: Reshaping brain rhythms with neuromodulation. Interface Focus 2011, 1, 61–74. [Google Scholar] [CrossRef]
- Engel, A.K.; Fries, P.; Singer, W. Dynamic predictions: Oscillations and synchrony in top-down processing. Nat. Rev. Neurosci. 2001, 2, 704–716. [Google Scholar] [CrossRef]
- Hutchison, W.D.; Dostrovsky, J.O.; Walters, J.R.; Courtemanche, R.; Boraud, T.; Goldberg, J.; Brown, P. Neuronal oscillations in the basal ganglia and movement disorders: Evidence from whole animal and human recordings. J. Neurosci. Off. J. Soc. Neurosci. 2004, 24, 9240–9243. [Google Scholar] [CrossRef]
- Buzsáki, G.; Draguhn, A. Neuronal oscillations in cortical networks. Science 2004, 304, 1926–1929. [Google Scholar] [CrossRef] [PubMed]
- Czanner, G.; Sarma, S.V.; Ba, D.; Eden, U.T.; Wu, W.; Eskandar, E.; Lim, H.H.; Temereanca, S.; Suzuki, W.A.; Brown, E.N. Measuring the signal-to-noise ratio of a neuron. Proc. Natl. Acad. Sci. USA 2015, 112, 7141–7146. [Google Scholar] [CrossRef] [PubMed]
- Gray, C.M.; Singer, W. Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc. Natl. Acad. Sci. USA 1989, 86, 1698–1702. [Google Scholar] [CrossRef] [PubMed]
- Buzsáki, G. Rhythms of the Brain; Oxford University Press: Oxford, UK, 2006. [Google Scholar] [CrossRef]
- Jarvis, M.R.; Mitra, P.P. Sampling properties of the spectrum and coherency of sequences of action potentials. Neural Comput. 2001, 13, 717–749. [Google Scholar] [CrossRef]
- Moran, A.; Bar-Gad, I. Revealing neuronal functional organization through the relation between multi-scale oscillatory extracellular signals. J. Neurosci. Methods 2010. [Google Scholar] [CrossRef] [PubMed]
- Andres, D.S.; Cerquetti, D.F.; Merello, M. Turbulence in Globus pallidum neurons in patients with Parkinson’s disease: Exponential decay of the power spectrum. J. Neurosci. Methods 2011, 197, 14–20. [Google Scholar] [CrossRef] [PubMed]
- Mazzoni, A.; Broccard, F.D.; Garcia-Perez, E.; Bonifazi, P.; Ruaro, M.E.; Torre, V. On the Dynamics of the Spontaneous Activity in Neuronal Networks. PLoS ONE 2007, 2, e439. [Google Scholar] [CrossRef]
- Bédard, C.; Kröger, H.; Destexhe, A. Does the 1/f Frequency Scaling of Brain Signals Reflect Self-Organized Critical States? Phys. Rev. Lett. 2006, 97, 118102. [Google Scholar] [CrossRef]
- Mitaim, S.; Kosko, B. Adaptive stochastic resonance. Proc. IEEE 1998. [Google Scholar] [CrossRef]
- Paffi, A.; Camera, F.; Apollonio, F.; D’Inzeo, G.; Liberti, M. Restoring the encoding properties of a stochastic neuron model by an exogenous noise. Front. Comput. Neurosci. 2015, 9, 1–11. [Google Scholar] [CrossRef][Green Version]
- Orcioni, S.; Paffi, A.; Camera, F.; Apollonio, F.; Liberti, M. Automatic decoding of input sinusoidal signal in a neuron model: Improved SNR spectrum by low-pass homomorphic filtering. Neurocomputing 2017, 267, 605–614. [Google Scholar] [CrossRef]
- Lindner, B.; Schimansky-Geier, L.; Longtin, A. Maximizing spike train coherence or incoherence in the leaky integrate-and-fire model. Phys. Rev. E 2002, 66, 031916. [Google Scholar] [CrossRef] [PubMed]
- Droste, F.; Lindner, B. Exact results for power spectrum and susceptibility of a leaky integrate-and-fire neuron with two-state noise. Phys. Rev. E 2017, 95, 012411. [Google Scholar] [CrossRef]
- Ozer, M.; Perc, M.; Uzuntarla, M.; Koklukaya, E. Weak signal propagation through noisy feedforward neuronal networks. NeuroReport 2010, 21, 338–343. [Google Scholar] [CrossRef] [PubMed]
- Paffi, A.; Apollonio, F.; D’Inzeo, G.; Liberti, M. Stochastic resonance induced by exogenous noise in a model of a neuronal network. Netw. Comput. Neural Syst. 2013, 24, 99–113. [Google Scholar] [CrossRef] [PubMed]
- Goychuk, I.; Hänggi, P. Nonstationary stochastic resonance viewed through the lens of information theory. Eur. Phys. J. B 2009, 69, 29–35. [Google Scholar] [CrossRef]
- Wiesenfeld, K.; Jaramillo, F. Minireview of stochastic resonance. Chaos Interdiscip. J. Nonlinear Sci. 1998, 8, 539–548. [Google Scholar] [CrossRef]
- Voronenko, S.O.; Stannat, W.; Lindner, B. Shifting Spike Times or Adding and Deleting Spikes—How Different Types of Noise Shape Signal Transmission in Neural Populations. J. Math. Neurosci. 2015, 5, 1. [Google Scholar] [CrossRef][Green Version]
- Orcioni, S.; Paffi, A.; Camera, F.; Apollonio, F.; Liberti, M. Automatic decoding of input sinusoidal signal in a neuron model: High pass homomorphic filtering. Neurocomputing 2018, 292, 165–173. [Google Scholar] [CrossRef]
- Biagetti, G.; Crippa, P.; Orcioni, S.; Turchetti, C. Homomorphic Deconvolution for MUAP Estimation From Surface EMG Signals. IEEE J. Biomed. Health Informatics 2017, 21, 328–338. [Google Scholar] [CrossRef]
- Abbott, L. Lapicque’s introduction of the integrate-and-fire model neuron (1907). Brain Res. Bull. 1999, 50, 303–304. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Mainen, Z.; Sejnowski, T. Reliability of spike timing in neocortical neurons. Science 1995, 268, 1503–1506. [Google Scholar] [CrossRef] [PubMed]
- Halliday, D.M.; Rosenberg, J.R. Time and Frequency Domain Analysis of Spike Train and Time Series Data. In Modern Techniques in Neuroscience Research; Windhorst, U., Johansson, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 503–543. [Google Scholar]
- Brillinger, D.R. Comparative aspects of the study of ordinary time series and of point processes. In Developments in Statistics; Krishnaiah, P.R., Ed.; Academic Press: Cambridge, MA, USA, 1978; pp. 33–133. [Google Scholar]
- Wald, A. Some Generalizations of the Theory of Cumulative Sums of Random Variables. Ann. Math. Stat. 1945, 16, 287–293. [Google Scholar] [CrossRef]
- Rubinstein, J. Threshold fluctuations in an N sodium channel model of the node of Ranvier. Biophys. J. 1995, 68, 779–785. [Google Scholar] [CrossRef]
- Mino, H.; Rubinstein, J.T.; White, J.A. Comparison of Algorithms for the Simulation of Action Potentials with Stochastic Sodium Channels. Ann. Biomed. Eng. 2002, 30, 578–587. [Google Scholar] [CrossRef] [PubMed]
- James, F. Monte Carlo theory and practice. Rep. Prog. Phys. 1980, 43, 1145–1189. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Dynamical Systems in Neuroscience; The MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Schneidman, E.; Freedman, B.; Segev, I. Ion Channel Stochasticity May Be Critical in Determining the Reliability and Precision of Spike Timing. Neural Comput. 1998, 10, 1679–1703. [Google Scholar] [CrossRef]
- White, J.A.; Rubinstein, J.T.; Kay, A.R. Channel noise in neurons. Trends Neurosci. 2000, 23, 131–137. [Google Scholar] [CrossRef]
- Ostrovskii, V.Y.; Karimov, T.I.; Solomevich, E.P.; Kolev, G.Y.; Butusov, D.N. Numerical Effects in Computer Simulation of Simplified Hodgkin-huxley Model. In Proceedings of the 24th International Conference on Oral and Maxillofacial Surgery, ICoMS’19, Rio de Janeiro, Brazil, 21–24 May 2019; ACM Press: New York, NY, USA, 2019; pp. 92–95. [Google Scholar] [CrossRef]
- Rowat, P.F.; Greenwood, P.E. The ISI distribution of the stochastic Hodgkin-Huxley neuron. Front. Comput. Neurosci. 2014, 8, 111. [Google Scholar] [CrossRef][Green Version]
- Kostal, L.; Lansky, P.; Stiber, M. Statistics of inverse interspike intervals: The instantaneous firing rate revisited. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 106305. [Google Scholar] [CrossRef]
- Dummer, B.; Wieland, S.; Lindner, B. Self-consistent determination of the spike-train power spectrum in a neural network with sparse connectivity. Front. Comput. Neurosci. 2014, 8. [Google Scholar] [CrossRef] [PubMed]
- Matzner, A.; Bar-Gad, I. Quantifying Spike Train Oscillations: Biases, Distortions and Solutions. PLoS Comput. Biol. 2015, 11, e1004252. [Google Scholar] [CrossRef] [PubMed]
| Current Density | Patch | ||||
|---|---|---|---|---|---|
| [A/cm] | [m] | [Hz] | [Hz] | [Hz] | [Hz] |
| 11 | 92.5 | 90.5 | 87.9 | 96.2 | |
| 20 | 100 | 89.5 | 88.5 | 88.6 | 91.0 |
| 300 | 89.5 | 89 | 89.3 | 91.0 | |
| 11 | 78 | 76.5 | 72.1 | 82.5 | |
| 10 | 100 | 73 | 72 | 69.6 | 76.9 |
| 300 | 72.5 | 72 | 70.7 | 75.2 | |
| 11 | 73 | 71 | 65.4 | 75.4 | |
| 7 | 100 | 66.5 | 65.5 | 59.8 | 69.2 |
| 300 | 65 | 64.5 | 57.9 | 66.4 |
| Peaks | 1 | 2 | 3 | 4 | 5 | ||
|---|---|---|---|---|---|---|---|
| Current Density | Patch | Error | Mean Abs | ||||
| [A/cm] | [m] | [Hz] | Error [Hz] | ||||
| 11 | 2 | 0 | 2.5 | 1.5 | |||
| 20 | 100 | 1 | 1 | 0.5 | 1 | 1 | 0.9 |
| 300 | 0.5 | 0.5 | 0.5 | 1 | 0.5 | 0.6 | |
| 11 | 1.5 | 0.5 | −1.5 | 1.17 | |||
| 10 | 100 | 1 | 1.5 | 1 | 0 | 1.5 | 1.0 |
| 300 | 0.5 | 1.5 | 1.0 | 0.5 | 0.5 | 0.8 | |
| 11 | 2 | 1.0 | 1.5 | 1.5 | |||
| 7 | 100 | 1.0 | 1.0 | 0.5 | 0 | 1.5 | 0.8 |
| 300 | 0.5 | 1.0 | 1.0 | 0.5 | 0.5 | 0.7 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orcioni, S.; Paffi, A.; Apollonio, F.; Liberti, M. Revealing Spectrum Features of Stochastic Neuron Spike Trains. Mathematics 2020, 8, 1011. https://doi.org/10.3390/math8061011
Orcioni S, Paffi A, Apollonio F, Liberti M. Revealing Spectrum Features of Stochastic Neuron Spike Trains. Mathematics. 2020; 8(6):1011. https://doi.org/10.3390/math8061011
Chicago/Turabian StyleOrcioni, Simone, Alessandra Paffi, Francesca Apollonio, and Micaela Liberti. 2020. "Revealing Spectrum Features of Stochastic Neuron Spike Trains" Mathematics 8, no. 6: 1011. https://doi.org/10.3390/math8061011
APA StyleOrcioni, S., Paffi, A., Apollonio, F., & Liberti, M. (2020). Revealing Spectrum Features of Stochastic Neuron Spike Trains. Mathematics, 8(6), 1011. https://doi.org/10.3390/math8061011







