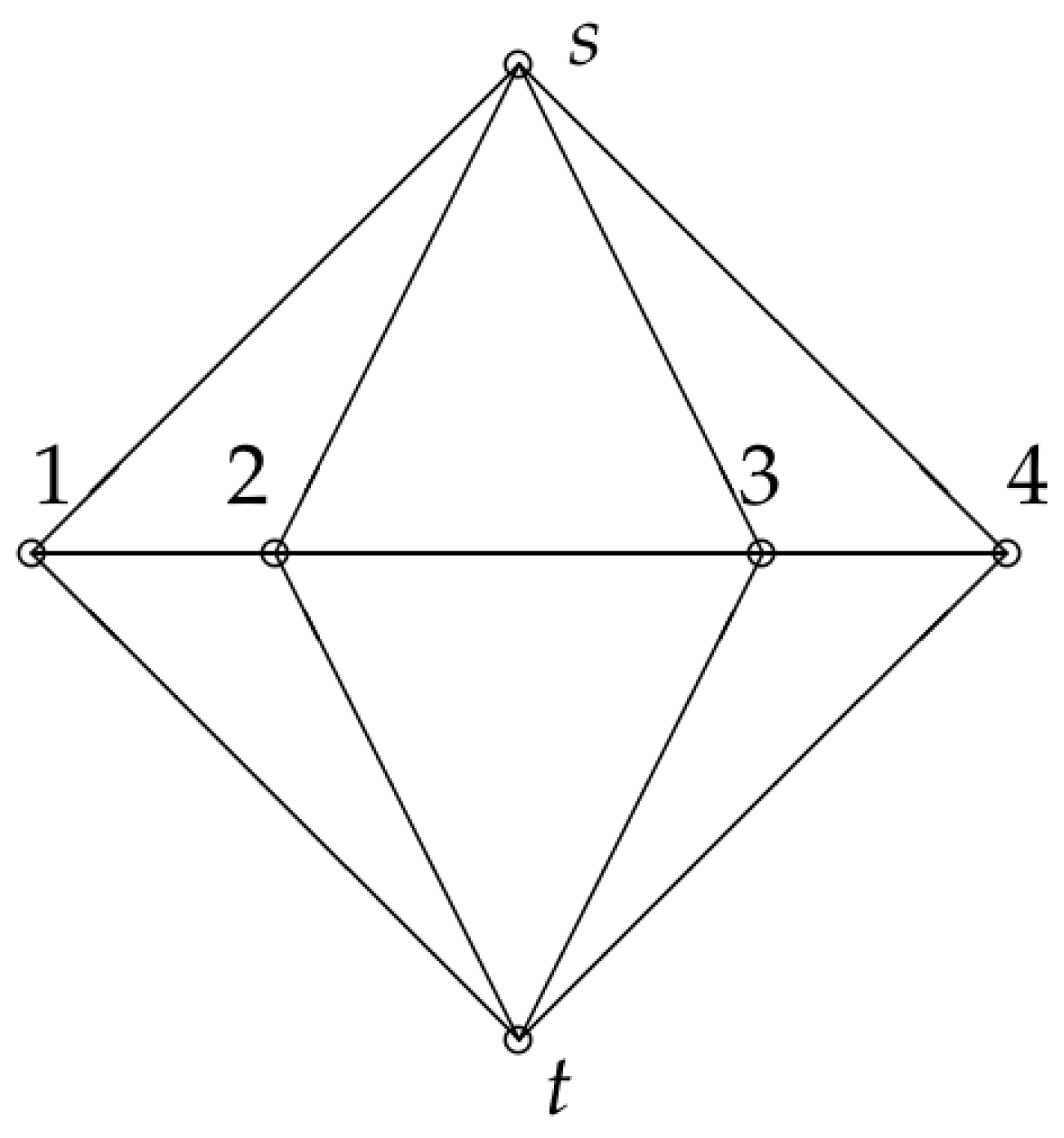
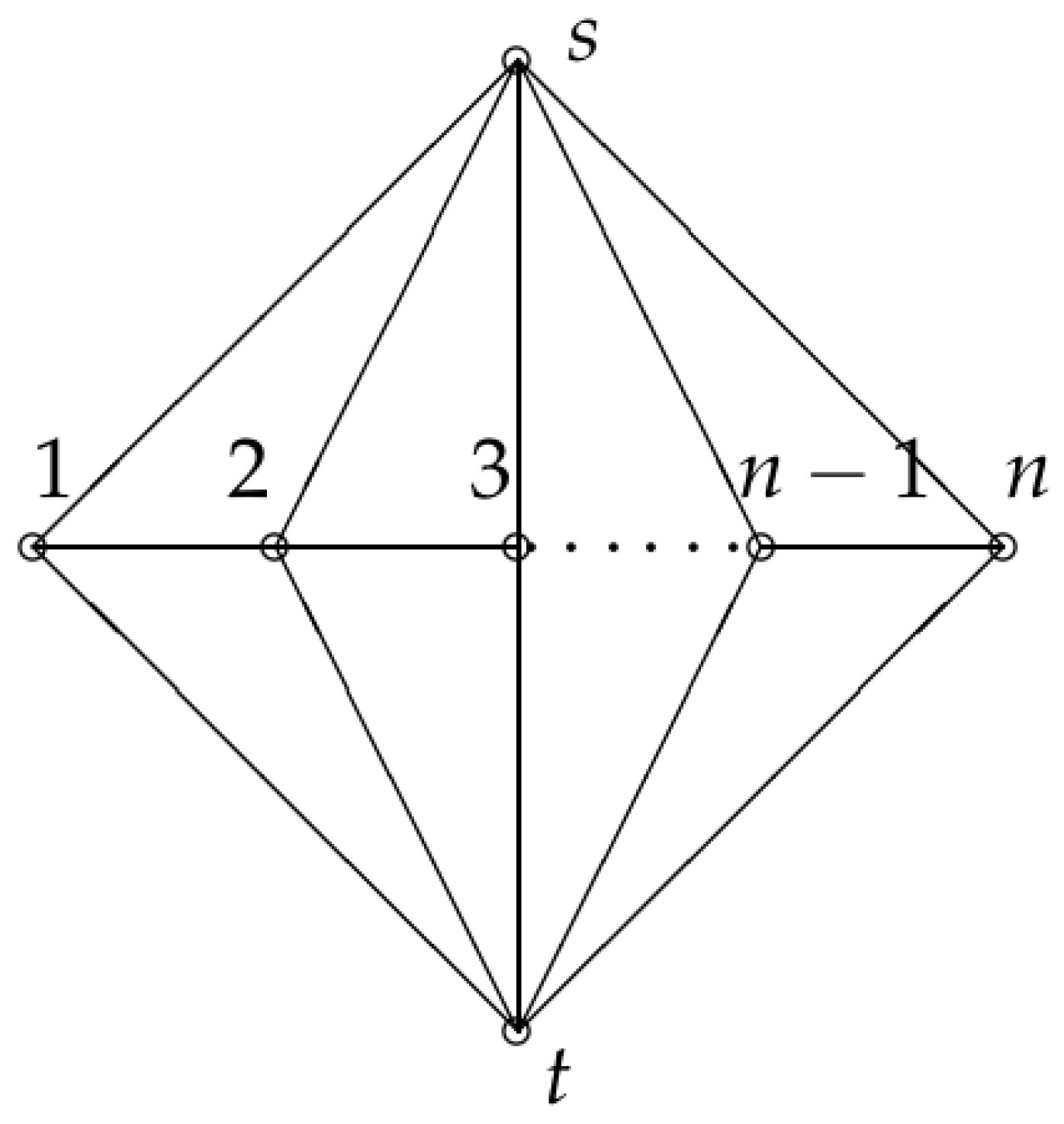
3. Endomorphism Spectra of Double Fan Graphs
Let
be a double fan graph as shown in
Figure 2 and
. Denote by
the subset of
A containing all the odd numbers and by
the subset of
A containing all the even numbers.
Lemma 1. ([16]) Let X be a graph and . Then if and only if is an induced subgraph of X. Lemma 2. Let . Then , or .
(1) If , then .
(2) If for some , then , or , or .
(3) If and for some , then , or .
Proof. (1) Let and . Then . Since the subgraph of induced by A is , .
(2) If , there are three cases:
Case 1. for some . Since s and t are adjacent to all vertices of A, and are adjacent to all vertices of . Note that i is adjacent to at most 4 vertices. If , then . If , then . If , then .
Case 2. and for some . Since s and t are adjacent to all vertices of A, i and j are adjacent to all vertices of . Thus . If has two vertices, then . If has three vertices, then . Thus (3) is proved.
Case 3. and . Without loss of generalization, suppose that for some and . Since t is adjacent to all vertices of A and , . Now has two adjacent vertices and . As s is adjacent to all vertices of A, i is adjacent to all vertices of . In particular, i is adjacent to and . Thus the subgraph of induced by is isomorphic to . This is impossible since the subgraph of induced by A is a path. □
Lemma 3. Let be a double fan graph. Then if and only if .
Proof. Necessity. We only need to prove that
for any
. Define a mapping
f on
by
Then and . Note that , and for any and . Then .
Sufficiency. If , there are only two vertices s and t which are not adjacent in . Let . Then . Note that . Then . If , then there are two pairs of vertices in , which are not adjacent. They are 1 and 3, s and t. Let . If , then and , or and . Note that and . Thus . Therefore for . □
Lemma 4. Let be a double fan graph with , as shown in Figure 3. If n is odd, then ; If n is even, then . Proof. Let . By Lemma 2, or .
(1) Suppose that
. By Lemma 2 (1),
. Thus the number of endomorphisms of
such that
and
is equal to
. A similar argument will show that the number of endomorphisms is equal to
for the case of
and
,
and
. Hence there are
endomorphisms in this case. It is known from [
17] that
(2) Suppose that . By Lemma 2, there are three cases:
Case 1. Assume that . Then and . There are subgraphs in isomorphic to . Select a subgraph X of such that . Without loss of generality, let , where and . Since , or . At the same time, f can map to in two ways. Therefore there are endomorphisms in this case.
Case 2. Assume that . Then for some with , or for some and with and . There are three cases:
(i) Assume that and . If n is odd, then and . Now there are subgraphs in which are isomorphic to and there are ways to divide B into two non-empty subsets and . Clearly, there are two ways to map to and there are two ways to map to . Similarly, there are ways to divide C into two non-empty subsets and . Now there are two ways to map to and there are two ways to map to . Therefore, there are endomorphisms in this case. If n is even, a similar argument will show that there are endomorphisms.
(ii) Assume that and . Then there are endomorphism images. If n is odd, there are ways to divide B into two non-empty subsets and and there are ways to divide C into two non-empty subsets and . If , then there are two ways to map to . If , then there are two ways to map to . Therefore, there are endomorphisms in this case. If n is even, a similar argument will show that there are endomorphisms.
(iii) Assume that and for some and . Then and there are endomorphisms images. Note that and . Now there are two ways map to . Analogously for the case of and . Therefore, there are endomorphisms in this case.
Therefore, if and n is odd, then there are endomorphisms. If and n is even, then there are endomorphisms.
Case 3. Assume that . Then there are subgraphs in isomorphic to . Select a subgraph Z of such that . Then Z has three vertices in A. Suppose for some such that and . Then and , or and , or .
(i) If n is odd, then and . Note that there are ways to divide B into two non-empty subsets and and there are ways to divide C into two non-empty subsets and .
If , then there are ways to map the vertices in B to and there are ways to map vertices in C to , or there are ways to map the vertices in B to and there are ways to map the vertices in C to . Therefore, there are endomorphisms in this case.
If , and , then there are ways to map the vertices in B to . If , and , then there are ways to map vertices in C to . It is also analogous for the case of and . Therefore, there are endomorphisms in this case.
(ii) If n is even, then . Thus, there are ways to divide B into two non-empty subsets and and there are ways to divide C into two non-empty subsets and .
If , then there are endomorphisms. If and , then there are endomorphisms. Analogously for the case of and . Then there are endomorphisms.
Therefore, if and n is odd, then there are endomorphisms. If and n is even, then there are endomorphisms.
From the above discussion, we finish our proof. □
Lemma 5. Let be a double fan graph with . Then . If n is odd, then ; If n is even and , then , where and is the Fibonacci sequence.
Proof. Let . By Lemma 2, , or . If , then . It is easy to check that . If , then , or , or . If or , then is an induced subgraph, and so .
In the following, we assume that . Clearly, there are subgraphs in isomorphic to . Select a subgraph Y of such that . Without loss of generality, suppose for some such that and . Let such that , , and . Now f is not half-strong if and only if f maps to and maps to , or f maps to and maps to . There are three cases:
Case 1. Assume that . Then there are only one way to divide A into four non-empty subsets . It is easy to see that there are 2 ways to map to and there are 2 ways to map to . Similarly, there are 2 ways to map to and there are 2 ways to map to . Note that there are two subgraphs in isomorphic to . Thus there are 16 endomorphisms of which are not half-strong.
Case 2. Assume that n is odd. Then , where and is the Fibonacci sequence. It is easy to see that there are 2 ways to map to and there are 2 ways to map to . Similarly, there are 2 ways to map to and there are 2 ways to map to . Note that there are subgraphs in isomorphic to . Thus, there are endomorphisms of which are not half-strong in this case.
Case 3. Assume that n is even and . Then . Thus, there are endomorphisms of , which are not half-strong.
From the above discussion, we get the results of Lemma 5 to finish our proof. □
Lemma 6. Let be a double fan graph. Then if and only if .
Proof. Necessity. We only need to prove that
for any
. Define a mapping
f on
by
Then . It is not hard to show that , and . Note that . Then . Therefore, .
Sufficiency. If , then by the proof of Lemma 3. Therefore, for . □
Lemma 7. Let be such that . Then if and only if .
Proof. Necessity. Let be such that . Then . Let be such that . Since f is locally-strong, for every there exists such that and analogously for preimage of j. Note that and . Then .
Sufficiency. Let be such that . If , then . Clearly, s and t are adjacent to all vertices of . If , then . Now we have . Since , for every preimage there exists a preimage such that and analogously for preimage of j. Note that and . Then . □
Proof. Let
. Firstly, suppose that
. By Lemma 7,
if and only if
. It is known from [
18] that
. Now we have
and
, or
and
, or
, or
. Thus, we have
endomorphisms in this case.
Next, suppose that for some . By Lemma 2, , or , or . There are three cases.
Case 1. Assume that . Then and . The subgraphs of induced by , , have no isolated vertices. Then . There are endomorphisms of by Lemma 4.
Case 2. Assume that . Denote and . Then it is easy to see that if and only if n is odd and . Now for some such that , or for some and such that and . If , then there are endomorphism images. Note that there are two ways to map to and there are two ways to map to . Thus there are locally strong endomorphisms. If , then there are endomorphism images. Now and . Note that there are two ways to map to . Thus, there are locally strong endomorphisms. Therefore, there are locally strong endomorphisms in this case.
Case 3. Assume that . Then f is not locally strong.
Finally, suppose that and for some . By Lemma 2, , or .
(1) If , it is easy to check that . Note that the subgraphs of induced by , , , , have no isolated vertices. Then . By Lemma 4, There are endomorphisms in this case.
(2) If , then for any . Hence there are no locally endomorphisms in this case.
From the discussion above, we deduce Lemma 8 to finish our proof. □
Lemma 9. if and only if .
Proof. Necessity. We only need to show that
for any
. Define a mapping
f on
by
It is not difficult to show that . Therefore, .
Sufficiency. If , then by the proof of Lemma 3. If , then there exist only two positive integers 1 and 3 such that , . Let , then , or , or or . If , then . If , then . It is easy to check that . If or , it is a routine matter to check that . Therefore, we have . □
Lemma 10. if and only if .
Proof. Necessity. We show that
. Define a mapping
f on
by
It is easy to check that , and . Then .
Sufficiency. If , then by the proof of Lemma 3. In the following, we suppose that . Let .
(1) If , then . Since , . Note that and . Then there exists adjacent to every vertex of B. This is impossible since each vertex of A is adjacent to at most two vertices of A.
(2) If is not isomorphic to . Then contains at least 3 vertices. Since , there exist such that . Suppose there exist such that and . Then there exists a preimage of such that is adjacent to both i and j. Similarly, there exists such that is adjacent to both i and j. Thus forms a cycle . This is impossible since the subgraph of induced by A is a path. Suppose there exists only one vertex such that . Then there exists such that since . Now there exists such that is adjacent to both i and j, and there exists such that is adjacent to . Thus is adjacent to 3 vertices of A. This is a contradiction since each vertex of A is adjacent to at most 2 vertices in A. Consequently, for . □
Lemma 11. for any .
Proof. Define a mapping
f on
by
It is not hard to check that , but . Therefore, . □
Proof. Let . If , then and . So . If , then . Denote by Y the subgraph of induced by . Then . Thus . If , then . If and , then the number of automorphisms of is equal to the number of automorphisms of . It is 2. And analogously for and . Therefore . □
Lemma 13. If , then .
Proof. Assume . Let . Then there exist such that . Then . Thus , or . If , then . Analogously for . Hence, the number of strong endomorphisms of which are not automorphism is 4. By Lemma 12, . Therefore, . □
Now we obtain the main result in this paper.
Theorem 1. Let be a double fan graph. Thenwhere Proof. This follows immediately from Lemmas 4, 5, 7–12. □
Theorem 2. Let be a double fan graph. Then Proof. This follows directly from Lemmas 3, 5, 8–10. □