Linear Operators That Preserve Two Genera of a Graph

Abstract

If a graph can be embedded in a smooth orientable surface of genus g without edge crossings and can not be embedded on one of genus $g-1$ without edge crossings, then we say that the graph has genus g. We consider a mapping on the set of graphs with m vertices into itself. The mapping is called a linear operator if it preserves a union of graphs and it also preserves the empty graph. On the set of graphs with m vertices, we consider and investigate those linear operators which map graphs of genus g to graphs of genus g and graphs of genus $g+j$ to graphs of genus $g+j$ for $j\le g$ and m sufficiently large. We show that such linear operators are necessarily vertex permutations.

1. Introduction

Let ${\mathcal{G}}_n$ denote the set of all simple loopless graphs on n vertices. Determining whether a graph belongs to some specified set is sometimes difficult. For example, finding the genus of a graph is an NP-hard problem. A good method of finding families of graphs of a specific genus is to consider operators on known families of graphs of specific genus.

A mapping T on ${\mathcal{G}}_n$ is called a linear operator if it preserves the unions (that is, $T(G_1\cup G_2)=T\left(G_1\right)\cup T\left(G_2\right)$ for any graphs $G_1$ and $G_2$), and preserves the edgeless graph, $\overline{K_n}$, in ${\mathcal{G}}_n$.

Such linear operators were studied by Pullman [1] in 1985 and by Hershkowitz [2] in 1987. Those mappings that preserve the clique covering number were studied in [1] and the mappings that preserve maximum cycle length were studied in [2]. The mappings that preserve chromatic number and planarity were studied in [3].

For a graph G, let $V\left(G\right)$ denote the vertex set and $E\left(G\right)$ denote the edge set so that an edge in $E\left(G\right)$ is represented by an unordered pair of vertices, $\{u,v\}$, or simply $uv$. Isolated vertices does not affect the properties that we are investigating. So, we may think of nonempty subgraph $\widehat{G}$ of G, which is obtained by deleting its isolated vertices from G. We now adopt the convention that “G has a property” means “$\widehat{G}$ has that property”. Therefore if we say that “E is an edge” means that $\widehat{E}=K_2$ and if we say that “G is a 3-cycle”, we mean that “$\widehat{G}$ is a 3-cycle”.

Let the vertex set of the graphs in ${\mathcal{G}}_n$ be $\{v_1,v_2,\cdots ,v_n\}$. If the edge set of a graph E consists only of the edge $v_i{v}_j$, we denote E by $E_{i,j}$. A linear operator $T:{\mathcal{G}}_n\to {\mathcal{G}}_n$ is called a vertex permutation ([2]) if there is a permutation, $\tau$, of $\{1,2,\cdots ,n\}$ such that if $v_i{v}_j$ is an edge of G, $i\ne j$, then $v_{\tau \left(i\right)}{v}_{\tau \left(j\right)}$ is an edge of $T\left(G\right)$, which is equivalent to

$$T\left(E_{i,j}\right)=E_{\tau \left(i\right),\tau \left(j\right)},$$

(1)

for all $i\ne j$.

We say that a linear operator T preserves a set $\mathcal{S}$ if $X\in \mathcal{S}$ implies that $T\left(X\right)\in \mathcal{S}$. The linear operator T strongly preserves the set $\mathcal{S}$ if

$$X\in \mathcal{S}\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}T\left(X\right)\in \mathcal{S}.$$

(2)

Thus, “T strongly preserves the set $\mathcal{S}$” means that “T preserves the set $\mathcal{S}$ and T preserves the complement ${\mathcal{G}}_n\backslash \mathcal{S}$”.

If $T:{\mathcal{G}}_n\to {\mathcal{G}}_n$ is a linear operator that maps the whole set ${\mathcal{G}}_n$ to a single element, then T preserves any set that contains that single element. So, for our investigation, additional conditions must be added to the linear operator as we see in the following example.

Example 1.

Let P be the Petersen graph, Then P is a 3-regular graph. Let $T:{\mathcal{G}}_{10}\to {\mathcal{G}}_{10}$ be defined by $T\left(A\right)=P$ for all $A\ne \overline{K}$ and $T\left(\overline{K}\right)=\overline{K}$. Then T is a linear operator and preserves 3-regular graphs, but T maps every graph A except $\overline{K}$ to the 3-regular graph $P.$ Therefore T strongly preserves no set of graphs except P and $\overline{K}$.

Let h be a function on ${\mathcal{G}}_n$ and $T:{\mathcal{G}}_n\to {\mathcal{G}}_n$ be a linear operator. The operator T is said to preserve the function h if T preserves the set $\{A\in {\mathcal{G}}_n|h\left(A\right)=k\}$ for each $k\in h\left({\mathcal{G}}_n\right)$, the image of h. This is equivalent that

$$\begin{gathered} T\mathrm{preserves}h\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if},\mathrm{for}\mathrm{each}k\in h\left({\mathcal{G}}_n\right), \\ T\mathrm{strongly}\mathrm{preserves}{h}^{-1}\left(k\right). \end{gathered}$$

(3)

Let $\epsilon \left(G\right)$ denote the number of edges in G, i.e., $\epsilon \left(G\right)=\left|E\right(G\left)\right|,$ the cardinality of the set $E\left(G\right)$. We say that a graph G is a k-star ([3]) if G is consisted of k edges sharing a common vertex. Then a 2-star is a path of two connected edges.

Let G and H be graphs in ${\mathcal{G}}_n$ and $E\left(G\right)\subseteq E\left(H\right)$. Then we say that G is dominated by H or H dominates G, and we denote $G⊑H$.

We say that the genus of a surface is 0 when the surface is a sphere or a plane. A surface has genus 1 if it is equivalent to a torus or a sphere with 1 “handle”. An orientable smooth surface has genus k if it is equivalent to a surface with k holes, or a sphere with k “handles”.

The genus of a graph is defined as the genus of the simplest surface in which it can be embedded (drawn) without crossings of edges. There are well known facts such that the genus of a graph is 0 (i.e., the surface is planar) if it is not a subdivision of a $K_5$ or $K_{3,3}$, where $K_5$ is the complete graph on 5 vertices, and $K_{3,3}$ is the complete bipartite graph the vertex bipartition being two sets each of three members.

For $G\in {\mathcal{G}}_n$, let us denote the genus of G by $\gamma \left(G\right)$. Thus, $\gamma$ is a function $\gamma :{\mathcal{G}}_n\to {\mathbb{Z}}_{+}$, the set of nonnegative integers, which is defined by $\gamma \left(G\right)=h$ if G has genus h.

For a graph G with $\gamma \left(G\right)=h$, if we add any edge E to G then $G\cup E$ will have genus at most $h+1$, since at most one “handle” should be attached to the surface to embed the edge. For more known facts on the genus of a graph and embedding, we refer [4] or the following mathematical web sites:http://mathworld.wolfram.com/GraphTheory.html. https://en.wikipedia.org/wiki/Graph_theory.

Now, we define a function $\phi$ on the set of natural integers $\mathbb{N}$, such that ${\mathcal{G}}_n$ has a graph G with $\gamma \left(G\right)=h$. That is, define $\phi :\mathbb{N}\to \mathbb{N}$ by $\phi \left(h\right)=n$ if and only if ${\mathcal{G}}_n$ contains a graph G with $\gamma \left(G\right)=h$ and ${\mathcal{G}}_{n-1}$ does not. As an example, $\phi \left(1\right)=5$ since complete graph $K_5$ has genus 1 and each graph on four vertices has genus 0. That is, $\phi \left(h\right)$ gives the minimum $n\in \mathbb{N}$ such that ${\mathcal{G}}_n$ has a graph G with $\gamma \left(G\right)=h$. Also, extending this function $\phi$ to the nonnegative integers, we define $\phi \left(\overline{K_n}\right)=0$.

In [5] the following theorem was established:

Theorem 1.

([5] Theorem 3.7). For a nonnegative integer h, let $n\ge 6$ if $h=0\mathrm{or}1$, and $n\ge 8+\phi (h-1)$ if $h\ge 2$. If $T:{\mathcal{G}}_n\to {\mathcal{G}}_n$ is a linear operator, then, the following are eqivalent:

1. 

T preserves consecutive two genera h and $h+1$;

2. 

T strongly preserves genus h;

3. 

T preserves genus h and is bijective;

4. 

T preserves genus h and $T\left(K_n\right)=K_n$;

5. 

T maps edges to edges and T preserves genus h for $h\ge 1$;

6. 

T is a vertex permutation.

In this article, we extend these results. The following join of two graphs will be used.

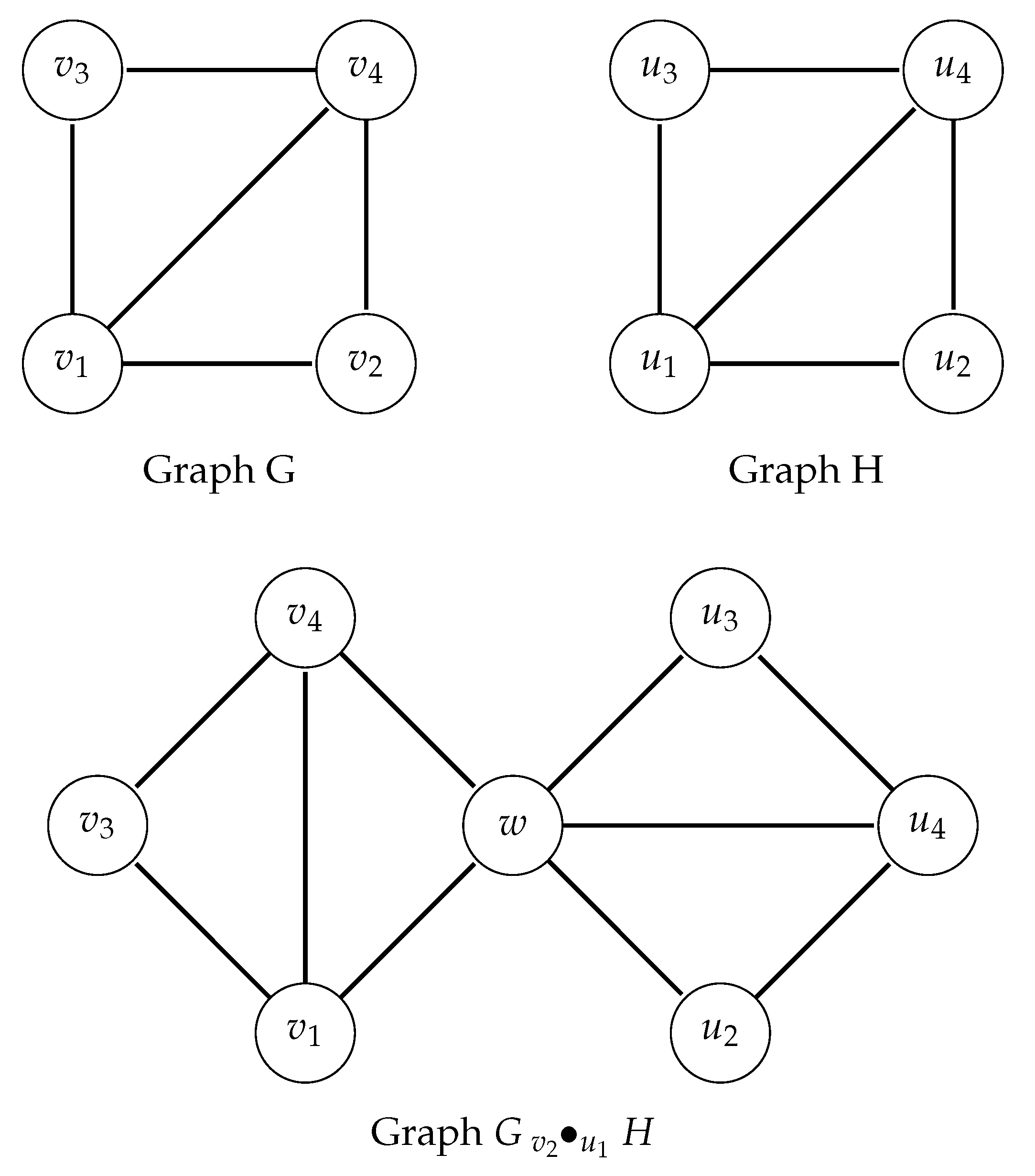
Definition 1.

Let $u,v,\mathrm{and}w$ be vertices. Let $G\in {\mathcal{G}}_q$, $H\in {\mathcal{G}}_r$, $V\left(G\right)\cap V\left(H\right)=\varnothing$, $u\in V\left(G\right)$, $v\in V\left(H\right)$, and $w\notin V\left(G\right)\cup V\left(H\right)$. Define the$(u,v)$-append ofGandH, $G{}_u{•}_{v}H$, to be the graph on $r+q-1$ vertices whose vertex set is $\left(V\right(G)\backslash \{u\left\}\right)\cup \left(V\right(H)\backslash \{v\left\}\right)\cup \left\{w\right\}$ and let the edge set of $G{}_u{•}_{v}H$ to be the set $\left\{xy\right|xy\in E\left(G\right),x,y\ne u\}\cup \{xy|xy\in E(H),x,y\ne v\}\cup \left\{xw\right|xu\in E\left(G\right)\}\cup \{xw|xv\in E(H\left)\right\}$. See Figure 1. If the vertex u in G is not specified, that is the choice of vertex u is arbitrary, we write $G{•}_{v}H$ or $H{}_v•G$, and if neither is specified we write $G•H$.

For example, if G is a graph one of whose vertices is v we write $K_4{•}_{v}G$ since any choice of a vertex from $K_4$ will give the same graph appended to the vertex v of G. Similarly, if $C_6$ is a 6 cycle, we write $K_4•C_6$, since for any choices of vertices of $K_4$ and any choice of vertices of $C_6$ give the same appended graph. Further, when appending more than two graphs, we use a sequence of vertices $w_1,w_2,\cdots$ so that for $v_1\in G_1$, $v_2,u_2\in G_2$, etc., the graph $G_1{}_{v_1}{•}_{u_2}{G}_2{}_{v_2}{•}_{u_3}{G}_3\cdots$ is well defined. 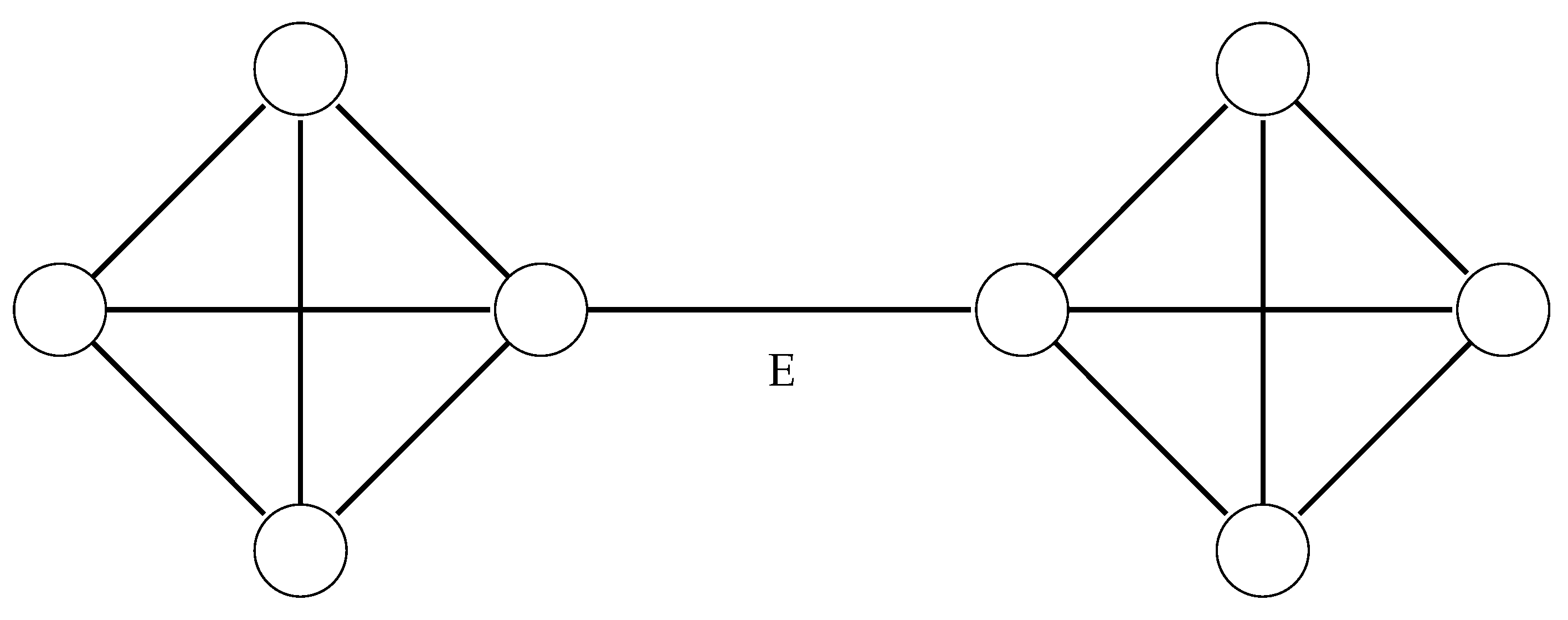In Figure 2, we show the appending of two $K_4$’s to the ends of an edge E.

2. A Construction

We define the box-sum of graphs $K_5⊞F$ where F is a forest. We assume that the number n of vertices in ${\mathcal{G}}_n$ is at least four times the number of edges in the forest plus the number of components of F.

We begin defining $K_5⊞H$ where H is a tree as follows: Let H be a tree with nonisolated vertex set $\{{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_{q+1}\}$ and with q edges, $E_i=\left\{{\mathbf{u}}_1^{\left(i\right)}{\mathbf{u}}_2^{\left(i\right)}\right\},i=1,\cdots ,q$, where ${\mathbf{u}}_1^{\left(i\right)},{\mathbf{u}}_2^{\left(i\right)}\in \{{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_{q+1}\}$. To each edge $E_i={\mathbf{u}}_1^{\left(i\right)}{\mathbf{u}}_2^{\left(i\right)}$, of H assign the vertices ${\mathbf{w}}_1^{\left(i\right)},{\mathbf{w}}_2^{\left(i\right)},{\mathbf{w}}_3^{\left(i\right)}\in \{{\mathbf{v}}_{q+2},{\mathbf{v}}_{q+3},\cdots ,{\mathbf{v}}_n\}$ and such that for $i\ne j$,

$$\{{\mathbf{w}}_1^{\left(i\right)},{\mathbf{w}}_2^{\left(i\right)},{\mathbf{w}}_3^{\left(i\right)}\}\cap \{{\mathbf{w}}_1^{\left(j\right)},{\mathbf{w}}_2^{\left(j\right)},{\mathbf{w}}_3^{\left(j\right)}\}=\varnothing .$$

Let $K_5^{\left(i\right)}$ be the complete graph induced by the set of vertices

$$\{{\mathbf{u}}_1^{\left(i\right)}{\mathbf{u}}_2^{\left(i\right)},{\mathbf{w}}_1^{\left(i\right)},{\mathbf{w}}_2^{\left(i\right)},{\mathbf{w}}_3^{\left(i\right)}\}.$$

Let $K_5⊞H={\bigcup }_{i=1}^q{K}_5^{\left(i\right)}$. Then, $K_5⊞H$ is a graph on $4\epsilon \left(H\right)+1$ vertices such that

• H is a subgraph of $K_5⊞H$;
• $K_5⊞H$ contains q blocks;
• each block is isomorphic to $K_5$; and
• exactly one edge of H is dominated by each block of $K_5⊞H$.

Let $F=H_1\cup \cdots \cup H_{\ell }$ be a forest with disjoint trees $H_1,\cdots ,H_{\ell }$. Let $\{{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_s\}$ be the set of nonisolated vertices of F, and let F have a total of r edges, $E_i=\left\{{\mathbf{u}}_1^{\left(i\right)}{\mathbf{u}}_2^{\left(i\right)}\right\},i=1,\cdots ,r$, where ${\mathbf{u}}_1^{\left(i\right)},{\mathbf{u}}_2^{\left(i\right)}\in \{{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_s\}$.

Let $\{{\mathbf{w}}_1^{\left(i\right)},{\mathbf{w}}_2^{\left(i\right)},{\mathbf{w}}_3^{\left(i\right)}|i=1,\cdots ,r\}$ be a set of vertices in $\{{\mathbf{v}}_{s+1},\cdots ,{\mathbf{v}}_n\}$ such that

$$\{{\mathbf{w}}_1^{\left(i\right)},{\mathbf{w}}_2^{\left(i\right)},{\mathbf{w}}_3^{\left(i\right)}\}\cap \{{\mathbf{w}}_1^{\left(j\right)},{\mathbf{w}}_2^{\left(j\right)},{\mathbf{w}}_3^{\left(j\right)}\}=\varnothing .$$

Let $K_5^{\left(i\right)}$ be the complete graph induced by the set of vertices

$$\{{\mathbf{u}}_1^{\left(i\right)}{\mathbf{u}}_2^{\left(i\right)},{\mathbf{w}}_1^{\left(i\right)},{\mathbf{w}}_2^{\left(i\right)},{\mathbf{w}}_3^{\left(i\right)}\}.$$

Let

$$K_5⊞F_1=\bigcup _{i=1}^r{K}_5^{\left(i\right)}=\bigcup _{i=1}^l{K}_5⊞H_i.$$

Then $K_5⊞F$ is a graph such that

• F is a subgraph of $K_5⊞F$;
• $K_5⊞F$ contains ℓ components and a total of $\epsilon \left(H_1\right)+\epsilon \left(H_2\right)+\cdots +\epsilon \left(H_{\ell }\right)$ (= s) blocks;
• the ith component of $K_5⊞F$ is $K_5⊞H_i$;
• exactly one edge of F is dominated by each block of each component of $K_5⊞F$;
• The genus of $K_5⊞F$ is s, the number of edges in F.

Note that $K_5⊞F$ is not unique, it depends on the choice of vertices $w^{\left(1\right)},w^{\left(2\right)},$$\cdots ,w^{(\ell -1)}$ and $v^{\left(2\right)},v^{\left(3\right)},\cdots ,v^{(\ell )}$.

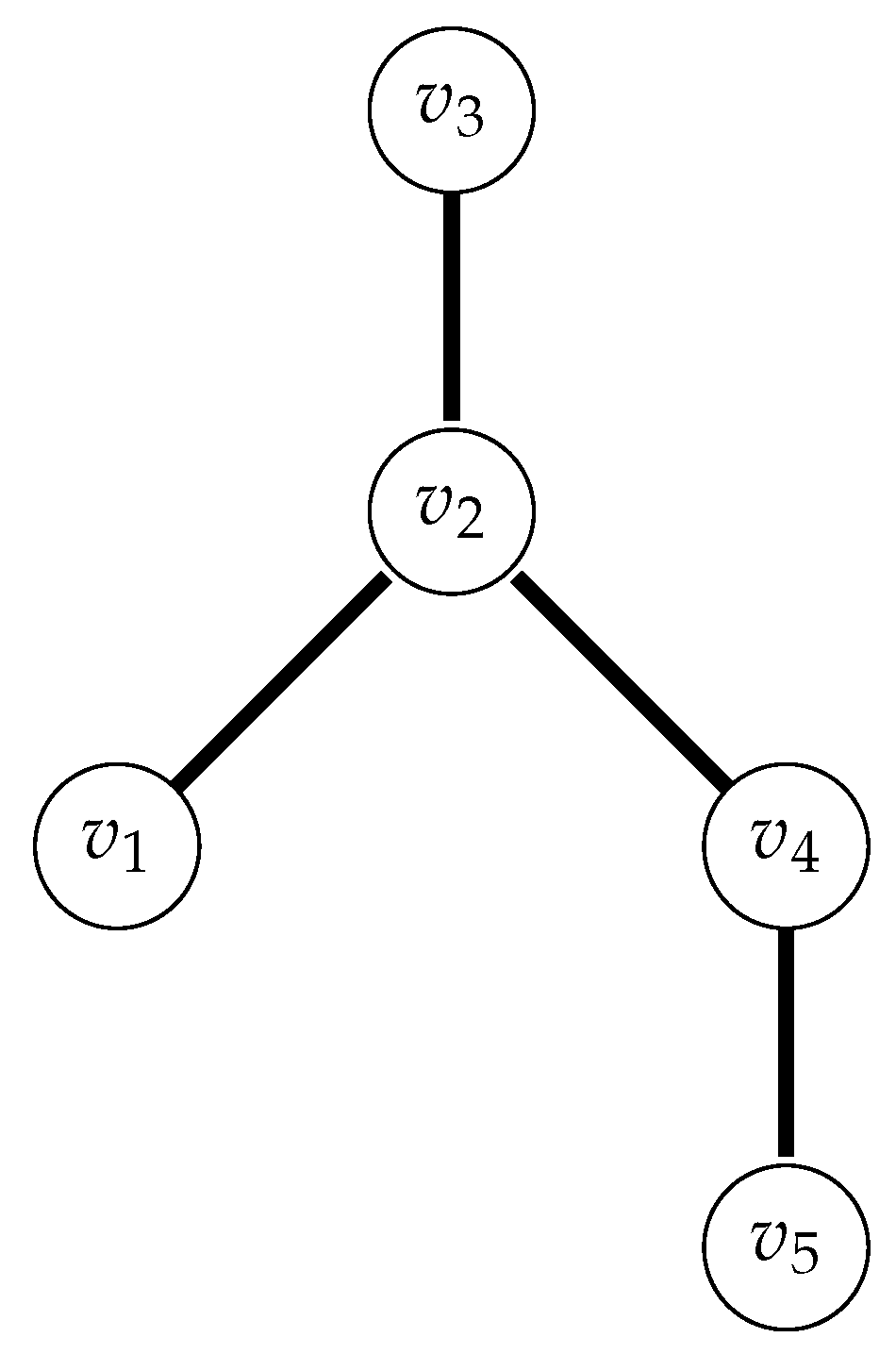
Example 2.

In Figure 3 we see a tree H and in Figure 4 we see the graph $K_5⊞H$ with the bold edges indicating the original tree H.

3. Linear Operators That Preserve Two Genera of a Graph

Let $\mathcal{X}$ be a subset of ${\mathcal{G}}_n$ and let $\bigcup \mathcal{X}={\cup }_{X\in \mathcal{X}}X$. So that $\bigcup ker\left(T\right)$ is the largest graph in $ker\left(T\right)$. Let $\epsilon \left(G\right)=\left|E\right(G\left)\right|$, the number of edges in the graph G and let $\mathcal{E}$ be the set of all edge graphs in ${\mathcal{G}}_n$.

Let $T:{\mathcal{G}}_n\to {\mathcal{G}}_n$ be a linear operator.

• Let $\mathcal{N}\left(T\right)=ker\left(T\right)\cap \mathcal{E}$. Let $N\left(T\right)=\bigcup ker\left(T\right)$ and let $F_N\left(T\right)$ be a spanning forest of $N\left(T\right)$.
• Let $\mathcal{W}\left(T\right)=\{E\in \mathcal{E}|\exists F\in \mathcal{E}\ni E⊑T\left(F\right)\}$, $W\left(T\right)=\bigcup \mathcal{W}$ and $F_W\left(T\right)$ be a spanning forest of $W\left(T\right)$.
• Let $\mathcal{U}\left(T\right)=\mathcal{N}\left(T\right)\cup \mathcal{W}\left(T\right)$, $U\left(T\right)=N\left(T\right)\cup W\left(T\right)$ and $F_U\left(T\right)$ be a spanning forest of $U\left(T\right)$.

In the following lemma we shall use the function $\phi :\mathbb{N}\to \mathbb{N}$ defined above Theorem 1 such that $\phi \left(h\right)$ gives the minimum $n\in \mathbb{N}$ such that ${\mathcal{G}}_n$ has a graph G with $\gamma \left(G\right)=h$. Further recall that an idempotent operator, L, is one for which $L^2=L$.

Lemma 1.

Let k and j be positive integers and let $n\ge 4j+\phi \left(k\right)$. Let $L:{\mathcal{G}}_n\to {\mathcal{G}}_n$ be an idempotent linear operator that preserves the set of graphs of genus k and the set of graphs of genus $k+j$. Then, $\epsilon \left(F_U\left(L\right)\right)<j$.

Proof. 

Suppose that $\epsilon \left(F_U\left(L\right)\right)\ge j$. Let $F_U\left(L\right)=E_1\cup E_2\cup \cdots \cup E_{\epsilon \left(F_u\left(L\right)\right)}$ where each $E_i$ is an edge, and label the edges so that $E_1\cup \cdots \cup E_{\ell }⊑W\left(L\right)$ and $E_{\ell +1}\cup \cdots \cup E_{\epsilon \left(F_U\left(L\right)\right)}⊑N\left(L\right)$. Further, for $E\in W\left(L\right)$, since L is idempotent and $E⊑L\left(F\right)$, $L\left(E\right)⊑L^2\left(F\right)=L\left(F\right)$.

Let $\tilde{F}=E_1\cup E_2\cup \cdots \cup E_j$, and consider $K_5⊞\tilde{F}$. Then, $K_5⊞\tilde{F}$ has genus j, and meets $4j+1$ vertices. Let Q be a graph of genus k on $n-4j$ vertices and let $G=(K_5⊞\tilde{F})•Q$. G meets all the vertices of $K_5⊞\tilde{F}(4j+1\mathrm{vertices})$ and all the vertices of $Q(n-4j\mathrm{vertices})$. Since in G, $(K_5⊞\tilde{F})$ and Q share one vertex, G meets n vertices. Then $\gamma \left(G\right)=k+j$ and $\gamma (G\backslash (E_1\cup E_2\cup \cdots \cup E_j))=k$ since the deletion of each edge in $\tilde{F}$ reduces the genus of $(K_5⊞\tilde{F})$ by one and hence reduces the genus of G by one. Let $F_i,i=1,\cdots ,\ell$ be edges dominated by G such that $E_i⊑L\left(F_i\right)$.

Now, $G=[G\backslash (E_1\cup E_2\cup \cdots \cup E_j)]\cup (E_1\cup E_2\cup \cdots \cup E_j)=[G\backslash (E_1\cup E_2\cup \cdots \cup E_j)]\cup (E_1\cup E_2\cup \cdots \cup E_j)\cup (F_1\cup \cdots \cup F_{\ell })$, since $G\backslash (E_1\cup E_2\cup \cdots \cup E_j)⊒(F_1\cup \cdots \cup F_{\ell })$. Thus $G\backslash (E_1\cup E_2\cup \cdots \cup E_j)=[G\backslash (E_1\cup E_2\cup \cdots \cup E_j)]\cup (F_1\cup \cdots \cup F_{\ell })$. So

$$\begin{array}{ccc}\hfill L\left(G\right)& =& L([G\backslash (E_1\cup E_2\cup \cdots \cup E_j)]\cup (E_1\cup E_2\cup \cdots \cup E_j))\hfill \\ & =& L([G\backslash (E_1\cup E_2\cup \cdots \cup E_j)]\cup (E_1\cup E_2\cdots \cup E_j)\cup (F_1\cup \cdots \cup F_{\ell }))\hfill \\ & =& L(G\backslash (E_1\cup E_2\cup \cdots \cup E_j))\cup L(E_{\ell +1}\cup \cdots \cup E_j)\hfill \\ & =& L(G\backslash (E_1\cup E_2\cup \cdots \cup E_j))\hfill \end{array}$$

since $L(E_{\ell +1}\cup \cdots \cup E_j)=\overline{K}$. We now have that $k+j=\gamma \left(G\right)=\gamma \left(L\left(G\right)\right)=\gamma \left(L(G\backslash (E_1\cup E_2\cup \cdots \cup E_j))\right)$ and $k=\gamma (G\backslash (E_1\cup E_2\cup \cdots \cup E_j))=\gamma \left(L(G\backslash (E_1\cup E_2\cup \cdots \cup E_j))\right)$, a contradiction since $L\left(G\right)=L(G\backslash (E_1\cup E_2\cup \cdots \cup E_j))$. Thus, $\epsilon \left(F_U\left(L\right)\right)<j$. □

Lemma 2.

Let $1\le j\le 5$ and let $n\ge 4j+\phi \left(k\right)$. If $L:{\mathcal{G}}_n\to {\mathcal{G}}_n$ is an idempotent linear operator that preserves graphs of genus k and graphs of genus $k+j$ then L is the identity mapping.

Proof. 

Consider $F_U\left(L\right)$. By Lemma 1 $\epsilon \left(F_U\left(L\right)\right)<j$. Note, if $F_U\left(L\right)=\overline{K}$ then L is the identity, so we assume that $1\le \epsilon \left(F_U\left(L\right)\right)\le j-1\le 4$. Thus, the vertices incident with a tree dominated by $F_U\left(L\right)$ induces a subgraph of a $K_5$, by permuting vertices, we may suppose that the $K_5=K_5^{\left(1\right)}$ is induced by vertices $\{v_1,v_2,v_3,v_4,v_5\}$. Further, if F is any edge, $L\left(F\right)⊑F\cup K_5^{\left(1\right)}$. Let $K_5^{\left(i\right)},i=2,\cdots j$ be appended so that for H a graph of genus k on $n-4j$ vertices, $G=K_5^{\left(1\right)}•K_5^{\left(2\right)}•\cdots •K_5^{\left(j\right)}•H$ dominates edges whose images dominate $F_W\left(L\right)$.

Let $F_2,\cdots ,F_j$ be edges dominated by $K_5^{\left(2\right)},\cdots K_5^{\left(j\right)}$ respectively such that $L(F_2.\cup ,\cdots .\cup ,F_j)⊒F_W\left(L\right)$.

Then $\gamma \left(G\right)=k+j$ and $\gamma (G\backslash (F_U\left(L\right)\cup F_2\cup \cdots \cup F_j))=k$, so that $\gamma \left(L\right(G\left)\right)=k+j$ and $\gamma \left(L(G\backslash (F_U\left(L\right)\cup F_2\cup \cdots \cup F_j))\right)=k$. But,

$$\begin{array}{ccc}\hfill L\left(G\right)& =& L([G\backslash (F_U\left(L\right)\cup F_2\cup \cdots \cup F_j)]\cup [F_U\left(L\right)\cup F_2\cup \cdots \cup F_j])\hfill \\ & =& L\left([G\backslash (F_U\left(L\right)\cup F_2\cup \cdots \cup F_j)]\right)\cup L\left([F_U\left(L\right)\cup F_2\cup \cdots \cup F_j]\right)\hfill \\ & =& L\left([G\backslash (F_U\left(L\right)\cup F_2\cup \cdots \cup F_j)]\right)\cup L(F_2\cup \cdots \cup F_j).\hfill \end{array}$$

But $L(F_2\cup \cdots \cup F_j)$ adds at most $j-1$ to the genus of $L(G\backslash (F_U\left(L\right)\cup F_2\cup \cdots \cup F_j))$. That is $\gamma \left(L(G\backslash (F_U\left(L\right)\cup F_2\cup \cdots \cup F_j))\right)\le k+j-1$.

That is $L\left(G\right)=L(G\backslash (F_U\left(L\right)\cup F_2\cup \cdots \cup F_j))$, so $k+j=\gamma \left(L\left(G\right)\right)=\gamma \left(L(G\backslash (F_U\left(L\right)\cup F_2\cup \cdots \cup F_j))\right)\le k+j-1$, a contradiction.

We have shown that $\epsilon \left(F_U\left(L\right)\right)=0$ and hence L is the identity. □

The following lemma was obtained in [6], but we include the proof for completeness.

Lemma 3

([6] Lemma 2.5). Let $\mathcal{K}$ be a finite set and $\varphi :\mathcal{K}\to \mathcal{K}$ be arbitrary mapping. Then there is some natural number r such that ${\varphi }^r$ (the r-th power of ϕ) is idempotent.

Proof. 

Since $\mathcal{K}$ is finite, and $\varphi$ can be considered a subset of $\mathcal{K}\times \mathcal{K}$, the set $\{\varphi ,{\varphi }^2,{\varphi }^3,\dots ,{\varphi }^{\ell },\dots \}$ is a finite set. Thus there exist two nonnegative integers $a,b$ with $1\le a<b$ such that ${\varphi }^a={\varphi }^b$. Let $d=b-a$. Since ${\varphi }^a={\varphi }^b={\varphi }^{(a+d)}$, if k is a nonnegative integer, then ${\varphi }^{(a+kd)}={\varphi }^{(a+d)+(k-1)d}={\varphi }^{(a+(k-1\left)d\right)}$, etc. So that for any nonnegative integer k, ${\varphi }^{(a+kd)}={\varphi }^a$.

Suppose that c is a nonnegative integer with $c\ge a$. Then $c=a+z$ for some nonnegative integer z. Thus, ${\varphi }^{c+kd}={\varphi }^{(a+z+kd)}={\varphi }^{(a+kd)+z}={\varphi }^{(a+z)}={\varphi }^c$. That is, for any nonnegative integers $c,k$ with $c\ge a$, ${\varphi }^{c+kd}={\varphi }^c$.

Now, let $d=b-a$, then $d\ge 1$ since $b>a$. Thus, $ad\ge a$. Hence it follows that ${\varphi }^{(ad+kd)}={\varphi }^{ad}$. For $k=a$ we have ${\left({\varphi }^{ad}\right)}^2={\varphi }^{2ad}={\varphi }^{(ad+ad)}={\varphi }^{ad}$. That is ${\varphi }^{ad}$ is idempotent. □

Theorem 2.

Let $1\le j\le 5$ and $j\le h$ be positive integers and let $n\ge 4j+4+\phi \left(h\right)$. If $T:{\mathcal{G}}_n\to {\mathcal{G}}_n$ is a linear operator that preserves graphs of genus h and graphs of genus $h+j$ then T is a vertex permutation.

Proof. 

Let L be a power of T that is idempotent as guaranteed by Lemma 3. By Lemma 2, L is the identity. It follows that T must be bijective since L is a power of T. Since $4j+4+\phi \left(h\right)\ge 8+\phi (h-1)$, by Theorem 1 the theorem follows. □

4. Conclusions

In this article, we continue our investigation on the linear operators that preserve the genera of a graph. Now we showed that those linear operators are the form of vertex permutations. And we added some equivalent conditions of the linear operators on the set of graphs that preserve the genera of a graph, say, the linear operator that preserves two genera h and $h+j$ of a graph. For further investigation, we give a conjecture:

Conjecture. If $T:{\mathcal{G}}_n\to {\mathcal{G}}_n$ is a linear operator that preserves any two genera h and k of a graph, then T is a vertex permutation.