Abstract
In this work, we identified the characteristics of unsteady magnetohydrodynamic (MHD) flow of ferrofluid past a radiated stretching surface. Cobalt–kerosene ferrofluid is considered and the impacts of Navier slip and convective heating are additionally considered. The mathematical model which describes the problem was built from some partial differential equations and then converted to self-similar equations with the assistance of the Lie group method; after that, the mathematical model was solved numerically with the aid of Runge–Kutta–Fehlberg method. Graphical representations were used to exemplify the impact of influential parameters on dimensionless velocity and temperature profiles; the obtained results for the skin friction coefficient and Nusselt number were also examined graphically. It was demonstrated that the magnetic field, Navier slip, and solid volume fraction of ferroparticles tended to reduce the dimensionless velocity, while the radiation parameter and Biot number had no effects on the dimensionless velocity. Moreover, the magnetic field and solid volume fraction increase skin friction whereas Navier slip reduces the skin friction. Furthermore, the Navier slip and magnetic field reduce the Nusselt number, whereas solid volume fraction of ferroparticles, convective heating, and radiation parameters help in increasing the Nusselt number.
1. Introduction
Flow and convective heat transfer through a stretching surface play an essential role in research due to their presence in many engineering and industrial applications. Many authors have emphasized this and the details are found in [1,2,3]. To overcome the poor thermal conductivity and increase the other thermophysical properties of the conventional fluids, nanoparticles were suspended in a base fluid. These nanoparticles are called nanofluids and can be generated from diverse operations or chemical deposition mechanisms. Enchantment in the surface area and the rate of heat transfer occurred and many improvements have recently been performed for this issue [4]. This scheme of nanofluid is processed by integrating the pure fluid and classical equations of mass. Many investigations ofnanofluid flow can be found in [5,6].
Heat transfer has been improved by adding nano-sized particles to a base fluid, as has been extensively enacted in heating and cooling methods in engineering and industries. The nano-scaled particles and the host fluid molecules are almost the same size and are identified as stable suspensions for an extended period. Convective thermal transport characteristics of nanofluids depend on the flow model, the volume fraction of nanofluid and shape of the particles [7,8,9,10,11,12,13,14]. Electronic gadgets, design of turbomachines, biomedicine, transportation, lubrication, enhanced oil recovery, lasers, petroleum drilling operations, and manufacturing process are some of the applications. The study of the combination of the fluid flow dynamic traits and the trait of electromagnetism is called magneto-hydrodynamics (MHD). It is a technique where the activities can be arrested electrically, associated with fluid flow in the presence of a magnetic flux field. The particles suspended in the fluid are controlled by the applied magnetic field and restructure their concentration; thus, the irregular heat transfer of the flow will be changed. A few situations with MHD issues are like the prediction of room climate, magneto-optical wavelength filters, estimations of stream rates of refreshments in the nourishment industry, optical switches and optical modulators. Magneto-nanoparticles are highly used in cancer therapy, MRI, magnetic drug targeting, hyperthermia, magnetic cell separation and drug delivery. They likewise have uses in geophysics; this is connected to thinking about stellar and solar structures, design of MHD pumps, etc. Several other significant investigations in this concern are due to [15,16,17,18,19,20,21].
Finally, Lie-group methods and their invariants offer a powerful, sophisticated, and methodical technique to obtain group-invariant solutions which are called self-similarity transformations. Self-similarity transformations achieved reduction of the independent variable numbers of a set of PDEs, leading to conversion of the non-linear governing PDEs into ODEs. Analysis using Lie groups has been executed by many scientists and applied mathematicians in many investigations [22,23,24,25,26,27,28].
In the current work, we analyze the unsteady MHD flow of ferrofluid and convective heat transfer confined by a radiate stretched sheet with the influence of Navier slip and convective heating. The mathematical model was solved numerically with the aid of Runge–Kutta–Fehlberg method. The aspects of various parameters such as velocity, temperature, shear stress fields and skin friction coefficient parameters associated with the current analysis are graphically examined. The recent advancements in modern technology have stimulated research interest in the analysis of boundary layer ferrofluid flow overstretching surfaces for its use in various engineering and industrial applications, such as paper production, fiberglass production, several engineering processes like solar power technology, etc.
2. Problem Formulation
In the current research, it is assumed that a 2D unsteady magneto-forced convective flow of ferrofluid past a radiate stretchable surface with impacts on Navier slip and convective heating are additionally considered. In this work, Cobalt is considered and is treated as a base nanoparticle, with kerosene as a base ferrofluid. The stretchable surface switches on from a fine slot, which is positioned at the starting point of a 2D coordinate system (x, y). At this point, the x-axis is considered all along the stretching direction of the sheet, having stretched velocity , which is applied vertically to the sheet externally. A constant magnetic strength is applied normal to the sheet. The mathematical model describing the system is (see Chamkha [29])
Subjected to the corresponding boundary conditions (see [30,31,32,33,34]):
where t, u and v are the time and velocity components along the x and y axes and T is the temperature in the fluid phase. stands for the density. stands for viscosity. Stands for the ferrofluid volumetric thermal expansion coefficient. σff stands for electrical conductivity. stands for the thermal diffusivity of the ferrofluid. L stands for the slip coefficient, which represents Navier slip, and hf stands for the heat transfer coefficient. Tf stands for the uniform temperature of the stretchable surface. kff stands for the thermal conductivity of ferrofluid. stands for the specific heat of the ferrofluid at a constant pressure. The radiative heat flux qr is approached according to the Rosseland approximation (see [35,36]):
where βR and σ1 stand for the mean absorption coefficient and the Stefan–Boltzmann constant. As carried out by Raptis [35], the fluid-phase temperature variations within the flow are approached to be adequately tiny so that T4 may be obvious as a linear function of temperature. This is created by extending T4 in a Taylor series on the free-stream temperature T∞ and removing higher-order terms to yield
By applying Equations (5) and (6) in the last term of Equation (3), we obtain
In the current investigation, the following thermophysical relations are applied [37];
Here, χ is nanoparticle volume fraction. Table 1 represents the thermophysical properties of ferrofluid.

Table 1.
Thermophysical properties of kerosene, water and cobalt [37].
In this stage, the expressions for u, v, and θ will be defined as:
Substituting Equations (7)–(9) into Equations (1)–(4), we obtain
3. Lie Group Framework
Obtaining the solutions of the PDEs (partial differential equations) (10)–(12) governing the investigation understudy is equivalent to satisfying the constant solutions of these equations under a special continuous one-parameter group. The proposed technique is to search for a transformation group from the primary collection of one parameter scaling transformation. The facilitated form of Lie group framework, namely, the scaling group of transformations Δ (see [38,39,40,41,42,43,44,45,46]), will be presented here:
where are transformation parameters and ε is a small parameter whose interrelationship will be determined by our investigation. Equation (13) may be scrutinized as a point transformation, which transfers the coordinates to Substituting transformations Equation (13) in Equations (10)–(12), we obtain;
The following relations should be determined to reserve the system to be constant:
These relations give
and the one-parameter group of transformations can be obtained as
Developing by Taylor’s technique in powers of ε, we obtain:
which yields
where Γ1, Γ2, and Γ3 are arbitrary functions which should be determined by its equations. η and τ are the similarity variable and dimensionless time.
To avert the fluid properties manifesting explicitly in the coefficients of the above equations, determining mass balance in Equation (1), with keeping generality, we have dropped three different convenient arbitrary constants based on the transformations performed previously by Nabwey [25] and Chamkha [29] as follows:
As a consequence, we find
with the assistance of these formulations in Equation (22). Equations (10)–(12) are characterized as
subject to the following boundary conditions:
where stands for the Hartmann number. stands for Biot number. stands for the radiation parameter. stands for the velocity slip parameter.
The local skin-drag coefficient and local Nusselt number can be written respectively, as
4. Numerical Method
Following [47,48], Equations (23) and (24), subject to (25), will be solved using the local similarity method, where the first derivatives with respect to are neglected and the Equations (23) and (24) with boundary conditions (25) can be re-written as
The boundary conditions (25) remain the same. These ordinary differential equations with the boundary conditions (25) can be solved numerically by applying the Runge–Kutta–Fehlberg method (RKF7 45). Following [47,48], for the local non-similarity solution, now we hold all the terms by assuming the new auxiliary functions and , which are defined by
Thus, Equations (23) and (24) can be expressed as
subject to the same condition in (25). The new ODEs (31)–(32), subject to (25) represent a local non-similarity model for the problem under consideration. Equations (31) and (32) and the boundary conditions (25) are now differentiated w.r.t. , simplified and the derivatives w.r.t. are neglected again. These equations represent a local similarity model and can be expressed as;
The ODEs (31)–(33) subject to (25) and (34) were solved numerically by employing the Runge–Kutta–Fehlberg technique (RKF45) using MAPLE-19 software (MAPLE 2019.0, Maplesoft, Waterloo, ON, Canada). This method is generally known as one of the most excellent methods available for obtaining the solutions of nonlinear differential equations and provides more accurate results. The step size was selected. For the similarity variable , Equations (25) and (34), were replaced as
The selection of guarantees that all numerical solutions approached the asymptotic values properly.
5. Results and Discussions
In this study, we investigated the unsteady magento-flow and heat transfer of Cobalt–kerosene ferrofluid past a stretchable surface. The influences of several key parameters on the dimensionless velocity , temperature , skin friction , and Nusselt number are examined. The Lie group method is employed to reduce partial differential equations and local similar and non-similar models are solved employing the RK-45 technique.
The effects of the magnetic field Ha and dimensionless time τ on the velocity are symbolized in Figure 1a and on the dimensionless temperature in Figure 1b, respectively. As the time increases, the velocity at the surface rises. The magnetic field generates Lorentz strength on the fluid particles, which resist the fluid and reduce the fluid velocity, as shown in Figure 1a. Consequently, the velocity boundary layer thickness decreases. Due to the decline in velocity, the temperature increases. In the thermal boundary layer, the temperature declines to the ambient temperature. The thermal boundary layer thickness reduces with an enlargement of the dimensionless time, as exhibited in Figure 1b. The influence of the solid volume fraction of nanoparticles χ and Navierslip δ on the velocity and temperature is depicted in Figure 2a,b when τ = 0.5. In the absence of slip, the velocity is found to be higher for the pure regular fluid. At the surface, the velocity decreases with the increase in the slip and solid volume fraction, as shown in Figure 2a. No appreciable impact of χ could be observed at the surface as well as within the velocity boundary layer. The velocity boundary layer thickness enlarges with δ, which enlarges the thermal resistance and reduces the heat transfer rate; see Figure 2b. The variation of the dimensionless temperature with the solid volume fraction χ is depicted in Figure 2b. In the absence of slip, the temperature is lower at the wall and intensifies with δ. As expected, the temperature at the wall is higher for the regular fluid and dwindles with an intensify in the solid volume fraction χ. This is due to the higher thermal conductivity of Cobalt nanoparticles. With the addition of nanoparticles, the thermal conductivity of the ferrofluid increases and the heat transfer rate is enhanced.
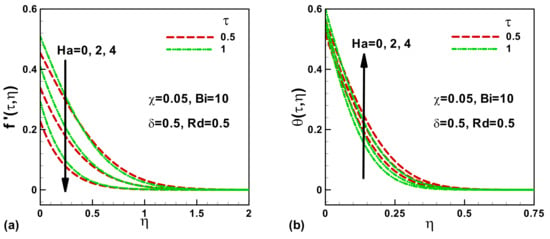
Figure 1.
Effects of magnetic field Ha and dimensionless time τ on (a) dimensionless velocity, and (b) dimensionless temperature.
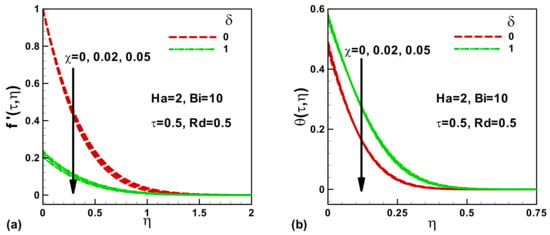
Figure 2.
Effects of solid volume fraction of nanoparticles χ and Navier slip δ on (a) dimensionless velocity and (b) dimensionless temperature.
Figure 3a,b presents the effects of radiation parameter Rd and Biot number Bi on the velocity and temperature curves. It is important to note that equations of momentum and energy are independent of each other. The momentum equation and the velocity boundary conditions are independent of the radiation parameter Rd and convective heating parameter Bi. Therefore, there is no influence of these parameters on the velocity, which is obvious from Figure 3a. On the other side, the surface temperature increases significantly with a strengthen in both Rd and Bi. As a result, the thermal boundary layer thickness is boosted, with an increase in both parameters, as depicted in Figure 3b. The radiation parameter Rd reveals an enhancement in radiative heat, which improves the thermal state of fluid, causing its surface temperature to increase. Similarly, as the convective heating parameter increases and tends to infinity, the convective boundary condition changes to an isothermal boundary condition.
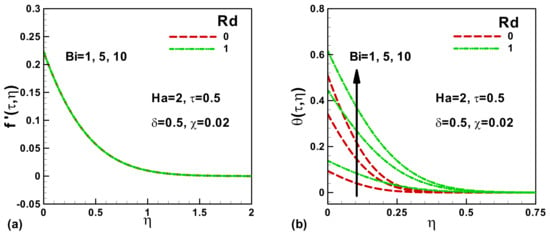
Figure 3.
Effects of Biot number Bi and radiation parameter Rd on (a) dimensionless velocity and (b) dimensionless temperature.
The variations in skin friction and Nusselt number with the magnetic field Ha are depicted in Figure 4 and Figure 5 for different values of the velocity slip δ and the solid volume fraction χ at τ = 1 and τ = 2, respectively. In the presence of magnetic strength, a Lorentz force is generated which resists the fluid and reduces the velocity curve. Therefore, the skin friction enhances with Ha, as shown in Figure 4 and Figure 5a at different dimensionless times. As expected, the skin friction increases with dimensionless time τ. In the absence of velocity slip δ, the velocity curves are higher at the surface and decline with an increment in slip parameter δ. Consequently, the skin friction declines with the boosting of slip parameter δ. For the pure regular fluid, the skin friction is lower and increases with a rise in the solid volume fraction χ. This is due to an evolution in the ferrofluid density with the increased volume fraction of cobalt nanoparticles. Figure 4 and Figure 5b illustrate the variation of Nusselt number with the magnetic field Ha and the volume fraction of ferroparticles χ at different dimensionless times. Like skin friction, Nusselt number also increases with dimensionless time. Due to Lorentz force, the dimensionless velocity decreases and, as a result, the Nusselt number is reduced with an increasing magnetic field. Similarly, the velocity decreases due to an intension in the slip and the Nusselt number reduces. The thermal conductivity of ferroparticles increases with an increase in the volume fraction of ferroparticles. Consequently, the Nusselt number increases with increasing χ.
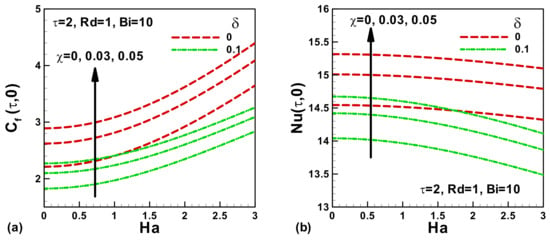
Figure 4.
Effects of solid volume fraction of nanoparticles χ, magnetic Ha, and Navier slip δ parameters on (a) skin friction, and (b) Nusselt number when τ = 1.
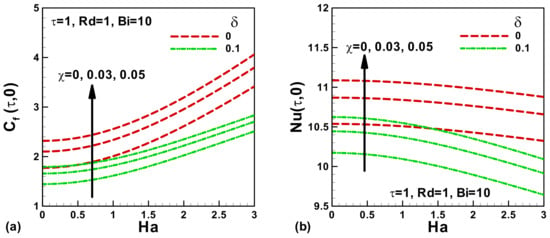
Figure 5.
Effects of solid volume fractions of nanoparticles χ, magnetic Ha and Navierslip δ parameters on (a) skin friction, and (b) Nusselt number when τ = 2.
Figure 6a, b presents the comparison of Nusselt numbers for kerosene oil and water for the same parameters. Due to the smaller Prandtl number Pr for water, the Nusselt numbers are found to be lower than kerosene. The Prandtl number Pr compares the rate of thermal diffusion in comparison to the rate of momentum diffusion. The higher the Prandtl number Pr, the higher the Nusselt number will be. It is also noticed that an increase in the Biot number Bi and radiation parameter Rd leads to an increase in the Nusselt number. These Nusselt numbers also become greater with increasing dimensionless time.
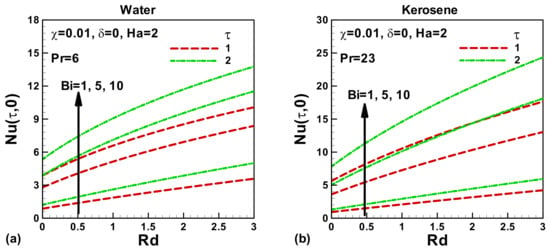
Figure 6.
Effects of Biot number Bi, dimensionless time τ, and radiation parameter Rd on Nusselt number for (a) water and (b) kerosene oil as base fluid.
6. Conclusions
In this study, application of the scaling group of transformations to the unsteady magneto-flow of ferrofluid past a stretching surface was employed. The impacts of Navier slip, radiation and solid volume fraction of ferroparticles, as well as convective heating, were also investigated. From this study, it was concluded that:
- Employing the Lie group framework, the symmetries of the partial differential equations are presented exclusively in this investigation, these equations are reduced to self-similar equations utilizing translational and scaling symmetries. Numerical solutions for scaling symmetry are obtained applying the Runge–Kutta–Fehlberg method.
- The magnetic field, Navier slip, and solid volume fraction of ferroparticles tend to reduce the dimensionless velocity.
- The radiation parameter and Biot number have no effects on the dimensionless velocity.
- Magnetic field, radiation, Biot number, and Navier slip increase the surface temperature, whereas the solid volume fraction of ferroparticles reduces the surface temperature.
- The magnetic field, dimensionless time and solid volume fraction increase skin friction, whereas Navier slip reduces the skin friction.
- The magnetic field and Navier slip reduce the Nusselt number, whereas solid volume fraction of ferroparticles, convective heating, and radiation parameters help in increasing the Nusselt number.
- The Nusselt number for kerosene oil is higher than for water.
Author Contributions
Supervision, H.A.N.; Investigation, H.A.N., W.A.K. and A.M.R.; Methodology, H.A.N., W.A.K. and A.M.R.; Writing – original draft, H.A.N., W.A.K. and A.M.R.; Writing – review & editing, H.A.N., W.A.K. and A.M.R.; Funding acquisition, H.A.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deanship of Scientific Research at Prince Sattam bin Abdulaziz University under the research project No. 2020/01/14307.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haq, R.; Nadeem, S.; Khan, Z.H.; Akbar, N.S. Thermal radiation and slip effects on MHD stagnation point over of nano fluid over a stretching sheet. J. Phys. 2015, 6, 7–13. [Google Scholar]
- Kudenattia, R.B.; Kirsurb, S.R.; Achalab, L.N.; Bujurkec, N.M. MHD boundary layer flow over a non-linear stretching boundary with suction and injection. Int. J. Non Linear Mech. 2013, 50, 58–67. [Google Scholar] [CrossRef]
- Yigra, Y.; Tesfay, D. Magneto-hydrodynamic flow of viscous fluid over a non-linearly stretching sheet. J. Fluid Mech. 2014, 1, 1–11. [Google Scholar]
- Das, S.K.; Choi, S.U.S.; Yu, W.; Pradeep, T. Nanofluids-Science and Technology; John Wiley & Sons Publishers: Hoboken, NJ, USA, 2007. [Google Scholar]
- Tlili, I.; Nabwey, H.A.; Ashwinkumar, G.P.; Sandeep, N. 3-D magnetohydrodynamic AA7072-AA7075/methanol hybrid nanofluid flow above an uneven thickness surface with slip effect. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Abdelmalek, Z.; Khan, S.U.; Waqas, H.; Nabwey, H.A.; Tlili, I. Utilization of second order slip, activation energy and viscous dissipation consequences in thermally developed flow of third grade nanofluid with gyrotactic microorganisms. Symmetry 2020, 12, 309. [Google Scholar] [CrossRef]
- Kumar, S.; Prasad, S.K.; Banerjee, J. Analysis of flow and thermal field in nanofluid using a single phase thermal dispersion model. Appl. Math. Model. 2010, 34, 573–592. [Google Scholar] [CrossRef]
- Wang, F.C.; Wu, H.A. Enhanced oil droplet detachment from solid surfaces in charged nanoparticle suspensions. Soft Matter. 2013, 9, 7974–7980. [Google Scholar] [CrossRef]
- Bég, O.A.; Espinoza, D.E.S.; Kadir, A.; Shamshuddin, M.; Sohail, A. Experimental study of improved rheology and lubricity of drilling fluids enhanced with nanoparticles. Appl. Nanosci. 2018, 8, 1069–1090. [Google Scholar] [CrossRef]
- Zhu, J.; Cao, J. Effects of nanolayer and second order slip on unsteady nanofluid flow past a wedge. Mathematics 2019, 7, 1043. [Google Scholar] [CrossRef]
- Avramenko, A.A.; Shevchuk, I.V.; Tyrinov, A.I.; Blinov, D.G. Heat transfer in stable film boiling of a nanofluid over a vertical surface. Int. J. Therm. Sci. 2015, 92, 106–118. [Google Scholar] [CrossRef]
- Avramenko, A.A.; Shevchuk, I.V.; Tyrinov, A.I.; Blinov, D.G. Heat transfer at film condensation of stationary vapor with nanoparticles near a vertical plate. Appl. Therm. Eng. 2014, 73, 391–398. [Google Scholar] [CrossRef]
- Avramenko, A.A.; Shevchuk, I.V.; Tyrinov, A.I.; Blinov, D.G. Heat transfer at film condensation of moving vapor with nanoparticles over a flat surface. Int. J. Heat Mass Transf. 2015, 82, 316–324. [Google Scholar] [CrossRef]
- Avramenko, A.A.; Shevchuk, I.V. Lie group analysis and general forms of self-similar parabolic equations for fluid flow, heat and mass transfer of nanofluids. J. Therm. Anal. Calorim. 2019, 135, 223–235. [Google Scholar] [CrossRef]
- Murthy, P.V.S.N.; RamReddy, C.; Chamkha, A.J.; Rashad, A.M. Magnetic effect on thermally stratified nanofluid saturated non-darcy porous medium under convective boundary condition. Int. Commun. Heat Mass Transf. 2013, 47, 41–48. [Google Scholar] [CrossRef]
- Rashad, A.M. Impact of thermal radiation on MHD slip flow of a ferrofluid over a nonisothermal wedge. J. Magn. Magn. Mater. 2017, 422, 25–31. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Nabwey, H.A.; Abdelrahman, Z.M.A.; Rashad, A.M. Mixed bioconvective flow over a wedge in porous media drenched with a nanofluid. J. Nanofluids 2019, 8, 1692–1703. [Google Scholar] [CrossRef]
- Nabwey, H.A.; Hashmi, M.S.; Khan, S.U.; Tlili, I. A theoretical analysis for mixed convection flow of Maxwell fluid between two infinite isothermal stretching disks with heat source/sink. Symmetry 2020, 12, 62. [Google Scholar]
- Kumar, K.G.; Ramesh, G.K.; Gireesha, B.J.; Rashad, A.M. On stretched magnetic flow of Carreau nanofluid with slip effects and nonlinear thermal radiation. Nonlinear Eng. 2019, 8, 340–349. [Google Scholar] [CrossRef]
- Rashad, A.M.; Nabwey, H.A. Gyrotactic mixed bioconvection flow of a nanofluid past a circular cylinder with convective boundary condition. J. Taiwan Inst. Chem. Eng. 2019, 99, 9–17. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Rashad, A.M.; Alsabery, A.I.; Abdelrahman, Z.M.A.; Nabwey, H.A. Impact of partial slip on magneto-ferrofluids mixed convection flow in enclosure. J. Therm. Sci. Eng. Appl. 2020, 12. [Google Scholar] [CrossRef]
- Ferdows, M.; Nabwey, A.H.; Rashad, A.M.; Uddin, M.J.; Alzahrani, F. Boundary layer flow of a nanofluid past a horizontal flat plate in a Darcy porous medium: A Lie group approach. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019. [Google Scholar] [CrossRef]
- Nabwey, H.A.; El-Mkyn, H.A. Lie group analysis of thermophoresis on a vertical surface in a porous medium. J. King Saud Univ. Sci. 2019, 31, 1048–1055. [Google Scholar] [CrossRef]
- Nabwey, H.A.; Boumazgour, M.; Rashad, A.M. Group method analysis of mixed convection stagnation-point flow of non-Newtonian nanofluid over a vertical stretching surface. Indian J. Phys. 2017, 91, 731–742. [Google Scholar] [CrossRef]
- Nabwey, H.A.; EL-Kabeir, S.M.M.; Rashad, A.M. Lie group analysis of effects of radiation and chemical reaction on heat and mass transfer by unsteady slip flow from a non-isothermal stretching sheet immersed in a porous medium. J. Comput. Theor. Nanosci. 2015, 12, 4056–4062. [Google Scholar] [CrossRef]
- Bakier, A.Y.; Rashad, A.M.; Mansour, M.A. Group method analysis of melting effect on MHD mixed convection flow from radiate vertical plate embedded in a saturated porous media. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2160–2170. [Google Scholar] [CrossRef]
- EL-Kabeir, S.M.M.; EL-Hakiem, M.A.; Rashad, A.M. Group method analysis of combined heat and mass transfer by MHD non-Darcy non-Newtonian natural convection adjacent to horizontal cylinder in a saturated porous medium. Appl. Math. Model. 2008, 32, 2378–2395. [Google Scholar] [CrossRef]
- EL-Kabeir, S.M.M.; EL-Hakiem, M.A.; Rashad, A.M. Lie group analysis of unsteady MHD three dimensional by natural convection from an inclined stretching surface saturated porous medium. J. Comput. Appl. Math. 2008, 213, 582–603. [Google Scholar] [CrossRef]
- Chamkha, A.J. Unsteady hydromagnetic flow and heat transfer from a non-isothermal stretching sheet immersed in a porous medium. Int. Comm. Heat Mass Transf. 1998, 25, 899–906. [Google Scholar] [CrossRef]
- Noghrehabadi, A.; Pourrajab, R.; Ghalambaz, M. Effect of partial slip boundary condition on the flow and heat transfer of nanofluids past stretching sheet prescribed constant wall temperature. Int. J. Therm. Sci. 2012, 54, 253–261. [Google Scholar] [CrossRef]
- Rashad, A.M.; Ismael, M.A.; Chamkha, A.J.; Mansour, M.A. MHD mixed convection of localized heat source/sink in a nanofluid-filled lid-driven square cavity with partial slip. J. Taiwan Inst. Chem. Eng. 2016, 68, 173–186. [Google Scholar] [CrossRef]
- Ismael, M.A.; Pop, I.; Chamkha, A.J. Mixed convection in a lid-driven square cavity with partial slip. Int. J. Therm. Sci. 2014, 82, 47–61. [Google Scholar] [CrossRef]
- Hafidzuddin, E.H.; Nazar, R.; Arifin, N.M.; Pop, I. Effects of anisotropic slip on three-dimensional stagnation-point flow past a permeable moving surface. Eur. J. Mech. B Fluids 2017, 65, 515–521. [Google Scholar] [CrossRef]
- Roşca, A.V.; Roşca, N.C.; Pop, I. Axisymmetric stagnation point flow and heat transfer towards a permeable moving flat plate with surface slip condition. Appl. Math. Comput. 2014, 233, 139–151. [Google Scholar] [CrossRef]
- Raptis, A. Radiation and free convection flow through a porous medium. Int. Comm. Heat Mass Transf. 1998, 25, 289–295. [Google Scholar] [CrossRef]
- EL-Hakiem, M.A.; Rashad, A.M. Effect of radiation on non-Darcy free convection from a vertical cylinder embedded in a fluid-saturated porous medium with a temperature-dependent viscosity. J. Porous Media 2007, 10, 209–218. [Google Scholar]
- Sheikholeslami, M.; Gorji-Bandpy, M. Free convection of ferrofluid in a cavity heated from below in the presence of an external magnetic field. Power Technol. 2014, 256, 490–498. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Layek, G.C.; Samad, S.A. Study of MHD boundary layer flow over a heated stretching sheet with variable viscosity. Int. J. Heat Mass Transf. 2005, 48, 4460–4466. [Google Scholar] [CrossRef]
- Reddy, G.V.R.; Chamkha, A.J. Lie group analysis of chemical reaction effects on MHD free convection dissipative fluid flow past an inclined porous surface. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1557. [Google Scholar] [CrossRef][Green Version]
- Ibragimov, N.H. CRC Handbook of Lie Group Analysis of Differential Equations; CRC Press: Boca Raton, FL, USA, 1995; Volume 3. [Google Scholar]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000; Volume 107. [Google Scholar]
- Yürüsoy, M.; Pakdemirli, M.; Noyan, Ö.F. Lie group analysis of creeping flow of a second grade fluid. Int. J. Non Linear Mech. 2001, 36, 955–960. [Google Scholar] [CrossRef]
- Yürüsoy, M.; Pakdemirli, M. Exact solutions of boundary layer equations of a special non-Newtonian fluid over a stretching sheet. Mech. Res. Commun. 1999, 26, 171–175. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Bhuvaneswari, M.; Kandaswamy, P.; Ramasami, E.K. Lie group analysis of natural convection heat and mass transfer in an inclined porous surface with heat generation. Int. J. Appl. Math. Mech. 2006, 2, 34–40. [Google Scholar]
- Sivasankaran, S.; Bhuvaneswari, M.; Kandaswamy, P.; Ramasami, E.K. Lie group analysis of natural convection heat and mass transfer in an inclined surface. Nonlinear Anal. Model. Control 2006, 11, 201–212. [Google Scholar]
- Sparrow, E.M.; Quack, H.; Boerner, C.J. Local non-similarity boundary-layer solutions. AIAA J. 1970, 8, 1936–1942. [Google Scholar] [CrossRef]
- Minkowycz, W.J.; Sparrow, E.M. Numerical solution scheme for local non-similarity boundary-layer analysis. Numer. Heat Transf. Part B Fundam. Int. J. Comput. Methodol. 1978, 1, 69–85. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).