On the Efficient Monitoring of Multivariate Processes with Unknown Parameters

Abstract

Control charts are commonly used tools that deal with monitoring of process parameters in an efficient manner. Multivariate control charts are more practical and are of greater importance for timely detection of assignable causes in multiple quality characteristics. This study deals with multivariate memory control charts to address smaller shifts in process mean vector. By adopting a new homogeneous weighting scheme, we have designed an efficient structure for multivariate process monitoring. We have also investigated the effect of an estimated variance covariance matrix on the proposed chart by considering different numbers and sizes of subgroups. We have evaluated the performance of the newly proposed multivariate chart under different numbers of quality characteristics and varying sample sizes. The performance measures used in this study include average run length, standard deviation run length, extra quadratic loss, and relative average run length. The performance analysis revealed that the proposed control chart outperforms the usual scheme under both known and estimated parameters. An application of the study proposal is also presented using a data set related to Olympic archery, for the monitoring of the location of arrows over the concentric rings on the archery board.

1. Introduction

Statistical process control (SPC) is a collection of useful tools that handle the variations occurring in process parameters. It helps us to monitor any irregularities happening in the process behavior with respect to parameters of concern such as location and dispersion. It is comprised of many useful tools including a cause-and-effect diagram, check sheet, control chart, histogram, pareto chart, scatter diagram, and flowchart (stratification). A combination of all such tools is formally known as an SPC took-kit. All of these SPC tools have their own specific objectives, for example, the cause-and-effect diagram identifies the possible causes for a problem and carries out sorting of ideas into useful categories, the check sheet is used to collect and analyze data, the pareto chart filters the more significant factors, the scatter diagram shows the relationships among different factors in the process, and the flow chart separates the data gathered from various sources. The control chart gets the highest rank in the SPC tool-kit because of its ability to study/analyze process abnormalities over time. These abnormalities cause variations in the process output that may lead to deterioration of the process quality. These variations may be natural (random) or un-natural (systematic) and control charts have the ability to differentiate between these two types of variations. The natural variations are acceptable to the process, but un-natural variations are of concern to the process engineers, as delay in their identification may result into huge loss to the process owners.

In real process scenarios, we come across different quality characteristics of interest that need our attention in a process. This leads us to simultaneous handling of such variables in a multivariate set up, named multivariate SPC. The multivariate control charts are very important tools in timely identification of any changes in multiple quality characteristics of interest in a process. In the recent decades, multivariate control charts received attention because of advancements in computational facilities used as main barriers in their implementation. The three popular categories of univariate control charts (Shewhart, exponential weighted moving average (EWMA), and cumulative sum (CUSUM)) are equally effective in multivariate setup, namely, multivariate Shewhart (the well know Hotelling’s T2, [1,2]); multivariate EWMA, that is, MEWMA ([3,4]); and multivariate CUSUM, that is, MCUSUM ([5,6,7]).

The literature on multivariate SPC control charts spans multiple directions that might be of concern in process monitoring such as detections of shifts in mean vector and variance covariance matrix, interpretations of out of control signals, principal components, regression adjustments and so on. The authors of [8] discussed multivariate charts for the monitoring of individual observations. The study of [3] gave a review on multivariate control charts. Other studies [5,6,9] have extended the ideology of the study of [10] towards designing quality control charts with the scope of monitoring two or more related characteristics jointly. The work of [9] suggested the use of simultaneously classical CUSUM control charts for related observations. The authors of [5] recommended two multivariate CUSUM control charts for jointly monitoring of related characteristics. First, the multivariate CUSUM chart converts the related characteristics into scalar quantity, and then formulates the structure of the control chart, while the second CUSUM procedure forms a CUSUM vector directly from the observations. Later, the work of [6] also recommended two multivariate CUSUM control charts, name $M{C}_1$ and $M{C}_2$. The input statistic of the $M{C}_1$ control chart is based on a quadratic form using a vector of accumulated observations. The $M{C}_2$ control chart uses the scalar quantity computed through a quadratic form based on the current observation vector.

The work of [11] extended the idea of [12] for related quality characteristics, and proposed a multivariate exponential weighted moving average (MEWMA) control chart. Some of the modification in multivariate classical control charts can be seen in [13,14,15,16,17,18,19,20,21,22,23] and the references therein. The authors of [24] extended the study of [25] known as a homogeneously weighted moving average (HWMA) control chart for the multivariate setup, and named it the MHWMA control chart. The HWMA and MHWMA control charts assign a specific weight to the current observation, and the remaining weight is equally assigned to the rest of the observations for effective process monitoring.

The remaining part of the article is arranged as follows: Section 2 describes the preliminaries and some existing multivariate control charts available; Section 3 provides the charring structure of proposed multivariate control chart; Section 4 provides performance measures and evaluation of the proposed chart and estimation effects, along with a comparative analysis with some existing charts; Section 5 provides an illustrative example that demonstrates the implementation of the proposal; and finally, Section 6 concludes the study and provides some future recommendations.

2. Preliminaries and Existing Multivariate Control Charts

Let $X$be a $p$ dimensional vector $\left(X_{p\times 1}\right)$ having multivariate normal distribution with $\mathsf{\mu }$ (mean vector) and $\Sigma$ (variance-covariance matrix), written as follows: $X~{\mathcal{N}}_p\left(\mathsf{\mu },\Sigma \right)$. Here, $\mathsf{\mu }$ is $p\times 1$ mean vector $\left({\mathsf{\mu }}_{p\times 1}\right)$ and $\Sigma$ is a $p\times p$ matrix$\left({\Sigma }_{p\times p}\right)$. For our study purposes, we will use ${\mathsf{\mu }}_0$ for the known mean vector and ${\Sigma }_0$ for the known variance–covariance matrix. The $X$, $\mathsf{\mu }$, $\Sigma$ are defined, respectively, as follows:

$$\begin{gathered} X={[{\mathrm{X}}_1{\mathrm{X}}_2{\mathrm{X}}_3\dots {\mathrm{X}}_p]}^{\prime } \\ \mathsf{\mu }={[{\mathsf{\mu }}_1{\mathsf{\mu }}_2{\mathsf{\mu }}_3\dots {\mathsf{\mu }}_p]}^{\prime } \\ \Sigma =\left[\begin{array}{cc}\begin{array}{c}{\sigma }_1^2\\ \begin{array}{c}{\sigma }_{21}\\ ⋮\\ {\sigma }_{p1}\end{array}\end{array}& \begin{array}{ccc}\begin{array}{c}{\sigma }_{11}\\ \begin{array}{c}{\sigma }_2^2\\ ⋮\\ {\sigma }_{p1}\end{array}\end{array}& \begin{array}{c}\cdots \\ \begin{array}{c}\cdots \\ \ddots \\ \cdots \end{array}\end{array}& \begin{array}{c}{\sigma }_{1p}\\ \begin{array}{c}{\sigma }_{21}\\ ⋮\\ {\sigma }_p^2\end{array}\end{array}\end{array}\end{array}\right] \end{gathered}$$

Let $X_t=\left[x_{i1t}{x}_{i2t}{x}_{i3t}\dots x_{ipt}\right]$ be the $t^{th}$ sample matrix consisting of $x_{ijt}$ as the $i^{th}$ ($i=1,2,\cdots ,n$) observation of the $j^{th}$ ($j=1,2,\cdots ,p$) quality charectersitic on the $t^{th}$ ($t=1,2,\cdots ,m$) sample. The multivariate data structure can be presented as given in Table A1 (Appendix A).

Let ${\overline{X}}_t$ and $S_t$ be the $p$ dimensional $t^{th}$ sample mean vector and sample variance–covariance matrix $({\overline{X}}_{p\times 1}$and$S_{p\times p}$), respectively. These are defined as follows:

${\overline{X}}_t={\left[\begin{array}{cc}\begin{array}{cc}{\overline{X}}_{1t}& {\overline{X}}_{2t}\end{array}& \begin{array}{cc}\cdots & {\overline{X}}_{pt}\end{array}\end{array}\right]}^{\prime }=\left[\begin{array}{c}{\overline{X}}_{1t}\\ {\overline{X}}_{\begin{array}{c}2t\\ ⋮\\ {\overline{X}}_{pt}\end{array}}\end{array}\right]$, ${\overline{X}}_{kt}=\frac{1}{n}{\displaystyle \sum }_{i=1}^{n}n{x}_{ikt}$, for $k=1,2,,\dots ,p$ and

Analogue with $S_t=\left[S_{klt}\right]$, where

$$\begin{gathered} S_{kkt}=S_{kt}^2=\frac{1}{n-1}{\displaystyle \sum }_{i-1}^n{\left(x_{ikt}-{\overline{X}}_{kt}\right)}^2 \\ {S}_{kkt}=S_{kt}^2=\frac{1}{n-1}{\displaystyle \sum }_{i-1}^n\left(x_{ikt}-{\overline{X}}_{kt}\right)\left(x_{ikt}-{\overline{X}}_{kt}\right). \end{gathered}$$

In practice, when ${\mathsf{\mu }}_0$ and ${\Sigma }_0$ are unknown, both are estimated from $m$in-control Phase I for each sample of sample size$n$ as follows:

$$\stackrel{\overline{¯}}{X}=\frac{{{\displaystyle \sum }}_{t=1}^m{\overline{X}}_t}{m}\mathrm{and}\overline{S}=\left[\begin{array}{c}\begin{array}{cc}\begin{array}{cc}{\overline{s}}_1^2& {\overline{s}}_{12}\end{array}& \begin{array}{cc}\cdots & {\overline{s}}_{1p}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{cc}\begin{array}{cc}{\overline{s}}_{21}& {\overline{s}}_1^2\end{array}& \begin{array}{cc}\cdots & {\overline{s}}_{2p}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{cc}\begin{array}{cc}⋮& ⋮\end{array}& \begin{array}{cc}\ddots & ⋮\end{array}\end{array}\\ \begin{array}{cc}\begin{array}{cc}{\overline{s}}_{p1}& {\overline{s}}_{p2}\end{array}& \begin{array}{cc}\cdots & {\overline{s}}_p^2\end{array}\end{array}\end{array}\end{array}\end{array}\right]$$

where ${\overline{S}}_j^2=\frac{{{\displaystyle \sum }}_{t=1}^m{S}_{jt}^2}{m}$and ${\overline{S}}_{jl}=\frac{{{\displaystyle \sum }}_{t=1}^m{S}_{jlt}}{m}\forall j\ne l$. The diagonal elements of are means of sample variances associated to $j^{th}$ quality characteristics $p$ and off-diagonal are means of sample covariances, obtained from $m$ samples. It is to be missioned that $\overline{X}$ refers to the mean vector of a particular sub-group, while $\stackrel{\overline{¯}}{X}$ refers to overall the mean vector of all the m sub-groups.

We provide brief details of some common multivariate chats and propose a new control chart (for known and unknown parameters) for the mean vector.

2.1. Existing Multivariate Charts

The following section expresses the charting structures of existing multivariate control charts including ${\chi }^2$/Hotelling’s $T^2$, $MCUSU{M}_c$, $MCUSU{M}_{PR}$, $MEWM{A}_L$, and $MHWM{A}_A$ charts by [2,5,6,11,24], respectively.

2.1.1. ${\chi }^2$ and Hotelling’s $T^2$ Charts

The Shewhart multivariate process control chart based on the weighted Mahalanobis distance of the sample mean from the process mean is (cf. [2]) as follows:

$${\chi }_t^2=n{\left({\overline{X}}_t-{\mathsf{\mu }}_0\right)}^{\prime }{\Sigma }_0^{-1}\left({\overline{X}}_t-{\mathsf{\mu }}_0\right)$$

$$\forall t=1,2,\cdots ,m.$$

(1)

As $X~{\mathcal{N}}_p\left({\mathsf{\mu }}_0,{\Sigma }_0\right)$, the control charting statistics (1) follows ${\chi }_t^2$ distribution (Chi-square probability distribution with t degrees of freedom), which gives an out-of-control signal, if${\chi }_t^2>h_0$, where $h_0={\chi }_{\alpha ,p}^2$. (${\chi }_{\alpha ,p}^2$ is the $p$-dimensional ${\alpha }^{th}$ upper percentage point of the ${\chi }^2$ distribution) is a specified control limit. The study of [1] proposed the special case of (1) to monitor sample point as ${\left(X-{\mathsf{\mu }}_0\right)}^{\prime }{\Sigma }_0^{-1}\left(X-{\mathsf{\mu }}_0\right)$ for$n=1$. By replacing ${\mathsf{\mu }}_0$ and ${\Sigma }_0$ with $\stackrel{\overline{¯}}{X}$ and $\overline{S}$, respectively, the expression (1) becomes the following:

$$T_t^2=n{\left(\overline{X}-\stackrel{\overline{¯}}{X}\right)}^{\prime }{\overline{S}}^{-1}\left(\overline{X}-\stackrel{\overline{¯}}{X}\right)$$

(2)

Under the assumption that the $m$ samples are independent and the joint distributions of the $p$ variables is the multivariate normal, $T_t^2$ follows $\frac{p\left(m-1\right)\left(n-1\right)}{mn-m-p+1}$ times $F_{v_1,v_2}$ distribution with degree of freedom $v_1=p$ and (cf. [26]). Expression (2) becomes $T_t^2={\left(X-\overline{X}\right)}^{\prime }{\overline{S}}^{-1}\left(X-\overline{X}\right)$ at $n=1$, which is called Hotelling’s $T^2$ chart for individuals (cf. [7]). The Hotelling’s $T^2$ chart gives an out-of-control signal if $T_t^2>h_1$, where $h_1=\frac{p\left(m-1\right)\left(n-1\right)}{mn-m-p+1}{F}_{\alpha ,v_1,v_2}$.

2.1.2. ${\mathrm{MCUSUM}}_{\mathrm{C}}$ Chart

The study of [5] proposed two multivariate CUSUM charts. One of these charts (the superior one) is based on the charting statistics:

$$C_t=\sqrt{{\left(S_{t-1}+{\overline{X}}_t-{\mathsf{\mu }}_0\right)}^{\prime }{\Sigma }_0^{-1}\left(S_{t-1}+{\overline{X}}_t-{\mathsf{\mu }}_0\right)}.$$

(3)

where $S_t=0\mathrm{if}{C}_t\le k$, $S_t=\left(S_{t-1}+{\overline{X}}_t-{\mathsf{\mu }}_0\right)\left(1-k/C_t\right)\mathrm{if}{C}_t>k$, $S_0=0$, and $k=0.5\frac{n{\left(\mu -{\mu }_0\right)}^{\prime }{\Sigma }_0^{-1}\left(\mu -{\mu }_0\right)}{\sqrt{n{\left(\mu -{\mu }_0\right)}^{\prime }{\Sigma }_0^{-1}\left(\mu -{\mu }_0\right)}}\forall k>0$. The MCUSUM chart gives an out-of-control alarm if

$$T_{t\left(C\right)}^2=S_t^{\prime }{\Sigma }_0^{-1}{S}_t>h_2.$$

(4)

where $h_2$ is chosen to achieve a desired value of in-control average run length (ARL).

2.1.3. ${\mathrm{MCUSUM}}_{PR}$ Chart

The work of [6] proposed two invariant multivariate CUSUM charts. Both charts are based on the quadratic forms of the mean vector and can be distinguished with respect to the accumulation (i.e., the sum).

$\mathit{M}{\mathit{C}}_1$Chart: The $M{C}_1$ accumulates the $X$ vectors and then generates the quadratic forms, while in$M{C}_2$, initially, the quadratic form is produced for each $X$, and then these are accumulated at a later stage.

$$C_t^1={\displaystyle \sum }_{l=t-n_t+1}^t\left(X_l-{\mathsf{\mu }}_0\right)$$

(5)

where $n_t$ the number of subgroups since the most recent renewal (i.e., zero value) of the CUSUM. As $C_t^1/n_t$ can be written as

$$\frac{C_t^1}{n_t}=\left(\frac{1}{n_t}{\displaystyle \sum }_{l=t-n_t+1}^t{X}_l\right)-{\mathsf{\mu }}_0$$

the vector $C_t^1/n_t$ represents the difference between the accumulated sample average and the target mean. Therefore, at time$t$, the multivariate process mean may be estimated as $C_t^1/n_t+{\mathsf{\mu }}_0$. The norm of $C_t^1$ is a measure of the distance between the estimate and the target, mathematically defined as follows:

$$\Vert C_t^1\Vert =\sqrt{C_t^1{}^{\prime }{\Sigma }_0^{-1}{C}_t^1}$$

A multivariate control chart can be constructed by defining $M{C}_1$ chart as

$${\mathrm{MC}}_{1_{\mathrm{t}}}=\max \{\Vert {\mathrm{C}}_{\mathrm{t}}^1\Vert -\mathrm{k}{\mathrm{n}}_{\mathrm{t}},0\}$$

(6)

and

$${\mathrm{n}}_{\mathrm{t}}=\{\begin{array}{cc}{\mathrm{n}}_{\mathrm{t}-1}+1& {\mathrm{if}\mathrm{MC}}_{1_{\mathrm{t}-1}}>0\\ 1& \mathrm{otherwise}\end{array}$$

(7)

The multivariate process thorough this multivariate CUSUM chart will be declared as out-of-control if$M{C}_{1_t}>h_3$, where $h_3$ is chosen to achieve a desired value of in-control ARL.

$\mathit{M}{\mathit{C}}_2$Chart: In the $M{C}_1$ chart, if accumulation function is applied after taking the square of the distance of each sample mean from ${\mathsf{\mu }}_0$, it results in a new structure. As a result, we evaluate ${\mathrm{D}}_t^2$ of the $t^{th}$ sample mean as follows:

$${\mathrm{D}}_{\mathrm{t}}^2={\left({\mathrm{X}}_{\mathrm{t}}-{\mathsf{\mu }}_0\right)}^{\prime }{\Sigma }_0^{-1}\left({\mathrm{X}}_{\mathrm{t}}-{\mathsf{\mu }}_0\right)$$

(8)

having a ${\chi }^2$ with $p$ degrees of freedom (on-target) and a non-central ${\chi }^2$ (off-target). A one-sided CUSUM structure is given as follows:

$${\mathrm{MC}}_{2_{\mathrm{t}}}=\max \left\{0,{\mathrm{MC}}_{2_{\mathrm{t}-1}}+{\mathrm{D}}_{\mathrm{t}}^2-\mathrm{k}\right\}$$

(9)

where $M{C}_{2_0}$= 0. An out-of-control signal is alarmed if$M{C}_{2_t}>h_3^{\prime }$, where $h_3^{\prime }$ is set according to a desired in-control ARL.

2.1.4. ${\mathrm{MEWMA}}_L$ Chart

The work of [11] developed the multivariate EWMA (${\mathrm{MEWMA}}_L$) chart to quickly detect shifts in the process mean vector $\mathsf{\mu }$ from the target vector ${\mu }_0$, and its statistic is defined as follows:

$$Z_t=\mathsf{\lambda }{\overline{X}}_t+\left(I-\mathsf{\lambda }\right)Z_{t-1}$$

(10)

where, initially, ${\mathrm{Z}}_0={\mu }_0$, $\mathsf{\lambda }=\mathrm{diag}\left({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_p\right)$ of the smoothing constant with $0<{\lambda }_j\le 1$, $j=1,2,...,p$ (usually in practice ${\lambda }_1={\lambda }_2=\dots ={\lambda }_p=\lambda$), and $I$ is the identity matrix (cf. [11]). The process gives an out-of-control signal in ${\mathrm{MEWMA}}_L$ chart when

$${\mathrm{T}}_{\mathrm{t}\left(\mathrm{L}\right)}^2={\left({\mathrm{Z}}_{\mathrm{t}}-{\mathsf{\mu }}_0\right)}^{\prime }{\Sigma }_{{\mathrm{Z}}_{\mathrm{t}}}^{-1}\left({\mathrm{Z}}_{\mathrm{t}}-{\mathsf{\mu }}_0\right)>{\mathrm{h}}_4$$

(11)

where $h_4$ is selected to get the chosen in-control average run length. The term ${\Sigma }_{Z_t}$ is an asymptotic variance–covariance matrix (as$t\to \infty$) defined as ${\Sigma }_{Z_t}=\frac{\lambda }{2-\lambda }{\Sigma }_0$, while ${\Sigma }_{Z_t}=\frac{\lambda \left[1-{\left(1-\lambda \right)}^{2t}\right]}{2-\lambda }{\Sigma }_0$ is the time varying variance–covariance matrix. Symbolically, for the ${\mathrm{MEWMA}}_L$ chart for asymptotic and time varying cases, we may write as ${\mathrm{MEWMA}}_{L_{as}}$ and ${\mathrm{MEWMA}}_{L_{tv}}$, respectively. It is to be noted that, when$\lambda =1$, the ${\mathrm{MEWMA}}_L$ chart is converted to Hotelling’s $T^2$ chart. (cf. [11]).

2.1.5. ${\mathrm{MHWMA}}_A$ Chart

The study of [24] proposed a multivariate homogeneously weighted moving average (${\mathrm{MHWMA}}_A$) chart for the mean vector. The plotting statistic of ${\mathrm{MHWMA}}_A$ chart is given as follows:

$${\mathrm{H}}_{\mathrm{t}}={\mathsf{\lambda }\mathrm{X}}_{\mathrm{t}}+\left(\mathrm{I}-\mathsf{\lambda }\right){\overline{\mathrm{X}}}_{\mathrm{t}-1}$$

(12)

where ${\overline{X}}_{t-1}$ represents the sample average of the previous information up to and including the $t-1$ observation, ${\overline{X}}_0={\mathsf{\mu }}_0$. For the case of equal $\lambda s$, the $\mathsf{\lambda }$ will be $\mathsf{\lambda }=\mathrm{diag}\left(\lambda ,\lambda ,\dots ,\lambda \right)$ in Equation (12).

The chart indicates a signal if

$${\mathrm{T}}_{\mathrm{t}\left(\mathrm{A}\right)}^2={\left({\mathrm{H}}_{\mathrm{t}}-{\mathsf{\mu }}_0\right)}^{\prime }{\Sigma }_{{\mathrm{H}}_{\mathrm{t}}}^{-1}\left({\mathrm{H}}_{\mathrm{t}}-{\mathsf{\mu }}_0\right)>{\mathrm{h}}_5$$

(13)

where $h_5$ and $\mathsf{\lambda }$ are set based on the in-control average run length ($ARL$), and ${\Sigma }_{H_t}$ refers to the variance–covariance matrix defined as follows:

$${\Sigma }_{{\mathrm{H}}_{\mathrm{t}}}=\{\begin{array}{cc}{\mathsf{\lambda }}^2{\Sigma }_0& \mathrm{if}\mathrm{t}=1\\ {\mathsf{\lambda }}^2{\Sigma }_0+{\left(\mathrm{I}-\mathsf{\lambda }\right)}^2\frac{{\Sigma }_0}{\mathrm{t}-1}& \mathrm{if}\mathrm{t}>1\end{array}$$

(14)

If $p$ = 1, the monitoring statistic in Equation (12) becomes $H_t=\lambda X_t+\left(1-\lambda \right){\overline{X}}_{t-1}$ and the variance of $H_t$ in Equation (14) becomes ${\sigma }_{H_t}^2={\mathsf{\lambda }}^2{\sigma }_0^2$($\mathrm{if}t=1$) and ${\sigma }_{H_t}^2={\mathsf{\lambda }}^2{\sigma }_0^2+{\left(1-\mathsf{\lambda }\right)}^2\frac{{\sigma }_0^2}{t-1}$($\mathrm{if}t>1$). Further details can be seen in [24].

3. The Proposed $MHWM{A}_p$ Control Chart for Subgroups

The proposed multivariate homogeneous weighted moving average (${\mathrm{MHWMA}}_P$) assigns a certain weight to current sample and the remaining weight is uniformly distributed among the previous samples. The charting statistic of this chart, for subgroups of size n, is defined as follows:

$${\mathrm{MH}}_{\mathrm{t}}={\mathsf{\lambda }\overline{\mathrm{X}}}_{\mathrm{t}}+\left(\mathrm{I}-\mathsf{\lambda }\right){\stackrel{\overline{¯}}{\mathrm{X}}}_{\mathrm{t}-1},\forall t=1,2,\cdots ,m.$$

(15)

This can also be extended as follows:

$$M{H}_t=\mathsf{\lambda }{\overline{X}}_t+\left[\left(\frac{I-\mathsf{\lambda }}{t-1}\right)\left\{{\overline{X}}_{t-1}+{\overline{X}}_{t-2}+...+{\overline{X}}_1\right\}\right]$$

(16)

where ${\overline{X}}_t$ denotes the sample mean vector for $t^{th}$ sample, and ${\stackrel{\overline{¯}}{X}}_{t-1}$ is the mean vector based on the means of $t-1$ preceding samples. Initially, the value of ${\overline{X}}_0$ is set equal to the in-control sample mean vector, that is, ${\overline{X}}_0={\mathsf{\mu }}_0$. As mentioned earlier, the quality characteristic$X_t\sim {\mathcal{N}}_p\left({\mathsf{\mu }}_0,{\Sigma }_0\right)$. So, it is a well-known fact that the distribution of the sample mean vector ${\overline{X}}_t$ is also normal with ${\mathsf{\mu }}_0$ and $\frac{{\Sigma }_0}{n}$, that is, ${\overline{X}}_t\sim {\mathcal{N}}_p\left({\mathsf{\mu }}_0,\frac{{\Sigma }_0}{n}\right)$ (cf. [27]). The process signals in ${\mathrm{MHWMA}}_P$ chart when

$$T_{t\left(P\right)}^2=n{\left(M{H}_t-{\mathsf{\mu }}_0\right)}^{\prime }{\Sigma }_{M{H}_t}^{-1}\left(M{H}_t-{\mathsf{\mu }}_0\right)>h_6$$

(17)

where $h_6$ is set according to a pre-specified in-control$ARL$, and ${\Sigma }_{M{H}_t}$ is the variance–covariance matrix at time $t$ defined as follows:

$${\Sigma }_{{\mathrm{MH}}_{\mathrm{t}}}=\{\begin{array}{cc}{\mathsf{\lambda }}^2\frac{{\Sigma }_0}{\mathrm{n}}& \mathrm{if}\mathrm{t}=1\\ {\mathsf{\lambda }}^2\frac{{\Sigma }_0}{\mathrm{n}}+{\left(\mathrm{I}-\mathsf{\lambda }\right)}^2\frac{{\Sigma }_0}{\mathrm{n}\left(\mathrm{t}-1\right)}& \mathrm{if}\mathrm{t}>1\end{array}$$

(18)

If $p$= 1, we have $M{H}_t=\lambda {\overline{X}}_t+\left(1-\lambda \right){\stackrel{\overline{¯}}{X}}_{t-1}$ (cf. Equation (15)), and the variance of ${\mathrm{MH}}_t$ in Equation (14) becomes ${\sigma }_{M{H}_t}^2={\mathsf{\lambda }}^2\frac{{\sigma }_0^2}{n}$($\mathrm{if}t=1$) and ${\sigma }_{M{H}_t}^2={\mathsf{\lambda }}^2\frac{{\sigma }_0^2}{n}+{\left(1-\mathsf{\lambda }\right)}^2\frac{{\sigma }_0^2}{n\left(t-1\right)}$($\mathrm{if}t>1$). The mean $\left(E\left(M{H}_t\right)\right)$ and variance $\left(V\left(M{H}_t\right)\right)$ under in-control situation are derived in the Appendix A.

Estimation of Unknown Parameters for MHWMA_P Chart for Subgroups

According to [4], the sampling distribution of charting statistics of a chart should be accounted for variation because it may seriously affect the in-control and out-of-control performance. The denial of this variation may cause a significant increase in the number of false alarms in the case of small sample size data in Phase I. The estimation error is inversely proportional to sample size of Phase I data ([4]).

As in the previous Section 2.1, we usually assume normality and known parameters such as mean vector and variance–covariance matrix (cf. [24]). However, these parameters, that is, ${\mathsf{\mu }}_0$ and ${\Sigma }_0$, are not always known in practice, and hence estimation is used, which ultimately affects charts’ performance. In this section, we study the performance of the MHWMA chart under the estimation case. When the ${\mathsf{\mu }}_0$ and ${\Sigma }_0$ are unknown, they are usually estimated based on $m$ subgroup (of a fixed size$n$) from an in-control${\mathcal{N}}_p\left({\mathsf{\mu }}_0,{\Sigma }_0\right)$, where $m>1$ and$m\left(n-1\right)>p$. The estimators of ${\mathsf{\mu }}_0$ and ${\Sigma }_0$ are ${\widehat{\mathsf{\mu }}}_0=\stackrel{\overline{¯}}{X}$ and${\widehat{\Sigma }}_0=\overline{S}$. The study of [27] showed that the in-control estimator of the mean vector $\stackrel{\overline{¯}}{X}\sim {\mathcal{N}}_p\left({\mathsf{\mu }}_0,\frac{{\Sigma }_0}{nm}\right)$ and the matrix$\left[m\left(n-1\right)\overline{S}\right]\sim Wishar{t}_p\left[{\Sigma }_0,m\left(n-1\right)\right]$.

In this study, we discuss two cases, namely Case I and Case II:

Case I: The values of ${\mathsf{\mu }}_0$ and ${\Sigma }_0$are known and the control limits for Case I are defined in (19);

Case II: The values of ${\mathsf{\mu }}_0$ and ${\Sigma }_0$are estimated from Phase I as $\widehat{\mathsf{\mu }}=\stackrel{\overline{¯}}{X}$. and $\widehat{\Sigma }=\overline{S}$ (derived in Appendix A–III). On the basis of $\widehat{\mathsf{\mu }}$ and $\widehat{\Sigma }$, the process gives an out-of-control signal in ${\mathrm{MHWMA}}_P$ chart when

$${\mathrm{T}}_{\mathrm{t}\left(\mathrm{P}\right)}^2=\mathrm{n}{\left({\mathrm{MH}}_{\mathrm{t}}-\widehat{\mathsf{\mu }}\right)}^{\prime }{\Sigma }_{{\mathrm{MH}}_{\mathrm{t}}}^{-1}\left({\mathrm{MH}}_{\mathrm{t}}-\widehat{\mathsf{\mu }}\right)>{\mathrm{h}}_6^{\prime }$$

(19)

where $h_6^{\prime }$ is chosen to achieve a desired in-control $ARL$ performance measure, and ${\mathbf{\Sigma }}_{{\mathrm{MH}}_{\mathit{t}}}$ is the covariance matrix at time point$t$ defined as follows:

$${\Sigma }_{{\mathrm{MH}}_{\mathrm{t}}}=\{\begin{array}{cc}{\mathsf{\lambda }}^2\frac{\widehat{\Sigma }}{\mathrm{n}}& \mathrm{if}\mathrm{t}=1\\ {\mathsf{\lambda }}^2\frac{\widehat{\Sigma }}{\mathrm{n}}+{\left(\mathrm{I}-\mathsf{\lambda }\right)}^2\frac{\widehat{\Sigma }}{\mathrm{n}\left(\mathrm{t}-1\right)}& \mathrm{if}\mathrm{t}>1\end{array}$$

(20)

The estimated mean $\left(E\left(M{H}_t\right)\right)$ and estimated variance $\left(V\left(M{H}_t\right)\right)$ under the in-control situation are derived in the Appendix A.

4. Performance Evaluations and Comparisons

The current section comprises of a set of performance measures that are based on the run length observations. These performance measures, namely, average run length ($ARL$), standard deviation of the run length $\left(SDRL\right),$extra quadratic loss ($EQL$), relative average run length ($RARL$), and performance comparison index ($PCI$), are analyzed to examine and compare the detection capability of different charts. The $ARL$ studies the performance of a chart at each shift separately, while$EQL$, $RARL$, and $PCI$ deal with the overall shift range. The term δ can be defined as$\delta =\sqrt{n{\left({\mathsf{\mu }}_1-{\mathsf{\mu }}_0\right)}^{\prime }{\Sigma }_0^{-1}\left({\mathsf{\mu }}_1-{\mathsf{\mu }}_0\right)}$, where ${\mathsf{\mu }}_1$ is out-of-control mean vector (cf. [24]). These measures are defined as follows.

Average Run Length (ARL) is the expected number of points prior to a point indicates an out-of-control signal by the chart. The $AR{L}_0$ and $AR{L}_1$ are two types of ARL mentioned as the in-control and out-of-control situation of a process, respectively. ARL₀ and ARL₁ are the average number of samples desired to get a false alarm in an in-control situation and a shift in an out-of-control situation, respectively. $AR{L}_1\le AR{L}_0$, a chart with a lower $AR{L}_1$ is considered as an efficient chart relative to another chart (cf. [28]). The best chart acquires a lower number of samples to detect the shift in the minimum ARL value. ARL has been used as a performance measure in many research articles such as [29,30].

Along with $ARL$, we have also reported standard deviation of run length ($SDRL$) to assess the behavior of the run length distribution (cf. [31]), which measure of the spread in the run length around its center.

Extra Quadratic Loss (EQL) is a measure used to assess the overall ability of a chart (cf. [32,33,34]). Mathematically, $\mathrm{EQL}={\left({\delta }_{max}-{\delta }_{min}\right)}^{-1}{{\displaystyle \int }}_{{\delta }_{min}}^{{\delta }_{max}}{\delta }^2\mathrm{ARL}\left(\delta \right)d\delta ,\forall \delta \in \left[{\delta }_{min},{\delta }_{max}\right]$. The distribution of $\delta$ is uniform with density function ${\left({\delta }_{max}-{\delta }_{min}\right)}^{-1}$ over the entire shift range $\left[{\delta }_{min},{\delta }_{max}\right]$ (cf. [28,35]). The probability distribution of $\delta$ (other than normal distribution) has a partial impact on EQL-based performance of charts (cf. [36]). The best performing chart has a minimum EQL value as compared with any competing chart. A control chart exhibiting superior EQL performance under uniform distribution of shift also offers superior performance under non-uniform cases.

Relative Average Run Length (RARL) inspects the overall performance of a chart relative a benchmark chart (cf. [33]). Mathematically, it is defined as $\mathrm{RARL}={\left({\delta }_{max}-{\delta }_{min}\right)}^{-1}{{\displaystyle \int }}_{{\delta }_{min}}^{{\delta }_{max}}\mathrm{ARL}\left(\delta \right)/{\mathrm{ARL}}_{\mathrm{opt}}\left(\delta \right)d\delta$, where $\mathrm{ARL}\left(\delta \right)$ and ${\mathrm{ARL}}_{\mathrm{opt}}\left(\delta \right)$ are the ARL of a specific chart and the standard charts, respectively, at$\delta$. For a standard chart, the RARL is equal to 1.

Performance Comparison Index (PCI) evaluates the performance of control charts based on the EQL. It is defined as the ratio of EQL value of a specific chart to EQL value of optimum chart (cf. [37]). Analogous with RARL, PCI may also get two values: PCI = 1 and PCI > 1 for best and competing charts, respectively. Mathematically, $PCI=EQL/EQ{L}_{opt}$. As RARL and PCI have similar interpretations, they may be used instead of each other. One may see more details of these performance measures in [32,37] and the references therein.

4.1. Monte Carlo Simulation Procedure

The Monte Carlo simulation technique is used to get am estimated solution of certain mathematical and statistical complixities. The literature on this simulation technique can be seen in [38,39,40], and the references therein. In order to find the values ARLs and SDRLs, a Monte Carlo simulation study based on 50,000 replications is carried out in R language (cf. [41]) by setting$AR{L}_0\approx 200$; $p=2,3,4,5,\mathrm{and}10$; $k_1=k_2=0.50$; and $\lambda =0.10$. For a suitable number of Monte Carlo simulation iterations in quality control, one may see [40,42,43]. The aforementioned computational methods are quite popular for control charts (cf. [44,45]). The calculation technique is described as follows:

• Generate the random samples from multivariable normal distribution and compute the values of the charting statistics Hotelling’s$T^2$,${\mathrm{MCUSUM}}_C$, ${MC}_1$, ${\mathrm{MEWMA}}_{L_{as}}$, ${\mathrm{MEWMA}}_{L_{tv}}$, and ${\mathrm{MHWMA}}_P$.
• Establish the control limits for all charting statistics.
• Calculate the values of ARL and SDRL for each charting statistics at changing shift values $\delta$ (0.50, 1.0, 1.5, 2.0, 2.5, and 3) for fixed$AR{L}_0=200$.

In order to compute other performance measures, we applied famous numerical integration procedures (such as Simpson/Trapezoidal methods) through these steps.

• Multiply ARL with ${\mathsf{\delta }}^2$ and inverse of range of $\delta$ values as $\left[0.50,3.0\right]$.
• Get $EQL$ by integrating the result (obtained in step i) over $\delta$ range using the Simpson or Trapezoidal integration technique.
• Take the ratio of the $ARL$s of a specific to optimum/standard charts and multiply with the inverse of entire range of $\delta$.
• Calculate $RARL$ by integrating the output over $\delta$ range.
• Get PCI by taking the ratio of $EQLs$ of a particular chart to the optimum/standard chart.

4.2. Performance Analysis and Comparisons

This section provides a comparative analysis of understudy and proposed charts using two methods, namely, (i) point to point shifts approach and (ii) entire shift range approach. The first approach is used to calculate ARL values, while the second is used to obtain the values of EQL, RARL, and PCI measures. The ARL values are obtained for understudy charts and the $\log \left(ARL\right)$ values are plotted along with $\delta$ values for a better comparative view (cf. Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5). On the basis of the ARL₁ values, we calculated the cumulative $EQL,RARL$, and $PCI$ values, namely, $CEQL,CRARL$, and $CPCI$, respectively, and the results are given in Table 1, Table 2 and Table 3. On the basis of Table 1, Table 2 and Table 3, we have also provided the superiority order understudy charts at varying choices of $p$ and δ in Table 4.

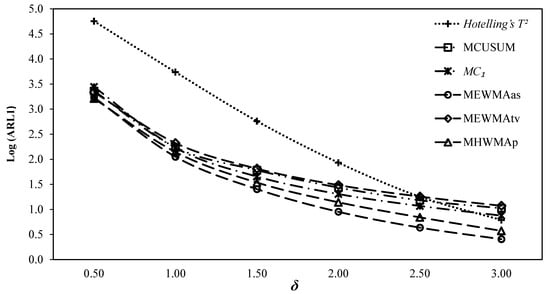
Figure 1. Average run length (ARL) comparisons for$p=2$. MEWMA, multivariate exponential weighted moving average; MHWMA, multivariate homogeneously weighted moving average; MCUSUM, multivariate CUSUM.

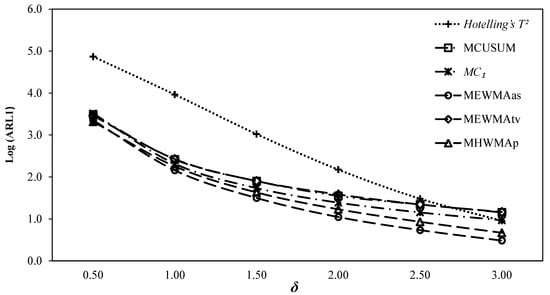
Figure 2. ARL comparisons for$p=3$.

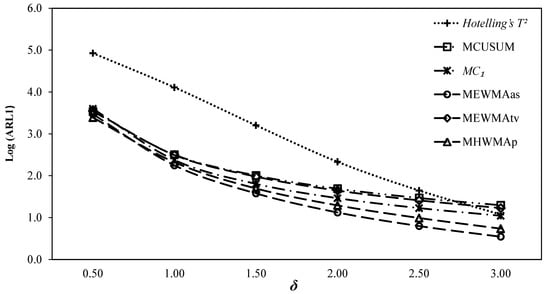
Figure 3. ARL comparisons for$p=4$.

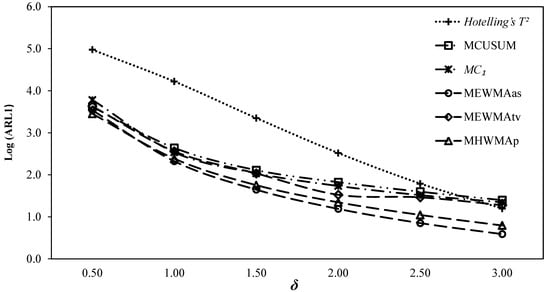
Figure 4. ARL comparisons for$p=5$.

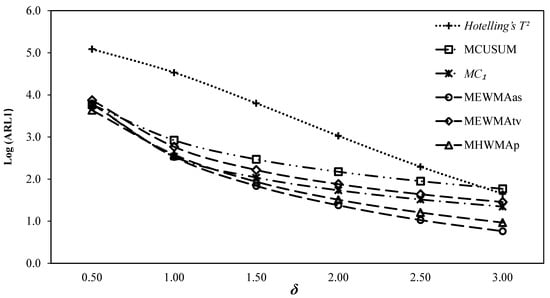
Figure 5. ARL comparisons for$p=10$.

Table 1. Cumulative extra quadratic loss (EQL) values for different charts. MEWMA, multivariate exponential weighted moving average; MHWMA, multivariate homogeneously weighted moving average; MCUSUM, multivariate CUSUM.

p	$p=2$						$p=3$
Chart	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp
δ	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10
0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
0.5	14.50	3.60	3.91	3.16	3.51	3.10	16.25	4.09	4.19	3.56	3.98	3.44
1	25.00	5.94	6.23	5.10	6.06	5.23	29.40	6.89	6.71	5.72	6.80	5.82
1.5	29.59	7.74	7.66	6.22	8.04	6.65	36.05	8.97	8.28	6.93	8.93	7.38
2	30.09	9.58	9.06	7.11	9.95	7.86	37.21	10.96	9.80	7.88	11.01	8.68
2.5	29.02	11.38	10.55	7.90	11.92	8.99	36.04	13.04	11.42	8.74	13.14	9.90
3	27.65	13.27	12.10	8.69	13.95	10.03	34.27	15.24	13.14	9.58	15.35	11.03
p	$p=4$						$p=5$
Chart	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp
δ	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10
0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
0.5	17.25	4.28	4.56	4.01	4.34	3.70	18.13	4.65	5.49	4.29	4.71	3.95
1	32.48	7.33	7.25	6.38	7.36	6.25	35.15	8.15	8.64	6.84	7.94	6.65
1.5	41.03	9.70	8.90	7.64	9.64	7.90	45.47	10.86	10.73	8.20	10.30	8.40
2	42.84	12.07	10.55	8.63	11.85	9.28	48.32	13.57	13.03	9.25	12.17	9.85
2.5	41.63	14.54	12.30	9.52	14.11	10.56	47.36	16.42	15.53	10.17	14.27	11.19
3	39.60	17.11	14.15	10.38	16.46	11.77	45.07	19.29	18.19	11.05	16.83	12.46
			p	$p=10$
			Chart	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp
			δ	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10
			0	NA	NA	NA	NA	NA	NA
			0.5	20.25	5.40	5.49	5.54	6.01	4.73
			1	43.45	10.05	8.64	8.66	9.99	8.03
			1.5	61.20	14.23	10.73	10.21	12.74	10.16
			2	68.77	18.38	13.03	11.41	15.41	11.83
			2.5	69.44	22.62	15.53	12.45	18.17	13.36
			3	66.93	26.90	18.19	13.44	21.03	14.84

Table 2. Cumulative relative average run length (RARL) values for different charts.

p	$p=2$						$p=3$
Chart	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp
δ	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10
0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
0.5	2.84	1.08	1.14	1.01	1.07	1.00	2.86	1.09	1.11	1.02	1.08	1.00
1	3.90	1.12	1.17	1.00	1.13	1.01	4.05	1.15	1.13	1.00	1.13	1.01
1.5	4.15	1.19	1.19	1.00	1.23	1.05	4.48	1.23	1.16	1.00	1.22	1.05
2	3.93	1.28	1.23	1.00	1.32	1.08	4.32	1.32	1.20	1.00	1.32	1.08
2.5	3.59	1.36	1.28	1.00	1.41	1.11	3.98	1.40	1.26	1.00	1.41	1.10
3	3.27	1.43	1.33	1.00	1.49	1.12	3.62	1.49	1.31	1.00	1.49	1.12
$\mathit{p}$	$p=4$						$p=5$
Chart	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp
δ	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10
0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
0.5	2.83	1.08	1.12	1.05	1.09	1.00	2.80	1.09	1.20	1.04	1.10	1.00
1	4.08	1.13	1.13	1.03	1.13	1.00	4.12	1.16	1.24	1.03	1.15	1.00
1.5	4.59	1.21	1.13	1.00	1.20	1.02	4.72	1.25	1.25	1.00	1.20	1.01
2	4.50	1.32	1.18	1.00	1.30	1.05	4.70	1.37	1.34	1.00	1.26	1.05
2.5	4.17	1.43	1.24	1.00	1.39	1.08	4.39	1.50	1.44	1.00	1.33	1.07
3	3.81	1.53	1.30	1.00	1.48	1.10	4.03	1.61	1.54	1.00	1.43	1.10
			$\mathit{p}$	$p=10$
			Chart	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp
			δ	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10
			0	NA	NA	NA	NA	NA	NA
			0.5	2.64	1.07	1.08	1.09	1.13	1.00
			1	4.15	1.17	1.07	1.07	1.19	1.00
			1.5	5.01	1.30	1.06	1.02	1.21	1.00
			2	5.32	1.49	1.11	1.00	1.29	1.02
			2.5	5.13	1.66	1.19	1.00	1.38	1.05
			3	4.78	1.82	1.28	1.00	1.47	1.08

Table 3. Cumulative performance comparison index (PCI) values for different charts.

p	$p=2$						$p=3$
Chart	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp
δ	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10
0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
0.5	4.68	1.16	1.26	1.02	1.13	1.00	4.72	1.19	1.22	1.03	1.15	1.00
1	4.90	1.16	1.22	1.00	1.19	1.03	5.14	1.20	1.17	1.00	1.19	1.02
1.5	4.76	1.24	1.23	1.00	1.29	1.07	5.20	1.29	1.19	1.00	1.29	1.07
2	4.23	1.35	1.28	1.00	1.40	1.11	4.72	1.39	1.24	1.00	1.40	1.10
2.5	3.67	1.44	1.33	1.00	1.51	1.14	4.12	1.49	1.31	1.00	1.50	1.13
3	3.18	1.53	1.39	1.00	1.60	1.15	3.58	1.59	1.37	1.00	1.60	1.15
p	$p=4$						$p=5$
Chart	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp
δ	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10
0	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
0.5	4.66	1.16	1.23	1.08	1.17	1.00	4.59	1.18	1.39	1.09	1.19	1.00
1	5.20	1.17	1.16	1.02	1.18	1.00	5.28	1.23	1.30	1.03	1.19	1.00
1.5	5.37	1.27	1.16	1.00	1.26	1.03	5.54	1.32	1.31	1.00	1.26	1.02
2	4.96	1.40	1.22	1.00	1.37	1.08	5.23	1.47	1.41	1.00	1.32	1.06
2.5	4.37	1.53	1.29	1.00	1.48	1.11	4.66	1.61	1.53	1.00	1.40	1.10
3	3.82	1.65	1.36	1.00	1.59	1.13	4.08	1.75	1.65	1.00	1.52	1.13
			p	$p=10$
			Chart	χ2	MCUSUMC	MC1	MEWMALas	MEWMALtv	MHWMAp
			δ	-	$k_1$ = 0.50	$k_2$ = 0.50	λ = 0.10	λ = 0.10	λ = 0.10
			0	NA	NA	NA	NA	NA	NA
			0.5	4.28	1.14	1.16	1.17	1.27	1.00
			1	5.41	1.25	1.08	1.08	1.24	1.00
			1.5	6.03	1.40	1.06	1.01	1.25	1.00
			2	6.03	1.61	1.14	1.00	1.35	1.04
			2.5	5.58	1.82	1.25	1.00	1.46	1.07
			3	4.98	2.00	1.35	1.00	1.57	1.10

Table 4. Superiority order of multivariate charts at varying $p\mathrm{and}\delta$.

$\mathit{p}$	δ	1	2	3	4	5	6
2	0.5	${\mathrm{MHWMA}}_P$	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	$M{C}_1$	${\chi }^2$
	1.0	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	${\mathrm{MCUSUM}}_C$	${\mathrm{MEWMA}}_{L_{tv}}$	$M{C}_1$	${\chi }^2$
	1.5	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MCUSUM}}_C$	${\mathrm{MEWMA}}_{L_{tv}}$	${\chi }^2$
	2.0	${\mathrm{MEWMA}}_{L_{as}}$		$M{C}_1$	${\mathrm{MCUSUM}}_C$	${\mathrm{MEWMA}}_{L_{tv}}$	${\chi }^2$
	2.5	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MCUSUM}}_C$	${\mathrm{MEWMA}}_{L_{tv}}$	${\chi }^2$
	3.0	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MCUSUM}}_C$	${\mathrm{MEWMA}}_{L_{tv}}$	${\chi }^2$
3	0.5	${\mathrm{MHWMA}}_P$	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	$M{C}_1$	${\chi }^2$
	1.0	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	${\chi }^2$
	1.5	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	${\chi }^2$
	2.0	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MCUSUM}}_C$	${\mathrm{MEWMA}}_{L_{tv}}$	${\chi }^2$
	2.5	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MCUSUM}}_C$	${\mathrm{MEWMA}}_{L_{tv}}$	${\chi }^2$
	3.0	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$		${\mathrm{MEWMA}}_{L_{tv}}$	${\chi }^2$
4	0.5	${\mathrm{MHWMA}}_P$	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MCUSUM}}_C$	${\mathrm{MEWMA}}_{L_{tv}}$	$M{C}_1$	${\chi }^2$
	1.0	${\mathrm{MHWMA}}_P$	${\mathrm{MEWMA}}_{L_{as}}$	$M{C}_1$	${\mathrm{MCUSUM}}_C$	${\mathrm{MEWMA}}_{L_{tv}}$	${\chi }^2$
	1.5	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	${\chi }^2$
	2.0	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	${\chi }^2$
	2.5	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	${\chi }^2$
	3.0	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	${\chi }^2$
5	0.5	${\mathrm{MHWMA}}_P$	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MCUSUM}}_C$	${\mathrm{MEWMA}}_{L_{tv}}$	$M{C}_1$	${\chi }^2$
	1.0	${\mathrm{MHWMA}}_P$	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	$M{C}_1$	${\chi }^2$
	1.5	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$		$M{C}_1$	${\mathrm{MCUSUM}}_C$	${\chi }^2$
	2.0	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	${\mathrm{MEWMA}}_{L_{tv}}$	$M{C}_1$	${\mathrm{MCUSUM}}_C$	${\chi }^2$
	2.5		${\mathrm{MHWMA}}_P$	${\mathrm{MEWMA}}_{L_{tv}}$	$M{C}_1$	${\mathrm{MCUSUM}}_C$
	3.0	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	${\mathrm{MEWMA}}_{L_{tv}}$	$M{C}_1$	${\mathrm{MCUSUM}}_C$
10	0.5	${\mathrm{MHWMA}}_P$	${\mathrm{MCUSUM}}_C$	$M{C}_1$	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MEWMA}}_{L_{tv}}$	${\chi }^2$
	1.0	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	${\chi }^2$
	1.5	${\mathrm{MHWMA}}_P$	${\mathrm{MEWMA}}_{L_{as}}$	$M{C}_1$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	${\chi }^2$
	2.0	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	${\chi }^2$
	2.5	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	${\chi }^2$
	3.0	${\mathrm{MEWMA}}_{L_{as}}$	${\mathrm{MHWMA}}_P$	$M{C}_1$	${\mathrm{MEWMA}}_{L_{tv}}$	${\mathrm{MCUSUM}}_C$	${\chi }^2$

In order to study the estimation effect of parameters on $AR{L}_0$ and$SDR{L}_0$, the related results are provided in Table 5 and Table 6, respectively. For this, we produced the $AR{L}_0$ and$SDR{L}_0$ values at$p\left(p=2,3,5,10\right)$ $n\left(n=3,5,10,15\right)\lambda (\lambda =0.10,0.20,0.30,0.40,0.50,0.60$);$m\left(m=20,30,50,100,200,300,500,\mathrm{and}\infty \right)$. For the suitable choice of subgroup size $K$, the literature may be recommended in this direction, for example, see [46,47] and the references therein. It is to be noted that the estimated $AR{L}_0$. and$SDR{L}_0$ results converge to the results for the known parameter if $m=\infty$.

Table 5. Estimation effect on ARL0 values.

$\mathit{p}$	$\mathit{n}$$\mathit{m}$	$\mathit{\lambda }=0.1$								$\mathit{\lambda }=0.2$
		20	30	50	100	200	300	500	∞	20	30	50	100	200	300	500	∞
2	3	91.1	110.3	132.8	156.8	175.2	182.2	187.7	199.9	113.4	129.0	147.6	167.7	181.4	187.0	192.4	200.3
	5	116.4	133.1	152.6	171.1	184.0	188.6	191.8	199.9	133.8	149.0	163.5	178.6	188.7	191.8	195.8	200.3
	10	144.7	158.1	171.6	183.8	191.0	194.1	196.8	199.9	157.6	169.2	180.3	189.3	195.1	196.9	198.6	200.3
	15	158.3	169.6	179.4	188.2	192.9	195.5	197.2	199.9	168.5	177.6	186.0	192.1	195.5	196.4	199.7	200.3
3	3	65.5	86.8	113.2	144.4	166.6	176.8	185.2	200.4	79.5	99.5	123.4	150.9	171.7	179.2	186.7	199.2
	5	94.6	114.6	138.2	162.9	179.8	187.1	192.1	200.4	107.8	126.4	146.8	169.0	182.3	187.7	192.3	199.2
	10	128.9	146.2	163.3	179.9	189.9	193.8	197.8	200.4	139.5	154.9	169.5	181.8	190.4	193.1	195.2	199.2
	15	146.4	160.4	173.8	186.9	193.6	196.5	199.0	200.4	156.2	166.2	178.1	187.5	193.3	194.6	196.1	199.2
4	3	48.2	69.4	96.5	131.2	158.4	170.3	181.2	199.5	60.2	80.4	107.3	139.0	164.2	175.3	183.7	199.8
	5	77.8	100.2	125.0	153.2	172.4	181.7	187.3	199.5	90.4	110.5	134.6	160.8	178.1	184.6	191.0	199.8
	10	116.0	134.4	154.2	174.2	186.1	190.8	194.4	199.5	127.3	143.9	162.0	177.7	189.0	191.6	195.4	199.8
	15	134.7	150.5	167.0	181.2	191.0	192.4	195.6	199.5	144.2	159.2	172.8	185.4	193.0	194.9	196.9	199.8
5	3	36.3	57.0	85.2	121.7	151.5	164.1	176.3	200.7	47.2	66.4	93.0	128.9	156.6	169.0	179.6	200.1
	5	65.8	88.5	115.3	145.8	168.6	178.4	186.4	200.7	77.1	97.7	123.8	153.6	173.8	181.7	188.9	200.1
	10	106.2	125.6	147.8	168.8	183.7	189.2	191.7	200.7	115.8	134.0	155.2	174.8	186.0	191.7	194.6	200.1
	15	126.4	143.4	162.1	178.2	187.8	192.0	194.9	200.7	135.7	151.7	168.3	182.4	190.8	193.4	195.5	200.1
10	3	8.9	22.3	47.6	88.0	125.6	144.3	162.6	200.7	16.9	30.4	52.6	90.8	128.2	146.8	164.9	200.5
	5	30.4	52.4	81.3	120.0	151.4	164.4	177.3	200.7	39.6	58.9	86.3	124.5	155.3	168.3	180.0	200.5
	10	71.4	95.2	122.1	153.0	172.5	180.8	189.0	200.7	77.8	100.9	127.1	157.4	176.4	183.3	190.5	200.5
	15	95.6	117.6	141.5	165.9	180.7	187.5	192.6	200.7	102.2	123.3	147.0	170.2	183.8	190.2	193.4	200.5
$\mathit{p}$	$\mathit{n}$	$\mathit{\lambda }=0.3$								$\mathit{\lambda }=0.4$
2	3	128.5	143.3	160.4	177.0	187.3	191.7	194.3	200.7	140.3	155.6	167.9	181.8	190.8	194.3	196.4	200.6
	5	146.6	159.8	173.5	184.2	193.1	195.9	198.0	200.7	156.8	169.2	180.1	189.0	195.6	196.9	199.4	200.6
	10	167.2	176.1	184.6	192.7	196.2	198.1	199.4	200.7	174.8	182.0	190.1	194.7	198.3	197.5	199.1	200.6
	15	177.2	184.1	190.3	195.9	198.4	198.9	200.2	200.7	183.1	187.7	192.3	196.9	199.0	199.2	199.8	200.6
3	3	87.1	108.2	131.7	158.9	175.9	183.6	189.7	199.9	95.1	115.6	140.8	165.0	181.5	187.3	193.0	200.4
	5	116.2	135.3	155.6	173.6	186.9	191.2	194.7	199.9	126.7	144.2	162.9	179.8	188.9	193.1	194.9	200.4
	10	149.0	162.2	175.0	186.9	192.8	195.4	197.9	199.9	157.2	169.0	180.8	191.1	195.4	197.4	198.3	200.4
	15	162.7	172.9	183.0	190.6	195.4	196.2	198.1	199.9	170.1	179.8	186.9	193.3	197.8	198.2	200.5	200.4
4	3	64.3	85.9	112.9	146.4	170.0	179.2	187.3	200.8	67.8	90.8	119.0	150.6	172.6	181.2	187.5	199.8
	5	97.6	118.4	142.5	167.5	183.3	188.1	192.5	200.8	103.6	124.5	148.0	171.3	184.2	190.4	195.1	199.8
	10	135.4	152.0	168.9	183.3	191.9	194.9	196.9	200.8	142.1	158.8	172.9	184.7	191.9	195.5	196.3	199.8
	15	152.1	165.5	179.4	189.9	195.9	197.1	198.6	200.8	158.6	169.9	182.2	190.7	194.1	196.7	197.4	199.8
5	3	48.3	68.9	98.1	134.0	160.6	173.2	182.4	199.8	50.7	72.2	102.4	139.6	164.8	175.5	184.7	200.6
	5	81.1	104.0	130.2	158.4	177.8	185.2	191.0	199.8	86.5	110.1	136.0	163.3	179.4	186.4	190.7	200.6
	10	122.4	142.0	161.4	178.3	189.0	193.2	195.1	199.8	129.4	148.1	164.3	180.5	190.5	193.7	195.8	200.6
	15	142.2	157.3	172.2	184.6	191.7	194.8	196.1	199.8	148.5	162.9	176.6	187.3	193.6	194.8	197.0	200.6
10	3	16.0	28.4	51.9	91.8	131.8	150.4	167.6	200.2	15.1	27.9	52.0	94.2	133.6	152.2	168.6	199.9
	5	38.7	59.1	88.9	128.8	159.1	171.0	182.0	200.2	39.1	60.4	91.8	131.8	162.2	172.9	182.5	199.9
	10	80.4	104.8	132.5	161.2	179.1	186.0	191.8	200.2	84.0	109.4	137.0	164.8	180.7	185.9	191.1	199.9
	15	106.9	128.6	151.9	173.5	186.7	191.5	194.1	200.2	110.1	132.3	154.6	175.0	186.9	191.5	193.9	199.9
$\mathit{p}$	$\mathit{n}$	$\mathit{\lambda }=0.5$								$\mathit{\lambda }=0.6$
2	3	151.2	162.6	173.4	185.2	191.6	194.1	196.1	200.4	158.0	169.4	178.8	187.5	192.7	196.1	197.1	200.1
	5	164.6	175.0	182.5	190.7	195.1	196.7	198.1	200.4	171.6	179.5	186.7	192.6	198.1	197.4	198.1	200.1
	10	180.1	185.8	192.1	194.7	198.1	200.2	197.7	200.4	184.3	189.3	192.6	196.2	199.3	198.9	199.3	200.1
	15	185.6	190.5	193.5	196.8	197.6	199.4	199.3	200.4	188.8	194.3	195.9	198.0	198.0	199.2	200.2	200.1
3	3	101.7	121.3	144.8	168.8	183.1	188.4	192.5	200.2	106.4	127.0	148.6	170.9	185.1	189.8	193.3	199.9
	5	132.7	148.7	166.2	182.3	190.2	192.4	195.7	200.2	137.2	154.3	169.1	184.3	191.7	195.5	196.6	199.9
	10	162.1	172.7	183.7	191.5	194.8	197.0	198.9	200.2	166.2	175.8	184.6	193.6	197.1	197.4	198.9	199.9
	15	172.2	180.3	187.2	194.8	196.6	196.5	199.1	200.2	176.0	184.4	190.8	195.1	197.4	199.0	198.8	199.9
4	3	72.3	95.3	123.8	155.2	174.5	184.2	189.2	200.1	75.0	99.2	127.9	156.4	177.4	184.3	189.5	199.5
	5	108.6	130.9	153.1	174.3	185.3	191.6	194.5	200.1	113.2	134.2	155.2	175.6	186.1	191.0	195.2	199.5
	10	146.5	161.1	176.6	186.6	193.0	194.6	198.0	200.1	150.7	164.5	177.2	189.0	194.2	196.1	197.2	199.5
	15	162.7	173.3	182.6	191.1	194.3	197.3	197.3	200.1	164.9	175.6	184.5	190.8	195.8	197.5	197.1	199.5
5	3	52.6	75.7	106.1	141.5	167.5	176.9	186.0	199.2	55.2	78.5	109.0	144.4	168.4	177.8	185.9	199.1
	5	90.3	114.4	140.3	166.0	182.1	186.9	191.9	199.2	93.8	117.3	143.0	167.5	182.2	188.3	191.5	199.1
	10	133.3	151.2	167.6	182.4	190.2	193.3	196.0	199.2	136.1	154.9	169.5	183.3	192.0	193.1	196.3	199.1
	15	153.1	165.5	177.3	188.1	192.2	195.0	196.2	199.2	154.5	168.3	179.2	189.0	192.7	195.4	197.5	199.1
10	3	14.6	27.9	52.9	96.2	135.6	154.1	171.1	199.7	14.6	28.0	54.3	98.3	138.0	155.2	171.5	199.3
	5	40.1	62.2	95.2	134.7	163.6	174.2	183.3	199.7	40.8	63.8	96.7	136.8	164.0	175.8	183.4	199.3
	10	87.3	111.8	139.9	165.9	181.9	186.7	192.2	199.7	88.6	114.4	141.0	167.6	182.3	189.2	192.8	199.3
	15	113.9	135.8	158.2	176.0	187.4	191.3	194.5	199.7	116.2	138.3	158.8	179.0	189.2	190.7	195.2	199.3

Table 6. Estimation effect on SDRL₀ values.

p	n m	$\mathit{\lambda }=0.1$								$\mathit{\lambda }=0.2$
		20	30	50	100	200	300	500	∞	20	30	50	100	200	300	500	∞
2	3	115.3	122.9	131.5	139.6	148.2	151.7	155.4	161.0	164.9	161.9	163.3	167.9	173.8	174.6	177.9	181.2
	5	123.8	129.1	138.2	145.8	152.2	154.3	156.3	161.0	155.9	161.4	166.6	170.2	174.8	177.0	178.4	181.2
	10	133.5	138.9	145.2	151.6	155.9	157.6	159.1	161.0	159.4	166.0	171.1	175.5	178.2	179.7	180.5	181.2
	15	138.7	145.3	149.4	154.7	156.7	157.9	159.4	161.0	164.5	169.5	172.2	177.0	178.0	178.9	181.1	181.2
3	3	83.3	96.6	111.7	128.2	141.5	148.3	153.4	163.1	101.7	117.1	130.7	149.0	161.3	167.4	173.0	181.4
	5	100.7	111.8	124.9	139.2	150.1	154.4	158.0	163.1	120.7	131.2	144.7	160.7	169.2	172.9	176.6	181.4
	10	119.4	129.0	139.2	149.0	155.9	159.2	161.6	163.1	138.8	150.3	160.1	169.0	174.7	176.5	177.8	181.4
	15	128.9	137.6	145.6	154.2	158.5	160.9	162.6	163.1	150.7	157.0	165.6	172.6	176.2	177.0	178.2	181.4
4	3	64.1	78.0	94.9	116.7	135.2	143.0	150.3	163.9	71.0	88.5	111.1	134.8	153.8	163.1	169.7	183.5
	5	84.8	97.8	112.8	130.9	143.9	151.1	154.1	163.9	95.6	111.3	130.5	152.0	165.6	170.8	175.3	183.5
	10	107.3	118.8	131.0	144.9	153.9	158.0	160.2	163.9	125.5	138.1	152.0	164.1	173.7	175.3	178.8	183.5
	15	118.8	129.1	140.3	150.1	157.7	159.1	160.8	163.9	137.8	149.5	159.8	169.9	176.5	177.7	180.1	183.5
5	3	51.5	67.2	84.8	108.5	129.5	137.1	147.1	165.5	51.9	68.8	92.6	123.3	146.3	157.1	165.9	184.3
	5	72.5	87.1	103.9	124.4	140.9	148.2	155.2	165.5	78.9	96.8	118.2	143.3	159.8	167.6	173.6	184.3
	10	98.5	110.9	126.2	141.0	152.2	156.5	158.5	165.5	111.8	126.0	145.3	161.1	171.3	176.3	179.0	184.3
	15	111.6	123.5	135.9	148.3	156.1	158.6	161.4	165.5	128.6	140.8	156.1	168.3	174.9	177.9	178.3	184.3
10	3	19.1	33.4	52.6	80.0	106.2	121.1	136.2	168.3	18.3	29.6	48.6	83.8	117.9	134.8	152.3	184.8
	5	40.9	56.3	75.0	102.5	126.9	137.7	147.4	168.3	37.6	53.8	79.2	114.0	142.5	154.5	164.8	184.8
	10	68.9	84.7	103.8	127.5	144.0	151.1	157.7	168.3	71.2	92.6	116.3	145.0	162.7	168.5	174.7	184.8
	15	85.1	101.1	119.1	138.5	151.0	155.2	161.0	168.3	93.6	111.9	134.8	156.7	168.8	175.5	178.8	184.8
$\mathit{p}$	$\mathit{n}$	$\mathit{\lambda }=0.3$								$\mathit{\lambda }=0.4$
2	3	223.0	202.2	198.1	193.4	190.0	191.8	191.6	192.7	245.9	233.5	213.0	204.2	201.1	199.1	197.8	196.6
	5	191.3	189.7	188.6	189.5	190.3	191.2	192.8	192.7	211.1	206.7	201.5	198.1	197.3	198.0	198.5	196.6
	10	183.5	185.3	187.2	191.2	191.6	191.2	193.2	192.7	197.9	195.9	197.3	197.4	197.5	195.4	197.2	196.6
	15	186.0	187.2	188.8	190.5	192.1	192.5	193.4	192.7	197.0	195.2	195.7	197.0	197.0	197.1	197.5	196.6
3	3	128.8	141.7	154.1	169.0	178.3	182.3	186.1	193.3	147.9	157.2	170.9	179.8	186.8	191.0	194.3	196.2
	5	140.2	153.1	166.2	174.0	184.7	187.7	189.8	193.3	161.7	167.3	178.5	187.2	190.4	193.2	192.6	196.2
	10	160.2	168.2	175.7	182.8	189.1	190.2	190.3	193.3	175.7	179.9	186.8	193.3	194.5	195.2	196.1	196.2
	15	168.4	175.3	181.5	186.3	189.3	189.3	189.9	193.3	180.3	186.1	189.6	192.9	196.6	196.0	197.5	196.2
4	3	84.8	104.7	126.8	153.4	171.4	177.0	183.7	194.5	97.8	116.8	141.3	161.7	177.5	183.0	188.5	196.6
	5	113.7	129.6	149.2	168.3	180.8	184.3	187.9	194.5	125.1	143.0	159.2	176.8	185.5	191.1	193.9	196.6
	10	143.0	155.8	168.6	179.8	185.2	189.0	191.7	194.5	154.8	169.0	178.1	186.1	190.0	195.1	194.1	196.6
	15	154.6	166.7	177.7	184.9	190.1	191.3	192.7	194.5	166.1	175.0	184.2	190.1	191.2	195.3	194.6	196.6
5	3	59.0	79.6	106.8	137.9	160.6	171.0	179.0	192.4	68.0	88.4	118.2	148.7	170.3	177.9	184.1	197.5
	5	91.1	111.5	134.3	158.3	175.2	180.6	186.8	192.4	102.5	123.6	145.2	167.3	179.7	186.4	189.6	197.5
	10	127.9	145.2	161.0	175.6	184.7	187.9	188.9	192.4	139.6	155.0	167.2	182.5	188.4	191.9	193.3	197.5
	15	144.2	156.4	169.8	179.3	186.3	188.4	190.2	192.4	155.0	167.2	178.7	186.5	191.2	191.8	195.1	197.5
10	3	16.4	28.5	51.9	91.0	129.9	146.6	164.2	194.4	16.1	29.5	54.7	97.6	134.9	154.3	169.2	197.8
	5	38.9	59.2	88.1	127.0	155.0	166.6	176.1	194.4	41.5	63.7	94.7	133.7	162.6	172.0	181.6	197.8
	10	79.5	103.5	129.9	156.9	174.0	180.4	186.1	194.4	87.6	111.8	139.3	163.9	179.4	184.1	188.5	197.8
	15	105.7	126.4	148.3	168.1	180.7	186.4	189.0	194.4	112.7	134.2	154.0	175.0	185.9	189.1	191.7	197.8
$\mathit{p}$	$\mathit{n}$	$\mathit{\lambda }=0.5$								$\mathit{\lambda }=0.6$
2	3	273.9	248.4	222.2	209.2	203.4	201.3	199.1	197.6	285.3	256.6	229.7	213.2	205.8	205.8	201.7	198.5
	5	224.5	217.0	206.5	201.5	198.7	200.1	198.4	197.6	238.1	225.9	212.8	205.9	203.3	201.7	199.1	198.5
	10	204.4	203.8	201.1	198.2	199.1	200.2	197.8	197.6	213.9	208.4	205.0	201.1	201.2	200.3	199.5	198.5
	15	203.7	200.9	199.6	199.4	197.8	198.2	199.0	197.6	207.3	205.9	202.9	200.6	199.1	199.3	199.5	198.5
3	3	166.2	170.9	178.4	186.3	191.6	194.3	194.9	199.0	178.0	182.0	183.8	191.3	195.7	195.9	195.6	199.3
	5	171.7	177.2	183.9	191.1	194.2	194.0	196.4	199.0	179.1	184.5	189.7	194.9	196.5	197.5	198.3	199.3
	10	182.7	186.4	192.6	194.7	195.8	197.1	198.6	199.0	187.5	191.6	193.1	199.2	199.7	198.0	197.8	199.3
	15	185.7	189.5	192.0	197.6	196.6	195.7	197.0	199.0	189.7	194.5	197.0	197.4	199.0	198.9	199.5	199.3
4	3	108.1	125.5	150.1	170.4	181.9	189.7	191.9	198.9	112.2	134.8	155.0	172.0	186.3	190.9	192.8	199.0
	5	136.2	152.6	168.1	183.1	188.7	193.3	196.1	198.9	143.1	157.1	171.6	183.5	190.4	193.7	196.7	199.0
	10	162.3	172.1	184.5	190.0	194.4	193.6	197.3	198.9	169.5	177.0	184.0	192.5	196.0	197.8	198.2	199.0
	15	173.7	179.7	185.8	192.7	195.2	197.3	196.9	198.9	175.2	183.4	190.7	193.4	196.2	197.8	196.4	199.0
5	3	74.9	96.8	125.5	152.0	174.6	181.9	188.3	197.5	80.0	102.3	128.3	158.5	175.7	182.2	188.2	198.3
	5	111.0	131.0	152.6	171.3	185.1	187.9	192.4	197.5	115.6	135.5	155.6	175.2	185.4	189.2	191.5	198.3
	10	146.2	160.6	173.4	185.4	190.9	193.4	196.4	197.5	149.4	165.0	176.1	186.0	193.5	193.0	197.0	198.3
	15	162.8	171.0	179.9	189.3	192.2	194.3	194.5	197.5	163.7	174.9	182.8	190.2	193.4	195.1	197.5	198.3
10	3	16.3	31.3	58.4	101.3	137.9	155.7	172.1	199.3	16.8	31.8	60.6	103.9	141.9	158.7	173.9	199.3
	5	44.3	66.9	101.2	138.9	165.2	176.1	183.7	199.3	45.8	70.0	102.7	140.7	166.3	177.2	184.9	199.3
	10	92.6	115.7	143.0	166.4	182.8	186.8	191.0	199.3	94.4	120.1	145.3	169.4	183.9	189.5	191.7	199.3
	15	118.0	138.8	159.1	176.8	187.2	190.9	192.8	199.3	120.9	142.2	161.6	180.4	189.6	190.8	195.0	199.3

The best performing chart will exhibit the lowest ARL curve, which means that a lower number of samples are required for a shift in the detection.The findings are summarized as follows.

CASE I: Analysis under known parameters

It can be observed from the ARL curve for $p=2$ (cf. in Figure 1) that $MHWM{A}_P$ and $MEWM{A}_{L_{as}}$ charts outperform$MEWM{A}_{L_{tv}}$, $MCUSU{M}_C$, $M{C}_1$, and Hotelling’s $T^2$ charts. The $MHWM{A}_P$ chart has smaller ARL values at $\delta =0.50$, and larger values at $\delta \left(\delta =1,1.5,2,2.5,\mathrm{and}3\right)$ than the ${\mathrm{MEWMA}}_{L_{as}}$ chart. The ${\mathrm{MEWMA}}_{L_{tv}}$ chart has a smaller ARL value than $\mathrm{MCUSUM}$ at $\delta =0.5$, and vice versa at$\delta =1$. The $M{C}_1$ chart has smaller values than the ${\mathrm{MCUSUM}}_C$ and ${\mathrm{MEWMA}}_{L_{tv}}$ charts, respectively, at $\delta =1.5-3$, while the traditional Hotelling’s $T^2$ chart has minimum ARL values at all values of$\delta$.

Overall, it can be observed that the ${\mathrm{MHWMA}}_P$ chart outperforms the other charts at small shifts, while the ${\mathrm{MEWMA}}_{L_{as}}$ chart does with the increasing shift. The Hotelling’s $T^2$ chart exhibits the worst performance at the shift range of$0.5-3.0$, while the other charts exhibit performance in between the best and worst charts. The above performance order based on the cumulative performance measures provided in Table 1, Table 2 and Table 3 for$p=2$ can be observed in Table 4.

It can be observed from the ARL curve for $p=3$ given in Figure 2 that the ${\mathrm{MHWMA}}_P$ and ${\mathrm{MEWMA}}_{L_{as}}$ charts outperform${\mathrm{MEWMA}}_{L_{tv}}$,${\mathrm{MCUSUM}}_C$, $M{C}_1$, and Hotelling’s $T^2$ charts. The $MHWM{A}_P$ chart has smaller ARL values at $\delta =0.50$, and larger values at $\delta =1,1.5,2,2.5,\mathrm{and}3$ than the ${\mathrm{MEWMA}}_{L_{as}}$ chart. The $MEWM{A}_{L_{tv}}$ chart has a smaller ARL value than ${\mathrm{MCUSUM}}_C$ at$\delta =0.5$. The $M{C}_1$ chart has smaller values than the ${\mathrm{MEWMA}}_{L_{tv}}$ and ${\mathrm{MCUSUM}}_C$ charts, respectively, at $\delta =1\mathrm{and}1.5$ and the ${\mathrm{MCUSUM}}_C$ and ${\mathrm{MEWMA}}_{L_{tv}}$ charts, respectively, at$\delta =2-3$. The usual Hotelling’s $T^2$ chart has minimum $ARL$ values at all values of$\delta$.

Overall, it can be observed that the ${\mathrm{MHWMA}}_P$. chart exhibits the best performance compared with the other charts at small shifts, while the ${\mathrm{MEWMA}}_{L_{as}}$ chart does with the increasing shift. The Hotelling’s $T^2$ chart exhibits the worst performance at the entire shift range, while the other charts exhibit performance in between the best and worst charts. The above performance order based on the cumulative performance measures provided in Table 1, Table 2 and Table 3 for$p=3$ can be observed in Table 4.

It can be observed from the ARL curve for $p=4$ given in Figure 3 that the ${\mathrm{MHWMA}}_P$ and ${\mathrm{MEWMA}}_{L_{as}}$ charts outperform${\mathrm{MEWMA}}_{L_{tv}}$, ${\mathrm{MCUSUM}}_C$, $M{C}_1$, and Hotelling’s $T^2$ charts. The ${\mathrm{MHWMA}}_P$ chart has smaller ARL values at $\delta =0.50\mathrm{and}1$, and larger values at $\delta =1.5,2,2.5,\mathrm{and}3$ than the ${\mathrm{MEWMA}}_{L_{as}}$ chart. The ${\mathrm{MCUSUM}}_C$ chart has smaller ARL values than the ${\mathrm{MEWMA}}_{L_{tv}}$ and $M{C}_1$ charts, respectively, at$\delta =0.5$. The $M{C}_1$ chart has smaller values than the ${\mathrm{MCUSUM}}_C$ and ${\mathrm{MEWMA}}_{L_{tv}}$ charts, respectively, at $\delta =1$and the ${\mathrm{MEWMA}}_{L_{tv}}$ and ${\mathrm{MCUSUM}}_C$ charts, respectively, at$\delta =1.5-3$. The usual Hotelling’s $T^2$ chart has minimum $ARL$ values at all values of$\delta$.

Overall, it can be observed that the ${\mathrm{MHWMA}}_P$ chart exhibits the best performance compared with the other charts at small shifts, while the ${\mathrm{MEWMA}}_{L_{as}}$ chart does with the increasing shift. The Hotelling’s $T^2$ chart exhibits the worst performance at the entire shift range, while the other charts exhibit performance in between the best and worst charts. The above performance order based on the cumulative performance measures provided in Table 1, Table 2 and Table 3 for$p=4$ can be observed in Table 4.

It can be observed from the ARL curve for $p=5$ given in Figure 4 that the ${\mathrm{MHWMA}}_P$ and ${\mathrm{MEWMA}}_{L_{as}}$ charts outperform${\mathrm{MEWMA}}_{L_{tv}}$, ${\mathrm{MCUSUM}}_C$, $M{C}_1$, and Hotelling’s $T^2$ charts. The ${\mathrm{MHWMA}}_P$ chart has smaller $ARL$ values at $\delta =0.50\mathrm{and}1$, and larger values at $\delta =1.5,2,2.5,\mathrm{and}3$ than the ${\mathrm{MEWMA}}_{L_{as}}$ chart. The ${\mathrm{MCUSUM}}_C$ chart has smaller ARL values than the ${\mathrm{MEWMA}}_{L_{tv}}$ and $M{C}_1$ charts, respectively, at$\delta =0.5$. The ${\mathrm{MEWMA}}_{L_{tv}}$ chart has smaller values than the ${\mathrm{MCUSUM}}_C$ and $M{C}_1$ charts, respectively, at $\delta =1$and the $M{C}_1$ and ${\mathrm{MCUSUM}}_C$ charts, respectively, at$\delta =1.5,3$. The usual Hotelling’s $T^2$ chart has minimum ARL values at all values of$\delta$.

Overall, it can be observed that the ${\mathrm{MHWMA}}_P$ chart exhibits the best performance compared with the other charts at small shifts, while the ${\mathrm{MEWMA}}_{L_{as}}$ chart does with the increasing shift. The Hotelling’s $T^2$ chart exhibits the worst performance at the entire shift range, while the other charts exhibit performance in between the best and worst charts. The above performance order based on the cumulative performance measures provided in Table 1, Table 2 and Table 3 for$p=5$ can be observed in Table 4.

It can be observed from the ARL curve for $p=10$ given in Figure 5 that ${\mathrm{MHWMA}}_P$ performs better than the${\mathrm{MCUSUM}}_C$, $M{C}_1$, and ${\mathrm{MEWMA}}_{L_{as}}$ charts at $\delta =0.5,1,\mathrm{and}1.5$, respectively, but shows inferior performance o the ${\mathrm{MEWMA}}_{L_{as}}$ chart at $\delta =2-3$, respectively. The ${\mathrm{MEWMA}}_{L_{as}}$ chart shows better performance than the ${\mathrm{MEWMA}}_{L_{tv}}$ and${\mathrm{MCUSUM}}_C$ charts at$\delta =1$. The $M{C}_1$ chart shows better performance than the ${\mathrm{MEWMA}}_{L_{as}}$. and ${\mathrm{MEWMA}}_{L_{tv}}$ charts, respectively, at$\delta =0.5$ and the ${\mathrm{MEWMA}}_{L_{tv}}$ $\mathrm{and}{\mathrm{MCUSUM}}_C$ charts, respectively, at$\delta =1.5,3$. The usual Hotelling’s $T^2$ chart has minimum ARL values at all values of$\delta$.

Overall, it can be observed that the ${\mathrm{MHWMA}}_P$ chart exhibits the best performance compared with the other charts at small shifts, while the ${\mathrm{MEWMA}}_{L_{as}}$ chart does with the increasing shift. The Hotelling’s $T^2$ chart exhibits the worst performance at the entire shift range, while the other charts exhibit performance in between the best and worst charts. The above performance order based on the cumulative performance measures provided in Table 1, Table 2 and Table 3 for$p=10$ can be observed in Table 4.

Some specific findings regarding Case I are listed below:

• The $AR{L}_1$ values of the proposed ${\mathrm{MHWMA}}_P$ and other competing charts decrease as the value of $p$ decreases, and vice versa. For example, at $\delta =0.50$ and $p=$2, 3, 4, 5, 10, the $AR{L}_1$ values of ${\mathrm{MHWMA}}_P$ chart are 24.80, 27.55, 29.61, 31.56, and 37.87, respectively. This reveals that the detection ability of charts improves as the number of variables increases in multivariate monitoring. A similar type of behavior can be observed for other charts (see Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5).
• The ${\mathrm{MHWMA}}_P$ chart exhibits the best performance at small$\delta$ followed by${\mathrm{MEWMA}}_{L_{as}}$. For example, at$\delta =0.50$, the $AR{L}_1$ values of ${\mathrm{MHWMA}}_P$ chart are 3.44, 3.70, 3.95, and 4.73, while those of the ${\mathrm{MEWMA}}_{L_{as}}$ chart are 3.56, 4.56, 4.29, and 5.54 for $p=$2, 3, 4, and 5, respectively. At$\delta =1.0$, the $AR{L}_1$ values of ${\mathrm{MEWMA}}_{L_{as}}$ chart are 5.10, 5.72, 6.38, and 6.84, while those of the ${\mathrm{MHWMA}}_P$ chart are 5.23, 5.82, 6.25, and 6.65 for $p=$2, 3, 4, and 5, respectively (see Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5).
• The Hotelling’s $T^2$ chart exhibits the most inferior performance among all charts. For example, for $p=2$ and $\delta =0.50$, the $AR{L}_1=116$ for Hotelling’s $T^2$ chart, while $AR{L}_1=$28.8, 31.3, 25.3, 28.1, and 24.8 for ${\mathrm{MCUSUM}}_C$, $M{C}_1$, ${\mathrm{MEWMA}}_{L_{as}}$, ${\mathrm{MEWMA}}_{L_{tv}}$, and ${\mathrm{MHWMA}}_P$ charts, respectively. Similarly, for $p=10$ and $\delta =0.50$, the $AR{L}_1=162$ for Hotelling’s $T^2$ chart, while $AR{L}_1=$43.2, 43.9, 44.3, 44.1, and 37.87 for ${\mathrm{MCUSUM}}_C$, $M{C}_1$, ${\mathrm{MEWMA}}_{L_{as}}$, ${\mathrm{MEWMA}}_{L_{tv}}$, and ${\mathrm{MHWMA}}_P$ charts, respectively. The inferiority of Hotelling’s $T^2$ chart can be observed for other choices of$p$ (see Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5).

CASE II: Analysis under estimated parameters

In order to examine the estimation effect of unknown parameters, we have observed that the$AR{L}_0$ and$SDR{L}_0$ values are affected because of the control limits based on estimated values of parameters. The detailed results about the estimation effect of parameters on $AR{L}_0$ and$SDR{L}_0$ values (at varying choices of$p$, $\lambda$, $n$, and $m$), provided in Table 5 and Table 6, respectively, are given as follows:

• The $AR{L}_0$ values are inversely related with the value of$p$ in the case of estimated parameters. This means that, as the number of variables increases in the multivariate set up, the $AR{L}_0$ values decrease. For example, for$\lambda =0.1$, $m=20$, and $n=3$, the $AR{L}_0=$ 91.12, 65.51, 48.25, 36.36, and 8.87 at $p=$ 2, 3, 4, 5, and 10, respectively (see Table 5). We may also oberserv behavior of the $SDR{L}_0=$ 115.34, 83.32, 64.08, 51.48, and 19.13 at $p=$ 2, 3, 4, 5, and 10, respectively (see Table 6).
• The $AR{L}_0$ values based on estimated parameters decrease as the value of smoothing parameter $\lambda$ increases. This means that the in-control $AR{L}_0$ moved downward as $\lambda \to 1$. For example, at$n=3\mathrm{and}m=50,$ the $AR{L}_0$= 132.80, 147.64, 160.42, 167.85, 173.39, and 178.77 at $\lambda =0.10,0.20,0.30,0.40,0.50,\mathrm{and}0.60,$ respectively (see Table 5). Similarly, we may observe the $SDR{L}_0$ results at $n=3\mathrm{and}m=50$, where the $SDR{L}_0$= 131.47, 163.29, 198.09, 212.99, 222.16, and 229.72 at $\lambda =0.10,0.20,0.30,0.40,0.50,\mathrm{and}0.60,$ respectively (see Table 6).
• As the sample size $n$and/or sub-group size $m$increase, the false alarms produced by ${\mathrm{MHWMA}}_P$ chart decrease, which means that the estimated version of $AR{L}_0$ converges to $200$ as$m\to \infty$. For instance, for$\lambda =0.1$, as $n$ increases from 3 to 15, the $AR{L}_0$ increases from 110.26 to 169.61.72 at $m=30$; as $m$ increases from 30 to 500, the $AR{L}_0$ increases from 110.26 to 187.72 at $n=3$ (see Table 5). Similar behavior of the $SDR{L}_0$ results can be observed as $\lambda =0.1$, because, if $n$ increases from 3 to 15, the $SDR{L}_0$ increases from 122.86 to 145.34 at $n=3$; if $m$ increases from 30 to 500, the $SDR{L}_0$ increases from 122.86 to 155.36 at $n=3$ (see Table 6).

The Corrected Control Limits: As we observed in Case II above, $AR{L}_0$ values are affected owing to the estimation effects in our control limits. Consequently, it is necessary to revise the control limits’ coefficient in order to attain the desired$AR{L}_0$. For our study purposes, we have worked out the corrected control limits coefficients for our proposed chart at various choices of$p\left(p=2,3,5,10\right),n\left(n=3,5,10,15\right)$,$\lambda (\lambda =0.10,0.20$), and $m(m=20,30,50,100,200,300,500,\mathrm{and}\infty$). The resulting coefficients are provided in Table 7 at some useful combinations of $\mathit{p}$, $\mathit{n},\mathit{\lambda }and\mathit{m}$. Moreover, we have also produced some selective graphs of the control limits’ coefficient ${\mathit{h}}_{\mathbf{6}}$ versus $\mathit{m}$ at various choices of $\mathit{p}$, $\mathit{n}$, and $\mathit{\lambda }$. The resulting graphs are provided in Figure 6 and Figure 7. It may observed from these tables and figures that the corrected limits get closer to the known limit (limit of the case of known parameter) with the increase in either $\mathit{n}$ or $\mathit{m}$ or both of these quantities.

Table 7. Corrected control limits coefficients h_6.

$\mathit{p}$	$\mathit{n}$$\mathit{m}$	$\mathit{\lambda }=0.1$								$\mathit{\lambda }=0.2$
		20	30	50	100	200	300	500	∞	20	30	50	100	200	300	500	∞
2	3	115.3	122.9	131.5	139.6	148.2	151.7	155.4	161.0	164.9	161.9	163.3	167.9	173.8	174.6	177.9	181.2
	5	123.8	129.1	138.2	145.8	152.2	154.3	156.3	161.0	155.9	161.4	166.6	170.2	174.8	177.0	178.4	181.2
	10	133.5	138.9	145.2	151.6	155.9	157.6	159.1	161.0	159.4	166.0	171.1	175.5	178.2	179.7	180.5	181.2
	15	138.7	145.3	149.4	154.7	156.7	157.9	159.4	161.0	164.5	169.5	172.2	177.0	178.0	178.9	181.1	181.2
3	3	83.3	96.6	111.7	128.2	141.5	148.3	153.4	163.1	101.7	117.1	130.7	149.0	161.3	167.4	173.0	181.4
	5	100.7	111.8	124.9	139.2	150.1	154.4	158.0	163.1	120.7	131.2	144.7	160.7	169.2	172.9	176.6	181.4
	10	119.4	129.0	139.2	149.0	155.9	159.2	161.6	163.1	138.8	150.3	160.1	169.0	174.7	176.5	177.8	181.4
	15	128.9	137.6	145.6	154.2	158.5	160.9	162.6	163.1	150.7	157.0	165.6	172.6	176.2	177.0	178.2	181.4
4	3	64.1	78.0	94.9	116.7	135.2	143.0	150.3	163.9	71.0	88.5	111.1	134.8	153.8	163.1	169.7	183.5
	5	84.8	97.8	112.8	130.9	143.9	151.1	154.1	163.9	95.6	111.3	130.5	152.0	165.6	170.8	175.3	183.5
	10	107.3	118.8	131.0	144.9	153.9	158.0	160.2	163.9	125.5	138.1	152.0	164.1	173.7	175.3	178.8	183.5
	15	118.8	129.1	140.3	150.1	157.7	159.1	160.8	163.9	137.8	149.5	159.8	169.9	176.5	177.7	180.1	183.5
5	3	51.5	67.2	84.8	108.5	129.5	137.1	147.1	165.5	51.9	68.8	92.6	123.3	146.3	157.1	165.9	184.3
	5	72.5	87.1	103.9	124.4	140.9	148.2	155.2	165.5	78.9	96.8	118.2	143.3	159.8	167.6	173.6	184.3
	10	98.5	110.9	126.2	141.0	152.2	156.5	158.5	165.5	111.8	126.0	145.3	161.1	171.3	176.3	179.0	184.3
	15	111.6	123.5	135.9	148.3	156.1	158.6	161.4	165.5	128.6	140.8	156.1	168.3	174.9	177.9	178.3	184.3
10	3	19.1	33.4	52.6	80.0	106.2	121.1	136.2	168.3	18.3	29.6	48.6	83.8	117.9	134.8	152.3	184.8
	5	40.9	56.3	75.0	102.5	126.9	137.7	147.4	168.3	37.6	53.8	79.2	114.0	142.5	154.5	164.8	184.8
	10	68.9	84.7	103.8	127.5	144.0	151.1	157.7	168.3	71.2	92.6	116.3	145.0	162.7	168.5	174.7	184.8
	15	85.1	101.1	119.1	138.5	151.0	155.2	161.0	168.3	93.6	111.9	134.8	156.7	168.8	175.5	178.8	184.8

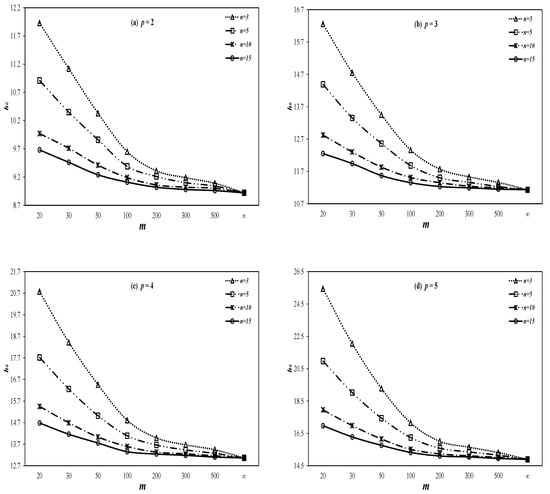
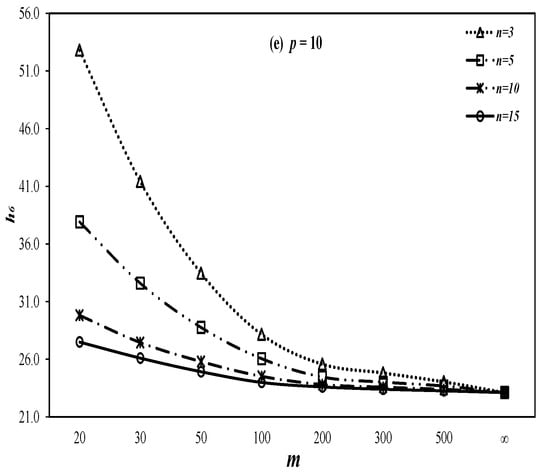
Figure 6. Control limit curves of proposed chart under estimated parameters with λ = 0.1.

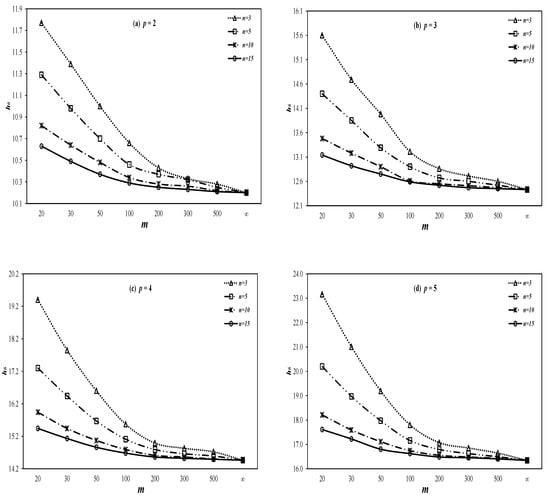
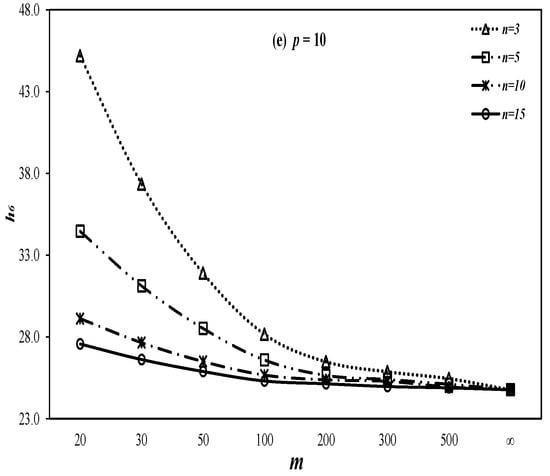
Figure 7. Control limit curves of proposed chart under estimated parameters with λ = 0.2.

Case when the parent distribution is heavy tailed: Throughout the paper so far, we have assumed that the variables of interest follow a multivariate normal distribution. This subsection provides the effect of deviation from normality in terms of a heavy tailed distribution, that is, multivariate t-distribution. The in-control ARL values for the proposed chart under known parameters case are given in Table 8, where the data are generated from multivariate t-distribution with $v$ degrees of freedom. The table clearly shows that the ARL values of the proposed chart get close to 200 as we increase the value of $v$, and finally $v\to \infty$ implies $\mathit{A}\mathit{R}\mathit{L}\to \mathbf{200}$. This is in line with the multivariate distributional theory that the multivariate T-distribution tends to multivariate normal distribution as $v\to \infty$. For the smaller values of $\mathit{v}$, the ARLs are substantially smaller than 200, implying that the constants evaluated in Table 7 are not appropriate.

Table 8. ARL values of MHWMA chart for multivariate T-distribution.

$\mathit{p}$	$\mathit{\lambda }$							$\mathit{v}$
		∞	5000	1000	500	100	50	20	10	5	4	3	2	1
2	0.1	199.89	199.43	197.51	193.35	176.68	158.15	117.46	79.07	42.39	32.55	22.41	12.6	4.92
	0.2	200.3	199.63	196.87	192.41	165.48	140.12	93.04	57.25	29.59	23.32	16.62	10.22	4.63
	0.3	200.73	199.7	195.68	192.06	160.02	131.26	81.79	47.5	23.71	18.67	13.55	8.65	4.22
	0.4	200.64	199.99	194.8	190.95	157.54	127.04	76.56	42.22	20.78	16.27	11.92	7.7	3.95
	0.5	200.36	198.7	194.69	190.18	154.39	124.89	73.36	39.86	19.15	14.9	10.83	7.07	3.69
	0.6	200.13	198.57	195.15	190.69	154.52	122.98	71.67	38.52	18.24	14.08	10.29	6.7	3.56
3	0.1	200.44	200.06	199.3	196.08	174.24	153.42	108.93	69.87	35.21	26.84	17.98	10.06	4.18
	0.2	199.19	198.25	194.61	189.93	157.81	128.95	80.85	47.88	23.98	18.83	13.48	8.31	3.97
	0.3	199.9	198.92	193.96	188.38	151.06	118.84	69.15	38.39	18.93	14.88	10.93	7.09	3.67
	0.4	200.4	198.62	194.48	188.51	148.31	113.97	63.8	33.87	16.42	12.93	9.55	6.29	3.39
	0.5	200.23	198.15	193.47	186.7	146.04	112.35	60.97	31.64	14.93	11.74	8.66	5.81	3.21
	0.6	199.92	198.64	193	186.51	145.67	111.16	59.5	30.25	14.07	11	8.09	5.47	3.08
4	0.1	199.49	198.86	197.87	194.06	168.85	146.21	100.81	62.12	30.44	22.92	15.38	8.63	3.76
	0.2	199.83	199.78	194.85	188.48	152.47	121.23	72.95	41.7	20.78	16.22	11.58	7.26	3.62
	0.3	200.81	199.71	192.86	187.14	143.99	110.93	61.56	33.18	16.23	12.81	9.45	6.21	3.33
	0.4	199.84	198.59	193.88	186.42	140.98	105.57	55.55	28.88	13.95	11.02	8.21	5.53	3.11
	0.5	200.07	198.87	192.59	184.21	138.15	102.51	52.46	26.4	12.57	9.91	7.43	5.06	2.95
	0.6	199.49	198.25	192.16	183.7	137.65	100.5	50.87	25.05	11.78	9.25	6.92	4.79	2.82
5	0.1	200.68	199.94	196.38	191.28	165.48	140.99	94.31	56.76	27.04	20.17	13.53	7.59	3.49
	0.2	200.06	198.86	192.79	187.55	146.82	114.83	66.32	37.53	18.46	14.35	10.34	6.54	3.37
	0.3	199.8	197.01	190.67	184.02	138.07	102.94	55.22	29.06	14.41	11.38	8.42	5.66	3.12
	0.4	200.61	197.44	191.48	182.25	133.8	96.89	49.14	25.15	12.27	9.73	7.37	5.01	2.93
	0.5	199.16	196.97	190.67	181.13	130.2	93.9	46.29	22.84	11.01	8.72	6.63	4.6	2.76
	0.6	199.11	196.89	189.76	182.08	129.63	92.41	44.17	21.68	10.24	8.16	6.18	4.35	2.66
10	0.1	200.68	199.95	195.09	189.11	153.14	123.52	75.04	41.61	18.26	13.53	9.08	5.48	2.91
	0.2	200.51	197.82	190.02	181.02	127.12	92.08	48.82	26.06	12.67	9.99	7.37	4.86	2.79
	0.3	200.24	198.84	188.31	177.04	115.77	78.76	38	19.65	9.84	7.96	6.08	4.27	2.63
	0.4	199.87	196.52	184.71	171.38	105.8	66.8	28.1	13.56	6.84	5.61	4.48	3.36	2.26
	0.5	199.69	197.41	186.16	173.29	107.8	68.81	29.9	14.57	7.4	6.07	4.81	3.55	2.34
	0.6	199.32	196.56	186.13	172.82	105.69	66.64	28.08	13.43	6.87	5.6	4.46	3.34	2.26

5. An Application

Illustrating the proposed control charts using a real dataset is common practice; see, for example, [48]. For illustration purpose in the current study, we used a data set related to Olympic archery, for the monitoring of location of arrows over the concentric rings on the archery board (cf. [7]). Target archery is the most standard form of archery directed by the World Archery Federation, in which participants shoot at stationary circular targets at varying distances. The size of the target varies and is usually measured as a 122 cm face for a distance of 70 m, all containing 10 concentric rings, representing different sectors to score. The outermost two rings (rings 1 and 2) are white, rings 3 and 4 are black, rings 5 and 6 are blue, rings 7 and 8 are red, and rings 9 and 10 (the innermost) are gold (cf. Figure 8a).

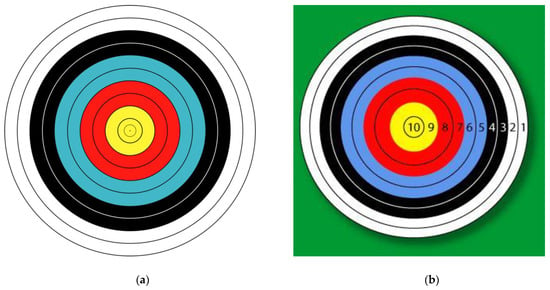
Figure 8. Description of target archery.

The scoring criterion is as follows: we add up all the points based on the arrows hitting different rings as mentioned above. The innermost ring gets a score of 10 and the outermost ring gets a score of 1, and for the inner rings, the score gradually decrease from 10 to 1 (cf. Figure 8b). The first 72 shots in finishes of three arrows of the ranking round of a particular archer with 24 subgroups were collected when the process was working under in-control state (i.e., Phase I) in order to estimate the unknown parameters. We used these estimated values of parameters and computed trail control limits. By plotting the Phase I data on these trail control limits, we found the first six points out of the control limits (which means that the process was not in-control when these samples were collected). Hence, we discarded first six samples from our Phase I data and revised our estimates to compute revised control limits.

Now, we have 18 subgroups containing 54 shoots of the elimination round in Phase I, and another 18 additional subgroups consisting of 54 shoots of the elimination round with the same subgroup size, which were collected in Phase II. Setting in-control $AR{L}_0=200$ under Hotelling’s $T^2$, the ${\mathrm{MEWMA}}_{L_{as}}\left({\mathrm{MEWMA}}_{as}\right)$, and ${\mathrm{MHWMA}}_P$ charts are made with $h_0=12.20$, $h_4=11.21$, $h_6=11.60$, and $\lambda =0.25$, respectively. In order to demonstrate the application of study, we plotted the values of charting statistics (calculated from Phase I and Phase II data) of the Hotelling’s $T^2$, ${\mathrm{MEWMA}}_{L_{as}}$, and ${\mathrm{MHWMA}}_P$ charts against their respective control limits in Figure 9.

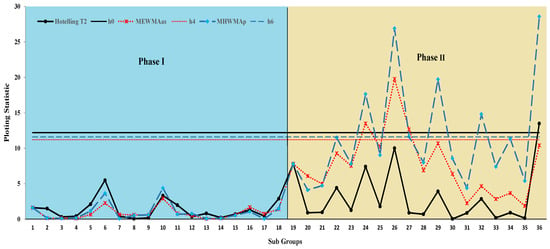
Figure 9. Comparison of proposed and existing chart under the target archery dataset.

From Figure 9, it can be observed that the Hotelling’s$T^2$, ${\mathrm{MEWMA}}_{L_{as}}$, and ${\mathrm{MHWMA}}_P$ charts are detecting an upward and downward shift in the process. The Hotelling’s $T^2$ chart indicates the first out-of-control signal at the last sample, while the ${\mathrm{MEWMA}}_{L_{as}}$ chart triggers the first out-of-control signal at the 24th sample. The proposed ${\mathrm{MHWMA}}_P$ chart detects the first out-of-control signal at the 24th sample (cf. Figure 9). Moreover, the Hotelling’s $T^2$, ${\mathrm{MEWMA}}_{L_{as}}$, and proposed ${\mathrm{MHWMA}}_P$ charts detect 1, 3, and 7 out-of-control signals (cf. Figure 9), respectively, which means that the proposed ${\mathrm{MHWMA}}_P$ chart has better detection ability than the other charts. These results display the supremacy of the proposed chart against the competing charts, and these results are also consistent with the findings of the study.

The property of better detection ability of MHWMAp chart claimed in Section 5 has a strong connection with the findings of Section 4, where the superiority of the proposal is established based on RL properties. These properties are based on the repeated iterations from a theoretical model by fixing ARL0 at a specific level for all of the charts under investigation, in order to maintain uniformity in performance evaluation. The RL analysis is also carried out at varying shifts, and the resulting outcomes are presented in tabular and graphical forms (cf. Table 1, Table 2, Table 3 and Table 4 and Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5), where the study proposal exhibits a clear dominance over others. Therefore, the feature of better detection in our application leads to justified conclusions, which will be acceptable to practitioners and quality control engineers.

6. Summary, Conclusions, and Future Recommendations

In this study, we proposed a new weighting scheme to design an efficient structure for proposed multivariate homogeneous weighted moving average ${\mathrm{MHWMA}}_P$ chart. We developed the control charting structure of the proposed $MHWM{A}_P$ chart along with some existing Hotelling’s$T^2$,${\mathrm{MCUSUM}}_C$, $M{C}_1$, ${\mathrm{MEWMA}}_{L_{as}}$, and ${\mathrm{MEWMA}}_{L_{tv}}$ charts. We investigated the performance of all charts under different numbers of quality characteristics and varying sample sizes and perceived that the performance of charts improves as the number of variables increases in the monitoring of the multivariate process. Overall, the proposed chart exhibits the best performance and Hotelling’s $T^2$ chart shows the worst performance. The performance of the proposed chart is seriously affected by the usage of a small number of Phase I samples at the estimation stage. Moreover, the in-control performance of the proposed chart is inversely related to the increment in the number of variables and smoothing parameter.

The current study can be extended by using different sampling strategies including ranked set sampling, two phases sampling, and so on in multivariate control charting. Moreover, the current study may also be extended for different runs rules schemes of quality control. Last, but not least, the current study can be of potential use in manufacturing and services processes.