Software Reliability for Agile Testing
Abstract
1. Introduction
2. Mathematical Derivations
2.1. Notation
2.2. Multinomial Distribution of Bug Counts
2.3. Conditioning on History
2.4. Extension to Multiple Features
2.5. Bayesian Estimation
- input data: the , , upper bounds for the indices f and i, and time point at which a feature starts;
- parameters: total bugs remaining, , with a lower bound of 0; the ; the hyperpriors for the truncated normal distributions of and ;
- transformed parameters: is considered a transformed parameter, calculated from a combination of data and a model parameter, ;
- model: distributions for and , hyperpriors for these, and a specification of log likelihood contributions by a double for-loop over features and over sprints, where the feature starting sprints are used.
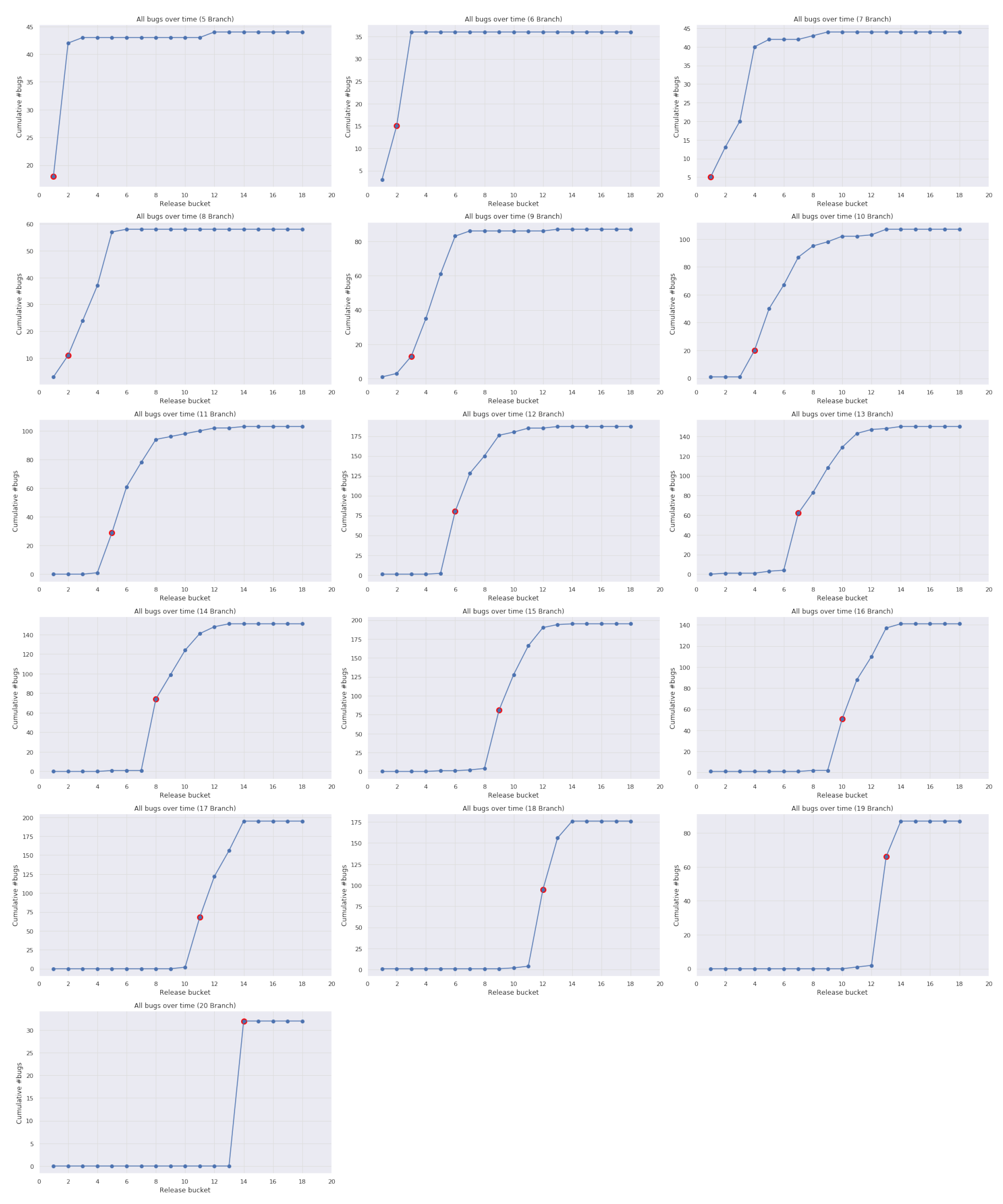
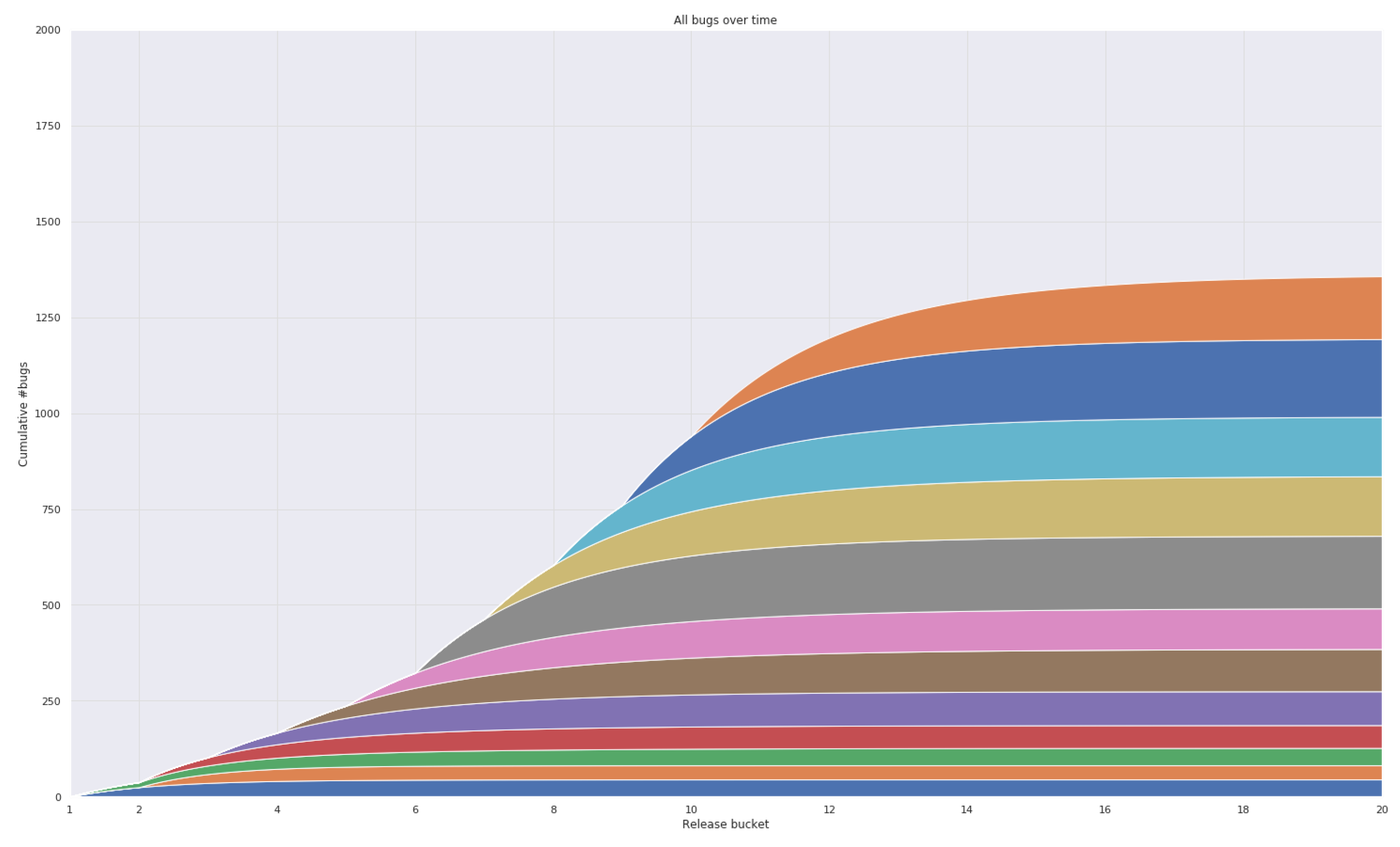
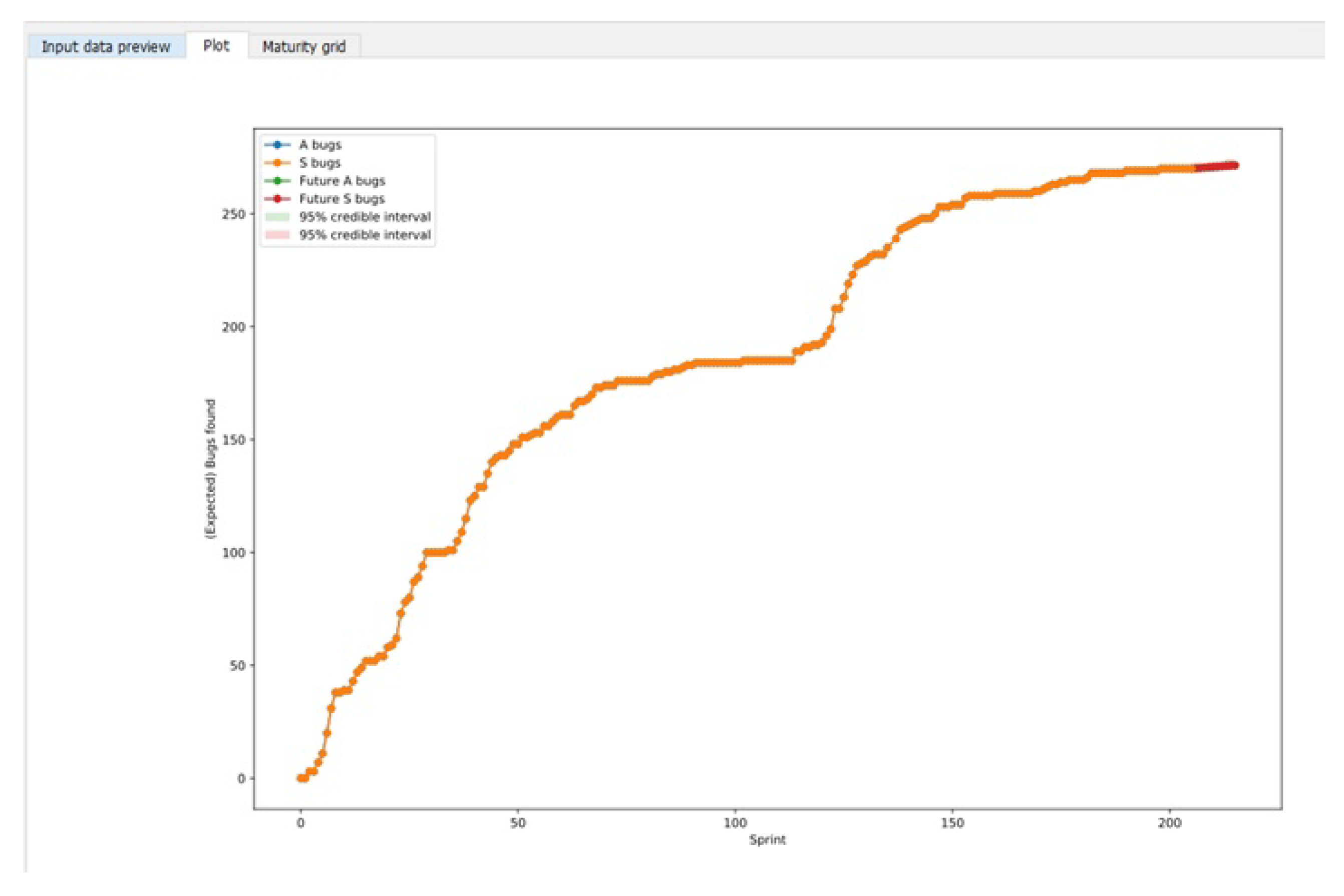
3. Use Cases
3.1. Case 1: Firefox Data
3.2. Case 2: Industrial Data
4. Discussion
- can assess or predict the to-be-achieved reliability;
- based on the observations of software failures during testing and/or operational use.
- how many errors are still left in the software?
- what is the probability of having no failures in a given time period?
- what is the expected time until the next software failure will occur?
- what is the expected number of total software failures in a given time period?
- gather more data from the software development teams;
- connect to the field quality community to gather field data of software tickets;
- using the field data determine the validity of the approach;
- make software reliability calculation part of the development process;
- automate the Python code such that ticket-feature data can be imported on-the-fly;
- include machine learning techniques and online failure prediction methods, which can be used to predict if a failure will happen 5 min from now [36];
- not focus on a specific software reliability model but rather assess forecast accuracy and then improve forecasts as was demonstrated by Zhao et al. [37];
- classify the expected shape of defect inflow prior to the prediction [18].
Author Contributions
Funding
Conflicts of Interest
References
- Van Driel, W.; Fan, X. Solid State Lighting Reliability: Components to Systems; Springer: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Van Driel, W.; Fan, X.; Zhang, G. Solid State Lighting Reliability: Components to Systems Part II; Springer: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Papp, Z.; Exarchakos, G. (Eds.) Runtime Reconfiguration in Networked Embedded Systems—Design and Testing Practice; Springer: Singapore, 2016. [Google Scholar] [CrossRef]
- Van Driel, W.; Schuld, M.; Wijgers, R.; Kooten, W. Software reliability and its interaction with hardware reliability. In Proceedings of the 15th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Ghent, Belgium, 7–9 April 2014. [Google Scholar]
- Abdel-Ghaly, A.A.; Chan, P.Y.; Littlewood, B. Evaluation of competing software reliability predictions. IEEE Trans. Softw. Eng. 1986, SE-12, 950–967. [Google Scholar] [CrossRef]
- Bendell, A.; Mellor, P. (Eds.) Software Reliability: State of the Art Report; Pergamon Infotech Limited: Maidenhead, UK, 1986. [Google Scholar]
- Lyu, M. (Ed.) Handbook of Software Reliability Engineering; McGraw-Hill and IEEE Computer Society: New York, NY, USA, 1996. [Google Scholar]
- Pham, H. (Ed.) Software Reliability and Testing; IEEE Computer Society Press: Los Alamitos, CA, USA, 1995. [Google Scholar]
- Xie, M. Software reliability models—Past, present and future. In Recent Advances in Reliability Theory (Bordeaux, 2000); Stat. Ind. Technol.; Birkhäuser Boston: Boston, MA, USA, 2000; pp. 325–340. [Google Scholar]
- Bishop, P.; Povyakalo, A. Deriving a frequentist conservative confidence bound for probability of failure per demand for systems with different operational and test profiles. Reliab. Eng. Syst. Safety 2017, 158, 246–253. [Google Scholar] [CrossRef]
- Adams, E. Optimizing preventive service of software products. IBM J. Res. Dev. 1984, 28, 2–14. [Google Scholar] [CrossRef]
- Miller, D. Exponential order statistic models of software reliability growth. IEEE Trans. Softw. Eng. 1986, SE-12, 12–24. [Google Scholar] [CrossRef]
- Joe, H. Statistical Inference for General-Order-Statistics and Nonhomogeneous-Poisson-Process Software Reliability Models. IEEE Trans. Software Eng. 1989, 15, 1485–1490. [Google Scholar] [CrossRef]
- Jelinski, Z.; Moranda, P. Software Reliability Research. In Statistical Computer Performance Evaluation; Freiberger, W., Ed.; Academic Press: Cambridge, MA, USA, 1972; pp. 465–497. [Google Scholar]
- Xie, M.; Hong, G. Software reliability modeling, estimation and analysis. In Advances in Reliability; North-Holland: Amsterdam, The Netherlands, 2001; Volume 20, pp. 707–731. [Google Scholar]
- Almering, V.; Van Genuchten, M.; Cloudt, G.; Sonnemans, P. Using Software Reliability Growth Models in Practice. Softw. IEEE 2007, 24, 82–88. [Google Scholar] [CrossRef]
- Pham, H. (Ed.) System Software Reliability; Springer: London, UK, 2000. [Google Scholar] [CrossRef]
- Rana, R.; Staron, M.; Berger, C.; Hansson, J.; Nilsson, M.; Törner, F.; Meding, W.; Höglund, C. Selecting software reliability growth models and improving their predictive accuracy using historical projects data. J. Syst. Softw. 2014, 98, 59–78. [Google Scholar] [CrossRef]
- Xie, M.; Hong, G.; Wohlin, C. Modeling and analysis of software system reliability. In Case Studies in Reliability and Maintenance; Blischke, W., Murthy, D., Eds.; Wiley: New York, NY, USA, 2003; Chapter 10; pp. 233–249. [Google Scholar]
- Dalal, S.R.; Mallows, C.L. When should one stop testing software? J. Amer. Statist. Assoc. 1988, 83, 872–879. [Google Scholar] [CrossRef]
- Zacks, S. Sequential procedures in software reliability testing. In Recent Advances in Life-Testing and Reliability; CRC: Boca Raton, FL, USA, 1995; pp. 107–126. [Google Scholar]
- Johnson, N.; Kemp, A.; Kotz, S. Univariate Discrete Distributions; Wiley Series in Probability and Statistics; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Blumenthal, S.; Dahiya, R. Estimation of sample size with grouped data. J. Stat. Plan. Inference 1995, 44, 95–115. [Google Scholar] [CrossRef]
- Littlewood, B.; Verrall, J.L. Likelihood function of a debugging model for computer software reliability. IEEE Trans. Rel. 1981, 30, 145–148. [Google Scholar] [CrossRef]
- Bai, C.G. Bayesian network based software reliability prediction with an operational profile. J. Syst. Softw. 2005, 77, 103–112. [Google Scholar] [CrossRef]
- Basu, S.; Ebrahimi, N. Bayesian software reliability models based on martingale processes. Technometrics 2003, 45, 150–158. [Google Scholar] [CrossRef]
- Littlewood, B.; Sofer, A. A Bayesian modification to the Jelinski-Moranda software reliability growth model. Softw. Eng. J. 1987, 2, 30–41. [Google Scholar] [CrossRef]
- Littlewood, B. Stochastic reliability-growth: A model for fault-removal in computer-programs and hardware-designs. IEEE Trans. Reliab. 1981, 30, 313–320. [Google Scholar] [CrossRef]
- Team, T.S.D. Stan Python Code. 2018. Available online: https://mc-stan.org/ (accessed on 15 November 2018).
- Lamkanfi, A.; Perez, J.; Demeyer, S. The Eclipse and Mozilla Defect Tracking Dataset: a Genuine Dataset for Mining Bug Information. In Proceedings of the MSR ’13 10th Working Conference on Mining Software Repositories, San Francisco, CA, USA, 18–19 May 2013. [Google Scholar]
- Depaoli, S.; van de Schoot, R. Improving Transparency and Replication in Bayesian Statistics: The WAMBS-Checklist. Psychol. Methods 2017, 22, 240–261. [Google Scholar] [CrossRef] [PubMed]
- Janczarek, P.; Sosnowski, J. Investigating software testing and maintenance reports: case study. Inf. Softw. Technol. 2015, 58, 272–288. [Google Scholar] [CrossRef]
- Rathore, S.; Kumar, S. An empirical study of some software fault prediction techniques for the number of faults prediction. Soft Comput. 2017, 21, 7417–7434. [Google Scholar] [CrossRef]
- Sosnowski, J.; Dobrzyński, B.; Janczarek, P. Analysing problem handling schemes in software projects. Inf. Softw. Technol. 2017, 91, 56–71. [Google Scholar] [CrossRef]
- Atlassian. JIRA Software Description. 2020. Available online: https://www.atlassian.com/software/jira (accessed on 12 May 2020).
- Salfner, F.; Lenk, M.; Malek, M. A survey of online failure prediction methods. ACM Comput. Surv. 2010, 42, 12–24. [Google Scholar] [CrossRef]
- Zhao, X.; Robu, V.; Flynn, D.; Salako, K.; Strigini, L. Assessing the Safety and Reliability of Autonomous Vehicles from Road Testing. In Proceedings of the 30th International Symposium on Software Reliability Engineering (ISSRE), Berlin, Germany, 28 October–1 November 2019. [Google Scholar]




| Symbol | Random | Domain | Meaning |
|---|---|---|---|
| a | No | Initial number of bugs | |
| b | No | Rate of bug detection | |
| Yes | Time at which bug i is found | ||
| L | No | Number of intervals | |
| No | End time of interval i | ||
| Yes | Number of bugs found in the time interval | ||
| Yes | Cumulative number of bugs detected until , |
| Branch | Average | Stdev |
|---|---|---|
| +1 | 4.5 | 3.5 |
| +5 | 12.0 | 4.0 |
| +10 | 15.2 | 3.8 |
| Sprint | Average | Stdev |
|---|---|---|
| +1 | 0.2 | 0.8 |
| +5 | 0.8 | 2.2 |
| +10 | 1.5 | 2.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
van Driel, W.D.; Bikker, J.W.; Tijink, M.; Di Bucchianico, A. Software Reliability for Agile Testing. Mathematics 2020, 8, 791. https://doi.org/10.3390/math8050791
van Driel WD, Bikker JW, Tijink M, Di Bucchianico A. Software Reliability for Agile Testing. Mathematics. 2020; 8(5):791. https://doi.org/10.3390/math8050791
Chicago/Turabian Stylevan Driel, Willem Dirk, Jan Willem Bikker, Matthijs Tijink, and Alessandro Di Bucchianico. 2020. "Software Reliability for Agile Testing" Mathematics 8, no. 5: 791. https://doi.org/10.3390/math8050791
APA Stylevan Driel, W. D., Bikker, J. W., Tijink, M., & Di Bucchianico, A. (2020). Software Reliability for Agile Testing. Mathematics, 8(5), 791. https://doi.org/10.3390/math8050791





