On Distance Signless Laplacian Spectral Radius and Distance Signless Laplacian Energy

Abstract

In this article, we find sharp lower bounds for the spectral radius of the distance signless Laplacian matrix of a simple undirected connected graph and we apply these results to obtain sharp upper bounds for the distance signless Laplacian energy graph. The graphs for which those bounds are attained are characterized.

1. Introduction and Preliminaries on Distance Matrix

Let $G=\left(V\right(G),E(G\left)\right)$ be a connected simple undirected graph with vertices set $V\left(G\right)$ and edges set $E\left(G\right)$. The distance $d\left(v_i,v_j\right)$ between the vertices $v_i$ and $v_j$ of G is equal to the length of (number of edges in) the shortest path that connects $v_i$ and $v_j$. The distance matrix of graph G is an $n\times n$ matrix such that the entry $(i,j)$ is equal to the distance between vertices $v_i$ and $v_j$ of the graph G. This is $D_{i,j}\left(G\right)=d_{i,j}=d(v_i,v_j)$.

Definition 1.

Let G be a simple connected graph with $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$. The distance degree of a vertex v, denoted by $T{r}_G\left(v\right)$ is defined to be the sum of the distances from v to all other vertices in G, that is,

$$T{r}_G\left(v\right)=\sum _{u\in V\left(G\right)}d\left(u,v\right).$$

The distance degree is also called the first distance degree or Transmission of a vertex v.

Let $Tr\left(G\right)$ be the $n\times n$ diagonal matrix defined by $T{r}_{i,i}\left(G\right)=T{r}_G\left(v_i\right)$.

For abbreviation, for $i=1,\dots ,n$, we write $T{r}_i$ instead of $T{r}_G\left(v_i\right)$ when no confusion can arise.

Definition 2.

A connected graph G is called a k-distance degree regular graph if $T{r}_i=k$ for all $i=1,2,\dots ,n$.

The Wiener index of a graph G, denoted by $W\left(G\right)$, was introduced by Wiener [1] and is defined by

$$W\left(G\right)=\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{D}_{i,j}\left(G\right)=\frac{1}{2}\sum _{u,v\in V\left(G\right)}d\left(u,v\right).$$

It is clear,

$$W\left(G\right)=\frac{1}{2}\sum _{v\in V\left(G\right)}T{r}_G\left(v\right).$$

In [2], Aouchiche and Hansen introduced the distance signless Laplacian matrix of a connected graph G as the $n\times n$ matrix defined by $DQ\left(G\right)=Tr\left(G\right)+D\left(G\right)$, where $D\left(G\right)$ is the distance matrix of G and $Tr\left(G\right)$ is the diagonal matrix of vertex transmissions of G. Furthermore, they prove the equivalence between the distance Laplacian matrix, distance signless Laplacian matrix and the distance spectra for the class of transmission regular graphs.

Since $D\left(G\right)$ and $DQ\left(G\right)$ are real symmetric matrices, we can denote

$${\lambda }_1\left(D\left(G\right)\right)\ge {\lambda }_2\left(D\left(G\right)\right)\ge \dots \ge {\lambda }_{n-1}\left(D\left(G\right)\right)\ge {\lambda }_n\left(D\left(G\right)\right)$$

and

$${\lambda }_1\left(DQ\left(G\right)\right)\ge {\lambda }_2\left(DQ\left(G\right)\right)\ge \dots \ge {\lambda }_{n-1}\left(DQ\left(G\right)\right)\ge {\lambda }_n\left(DQ\left(G\right)\right)$$

to the eigenvalues of $D\left(G\right)$ and $DQ\left(G\right)$, respectively.

We recall that the spectral radius of a matrix A is $\rho \left(A\right)=\underset{1\le i\le n}{max}\left\{\right|{\lambda }_i\left(A\right)\left|\right\}$ where, for $i=1,\dots ,n$, ${\lambda }_i\left(A\right)$ are the eigenvalues of matrix A.

Theorem 1

([3]). If A is a nonnegative matrix then its spectral radius $\rho \left(A\right)$ is an eigenvalue of A and it has an associated nonnegative eigenvector. Furthermore, if A is irreducible, then $\rho \left(A\right)$ is a simple eigenvalue of A with an associated positive eigenvector.

Clearly, $D\left(G\right)$ and $DQ\left(G\right)$ are irreducible nonnegative matrices; then, $\rho \left(D\right(G\left)\right)$ and $\rho \left(DQ\right(G\left)\right)$ are a simple eigenvalues of $D\left(G\right)$ and $DQ\left(G\right)$, respectively. Moreover, $DQ\left(G\right)$ is a positive semidefinite matrix, i.e., all its eigenvalues are nonnegative.

In several articles, different authors find upper and lower bounds for the distance signless Laplacian spectral radius. In [4], Hong and You gave a lower bound on the distance signless Laplacian spectral radius in terms of the sum row of matrix. In [5], the authors determined the graphs with minimum distance signless Laplacian spectral radius among the the trees, unicyclic graphs and bipartite graphs with fixed numbers of vertices, respectively, and determined the graphs with minimum distance signless Laplacian spectral radius among the connected graphs with fixed numbers of vertices and pendant vertices and the connected graphs with fixed number of vertices and connectivity, respectively. In [6], the authors gave a lower bound on the distance Laplacian spectral radius in terms of largest sum row of the distance matrix and they characterized that the extremal graph attains the maximum distance spectral radius in terms of order and the clique number of graph. In [7], Alhevaz et al. determined some upper and lower bounds on the distance signless Laplacian spectral radius of G based on its order and independence number and characterized the extremal graphs. In [8], the authors gaive bounds of the spectral radius of distance Laplacian and distance signless Laplacian matrices.

Connected simple undirected graphs are of great interest in molecular topology, a field of chemistry which reduces the molecule to a connected simple undirected graph. Eigenvalues and characteristic polynomial have found their use in the characterization of chemical compounds. On applications of eigenvalues, characteristic polynomial, distance matrix and graph invariants to chemistry, we mention the works in [9,10,11,12,13,14,15,16,17,18,19].

On the other hand, the energy of a graph is a concept defined in 1978 by Ivan Gutman [20] and originating from theoretical chemistry. Let $A\left(G\right)$ be an adjacency matrix of a graph G of order n; then, the energy of the graph G is $E\left(G\right)={\displaystyle \sum _{i=1}^n}\left|{\lambda }_i\left(A\left(G\right)\right)\right|$. Several authors study the energy of bipartite graphs, cyclic and acyclic graphs, regular graph (see, e.g., [21,22,23,24,25], and for more details on graph energy, see [26,27]). The concept energy of a graph has been extended to different matrices associated with a graph: let M be a matrix associated with a graph G; then, the energy of matrix M is defined in [28] by

$$E_M\left(G\right)=\sum _{i=1}^n|{\lambda }_i\left(M\left(G\right)\right)-\overline{\lambda }\left(M\left(G\right)\right)|,$$

(1)

where $\overline{\lambda }\left(M\left(G\right)\right)$ is the average of eigenvalues of M. In addition, some important applications of the Laplacian spectra and Laplacian energy are covered in Section 2.2 and 3.6 in [19].

About distance signless Laplacian energy, in [7], Alhevaz et al. gave a description of the distance signless Laplacian energy of the join of regular graphs in terms of their adjacency spectrum. In [29], Das et al. proved that the complete graph and the star give the smallest distance signless Laplacian energy among all the graphs and trees of order n, respectively. In [30], the authors gave upper bounds on the distance energy, distance Laplacian energy and distance signless Laplacian energy. Moreover, they characterized the graphs attaining the corresponding upper bound.

In this work, we find new sharp lower bounds on the distance signless Laplacian spectral radius and we find new upper bounds on the distance signless Laplacian energy.

To finish this section, we recall some results that are used in this article. The next theorem can be found, in simple form, in A. Cauchy’s “Cours d’Analyse” of 1821, which were the lecture notes used at the Ecole Polytechnique of Paris [31]; the version to be presented and its proof can be found in [32].

Theorem 2.

(Cauchy’s Interlacing Theorem) [32] Let A be a symmetric matrix of order n. Let B be a principal submatrix of order m obtained by deleting both ith row and ith column of A, for some values of i. Suppose A has eigenvalues ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_n$ and B has eigenvalues ${\beta }_1\ge {\beta }_2\ge \dots \ge {\beta }_m$. Then,

$${\lambda }_{n-m+k}\le {\beta }_k\le {\lambda }_k,$$

for $k=1,2,\dots ,m$.

We recall that the Frobenius norm of an $n\times n$ matrix $M=\left(m_{i,j}\right)$ is

$${\left|\right|M\left|\right|}_F=\sqrt{\sum _{i=1}^n\sum _{j=1}^n{\left|m_{i,j}\right|}^2}.$$

Moreover, if M is a normal matrix, then ${\left|\right|M\left|\right|}_F^2={\displaystyle \sum _{i=1}^n}{\left|{\lambda }_i\left(M\right)\right|}^2$ where ${\lambda }_1\left(M\right),\dots ,{\lambda }_n\left(M\right)$ are the eigenvalues of M. In particular,

$${\left|\right|D\left(G\right)\left|\right|}_F^2=\sum _{i=1}^n({\lambda }_i{\left(D\left(G\right)\right)}^2{ \mathrm{and} \left|\right|DQ\left(G\right)\left|\right|}_F^2=\sum _{i=1}^n({\lambda }_i{\left(DQ\left(G\right)\right)}^2.$$

It is clear that,

$${\parallel DQ\left(G\right)\parallel }_F\ge \rho \left(DQ\left(G\right)\right).$$

(2)

Definition 3

([33]). Let G be a simple connected graph with $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$, distance matrix $D_{i,j}=\left(d_{i,j}\right)$ and the distance degree sequence $\{T{r}_1,T{r}_2,\dots ,T{r}_n\}$, such that $T{r}_1\ge T{r}_2\ge \dots \ge T{r}_n$. Then, the second distance degree of a vertex $v_i$, denoted by $T_i$, is defined to be

$$T_i=\sum _{j=1}^n{d}_{i,j}T{r}_j.$$

Lemma 1

([33]). Let G be a simple connected graph of order n with distance degree sequence $\{T{r}_1,T{r}_2,\dots ,T{r}_n\}$ and second distance degree sequence $\{T_1,T_2,\dots ,T_n\}$. Then,

$$T{r}_1^2+T{r}_2^2+\dots +T{r}_n^2=T_1+T_2+\dots +T_n.$$

2. Lower Bounds on the Distance Signless Laplacian Spectral Radius

In this section, we obtain new bounds on the distance signless Laplacian radius in terms of parameters that depend on the distance between the vertices and the order of the graph. Before that, we give some known results.

Lemma 2

[2]). A connected graph G has only two distinct distance signless Laplacian eigenvalues if and only if G a complete graph.

Theorem 3

([2]). Let G be a connected graph on n vertices and m edges, with $m\ge n$. Consider the connected graph $\tilde{G}$ obtained from G by the deletion of an edge. Let

$$\rho \left(DQ\left(G\right)\right),{\lambda }_2\left(DQ\left(G\right)\right),\dots ,{\lambda }_n\left(DQ\left(G\right)\right)$$

and

$$\rho \left(DQ\left(\tilde{G}\right)\right),{\lambda }_2\left(DQ\left(\tilde{G}\right)\right),\dots ,{\lambda }_n\left(DQ\left(\tilde{G}\right)\right)$$

be the distance signless Laplacian spectra of G and $\tilde{G}$, respectively. Then, for all $i=1,\dots ,n$,

$${\lambda }_i\left(DQ\left(G\right)\right)\le {\lambda }_i(DQ(\tilde{G})).$$

Corollary 1.

Let G be a connected graph on n vertices. Then,

$$2(n-1)\le \rho \left(DQ\right(G\left)\right).$$

Let $\mathbf{e}$ be the n-dimensional vector of ones.

Theorem 4

([5]). Let G be a connected graph of order $n>2$. Then,

$$\rho \left(DQ\left(G\right)\right)\ge \frac{4W\left(G\right)}{n}.$$

The equality holds if and only if G is a distance degree regular graph.

Theorem 5.

Let G be a simple connected graph, such that, for $i=1,\dots ,n$, $T{r}_i$ is the distance degree of vertex $v_i$. Then,

$$\rho \left(DQ\left(G\right)\right)\ge 2\sqrt{\frac{T{r}_1^2+T{r}_2^2+\dots +T{r}_n^2}{n}}.$$

The equality holds if and only if G is a distance degree regular graph.

Proof. 

Let $\mathbf{x}={[x_1,x_2,\dots ,x_n]}^T$ be the unit positive Perron eigenvector of $DQ\left(G\right)$ corresponding to $\rho \left(DQ\right(G\left)\right)$.

We take the unit positive vector $\mathbf{y}=\frac{1}{\sqrt{n}}\mathbf{e}$. Then, we have

$$\rho \left(DQ\left(G\right)\right)=\sqrt{\rho {\left(DQ\left(G\right)\right)}^2}=\sqrt{{\mathbf{x}}^T{\left(DQ\left(G\right)\right)}^2\mathbf{x}}\ge \sqrt{{\mathbf{y}}^T{\left(DQ\left(G\right)\right)}^2\mathbf{y}}.$$

(3)

Since $\left(DQ\left(G\right)\right)\mathbf{y}=\frac{1}{\sqrt{n}}{[2T{r}_1,2T{r}_2,\dots ,2T{r}_n]}^T$, we obtain

$${\mathbf{y}}^T{\left(DQ\left(G\right)\right)}^2\mathbf{y}=\frac{4\left(T{r}_1^2+T{r}_2^2+\dots +T{r}_n^2\right)}{n}.$$

Therefore,

$$\rho \left(DQ\left(G\right)\right)\ge 2\sqrt{\frac{T{r}_1^2+T{r}_2^2+\dots +T{r}_n^2}{n}}.$$

Now, we assume that the equality holds. By Equation (3), we have that $\mathbf{y}$ is the positive eigenvector corresponding to $\rho \left(DQ\right(G\left)\right)$. From $DQ\left(G\right)\mathbf{y}=\rho \left(DQ\right(G\left)\right)\mathbf{y}$, we obtain that $2T{r}_i=\rho \left(DQ\left(G\right)\right)$, for $i=1,\dots ,n$. Therefore, the graph G is a $\frac{\rho \left(DQ\right(G\left)\right)}{2}$-distance degree regular graph.

Conversely, if G is a distance degree regular graph, then the matrix $DQ\left(G\right)$ has constant row sum, $2T{r}_1=2T{r}_2=\dots =2T{r}_n=k$. From Theorem 1, $k=\rho \left(DQ\right(G\left)\right)$. However,

$$\rho \left(DQ\left(G\right)\right)=k=\sqrt{\frac{n{k}^2}{n}}=\sqrt{\frac{4T{r}_1^2+4T{r}_2^2+\dots +4T{r}_n^2}{n}}.$$

Therefore, the equality holds. □

Theorem 6.

Let G be a simple connected graph, such that, for $i=1,\dots ,n$, $T{r}_i$ is the distance degree of vertex $v_i$ and $T_i$ is the second distance degree of vertex $v_i$. Then,

$$\rho \left(DQ\left(G\right)\right)\ge \sqrt{\frac{{(T{r}_1^2+T_1)}^2+{(T{r}_2^2+T_2)}^2+\dots +{(T{r}_n^2+T_n)}^2}{T{r}_1^2+T{r}_2^2+\dots +T{r}_n^2}}.$$

The equality holds if and only if $(T{r}_i+\frac{T_i}{T{r}_i})$ is constant for all i.

Proof. 

Using $\mathbf{y}=\frac{1}{\sqrt{T{r}_1^2+T{r}_2^2+\dots +T{r}_n^2}}{[T{r}_1,T{r}_2,\dots ,T{r}_n]}^T$, the proof is similar to the previous theorem. □

Remark 1.

Notice that the lower bound given in Theorem 6 improves the lower bound given in Theorem 5 and the lower bound given in Theorem 5 improves the lower bound given in Theorem 4.

In fact, we observe that

$$n\sum _{i=1}^n{(T{r}_i^2+T_i)}^2\ge {\left(\sum _{i=1}^n(T{r}_i^2+T_i)\right)}^2={\left(\sum _{i=1}^{n}T{r}_i^2+\sum _{i=1}^n{T}_i\right)}^2.$$

From Lemma 1, we have ${\displaystyle \sum _{i=1}^n}{T}_i={\displaystyle \sum _{i=1}^n}T{r}_i^2$. Then,

$$n\sum _{i=1}^n{(T{r}_i^2+T_i)}^2\ge 4{\left(\sum _{i=1}^{n}T{r}_i^2\right)}^2.$$

Moreover, we recall that, ${\left({\displaystyle \sum _{i=1}^n}T{r}_i\right)}^2\le n{\displaystyle \sum _{i=1}^n}T{r}_i^2$. Thus,

$$\begin{array}{ccc}\hfill \sqrt{\frac{{\displaystyle \sum _{i=1}^n}{(T{r}_i^2+T_i)}^2}{{\displaystyle \sum _{i=1}^n}T{r}_i^2}}& \ge & \sqrt{\frac{4{\left({\displaystyle \sum _{i=1}^n}T{r}_i^2\right)}^2}{n{\displaystyle \sum _{i=1}^n}T{r}_i^2}}=2\sqrt{\frac{\left({\displaystyle \sum _{i=1}^n}T{r}_i^2\right)}{n}}\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill 2\sqrt{\frac{{\displaystyle \sum _{i=1}^n}T{r}_i^2}{n}}& \ge & 2\sqrt{\frac{{\left({\displaystyle \sum _{i=1}^n}T{r}_i\right)}^2}{n^2}}=\frac{4W\left(G\right)}{n}.\hfill \end{array}$$

Definition 4

([34]). For $i=1,\dots ,n$, the sequence $M_1^{\left(1\right)},M_2^{\left(2\right)},\dots ,M_i^{\left(t\right)},\dots$ is defined as follows: fix $\alpha \in \mathbb{R}$, let $M_i^{\left(1\right)}={\left(T{r}_i\right)}^{\alpha }$ and for each $t\ge 2$, let $M_i^{\left(t\right)}={\displaystyle \sum _{j=1}^n}{d}_{i,j}{M}_j^{(t-1)}$.

Remark 2.

For $\alpha =1$ and $i=1,\dots ,n$: $M_i^{\left(1\right)}=T{r}_i$ and $M_i^{\left(2\right)}=T_i$.

A generalization of Theorem 6 is the next theorem.

Theorem 7.

Let G be a connected graph, α be a real number and t be an integer. Then,

$$\rho \left(DQ\left(G\right)\right)\ge \sqrt{\frac{{\displaystyle \sum _{i=1}^n}{\left(T{r}_i{M}_i^{\left(t\right)}+M_i^{(t+1)}\right)}^2}{{\displaystyle \sum _{i=1}^n}{\left(M_i^{\left(t\right)}\right)}^2}}.$$

The equality holds (for particular values of α and t) if and only if $T{r}_i+\frac{M_i^{(t+1)}}{M_i^{\left(t\right)}}$ is constant for all i.

Proof. 

Let $\mathbf{x}={[x_1,x_2,\dots ,x_n]}^T$ be the unit positive Perron eigenvector of $DQ\left(G\right)$ corresponding to $\rho \left(DQ\right(G\left)\right)$. Let $\mathbf{y}$ be the unit positive vector defined by

$$\mathbf{y}=\frac{1}{\sqrt{{\displaystyle \sum _{i=1}^n}{\left(M_i^{\left(t\right)}\right)}^2}}{[M_1^{\left(t\right)},M_2^{\left(t\right)},\dots ,M_n^{\left(t\right)}]}^T.$$

Since

$$\rho \left(DQ\left(G\right)\right)=\sqrt{\rho {\left(DQ\left(G\right)\right)}^2}=\sqrt{{\mathbf{x}}^T{\left(DQ\left(G\right)\right)}^2\mathbf{x}}\ge \sqrt{{\mathbf{y}}^T{\left(DQ\left(G\right)\right)}^2\mathbf{y}}$$

(4)

and

$$\left(DQ\left(G\right)\right)\mathbf{y}=\frac{1}{\sqrt{{\displaystyle \sum _{i=1}^n}{\left(M_i^{\left(t\right)}\right)}^2}}{\left[T{r}_1{M}_1^{\left(t\right)}+M_1^{(t+1)},T{r}_2{M}_1^{\left(t\right)}+M_2^{(t+1)},\dots ,T{r}_n{M}_n^{\left(t\right)}+M_n^{(t+1)}\right]}^T,$$

we obtain

$${\mathbf{y}}^T{\left(DQ\left(G\right)\right)}^2\mathbf{y}=\frac{{\displaystyle \sum _{i=1}^n}{\left(T{r}_i{M}_i^{\left(t\right)}+M_i^{(t+1)}\right)}^2}{{\displaystyle \sum _{i=1}^n}{\left(M_i^{\left(t\right)}\right)}^2}.$$

Therefore,

$$\rho \left(DQ\left(G\right)\right)\ge \sqrt{\frac{{\displaystyle \sum _{i=1}^n}{\left(T{r}_i{M}_i^{\left(t\right)}+M_i^{(t+1)}\right)}^2}{{\displaystyle \sum _{i=1}^n}{\left(M_i^{\left(t\right)}\right)}^2}}.$$

Now, we assume that the equality holds. By Equation (4), we have that $\mathbf{y}$ is the positive eigenvector corresponding to $\rho \left(DQ\right(G\left)\right)$. From $DQ\left(G\right)\mathbf{y}=\rho \left(DQ\right(G\left)\right)\mathbf{y}$, we obtain that $T{r}_i+\frac{M_i^{(t+1)}}{M_i^{\left(t\right)}}=\rho \left(DQ\left(G\right)\right)$, for $i=1,\dots ,n$.

Conversely if $T{r}_i+\frac{M_i^{(t+1)}}{M_i^{\left(t\right)}}=k$, then $T{r}_i{M}_i^{\left(t\right)}+M_i^{(t+1)}=k{M}_i^{\left(t\right)}$ for all $i\in \{1,2,\dots ,n\}$. Hence,

$$\begin{array}{ccc}\hfill \left(DQ\right(G\left)\right)\mathbf{y}& =& \frac{1}{\sqrt{{\displaystyle \sum _{i=1}^n}{\left(M_i^{\left(t\right)}\right)}^2}}{[k{M}_1^{\left(t\right)},k{M}_2^{\left(t\right)},\dots ,k{M}_n^{\left(t\right)}]}^T=k\mathbf{y}.\hfill \end{array}$$

Therefore, k is a eigenvalue of $DQ\left(G\right)$ and $\mathbf{y}$ its corresponding eigenvector. We recall that $\mathbf{y}$ is a positive vector, applying the Theorem 1, we obtain $k=\rho \left(DQ\right(G\left)\right)$. To finish, we show that

$$\rho \left(DQ\left(G\right)\right)=k=\sqrt{\frac{{\displaystyle \sum _{i=1}^n}{k}^2{\left(M_i^{\left(t\right)}\right)}^2}{{\displaystyle \sum _{i=1}^n}{\left(M_i^{\left(t\right)}\right)}^2}}=\sqrt{\frac{{\displaystyle \sum _{i=1}^n}{\left(T{r}_i{M}_i^{\left(t\right)}+M_i^{(t+1)}\right)}^2}{{\displaystyle \sum _{i=1}^n}{\left(M_i^{\left(t\right)}\right)}^2}}.$$

□

Example 1.

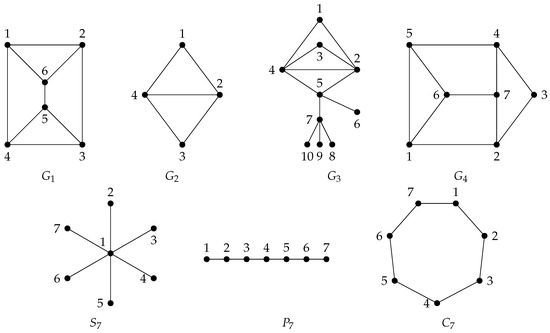
For $i=1,\dots ,7$, let $G_i$ be the graphs given in Figure 1. In particular, $G_5, G_6$ and $G_7$ are the star, path and cycle on seven vertices, denoted by $S_7$, $P_7$ and $C_7$, respectively.

Figure 1. Examples of seven connected simple undirected graphs.

We observe that $G_1$ is a 7-distance degree regular graph and $C_7$ is a 12-distance degree regular graph. In Table 1 we show the lower bounds for $\rho \left(DQ\left(G_i\right)\right)$, using six decimal places.

Table 1. Lower bounds for r(DQ(Gi)), using six decimal places, where Gi is given in Figure 1

	${\mathit{G}}_1$	${\mathit{G}}_2$	${\mathit{G}}_3$	${\mathit{G}}_4$	${\mathit{S}}_7$	${\mathit{P}}_7$	${\mathit{C}}_7$
$\rho \left(DQ\right(G\left)\right)$	14	$7.236067$	$43.543838$	$19.080481$	$21.389866$	$34.508309$	24
Theorem 4	14	7	$41.2$	$18.857142$	$20.571428$	32	24
Theorem 5	14	$7.071067$	$41.923740$	$18.913336$	$20.866925$	$32.741411$	24
Theorem 6	14	$7.211102$	$43.318868$	$19.039390$	$21.352497$	$34.223366$	24
Theorem 7 $\alpha =1\wedge t=1$	14	$7.211102$	$43.318868$	$19.039390$	$21.352497$	$34.223366$	24
Theorem 7 $\alpha =1\wedge t=2$	14	$7.197090$	$43.254373$	$19.030900$	$21.340541$	$34.042264$	24
Theorem 7 $\alpha =1\wedge t=3$	14	$7.199505$	$43.264033$	$19.033222$	$21.341225$	$34.081419$	24
Theorem 7 $\alpha =1\wedge t=4$	14	$7.199129$	$43.261693$	$19.032408$	$21.341188$	$34.073923$	24
Theorem 7 $\alpha =2\wedge t=1$	14	$7.230827$	$43.507702$	$19.078663$	$21.376257$	$34.443494$	24
Theorem 7 $\alpha =2\wedge t=2$	14	$7.181322$	$43.190400$	$19.018253$	$21.332838$	$33.830677$	24
Theorem 7 $\alpha =2\wedge t=3$	14	$7.201677$	$43.271151$	$19.035480$	$21.341620$	$34.115449$	24
Theorem 7 $\alpha =2\wedge t=4$	14	$7.198779$	$43.259397$	$19.031369$	$21.341167$	$34.067028$	24
Theorem 7 $\alpha =-1\wedge t=1$	14	$6.811754$	$38.9303735$	$18.725749$	$19.105982$	$30.246953$	24
Theorem 7 $\alpha =-1\wedge t=2$	14	$7.222337$	$43.377491$	$19.044974$	$21.368542$	$34.352322$	24
Theorem 7 $\alpha =-1\wedge t=3$	14	$7.194507$	$43.242240$	$19.028687$	$21.339406$	$34.000209$	24
Theorem 7 $\alpha =-1\wedge t=4$	14	$7.199892$	$43.266253$	$19.033852$	$21.341285$	$34.089018$	24
Theorem 7 $\alpha =-2\wedge t=1$	14	$6.472952$	$34.761644$	$18.501026$	$15.666680$	$27.454188$	24
Theorem 7 $\alpha =-2\wedge t=2$	14	$7.230194$	$43.423747$	$19.048631$	$21.384377$	$34.421688$	24
Theorem 7 $\alpha =-2\wedge t=3$	14	$7.191858$	$43.228397$	$19.026696$	$21.337653$	$33.958092$	24
Theorem 7 $\alpha =-2\wedge t=4$	14	$7.200275$	$43.268215$	$19.034333$	$21.341377$	$34.096220$	24

3. Upper Bounds on the Distance Signless Laplacian Energy

In this section, we obtain new bounds on the distance signless Laplacian energy in terms of spectral radius and parameters that depend on the distance between the vertices and the order of the graph. Previously, we extend the ideas given by Koolen and Moulton [35] to the distance signless Laplacian matrix and we use the lower bounds of spectral radius obtained in the previous section.

Theorem 8.

Let G be a connected graph on n vertices. Then,

$$E_{DQ}\le \rho \left(DQ\left(G\right)\right)-\frac{2W\left(G\right)}{n}+\sqrt{(n-1)\left[{\parallel DQ\left(G\right)\parallel }^2-\frac{4W{\left(G\right)}^2}{n}-{\left(\rho \left(DQ\left(G\right)\right)-\frac{2W\left(G\right)}{n}\right)}^2\right]}.$$

(5)

Moreover,

1. 

The function $F\left(x\right)=x-\frac{2W\left(G\right)}{n}+\sqrt{(n-1)\left[{\left|\right|DQ\left(G\right)\left|\right|}^2-\frac{4W{\left(G\right)}^2}{n}-{\left(x-\frac{2W\left(G\right)}{n}\right)}^2\right]}$ is strictly decreasing in the interval

$$\sqrt{\frac{{\parallel DQ\parallel }^2}{n}-\frac{4W{\left(G\right)}^2}{n^2}}+\frac{2W\left(G\right)}{n}<x\le \sqrt{{\parallel DQ\parallel }^2-\frac{4W{\left(G\right)}^2}{n}}+\frac{2W\left(G\right)}{n}.$$

2. 

Equality holds if and only if either G is a complete graph or G has at most three distinct distance signless Laplacian eigenvalues. In particular, if G has three distinct distance signless Laplacian eigenvalues, these are $\frac{2W\left(G\right)}{n}$, $\frac{-2W\left(G\right)}{n}$ and $\rho \left(DQ\left(G\right)\right)\ne \frac{\pm 2W\left(G\right)}{n}$.

Proof. 

From Equation (1), we have that distance signless Laplacian energy of a graph G is

$$E_{DQ}\left(G\right)=\sum _{i=1}^n|{\lambda }_i\left(DQ\left(G\right)\right)-\overline{\lambda }\left(DQ\left(G\right)\right)|.$$

We observe that

$$\overline{\lambda }\left(DQ\left(G\right)\right)=\frac{trace\left(DQ\right(G\left)\right)}{n}=\frac{{\displaystyle \sum _{i=1}^n}T{r}_i\left(G\right)}{n}=\frac{2W\left(G\right)}{n}.$$

(6)

On the other hand,

$$E_{DQ}\left(G\right)=\rho \left(DQ\left(G\right)\right)-\overline{\lambda }\left(DQ\left(G\right)\right)+\sum _{i=2}^n|{\lambda }_i\left(DQ\left(G\right)\right)-\overline{\lambda }\left(DQ\left(G\right)\right)|.$$

Using the Cauchy–Schwarz inequality, we obtain

$$\begin{array}{c}\hfill {\left(E_{DQ}\left(G\right)-\rho \left(DQ\left(G\right)\right)+\overline{\lambda }\left(DQ\left(G\right)\right)\right)}^2\le (n-1)\sum _{i=2}^n{\left({\lambda }_i\left(DQ\left(G\right)\right)-\overline{\lambda }\left(DQ\left(G\right)\right)\right)}^2.\end{array}$$

(7)

where

$$\begin{array}{ccc}\hfill \sum _{i=2}^n{\left({\lambda }_i\left(DQ\left(G\right)\right)-\overline{\lambda }\left(DQ\left(G\right)\right)\right)}^2& =& \sum _{i=2}^n\left({\lambda }_i{\left(DQ\left(G\right)\right)}^2-2{\lambda }_i\left(DQ\left(G\right)\right)\overline{\lambda }\left(DQ\left(G\right)\right)+\overline{\lambda }{\left(DQ\left(G\right)\right)}^2\right).\hfill \end{array}$$

For simplicity, we omit the $\left(DQ\right(G\left)\right)$ notation; then,

$$\begin{array}{ccc}\hfill \sum _{i=2}^n{\left({\lambda }_i\left(DQ\left(G\right)\right)-\overline{\lambda }\left(DQ\left(G\right)\right)\right)}^2& =& \sum _{i=2}^n{\lambda }_i^2-2\overline{\lambda }\sum _{i=2}^n{\lambda }_i+(n-1){\overline{\lambda }}^2\hfill \\ \hfill & =& {\parallel DQ\parallel }_F^2-\rho {\left(G\right)}^2-2\overline{\lambda }\sum _{i=1}^n{\lambda }_i+2\overline{\lambda }\rho \left(G\right)+(n-1){\overline{\lambda }}^2\hfill \\ \hfill & =& {\parallel DQ\parallel }_F^2-2\overline{\lambda }\sum _{i=1}^n{\lambda }_i+n{\overline{\lambda }}^2-{(\rho \left(G\right)-\overline{\lambda })}^2\hfill \end{array}$$

Using the equalities given in Equation (6), we have

$$\begin{array}{ccc}\hfill \sum _{i=2}^n{\left({\lambda }_i\left(DQ\right)-\overline{\lambda }\left(DQ\right)\right)}^2& =& {\parallel DQ\parallel }_F^2-\frac{4W\left(G\right)}{n}2W\left(G\right)+n\frac{4W{\left(G\right)}^2}{n^2}-{(\rho \left(G\right)-\overline{\lambda })}^2\hfill \\ \hfill & =& {\parallel DQ\parallel }_F^2-\frac{4W{\left(G\right)}^2}{n}-{\left(\rho \left(G\right)-\frac{2W\left(G\right)}{n}\right)}^2.\hfill \end{array}$$

Then, from the inequality in Equation (7), we conclude that

$$E_{DQ}\le \rho \left(G\right)-\frac{2W\left(G\right)}{n}+\sqrt{(n-1)\left[{\parallel DQ\left(G\right)\parallel }^2-\frac{4W{\left(G\right)}^2}{n}-{\left(\rho \left(G\right)-\frac{2W\left(G\right)}{n}\right)}^2\right]}.$$

Moreover, let

$$F\left(x\right)=\left(x-\frac{2W\left(G\right)}{n}\right)+\sqrt{(n-1)\left[{\parallel DQ\left(G\right)\parallel }^2-\frac{4W{\left(G\right)}^2}{n}-{\left(x-\frac{2W\left(G\right)}{n}\right)}^2\right]}$$

be a real function. We observe that the function F is a strictly decreasing on the interval

$$\sqrt{\frac{{\parallel DQ\left(G\right)\parallel }^2}{n}-\frac{4W{\left(G\right)}^2}{n^2}}+\frac{2W\left(G\right)}{n}<x\le \sqrt{{\parallel DQ\parallel }^2-\frac{4W{\left(G\right)}^2}{n}}+\frac{2W\left(G\right)}{n}.$$

Now, the equality in Equation (5) holds if and only if the equality in Equation (7) holds, which is, for $i=2,\dots ,n$,

$$\left|{\lambda }_2\left(DQ\left(G\right)\right)-\frac{2W\left(G\right)}{n}\right|=\dots =\left|{\lambda }_n\left(DQ\left(G\right)\right)-\frac{2W\left(G\right)}{n}\right|$$

Therefore, only three cases are possible: (i) the graph G has only one distance signless Laplacian eigenvalues; (ii) the graph G has only two distinct distance signless Laplacian eigenvalues; or (iii) G is a graph with three distinct distance signless Laplacian eigenvalues.

In Case (i), we conclude that $G=K_1$.

In Case (ii), from Lemma 2, we conclude that $G=K_n$.

In Case (iii), we have that $\rho \left(DQ\left(G\right)\right)\ne \frac{2W\left(G\right)}{n}$ and there is r such that ${\lambda }_2=\dots ={\lambda }_r=-{\lambda }_{r+1}=\dots =-{\lambda }_n=\frac{2W\left(G\right)}{n}$, we conclude that $DQ\left(G\right)$ have exactly three distinct eigenvalues.

Conversely, the result is immediate. □

Lemma 3.

Let G be a connected graph. Then,

$${\parallel DQ\left(G\right)\parallel }^2>\frac{4{\left(W\left(G\right)\right)}^2}{n}.$$

Proof. 

Since ${\displaystyle \sum _{i=1}^n}{\left[{\lambda }_i\left(DQ\left(G\right)\right)-\frac{2W\left(G\right)}{n}\right]}^2>0$, the result is immediate. □

Lemma 4

([30]). Let m and n be natural numbers such that $m\ge n>2$. Let $a_1,a_2,\dots ,a_m$ be positive real numbers. Then,

$$\frac{2}{n}{\left(\sum _{i=1}^m{a}_i\right)}^2>\sum _{i=1}^m{a}_i^2.$$

Lemma 5.

Let G be a connected graph. Then,

$$\begin{array}{c}\hfill \sqrt{\frac{{\parallel DQ\left(G\right)\parallel }^2}{n}-\frac{4{\left(W\left(G\right)\right)}^2}{n^2}}<\frac{2W\left(G\right)}{n}.\end{array}$$

(8)

Proof. 

From Lemma 3, $\frac{{\parallel DQ\left(G\right)\parallel }^2}{n}-\frac{4{\left(W\left(G\right)\right)}^2}{n^2}>0$. Thus, the inequality in Equation (8) is equivalent to

$${\parallel DQ\left(G\right)\parallel }^2<\frac{2{\left(2W\left(G\right)\right)}^2}{n}.$$

We recall that

$${\parallel DQ\left(G\right)\parallel }^2=\sum _{i=1}^n{\left({\lambda }_i\left(DQ\left(G\right)\right)\right)}^2 \mathrm{and} 2W\left(G\right)=\sum _{i=1}^n{\lambda }_i\left(DQ\left(G\right)\right).$$

Now, using Lemma 4, we have

$$\begin{array}{c}\hfill \frac{2{\left(2W\left(G\right)\right)}^2}{n}=\frac{2{\left({\displaystyle \sum _{i=1}^n}{\lambda }_i\left(DQ\left(G\right)\right)\right)}^2}{n}>\sum _{i=1}^n{\left({\lambda }_i\left(DQ\left(G\right)\right)\right)}^2={\parallel DQ\left(G\right)\parallel }^2.\end{array}$$

□

Lemma 6.

$$\rho \left(DQ\left(G\right)\right)\le \sqrt{{\parallel DQ\left(G\right)\parallel }^2-\frac{4W{\left(G\right)}^2}{n}}+\frac{2W\left(G\right)}{n}.$$

Proof. 

In fact, using ${\parallel DQ\left(G\right)\parallel }^2-\frac{4W{\left(G\right)}^2}{n}>{\parallel DQ\left(G\right)\parallel }^2$ and the inequality in Equation (2) we obtain the result. □

Then, we obtain the next three theorems.

Theorem 9.

Let G be a connected graph on n vertices. Then,

$$E_{DQ}\left(G\right)\le \frac{2W\left(G\right)}{n}+\sqrt{(n-1)\left[{\parallel DQ\left(G\right)\parallel }^2-\frac{4(n+1)W{\left(G\right)}^2}{n^2}\right]}.$$

Moreover, the equality holds if and only if either G is a complete graph or G is a distance degree regular graph with at most three distinct distance signless Laplacian eigenvalues: $\frac{2W\left(G\right)}{n}$, $\frac{-2W\left(G\right)}{n}$ and $\rho \left(DQ\left(G\right)\right)=\frac{4W\left(G\right)}{n}$.

Proof. 

From Lemma 5, we obtain

$$\begin{array}{c}\hfill \sqrt{\frac{{\parallel DQ\left(G\right)\parallel }^2}{n}-\frac{4W{\left(G\right)}^2}{n^2}}+\frac{2W\left(G\right)}{n}<\frac{4W\left(G\right)}{n}\end{array}$$

(9)

and, from Theorem 4 and Lemma 6, we have

$$\begin{array}{c}\hfill \frac{4W\left(G\right)}{n}\le \sqrt{{\parallel DQ\left(G\right)\parallel }^2-\frac{4W{\left(G\right)}^2}{n}}+\frac{2W\left(G\right)}{n}.\end{array}$$

Then, applying Theorem 8, we conclude that

$$E_{DQ}\left(G\right)\le F\left(\frac{4W\left(G\right)}{n}\right)=\frac{2W\left(G\right)}{n}+\sqrt{(n-1)\left[{\parallel DQ\left(G\right)\parallel }^2-\frac{4(n+1)W{\left(G\right)}^2}{n^2}\right]}.$$

Moreover, the equality holds if and only if the conditions of equality given in Theorems 5 and 8 are satisfied and the fact that $E_{DQ}\left(G\right)=F\left(\rho \left(G\right)\right)$. □

Theorem 10.

Let G be a connected graph on n vertices. Then,

$$\begin{array}{ccc}\hfill E_{DQ}\left(G\right)& \le & 2\left(\sqrt{\frac{{\displaystyle \sum _{i=1}^n}T{r}_i^2}{n}}-\frac{W\left(G\right)}{n}\right)\hfill \\ \hfill & & +\sqrt{(n-1)\left[{\parallel DQ\left(G\right)\parallel }^2-\frac{4W{\left(G\right)}^2}{n}-4{\left(\sqrt{\frac{{\displaystyle \sum _{i=1}^n}T{r}_i^2}{n}}-\frac{W\left(G\right)}{n}\right)}^2\right]}.\hfill \end{array}$$

Moreover, the bound is achieved if and only if either G is a complete graph or G is a distance degree regular graph with at most three distinct distance signless Laplacian eigenvalues: $\frac{2W\left(G\right)}{n}$, $\frac{-2W\left(G\right)}{n}$ and $\rho \left(DQ\left(G\right)\right)=2\sqrt{\frac{{\displaystyle \sum _{i=1}^n}T{r}_i^2}{n}}$.

Proof. 

From Remark 1,

$$\frac{4W\left(G\right)}{n}\le 2\sqrt{\frac{{\displaystyle \sum _{i=1}^n}T{r}_i^2}{n}}\le \rho \left(DQ\left(G\right)\right).$$

Now, using Equation (9) and Lemma 6, we have

$$\begin{array}{c}\hfill \sqrt{\frac{{\parallel DQ\left(G\right)\parallel }^2}{n}-\frac{4W{\left(G\right)}^2}{n^2}}+\frac{2W\left(G\right)}{n}<2\sqrt{\frac{{\displaystyle \sum _{i=1}^n}T{r}_i^2}{n}}\end{array}$$

and

$$\begin{array}{c}\hfill 2\sqrt{\frac{{\displaystyle \sum _{i=1}^n}T{r}_i^2}{n}}\le \sqrt{{\parallel DQ\left(G\right)\parallel }^2-\frac{4W{\left(G\right)}^2}{n}}+\frac{2W\left(G\right)}{n}.\end{array}$$

Applying Theorem 8, the bound is obtained.

To show that the bound is achieved, we use the conditions of equality given in Theorems 5 and 8 and the fact that $E_{DQ}\left(G\right)=F\left(\rho \left(G\right)\right)$. □

Theorem 11.

Let G be a connected graph on n vertices. Then,

$$\begin{array}{ccc}\hfill E_{DQ}\left(G\right)& \le & \left(\sqrt{\frac{{\displaystyle \sum _{i=1}^n}{(T{r}_i^2+T_i)}^2}{{\displaystyle \sum _{i=1}^n}T{r}_i^2}}-\frac{2W\left(G\right)}{n}\right)\hfill \\ \hfill & & +\sqrt{(n-1)\left[{\parallel DQ\left(G\right)\parallel }^2-\frac{4W{\left(G\right)}^2}{n}-{\left(\sqrt{\frac{{\displaystyle \sum _{i=1}^n}{(T{r}_i^2+T_i)}^2}{{\displaystyle \sum _{i=1}^n}T{r}_i^2}}-\frac{2W\left(G\right)}{n}\right)}^2\right]}.\hfill \end{array}$$

Moreover, the equality holds if and only if either G is a complete graph or $\left(a\right)$$(T{r}_i+\frac{T_i}{T{r}_i})$ is constant for all i on G and $\left(b\right)$ G has at most three distinct distance signless Laplacian eigenvalues $\frac{2W\left(G\right)}{n}$, $\frac{-2W\left(G\right)}{n}$ and $\rho \left(DQ\left(G\right)\right)=\sqrt{\frac{{\displaystyle \sum _{i=1}^n}{(T{r}_i^2+T_i)}^2}{{\displaystyle \sum _{i=1}^n}T{r}_i^2}}$.

Proof. 

The proof is similar to given in Theorem 10. □

Remark 3.

From Remark 1 and Theorem 8, we observe that the upper bound given in Theorem 10 improves the upper bound given in Theorem 9 and the upper bound given in Theorem 11 improves the upper bound given in Theorem 10.

Example 2.

We consider the graphs $G_1$, $G_2$, $G_3$, $G_4$, $G_5=S_7$, $G_6=P_7$ and $G_7=C_7$ given in Example 1 and $F\left(x\right)$ given in Theorem 8. Using six decimal places, we obtain the upper bounds for distance signless Laplacian energy, as shown in the Table 2.

Table 2. Upper bounds for EDQ(Gi), using six decimal places, where Gi is given in Figure 1.

	${\mathit{G}}_1$	${\mathit{G}}_2$	${\mathit{G}}_3$	${\mathit{G}}_4$	${\mathit{S}}_7$	${\mathit{P}}_7$	${\mathit{C}}_7$
$E_{DQ}\left(G\right)$	14	$7.472200$	$54.287676$	$19.796514$	$22.208371$	$41.857600$	24
$F\left(\frac{4W\left(G\right)}{n}\right)$	$16.219544$	8	$71.515224$	$23.460734$	$27.191289$	$52.3318$	$29.663521$
$F\left(2\sqrt{\frac{{\displaystyle \sum _{i=1}^n}T{r}_i^2}{n}}\right)$	$16.219544$	$7.900272$	$69.482675$	$23.287817$	$26.354659$	$51.010236$	$29.663521$
$F\left(\sqrt{\frac{{\displaystyle \sum _{i=1}^n}{(T{r}_i^2+T_i)}^2}{{\displaystyle \sum _{i=1}^n}T{r}_i^2}}\right)$	$16.219544$	$7.671303$	$64.745970$	$22.880250$	$24.695026$	$47.607854$	$29.663521$

4. Conclusions

In this paper, we find sharp lower bounds for the spectral radius of the distance signless Laplacian matrix of a simple undirected connected graph G and we apply these results to obtain sharp upper bounds for the distance signless Laplacian energy of G. The graphs for which those bounds are attained are characterized.