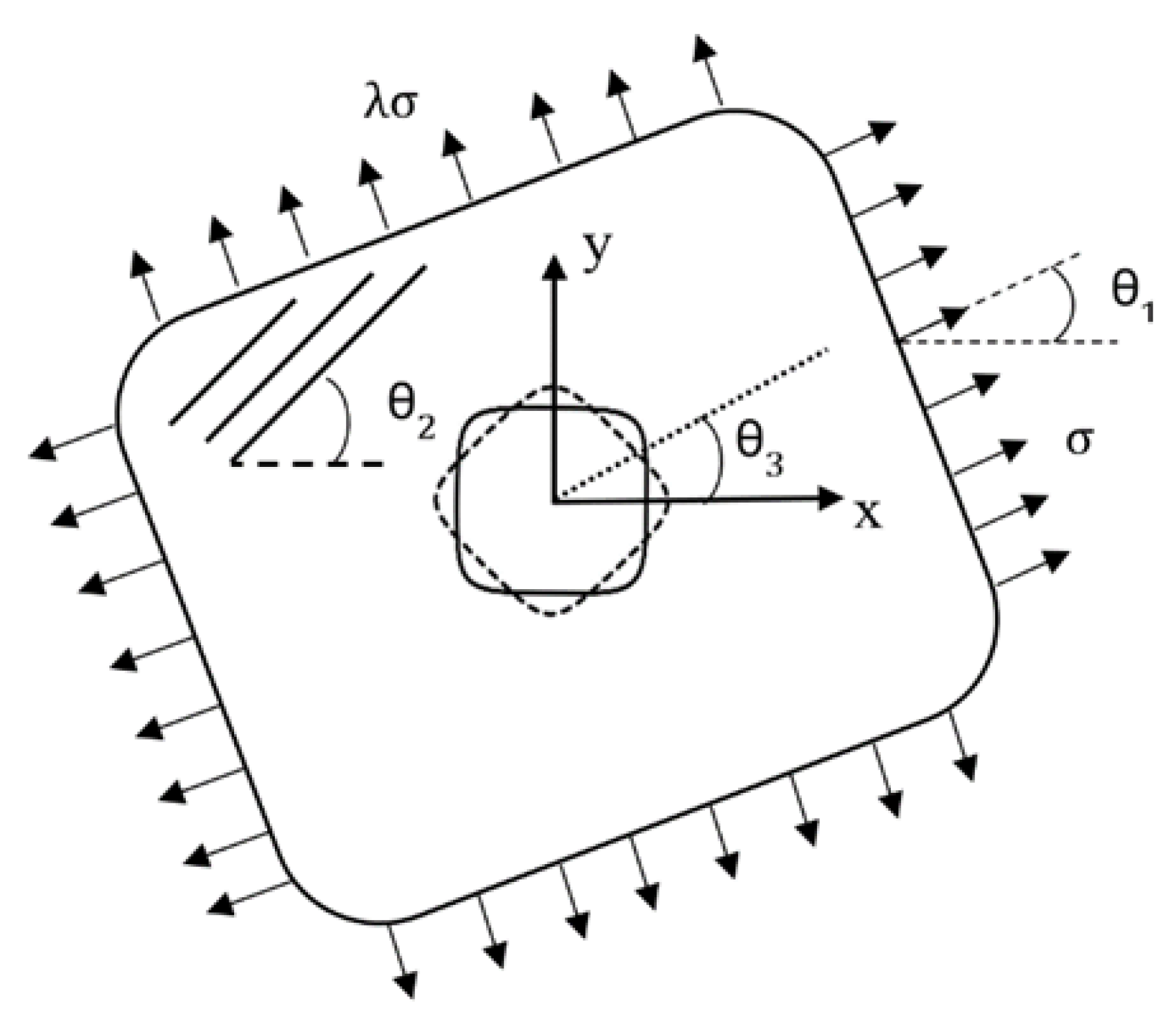
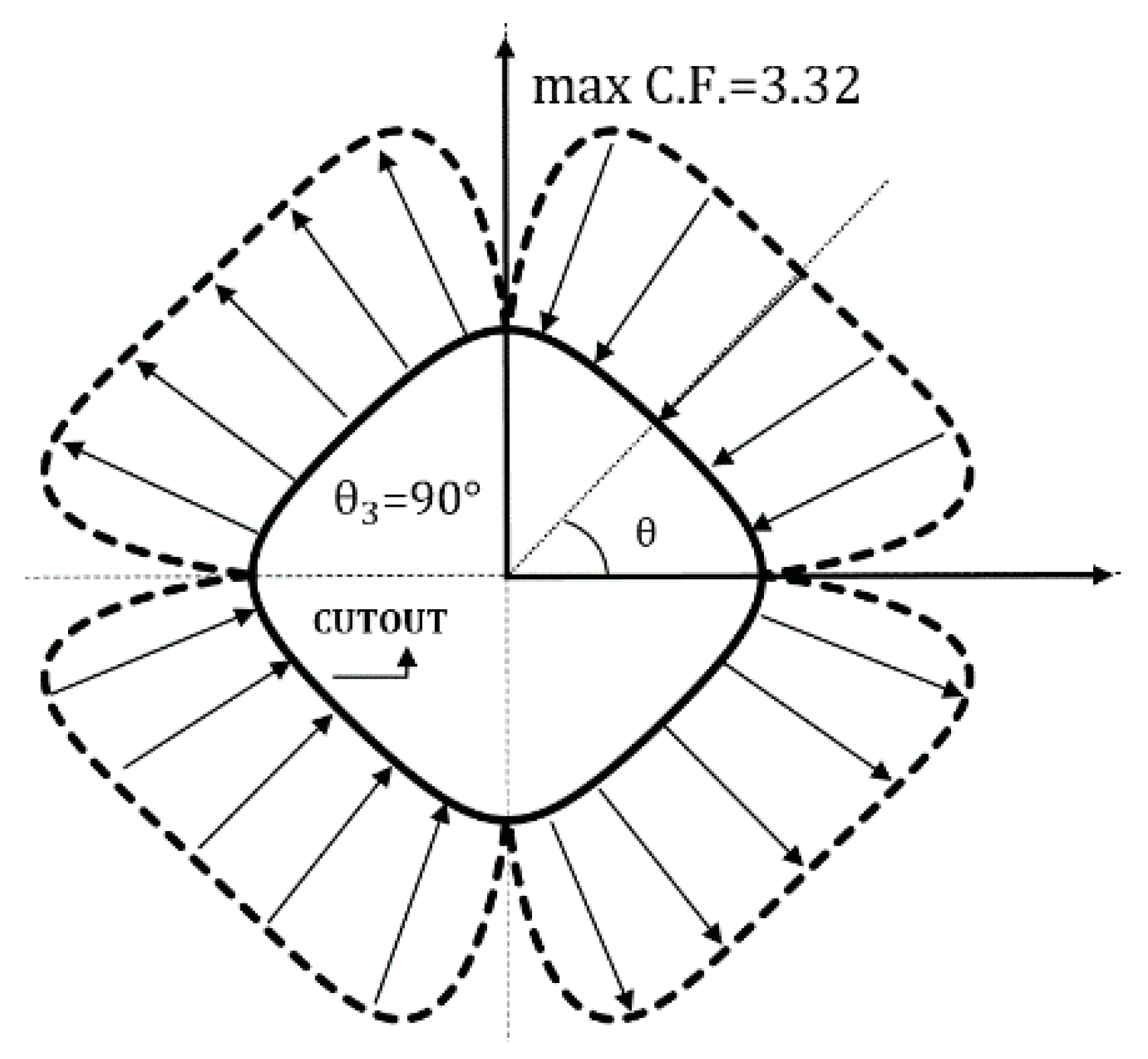
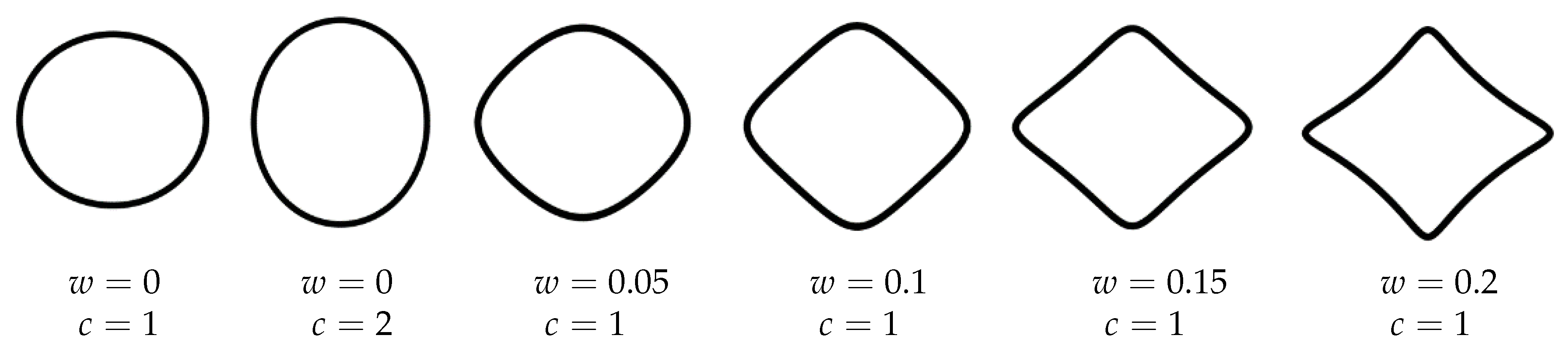Figure 1.
Infinite perforated orthotropic plate subject to biaxial loading ( is load angle, is fiber angle, and is cut out orientation).
Figure 1.
Infinite perforated orthotropic plate subject to biaxial loading ( is load angle, is fiber angle, and is cut out orientation).
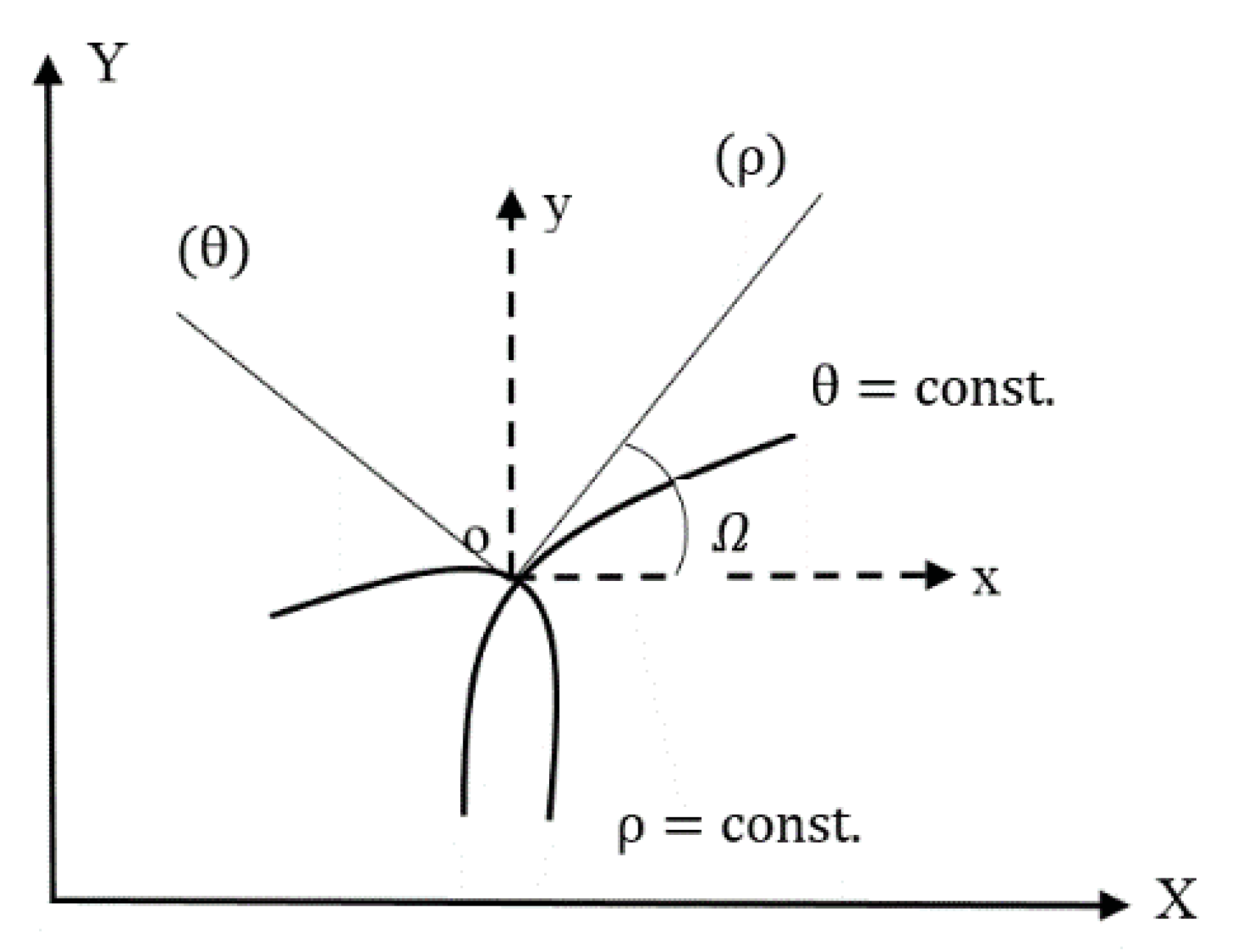
Figure 2.
Convert Cartesian coordinate () to curvilinear coordinate ().
Figure 2.
Convert Cartesian coordinate () to curvilinear coordinate ().
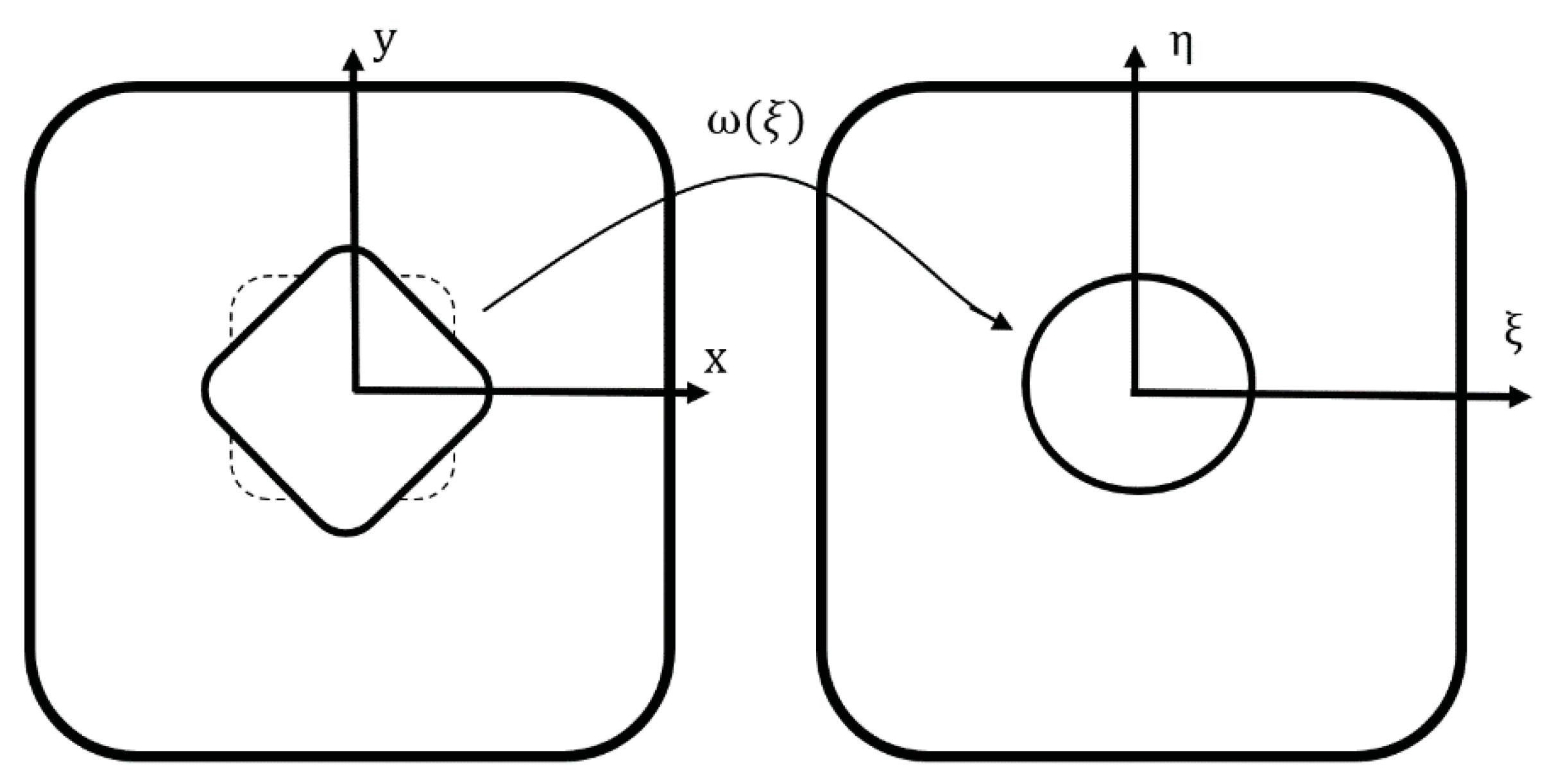
Figure 3.
Mapping a plate containing quasi-square cut out to a plate containing a circular cut out.
Figure 3.
Mapping a plate containing quasi-square cut out to a plate containing a circular cut out.
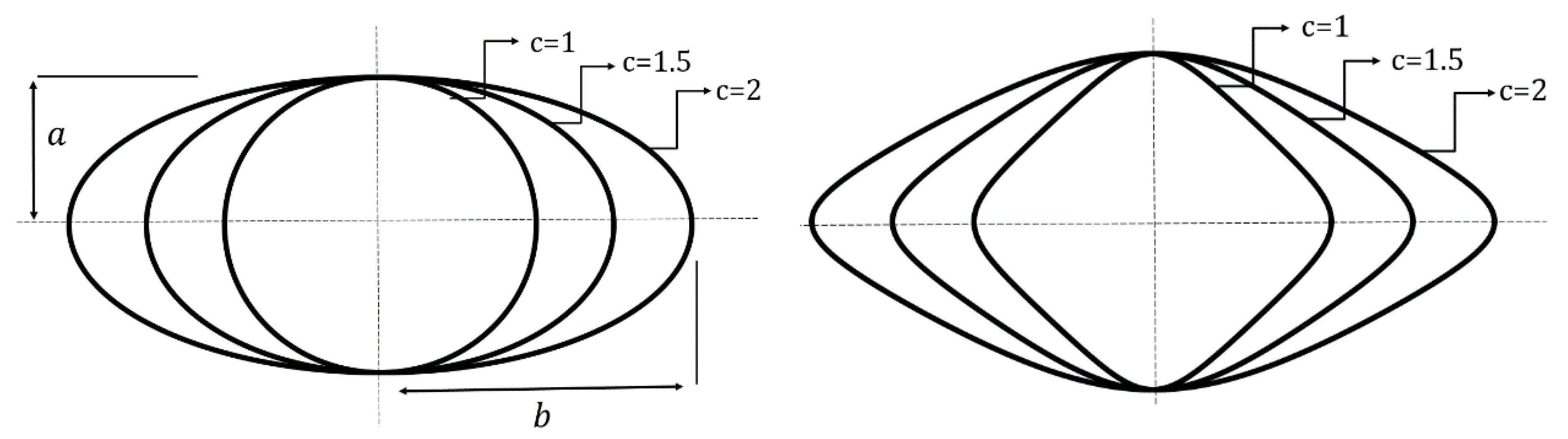
Figure 4.
Effect of w on the shape of quasi-square cutout ().
Figure 4.
Effect of w on the shape of quasi-square cutout ().
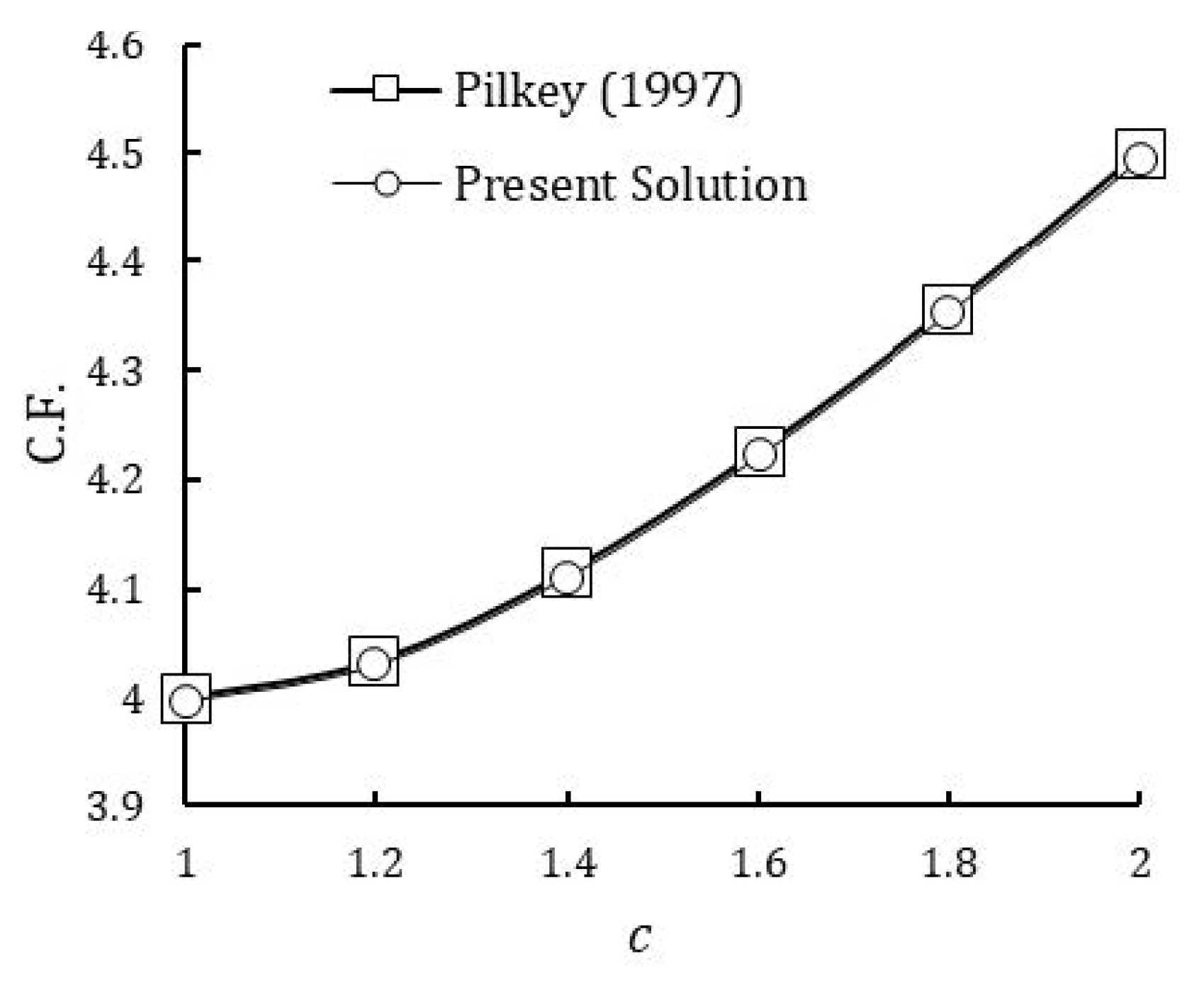
Figure 5.
Effect of c parameter on the shape of circular cutout , (left), effect of c parameter on the shape of quasi-square cutout , (right).
Figure 5.
Effect of c parameter on the shape of circular cutout , (left), effect of c parameter on the shape of quasi-square cutout , (right).
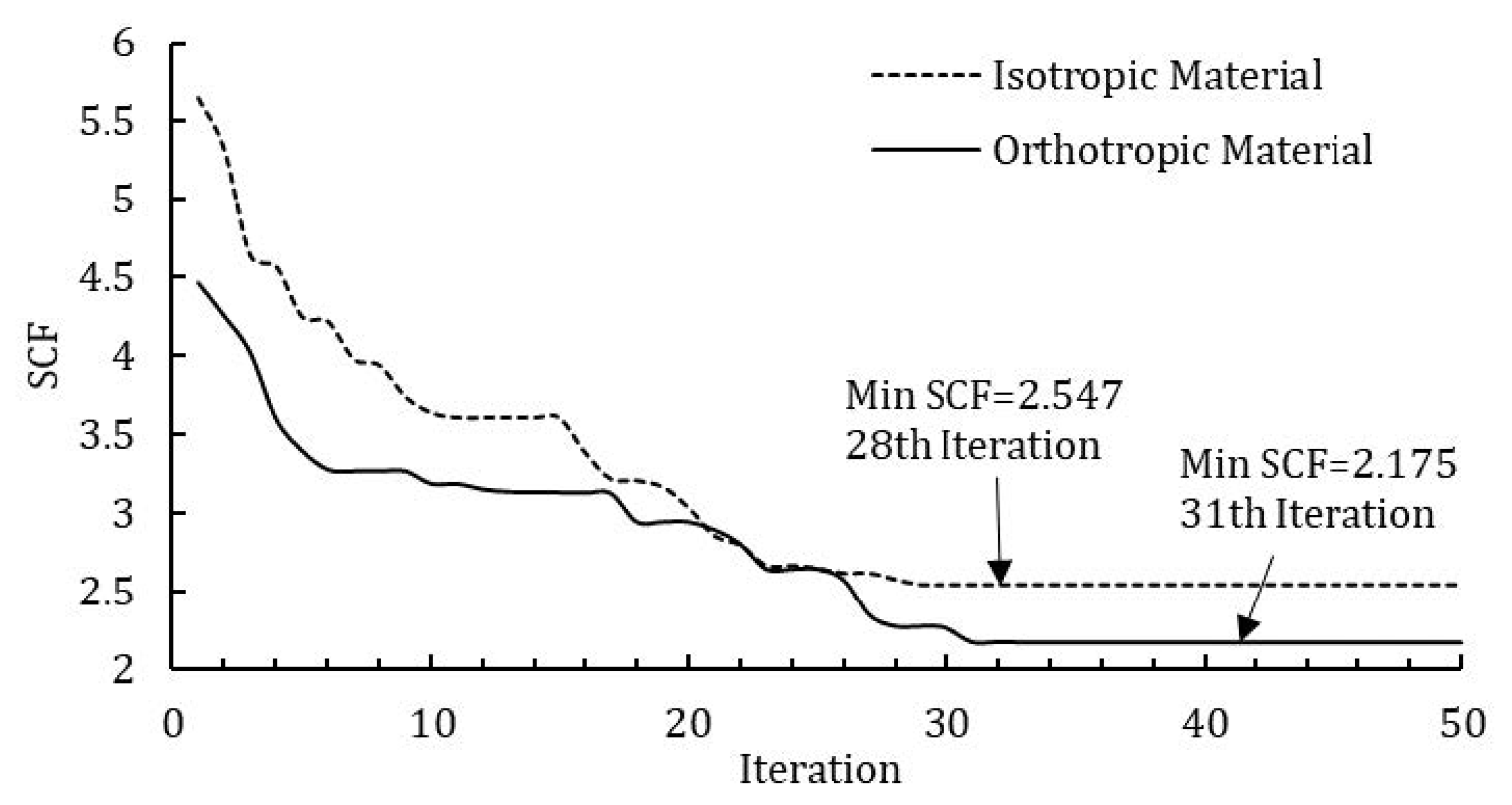
Figure 6.
Convergence diagram for optimum values with minimum SCF: isotropic material (Steel: , , and ) and orthotropic material (Graphite/Epoxy (T300/5208): , , , and ).
Figure 6.
Convergence diagram for optimum values with minimum SCF: isotropic material (Steel: , , and ) and orthotropic material (Graphite/Epoxy (T300/5208): , , , and ).
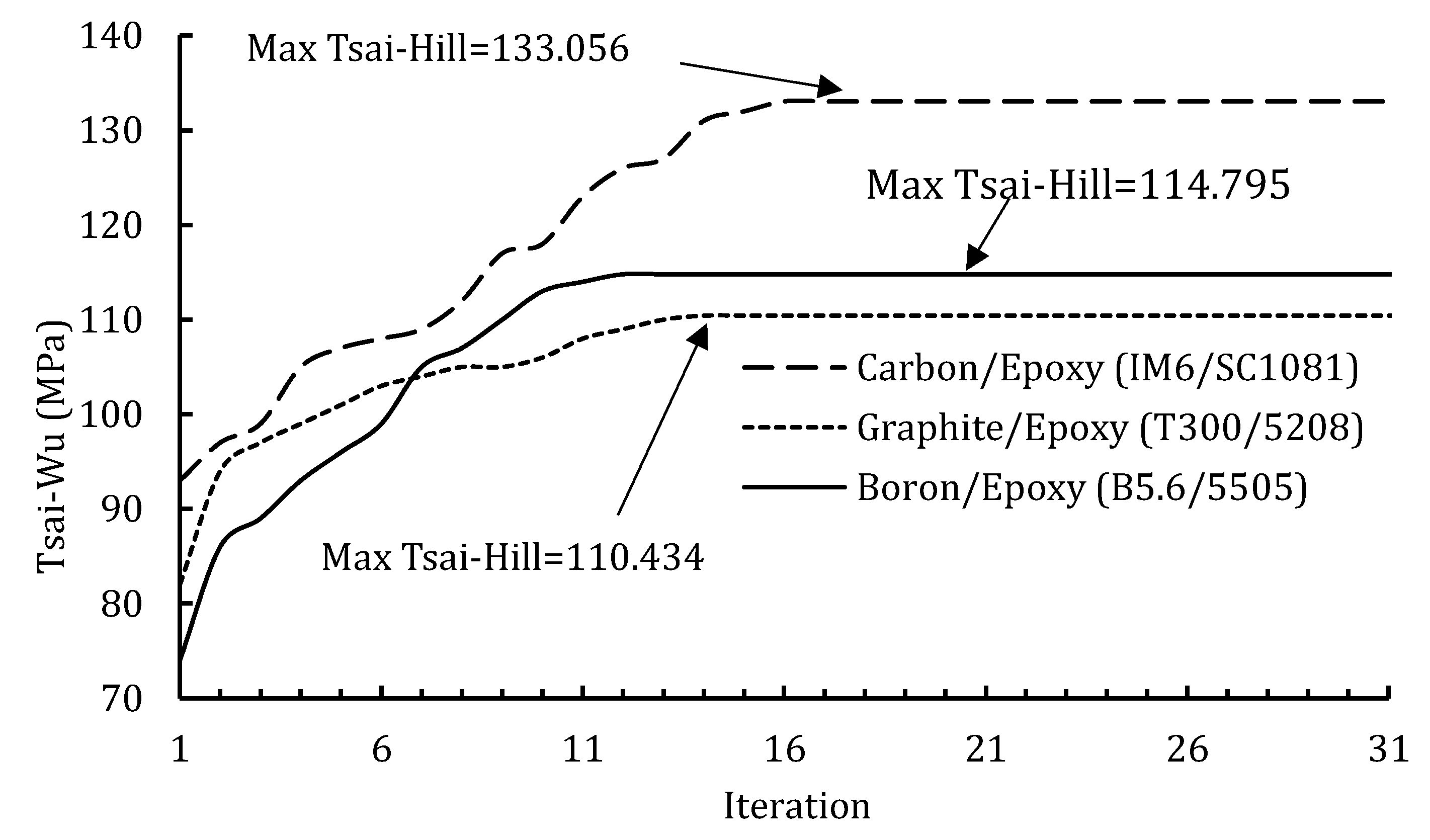
Figure 7.
Convergence diagram for optimum values according to the maximum values of Tsai-Hill (MPa) criterion. Carbon/Epoxy (IM6/SC1081) (), Graphite/Epoxy (T300/5208) (), and Boron/Epoxy (B5.6/5505) ().
Figure 7.
Convergence diagram for optimum values according to the maximum values of Tsai-Hill (MPa) criterion. Carbon/Epoxy (IM6/SC1081) (), Graphite/Epoxy (T300/5208) (), and Boron/Epoxy (B5.6/5505) ().
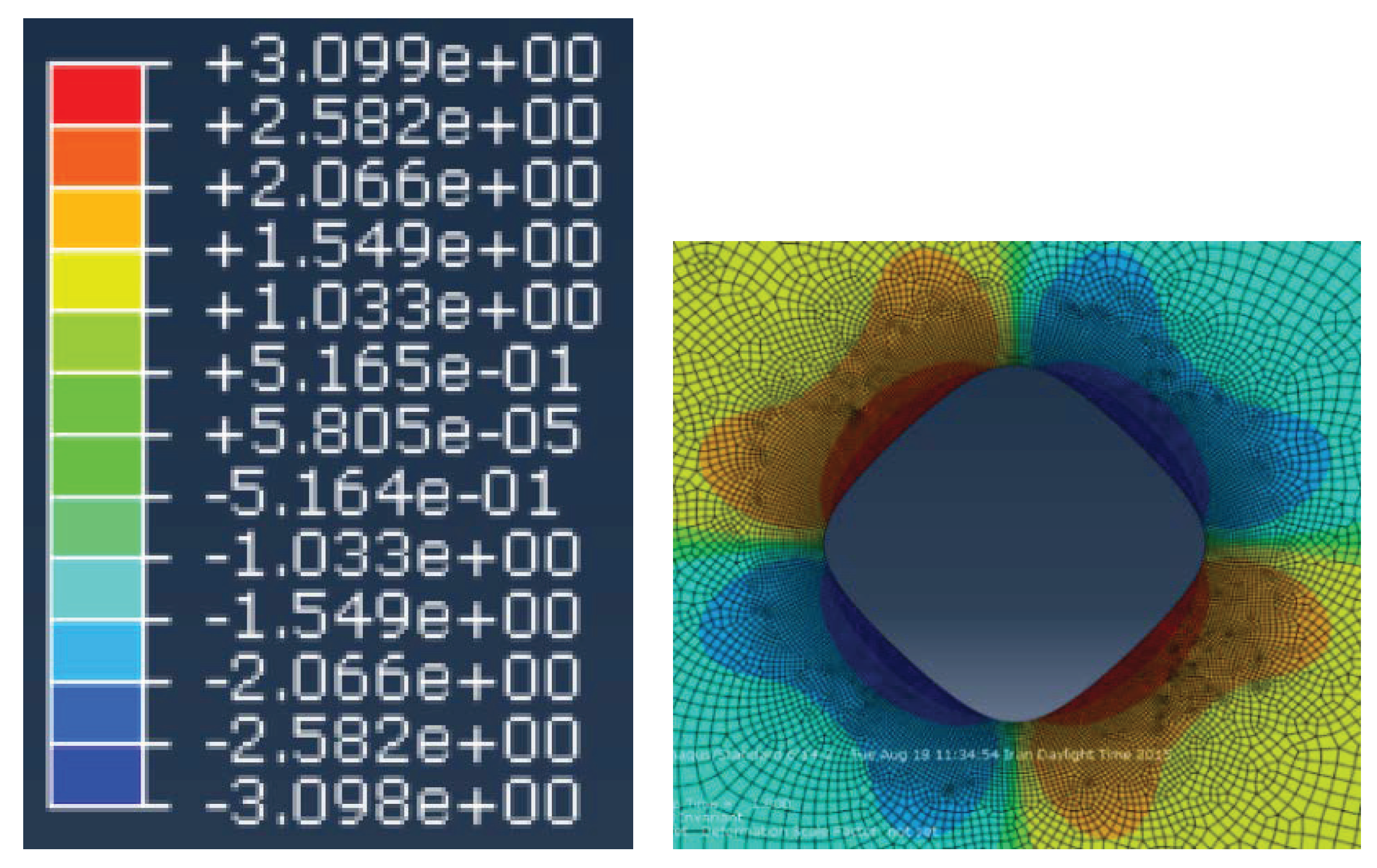
Figure 8.
Stress distribution around quasi-square cut out obtained from FEM ( and ).
Figure 8.
Stress distribution around quasi-square cut out obtained from FEM ( and ).
Figure 9.
Optimal stress distribution around quasi-square cutout computed by MATLAB.
Figure 9.
Optimal stress distribution around quasi-square cutout computed by MATLAB.
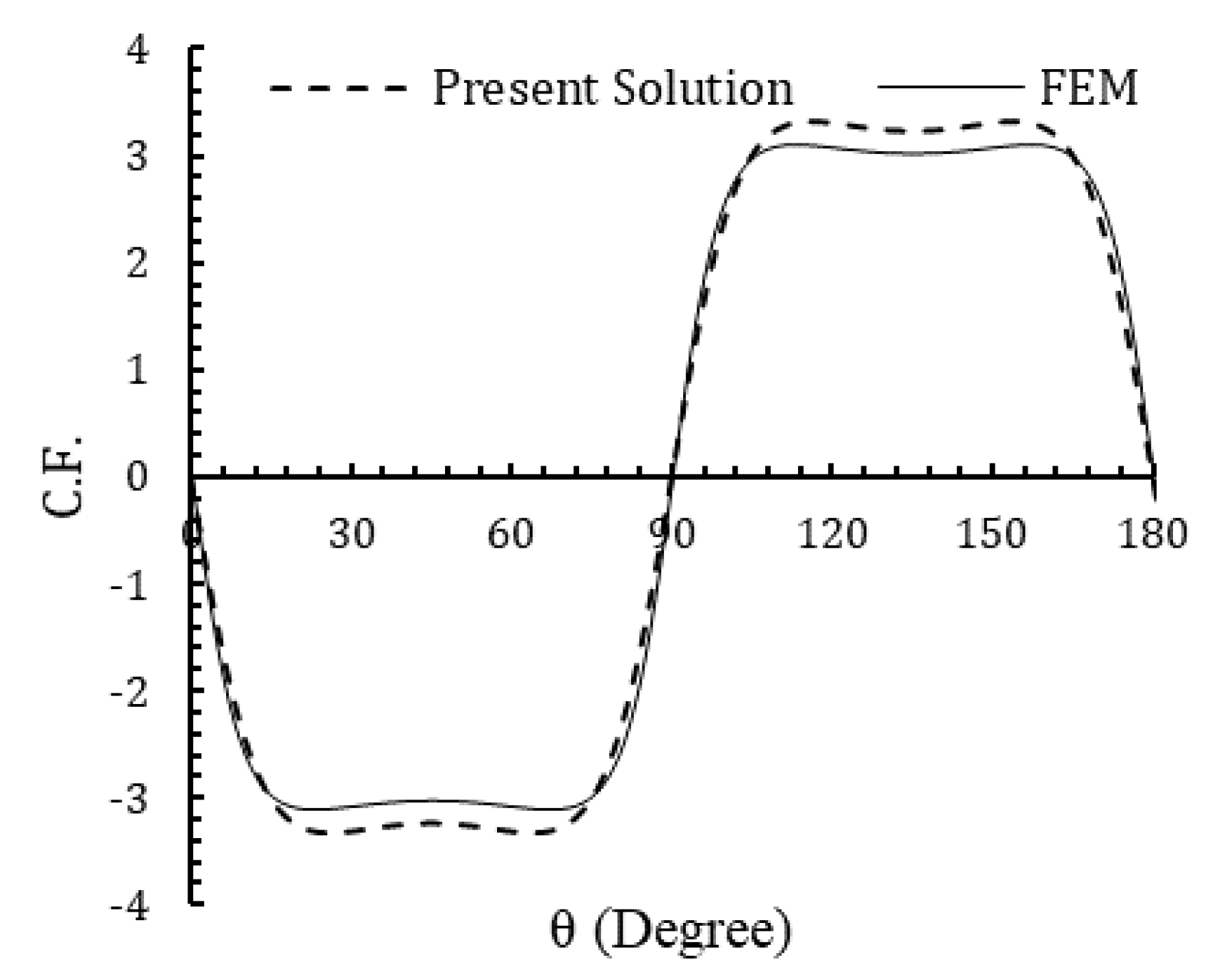
Figure 10.
Comparison of stress distribution around square cutout obtained by FEM and present solution (isotropic plate).
Figure 10.
Comparison of stress distribution around square cutout obtained by FEM and present solution (isotropic plate).
Figure 11.
Variation of SCF with aspect ratio of elliptical cut out by different methods for isotropic plate ().
Figure 11.
Variation of SCF with aspect ratio of elliptical cut out by different methods for isotropic plate ().
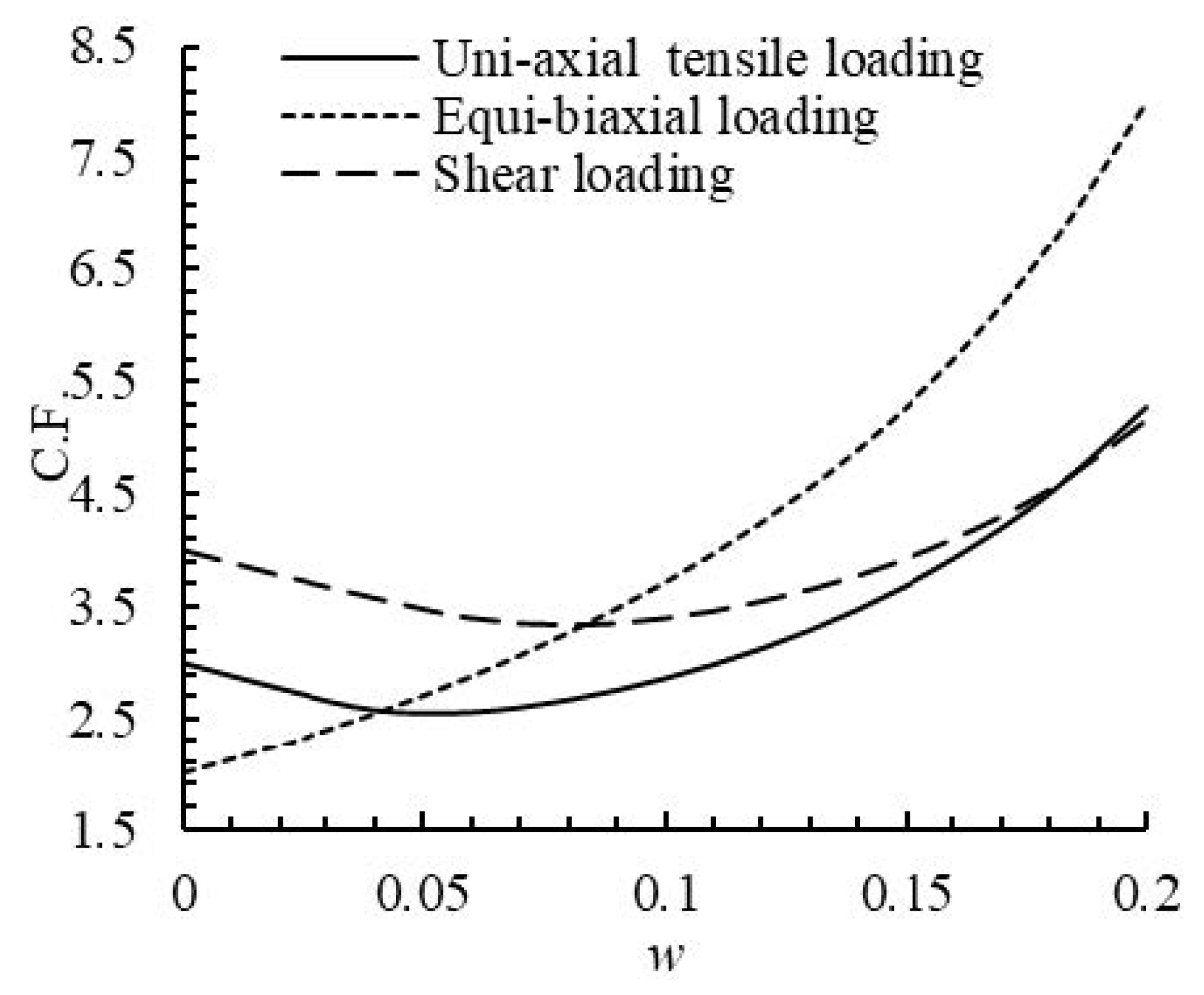
Figure 12.
Variations of the C.F. in terms of w in different loading ().
Figure 12.
Variations of the C.F. in terms of w in different loading ().
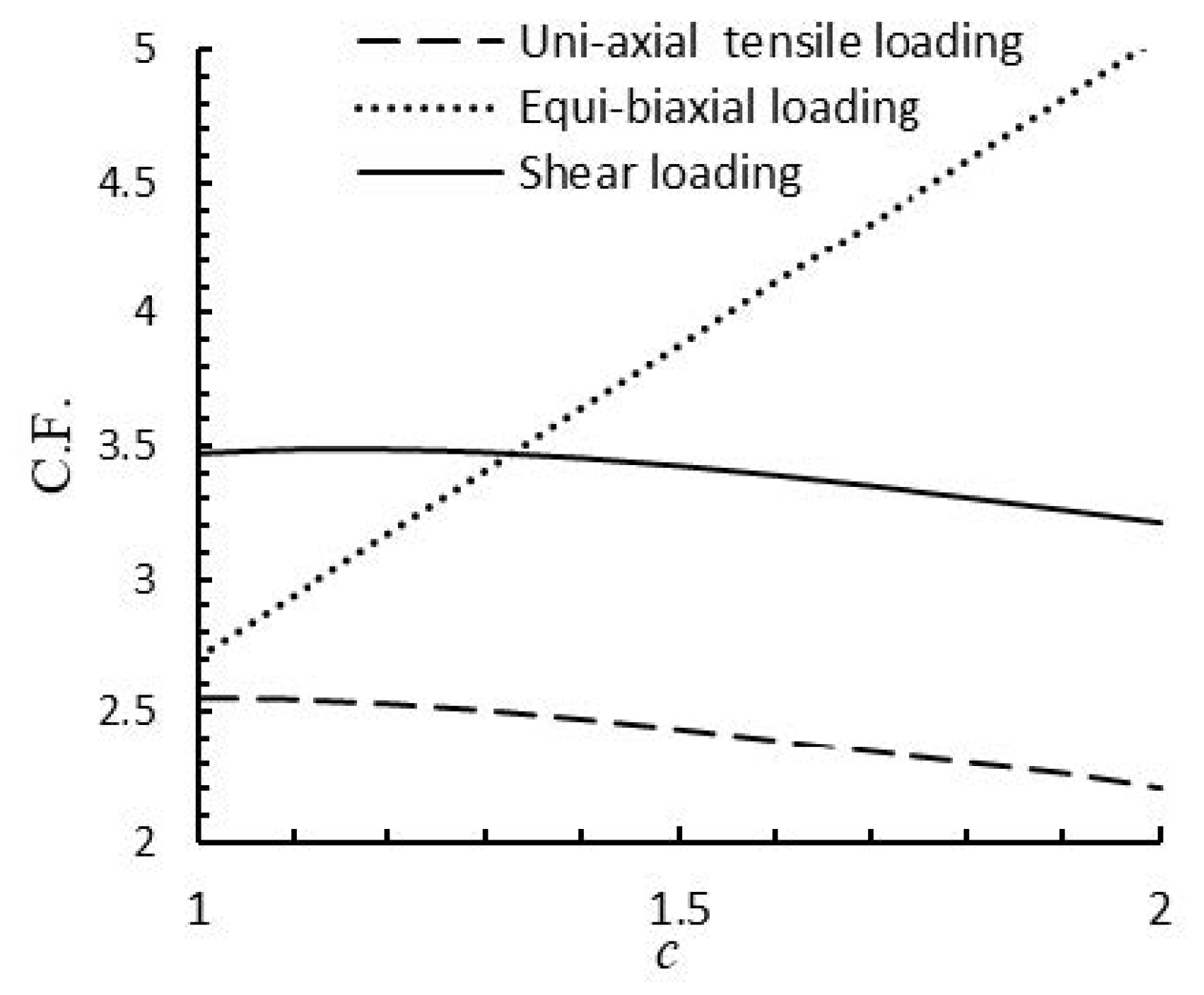
Figure 13.
Variations of the C.F. in terms of c for rectangular cutout ().
Figure 13.
Variations of the C.F. in terms of c for rectangular cutout ().
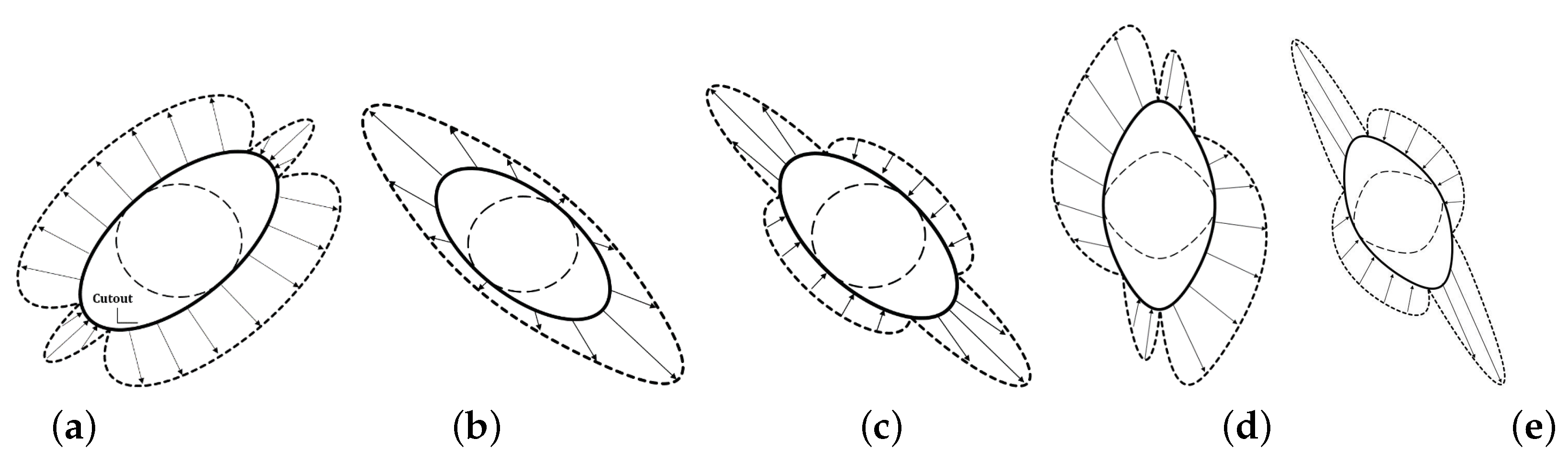
Figure 14.
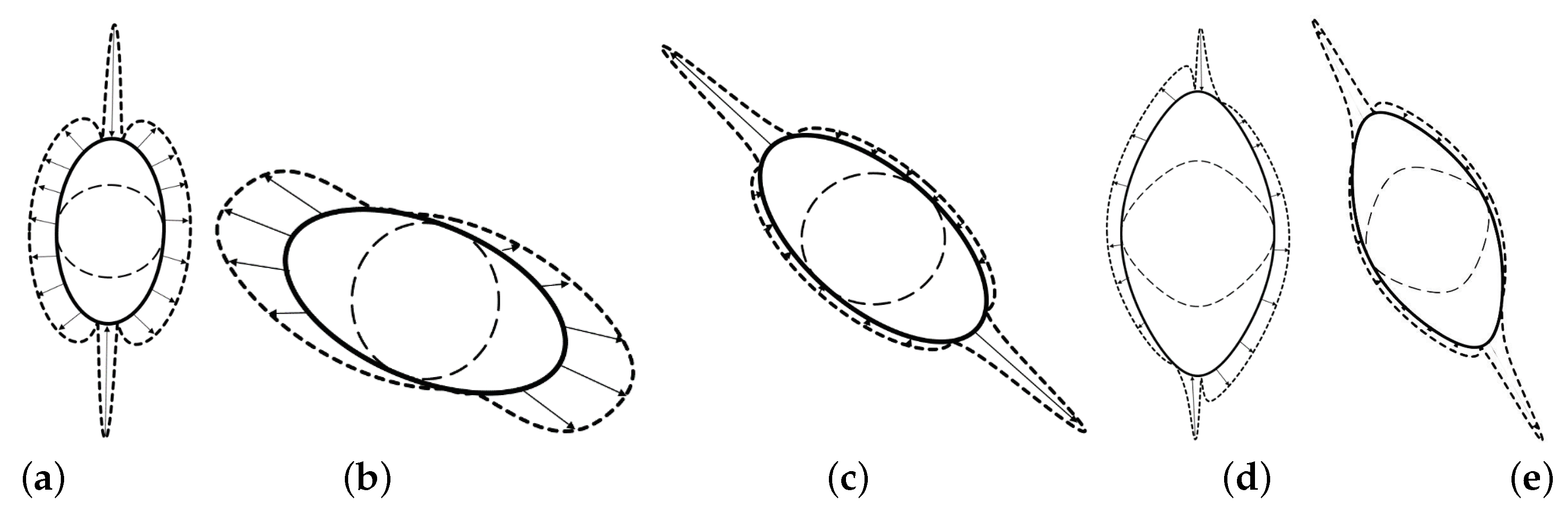
Stress distribution around different cutouts in an optimal condition for isotropic plates: (a) uniaxial tensile loading (, C.F. ), elliptical (, , ); (b) equibiaxial loading (, C.F. ), elliptical (, ); (c) shear loading (, C.F. ), elliptical (, ); (d) uniaxial tensile loading (, C.F. ), rectangular (, , ); and (e) shear loading (, C.F. ), rectangular (, ).
Figure 14.
Stress distribution around different cutouts in an optimal condition for isotropic plates: (a) uniaxial tensile loading (, C.F. ), elliptical (, , ); (b) equibiaxial loading (, C.F. ), elliptical (, ); (c) shear loading (, C.F. ), elliptical (, ); (d) uniaxial tensile loading (, C.F. ), rectangular (, , ); and (e) shear loading (, C.F. ), rectangular (, ).
Figure 15.
Distribution of the cost function around square cutout in an optimal state (uniaxial tensile loading).
Figure 15.
Distribution of the cost function around square cutout in an optimal state (uniaxial tensile loading).
Figure 16.
Distribution of the cost function around square cutout in an optimal state (equibiaxial loading).
Figure 16.
Distribution of the cost function around square cutout in an optimal state (equibiaxial loading).
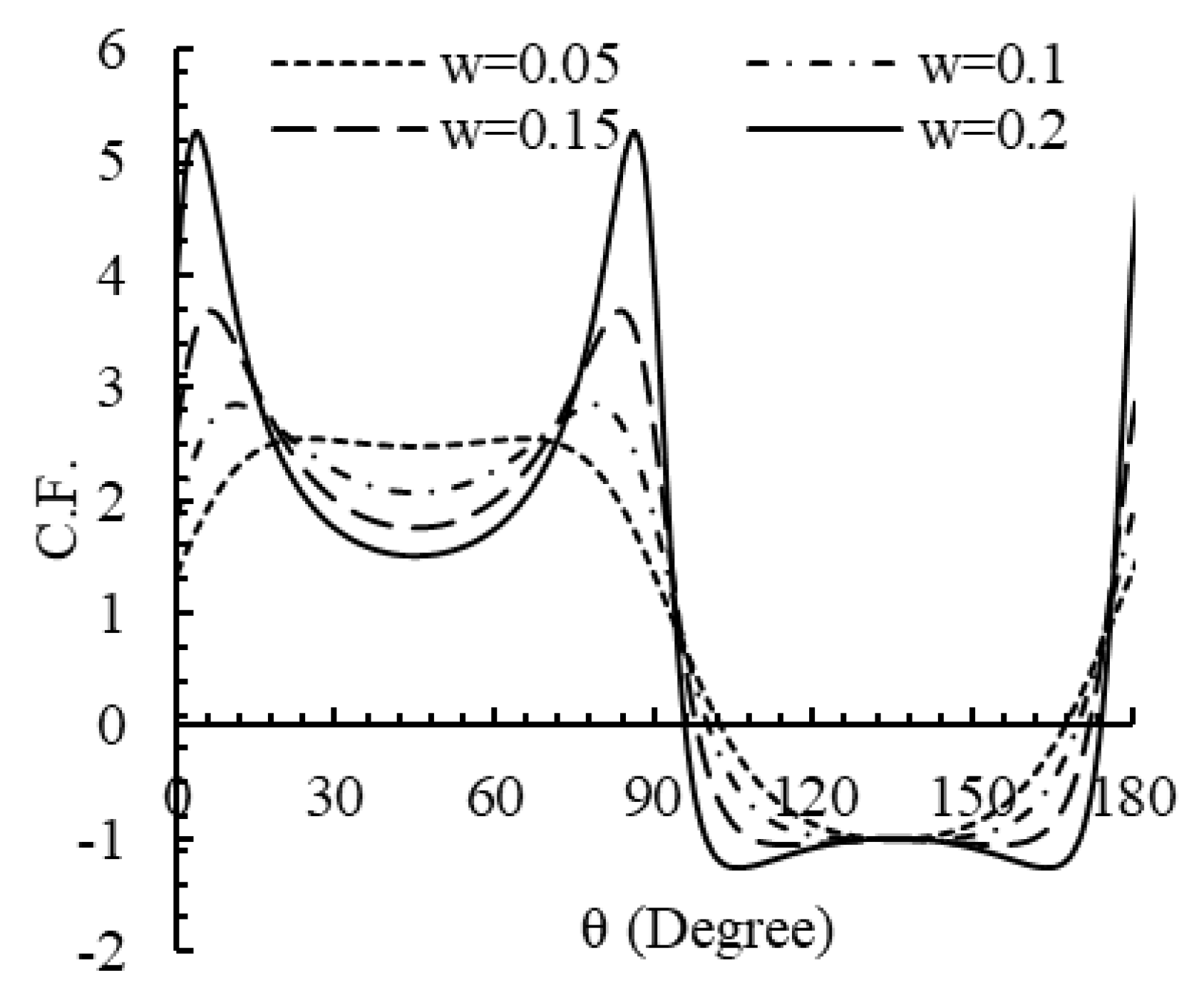
Figure 17.
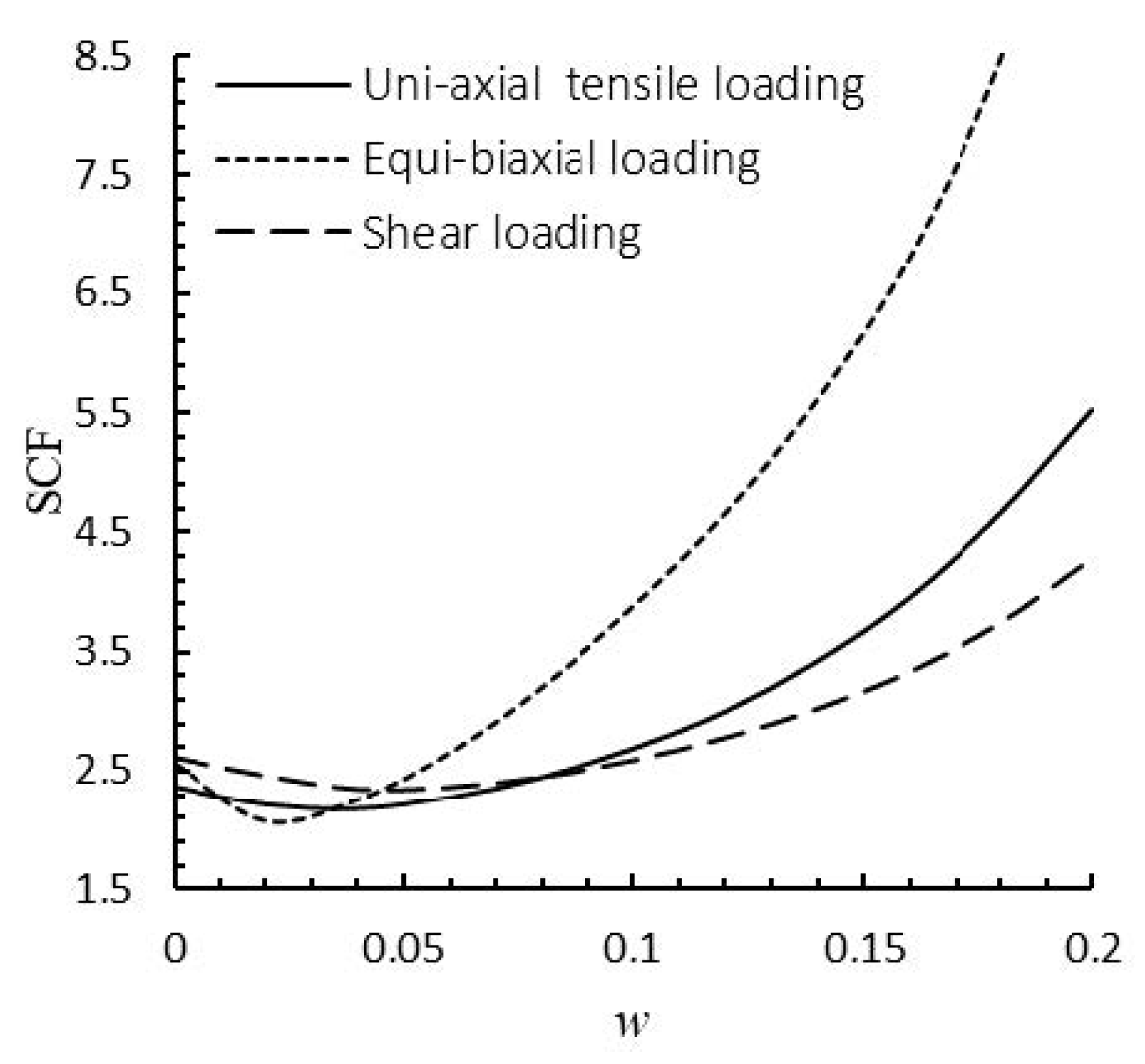
Variations of the SCF with w for quasi-square cutout ().
Figure 17.
Variations of the SCF with w for quasi-square cutout ().
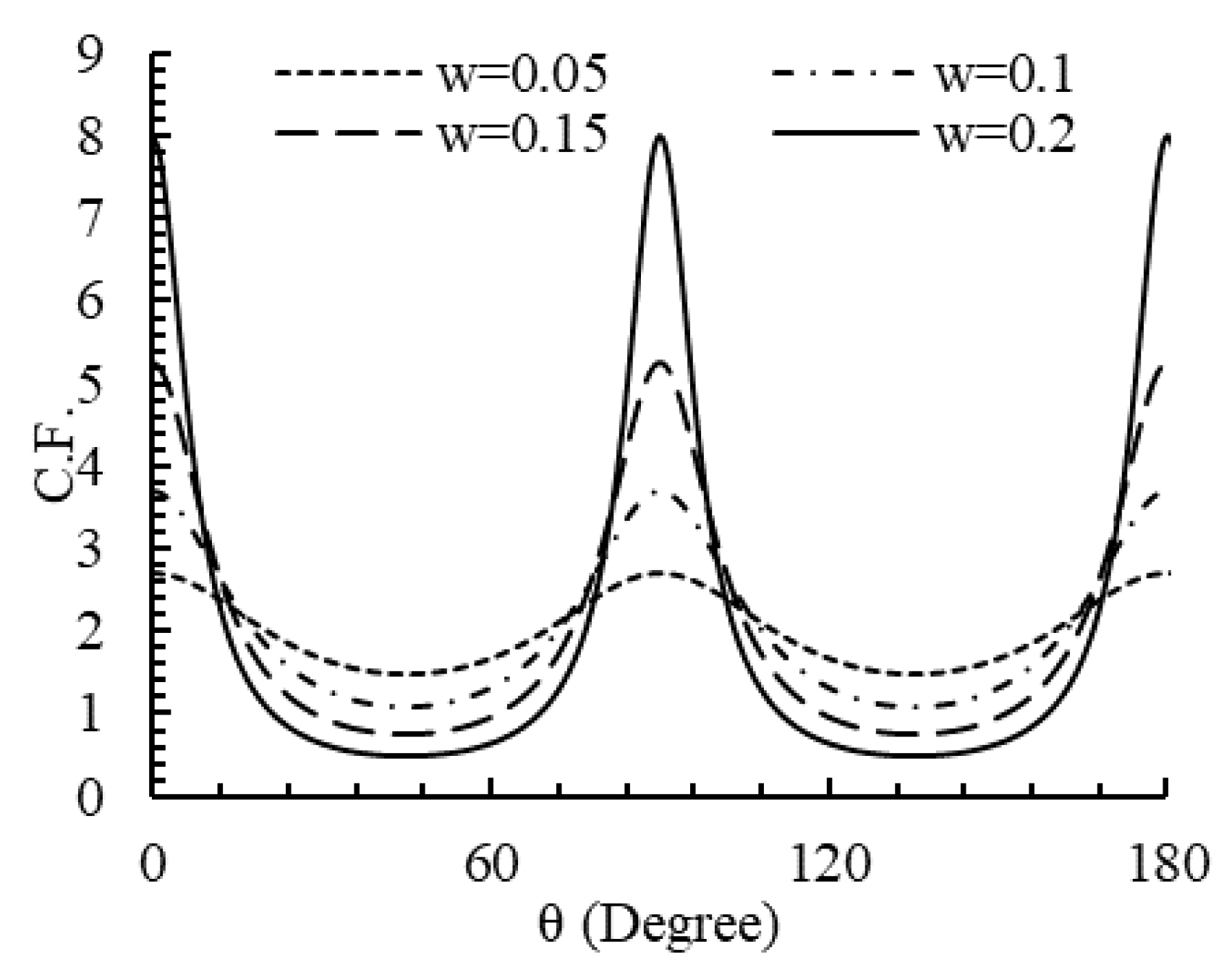
Figure 18.
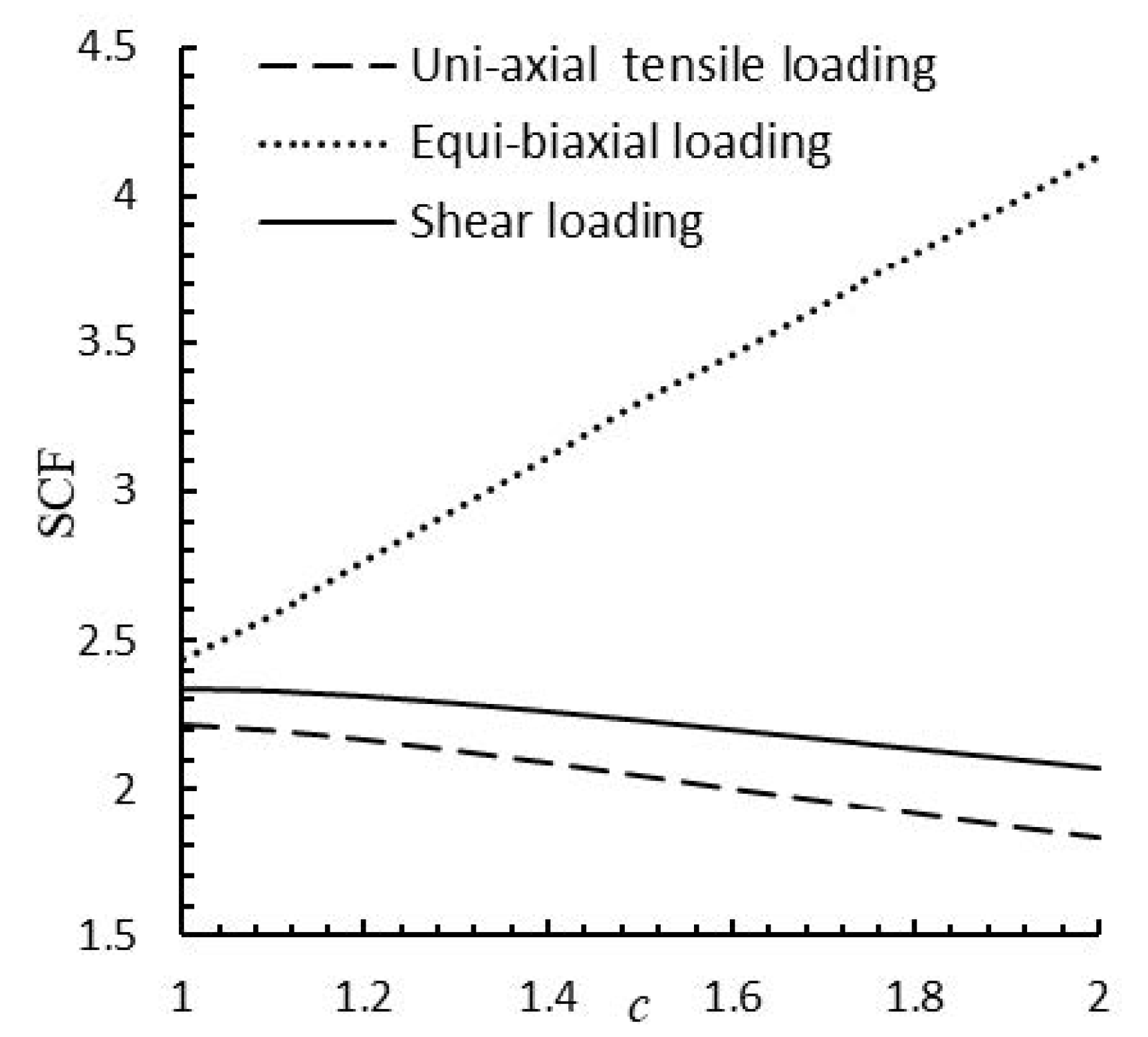
Variations of the SCF with c in different types of loadings ().
Figure 18.
Variations of the SCF with c in different types of loadings ().
Figure 19.
Stress distribution around cutout for graphite/epoxy plates in an optimal condition: (a) uniaxial tensile loading (, C.F. ), elliptical (, , , ); (b) equibiaxial loading (, C.F. ), elliptical (, , ); (c) shear loading (, C.F. ), elliptical (, , ); (d) uniaxial tensile loading (, C.F. ), rectangular (, , , ); and (e) shear loading (, C.F. ), rectangular (, , ).
Figure 19.
Stress distribution around cutout for graphite/epoxy plates in an optimal condition: (a) uniaxial tensile loading (, C.F. ), elliptical (, , , ); (b) equibiaxial loading (, C.F. ), elliptical (, , ); (c) shear loading (, C.F. ), elliptical (, , ); (d) uniaxial tensile loading (, C.F. ), rectangular (, , , ); and (e) shear loading (, C.F. ), rectangular (, , ).
Figure 20.
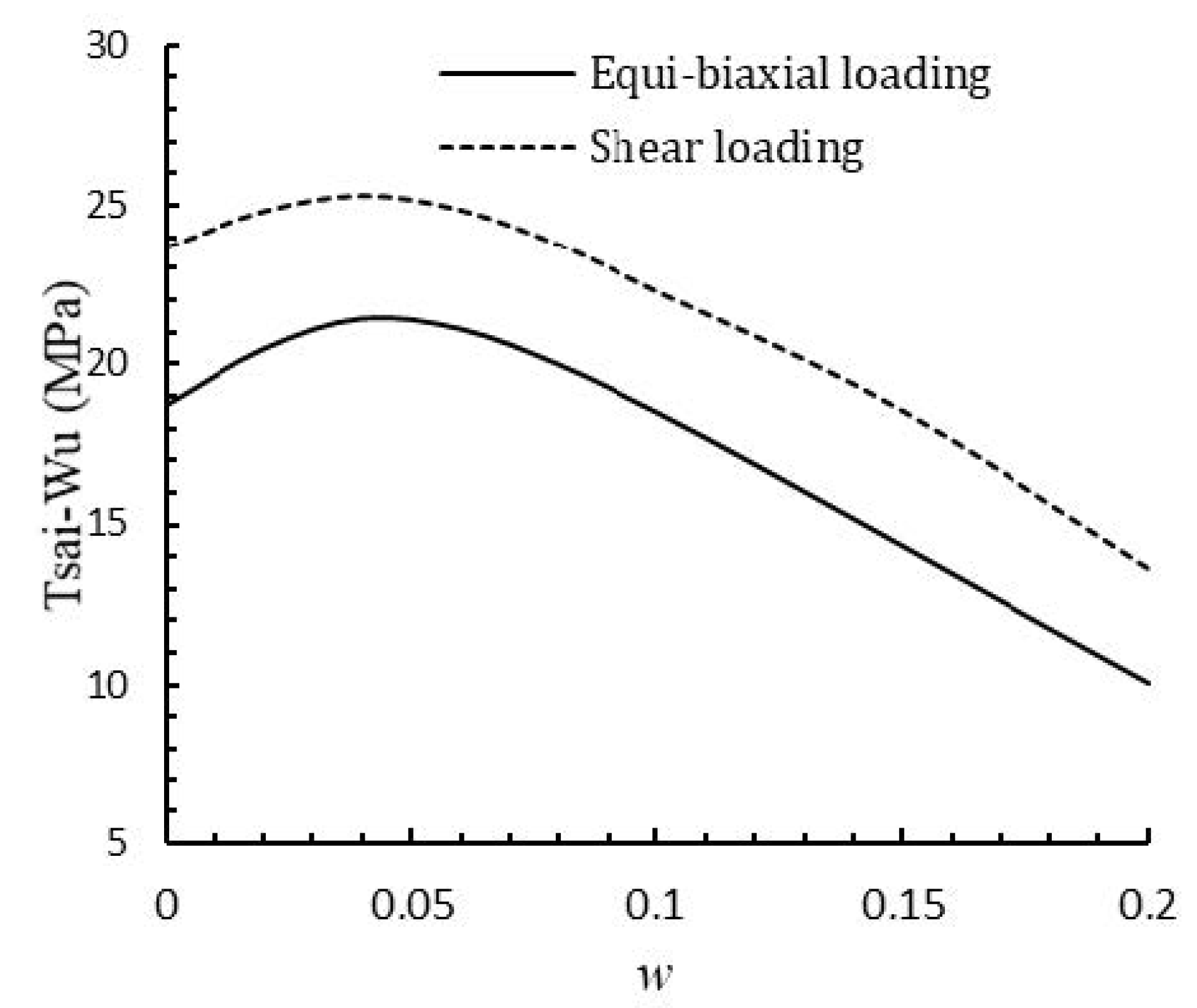
Strength variations of the graphite/epoxy with w ().
Figure 20.
Strength variations of the graphite/epoxy with w ().
Figure 21.
Strength variations of the graphite/epoxy with w in different values of c (Uniaxial tensile loading).
Figure 21.
Strength variations of the graphite/epoxy with w in different values of c (Uniaxial tensile loading).
Table 1.
The value of effective parameter for PSO algorithm.
Table 1.
The value of effective parameter for PSO algorithm.
| PSO Parameters | |
|---|
| Population Size | 40 |
| Maximum of Iteration | 50 |
| Cognitive Component | |
| Social Component | |
| Inertia Weight | |
Table 2.
Comparison of Tsai–Wu failure strength (MPa) obtained by present solution (p.s.) as well as those of Ukadgaonker and Rao [
73] (U&R).
Table 2.
Comparison of Tsai–Wu failure strength (MPa) obtained by present solution (p.s.) as well as those of Ukadgaonker and Rao [
73] (U&R).
| p.s. | U&R | | p.s. | U&R |
|---|
| 0 | 32.55 | 32.6 | 95 | 35.73 | 35.7 |
| 5 | 40.64 | 40.6 | 100 | 33091 | 33.1 |
| 10 | 58.045 | 58 | 105 | 30.756 | 30.8 |
| 15 | 185.28 | 185.3 | 110 | 28.676 | 28.7 |
| 20 | 166.18 | 166.2 | 115 | 26.813 | 26.8 |
| 25 | 181.79 | 181.8 | 120 | 25.14 | 25.1 |
| 30 | 198.51 | 198.5 | 125 | 23.64 | 23.6 |
| 35 | 181.2 | 181.2 | 130 | 22.32 | 22.3 |
| 40 | 150.93 | 150.9 | 135 | 22.32 | 22.3 |
| 45 | 123.42 | 123.4 | 140 | 20.23 | 20.2 |
| 50 | 102.07 | 102.1 | 145 | 19.52 | 19.5 |
| 55 | 86.027 | 86 | 150 | 19.12 | 19.1 |
| 60 | 73.9 | 73.9 | 155 | 19.108 | 19.1 |
| 65 | 64.55 | 64.50 | 160 | 19.64 | 19.6 |
| 70 | 57.177 | 57.2 | 165 | 20.93 | 20.9 |
| 75 | 51.234 | 51.2 | 170 | 23.27 | 23.3 |
| 80 | 46.343 | 46.3 | 175 | 27 | 27 |
| 85 | 42.244 | 42.2 | 180 | 35.7 | 180 |
| 90 | 38.751 | 38.8 | | | |
Table 3.
Material properties of the plate by Daniel and Ishai [
74].
Table 3.
Material properties of the plate by Daniel and Ishai [
74].
| | | | | | | | |
|---|
| | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | |
|---|
| Steel | - | - | - | 207 | 207 | 79.3 | 0.3 |
| Graphite/Epoxy (T300/5208) | 1500 | 40 | 68 | 181 | 10.3 | 7.17 | 0.28 |
| S-glass/Epoxy | 1280 | 49 | 69 | 43 | 8.9 | 4.5 | 0.27 |
| Woven-glass/Epoxy (7781/5245C) | 367 | 367 | 97.1 | 29.7 | 29.7 | 5.3 | 0.17 |
| E-glass/epoxy | 1080 | 39 | 89 | 39 | 8.6 | 3.8 | 0.28 |
| Carbon/Epoxy (IM6/SC1081) | 2860 | 49 | 83 | 177 | 10.8 | 7.6 | 0.27 |
| Boron/Epoxy (B5.6/5505) | 1380 | 56 | 62 | 201 | 21.7 | 5.4 | 0.17 |
| Glass/Epoxy | 1062 | 31 | 72 | 38.6 | 8.27 | 4.14 | 0.26 |
Table 4.
Optimal results for circular/elliptical cutout in isotropic plates.
Table 4.
Optimal results for circular/elliptical cutout in isotropic plates.
| | Optimal Values |
|---|
| | Uni-Axial Tensile Loading | Equi-Biaxial Loading | Shear Loading |
|---|
| | | | C.F. | | C.F. | | C.F. |
|---|
| 1 (circular) | 45 | - | - | 2.996 | - | 2.002 | - | 3.995 |
| (elliptical) | 45 | 134.55 | 89.55 | 2.331 | 45–135 | 2.996 | 44.33 | 3.330 |
| (elliptical) | 45 | 135 | 90 | 1.998 | 45–135 | 3.994 | 44.5 | 2.998 |
Table 5.
Optimal results for rectangular cutout in isotropic plates.
Table 5.
Optimal results for rectangular cutout in isotropic plates.
| | | Optimal Values |
|---|
| | | Uni-Axial Tensile Loading | Equi-Biaxial Loading | Shear Loading |
|---|
| | | | | C.F. | | C.F. | | C.F. |
|---|
| | 1 | 39.61 | 174.59 | 134.98 | 2.548 | 45–135 | 2.702 | 0-90-180 | 3.476 |
| 0.05 | 1.5 | 58.85 | 117.55 | 58.7 | 2.428 | 45–135 | 3.877 | 77 | 3.429 |
| | 2 | 70.13 | 0.00 | 70.13 | 2.208 | 45–135 | 5.052 | 26.9 | 3.214 |
| | 1 | 61.77 | 16.81 | 44.96 | 2.857 | 45–135 | 3.709 | 180 | 3.389 |
| 0.1 | 1.5 | 15.6 | 74 | 58.4 | 2.560 | 45–135 | 5.136 | 80.5 | 3.261 |
| | 2 | 17.82 | 131.32 | 135.5 | 2.293 | 45–135 | 5.136 | 15.8 | 3.141 |
| | 1 | 38.15 | 173.1 | 134.95 | 3.683 | 45–135 | 5.265 | 0-90-180 | 3.928 |
| 0.15 | 1.5 | 47 | 167.5 | 120.5 | 3.005 | 45–135 | 7.081 | 79.8 | 3.488 |
| | 2 | 39.15 | 106.9 | 67.75 | 2.566 | 45–135 | 8.897 | 16.35 | 3.240 |
| | 1 | 8.6 | 53.6 | 45 | 5.256 | 45–135 | 7.989 | 0-90-180 | 5.149 |
| 0.2 | 1.5 | 17.4 | 135.33 | 117.93 | 3.723 | 45–135 | 10.486 | 78 | 4.063 |
| | 2 | 87.6 | 17.3 | 70.3 | 2.988 | 45–135 | 12.983 | 18.23 | 3.564 |
Table 6.
All optimal values of design parameters for quasi-square cutout in isotropic plate ().
Table 6.
All optimal values of design parameters for quasi-square cutout in isotropic plate ().
| | All Optimal Values for Minimum SCF |
|---|
| | w | | | | C.F. | P.D. |
|---|
| Uniaxial tensile loading | 0.052 | 90 | 135 | 45 | 2.547 | 15% |
| Equibiaxial loading | 0.00 | - | - | - | 2.002 | 0.00% |
| Shear loading | 0.078 | - | 0-90-180 | - | 3.328 | 16.7% |
Table 7.
Optimal values of design variables in different aspect ratios of cutout ().
Table 7.
Optimal values of design variables in different aspect ratios of cutout ().
| | Optimal Values |
|---|
| | Uni-Axial Tensile Loading | Equi-Biaxial Loading | Shear Loading |
|---|
| | | | | SCF | | | SCF | | | SCF |
|---|
| 1 (circular) | 90 | 0 | - | - | 2.371 | 49 | - | 2.551 | 4 | - | 2.609 |
| | | | | | | | | | 5 | | |
| (elliptical) | 90 | 1.5 | 180 | 90 | 1.914 | 66.15 | 180 | 2.704 | 45.45 | 2.152 |
| | | | | | | | | | 5 | | |
| 2 (elliptical) | 88.6 | 0 | 178.6 | 90 | 1.685 | 0 | 69.3 | 3.397 | 4 | 45.3 | 1.924 |
| | | | | | | | | | 5 | | |
Table 8.
The optimal values of design variables in different values of bluntness w and aspect ratio of rectangular cutout c.
Table 8.
The optimal values of design variables in different values of bluntness w and aspect ratio of rectangular cutout c.
| | | Optimal Values |
|---|
| | | Uni-Axial Tensile Loading | Equi-Biaxial Loading | Shear Loading |
|---|
| | | | | | SCF | | | SCF | | | SCF |
|---|
| | 1 | 90 | 0 | 45 | 45 | 2.232 | 84.5 | 129.5 | 2.548 | 45 | 0 | 2.338 |
| 0.05 | 1.5 | 0 | 90 | 117 | 117 | 2.044 | 84.5 | 129.5 | 3.286 | 45 | 0 | 2.338 |
| | 2 | 77.5 | 0 | 180 | 102.5 | 1.826 | 16 | 84.7 | 4.126 | 43 | 26.4 | 2.073 |
| | 1 | 90 | 0 | 135 | 45 | 2.688 | 5.25 | 50.25 | 3.842 | 45 | 180 | 2.586 |
| 0.1 | 1.5 | 86.5 | 0 | 149.5 | 63 | 2.295 | 76.3 | 143.7 | 4.183 | 42.5 | 15 | 2.342 |
| | 2 | 74 | 0 | 175.5 | 101.5 | 1.979 | 90 | 19.5 | 5.184 | 47.12 | 67.87 | 2.136 |
| | 1 | 0 | 90 | 135 | 135 | 3.633 | 39.8 | 84.8 | 6.170 | 45 | 0 | 3.170 |
| 0.15 | 1.5 | 0 | 90 | 112.5 | 112.5 | 2.704 | 32.5 | 107.5 | 5.543 | 48 | 73.73 | 2.639 |
| | 2 | 85.8 | 15 | 6.4 | 79.4 | 2.193 | 33.8 | 1009.6 | 6.786 | 41.8 | 23.53 | 2.309 |
| | 1 | 73.5 | 17.5 | 98 | 44.5 | 5.216 | 35 | 170 | 10.76 | 45 | 90 | 4.286 |
| 0.2 | 1.5 | 22 | 90 | 98 | 76 | 3.196 | 33.6 | 138.6 | 7.856 | 49 | 71 | 3.121 |
| | 2 | 5 | 75.8 | 85.7 | 80.7 | 2.477 | 60 | 135 | 9.559 | 48 | 64.81 | 2.576 |
Table 9.
The optimal values of design variables in different values of bluntness w and aspect ratio of rectangular cutout c.
Table 9.
The optimal values of design variables in different values of bluntness w and aspect ratio of rectangular cutout c.
| | | Optimal Values in Different Bluntness for Rectangular Cutout |
|---|
| | | Uni-Axial Tensile Loading | Equi-Biaxial Loading | Shear Loading |
|---|
| | | | | T.W. (MPa)
| | | T.W. (MPa)
| | | T.W. (MPa)
|
|---|
| | 1 | 48.2 | 48.2 | - | 96.7702 | 61 | - | 18.7526 | 0 | - | 23.6921 |
| 0 | 1.5 | 32 | 31.7 | 126.4 | 135.8846 | 47 | 47 | 23.8670 | 90 | 180 | 25.8111 |
| | 2 | 90 | 90 | 0 | 167.7 | 90 | 90 | 27.6369 | 90 | 0 | 26.3309 |
| | 1 | 40.8 | 37.6 | 90.65 | 109.8832 | 66 | 21 | 21.4362 | 0 | 189 | 25.2117 |
| 0.05 | 1.5 | 88.55 | 86.4 | 154.4 | 124.5388 | 71 | 100 | 22.7636 | 90 | 0 | 29.1770 |
| | 2 | 43.8 | 42.65 | 121.8 | 150.7597 | 49 | 30 | 25.1931 | 0 | 90 | 28.5282 |
| | 1 | 44.65 | 47.9 | 87.3 | 96.8535 | 77.2 | 122.2 | 18.5250 | 90 | 0 | 22.2486 |
| 0.1 | 1.5 | 37.2 | 32 | 100.7 | 118.3234 | 41.5 | 70.5 | 20.8137 | 0 | 90 | 30.2795 |
| | 2 | 18.6 | 14.8 | 88.8 | 143.0703 | 90 | 107.5 | 23.3656 | 0 | 90 | 29.2944 |
| | 1 | 26.6 | 20 | 166.5 | 69.2347 | 45 | 90 | 14.3278 | 90 | 180 | 17.7315 |
| 0.15 | 1.5 | 37.2 | 32 | 100.7 | 118.3234 | 41.5 | 70.5 | 20.8137 | 90 | 0 | 27.4709 |
| | 2 | 71 | 75.3 | 180 | 120.9234 | 82.3 | 97 | 20.4352 | 90 | 0 | 27.8044 |
| | 1 | 54 | 54.3 | 98.8 | 47.8697 | 64 | 19 | 10.0770 | 0 | 180 | 13.6550 |
| 0.2 | 1.5 | 63.2 | 67.8 | 178 | 74.4147 | 68.7 | 46 | 14.0185 | 0 | 90 | 23.7177 |
| | 2 | 79.8 | 83.8 | 7.2 | 99.6860 | 55 | 51.7 | 17.2145 | 0 | 90 | 23.8164 |
Table 10.
The optimal values of design variables in different values of bluntness w and aspect ratio of quasi-triangular cutout c.
Table 10.
The optimal values of design variables in different values of bluntness w and aspect ratio of quasi-triangular cutout c.
| | | Optimal Values in Different Bluntness for Quasi-Triangular Cutout |
|---|
| | | Uni-Axial Tensile Loading | Equi-Biaxial Loading | Shear Loading |
|---|
| | | | | T.W. (MPa)
| | | T.W. (MPa)
| | | T.W. (MPa)
|
|---|
| | 1 | 61.2 | 59.6 | 127.7 | 88.3026 | 90 | 180 | 18.0113 | 90 | 0 | 22.6820 |
| 0.05 | 1.5 | 18.2 | 18.14 | 105.56 | 119.7700 | 17.23 | 17.67 | 21.7493 | 0 | 90 | 24.1125 |
| | 2 | 90 | 90 | 180 | 154.5169 | 0 | 0 | 25.7136 | 12.42 | 7.34 | 24.7409 |
| | 1 | 88.36 | 81.58 | 150.41 | 76.2248 | 90 | 180 | 16.3052 | 90 | 180 | 20.9688 |
| 0.1 | 1.5 | 46.91 | 47.95 | 150.59 | 107.7110 | 42.33 | 26.53 | 20.1418 | 81.63 | 14 | 22.5973 |
| | 2 | 90 | 90 | 180 | 138.6020 | 0 | 180 | 23.8684 | 75 | 20.23 | 23.2315 |
| | 1 | 58.27 | 61.72 | 112.61 | 65.3773 | 90 | 180 | 14.2295 | 90 | 180 | 18.8204 |
| 0.15 | 1.5 | 76.65 | 78.17 | 180 | 94.5733 | 19 | 4.25 | 18.3230 | 90 | 0 | 19.9144 |
| | 2 | 66.95 | 67.64 | 164.83 | 124.7309 | 14 | 6.63 | 22.1809 | 17.18 | 68.47 | 21.5115 |
| | 1 | 46.50 | 50.07 | 101.50 | 53.5819 | 90 | 0 | 12.0449 | 90 | 180 | 16.4227 |
| 0.2 | 1.5 | 54.07 | 55.80 | 156.74 | 82.2125 | 22.90 | 9.55 | 16.4221 | 11.72 | 73.92 | 18.4941 |
| | 2 | 48 | 47.16 | 130.74 | 111.5711 | 90 | 84.24 | 20.4724 | 70.44 | 23.17 | 19.6876 |
Table 11.
Optimal values of all design variables for square cutout ().
Table 11.
Optimal values of all design variables for square cutout ().
| | All Optimal Values |
|---|
| | All Optimal Values for minimum SCF | All Optimal Values for maximum Tsai–Wu |
|---|
| | w | | | | SCF | P.D. | w | | | | T.W. (MPa) | P.D. |
|---|
| Uniaxial | 0.035 | 0 | 90 | 135.5 | 2.175 | 8% | 0.052 | 86.7 | 88.4 | 39.4 | 110.4345 | 14% |
| Equibiaxial | 0.020 | - | 55 | 10 | 2.031 | 20% | 0.045 | - | 73.6 | 118.6 | 21.4945 | 14% |
| Shear | 0.045 | - | 44.5 | 90.5 | 2.336 | 10% | 0.039 | - | 90 | 0 | 25.3407 | 7% |
Table 12.
All optimal values of design parameters for another cutout ().
Table 12.
All optimal values of design parameters for another cutout ().
| | Uni-Axial Tensile Loading | Equi-Biaxial Loading | Shear Loading |
|---|
| | w | | | | T.W. (MPa) | w | | | T.W. (MPa) | w | | | T.W. (MPa) |
|---|
| Pentagonal | 0.00 | 90 | 90 | 180 | 96.3992 | 0.00 | 80.5 | 180 | 18.7526 | 0.00 | 90 | 39.5 | 23.6940 |
| Hexagonal | 0.013 | 0.00 | 0.00 | 180 | 99.2559 | 0.013 | 34 | 4 | 19.9764 | 0.00 | 90 | 15.5 | 23.6940 |
| Heptagonal | 0.00 | 90 | 90 | 121.5 | 96.4769 | 0.00 | 90 | 141 | 18.7526 | 0.00 | 0.00 | 76.5 | 23.6940 |
| Octagonal | 0.00 | 90 | 90 | 104.5 | 96.4769 | 0.005 | 88 | 20.5 | 19.4578 | 0.00 | 90 | 145.5 | 23.6940 |
Table 13.
Optimal values of the design parameters for different materials () with respect to Tsai–Wu.
Table 13.
Optimal values of the design parameters for different materials () with respect to Tsai–Wu.
| | Optimum Failure Strength Subjected to Uniaxial Tensile Loading |
|---|
| | Graphite/Epoxy (T300/5208) | S-Glass/Epoxy | Woven-Glass/Epoxy | Graphite/Epoxy | Carbon/Epoxy | E-Glass/Epoxy | Boron/Epoxy (B5.6/5505) |
|---|
| w | 0.052 | 0.032 | 0.047 | 0.072 | 0.050 | 0.089 | 0.056 |
| 86.7 | 36.6 | 68.7 | 36.4 | 40.6 | 29.7 | 90 |
| 88.4 | 35.2 | 78 | 46.23 | 37.7 | 20.7 | 90 |
| 39.4 | 175.3 | 18.5 | 155.4 | 180 | 0.00 | 135 |
| Optimal | 110.434 | 91.005 | 107.755 | 67.781 | 133.056 | 84.206 | 114.795 |
| Tsai–Wu | | | | | | | |
| P.D. | 14% | 5% | 10% | 2.5% | 13% | 1.5% | 19.5% |
| Tsai–Wu | 96.770 | 86.548 | 98.072 | 66.105 | 117.967 | 82.850 | 96.110 |
| (circular) | | | | | | | |