Inertial Iterative Schemes with Variable Step Sizes for Variational Inequality Problem Involving Pseudomonotone Operator

Abstract

Two inertial subgradient extragradient algorithms for solving variational inequality problems involving pseudomonotone operator are proposed in this article. The iterative schemes use self-adaptive step sizes which do not require the prior knowledge of the Lipschitz constant of the underlying operator. Furthermore, under mild assumptions, we show the weak and strong convergence of the sequences generated by the proposed algorithms. The strong convergence in the second algorithm follows from the use of viscosity method. Numerical experiments both in finite- and infinite-dimensional spaces are reported to illustrate the inertial effect and the computational performance of the proposed algorithms in comparison with the existing state of the art algorithms.

1. Introduction

This paper considers the problem of finding a point $\breve{u}\in \mathbb{E}$ such that

$$⟨\mathbb{A}\breve{u},u-\breve{u}⟩\ge 0,\forall u\in \mathbb{E},$$

(1)

where $\mathbb{E}$ is a nonempty closed convex subset of a real Hilbert space $\mathbb{H}$ and $\mathbb{A}$ is an operator on $\mathbb{H}$. The Variational Inequality (VI) problem Equation (1) is a fundamental problem in optimization theory which is applied in many areas of study, such as transportation problems, equilibrium, economics, engineering and so on (Refs. [1,2,3,4,5,6,7,8,9,10,11,12,13,14]).

There are many approaches to the VI problem, the basic one being the regularization and projection method. Many studies have been carried out and several algorithms have been considered and proposed (Refs. [5,15,16,17,18,19,20,21,22,23,24]). In this study, we are interested in the projection method.

The main iterative scheme in this study is given by

$$\left\{\begin{array}{c}{t}_n=u_n+{\varrho }_n(u_n-u_{n-1}),\hfill \\ s_n=P_{\mathbb{E}}\left(t_n-{\lambda }_n\mathbb{A}{t}_n\right),\hfill \\ T_n=\left\{u\in \mathbb{H}:⟨t_n-{\lambda }_n\mathbb{A}{t}_n-s_n,u-s_n⟩\le 0\right\}\hfill \\ u_{n+1}=P_{T_n}\left(t_n-{\lambda }_n\mathbb{A}{s}_n\right)n\ge 1.\hfill \end{array}\right.$$

(2)

where ${\varrho }_n$ is the inertial parameter with two different updating rules. The step size ${\lambda }_n$ is define to be self adaptively updated according to a new step size rule.

We now discuss the relationship between our scheme and the existing algorithms. The iterative scheme Equation (2) with a fixed step size is exactly the scheme proposed in [25] and without the inertial step, it reduces to the original subgradient extragradient scheme proposed by Censor et al. [26] where the underlying operator is monotone. The subgradient extragradient method has been studied, modified and improved by several researchers to produce variant methods. Most of these modifications used a fixed step size which depends on the factorials of the underlying operator such as strongly (inverse) modulus and Lipschitz constant. Therefore, algorithms with fixed step size require the prior knowledge of such factorials to be implemented. In a situation where such constants are difficult to compute or do not exist, such algorithms may be impossible to implement.

Recently, Yang et al. [27] proposed a modified subgradient algorithm with variable step size which does not require the knowledge of the Lipschitz constant for solving Equation (1). However, they considered the underlying operator to be monotone and the sequence generated converges weakly. Interested readers may refer to some recent articles that propose algorithms with variable step sizes which are independent of factorials of the underlying operator and Lipschitz constant (Refs. [28,29,30,31]). The question now is, can we have an iterative scheme involving a more general class of operators with a strong convergence and self-adaptive step size? We hence provide a positive answer to this question.

Inspired and motivated by [26,27], we proposed a self-adaptive subgradient extragradient algorithm by incorporating the inertial extrapolation step with the subgradient extragradient scheme. The aim of this modification is to obtain a self-adaptive scheme with fast convergence properties involving a more general class of operators. Moreover, we present a strong convergence version of the proposed algorithm by incorporating a viscosity method. The proposed schemes do not require prior knowledge of the Lipschitz constant of the operator. Furthermore, we present numerical experiments in finite- and infinite-dimensional spaces to illustrate the performance and the effect of the inertial step when compared to the existing algorithms in the literature.

The outline of this work is as follows: We give some definitions and Lemmas which we will use in our convergence analysis in the next section. We present the convergence analysis of our proposed schemes in Section 3 and lastly, in Section 4, we illustrate the inertial effect and the computational performance of our algorithms by giving some examples.

2. Preliminaries

This section recalls some known facts and necessary tools that we need for the convergence analysis of our method. Throughout this article, $\mathbb{H}$ is a real Hilbert space with inner product and norm denoted respectively as $⟨·,·⟩$ and $∥·∥$, $\mathbb{E}$ is a nonempty closed and convex subset of $\mathbb{H}$. The notation $u_j\rightharpoonup u(\mathrm{resp}{u}_j⟶u)$ is used to indicate that, respectively, the sequence $\left\{u_j\right\}$ converges weakly (strongly) to u. The following is known to hold in a Hilbert space:

$${\parallel t\pm s\parallel }^2={\parallel t\parallel }^2+{\parallel s\parallel }^2\pm 2⟨t,s⟩,$$

(3)

for every $t,s\in \mathbb{H}$ [32].

Definition 1.

Let $\mathbb{A}:\mathbb{H}⟶\mathbb{H}$ be a mapping defined on a real Hilbert space $\mathbb{H}$. $\mathbb{A}$ is said to be:

(1) 

Pseudomonotone if

$$⟨\mathbb{A}u,v-u⟩\ge 0,⟹⟨\mathbb{A}v,u-v⟩\ge 0\forall u,v\in \mathbb{E}.$$

(2) 

sequentially weakly continuous on $\mathbb{H}$ if $u_j\rightharpoonup u\in \mathbb{H},$ then $\mathbb{A}{u}_j\rightharpoonup \mathbb{A}u.$

Lemma 1.

[32] For any $\mathbb{E}\subset \mathbb{H}$ closed and convex and a metric projection from $\mathbb{H}$ onto $\mathbb{A}$. $v=P_{\mathbb{E}}u$ for any $u\in \mathbb{H}$, ⇔$⟨u-v,\omega -v⟩\le 0,\forall \omega \in \mathbb{E}.$

Lemma 2.

[33] For any $\mathbb{E}\subset \mathbb{H}$ closed and convex, for every u in $\mathbb{H}$, the following holds

i. 

$\parallel P_{\mathbb{E}}u-P_{\mathbb{E}}{v\parallel }^2\le ⟨P_{\mathbb{E}}u-P_{\mathbb{E}}v,u-v⟩$ for all $v\in \mathbb{H}$,

ii. 

$\parallel P_{\mathbb{E}}{u-v\parallel }^2\le {\parallel u-v\parallel }^2-{\parallel u-P_{\mathbb{E}}v\parallel }^2$ for all $v\in \mathbb{E}$.

For more properties of projection interested reader should see [33].

Lemma 3.

[34] Let $\mathbb{A}:\mathbb{E}⟶\mathbb{H}$ be a continuous and pseudomonotone mapping. Then $\breve{u}\in \Gamma$ if and only if $\breve{u}$ is a solution of the problem of finding $u\in \mathbb{E}$ such that $⟨\mathbb{A}v,v-u⟩\ge 0,\forall v\in \mathbb{E}.$

Lemma 4.

[35] Suppose $\left\{{\gamma }_n\right\}$, $\left\{{\varphi }_n\right\}$ and $\left\{{\varrho }_n\right\}$ be sequences in $[0,\infty )$ such that for all $n\ge 1$,

$${\gamma }_{n+1}\le {\gamma }_n+{\varrho }_n({\gamma }_n-{\gamma }_{n-1})+{\varphi }_n,\sum _{n=1}^{\infty }{\varphi }_n<\infty$$

and there exists $\varrho \in \mathbb{R}$ with $0\le {\varrho }_n\le \varrho \le 1$ for all $n\ge 1.$ Then the following are satisfied:

(i) 

${\sum }_{n=1}^{\infty }{[{\gamma }_n-{\gamma }_{n-1}]}_{+}<\infty$, where ${\left[a\right]}_{+}=max\{a,0\}$;

(ii) 

there exists ${\gamma }^{\ast }\in [0,\infty )$ with $lim{\gamma }_n={\gamma }^{\ast }$.

Lemma 5.

[36] Let $\mathbb{E}\subset \mathbb{H}$ be a nonempty set and a sequence $\left\{u_j\right\}$ in $\mathbb{H}$ such that the following are satisfied:

(a) 

for every $u\in \mathbb{E},{lim}_{j\to \infty }\parallel u_j-u\parallel$ exists;

(b) 

every sequentially weak cluster point of $\left\{u_j\right\}$ is in E.

Therefore, $\left\{u_j\right\}$ converges weakly in $\mathbb{E}.$

Lemma 6.

Let $\left\{{\varrho }_n\right\}$ be a nonnegative real number sequence, $\left\{{\gamma }_n\right\}$ be a sequence of real numbers in $(0,1)$ with ${\sum }_{n=1}^{\infty }{\gamma }_n=\infty$ and $\left\{{\delta }_n\right\}$ be a sequence of real numbers satisfying

$${\varrho }_{n+1}\le (1-{\gamma }_n){\varrho }_n+{\gamma }_n{\delta }_n,foralln\ge 1.$$

If ${lim\; sup}_{i\to \infty }{\delta }_{n_j}\le 0$ for every subsequence $\left\{{\varrho }_{n_j}\right\}$ of $\left\{{\varrho }_n\right\}$ satisfying $({\varrho }_{n_j+1}-{\varrho }_{n_j})\ge 0,$ then ${lim}_{n\to \infty }{\varrho }_n=0.$

3. A Self-Adaptive Subgradient Extragradient Scheme for Variational Inequality Problem

In this section, we give a detail description of our proposed algorithms. First, we present weak convergence analysis of the iterates generated by the algorithm to the solution of the VI problem Equation (1) involving pseudomonotone operator. We suppose the following assumptions for the analysis of our method.

Assumption 1.

A1 

The feasible set of Equation (1) is nonempty closed and convex subset of $\mathbb{H}$.

A2 

The solution set Γ of Equation (1) is nonempty.

A3 

$\mathbb{A}:\mathbb{H}⟶\mathbb{H}$ is pseudomonotone, L-Lipschitz continuous on $\mathbb{H}$ and sequentially weakly continuous on $\mathbb{E}.$

Remark 1.

For $0\le {\varrho }_n\le \varrho ,$ it can be observed from Equation (5) that ${\varrho }_n{\parallel u_n-u_{n-1}\parallel }^2\le \frac{1}{n^2}$ for all $n\in \mathbb{N}.$ This implies that

$$\sum _{n=1}^{\infty }{\varrho }_n{\parallel u_n-u_{n-1}\parallel }^2<\infty .$$

Algorithm 1 Adaptive Subgradient Extragradient Algorithm for Pseudomonotone Operator.

Initialization: Choose $u_{-1},u_0\in \mathbb{H},$ $\mu \in (0,1),$ $\varrho >0$ and ${\lambda }_0>0.$ Iterative Steps: Given the current iterates $u_{n-1}$ and $u_n\in \mathbb{H}$.    Step 1. Set $t_n$ as: $$t_n:=u_n+{\varrho }_n(u_n-u_{n-1}),$$ (4)    where $${\varrho }_n:=\left\{\begin{array}{cc}min\left\{\varrho ,\frac{1}{n^2{\parallel u_n-u_{n-1}\parallel }^2}\right\},\hfill & \mathrm{if}{u}_n\ne u_{n+1},\hfill \\ \varrho ,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ (5)    Step 2. Compute $$s_n=P_{\mathbb{E}}\left(t_n-{\lambda }_n\mathbb{A}{t}_n\right).$$    If $t_n=s_n$ or $\mathbb{A}{t}_n=0$, stop. Else, go to step 3.    Step 3. Construct $$T_n:=\left\{x\in \mathbb{H}:⟨t_n-{\lambda }_n\mathbb{A}{t}_n-s_n,x-s_n⟩\le 0\right\}.$$    Compute $$u_{n+1}=P_{T_n}\left(t_n-{\lambda }_n\mathbb{A}{s}_n\right).$$    where the stepsize sequence ${\lambda }_{n+1}$ is updated as follows: $${\lambda }_{n+1}:=\left\{\begin{array}{cc}min\left\{{\lambda }_n,{\mathsf{\Lambda }}_n\right\},\hfill & \mathrm{if}⟨\mathbb{A}{t}_n-\mathbb{A}{s}_n,u_{n+1}-s_n⟩>0\hfill \\ {\lambda }_n,\hfill & \mathrm{otherwise}0.\hfill \end{array}\right.$$ (6)    where $${\mathsf{\Lambda }}_n:=\frac{\mu (\parallel t_n-s_n{\parallel }^2-\parallel u_{n+1}-s_n{\parallel }^2)}{2⟨\mathbb{A}{t}_n-\mathbb{A}{s}_n,u_{n+1}-s_n⟩}$$ Set $n:=n+1$ and go back to Step 1.

Lemma 7.

The generated sequence $\left\{{\lambda }_n\right\}$ by Equation (6) is monotonically decreasing and bounded from below by $min\{\frac{\mu }{L},{\lambda }_0\}$

Proof. 

It can be observed that, the sequence $\left\{{\lambda }_n\right\}$ is monotonically decreasing. Since $\mathbb{A}$ is a Lipschitz function with Lipschitz’s constant $L,$ for $⟨\mathbb{A}{t}_n-\mathbb{A}{s}_n,u_{n+1}-s_n⟩>0$, we have

$$\begin{array}{cc}\hfill \frac{\mu (\parallel t_n-s_n{\parallel }^2-\parallel u_{n+1}-s_n{\parallel }^2)}{2⟨\mathbb{A}{t}_n-\mathbb{A}{s}_n,u_{n+1}-s_n⟩}& \ge \frac{\mu (\parallel t_n-s_n{\parallel }^2-\parallel u_{n+1}-s_n{\parallel }^2)}{2\parallel \mathbb{A}{t}_n-\mathbb{A}{s}_n\parallel \parallel u_{n+1}-s_n\parallel },\hfill \\ \hfill & \ge \frac{\mu (\parallel t_n-s_n{\parallel }^2-\parallel u_{n+1}-s_n{\parallel }^2)}{2L\parallel t_n-s_n\parallel \parallel u_{n+1}-s_n\parallel }\hfill \\ \hfill & \ge \frac{2\mu (\parallel t_n-s_n{\parallel }^2-\parallel u_{n+1}-s_n{\parallel }^2)}{2L\parallel t_n-s_n{\parallel }^2+{\parallel u_{n+1}-s_n\parallel }^2},\hfill \\ \hfill & \ge \frac{\mu }{L}\hfill \end{array}$$

□

Remark 2.

By Lemma 7, Equation (6) is well-defined and

$${\lambda }_{n+1}⟨\mathbb{A}{t}_n-\mathbb{A}{s}_n,u_{n+1}-s_n⟩\le \frac{\mu }{2}(\parallel t_n-s_n{\parallel }^2-\parallel u_{n+1}-s_n{\parallel }^2).$$

Next, the following lemma and its proof is crucial for the convergence analysis of the sequence generated by Algorithm 1.

Lemma 8.

Let $\mathbb{A}$ be an operator satisfying the Assumption 1 ($A3$). Then, for all $p\in \Gamma \ne \varnothing ,$ we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\breve{u}{\parallel }^2& \le \parallel t_n-\breve{u}{\parallel }^2-\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel t_n-s_n\parallel }^2\hfill \\ \hfill & -\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel u_{n+1}-s_n\parallel }^2.\hfill \end{array}$$

Proof. 

By Lemma 2 and the definition of $u_{n+1},$ we get

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\breve{u}{\parallel }^2& =\parallel P_{T_n}(t_n-{\lambda }_n\mathbb{A}{s}_n)-\breve{u}{\parallel }^2,\hfill \\ \hfill & \le \parallel (t_n-{\lambda }_n\mathbb{A}{s}_n)-\breve{u}{\parallel }^2-{\parallel (t_n-{\lambda }_n\mathbb{A}{s}_n)-u_{n+1}\parallel }^2,\hfill \\ \hfill & =\parallel t_n-\breve{u}{\parallel }^2-{\parallel t_n-u_{n+1}\parallel }^2+2{\lambda }_n⟨\breve{u}-u_{n+1},\mathbb{A}{s}_n⟩,\hfill \\ \hfill & =\parallel t_n-\breve{u}{\parallel }^2-{\parallel t_n-u_{n+1}\parallel }^2+2{\lambda }_n⟨\breve{u}-s_n,\mathbb{A}{s}_n-\mathbb{A}\breve{u}⟩\hfill \\ \hfill & +2{\lambda }_n⟨\breve{u}-s_n,\mathbb{A}\breve{u}⟩+2{\lambda }_n⟨s_n-u_{n+1},\mathbb{A}{s}_n⟩,\hfill \\ \hfill & \le \parallel t_n-\breve{u}{\parallel }^2-{\parallel t_n-u_{n+1}\parallel }^2+2{\lambda }_n⟨s_n-u_{n+1},\mathbb{A}{s}_n⟩,\hfill \\ \hfill & =\parallel t_n-\breve{u}{\parallel }^2-\parallel t_n-s_n{\parallel }^2-{\parallel u_{n+1}-s_n\parallel }^2+2{\lambda }_n⟨s_n-u_{n+1},\mathbb{A}{s}_n⟩\hfill \\ \hfill & -2⟨t_n-s_n,s_n-u_{n+1}⟩,\hfill \\ \hfill & =\parallel t_n-\breve{u}{\parallel }^2-\parallel t_n-s_n{\parallel }^2-{\parallel u_{n+1}-s_n\parallel }^2\hfill \\ \hfill & +2⟨t_n-{\lambda }_n\mathbb{A}{s}_n-s_n,u_{n+1}-s_n⟩.\hfill \end{array}$$

(7)

Using the definition of $s_n$ and the fact that $u_{n+1}\in T_n$, we have

$$\begin{array}{cc}\hfill ⟨t_n-{\lambda }_n\mathbb{A}{s}_n-s_n,u_{n+1}-s_n⟩& =⟨t_n-{\lambda }_n\mathbb{A}{t}_n-s_n,u_{n+1}-s_n⟩\hfill \\ \hfill & +⟨{\lambda }_n\mathbb{A}{t}_n-{\lambda }_n\mathbb{A}{s}_n,u_{n+1}-s_n⟩,\hfill \\ \hfill & \le {\lambda }_n⟨\mathbb{A}{t}_n-\mathbb{A}{s}_n,u_{n+1}-s_n⟩.\hfill \end{array}$$

(8)

Now, from the definition of ${\lambda }_{n+1}$, we have,

$$\begin{array}{cc}\hfill ⟨\mathbb{A}{t}_n-\mathbb{A}{s}_n,u_{n+1}-s_n⟩& \le \frac{1}{{\lambda }_{n+1}}\frac{\mu }{2}(\parallel t_n-s_n{\parallel }^2-\parallel u_{n+1}-s_n{\parallel }^2).\hfill \end{array}$$

(9)

Combining Equations (7)–(9), we obtain the required result. □

Lemma 9.

Let $\left\{t_n\right\}$ be a sequence generated by Algorithm 1 and Assumption $(A_1-A_3)$ is satisfied. If there exists a subsequence $\left\{t_{n_i}\right\}$ weakly convergent to $q\in \mathbb{H}$ with ${lim}_{i\to \infty }\parallel t_{n_i}-s_{n_i}\parallel =0.$ Then $q\in \Gamma .$

Proof. 

Since,

$$⟨t_{n_i}-{\lambda }_{n_i}\mathbb{A}{t}_{n_i}-s_{n_i},u-s_{n_i}⟩\le 0\mathrm{for}\mathrm{all}u\in \mathbb{E},$$

this implies that

$$\frac{1}{{\lambda }_{n_i}}⟨t_{n_i}-s_{n_i},u-s_{n_i}⟩\le ⟨\mathbb{A}{t}_{n_i},u-s_{n_i}⟩\mathrm{for}\mathrm{all}u\in \mathbb{E}.$$

Furthermore,

$$\frac{1}{{\lambda }_{n_i}}⟨t_{n_i}-s_{n_i},u-s_{n_i}⟩+⟨\mathbb{A}{t}_{n_i},s_{n_i}-t_{n_i}⟩\le ⟨\mathbb{A}{t}_{n_i},u-t_{n_i}⟩\mathrm{for}\mathrm{all}u\in \mathbb{E}.$$

(10)

By the hypothesis, $\left\{t_{n_i}\right\}$ is bounded, consequently, $\left\{s_{n_i}\right\}$ is also bounded, and from the Lipschitz continuity of $\mathbb{A}$, $\left\{\mathbb{A}{t}_{n_i}\right\}$ is bounded as well. Passing limit as $i\to \infty$ to Equation (10), we obtain

$$\underset{i\to \infty }{lim\; inf}⟨\mathbb{A}{t}_{n_i},u-t_{n_i}⟩\ge 0\mathrm{for}\mathrm{all}u\in \mathbb{E}.$$

(11)

Furthermore, we have

$$⟨\mathbb{A}{s}_{n_i},u-s_{n_i}⟩=⟨\mathbb{A}{s}_{n_i}-\mathbb{A}{t}_{n_i},u-t_{n_i}⟩+⟨\mathbb{A}{s}_{n_i},t_{n_i}-s_{n_i}⟩\mathrm{for}\mathrm{all}u\in \mathbb{E}.$$

(12)

$$\underset{i\to \infty }{lim\; inf}⟨\mathbb{A}{s}_{n_i},u-s_{n_i}⟩\ge 0.$$

The last inequality follows from Equations (11) and (12) and ${lim}_{i\to \infty }\parallel \mathbb{A}{t}_{n_i}-\mathbb{A}{s}_{n_i}\parallel =0$ (this follows from the fact that $\mathbb{A}$ is Lipschitz on $\mathbb{H},$ and ${lim}_{i\to \infty }\parallel t_{n_i}-s_{n_i}\parallel =0.$). Let $\left\{{\eta }_i\right\}$ be a decreasing sequence of positive numbers tending to 0 and for each $i,$ $N_i$ a smallest positive integer such that

$$⟨\mathbb{A}{s}_{n_j},u-s_{n_j}⟩+{\eta }_i\ge 0\mathrm{for}\mathrm{all}i\ge N_i.$$

(13)

It can be observed that the sequence $\left\{N_i\right\}$ is increasing. Moreover, assume $\mathbb{A}{s}_{n_i}\ne 0$ (otherwise $s_{n_i}$ is a solution), set

$${\rho }_{N_i}=\frac{\mathbb{A}{s}_{n_i}}{\parallel \mathbb{A}{s}_{n_i}{\parallel }^2},$$

therefore, for each i, we get $⟨\mathbb{A}{s}_{n_i},{\rho }_{N_i}⟩=1.$

It can be inferred from Equation (13) that for any i

$$⟨\mathbb{A}{s}_{n_i},u+{\eta }_i{\rho }_{N_i}-s_{n_i}⟩\ge 0.$$

By the pseudomonotonicity of $\mathbb{A},$ we have

$$⟨\mathbb{A}(u+{\eta }_i{\rho }_{N_i}),u+{\eta }_i{\rho }_{N_i}-s_{n_i}⟩\ge 0.$$

This implies that

$$⟨\mathbb{A}u,u-s_{n_i}⟩\ge ⟨\mathbb{A}u-\mathbb{A}(u+{\eta }_i{\rho }_{N_i}),u+{\eta }_i{\rho }_{N_i}-s_{n_i}⟩-{\eta }_i⟨\mathbb{A}u,{\rho }_{N_i}⟩.$$

(14)

To show that $q\in \Gamma$, to that end, we show that ${lim}_{i\to \infty }{\eta }_i{\rho }_{N_i}=0$. By the sequentially weakly lower semicontinuity of the norm mapping, we get

$$0<\parallel \mathbb{A}q\parallel \le \underset{i\to \infty }{lim\; inf}\parallel \mathbb{A}{s}_{n_i}\parallel .$$

Since, $\left\{s_{N_i}\right\}\subset \left\{s_{n_i}\right\}$ and ${\eta }_i\to 0$ as $i\to \infty ,$ we get

$$0\le \underset{i\to \infty }{lim\; sup}\parallel {\eta }_i{\rho }_{N_i}\parallel =\underset{i\to \infty }{lim\; sup}\left(\frac{{\eta }_i}{\parallel \mathbb{A}{s}_{n_i}\parallel }\right)\le \underset{i\to \infty }{lim\; sup}\frac{{\eta }_i}{\parallel \mathbb{A}{s}_{n_i}\parallel }=0.$$

Therefore, ${lim}_{i\to \infty }{\eta }_i{\rho }_{N_i}=0.$ Now, from the fact that $\mathbb{A}$ is uniformly bounded, $\left\{t_{n_i}\right\},\left\{{\rho }_{N_i}\right\},$ are bounded and ${lim}_{i\to \infty }{\eta }_i{\rho }_{N_i}=0,$ we obtain

$$\underset{i\to \infty }{lim\; inf}⟨\mathbb{A}u,u-s_{n_i}⟩\ge 0$$

Therefore, for all $u\in \mathbb{E},$ we have

$$⟨\mathbb{A}u,u-q⟩=\underset{i\to \infty }{lim}⟨\mathbb{A}u,u-s_{n_i}⟩=\underset{i\to \infty }{lim\; inf}⟨\mathbb{A}u,u-s_{n_i}⟩\ge 0.$$

By Lemma 3, $q\in \Gamma$ and hence the proof is complete. □

Remark 3.

As noted in [37,38], when the operator $\mathbb{A}$ is monotone, the sequentially weak- weak assumption is not needed in Lemma 9.

Theorem 1.

Let A be an operator satisfying the Assumption 1 ($A3$). Then, for all $p\in \Gamma \ne \varnothing ,$ the sequence $\left\{u_n\right\}$ generated by Algorithm 1, converges weakly to $\breve{u}.$

Proof. 

By Lemma 8, we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\breve{u}{\parallel }^2& \le \parallel t_n-\breve{u}{\parallel }^2-\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel t_n-s_n\parallel }^2\hfill \\ \hfill & -\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel u_{n+1}-s_n\parallel }^2.\hfill \end{array}$$

(15)

Moreover, from Equation (4), we have

$$\begin{array}{cc}\hfill \parallel t_n-\breve{u}{\parallel }^2& =\parallel u_n+{\varrho }_n(u_n-u_{n-1})-\breve{u}{\parallel }^2,\hfill \\ \hfill & =\parallel (1+\varrho )(u_n-p)-{\varrho }_n(u_{n-1}-\breve{u}){\parallel }^2,\hfill \\ \hfill & =(1+{\varrho }_n)\parallel u_n-\breve{u}{\parallel }^2-{\varrho }_n\parallel u_{n-1}-\breve{u}{\parallel }^2+{\varrho }_n(1+{\varrho }_n){\parallel u_n-u_{n-1}\parallel }^2.\hfill \end{array}$$

(16)

Substituting the last equation in Equation (15), we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\breve{u}{\parallel }^2& \le (1+{\varrho }_n)\parallel u_n-\breve{u}{\parallel }^2-{\varrho }_n\parallel u_{n-1}-\breve{u}{\parallel }^2+{\varrho }_n(1+{\varrho }_n){\parallel u_n-u_{n-1}\parallel }^2,\hfill \\ \hfill & -\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right)\parallel t_n-s_n{\parallel }^2-\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel u_{n+1}-s_n\parallel }^2.\hfill \\ \hfill & \le \parallel u_n-\breve{u}{\parallel }^2+{\varrho }_n(\parallel u_n-\breve{u}{\parallel }^2-\parallel u_{n-1}-\breve{u}{\parallel }^2),\hfill \\ \hfill & +{\varrho }_n(1+{\varrho }_n)\parallel u_n-u_{n-1}{\parallel }^2-\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel t_n-s_n\parallel }^2,\hfill \\ \hfill & -\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel u_{n+1}-s_n\parallel }^2.\hfill \end{array}$$

(17)

Observe that ${lim}_{n\to \infty }{\lambda }_n\frac{\mu }{{\lambda }_{n+1}}=\mu$ with $0<\mu <1$, thus, there exists $\aleph \ge 0$, such that for all $n\ge \aleph$ $0<{\lambda }_n\frac{\mu }{{\lambda }_{n+1}}<1$. Consequently, we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\breve{u}{\parallel }^2& \le \parallel u_n-\breve{u}{\parallel }^2+{\varrho }_n(\parallel u_n{-p\parallel }^2-\parallel u_{n-1}-\breve{u}{\parallel }^2),\hfill \\ \hfill & +{\varrho }_n(1+{\varrho }_n){\parallel u_n-u_{n-1}\parallel }^2.\hfill \end{array}$$

Now, comparing the last equation with Lemma 4, we have

$${\mathsf{\Gamma }}_n=\parallel u_n-\breve{u}{\parallel }^2\mathrm{and}{\phi }_n={\varrho }_n(1+{\varrho }_n){\parallel u_n-u_{n-1}\parallel }^2.$$

Therefore, we get

$$\sum _{n=1}^{\infty }{\left[\parallel u_n-\breve{u}{\parallel }^2-{\parallel u_{n-1}-\breve{u}\parallel }^2\right]}_{+}\le +\infty .$$

Consequently,

$$\underset{n\to \infty }{lim}{\left[\parallel u_n-\breve{u}{\parallel }^2-{\parallel u_{n-1}-\breve{u}\parallel }^2\right]}_{+}=0,$$

and ${lim}_{n\to \infty }{\parallel u_n-\breve{u}\parallel }^2$ exists. On the other hand, from Equation (17) we have

$$\begin{array}{cc}\hfill & \left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right)\parallel t_n-s_n{\parallel }^2+\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel u_{n+1}-s_n\parallel }^2\hfill \\ \hfill & \le \parallel u_n-\breve{u}{\parallel }^2-\parallel u_{n+1}-\breve{u}{\parallel }^2+{\varrho }_n(\parallel u_n-\breve{u}{\parallel }^2-\parallel u_{n-1}-\breve{u}{\parallel }^2)\hfill \\ \hfill & +{\varrho }_n(1+{\varrho }_n){\parallel u_n-u_{n-1}\parallel }^2,\hfill \\ \hfill & \le \parallel u_n-\breve{u}{\parallel }^2-{\parallel u_{n+1}-\breve{u}\parallel }^2+{\varrho }_n{\left[\parallel u_n-\breve{u}{\parallel }^2-{\parallel u_{n-1}-\breve{u}\parallel }^2\right]}_{+}\hfill \\ \hfill & +{\varrho }_n(1+{\varrho }_n){\parallel u_n-u_{n-1}\parallel }^2\mathrm{for}\mathrm{all}n\ge N.\hfill \end{array}$$

This implies that

$$\underset{n\to \infty }{lim}\parallel t_n-s_n\parallel =0.$$

Moreover, we obtain from Equation (4)

$$\parallel t_n-u_n{\parallel }^2={\varrho }_n^2\parallel u_n-u_{n-1}{\parallel }^2\le \alpha ·{\varrho }_n{\parallel u_n-u_{n-1}\parallel }^2\to 0\mathrm{as}n\to \infty ,$$

hence,

$$\underset{n\to \infty }{lim}\parallel t_n-u_n\parallel =0.$$

(18)

Since ${lim}_{n\to \infty }{\parallel u_n-\breve{u}\parallel }^2$ exists, therefore, the sequence $\left\{u_n\right\}$ is bounded. Let $\left\{u_{n_i}\right\}$ be a subsequence of $\left\{u_n\right\}$ such that $u_{n_i}\rightharpoonup z$, then from Equation (18) we have $t_{n_i}\rightharpoonup z.$ Now, since ${lim}_{n\to \infty }\parallel t_n-s_n\parallel =0,$ by Lemma 9 we get $z\in \Gamma .$ Consequently by Lemma 5, the sequence $\left\{u_n\right\}$ converges weakly to the solution of the VI problem. □

Notice that when ${\varrho }_n=0$ in Algorithm 1, then we have the following as a corollary.

Corollary 1.

Suppose that $\mathbb{A}:\mathbb{E}\to \mathbb{H}$ satisfies $\left(A_3\right)$ in Assumption 1. Let $\left\{u_n\right\}$ and $\left\{s_n\right\}$ be the sequences generated as follows:

i. 

Choose $u_0\in \mathbb{H},$ $\mu \in (0,1),$ and ${\lambda }_0>0.$

$$\left\{\begin{array}{c}{s}_n=P_{\mathbb{E}}(u_n-{\lambda }_n\mathbb{A}{u}_n),\hfill \\ u_{n+1}=P_{T_n}(u_n-{\lambda }_n\mathbb{A}{s}_n),\hfill \end{array}\right.$$

where $T_n=\{z\in \mathbb{H}:⟨u_n-{\lambda }_n\mathbb{A}{u}_n-s_n,z-s_n⟩\le 0\}.$ Moreover, the stepsize sequence ${\lambda }_{n+1}$ is updated as follows:

$${\lambda }_{n+1}=\left\{\begin{array}{cc}min\left\{\frac{\mu (\parallel u_n-s_n{\parallel }^2-\parallel u_{n+1}-s_n{\parallel }^2)}{2⟨{\mathbb{A}}_n-\mathbb{A}{s}_n,u_{n+1}-s_n⟩},{\lambda }_n\right\},\hfill & if⟨{\mathbb{A}}_n-\mathbb{A}{s}_n,u_{n+1}-s_n⟩>0\hfill \\ {\lambda }_n,\hfill & otherwise.\hfill \end{array}\right.$$

Then, the sequences $\left\{u_n\right\}$ and $\left\{s_n\right\}$ weakly converge to the solution $\breve{u}\in \Gamma$ of the VI problem.

Strong Convergence Analysis

In this subsection we present a modified version of Algorithm 1 by using viscosity method to establish a strong convergence. The modified algorithm similar to Algorithm 1 has adaptive step size, that is, the step size does not depend on the Lipschitz constant. Moreover, for the convergence analysis of the modified algorithm, the Lipschitz constant of the operator is not required.

For the convergence analysis, we suppose $g:\mathbb{H}⟶\mathbb{H}$ to be a contraction mapping with $\tau \in (0,1]$ as the contraction parameter. $\left\{{\zeta }_n\right\}$ is a positive sequence such that ${\zeta }_n=\circ \left({\gamma }_n\right)$ where $\left\{{\gamma }_n\right\}\subset (0,1)$ with:

$$\underset{n\to \infty }{lim}{\gamma }_n=0\mathrm{and}\sum _{n=1}^{\infty }{\gamma }_n=\infty .$$

The modified algorithm is as follows:

Algorithm 2 Adaptive Subgradient Extragradient Algorithm for Pseudomonotone Operator.

Initialization: Choose $u_{-1},u_0\in \mathbb{H},$ $\mu \in (0,1),$ $\varrho >0$ and ${\lambda }_0>0.$ Iterative Steps: Given the current iterates $u_{n-1}$ and $u_n\in \mathbb{H}$, choose ${\varrho }_n$ such that $0\le {\varrho }_n\le {\varrho }_n^{\ast },$ where $${\varrho }_n^{\ast }:=\left\{\begin{array}{cc}min\left\{\frac{{\zeta }_n}{\parallel u_n-x_{n+1}\parallel },\varrho \right\},\hfill & \mathrm{if}{u}_n\ne u_{n+1},\hfill \\ \varrho ,\hfill & \mathrm{otherwise}.\end{array}\right.$$ (19)    Step 1. Set $t_n$ as: $$t_n:=u_n+{\varrho }_n(u_n-u_{n-1}),$$ (20)    Step 2. Compute $$s_n=P_{\mathbb{E}}\left(t_n-{\lambda }_n\mathbb{A}{t}_n\right).$$    If $t_n=s_n$ or $\mathbb{A}{t}_n=0$, stop. Else, go to step 3.    Step 3. Construct $$T_n:=\left\{x\in \mathbb{H}:⟨t_n-{\lambda }_n\mathbb{A}{t}_n-s_n,x-s_n⟩\le 0\right\}.$$    Compute $$u_{n+1}={\gamma }_{n}g\left(z_n\right)+(1-{\gamma }_n)z_n,$$    where $$z_n=P_{T_n}\left(t_n-{\lambda }_n\mathbb{A}{s}_n\right).$$    where the stepsize sequence ${\lambda }_{n+1}$ is updated as follows: $${\lambda }_{n+1}:=\left\{\begin{array}{cc}min\left\{{\lambda }_n,{\mathsf{\Lambda }}_n\right\},\hfill & \mathrm{if}⟨\mathbb{A}{t}_n-\mathbb{A}{s}_n,u_{n+1}-s_n⟩>0,\hfill \\ {\lambda }_n\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$ (21)    where $${\mathsf{\Lambda }}_n:=\frac{\mu (\parallel t_n-s_n{\parallel }^2-\parallel z_n-s_n{\parallel }^2)}{2⟨\mathbb{A}{t}_n-\mathbb{A}{s}_n,z_n-s_n⟩}$$ Set $n:=n+1$ and go back to Step 1.

Remark 4.

It can be observed that from Equation (20) and ${\zeta }_n=\circ \left({\gamma }_n\right)$ that is ${lim}_{n\to \infty }\frac{{\zeta }_n}{{\gamma }_n}=0,$ we have for all $n\ge 1$

$$\underset{n\to \infty }{lim}\frac{{\zeta }_n}{{\gamma }_n}\parallel u_n-u_{n-1}\parallel \le \underset{n\to \infty }{lim}\frac{{\zeta }_n}{{\gamma }_n}=0.$$

Theorem 2.

Let $\mathbb{A}$ be an operator satisfying the Assumption 1 (A3). Then, for all $p\in \Gamma \ne \varnothing ,$ the sequence $\left\{u_n\right\}$ generated by Algorithm 2, converges strongly to $\breve{u}.$

Proof. 

To show that iterates generated by Algorithm 2 converges strongly to $\breve{u}\in \Gamma ,$ we consider four claims.

Claim I: The sequence $\left\{u_n\right\}$ generated by Algorithm 2 is bounded.

In fact, from Lemma 9,

$$\begin{array}{cc}\hfill \parallel z_n-\breve{u}{\parallel }^2& \le \parallel t_n-\breve{u}{\parallel }^2-\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel t_n-s_n\parallel }^2\hfill \\ \hfill & -\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel z_n-s_n\parallel }^2.\hfill \end{array}$$

(22)

Recall that there exists $\aleph \in \mathbb{N}$, such that for all $n\ge \aleph$ $0<{\lambda }_n\frac{\mu }{{\lambda }_{n+1}}<1$. This implies that $1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu >0$ for all $n\ge \aleph .$ Thus, from Equation (22) we get

$$\parallel z_n-\breve{u}{\parallel }^2\le {\parallel t_n-\breve{u}\parallel }^2\mathrm{for}\mathrm{all}n\ge N.$$

(23)

On the other hand,

$$\begin{array}{cc}\hfill \parallel t_n-\breve{u}\parallel & =\parallel u_n+{\varrho }_n(u_n-u_{n-1})-\breve{u}\parallel ,\hfill \\ \hfill & \le \parallel u_n-\breve{u}\parallel +\parallel {\varrho }_n(u_n-u_{n-1})\parallel ,\hfill \\ \hfill & =\parallel u_n-\breve{u}\parallel +{\gamma }_n·\frac{{\varrho }_n}{{\gamma }_n}\parallel (u_n-u_{n-1})\parallel .\hfill \end{array}$$

(24)

It follows from Remark 4 that for all $n\in \mathbb{N},$ there exists a constant $C_1$ such that

$$\frac{{\varrho }_n}{{\gamma }_n}\parallel (u_n-u_{n-1})\parallel \le C_1.$$

Putting Equation (23), Equation (24) and the last equation together, we obtain

$$\parallel z_n-\breve{u}\parallel \le \parallel t_n-\breve{u}\parallel \le \parallel u_n-\breve{u}\parallel +{\gamma }_n{C}_1\mathrm{for}\mathrm{all}n\ge \aleph .$$

(25)

On the other hand, we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\breve{u}\parallel & =\parallel {\gamma }_{n}g\left(z_n\right)+(1-{\gamma }_n)z_n-\breve{u}\parallel ,\hfill \\ \hfill & =\parallel {\gamma }_n(g\left(z_n\right)-\breve{u})+(1-{\gamma }_n)(z_n-\breve{u})\parallel ,\hfill \\ \hfill & \le {\gamma }_n\parallel g\left(z_n\right)-\breve{u}\parallel +(1-{\gamma }_n)\parallel z_n-\breve{u}\parallel ,\hfill \\ \hfill & \le {\gamma }_n\parallel g\left(z_n\right)-g\left(\breve{u}\right)\parallel +{\gamma }_n\parallel g\left(\breve{u}\right)-\breve{u}\parallel +(1-{\gamma }_n)\parallel z_n-\breve{u}\parallel ,\hfill \\ \hfill & \le {\gamma }_n\tau \parallel z_n-\breve{u}\parallel +{\gamma }_n\parallel g\left(\breve{u}\right)-\breve{u}\parallel +(1-{\gamma }_n)\parallel z_n-\breve{u}\parallel ,\hfill \\ \hfill & \le (1-(1-\tau ){\gamma }_n)\parallel z_n-\breve{u}\parallel +{\gamma }_n\parallel g\left(\breve{u}\right)-\breve{u}\parallel .\hfill \end{array}$$

(26)

Putting Equation (13) in Equation (26), we get

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\breve{u}\parallel & \le (1-(1-\tau ){\gamma }_n)\parallel u_n-\breve{u}\parallel +{\gamma }_n{C}_1+{\gamma }_n\parallel g\left(\breve{u}\right)-\breve{u}\parallel \mathrm{for}\mathrm{all}n\ge \aleph ,\hfill \\ \hfill & \le (1-(1-\tau ){\gamma }_n)\parallel u_n-\breve{u}\parallel +(1-\tau ){\gamma }_n\frac{C_1+{\gamma }_n\parallel g\left(\breve{u}\right)-\breve{u}\parallel }{1-\tau }\mathrm{for}\mathrm{all}n\ge \aleph ,\hfill \\ \hfill & \le max\left\{\parallel u_n-\breve{u}\parallel ,\frac{C_1+{\gamma }_n\parallel g\left(\breve{u}\right)-\breve{u}\parallel }{1-\tau }\right\}\mathrm{for}\mathrm{all}n\ge \aleph ,\hfill \\ \hfill & ⋮\hfill \\ \hfill & \le max\left\{\parallel u_n-\breve{u}\parallel ,\frac{C_1+{\gamma }_n\parallel g\left(\breve{u}\right)-\breve{u}\parallel }{1-\tau }\right\}\mathrm{for}\mathrm{all}n\ge \aleph ,\hfill \end{array}$$

Therefore, $\left\{u_n\right\}$ is bounded and thus, $\left\{t_n\right\},\left\{g\left(u_n\right)\right\}$ and $\left\{z_n\right\}$ are bounded.

Claim II:

$$\begin{array}{cc}\hfill & \left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right)\parallel t_n-s_n{\parallel }^2+\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel u_{n+1}-s_n\parallel }^2\hfill \\ \hfill & \le \parallel u_n-\breve{u}{\parallel }^2-{\parallel u_{n+1}-\breve{u}\parallel }^2+{\gamma }_n{C}_4.\hfill \end{array}$$

(27)

In fact, from Equation (26), we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\breve{u}{\parallel }^2& \le {\gamma }_n\parallel g\left(z_n\right)-\breve{u}{\parallel }^2+(1-{\gamma }_n){\parallel z_n-\breve{u}\parallel }^2,\hfill \\ \hfill & \le {\gamma }_n{\left(\parallel g\left(z_n\right)-g\left(\breve{u}\right)\parallel +\parallel g\left(\breve{u}\right)-\breve{u}\parallel \right)}^2+(1-{\gamma }_n){\parallel z_n-\breve{u}\parallel }^2,\hfill \\ \hfill & \le {\gamma }_n{\left(\tau \parallel z_n-\breve{u}\parallel +\parallel g\left(\breve{u}\right)-\breve{u}\parallel \right)}^2+(1-{\gamma }_n){\parallel z_n-\breve{u}\parallel }^2,\hfill \\ \hfill & ={\gamma }_n{\parallel z_n-\breve{u}\parallel }^2+{\gamma }_n\left(2\parallel z_n-\breve{u}\parallel ·\parallel g\left(\breve{u}\right)-\breve{u}\parallel +\parallel g\left(\breve{u}\right)-\breve{u}{\parallel }^2\right)\hfill \\ \hfill & +(1-{\gamma }_n){\parallel z_n-\breve{u}\parallel }^2,\hfill \\ \hfill & \le {\gamma }_n\parallel z_n-\breve{u}{\parallel }^2+(1-{\gamma }_n){\parallel z_n-\breve{u}\parallel }^2+{\gamma }_n{C}_2,\mathrm{for}\mathrm{some}{C}_2>0,\hfill \\ \hfill & =\parallel z_n-\breve{u}{\parallel }^2+{\gamma }_n{C}_2.\hfill \end{array}$$

(28)

Substituting Equation (22) into Equation (28), we obtain

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\breve{u}{\parallel }^2& \le \parallel t_n-\breve{u}{\parallel }^2-\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel t_n-s_n\parallel }^2\hfill \\ \hfill & -\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel z_n-s_n\parallel }^2+{\gamma }_n{C}_2.\hfill \end{array}$$

(29)

From Equation (25), we get

$$\begin{array}{cc}\hfill \parallel t_n-\breve{u}{\parallel }^2& \le {\left(\parallel u_n-\breve{u}\parallel +{\gamma }_n{C}_1\right)}^2,\hfill \\ \hfill & =\parallel u_n-\breve{u}{\parallel }^2+{\gamma }_n\left(2C_1\parallel u_n-\breve{u}\parallel +{\gamma }_n{C}_1^2\right),\hfill \\ \hfill & \le \parallel u_n-\breve{u}{\parallel }^2+{\gamma }_n{C}_3,\mathrm{for}\mathrm{some}{C}_3>0.\hfill \end{array}$$

(30)

Putting Equations (29) and (30), we have

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\breve{u}{\parallel }^2& \le \parallel u_n-\breve{u}{\parallel }^2+{\gamma }_n{C}_3-\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel t_n-s_n\parallel }^2\hfill \\ \hfill & -\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel z_n-s_n\parallel }^2+{\gamma }_n{C}_2.\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill & \left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right)\parallel t_n-s_n{\parallel }^2+\left(1-\frac{{\lambda }_n}{2{\lambda }_{n+1}}\mu \right){\parallel u_{n+1}-s_n\parallel }^2\hfill \\ \hfill & \le \parallel u_n-\breve{u}{\parallel }^2-{\parallel u_{n+1}-\breve{u}\parallel }^2+{\gamma }_n{C}_4,\hfill \end{array}$$

where $C_4={\gamma }_n{C}_3+{\gamma }_n{C}_2.$

Claim III:

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\breve{u}\parallel & \le (1-(1-\tau ){\gamma }_n)\parallel z_n-\breve{u}\parallel \hfill \\ \hfill & +(1-\tau ){\gamma }_n\left[\frac{2}{1-\tau }⟨g\left(\breve{u}\right)-\breve{u},u_{n+1}-\breve{u}⟩+\frac{3C}{1-\tau }·\frac{{\varrho }_n}{{\gamma }_n}\parallel u_n-u_{n-1}\parallel \right].\hfill \end{array}$$

(31)

In fact, we have

$$\begin{array}{cc}\hfill \parallel t_n{-p\parallel }^2& =\parallel u_n+{\varrho }_n(u_n-u_{n-1})-\breve{u}{\parallel }^2,\hfill \\ \hfill & \le \parallel u_n-\breve{u}{\parallel }^2+{\varrho }_n^2{\parallel u_n-u_{n-1}\parallel }^2+2{\varrho }_n⟨u_n-\breve{u},u_n-u_{n-1}⟩,\hfill \\ \hfill & \le \parallel u_n-\breve{u}{\parallel }^2+{\varrho }_n^2\parallel u_n-u_{n-1}{\parallel }^2+2{\varrho }_n\parallel u_n-\breve{u}\parallel \parallel u_n-u_{n-1}\parallel .\hfill \end{array}$$

(32)

Using the inequality $\parallel t+s\parallel \le {\parallel t\parallel }^2+2⟨s,t+s⟩,$ we get

$$\begin{array}{cc}\hfill \parallel u_{n+1}-\breve{u}{\parallel }^2& =\parallel {\gamma }_{n}g\left(z_n\right)+(1-{\gamma }_n)z_n-\breve{u}{\parallel }^2,\hfill \\ \hfill & =\parallel {\gamma }_n(g\left(z_n\right)-g\left(\breve{u}\right))+(1-{\gamma }_n)(z_n-\breve{u})+{\gamma }_n(g\left(\breve{u}\right)-\breve{u}){\parallel }^2,\hfill \\ \hfill & \le \parallel {\gamma }_n(g\left(z_n\right)-g\left(\breve{u}\right))+(1-{\gamma }_n)(z_n-\breve{u}){\parallel }^2+2{\gamma }_n⟨g\left(\breve{u}\right)-\breve{u},u_{n+1}-\breve{u}⟩,\hfill \\ \hfill & \le {\gamma }_n\parallel g\left(z_n\right)-g\left(\breve{u}\right){\parallel }^2+(1-{\gamma }_n){\parallel z_n-\breve{u}\parallel }^2+2{\gamma }_n⟨g\left(\breve{u}\right)-\breve{u},u_{n+1}-\breve{u}⟩,\hfill \\ \hfill & \le {\gamma }_n{\tau }^2\parallel z_n-\breve{u}{\parallel }^2+(1-{\gamma }_n){\parallel z_n-\breve{u}\parallel }^2+2{\gamma }_n⟨g\left(\breve{u}\right)-\breve{u},u_{n+1}-\breve{u}⟩,\hfill \\ \hfill & \le (1-(1-\tau ){\gamma }_n){\parallel z_n-\breve{u}\parallel }^2+2{\gamma }_n⟨g\left(\breve{u}\right)-\breve{u},u_{n+1}-\breve{u}⟩,\hfill \\ \hfill & \le (1-(1-\tau ){\gamma }_n){\parallel t_n-\breve{u}\parallel }^2+2{\gamma }_n⟨g\left(\breve{u}\right)-\breve{u},u_{n+1}-\breve{u}⟩,\hfill \end{array}$$

(33)

where the last inequality follows from Equation (23). Substituting Equation (32) into Equation (33), we get

$$\begin{array}{cc}\hfill \parallel u_{n+1}& -\breve{u}{\parallel }^2\hfill \\ \hfill & \le (1-(1-\tau ){\gamma }_n)\parallel u_n-\breve{u}{\parallel }^2+{\varrho }_n^2{\parallel u_n-u_{n-1}\parallel }^2\hfill \\ \hfill & +2{\varrho }_n\parallel u_n-\breve{u}\parallel \parallel u_n-u_{n-1}\parallel +2{\gamma }_n⟨g\left(\breve{u}\right)-\breve{u},u_{n+1}-\breve{u}⟩,\hfill \\ \hfill & \le (1-(1-\tau ){\gamma }_n){\parallel u_n-\breve{u}\parallel }^2+(1-\tau ){\gamma }_n\frac{2}{1-\tau }⟨g\left(\breve{u}\right)-\breve{u},u_{n+1}-\breve{u}⟩\hfill \\ \hfill & +{\varrho }_n\parallel u_n-u_{n-1}\parallel \left(2\parallel u_n-\breve{u}\parallel +{\varrho }_n\parallel u_n-u_{n-1}\parallel \right)\mathrm{for}\mathrm{all}n\ge \aleph ,\hfill \\ \hfill & \le (1-(1-\tau ){\gamma }_n)+(1-\tau ){\gamma }_n\frac{2}{1-\tau }⟨g\left(\breve{u}\right)-\breve{u},u_{n+1}-\breve{u}⟩\hfill \\ \hfill & +3C{\varrho }_n\parallel u_n-u_{n-1}\parallel \mathrm{for}\mathrm{all}n\ge \aleph ,\hfill \\ \hfill & \le (1-(1-\tau ){\gamma }_n)+(1-\tau ){\gamma }_n\frac{2}{1-\tau }⟨g\left(\breve{u}\right)-\breve{u},u_{n+1}-\breve{u}⟩\hfill \\ \hfill & +\frac{3C}{1-\tau }·\frac{{\varrho }_n}{{\gamma }_n}\parallel u_n-u_{n-1}\parallel \mathrm{for}\mathrm{all}n\ge \aleph ,\hfill \end{array}$$

where $M={sup}_{n\in \mathbb{N}}\left\{\parallel u_n-\breve{u}\parallel ,{\varrho }_n\parallel u_n-u_{n-1}\parallel \right\}>0.$

Claim IV: The sequence $\{\parallel u_n-\breve{u}\parallel \}$ converges to zero. From Lemma 6 it suffices to show that ${lim\; sup}_{k\to \infty }⟨g\left(\breve{u}\right)-\breve{u},u_{n+1}-\breve{u}⟩\le 0$ for every subsequence $\{\parallel u_{n_k}-\breve{u}\parallel \}$ of $\{\parallel u_n-\breve{u}\parallel \}$ such that

$$\underset{k\to \infty }{lim\; inf}\left(\parallel u_{n_k+1}-\breve{u}\parallel -\parallel u_{n_k}-\breve{u}\parallel \right).$$

(34)

To this end, let $\{\parallel u_{n_k}-\breve{u}\parallel \}$ be a subsequence of $\{\parallel u_n-\breve{u}\parallel \}$ such that Equation (34) is satisfied, then by claim II we get

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim\; sup}\left[\right(1-& \frac{{\lambda }_{n_k}}{2{\lambda }_{n_k+1}}\mu )\parallel t_{n_k}-v_{n_k}{\parallel }^2+\left(1-\frac{{\lambda }_{n_k}}{2{\lambda }_{n_k+1}}\mu \right){\parallel u_{n_k+1}-v_{n_k}\parallel }^2]\hfill \\ \hfill & \le \underset{k\to \infty }{lim\; sup}\left[\parallel u_{n_k}-\breve{u}{\parallel }^2-{\parallel u_{n_k+1}-\breve{u}\parallel }^2+{\gamma }_{n_k}{C}_4\right],\hfill \\ \hfill & \le \underset{k\to \infty }{lim\; sup}\left[\parallel u_{n_k}-\breve{u}{\parallel }^2-{\parallel u_{n_k+1}-\breve{u}\parallel }^2\right]++\underset{k\to \infty }{lim\; sup}{\gamma }_{n_k}{C}_4,\hfill \\ \hfill & \le -\underset{k\to \infty }{lim\; inf}\left[\parallel u_{n_k+1}-\breve{u}{\parallel }^2-{\parallel u_{n_k}-\breve{u}\parallel }^2\right],\hfill \\ \hfill & \le 0.\hfill \end{array}$$

Therefore,

$$\underset{k\to \infty }{lim}\parallel t_{n_k}-v_{n_k}\parallel =0$$

(35)

and

$$\underset{k\to \infty }{lim}\parallel z_{n_k}-v_{n_k}\parallel =0,$$

Next, we show that

$$\parallel u_{n_k+1}-u_{n_k}\parallel \to 0\mathrm{as}k\to \infty .$$

(36)

In fact, we have

$$\parallel u_{n_k+1}-z_{n_k}\parallel ={\gamma }_{n_k}\parallel z_{n_k}-g\left(z_{n_k}\right)\parallel \to 0\mathrm{as}k\to \infty ,$$

and

$$\parallel u_{n_k}-t_{n_k}\parallel ={\alpha }_{n_i}\parallel u_{n_k+1}-u_{n_k}\parallel ={\gamma }_{n_k}\frac{{\alpha }_{n_i}}{{\gamma }_{n_k}}\parallel u_{n_k+1}-u_{n_k}\parallel \to 0\mathrm{as}k\to \infty .$$

(37)

It now follows that, there exists a subsequence $\left\{u_{n_{k_j}}\right\}$ of $\left\{u_{n_k}\right\}$ such that, for some $z\in \mathbb{H},$ $u_{n_{k_j}}\rightharpoonup z,$ and

$$\underset{k\to \infty }{lim\; sup}⟨g\left(\breve{u}\right)-\breve{u},u_{n_k}-\breve{u}⟩=\underset{k\to \infty }{lim}⟨g\left(\breve{u}\right)-\breve{u},u_{n_{k_j}}-\breve{u}⟩=⟨g\left(\breve{u}\right)-\breve{u},z-\breve{u}⟩$$

(38)

From Equation (37), we have $t_{n_k}\rightharpoonup z\mathrm{as}k\to \infty ,$ which it follows from Equation (35) and Lemma 9 that $z\in \Gamma .$ From Equation (38) and the fact that $\breve{u}=P_{\Gamma }\circ g\left(\breve{u}\right),$ we have

$$\underset{k\to \infty }{lim\; sup}⟨g\left(\breve{u}\right)-\breve{u},u_{n_k}-\breve{u}⟩=⟨g\left(\breve{u}\right)-\breve{u},z-\breve{u}⟩\le 0.$$

(39)

Putting Equations (36) and (39) together, we get

$$\begin{array}{cc}\hfill \underset{k\to \infty }{lim\; sup}⟨g\left(\breve{u}\right)-\breve{u},u_{n_k+1}-\breve{u}⟩& \le \underset{k\to \infty }{lim\; sup}⟨g\left(\breve{u}\right)-\breve{u},u_{n_k}-\breve{u}⟩,\hfill \\ \hfill & =⟨g\left(\breve{u}\right)-\breve{u},z-\tilde{u}⟩,\hfill \\ \hfill & \le 0.\hfill \end{array}$$

(40)

Thus, the desired result follows from ${lim}_{n\to \infty }\frac{{\alpha }_{n_i}}{{\gamma }_{n_k}}\parallel u_{n_k+1}-u_{n_k}\parallel =0,$ Equation (40), Claim III and Lemma 6. □

4. Computational Experiments

Numerical experiments will be presented in this section to demonstrate the performance of our proposed methods. The Codes were run on a PC Intel(R) Core(TM)i5-6200 CPU @ 2.30GHz 2.40GHz, RAM 8.00 GB, MATLAB version 9.5 (R2018b). Throughout these examples y-axis and x-axis represent $D_n=\parallel u_{n+1}-u_n\parallel$ and number of iterations or execution time (in seconds) respectively. The following examples were considered for the numerical experiments of the two proposed algorithms.

Example 1.

Let an operator $\mathbb{A}$ be define on $\mathbb{E}\subset {\mathbb{R}}^n$ as follows

$$\mathbb{A}=(B{B}^T+S+D)u+q$$

where $q\in {\mathbb{R}}^n,$ B is an $n\times n$ matrix, S is an $n\times n$ skew-symmetric matrix, D is an $n\times n$ diagonal matrix, whose diagonal entries are nonnegative. These matrices and the vector q are randomly generated in $(0,1).$ The set $\mathbb{E}\subset {\mathbb{R}}^n$ is closed and convex and defined as

$$\mathbb{E}=\{u\in {\mathbb{R}}^n:Cu\le d\}$$

where C is an $100\times n$ matrix and d is a nonnegative vector. It is clear that $\mathbb{A}$ is monotone and L-Lipschitz continuous with $L=max\left(eig(B{B}^T+S+D)\right).$

Example 2.

The following problem which was considered by Sun [39] (page 9, example 5), with an operator defined as

$$\mathbb{A}u=Gu+Hu,$$

where

$$Gu=\left(g_{1}u,g_{2}u,\cdots ,g_{n}u\right),$$

$$Hu=Ex+d,$$

$$g_{i}u=u_{i-1}^2+u_i^2+u_{i-1}{u}_i+u_i{u}_{i+1},i=1,2,\cdots ,n{u}_0=u_{n+1}=0.$$

Here E is an $n\times n$ square matrix with entries defined as

$$e_{l,m}=\left\{\begin{array}{cc}4\hfill & m=l\hfill \\ 1\hfill & l-m=1\hfill \\ -2\hfill & l-m=-1\hfill \\ 0\hfill & otherwise,\hfill \end{array}\right.$$

while $d=(-1,-1,\cdots ,-1).$

Example 3.

Let $\mathbb{H}=l_2$ and $\mathbb{E}=\{u\in \mathbb{H}:\parallel u\parallel \le 5\}.$ Define an operator $\mathbb{A}$ as follows:

$$\mathbb{A}u=(7-\parallel u\parallel )u\forall u\in \mathbb{H},$$

where $\parallel u\parallel =\sqrt{{\sum }_i{\left|u_i\right|}^2}.$ Observe that the solution set $\Gamma \ne \varnothing$ and the operator is pseudomonotone but not monotone with Lipschitz constant $L=11.$ The projection onto $\mathbb{E}$ is explicitly computed as

$$P_{\mathbb{E}}u=\left\{\begin{array}{c}uif\parallel u\parallel \le 5,\hfill \\ \frac{5u}{\parallel u\parallel },otherwise.\hfill \end{array}\right.$$

4.1. Comparative Analysis for Algorithm 1

Here, we give the numerical experiment of Algorithm 1 in comparison with some existing algorithms in the literature. We use the following algorithms and their corresponding control parameters details.

• Dong et al. [19] on page 3 (shortly, iEgA) with ${\alpha }_n=0.40,$ ${\lambda }_n=0.80$ and $\mathsf{\tau }=\frac{1}{1.5L}.$
• Thong et al. [25] on page 5 (shortly, ISEGM), with $\alpha =0.20$ and $\mathsf{\tau }=\frac{0.5-2\alpha -0.5{\alpha }^2}{2L(0.5-\alpha +0.5{\alpha }^2)}.$
• Dong et al. [17] Algorithm 3.1 (shortly, iPCA), with ${\alpha }_n=0.40,$ $\gamma =1.5$ and $\mathsf{\tau }=\frac{1}{2L}.$
• Yang et al. [40] Algorithm 3.1 (shortly, Alg3.1), with ${\alpha }_n=0.15,$ $\mu =0.5$ and ${\lambda }_1=\frac{0.7}{\sqrt{26}}.$
• Thong et al. [41] Algorithm 3.1 (shortly, WISEGM), $\alpha =0.80,$ $\mu =0.9$ and ${\mathsf{\tau }}_1=1.$

For Algorithm 1 (shortly, Algo1) we chose $\varrho =0.50,$ $\mu =0.80$ and ${\lambda }_0=0.60.$ The results are shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8.

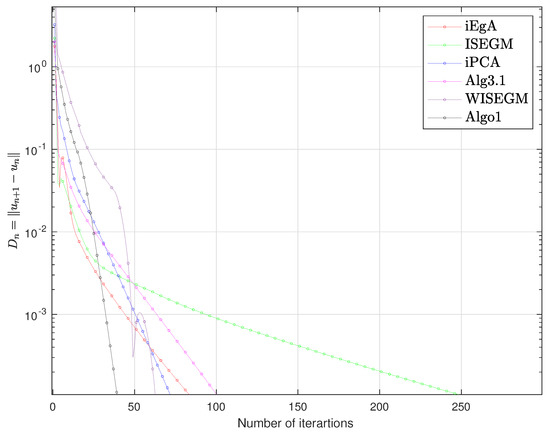
Figure 1. Example 1 in ${\mathbb{R}}^5$: Numbers of iterations are 85, 254, 73, 102, 63, 40 respectively.

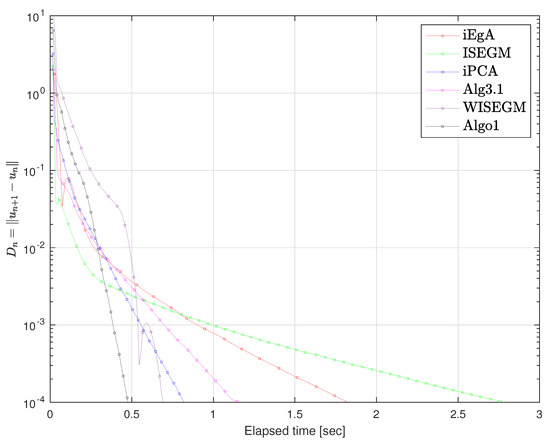
Figure 2. Example 1 in ${\mathbb{R}}^5$: Elapsed time 1.83, 2.78, 0.82, 1.25, 0.69, 0.48 respectively.

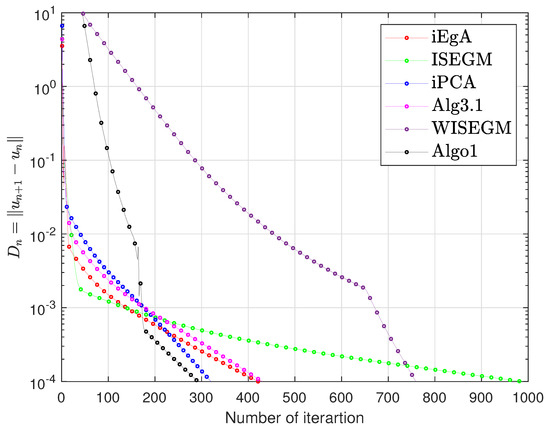
Figure 3. Example 1 in ${\mathbb{R}}^{50}$: Numbers of iterations 421, 985, 320, 430, 759, 292 respectively.

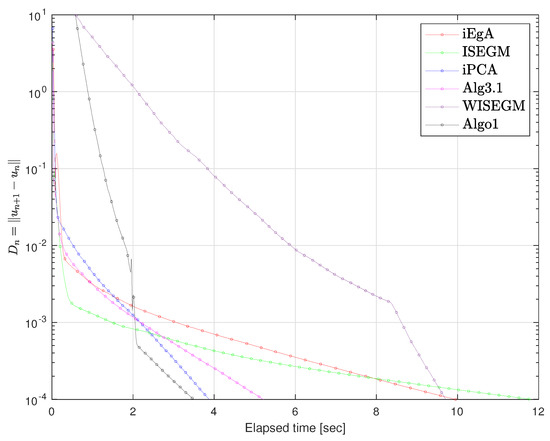
Figure 4. Example 1 in ${\mathbb{R}}^{50}$: Elapsed time 9.95, 11.79, 3.87, 5.19, 9.70, 3.41 respectively.

Figure 5. Example 2: Numbers of iterations are 45, 169, 155, 52, 60, 38 respectively.

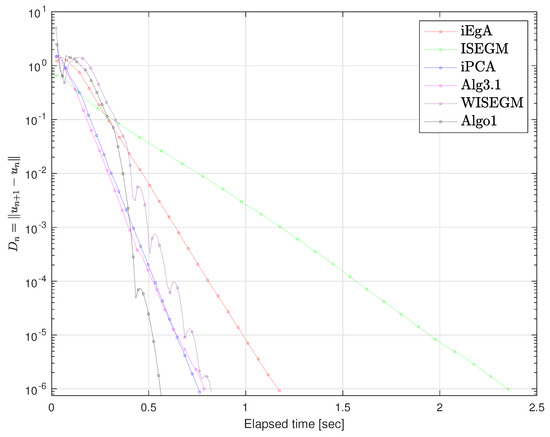
Figure 6. Example 2: Elapsed time are 1.17, 2.35, 0.76, 0.78, 0.82, 0.56 respectively.

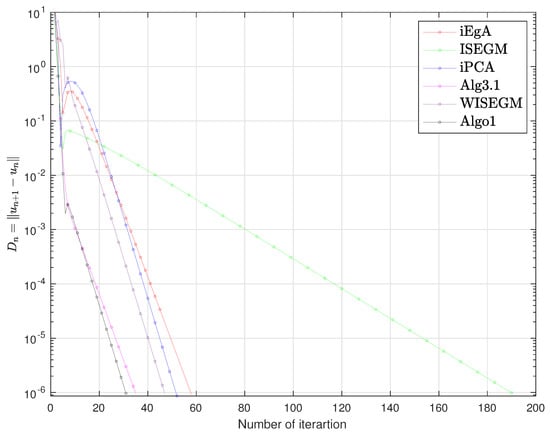
Figure 7. Example 3: Numbers of iterations are 58, 190, 52, 35, 47, 31 respectively.

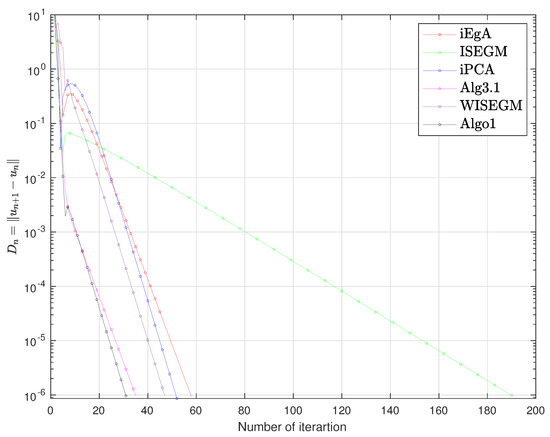
Figure 8. Example 3: Elapsed time are 2.94, 19.59, 2.73, 3.83, 4.76, 3.04 respectively.

It can be clearly seen from Figure 1, Figure 2, Figure 3 and Figure 4, Figure 5 and Figure 6 and Figure 7 and Figure 8 for Example 1, 2 and 3 respectively that the proposed algorithm has fewer iterations and less CPU time than the compared algorithms.

4.2. Comparative Results of Algorithm 2

For the numerical results of Algorithm 2, we used the following algorithms with strong convergence.

• Kraikaew et al. [42] on page 6 (shortly, hEgA), with ${\alpha }_k=\frac{1}{100(k+2)}$ and $\mathsf{\tau }=\frac{1}{1.5L}.$
• Yang et al. [27] Algorithm 2 (shortly, Alg.2), with ${\alpha }_k=\frac{1}{100(k+2)},$ $\mu =0.4$ and ${\lambda }_0=\frac{0.7}{L}.$
• Shehu et al. [29] Algorithm 4.3 (shortly, Algorithm4.3), with ${\alpha }_n=\frac{1}{13n+2},$ $\gamma =1.99$ and ${\lambda }_0=\frac{0.9}{L}.$
• Thong et al. [41] Algorithm 3.2 (shortly, SISEGM), with $\alpha =1,$ $\mu =0.9,$ $f\left(x\right)=\frac{1}{2x},$ ${\beta }_n=\frac{1}{n+1},$ ${ϵ}_n=\frac{1}{{(n+1)}^2}$ and ${\mathsf{\tau }}_1=1.$

For Algorithm 2 (shortly, Algo2), we take $\varrho =0.8,$ $\mu =0.9,$ $g\left(x\right)=\frac{1}{2x},$ ${\gamma }_n=\frac{1}{13n+2},$ ${ϵ}_n=\frac{1}{{(n+1)}^2}$ and ${\lambda }_0=0.5.$ The results are shown in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16.

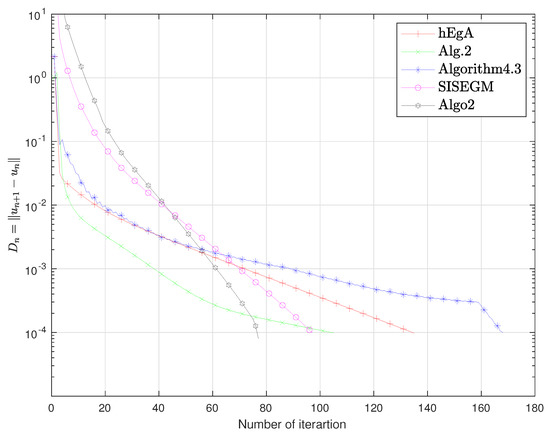
Figure 9. Example 1 in ${\mathbb{R}}^5$: Numbers of iterations are 135, 105, 168, 97, 77 respectively.

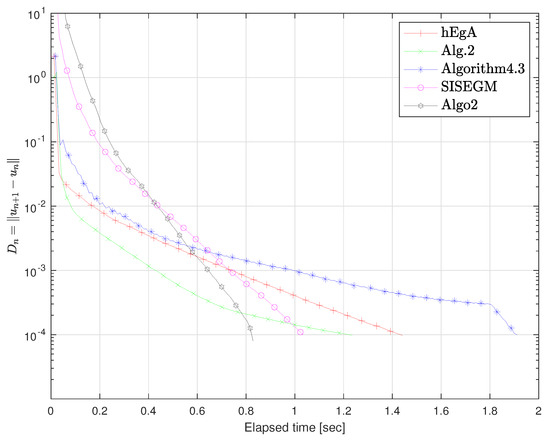
Figure 10. Example 1 in ${\mathbb{R}}^5$: Elapsed time 1.44, 1.23, 1.97, 1.03, 0.84 respectively.

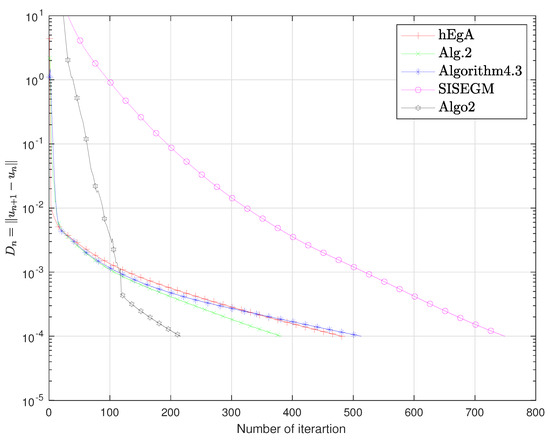
Figure 11. Example 1 in ${\mathbb{R}}^5$: Numbers of iterations are 482, 382, 513, 749, 216 respectively.

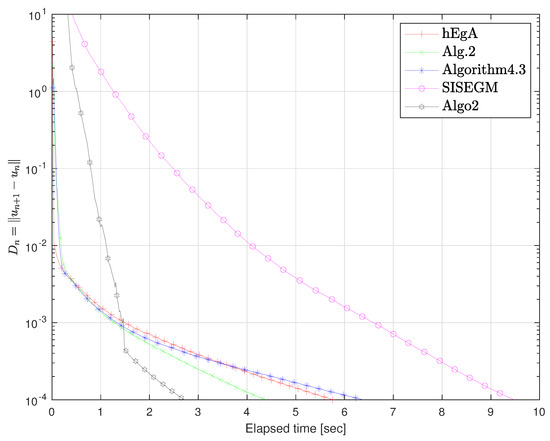
Figure 12. Example 1 in ${\mathbb{R}}^5$: Elapsed time 5.76, 4.38, 6.37, 9.47, 2.71 respectively.

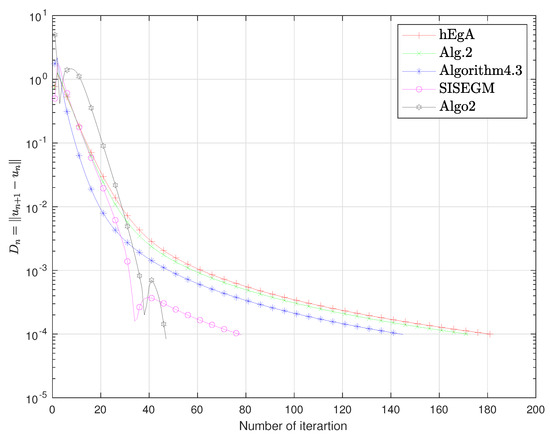
Figure 13. Example 2: Numbers of iterations are 181, 172, 145, 78, 47 respectively.

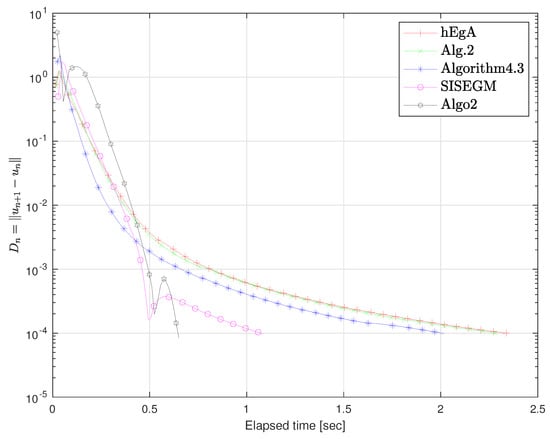
Figure 14. Example 2: Elapsed time 2.33, 2.29, 2.01, 1.08, 0.64 respectively.

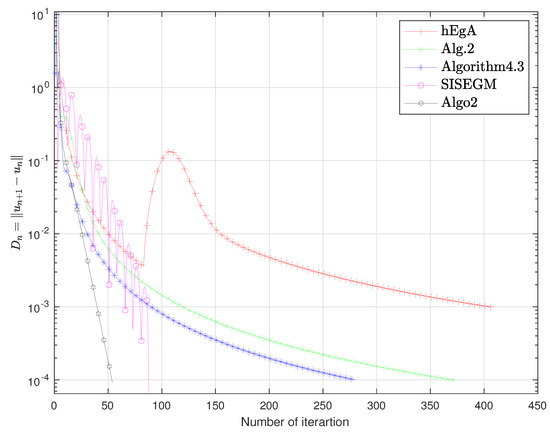
Figure 15. Example 3: Numbers of iterations are 406, 372, 280, 88, 54 respectively.

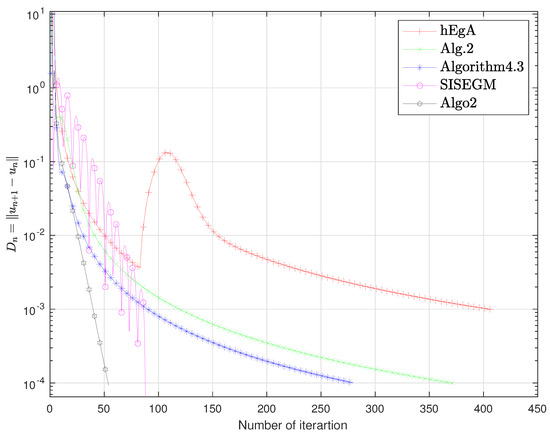
Figure 16. Example 3: Elapsed time 2.28, 2.40, 1.35, 0.58, 0.37 respectively.

For the strong convergent algorithm, it can be observed that for Example 1, 2 and 3 in Figure 9, Figure 10, Figure 11 and Figure 12, Figure 13 and Figure 14 and Figure 15 and Figure 16 respectively, the proposed algorithm is faster, more efficient and more robust than the compared existing algorithms.

5. Conclusions

A self-adaptive subgradient extragradient algorithms with an inertial extrapolation step is presented in this work. The proposed algorithms involve a more general class of operators, the iterates generated by the first scheme converge weakly to the solution of the variational inequality problem. Furthermore, a modified version of the proposed algorithm is given by using the viscosity method to obtain a strong convergence algorithm. The main advantage of the proposed algorithms is that they do not require the prior knowledge of the Lipchitz constant of the cost operator and the iterates generated converge faster to the solution of the problem due to the inertial extrapolation step. Numerical comparison of the proposed algorithms with some of the existing state of the art algorithms shows that the proposed algorithms are fast, robust and efficient.