Robust Dissipativity Analysis of Hopfield-Type Complex-Valued Neural Networks with Time-Varying Delays and Linear Fractional Uncertainties
Abstract
:1. Introduction
2. Problem Statement and Fundamentals
3. Main Results
Dissipativity Analysis
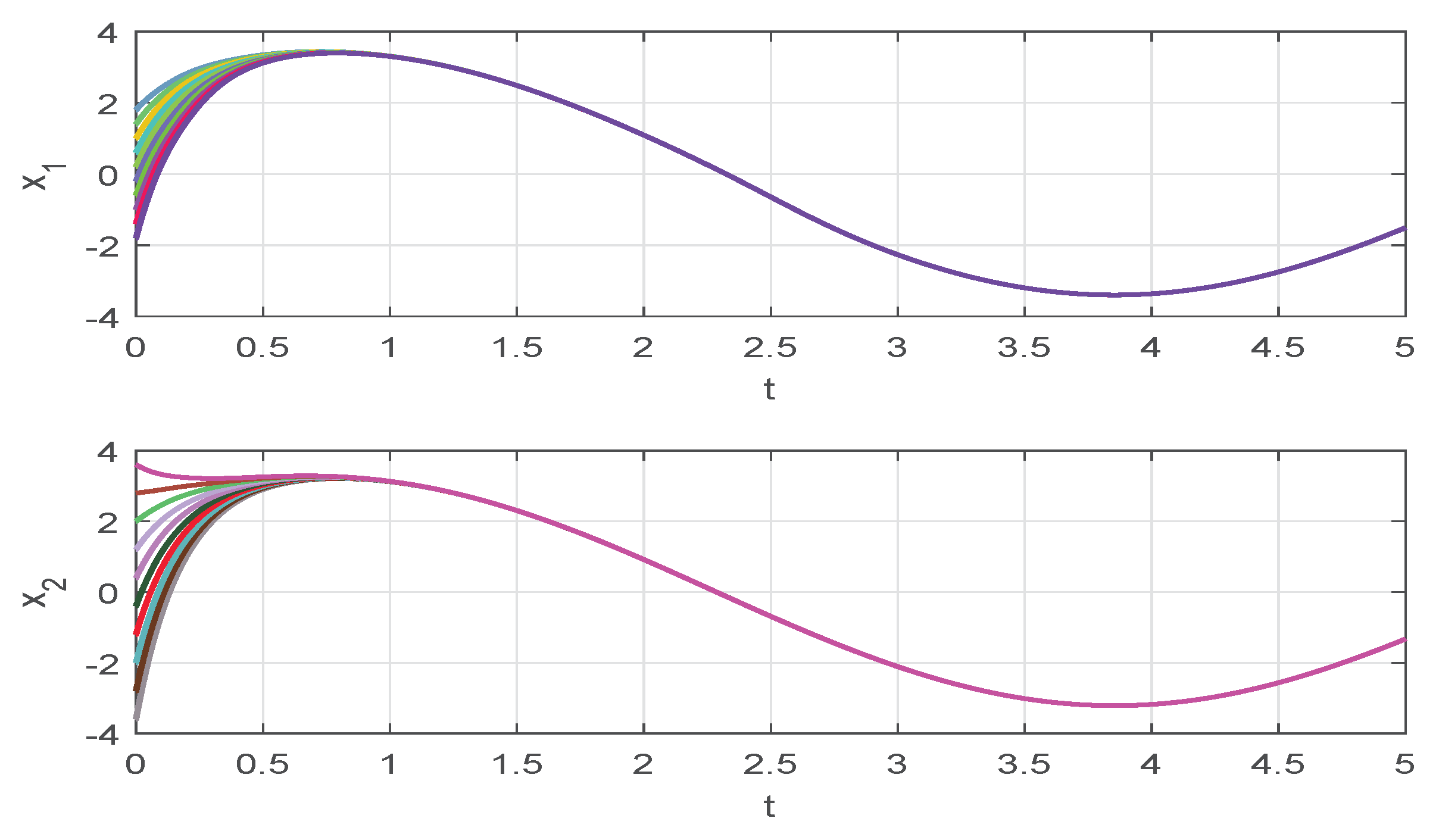
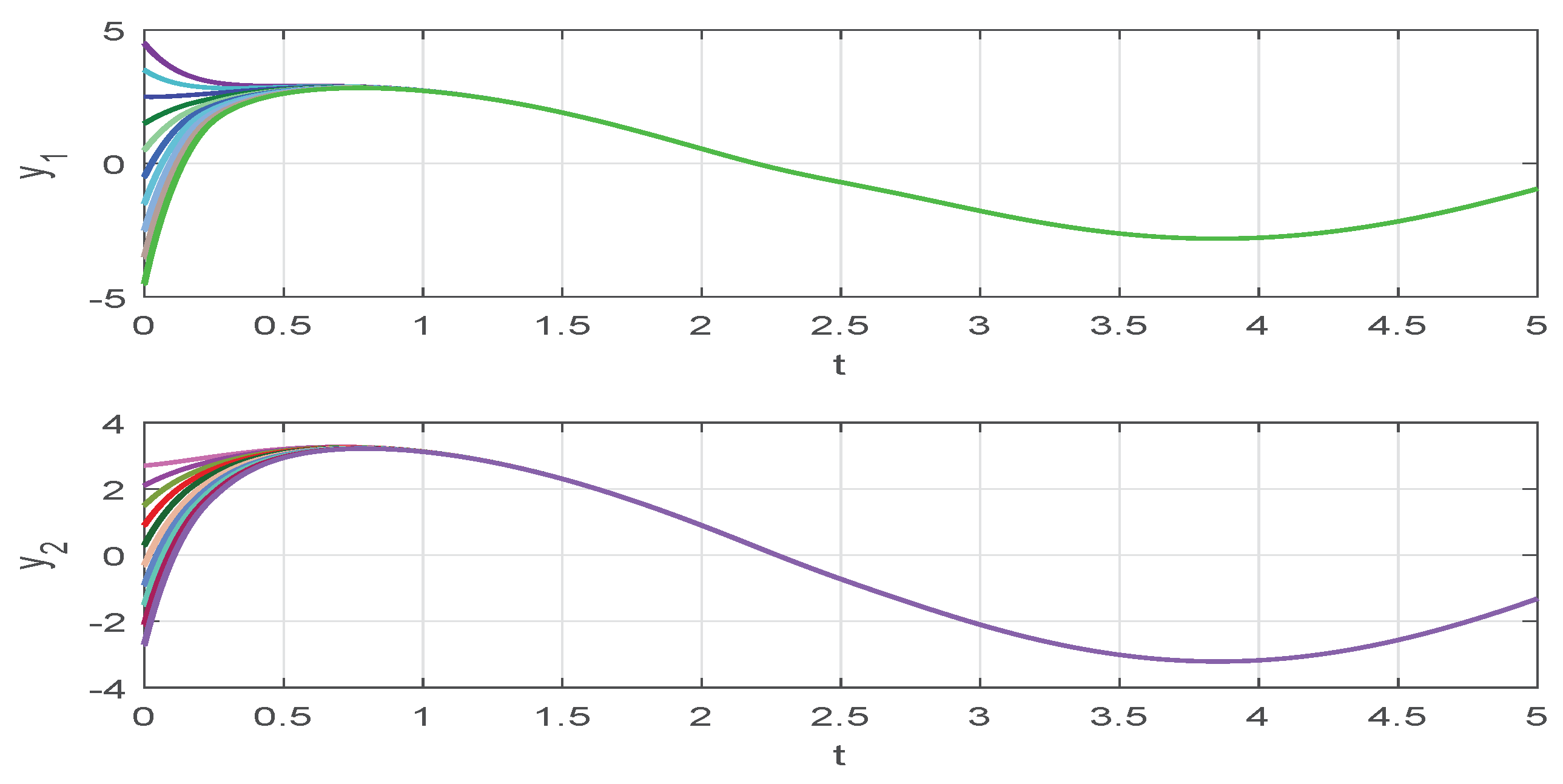
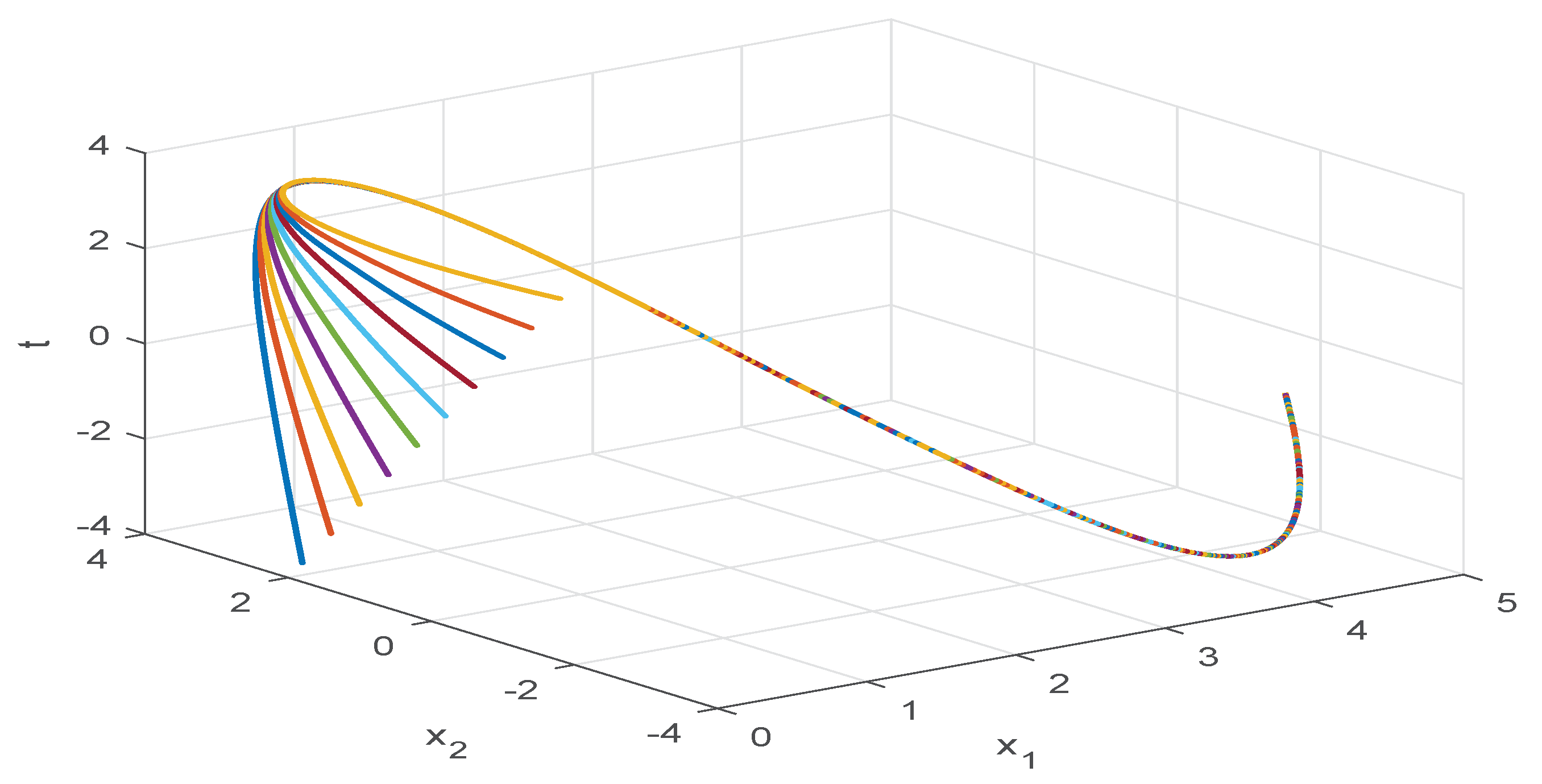
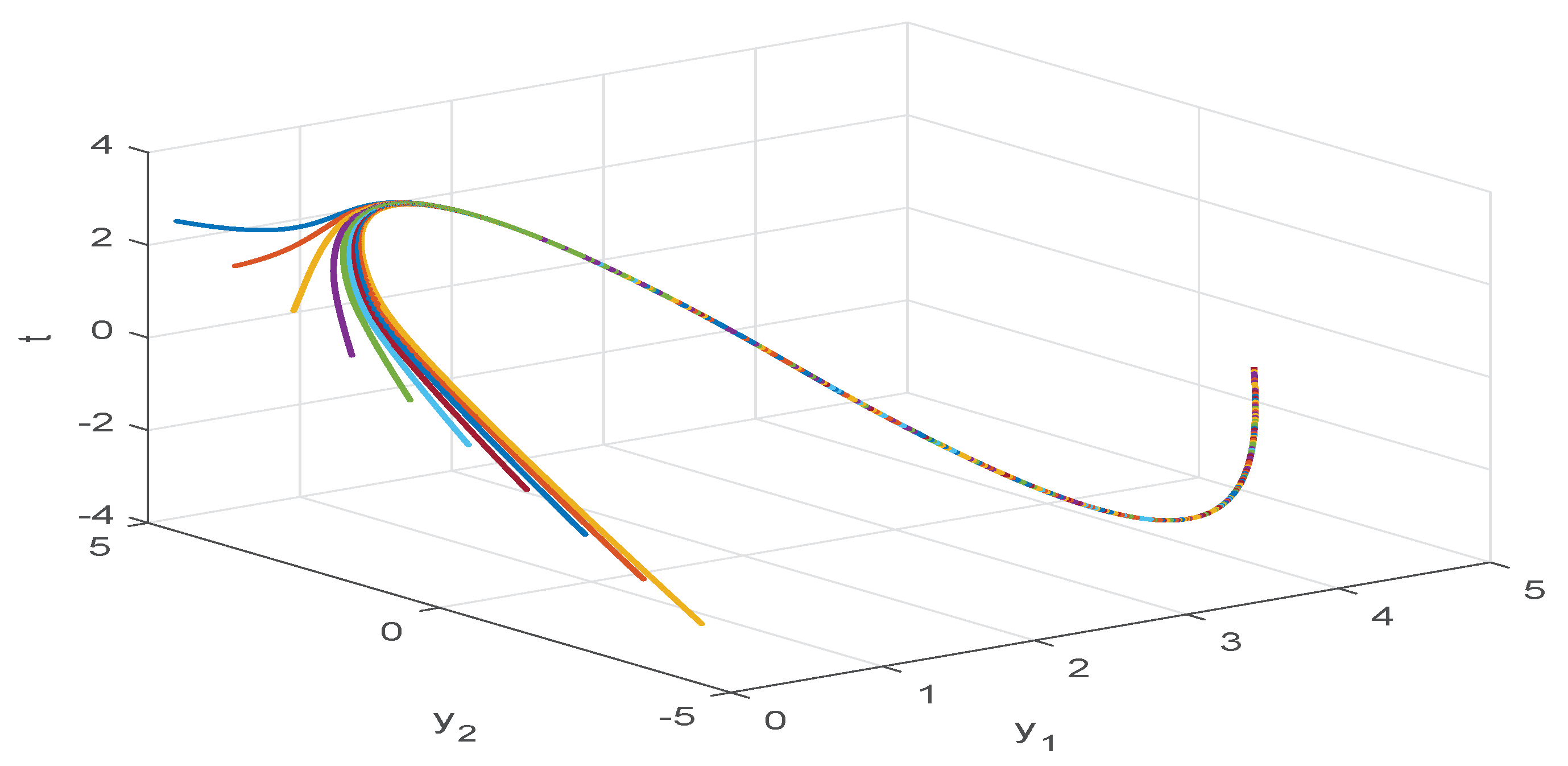
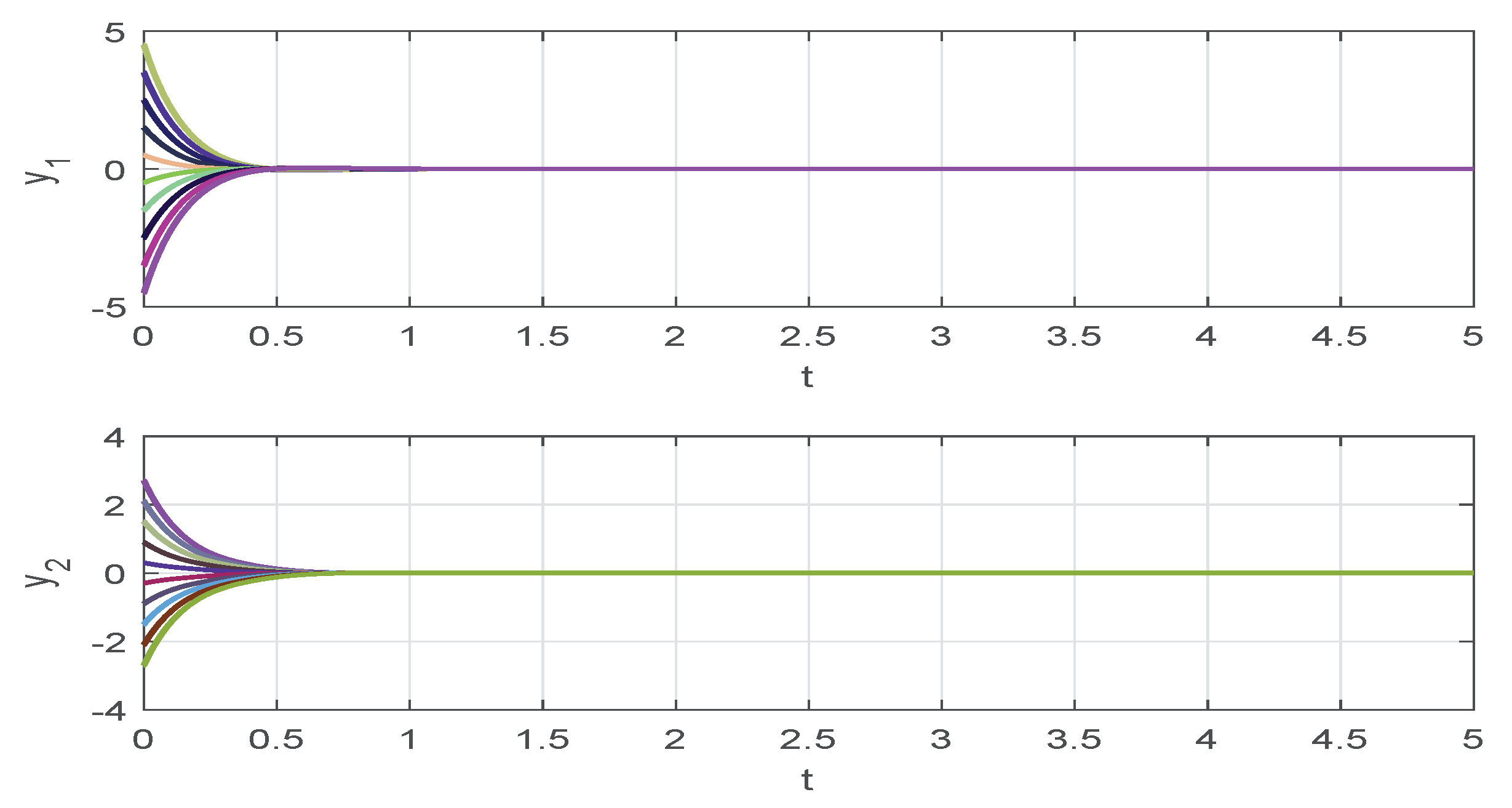
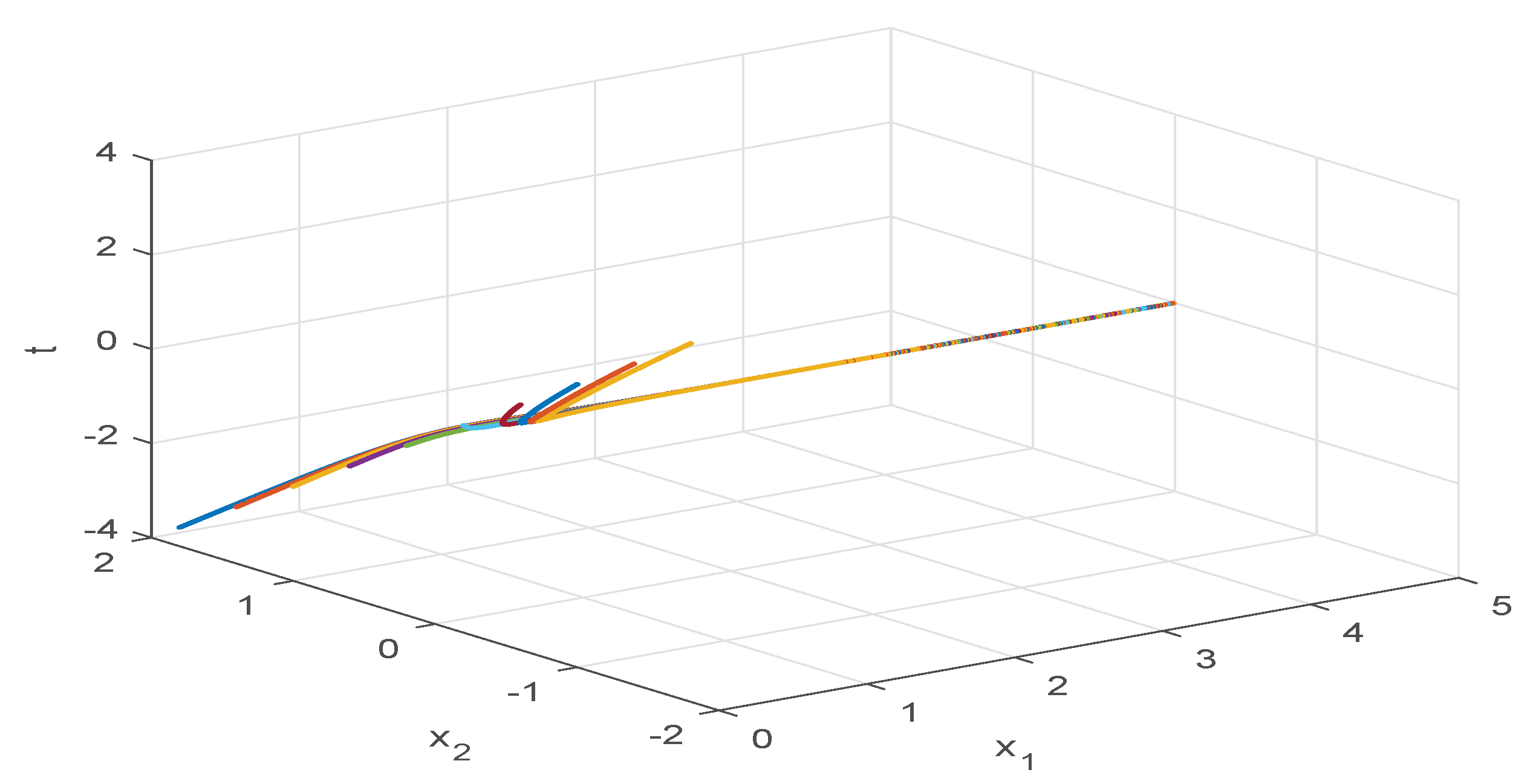
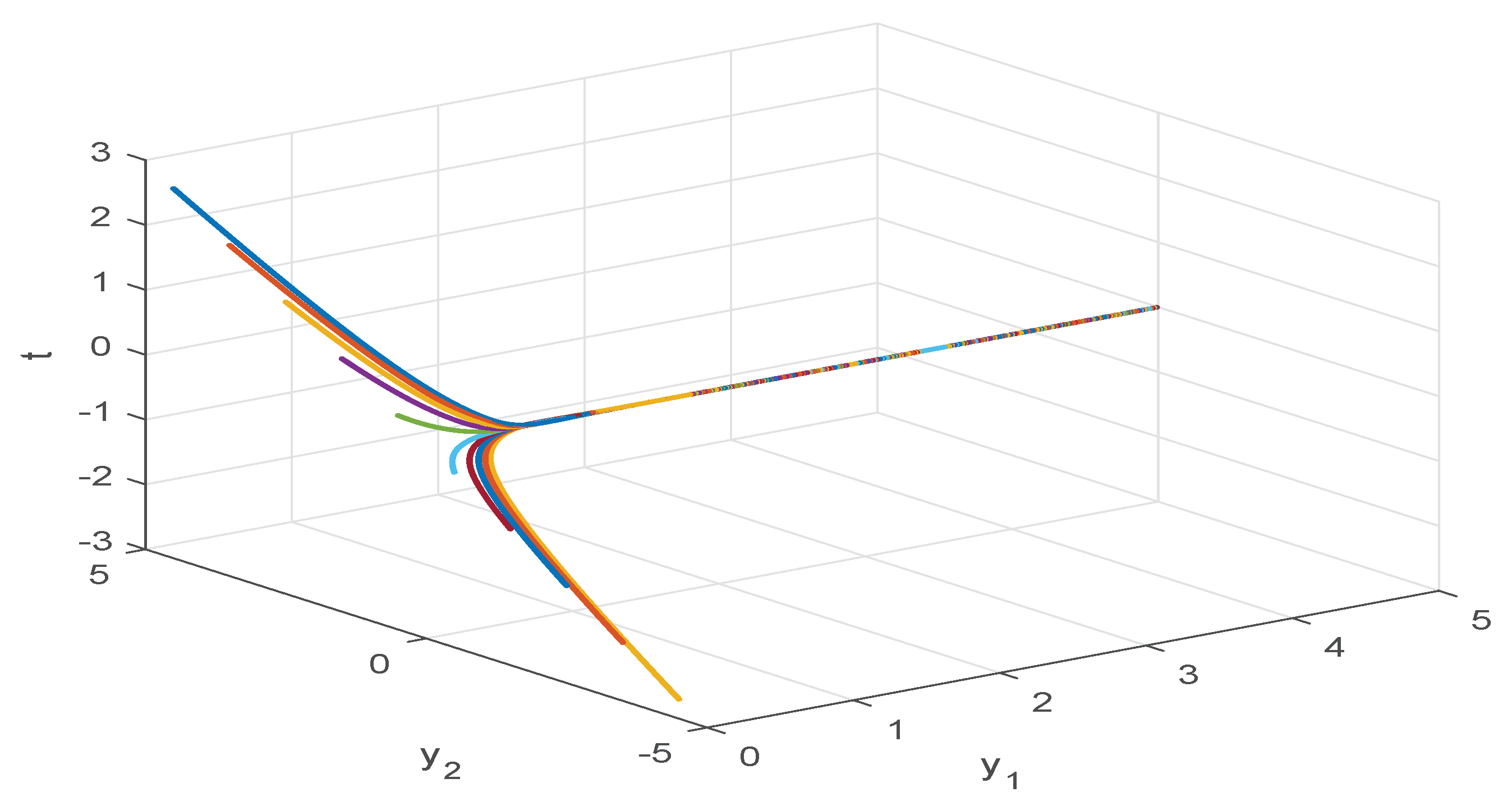
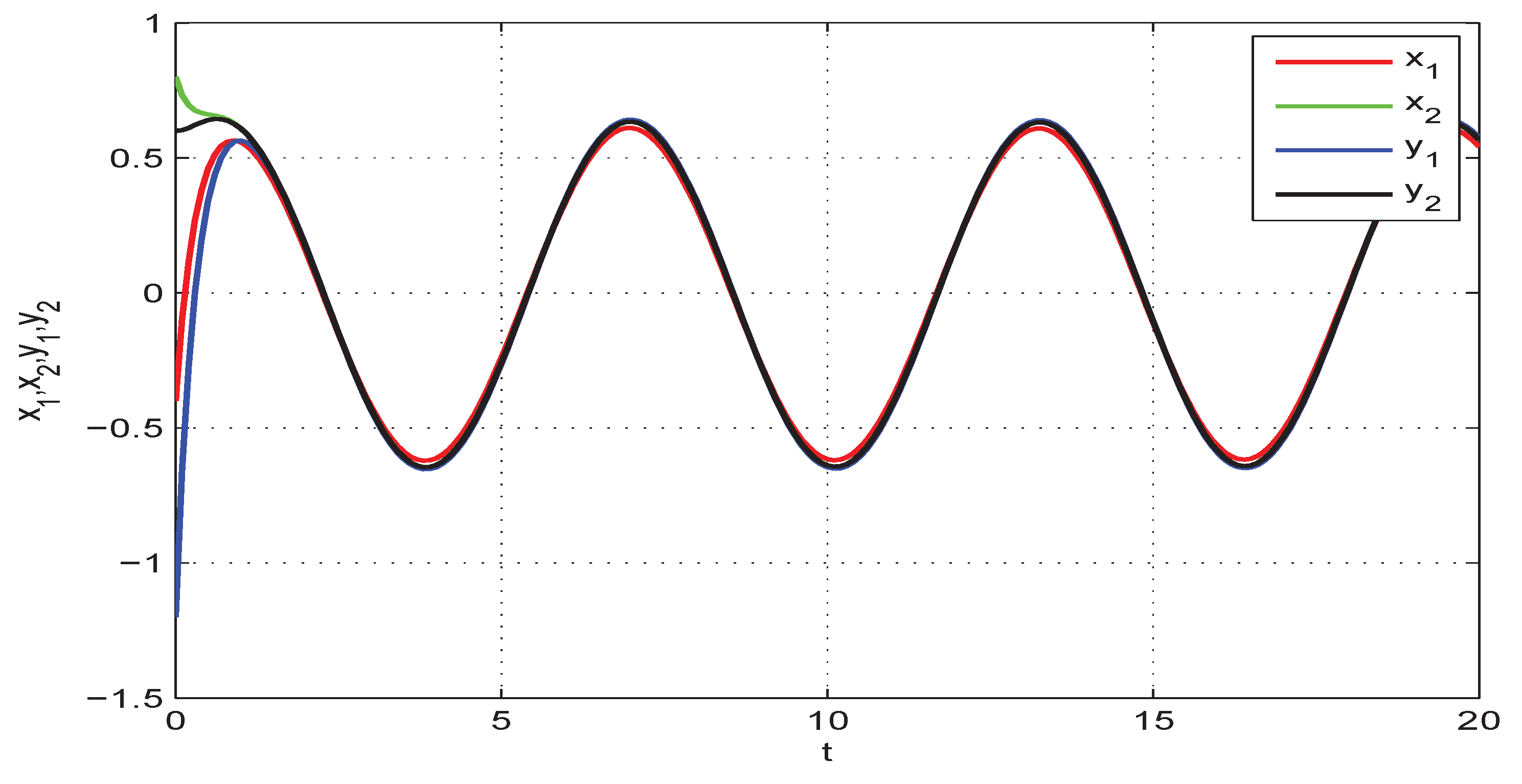
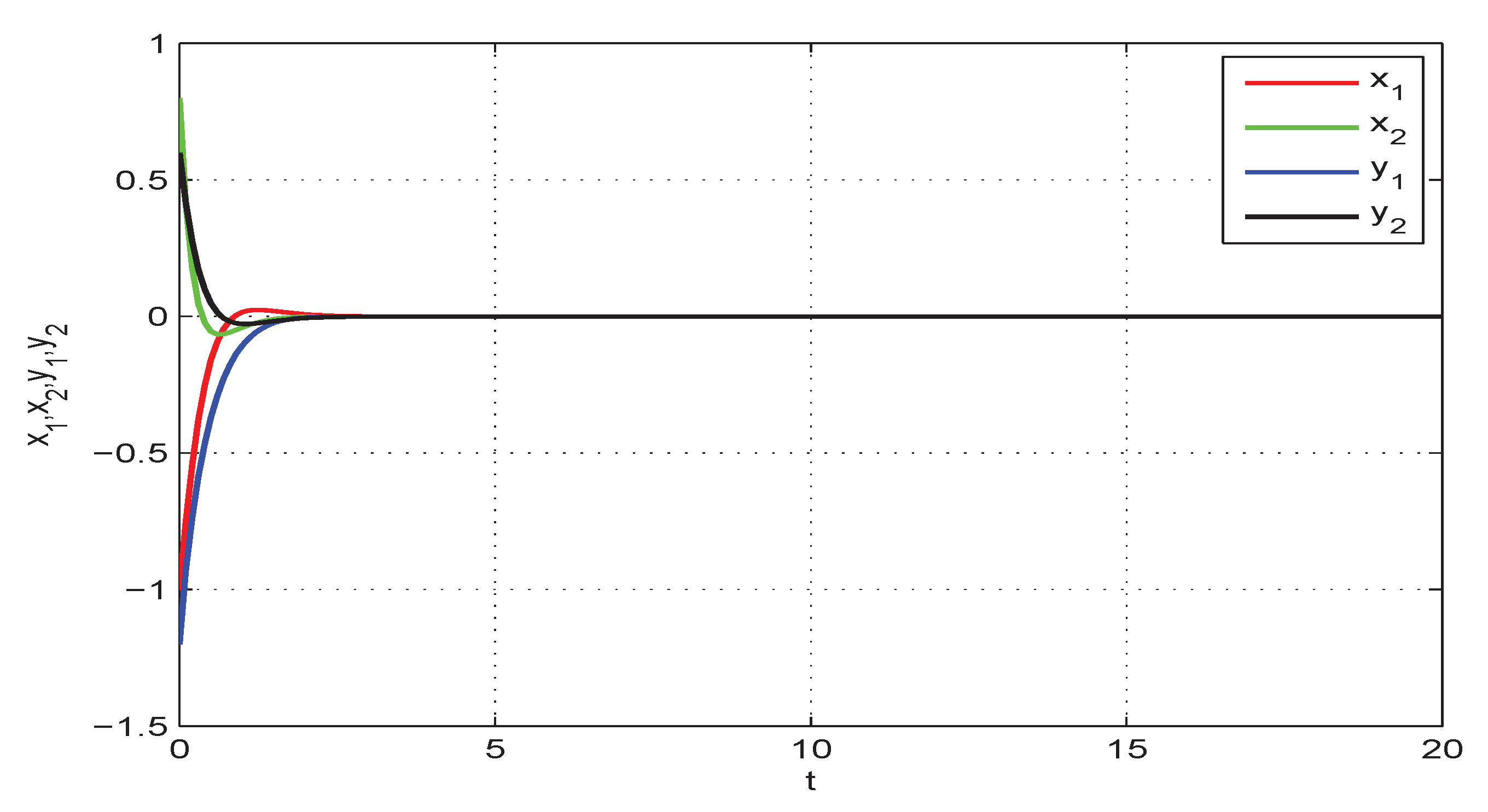
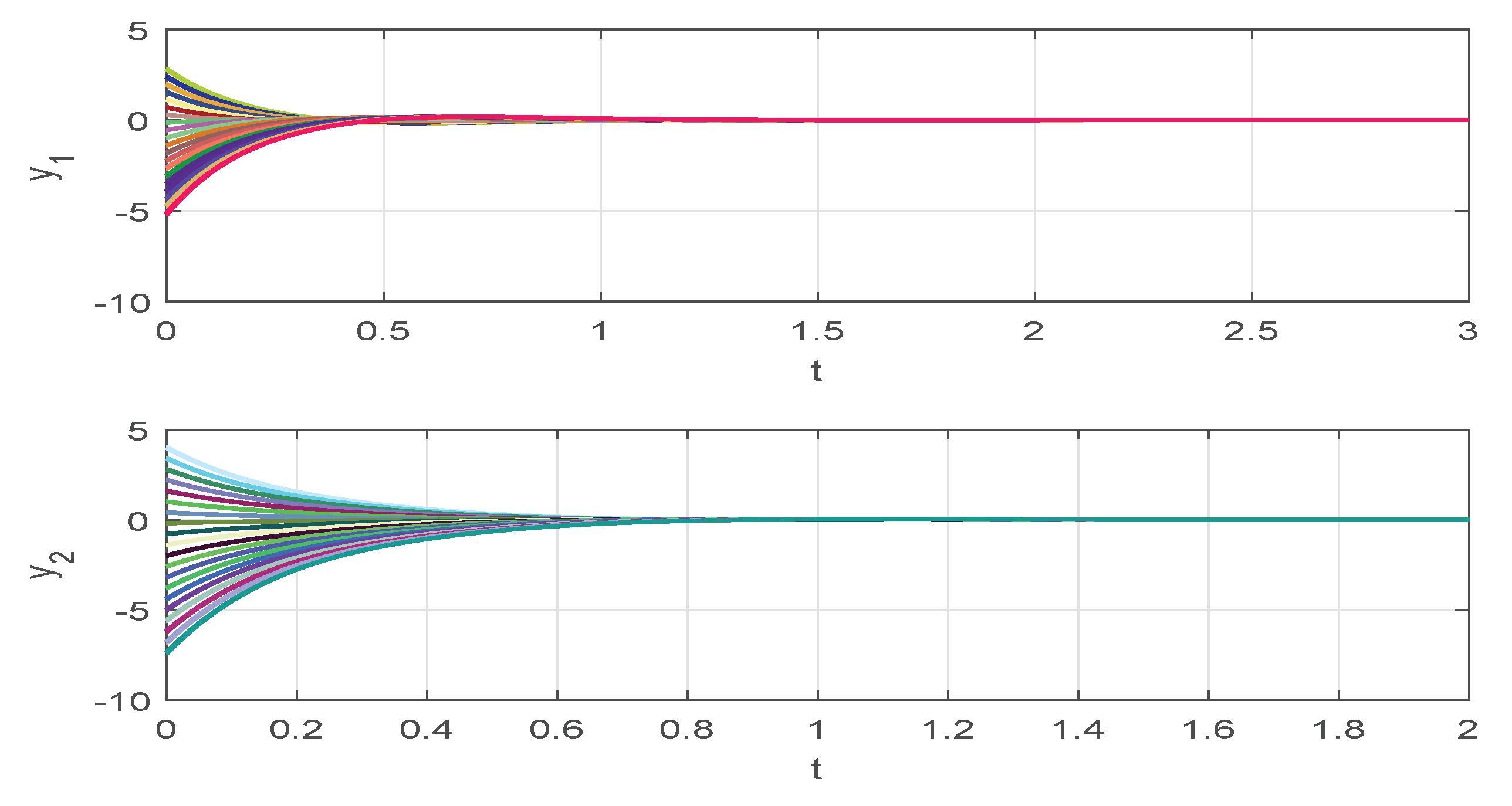
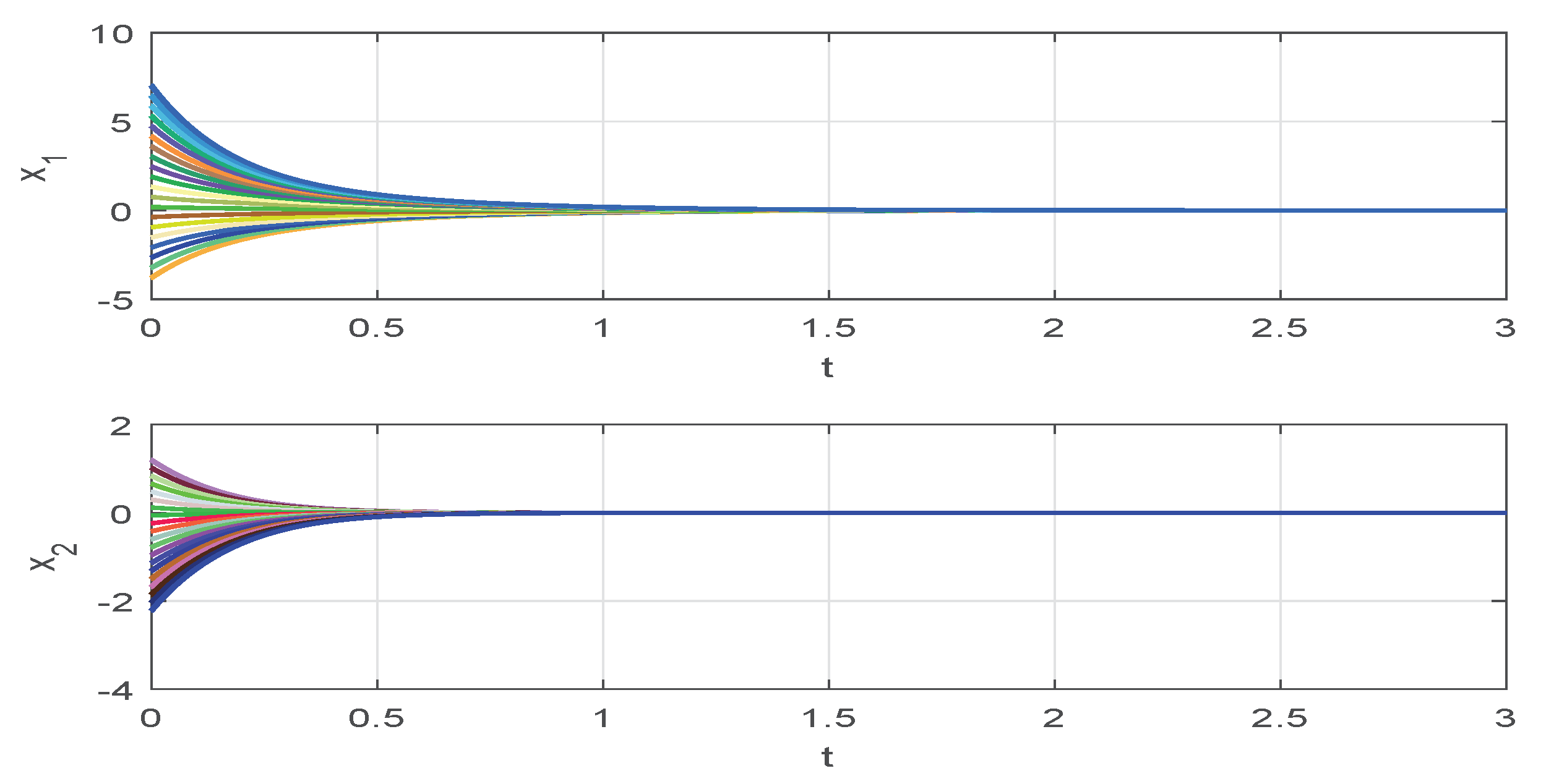
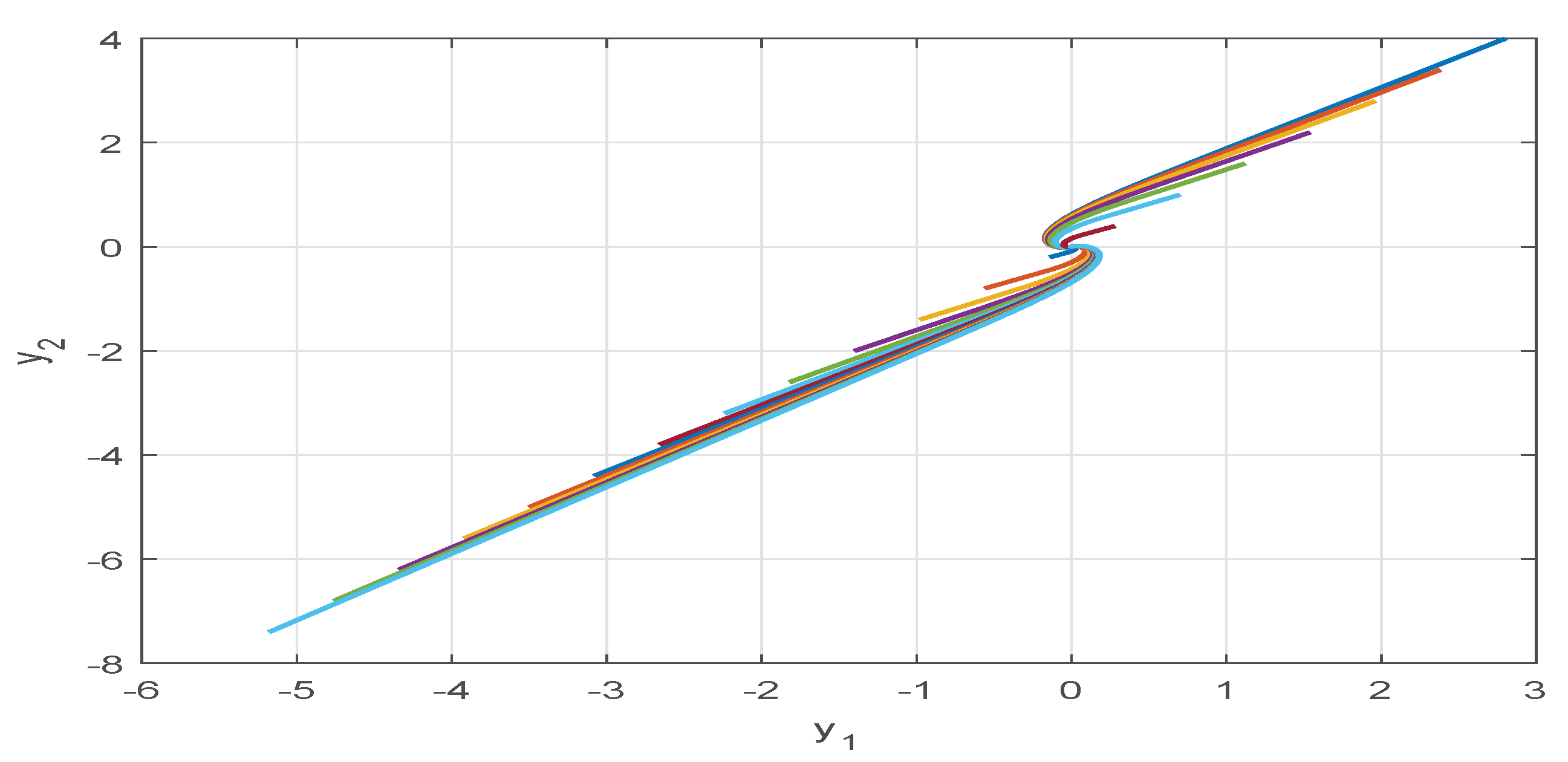
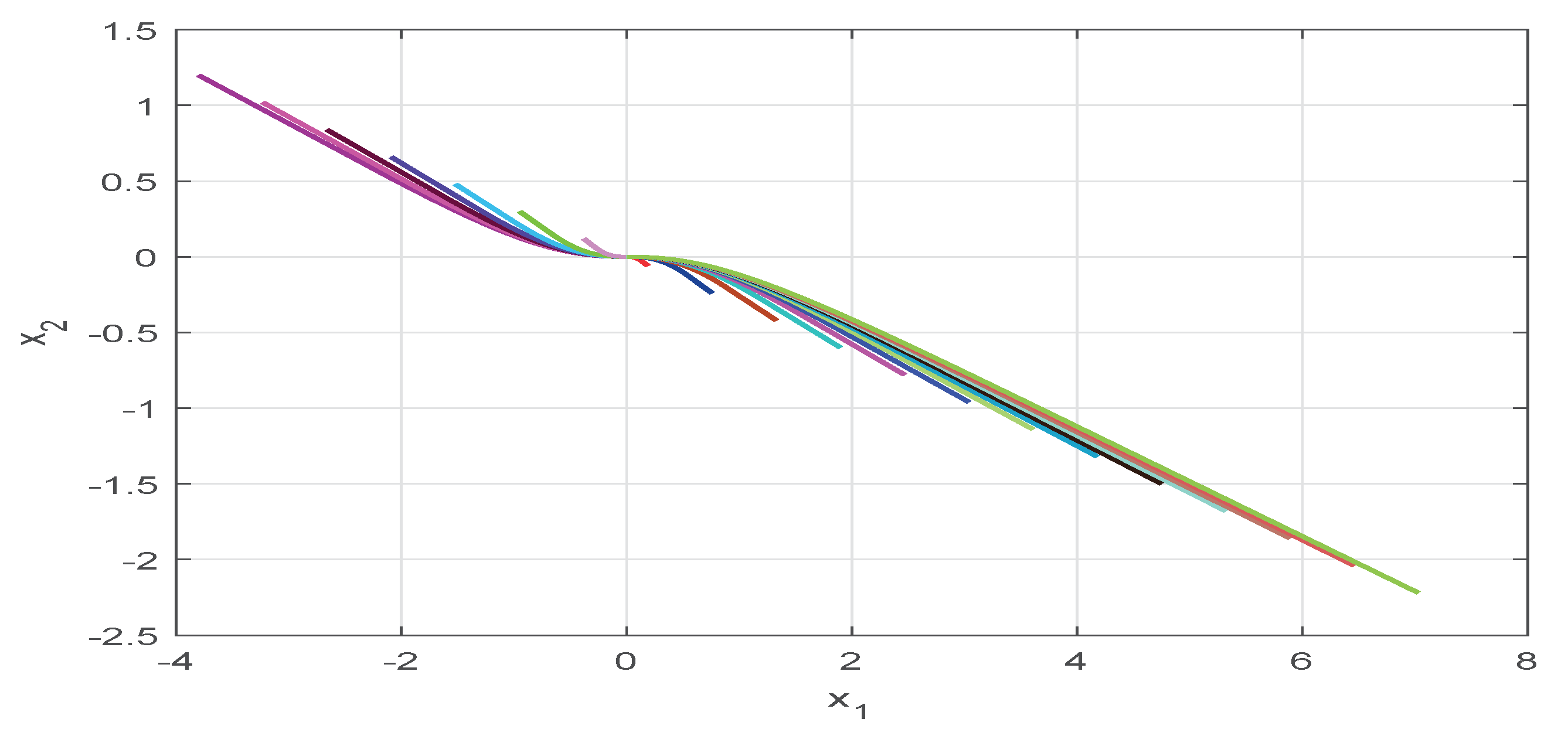
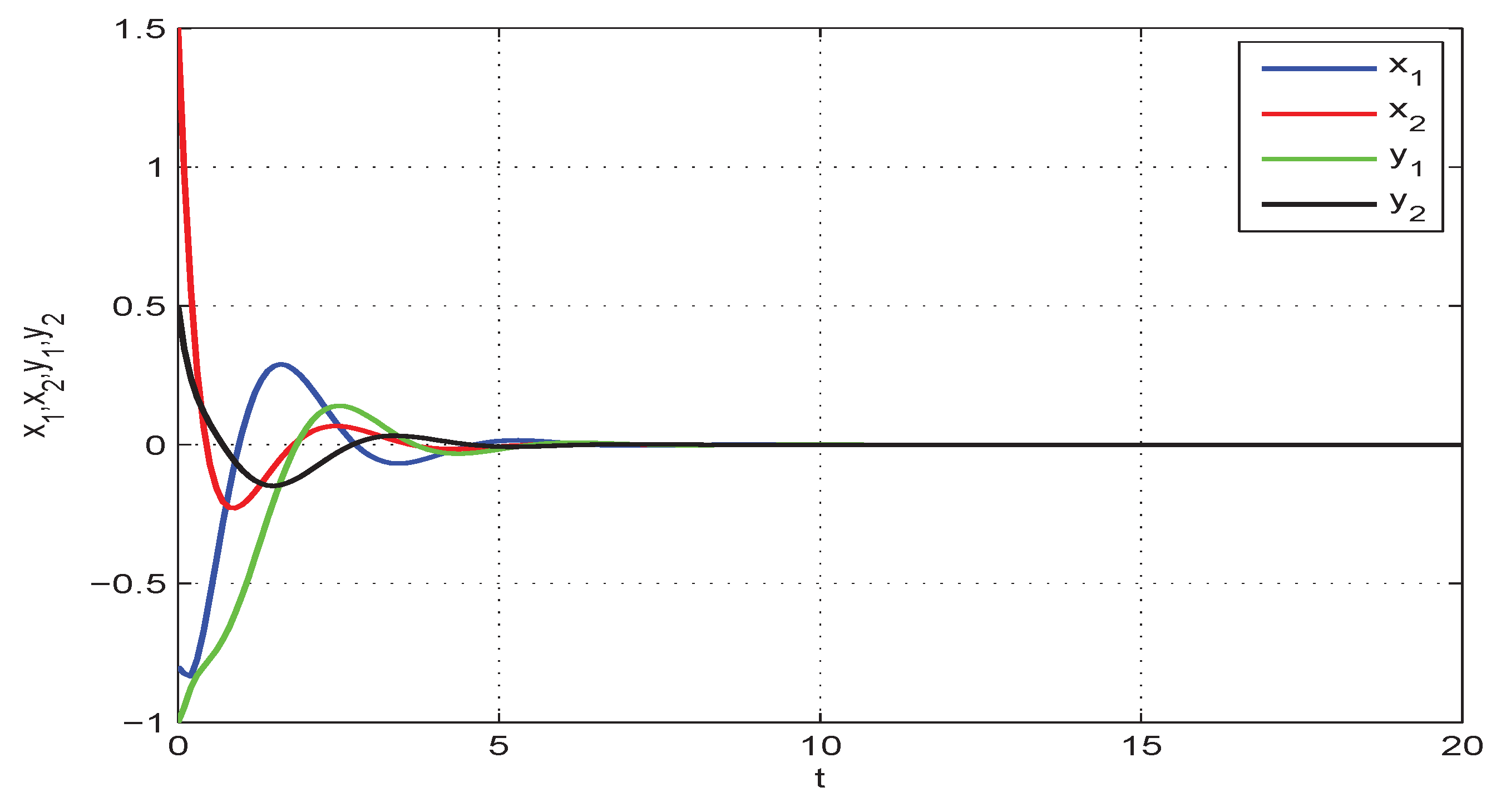
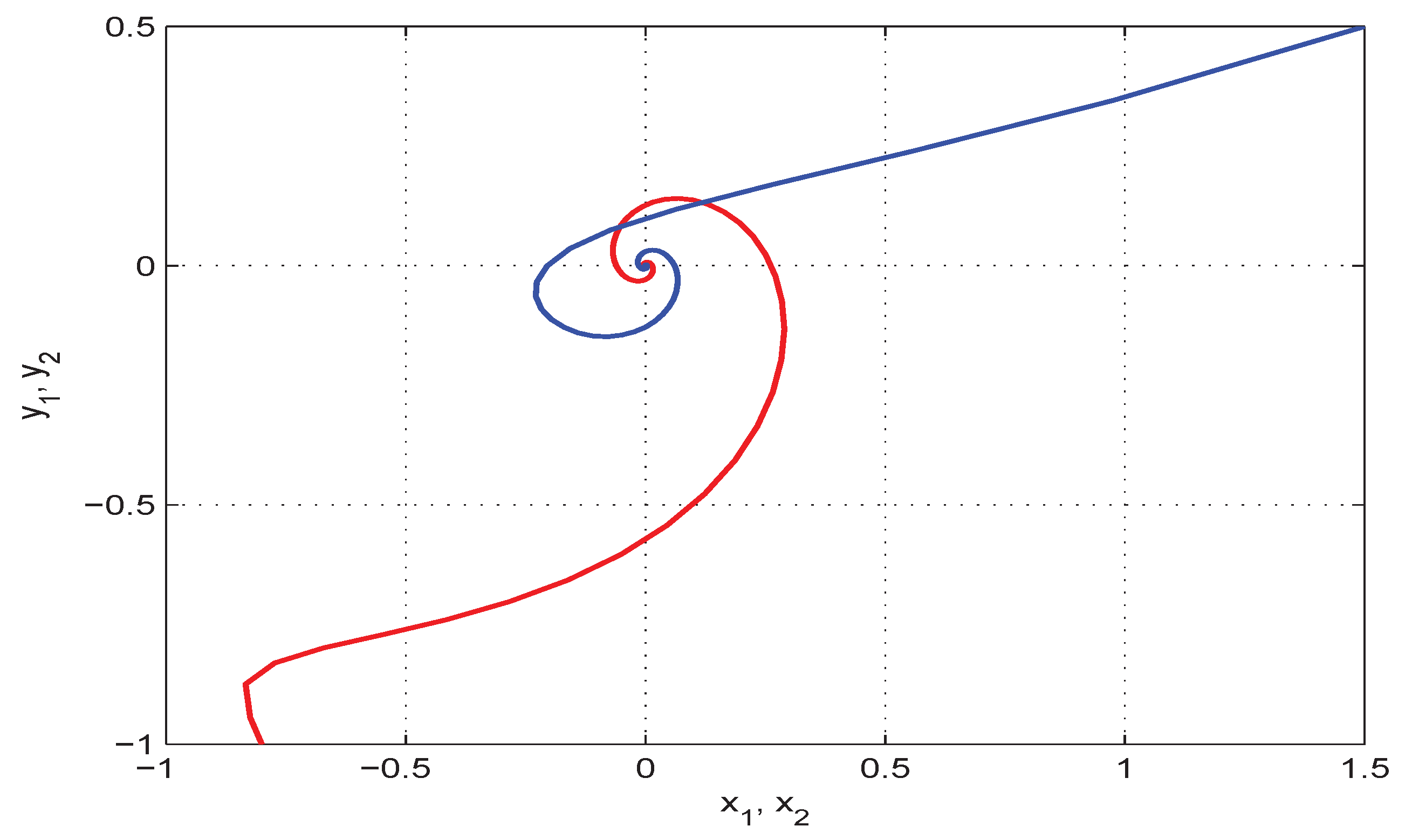
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, Z.; Guo, Z.; Huang, L.; Liu, X. Dynamical behavior of complex-valued Hopfield neural networks with discontinuous activation functions. Neural Process. Lett. 2017, 45, 1039–1061. [Google Scholar] [CrossRef]
- Song, Q.; Zhao, Z.; Liu, Y. Stability analysis of complex-valued neural networks with probabilistic time-varying delays. Neurocomputing 2015, 159, 96–104. [Google Scholar] [CrossRef]
- Sriraman, R.; Cao, Y.; Samidurai, R. Global asymptotic stability of stochastic complex-valued neural networks with probabilistic time-varying delays. Math. Comput. Simul. 2020, 171, 103–118. [Google Scholar] [CrossRef]
- Chen, X.; Song, Q. Global stability of complex-valued neural networks with both leakage time delay and discrete time delay on time scales. Neurocomputing 2013, 121, 254–264. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Cao, J.; Rajchakit, G.; Lim, C.P. Global robust synchronization of fractional order complex-valued neural networks with mixed time varying delays and impulses. Int. J. Control Autom. Syst. 2019, 17, 509–520. [Google Scholar]
- Gong, W.; Liang, J.; Kan, X.; Nie, X. Robust state estimation for delayed complex-valued neural networks. Neural Process. Lett. 2017, 46, 1009–1029. [Google Scholar] [CrossRef]
- Samidurai, R.; Sriraman, R.; Zhu, S. Leakage delay-dependent stability analysis for complex-valued neural networks with discrete and distributed time-varying delays. Neurocomputing 2019, 338, 262–273. [Google Scholar] [CrossRef]
- Samidurai, R.; Sriraman, R.; Cao, J.; Tu, Z. Effects of leakage delay on global asymptotic stability of complex-valued neural networks with interval time-varying delays via new complex-valued Jensen’s inequality. Int. J. Adapt. Control Signal Process. 2018, 32, 1294–1312. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, L. Global stability analysis for delayed complex-valued BAM neural networks. Neurocomputing 2016, 173, 2083–2089. [Google Scholar] [CrossRef]
- Subramanian, K.; Muthukumar, P. Global asymptotic stability of complex-valued neural networks with additive time-varying delays. Cogn. Neurodyn. 2017, 11, 293–306. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Guo, R.; Lin, C. Finite-time stability for delayed complex-valued BAM neural networks. Neural Process. Lett. 2018, 48, 179–193. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Zhou, D.; Lin, C.; Chen, J.; Wang, H. Finite-time stabilizability and instabilizability for complex-valued memristive neural networks with time delays. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 2371–2382. [Google Scholar] [CrossRef]
- Mishra, D.; Tolambiya, A.; Shukla, A.; Kalra, P. Stability analysis for higher order complex-valued Hopfield neural network. Neural Inf. Process. 2006, 4232, 608–615. [Google Scholar]
- Liu, D.; Zhu, S.; Ye, E. Synchronization stability of memristor-based complex-valued neural networks with time delays. Neural Netw. 2017, 96, 115–127. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Zhu, S.; Chang, W. Mean square exponential input-to-state stability of stochastic memristive complex-valued neural networks with time varying delay. Int. J. Syst. Sci. 2017, 48, 1966–1977. [Google Scholar] [CrossRef]
- Li, X.; Ding, D. Mean square exponential stability of stochastic Hopfield neural networks with mixed delays. Stat. Probab. Lett. 2017, 126, 88–96. [Google Scholar] [CrossRef]
- Wang, T.; Zhao, S.; Zhou, W.; Yu, W. Finite-time state estimation for delayed Hopfield neural networks with Markovian jump. Neurocomputing 2015, 156, 193–198. [Google Scholar] [CrossRef]
- Liu, L.; Deng, F. Stability analysis of time varying delayed stochastic Hopfield neural networks in numerical simulation. Neurocomputing 2018, 316, 294–305. [Google Scholar] [CrossRef]
- Park, M.J.; Kwon, O.M.; Ryu, J.H. Generalized integral inequality: Application to time-delay systems. Appl. Math. Lett. 2018, 77, 6–12. [Google Scholar] [CrossRef]
- Chen, J.; Xu, S.; Chen, W.; Zhang, B.; Ma, Q.; Zou, Y. Two general integral inequalities and their applications to stability analysis for systems with time-varying delay. Int. J. Robust Nonlinear Control 2016, 26, 4088–4103. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Ding, S.; Zhang, H. Refined Jensen-based multiple integral inequality and its application to stability of time-delay systems. IEEE/CAA J. Automat. Sinica 2018, 5, 758–764. [Google Scholar] [CrossRef]
- Kwon, O.M.; Park, M.J.; Park, J.H.; Lee, S.M.; Cha, E.J. Analysis on robust H∞ performance and stability for linear systems with interval time-varying state delays via some new augmented Lyapunov-Krasovskii functional. Appl. Math. Comput. 2013, 224, 108–122. [Google Scholar]
- Li, T.; Guo, L.; Sun, C. Robust stability for neural networks with time-varying delays and linear fractional uncertainties. Neurocomputing 2007, 71, 421–427. [Google Scholar] [CrossRef]
- Sakthivel, R.; Shi, P.; Arunkumar, A.; Mathiyalagan, K. Robust reliable H∞ control for fuzzy systems with random delays and linear fractional uncertainties. Fuzzy Set. Syst. 2016, 302, 65–81. [Google Scholar] [CrossRef]
- Samidurai, R.; Sriraman, R. Robust dissipativity analysis for uncertain neural networks with additive time-varying delays and general activation functions. Math. Comput. Simul. 2019, 155, 201–216. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Saif, A.W.A. Dissipativity analysis and design for uncertain Markovian jump systems with time-varying delays. Appl. Math. Comput. 2013, 219, 9681–9695. [Google Scholar] [CrossRef]
- Wu, Z.G.; Lam, J.; Su, H.; Chu, J. Stability and dissipativity analysis of static neural networks with time delay. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 199–210. [Google Scholar]
- Feng, Z.; Lam, J. Stability and dissipativity analysis of distributed delay cellular neural networks. IEEE Trans. Neural Netw. 2011, 22, 976–981. [Google Scholar] [CrossRef]
- Raja, R.; Raja, U.K.; Samidurai, R.; Leelamani, A. Dissipativity of discrete-time BAM stochastic neural networks with Markovian switching and impulses. J. Frankl. Inst. 2013, 350, 3217–3247. [Google Scholar] [CrossRef]
- Zeng, H.B.; Park, J.H.; Zhang, C.F.; Wang, W. Stability and dissipativity analysis of static neural networks with interval time-varying delay. J. Frankl. Inst. 2015, 352, 1284–1295. [Google Scholar] [CrossRef]
- Li, X.; Rakkiyappan, R.; Velmurugan, G. Dissipativity analysis of memristor-based complex-valued neural networks with time-varying delays. Inform. Sci. 2015, 294, 645–665. [Google Scholar] [CrossRef]
- Rajivganthi, C.; Rihan, F.A.; Lakshmanan, S. Dissipativity analysis of complex-valued BAM neural networks with time delay. Neural Comput. Appl. 2019, 31, 127–137. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Velmurugan, G.; Li, X.; Regan, D.O. Global dissipativity of memristor-based complex-valued neural networks with time-varying delays. Neural Comput. Appl. 2016, 27, 629–649. [Google Scholar] [CrossRef]
- Ramasamy, S.; Nagamani, G. Dissipativity and passivity analysis for discrete-time complex-valued neural networks with leakage delay and probabilistic time-varying delays. Int. J. Adapt. Control Signal Process. 2017, 31, 876–902. [Google Scholar] [CrossRef]
- Nagamani, G.; Ramasamy, S. Dissipativity and passivity analysis for discrete-time complex-valued neural networks with time-varying delays. Cogent Math. 2015, 2, 1048580. [Google Scholar] [CrossRef]
- Cao, Y.; Sriraman, R.; Shyamsundarraj, N.; Samidurai, R. Robust stability of uncertain stochastic complex-valued neural networks with additive time-varying delays. Math. Comput. Simul. 2020, 171, 207–220. [Google Scholar] [CrossRef]
- Liu, M.; Wang, X.; Zhang, Z.; Wang, Z. Dissipativity analysis of complex-valued stochastic neural networks with time-varying delays. IEEE Access 2019, 7, 165076–165087. [Google Scholar] [CrossRef]
- Cao, Y.; Samidurai, R.; Sriraman, R. Stability and stabilization analysis of nonlinear time-delay systems with randomly occurring controller gain fluctuation. Math. Comput. Simul. 2020, 171, 36–51. [Google Scholar] [CrossRef]
- Subramanian, K.; Muthukumar, P.; Lakshmanan, S. State feedback synchronization control of impulsive neural networks with mixed delays and linear fractional uncertainties. Appl. Math. Comput. 2018, 321, 267–281. [Google Scholar] [CrossRef]
- Hill, D.L.; Moylan, P.J. Dissipative dynamical systems: Basic input-output and state properties. J. Frankl. Inst. 1980, 309, 327–357. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chanthorn, P.; Rajchakit, G.; Ramalingam, S.; Lim, C.P.; Ramachandran, R. Robust Dissipativity Analysis of Hopfield-Type Complex-Valued Neural Networks with Time-Varying Delays and Linear Fractional Uncertainties. Mathematics 2020, 8, 595. https://doi.org/10.3390/math8040595
Chanthorn P, Rajchakit G, Ramalingam S, Lim CP, Ramachandran R. Robust Dissipativity Analysis of Hopfield-Type Complex-Valued Neural Networks with Time-Varying Delays and Linear Fractional Uncertainties. Mathematics. 2020; 8(4):595. https://doi.org/10.3390/math8040595
Chicago/Turabian StyleChanthorn, Pharunyou, Grienggrai Rajchakit, Sriraman Ramalingam, Chee Peng Lim, and Raja Ramachandran. 2020. "Robust Dissipativity Analysis of Hopfield-Type Complex-Valued Neural Networks with Time-Varying Delays and Linear Fractional Uncertainties" Mathematics 8, no. 4: 595. https://doi.org/10.3390/math8040595
APA StyleChanthorn, P., Rajchakit, G., Ramalingam, S., Lim, C. P., & Ramachandran, R. (2020). Robust Dissipativity Analysis of Hopfield-Type Complex-Valued Neural Networks with Time-Varying Delays and Linear Fractional Uncertainties. Mathematics, 8(4), 595. https://doi.org/10.3390/math8040595





