Convergence Rate of the Modified Landweber Method for Solving Inverse Potential Problems
Abstract
1. Introduction
2. Preliminary Results
3. Convergence Analysis
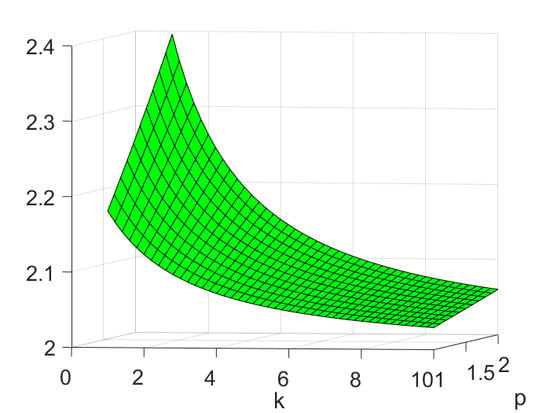
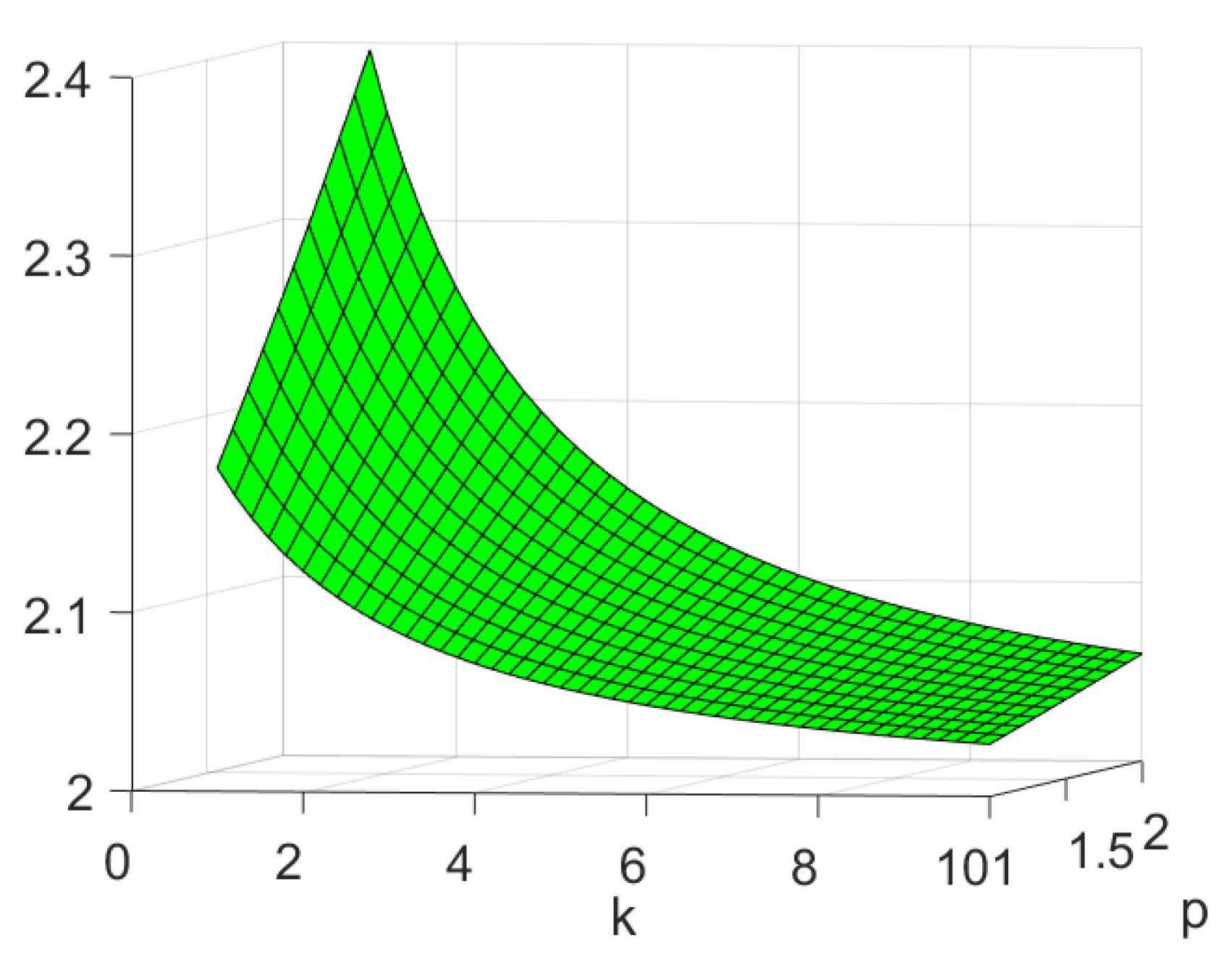
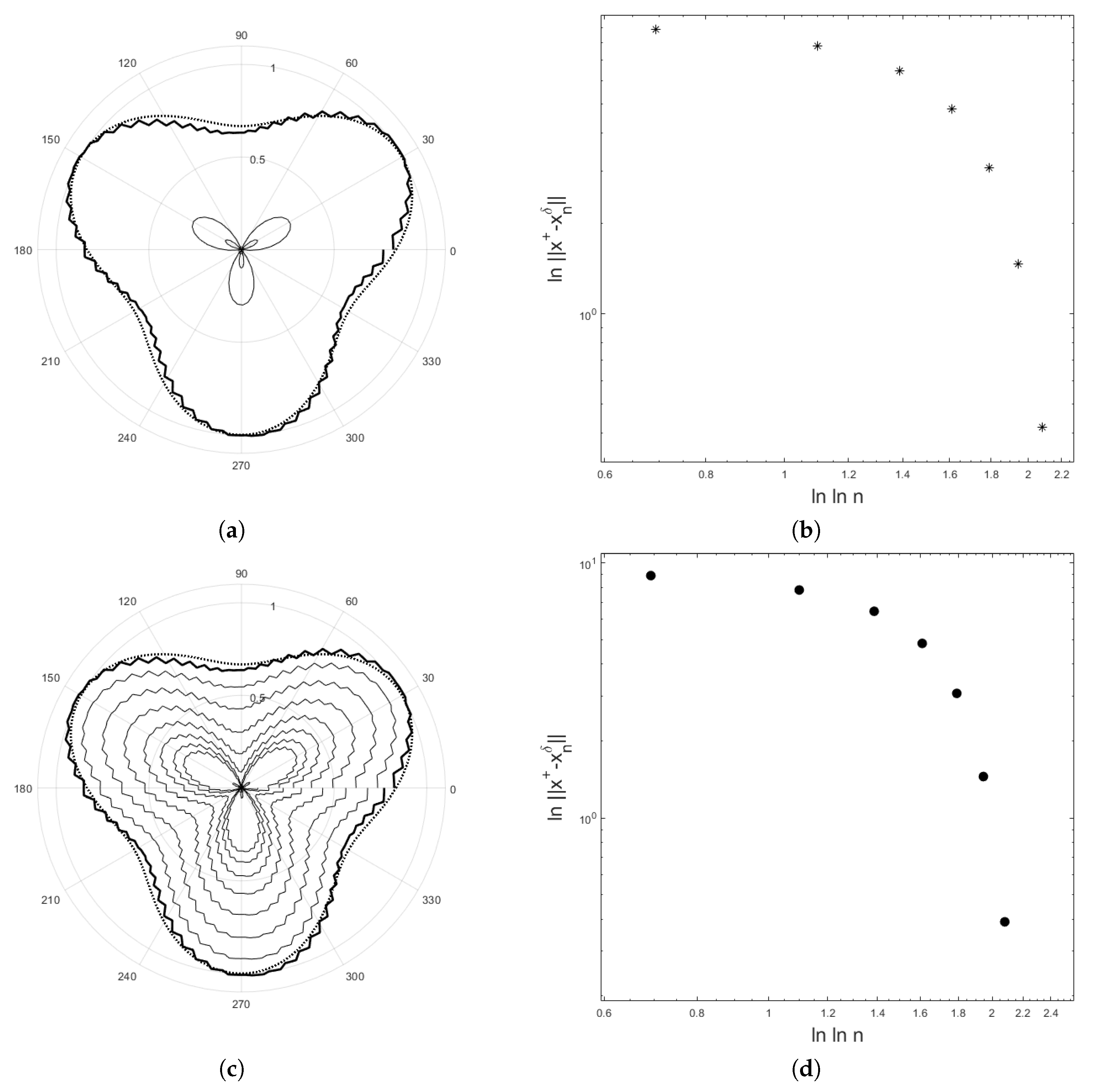
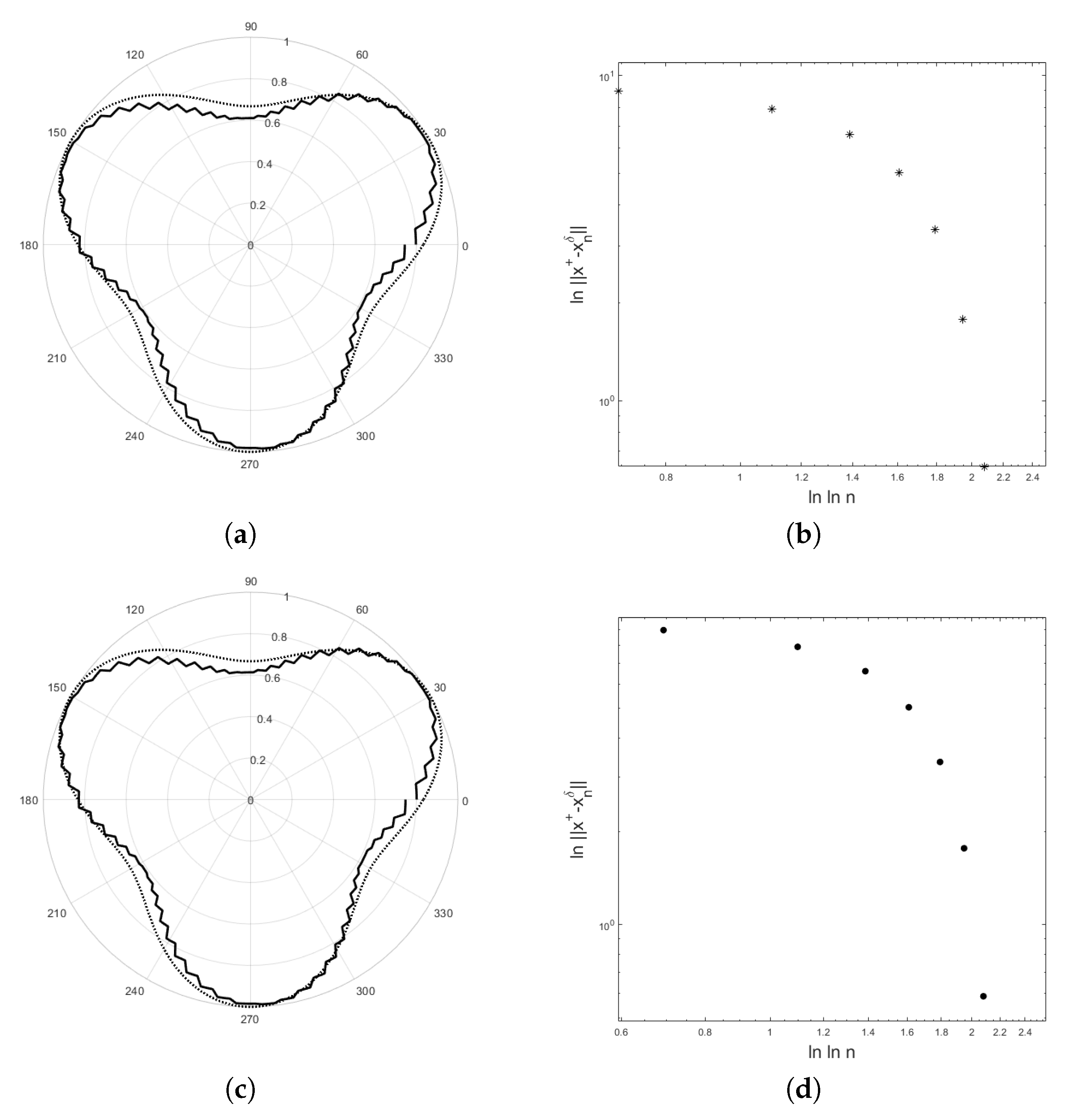
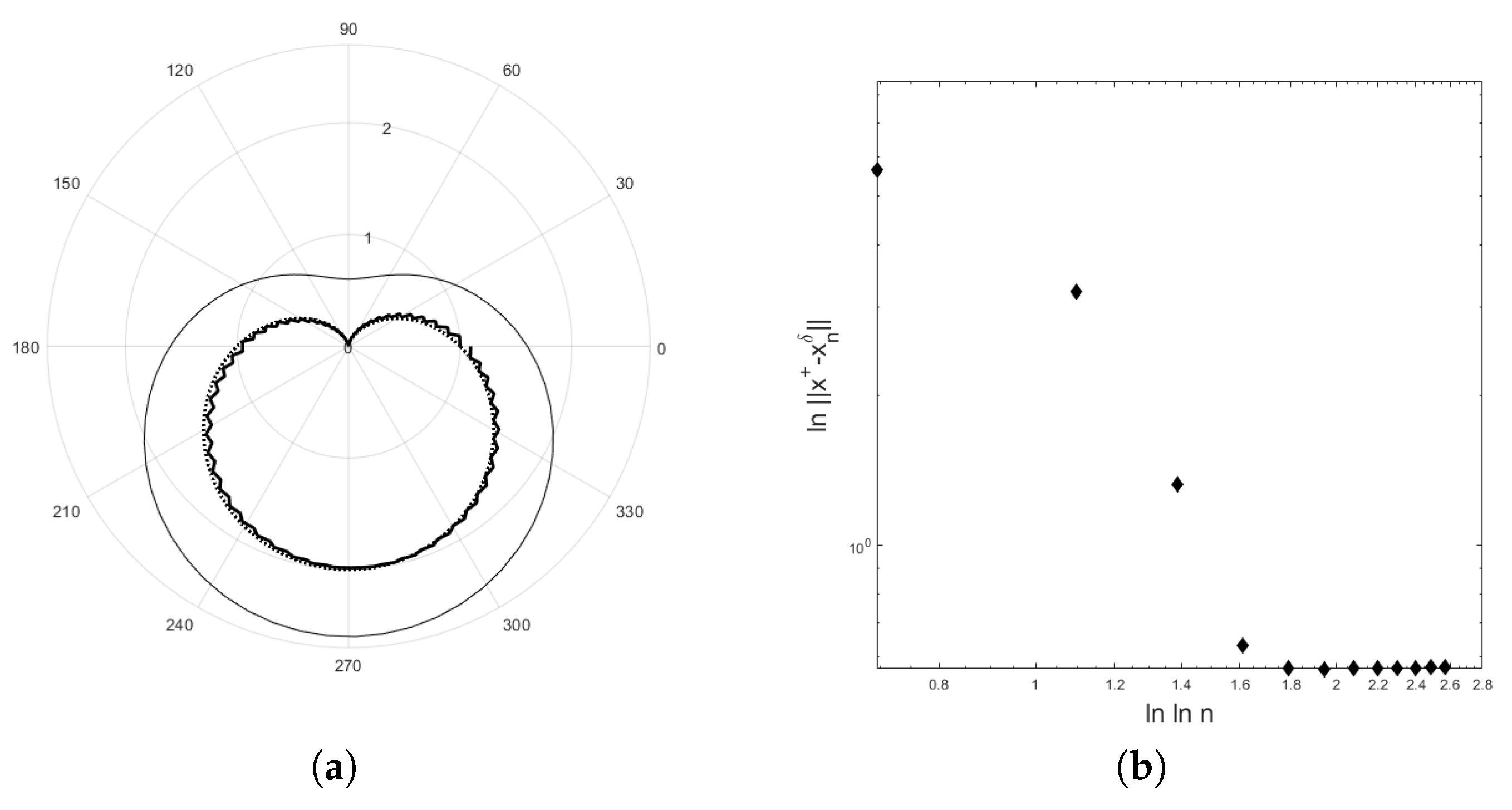
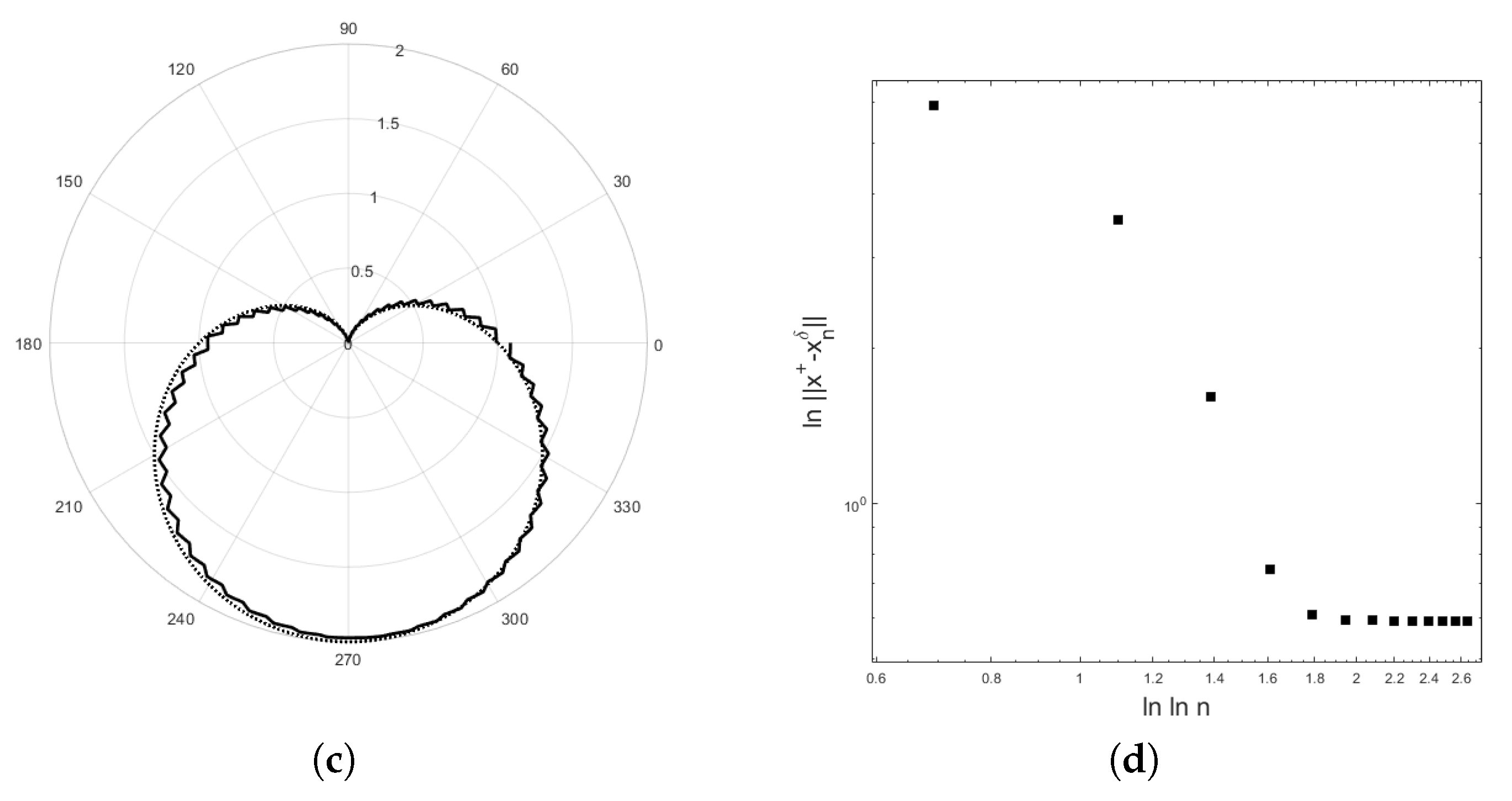
4. Application to an Inverse Potential Problem
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Böckmann, C.; Kammanee, A.; Braunß, A. Logarithmic convergence rate of Levenberg–Marquardt method with application to an inverse potential problem. J. Inv. Ill-Posed Probl. 2011, 19, 345–367. [Google Scholar] [CrossRef]
- Hettlich, F.; Rundell, W. Iterative methods for the reconstruction of an inverse potential problem. Inverse Probl. 1996, 12, 251–266. [Google Scholar] [CrossRef]
- Hettlich, F.; Rundell, W. A second degree method for nonlinear inverse problems. SIAM J. Numer. Anal. 1999, 37, 587–620. [Google Scholar] [CrossRef]
- Van den Doel, K.; Ascher, U. On level set regularization for highly ill-posed distributed parameter estimation problems. J. Comput. Phys. 2006, 216, 707–723. [Google Scholar] [CrossRef][Green Version]
- Hohage, T. Logarithmic convergence rates of the iteratively regularized Gauss—Newton method for an inverse potential and an inverse scattering problem. Inverse Probl. 1997, 13, 1279. [Google Scholar] [CrossRef]
- Pornsawad, P.; Sapsakul, N.; Böckmann, C. A modified asymptotical regularization of nonlinear ill-posed problems. Mathematics 2019, 7, 419. [Google Scholar] [CrossRef]
- Tautenhahn, U. On the asymptotical regularization of nonlinear ill-posed problems. Inverse Probl. 1994, 10, 1405–1418. [Google Scholar] [CrossRef]
- Zhang, Y.; Hofmann, B. On the second order asymptotical regularization of linear ill-posed inverse problems. Appl. Anal. 2018. [Google Scholar] [CrossRef]
- Pornsawad, P.; Böckmann, C. Modified iterative Runge-Kutta-type methods for nonlinear ill-posed problems. Numer. Funct. Anal. Optim. 2016, 37, 1562–1589. [Google Scholar] [CrossRef]
- Mahale, P.; Nair, M. Tikhonov regularization of nonlinear ill-posed equations under general source condition. J. Inv. Ill-Posed Probl. 2007, 15, 813–829. [Google Scholar] [CrossRef]
- Romanov, V.; Kabanikhin, S.; Anikonov, Y.; Bukhgeim, A. Ill-Posed and Inverse Problems: Dedicated to Academician Mikhail Mikhailovich Lavrentiev on the Occasion of his 70th Birthday; De Gruyter: Berlin, Germany, 2018. [Google Scholar]
- Scherzer, O. A modified Landweber iteration for solving parameter estimation problems. Appl. Math. Optim. 1998, 38, 45–68. [Google Scholar] [CrossRef]
- Deuflhard, P.; Engl, W.; Scherzer, O. A convergence analysis of iterative methods for the solution of nonlinear ill-posed problems under affinely invariant conditions. Inverse Probl. 1998, 14, 1081–1106. [Google Scholar] [CrossRef]
- Bakushinsky, A.; Kokurin, M.; Kokurin, M. Regularization Algorithms for Ill-Posed Problems; Inverse and Ill-Posed Problems Series; De Gruyter: Berlin, Germany, 2018. [Google Scholar]
- Schuster, T.; Kaltenbacher, B.; Hofmann, B.; Kazimierski, K. Regularization Methods in Banach Spaces; Radon Series on Computational and Applied Mathematics; De Gruyter: Berlin, Germany, 2012. [Google Scholar]
- Albani, V.; Elbau, P.; de Hoop, M.V.; Scherzer, O. Optimal convergence rates results for linear inverseproblems in Hilbert spaces. Numer. Funct. Anal. Optim. 2016, 37, 521–540. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kaltenbacher, B.; Neubauer, A.; Scherzer, O. Iterative Regularization Methods for Nonlinear Ill-Posed Problems; De Gruyter: Berlin, Germany; Boston, MA, USA, 2008. [Google Scholar]
- Louis, A.K. Inverse und Schlecht Gestellte Probleme; Teubner Studienbücher Mathematik, B. G. Teubner: Stuttgart, Germany, 1989. [Google Scholar]
- Vainikko, G.; Veterennikov, A.Y. Iteration Procedures in Ill-Posed Problems; Nauka: Moscow, Russia, 1986. [Google Scholar]
- Hanke, M.; Neubauer, A.; Scherzer, O. A convergence analysis of the Landweber iteration for nonlinear ill-posed problems. Numer. Math. 1995, 72, 21–37. [Google Scholar] [CrossRef]
- Böckmann, C.; Pornsawad, P. Iterative Runge-Kutta-type methods for nonlinear ill-posed problems. Inverse Probl. 2008, 24, 025002. [Google Scholar] [CrossRef][Green Version]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pornsawad, P.; Sungcharoen, P.; Böckmann, C. Convergence Rate of the Modified Landweber Method for Solving Inverse Potential Problems. Mathematics 2020, 8, 608. https://doi.org/10.3390/math8040608
Pornsawad P, Sungcharoen P, Böckmann C. Convergence Rate of the Modified Landweber Method for Solving Inverse Potential Problems. Mathematics. 2020; 8(4):608. https://doi.org/10.3390/math8040608
Chicago/Turabian StylePornsawad, Pornsarp, Parada Sungcharoen, and Christine Böckmann. 2020. "Convergence Rate of the Modified Landweber Method for Solving Inverse Potential Problems" Mathematics 8, no. 4: 608. https://doi.org/10.3390/math8040608
APA StylePornsawad, P., Sungcharoen, P., & Böckmann, C. (2020). Convergence Rate of the Modified Landweber Method for Solving Inverse Potential Problems. Mathematics, 8(4), 608. https://doi.org/10.3390/math8040608