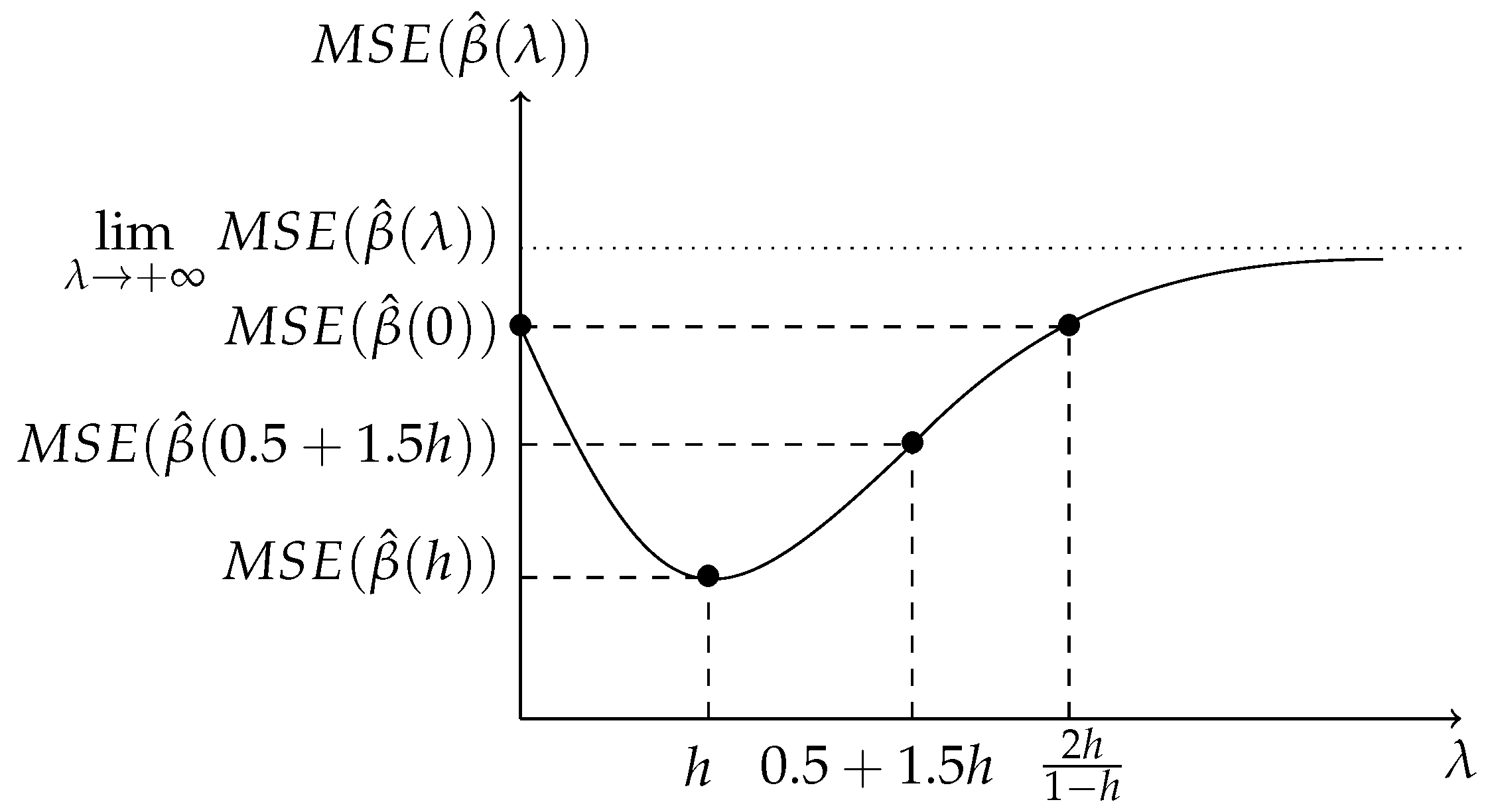1. Introduction
In the last fifty years, different methods have been developed to avoid the instability of estimates derived from collinearity (see, for example, Kiers and Smilde [
1]). Some of these methods can be grouped within a general denomination known as penalized regression.
In general terms, the penalized regression parts from the linear model (with
p variables and
n observations),
, and obtains the regularization of the estimated parameters, minimizing the following objective function:
where
is a penalty term that can take different forms. One of the most common penalty terms is the bridge penalty term ([
2,
3]) is given by
where
is a tuning parameter. Note that the ridge ([
4]) and the Lasso ([
5]) regressions are obtained when
and
, respectively. Penalties have also been called soft thresholding ([
6,
7]).
These methods are applied not only for the treatment of multicollinearity but also for the selection of variables (see, for example, Dupuis and Victoria-Feser [
8], Li and Yang [
9] Liu et al. [
10], or Uematsu and Tanaka [
11]), which is a crucial issue in many areas of science when the number of variables exceeds the sample size. Zou and Hastie [
12] proposed elastic net regularization by using the penalty terms
and
that combine the Lasso and ridge regressions:
Thus, the Lasso regression usually selects one of the regressors from among all those that are highly correlated, while the elastic net regression selects several of them. In the words of Tutz and Ulbricht [
13] “the elastic net catches all the big fish”, meaning that it selects the whole group.
From a different point of view, other authors have also presented different techniques and methods well suited for dealing with the collinearity problems: continuum regression ([
14]), least angle regression ([
15]), generalized maximum entropy ([
16,
17,
18]), the principal component analysis (PCA) regression ([
19,
20]), the principal correlation components estimator ([
21]), penalized splines ([
22]), partial least squares (PLS) regression ([
23,
24]), or the surrogate estimator focused on the solution of the normal equations presented by Jensen and Ramirez [
25].
Focusing on collinearity, the ridge regression is one of the more commonly applied methodologies and it is estimated by the following expression:
where
is the identity matrix with adequate dimensions and
K is the ridge factor (ordinary least squares (OLS) estimators are obtained when
). Although ridge regression has been widely applied, it presents some problems with current practice in the presence of multicollinearity and the estimators derived from the penalty come into these same problems whenever
:
In relation to the calculation of the variance inflation factors (VIF), measures that quantify the degree of multicollinearity existing in a model from the coefficient of determination of the regression between the independent variables (for more details, see
Section 2), García et al. [
26] showed that the application of the original data when working with the ridge estimate leads to non-monotone VIF values by considering the VIF as a function of the penalty term. Logically, the Lasso and the elastic net regression inherit this property.
By following Marquardt [
27]: “The least squares objective function is mathematically independent of the scaling of the predictor variables (while the objective function in ridge regression is mathematically dependent on the scaling of the predictor variables)”. That is to say, the penalized objective function will bring problems derived from the standardization of the variables. This fact has to be taken into account both for obtaining the estimators of the regressors and for the application of measures that detect if the collinearity has been mitigated. Other penalized regressions (such as Lasso and elastic net regressions) are not scale invariant and hence yield different results depending on the predictor scaling used.
Some of the properties of the OLS estimator that are deduced from the normal equations are not verified by the ridge estimator and, among others, the estimated values for the endogenous variable are not orthogonal to the residuals. As a result, the following decomposition is verified
When the OLS estimators are obtained (
), the third term is null. However, this term is not null when
K is not zero. Consequently, the relationship
is not satisfied in ridge regression, and the definition of the coefficient of determination may not be suitable. This fact not only limits the analysis of the goodness of fit but also affects the global significance since the critical coefficient of determination is also questioned. Rodríguez et al. [
28] showed that the estimators obtained from the penalties mentioned above inherit the problem of the ridge regression in relation to the goodness of fit.
In order to overcome these problems, this paper is focused on the raise regression (García et al. [
29] and Salmerón et al. [
30]) based on the treatment of collinearity from a geometrical point of view. It consists in separating the independent variables by using the residuals (weighted by the raising factor) of the auxiliary regression traditionally used to obtain the VIF. Salmerón et al. [
30] showed that the raise regression presents better conditions than ridge regression and, more recently, García et al. [
31] showed, among other questions, that the ridge regression is a particular case of the raise regression.
This paper presents the extension of the VIF to the raise regression showing that, although García et al. [
31] showed that the application of the raise regression guarantees a diminishing of the VIF, it is not guaranteed that its value is lower the threshold traditionally established as troubling. Thus, it will be concluded that an unique application of the raise regression does not guarantee the mitigation of the multicollinearity. Consequently, this extension complements the results presented by García et al. [
31] and determines, on the one hand, whether it is necessary to apply a successive raise regression (see García et al. [
31] for more details) and, on the other hand, the most adequate variable for raising and the most optimal value for the raising factor in order to guarantee the mitigation of the multicollinearity.
On the other hand, the transformation of variables is common when strong collinearity exists in a linear model. The transformation to unit length (see Belsley et al. [
32]) or standardization (see Marquardt [
27]) is typical. Although the VIF is invariant to these transformations when it is calculated after estimation by OLS (see García et al. [
26]), it is not guaranteed either in the case of the raise regression or in ridge regression as showed by García et al. [
26]. The analysis of this fact is one of the goals of this paper.
Finally, since the raise estimator is biased, it is interesting to calculate its mean square error (MSE). It is studied whether the MSE of the raise regression is less than the one obtained by OLS. In this case, this study could be used to select an adequate raising factor similar to what is proposed by Hoerl et al. [
33] in the case of the ridge regression. Note that estimators with MSE less than the one from OLS estimators are traditionally preferred (see, for example, Stein [
34], James and Stein [
35], Hoerl and Kennard [
4], Ohtani [
36], or Hubert et al. [
37]). In addition, this measure allows us to conclude whether the raise regression is preferable, in terms of MSE, to other alternative techniques.
The structure of the paper is as follows:
Section 2 briefly describes the VIF and the raise regression, and
Section 3 extends the VIF to this methodology. Some desirable properties of the VIF are analyzed, and its asymptotic behavior is studied. It is also concluded that the VIF is invariant to data transformation.
Section 4 calculates the MSE of the raise estimator, showing that there is a minimum value that is less than the MSE of the OLS estimator.
Section 5 illustrates the contribution of this paper with two numerical examples. Finally,
Section 6 summarizes the main conclusions of this paper.
4. MSE for Raise Regression
Since the estimator
obtained from Equation (
5) is biased, it is interesting to study its Mean Square Error (MSE).
Taking into account that, for
,
it is obtained that matrix
of the expression in Equation (
5) can be rewritten as
, where
Thus, we have
, and then, the estimator of
obtained from Equation (
5) is biased unless
, which only occurs when
, that is to say, when the raise regression coincides with OLS. Moreover,
where
denotes the trace of a matrix.
In that case, the MSE for raise regression is
where
.
We can obtain the MSE from the estimated values of
and
from the model in Equation (
2).
On the other hand, once the estimations are obtained and taking into account the
Appendix C,
minimizes
. Indeed, it is verified that
; that is to say, if the goal is exclusively to minimize the MSE (as in the work presented by Hoerl et al. [
33]),
should be selected as the raising factor.
Finally, note that, if , then for all .
6. Conclusions
The Variance Inflation Factor (VIF) is one of the most applied measures to diagnose collinearity together with the Condition Number (CN). Once the collinearity is detected, different methodologies can be applied as, for example, the raise regression, but it will be required to check if the methodology has mitigated the collinearity effectively. This paper extends the concept of VIF to be applied after the raise regression and presents an expression of the VIF that verifies the following desirable properties (see García et al. [
26]):
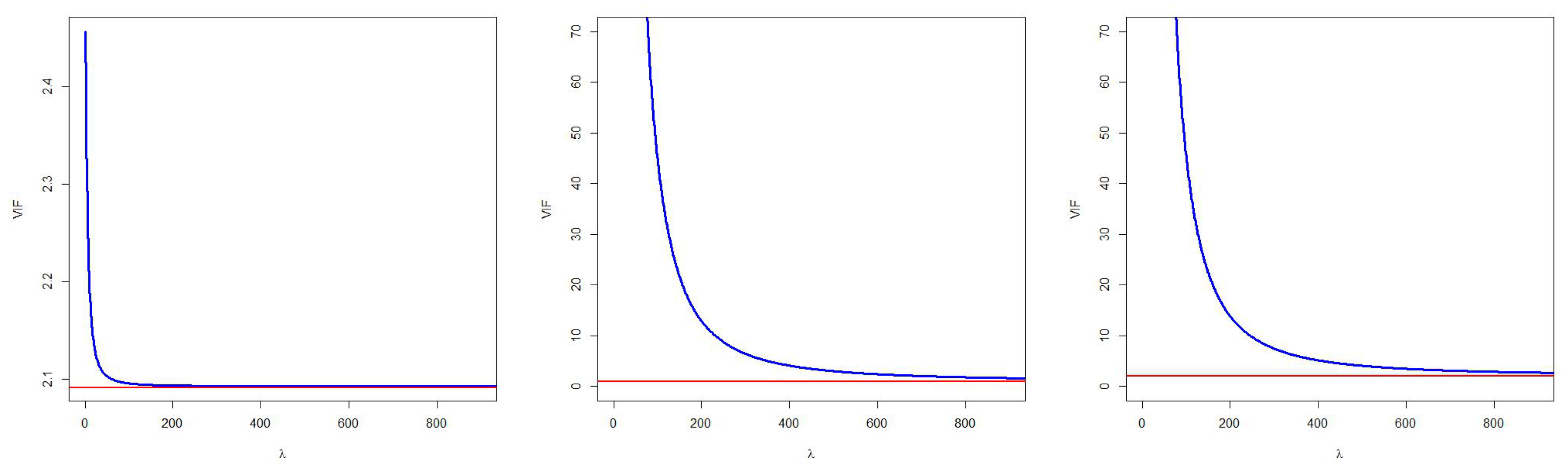
continuous in zero. That is to say, when the raising factor () is zero, the VIF obtained in the raise regression coincides with the one obtained by OLS;
decreasing as a function of the raising factor (). That is to say, the degree of collinearity diminishes as increases, and
always equal or higher than 1.
The paper also shows that the VIF in the raise regression is scale invariant, which is a very common transformation when working with models with collinearity. Thus, it yields identical results regardless of whether predictions are based on unstandardized or standardized predictors. Contrarily, the VIFs obtained from other penalized regressions (ridge regression, Lasso, and Elastic Net) are not scale invariant and hence yield different results depending on the predictor scaling used.
Another contribution of this paper is the analysis of the asymptotic behavior of the VIF associated with the raised variable (verifying that its limit is equal to 1) and associated with the rest of the variables (presenting an horizontal asymptote). This analysis allows to conclude that
It is possible to know a priori how far each of the VIFs can decrease simply by calculating their horizontal asymptote. This could be used as a criterion to select the variable to be raised, the one with the lowest horizontal asymptote being chosen.
If there is asymptote under the threshold established as worrying, the extension of the VIF can be applied to select the raising factor considering the value of that verifies for .
It is possible that the collinearity is not mitigated with any value of
. This can happen when at least one horizontal asymptote is greater than the threshold. In that case, a second variable has to be raised. García and Ramírez [
42] and García et al. [
31] show the successive raising procedure.
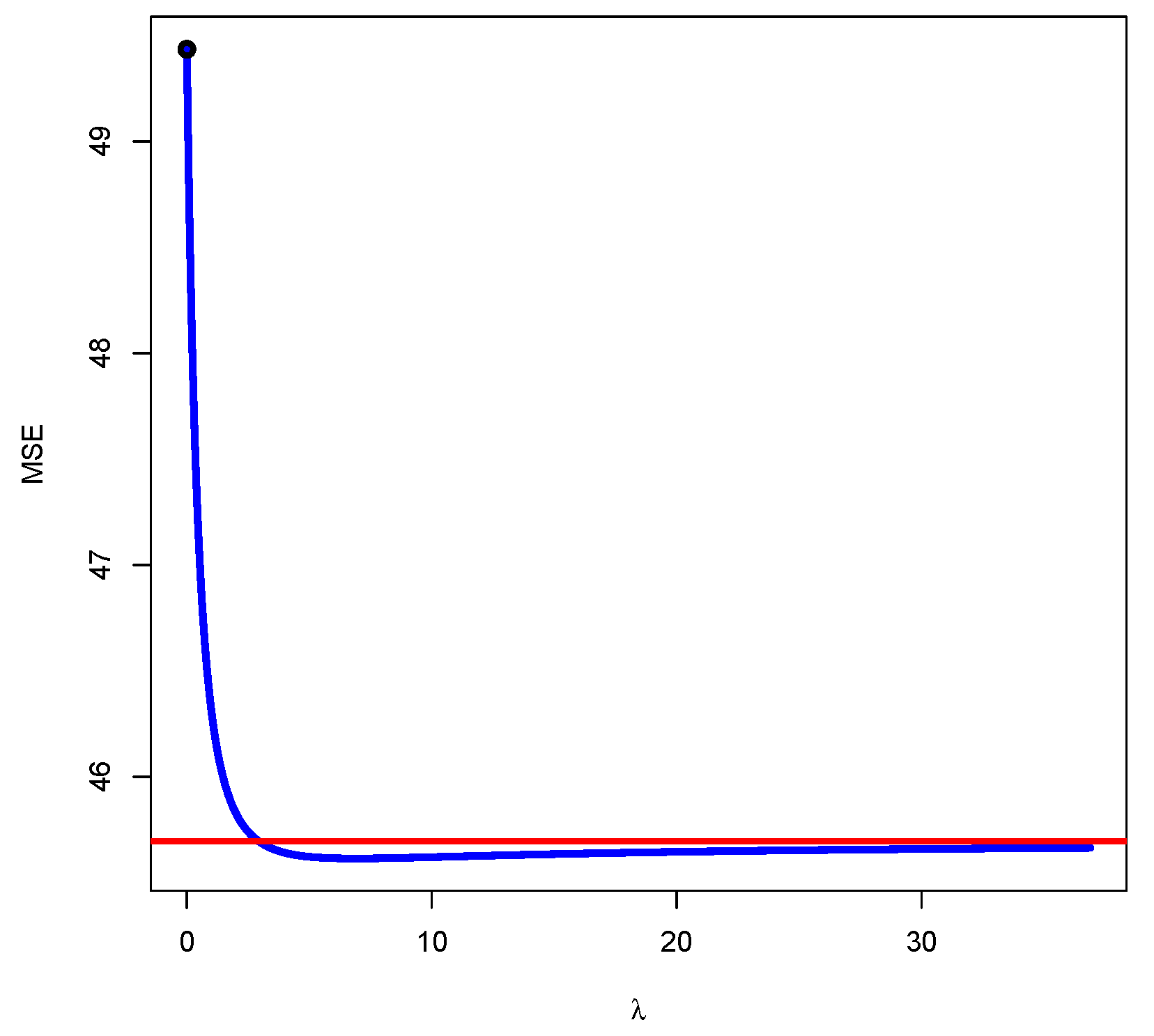
On the other hand, since the raise estimator is biased, the paper analyzes its Mean Square Error (MSE), showing that there is a value of that minimizes the possibility of the MSE being lower than the one obtained by OLS. However, it is not guaranteed that the VIF for this value of presents a value less than the established thresholds. The results are illustrated with two numerical examples, and in the second one, the results obtained by OLS are compared to the results obtained with the raise, ridge, and Lasso regressions that are widely applied to estimated models with worrying multicollinearity. It is showed that the raise regression can compete and even overcome these methodologies.
Finally, we propose as future lines of research the following questions:
The examples showed that the coefficients of variation increase after raising the variables. This fact is associated with an increase in the variability of the variable and, consequently, with a decrease of the near nonessential multicollinearity. Although a deeper analysis is required, it seems that raise regression mitigates this kind of near multicollinearity.
The value of the ridge factor traditionally applied, , leads to estimators with smaller MSEs than the OLS estimators with probability greater than 0.5. In contrast, the value of the raising factor always leads to estimators with smaller MSEs than OLS estimators. Thus, it is deduced that the ridge regression provides estimators with MSEs higher than the MSEs of OLS estimators with probability lower than 0.5. These questions seem to indicate that, in terms of MSE, the raise regression can present better behaviour than the ridge regression. However, the confirmation of this judgment will require a more complete analysis, including other aspects such as interpretability and inference.