Abstract
Accurate assessment of the efficiency of securities companies is of great significance to improve the competitiveness of companies, due to their increasingly important role in supporting economic development. As the main contribution, this paper proposes a novel efficiency estimation framework for securities companies based on data envelopment analysis (DEA), which takes into account operational risks and technical heterogeneity. First, the risk variable is incorporated in the evaluation system as an undesirable output through the setting of weak disposability. Subsequently, the meta-frontier model is introduced to consider the impact of the technical heterogeneity of different companies to improve the accuracy of the assessment. Furthermore, this article also provides the meta-frontier Malmquist model, which can be utilized to analyze in detail technological progress. Finally, the securities companies listed in the Chinese stock market were selected as samples for empirical analysis. The efficiency evaluation model for securities companies proposed in this paper will provide a reference for related evaluation issues.
1. Introduction
As the capital market comes of age, securities firms are playing an increasingly important role in sustaining market operations, maintaining a sound market environment and supporting the development of the real economy. The efficiency of these companies, therefore, will exert a direct influence on areas such as capital distribution in the market and the efficiency of investment and financing, which will subsequently affect the stability of economic development [1]. As a major indicator of the competitiveness of securities firms, operational efficiency has a direct bearing on the efficiency of China’s capital market and, further, on the operations of the national financial system as well as the rate and quality of national economic development [2]. In addition, The Chinese government announced that it will lift restrictions on foreign capital’s shareholding in Chinese securities companies from April 2020. This policy will significantly increase competition among Chinese securities companies. Against such a backdrop, research into the efficiency of Chinese securities firms is highly relevant to improving the managerial efficiency of businesses, boosting corporate competitiveness and maintaining the sustainable development of the financial system. How to scientifically evaluate the operational efficiency of China’s securities firms and enhance their competitiveness has thus become a major research topic.
Similar to many financial institutions, the efficiency of a securities company depends on various factors, such as operating income, personnel, assets and profits [3]. Without loss of generality, a securities company can make a profit by investing in personnel and assets. Thus, the performance of securities companies can be defined as the conversion efficiency of inputs and outputs, and companies with higher efficiency can be considered to have stronger competitiveness. To the best of our knowledge, research on the efficiency evaluation method has made great progress. Among them, DEA is a non-parametric method for evaluating the efficiency of multiple inputs and outputs. It has been widely used in various fields since it was proposed by Charnes, Cooper and Rhodes in 1978 [4,5]. Therefore, this paper introduces the DEA method as the basis to build a model that can be used to evaluate the efficiency of Chinese securities companies.
As research on the efficiency evaluation of securities companies, the main contributions of this paper can be summarized into the following aspects. First, the risk variable is incorporated into the evaluation system when estimating the efficiency of securities companies. Based on the weak disposability setting for undesirable output and the slack-based model (SBM), this paper constructs a novel DEA framework that includes the undesirable output. Subsequently, the meta-frontier model is introduced to consider the impact of the technology heterogeneity of different companies to improve the accuracy of the assessment. The method proposed above can be regarded as the first attempt to evaluate the efficiency of securities companies. Furthermore, the Malmquist method is also adopted to further analyze the technological progress of securities companies. Finally, based on the proposed non-parametric method, Chinese listed securities companies were selected for empirical analysis.
2. Literature Review
In recent years, studies on the competitiveness of securities companies have attracted broad attention from researchers [6,7], many of them approaching the topic from the perspective of efficiency. Zhang et al. [8] studied the technological progress parameters, efficiency and productivity of the US securities industry between 1980 and 2000 and discussed the reasons for the difference in efficiency. They suggested that the relative efficiency of the US securities industry has generally declined. Most companies fail to catch up with the production frontiers driven by a few large investment banks, which is the main reason for the decline in efficiency. Yeh, Wang and Chai [1] analyzed and compared the operational efficiency of 14 Taiwanese securities firms, taking into account the impact of financial assets. They found that by providing financial holding companies with sufficient capital and unhindered channels, the operating efficiency of securities companies can potentially be improved. Lao and Mo [9] used the Hicks–Moorsteen index to analyze the efficiency of 15 major listed Chinese securities firms in the period between 2010 and 2015. Research shows that the efficiency of the 15 listed security companies generally showed a “V” shape, and the diseconomies of scope led to a decrease in the efficiency of the security companies. Kao et al. [10] discussed the efficiency of financial holding companies in Taiwan and how financial reforms might enhance the efficiency of financial institutions. The analysis showed that the efficiency remains low in the first three years after the formation of the financial holding company. In addition, Li et al. [11] evaluated the performance and sustainability of Chinese securities firms’ collective assets management projects.
Although studies on the efficiency of securities firms can be found in the existing literature, some of their shortcomings still merit our attention. First, few studies so far have considered the impact of risk factors on efficiency. It is undeniable that securities companies, as institutions engaged in financial intermediation and financial investment, will also generate certain risks while obtaining income. Chinese securities firms have made great strides in terms of their size and total number in the past decades. However, compared with foreign-funded investment banks, they still face multiple challenges, particularly insufficiency in risk management capabilities [12]. That being the case, risk impact must be included when analyzing the efficiency of securities firms for greater reliability of results. Similar to the performance evaluation of banks, bringing the impact of risk assets into the equation will contribute to the accuracy of the efficiency evaluation of securities firms [3]. Also lacking from previous studies is the consideration of the potential technical heterogeneity across securities firms as a result of their differences in size, technology and risk management capabilities [13]. With technical heterogeneity excluded, the traditional DEA approach may produce less accurate results in efficiency evaluation [14]. Technical heterogeneity, therefore, is of great importance when using the DEA model to evaluate the efficiency of securities firms.
As for the efficiency evaluation methodology, the DEA method, as a non-parametric approach has been well-developed by scholars. The DEA method can obtain the weight of a set of optimal input and output indicators through optimization methods based on the data of the decision making units (DMUs) and then determine the efficiency [15]. The basic logic of the DEA method is to construct a set of homogeneous DMU convex combinations based on input-output data to obtain an effective production frontier. The relative efficiency of the DMU can be evaluated by judging the projection of the actual input-output data of the DMU onto the frontier [16]. Since the DEA method was proposed, it has gained the attention of many scholars and has been widely used in different fields [4,5].
The treatment of undesirable output and technical heterogeneity in the existing literature is also involved. Regarding the setting of the undesired output in the DEA method, it can be divided into strong disposability and weak disposability [17]. The first is strong disposability, which can reduce undesired output without reducing expected output [18]. In the case of strong disposability assumptions, the undesired output can be treated as input [19,20] or transform the data of the undesired output, including linear transformation, inverse transformation and exponential transformation [21,22,23]. The second is the assumption of weak disposability of undesired output, that is, to reduce undesired output requires additional input or the reduction of expected output [24,25]. It implies that the reduction of undesired output comes at the cost of expected output. Furthermore, in order to solve the problem of bias in efficiency evaluation results due to heterogeneity between DMUs, Battese et al. [26] introduced a meta-frontier model for different groups with different technologies. In a detailed analysis of technical efficiency considering technical heterogeneity, Chen and Yang [27] combined the Malmquist index and the meta-frontier model to analyze the changes of the frontier and the meta-frontier of DMUs in different groups.
3. Methodology
This section will first pin down the input and output variables for the evaluation of securities firms’ efficiency based on their operational process. An efficiency evaluation model will then be built on the basis of the SBM and the meta-frontier model, and efficiency decomposition parameters will be constructed from the perspectives of managerial and technical inefficiencies. Malmquist is also used for detailed analysis of technological changes.
3.1. Input and Output Variables
Before DEA is utilized to measure the efficiency, input and output variables should be determined. To the best of our knowledge, as a non-parametric estimation method, DEA does not require statistical correlation between input and output variables. However, it should be noted that the selection of variables cannot be arbitrary. In other words, it is generally believed that the principle to be followed is that the corresponding output can be obtained through the input of certain resources [5].
According to the actual operating process of a specific security firm, it is generally agreed that labor and capital inputs are the prerequisites for securities firms to make profits. Capital input in this paper mainly refers to securities firms’ operational expenses (E) and fixed assets (F), while labor input is represented by the number of laborers (L). Profits are generated through operations with the aforementioned inputs. As a major result of operations, the profit (P) is considered the desirable output. These input and output variables are consistent with those selected by Yeh, Wang and Chai [1]. Apart from desirable outputs, there are also undesirable outputs. The latter refers to operation-related assets of securities firms that may induce losses. According to the Measures for the Administration of the Risk Control Indicators of Securities Companies issued by China’s securities regulatory authorities, the total risk assets (R) reflect the operational risk of securities firms. This is regarded in this paper as a variable of undesirable outputs. The operational process of securities firms is shown in Figure 1.

Figure 1.
Operational process of securities firms.
3.2. Efficiency Evaluation Model
3.2.1. Efficiency Evaluation in SBM-DEA
Based on the operational process established in Figure 1, this section introduces the SBM-DEA to develop a modified efficiency evaluation model considering the impact of the risk factor. As a non-radial method, the SBM approach is better than the traditional DEA model in identifying output and input slacks, thus measuring securities firms’ operational efficiency in a more accurate manner [28,29]. For the risk variable that is regarded as an undesirable output in DEA, there are two kinds of settings, strong disposability and weak disposability [17]. The traditional DEA model assumes strong disposability in inputs and outputs. In the actual production process, however, extra inputs or reduced desirable outputs are normally required to reduce undesirable outputs [25]. Based on the weak disposability assumption of undesirable outputs put forward by Fare, Grosskopf and Hernandez-Sancho [24], an SBM-DEA based efficiency evaluation model is developed in this study as shown by model (1), which does not take into account the technical differences between different securities companies.
In model (1), suppose that there are n decision making units (DMUs), representing securities firms. λ is the coefficient of the linear input-output combination. In model (2), represents the efficiency value of the ith securities firm, of which the range is set to be [0,1], are the slack variables of input and output. The weak disposability setting of undesirable outputs is mainly reflected by , which indicates that risks and profits appear together and the change of one is proportional to that of the other. The weak disposability setting in mode (1) is consistent with that in Yu et al. [30]. The constraint refers to the returns to scale of securities firms. The value obtained through model (1) is pure technical efficiency.
To obtain the optimal value of the objective function, the non-linear model (1) can be converted into a linear program through the Charnes–Cooper transformation [4], where . As shown by model (2), the efficiency of a specific securities firm can be obtained by calculating the optimal values of variables .
3.2.2. Efficiency Evaluation in a Meta-Frontier SBM-DEA Model
The conventional DEA estimation is based on one unified reference technology. As illustrated in model (2), all DMUs are assumed to participate in the evaluation with the same technological benchmark. However, due to differences in the size and management capability between securities firms, such an assumption is usually at odds with reality [14]. Therefore, to more accurately measure the efficiency of securities firms, this paper, on the basis of the meta-frontier approach [31], proposes a modified DEA model that considers technical heterogeneity as follows. To measure technological heterogeneity, an independent technological benchmark is proposed for each group, which can be measured by a meta-frontier DEA model. This study proposes an improved meta-frontier SBM model with the weak disposability setting of undesirable output, which is shown in model (3).
In model (3), all the DMUs are divided into h groups (i.e., G1, G2,…, Gh). The superscript m means the evaluated DMU group. For example, denotes the E of DMU i in group m. represents the expected , which is the combination of h group frontiers.
The efficiency obtained through model (3) is based on the frontiers of different groups, which can be represented by GTE (group-frontier efficiency), while that obtained through model (2) is the is based on one unified reference technology, represented by MTE (meta-frontier efficiency). The range of both values is set to be [0,1]. According to O’Donnell, Rao and Battese [31], the technical gap ratio (TGR) between the group-frontier and the meta-frontier can be calculated using Equation (5). The TGR reflects the gap in production techniques; the higher the TGR is, the greater the gap.
According to Chiu et al. [32], the managerial inefficiency (represented by GMI) and the overall inefficiency (represented by MOI) could be calculated through efficiency decomposition using Equations (5) and (6) respectively. The GMI refers to a lack of efficiency caused mainly by internal factors regardless of technical heterogeneity between securities firms. Since technical diversity is unlikely to exist in a single group, such inefficiency is generally defined from a managerial perspective. The overall inefficiency level can be determined by combining the managerial inefficiency value and the technical gap ratio in Equations (4) and (5).
3.2.3. Efficiency Decomposition Model Based on Meta-Frontier-Malmquist
As a time series analysis technique, Färe et al. [33] first introduced the Malmquist index into the DEA model. Malmquist can evaluate the efficiency of different DMUs in two periods and the dynamic changes of production technology [34,35,36]. This article introduces the Malmquist index, which is used to analyze the changes in the efficiency production technology of securities companies. The DEA-Malmquist analysis framework proposed by Caves et al. [37] and Färe, Grosskopf, Lindgren and Roos [33] can analyze the Malmquist index, technical efficiency index and technological progress index in the meta-frontier. Since then, Chen and Yang [27] have combined the Malmquist index and the meta-frontier when analyzing the technical efficiency decomposition problem considering technical heterogeneity, which was used to analyze the changes of the frontier and meta-frontier of different grouped DMUs. According to Chen and Yang [27], their paper analyzes the changes in the frontier of securities companies and groups. The changes can be expressed by PTCU (pure technology catch-up) and PTRC (potential technological relative change). PTCU and PTCR can be obtained using Formula (7).
In Formula (7), and represent the efficiency of a specific DMU in period t and period t + 1 in the meta-frontier. is the efficiency obtained by replacing the data in period t with the DMU data in period t + 1. is the efficiency obtained by replacing data in period t + 1 with data in period t. Similarly, the efficiencies , , and in the group-frontier can be calculated as well.
In Formula (7), PTCU represents the pure technology catch-up index. If PTCU is greater than 1, it indicates that the gap between the actual technology of the evaluated decision unit and the meta-frontier technology tends to decrease, which means that there is a technology catch-up effect. PTRC is the potential technological relative change. This index reflects the relative movement speed of the meta-frontier. If the PTRC is less than 1, it indicates that the group-frontier moves more than the meta-frontier. That is, there is a catch-up effect of the group-frontier on the meta-frontier. If PTRC is greater than 1, it indicates that it is more difficult for the group-frontier to catch up with meta-frontier technology.
4. Empirical Analysis
4.1. Sampling and Data
To guarantee the accessibility of data, 30 securities firms listed in China’s A-share market were selected as samples for this study. They were divided, as shown by Table 1, into three groups—AA, A and BBB—according to the categorization standard set by the China Securities Regulatory Commission based on securities firms’ sizes and risk management capabilities [38]. All data were obtained from the annual report released by these listed securities firms. Related descriptive statistics are shown in Table 2.

Table 1.
Categorization of securities firms.

Table 2.
Descriptive statistics.
4.2. Securities Companies Efficiency Analysis
Based on the data of the 30 sample securities firms in the period between 2014 and 2018, the efficiency of different rated companies within different frontiers was calculated through model (2) and model (3) respectively. The results are shown in Table 3, where MTE is the meta-frontier efficiency and GTE, the group-frontier efficiency. Figure 2 shows the change of the average efficiency of different rated securities firms.

Table 3.
Group frontier efficiency (GFE) and meta-frontier efficiency (MFE) during 2014–2018.
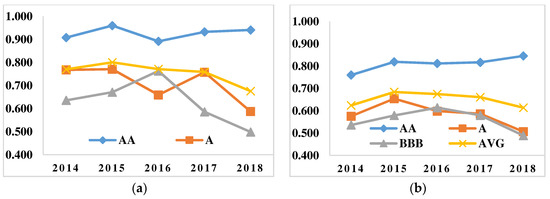
Figure 2.
The efficiency changes of the three types of securities companies in the group-frontier (a) and the meta-frontier (b).
The efficiency changes of the three types of securities companies in the group-frontier, as shown in Figure 2a, are selected to be analyzed first. It is obvious that securities companies with AA ratings had the highest efficiency, with an average efficiency of 0.926, and peaking in 2015 (0.960). Within this group, the average efficiency values of Guotai Junan, Tianfeng Securities and Merchants Securities all stood at 1 over the five years. Furthermore, the efficiency of CITIC Construction Investment Securities and Haitong Securities was above the average of this group, remaining 1 for four years. Guosen Securities had a relatively low efficiency value of just 0.752. In terms of efficiency changes, AA firms’ efficiency touched bottom in 2016 and picked up steadily in the following years.
Regarding A-rated firms’ efficiency, this changed following a trajectory identical to that of their AA counterparts during the first four years. However, the value dropped from 0.757 to 0.587 between 2017 and 2018, mainly since the efficiency value of Everbright Securities declined by 92.1% from 1 to 0.079 during the same period. This can be explained by Everbright Securities’ performance in 2018. In May 2018, Shanghai Jin Xin Investment Fund, a company jointly established by Everbright Securities’ fully-owned subsidiary Everbright Capital and Baofeng Technology, purchased the British sports rights distributor MPS for $1billion. However, the bankruptcy of MPS in October the same year led to a 96.57% year-on-year decrease of Everbright Securities’ net profit in 2018 [39]. Among A firms, ChinaLin Securities, Shenwan Hongyuan Securities and China Galaxy were all considered efficient in the DEA model.
Different from the efficiency change trajectories of A and AA firms, the efficiency of BBB companies surged in the first two years and overtook that of their A counterparts in 2016, with the average efficiency value being 0.763. However, it dipped during the last two years, standing at only 0.499 in 2018. Judged by the efficiency values, among BBB firms, Hongta Securities and GF Securities were both efficient in the DEA model over the studied period.
It is worth noting that the efficiency changes of the 30 selected firms, reflected by AVG in Figure 2a, was stable between 2014 and 2018. However, their overall efficiency level remained relatively low, the average values being 0.652. This means that efficiency varies substantially among these securities firms. The efficiency of these firms increased slightly between 2014 and 2015, but was then on the decline in the following three years. On a different note, from 2014, China’s stock market experienced a continuing increase until June 2015, when the market disaster hit, and then subsequently plunged. Fluctuations were seen again in 2018 due to China-US trade disputes. That being the case, the efficiency of the listed securities firms was generally consistent with the performance of the stock market.
Figure 2b illustrates the changing trend of the efficiency of a securities company without considering technological differences. The efficiency of the AA companies is still in a leading position. It can be seen that the efficiency showed an upward trend during 2013–2018, with an average efficiency of 0.811. From 2014 to 2015, the efficiency of both the BBB and A companies increased slightly. During 2016–2018, the efficiency of these two types of companies gradually decreased.
From the perspective of the average efficiency of all companies, the overall change trend of meta-frontier efficiency is similar to that of group-frontier. It is notable that the magnitude of the efficiency change of the three types of companies in the meta-frontier is significantly weaker than that in the group-frontier. It can be clearly found from Table 3 that there is a significant difference between the efficiency in the group-frontier and the meta-frontier. This is mainly because when the group-frontier is adopted as a reference, the efficiency obtained reflects the level of technology and management in the existing conditions of securities companies of the same category. However, when using the meta-frontier as a benchmark, efficiency reflects the level of efficiency under the most advanced management and technical conditions. In the following, the differences in efficiency and technical conditions will be further analyzed.
4.3. Efficiency Decomposition Analysis
In order to further analyze the reasons for the non-efficiency of securities companies, according to Equations (4)–(6), the TGR, GMI and MOI of securities companies can be measured. The MOI of 30 securities companies during the period is shown in Table 4. Figure 3 is the average TGR and GMI of securities companies from 2014 to 2018.

Table 4.
Overall inefficiency (MOI) of securities firms.
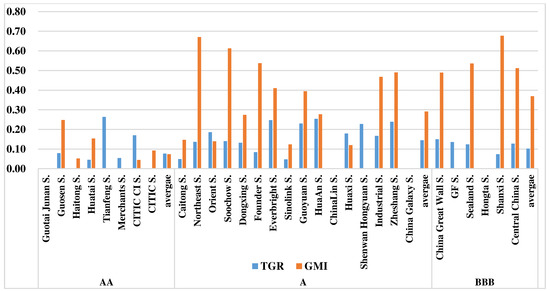
Figure 3.
Technical gap ratio (TGR) and managerial inefficiency (GMI) of the three groups.
The MOI of AA firms was 0.150, lower than A firms (0.436) and BBB firms (0.471). Among all the companies, Guotai Junan Securities, ChinaLin Securities, Hongta Securities and China Galaxy Securities all had 0 overall inefficiency, indicating that they were all efficient managerially and technically in the group-frontier. TGR reflects the discrepancy in technical capabilities—the higher the TGR, the more a firm’s technical strength differs from the overall level. According to the results, the TGR of AA firms was 0.08, lower than BBB firms (0.1) and A firms (0.14). This reflects that AA companies’ overall technical capabilities are higher than those of the other two groups. BBB and A firms have an improvement scope of 10% and 14% respectively in this regard. Within the AA group, Haitong Securities and Guotai Junan Securities both had a TGR of 0, indicating that their technical capabilities had reached the meta-frontier level. In particular, the managerial inefficiency value of Guotai Junan Securities was 0, which means that its managerial capabilities are also in a leading position. The efficiency of Tianfeng Securities and Merchants Securities was mainly influenced by technical factors as they both had 0 managerial inefficiency. Their technical capabilities need to be further strengthened.
Among A firms, ChinaLin Securities and China Galaxy Securities both had a TGR of 0 and their managerial inefficiency was 0 as well. This indicates that their technical and managerial capabilities are the greatest in the group, with others all having a TGR of more than 0.05. In particular, Everbright Securities and HuaAn Securities both had a TGR of 0.25, and Zheshang Securities and Shenwan Hongyuan Securities had a TGR of 0.24 and 0.23 respectively. There is still significant room for technical improvement for these companies. Within the same group, other than Orient Securities, Huaxi Securities and Shenwan Hongyuan Securities, all the others demonstrated a managerial inefficiency value higher than the TGR. Shenwan Hongyuan Securities’ inefficiency was mainly influenced by the technical gap. A firms’ average managerial inefficiency was 0.29 and the TGR was only 0.14. Among BBB firms, only Hongta Securities had 0 technical inefficiency and managerial inefficiency. All the others had similar TGR values of around 0.1. In terms of managerial inefficiency, BBB firms’ average level was 0.37, significantly higher than that of the other two groups. Within this group, Shanxi Securities’ managerial inefficiency value was 0.68, higher than that of all others, followed by Sealand Securities, Central China securities and China Great Wall Securities. Noticeably, GF Securities’ managerial inefficiency value was 0.
4.4. Analysis of Technical Changes
In order to evaluate the dynamic changes in technology of China’s listed securities companies, the PTCU and PTRC can be obtained using Formula (7), and the results are shown in Table 5.

Table 5.
Potential technology relative change (PTRC) and pure technology catch-up (PTCU) of securities companies.
From the perspective of technology catch-up, BBB companies performed best from 2013 to 2018, with a PTCU value of 1.1657. It is worth mentioning that the PTCU value of all BBB companies is greater than or equal to 1. Among them, the PTCU value of GF Securities is 1.687, which is at the highest. This could reflect the continuous increase of innovation and risk management level of this type of securities companies during the research period, which makes the gap between their technology level and those of the other two types of companies continue to decrease. Regarding the relative change of potential technology, the PTRC value of BBB companies is 0.891. Except for Hongta Securities, the rest of the companies are less than 1, indicating that the group-frontier movement speed of the companies in this group is faster than that of their meta-frontier counterparts, and there is a technology catch-up effect. This result also reflects the continuous improvement of the technical and risk management level of BBB rated companies during the research period.
During the research period, the overall technical level of A-rated companies showed a growth trend, with a PTCU value of 1.165. However, several of these companies have PTCU values less than 1, such as Northeast Securities, Soochow Securities and West China Securities. This phenomenon shows that the gap between these companies in the technical and risk management level during the research period has widened from the industry level. The PTRC of class A companies is 1.010, which is only slightly larger than 1, which shows that the movement level of the group-frontier of the group A companies is similar to that of the common front.
Different from the other two types of companies, AA companies have different performances in catching up with technology. Among them, China Merchants Securities and CITIC Construction Investment performed best, with PTCU values of 1.367 and 1.407, respectively. The two companies mentioned above have in common that they belong to a large state-owned financial holding group. This means that these two companies have advantages in talent recruitment and enterprise resource investment, which can explain the excellent performance of these two companies.
The PTCU of Haitong Securities, Cathay Securities and CITIC Securities is 1, which is consistent with the value of the TGR, which shows that these three securities companies can be regarded as leading companies in the securities industry. The PTCU of Tianfeng Securities and Guosen Securities is less than 1, indicating that the technology of these two companies has decreased compared with other companies in the AA group during the study period. From the perspective of PTRC, all AA-type companies are greater than 1, reflecting that the group production frontier movement is smaller than the meta production frontier. In fact, the overall technical capabilities of AA companies are already at a relatively high level, so compared with the other two companies, their technological development potential is relatively narrow.
4.5. Findings and Suggestions
In this article, 30 listed securities companies in China were selected as samples for empirical analysis. The main findings and corresponding suggestions are as follows. (1) The efficiency change in the meta-frontier is consistent with the efficiency change trend in the group-frontier. However, the efficiency change in the group-frontier is greater, indicating that the differentiation degree of the efficiency evaluation of different securities companies is higher than that of the meta-frontier model. There is a clear difference between the group-frontier efficiency value and the meta-frontier efficiency value. This difference could reflect the technology gap between the securities companies. Therefore, for the three types of companies, it is necessary to increase technical investment and improve technical level. (2) For AA companies, the overall efficiency level and technology are in the leading position in the industry, but the speed of its technological development is relatively slower than that of the other two companies, so it is necessary to continue technological innovation and maintain a leading position. Different with the efficiency fluctuations of the AA companies, the efficiency of A companies decreased during the period. The gap between the technology of this type of company and the frontier level is higher than that of the other two types of companies, indicating that the technology level of A-type companies has greater room for improvement. From the perspective of technological catch-up, the technological development of A-type companies is close to the industry level. (3) For BBB companies, the average efficiency of the group-frontier and meta-frontier during the research period is lower than that of the other two companies. From the perspective of efficiency decomposition, the technology catch-up performance of BBB companies is the best, which means that the technical level was significantly improved during the research period. However, from the perspective of management inefficiency, the average value of the management inefficiency of BBB companies is significantly higher than that of the other two groups, indicating that the management level is relatively weak. Therefore, for BBB companies to achieve efficiency improvement, they need to further strengthen their investment in technology, maintain the trend of technology catch-up, and at the same time strengthen their governance capabilities.
5. Conclusions
This paper proposes an improved DEA method, which takes the risk of securities companies as one of the influencing factors in the modelling process and builds a risk-adjusted efficiency evaluation model of securities companies. The model can analyze the efficiency in the meta-frontier and group-frontier separately, and based on the efficiency in the different frontiers, it can present the technology gap and management inefficiency of the securities company. In order to further analyze the technical changes of various types of securities companies, the meta-frontier Malmquist model is used to discuss the catch-up situation of securities companies during the research period. This paper proposes that the improved DEA model will more accurately evaluate the efficiency and technological development of securities companies and provide a model reference for the efficiency evaluation of securities companies.
Generally, three further research directions can be drawn from this research. Firstly, on the basis of analyzing the efficiency of considering the impact of risks, quantitatively analyze the risk management capabilities of securities companies is necessary. Secondly, it would be interesting to further explore the impact of risk management on the operating efficiency of securities companies. Thirdly, some suitable methods could be proposed to select data for estimating efficiency in the big data environment.
Author Contributions
conceptualization, J.Y.; data curation, Y.S.; funding acquisition, T.X. and J.Y.; methodology, T.X.; resources, T.X.; visualization, Y.S.; writing—original draft, Y.S.; writing—review and editing, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China grant number 71671125.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
To give a clear description, all the acronyms mentioned in this paper are listed in the following nomenclatures.
| CNY | Chinese Yuan |
| DEA | Data envelopment analysis |
| DMU | Decision-making unit |
| GFE | Efficiency in group-frontier |
| MFE | Efficiency in meta-frontier |
| MOI | Overall inefficiency |
| TGR | Technical gap ratio |
| GMI | Managerial inefficiency |
| PTCU | Pure technology catch-up |
| PTCR | Potential technological relative change |
| SBM | Slack-based Model |
References
- Yeh, C.-P.; Wang, K.-M.; Chai, K.-C. Measuring the efficiency of securities companies by corporate governance in a financial holding and non-financial holding system. Expert Syst. Appl. 2010, 37, 4671–4679. [Google Scholar] [CrossRef]
- Serifsoy, B. Stock exchange business models and their operative performance. J. Bank. Financ. 2007, 31, 2978–3012. [Google Scholar] [CrossRef]
- Yu, A.Y.; Shao, Y.L.; You, J.X.; Wu, M.G.; Xu, T. Estimations of operational efficiencies and potential income gains considering the credit risk for China?s banks. J. Oper. Res. Soc. 2019, 70, 2153–2168. [Google Scholar] [CrossRef]
- Cooper, W.W.; Seiford, L.M.; Zhu, J. Handbook on Data Envelopment Analysis; Springer Science & Business Media: Berlin, Germany, 2011; Volume 164. [Google Scholar]
- Zhu, J. Data Envelopment Analysis: A Handbook of Models and Methods; Springer: Boston, MA, USA, 2015; Volume 221. [Google Scholar]
- Piansoongnern, O.; Anurit, P. A Global Competitiveness Study of Thai Securities Industry: A Case Study of Factors Influencing Investors’ Loyalty to Securities Companies in Bangkok. Glob. J. Flex. Syst. Manag. 2007, 8, 1–16. [Google Scholar] [CrossRef]
- Qian, L.; Lou, L.; Jing, W. Research on Competitiveness of Listed Security Companies in China; Springer: Singapore, 2017. [Google Scholar]
- Zhang, W.D.; Zhang, S.; Luo, X. Technological progress, inefficiency, and productivity growth in the US securities industry, 1980–2000. J. Bus. Res. 2006, 59, 589–594. [Google Scholar] [CrossRef]
- Lao, G.; Mo, B. Study on the Efficiency and Total Factor Productivity of China’s Securities Companies—Based on Hicks-Moorsteen TFP Index Method. Technol. Invest. 2018, 9, 52–67. [Google Scholar] [CrossRef][Green Version]
- Kao, M.-C.; Lin, C.-T.; Xu, L. Do Financial Reforms Improve the Performance of Financial Holding Companies? The Case of Taiwan. Int. Rev. Financ. 2012, 12, 491–509. [Google Scholar] [CrossRef]
- Li, C.; Han, L.; Zhang, X. DEA-based performance evaluation and sustainable research on securities firms’ CAMS. In Proceedings of the 2nd International Conference on Information Science and Engineering, Hangzhou, China, 4–6 December 2010; IEEE: Hangzhou, China, 2011. [Google Scholar]
- Chao, L.; Yuan-rui, L.; Chao, J.; Yujie, M.; Chenqi, L.; Qiwei, X. Research on Systematic Risk Measurement and Evolution Characteristics of Chinas Securities Companies—Empirical Data from 20 Listed Securities Companies. Chin. J. Manag. Sci. 2019, 27, 11–22. [Google Scholar]
- Liu, X.; Sun, J.; Yang, F.; Wu, J. How ownership structure affects bank deposits and loan efficiencies: An empirical analysis of Chinese commercial banks. Ann. Oper. Res. 2018. [Google Scholar] [CrossRef]
- Ding, T.; Chen, Y.; Wu, H.Q.; Wei, Y.Q. Centralized fixed cost and resource allocation considering technology heterogeneity: A DEA approach. Ann. Oper. Res. 2018, 268, 497–511. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Li, F.; Emrouznejad, A.; Yang, G.L.; Li, Y.J. Carbon emission abatement quota allocation in Chinese manufacturing industries: An integrated cooperative game data envelopment analysis approach. J. Oper. Res. Soc. 2019. [Google Scholar] [CrossRef]
- Halkos, G.; Petrou, K.N. Treating undesirable outputs in DEA: A critical review. Econ. Anal. Policy 2019, 62, 97–104. [Google Scholar] [CrossRef]
- Fare, R.; Grosskopf, S.; Pasurka, C. Effects on Relative Efficiency in Electric-Power Generation Due to Environmental Controls. Resour. Energy 1986, 8, 167–184. [Google Scholar] [CrossRef]
- Tyteca, D. Linear programming models for the measurement of environmental performance of firms—Concepts and empirical results. J. Prod. Anal. 1997, 8, 183–197. [Google Scholar] [CrossRef]
- Macpherson, A.J.; Principe, P.P.; Shao, Y. Controlling for exogenous environmental variables when using data envelopment analysis for regional environmental assessments. J. Environ. Manag. 2013, 119, 220–229. [Google Scholar] [CrossRef]
- Scheel, H. Undesirable outputs in efficiency valuations. Eur. J. Oper. Res. 2001, 132, 400–410. [Google Scholar] [CrossRef]
- Seiford, L.M.; Zhu, J. Modeling undesirable factors in efficiency evaluation. Eur. J. Oper. Res. 2002, 142, 16–20. [Google Scholar] [CrossRef]
- Zhou, Z.X.; Xu, G.C.; Wang, C.; Wu, J. Modeling undesirable output with a DEA approach based on an exponential transformation: An application to measure the energy efficiency of Chinese industry. J. Clean. Prod. 2019, 236, 11. [Google Scholar] [CrossRef]
- Fare, R.; Grosskopf, S.; Hernandez-Sancho, F. Environmental performance: An index number approach. Resour. Energy Econ. 2004, 26, 343–352. [Google Scholar] [CrossRef]
- Yang, H.L.; Pollitt, M. The necessity of distinguishing weak and strong disposability among undesirable outputs in DEA: Environmental performance of Chinese coal-fired power plants. Energy Policy 2010, 38, 4440–4444. [Google Scholar] [CrossRef]
- Battese, G.E.; Prasada Rao, D.S.; O’Donnell, C.J. A metafrontier production function for estimation of technical efficiencies and technology gaps for firms operating under different technologies. J. Prod. Anal. 2004, 21, 91–103. [Google Scholar] [CrossRef]
- Chen, K.-H.; Yang, H.-Y. Extensions of the metafrontier Malmquist productivity index: An empirical study with cross-country macro-data. Taiwan Econ. Rev. 2008, 36, 551–588. [Google Scholar]
- Tone, K. A slacks-based measure of super-efficiency in data envelopment analysis. Eur. J. Oper. Res. 2002, 143, 32–41. [Google Scholar] [CrossRef]
- Wang, C.-N.; Luu, Q.-C.; Nguyen, T.-K.-L.; Day, J.-D. Assessing Bank Performance Using Dynamic SBM Model. Mathematics 2019, 7, 73. [Google Scholar] [CrossRef]
- Yu, A.Y.; You, J.X.; Zhang, H.; Ma, J.J. Estimation of industrial energy efficiency and corresponding spatial clustering in urban China by a meta-frontier model. Sustain. Cities Soc. 2018, 43, 290–304. [Google Scholar] [CrossRef]
- O’Donnell, C.J.; Rao, D.S.P.; Battese, G.E. Metafrontier frameworks for the study of firm-level efficiencies and technology ratios. Empir. Econ. 2008, 34, 231–255. [Google Scholar] [CrossRef]
- Chiu, C.R.; Liou, J.L.; Wu, P.I.; Fang, C.L. Decomposition of the environmental inefficiency of the meta-frontier with undesirable output. Energy Econ. 2012, 34, 1392–1399. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Lindgren, B.; Roos, P. Productivity developments in Swedish hospitals: A Malmquist output index approach. In Data Envelopment Analysis: Theory, Methodology, and Applications; Springer: Berlin, Germany, 1994; pp. 253–272. [Google Scholar]
- Lv, W.D.; Hong, X.X.; Fang, K.N. Chinese regional energy efficiency change and its determinants analysis: Malmquist index and Tobit model. Ann. Oper. Res. 2015, 228, 9–22. [Google Scholar] [CrossRef]
- Perez, K.; Gonzalez-Araya, M.C.; Iriarte, A. Energy and GHG emission efficiency in the Chilean manufacturing industry: Sectoral and regional analysis by DEA and Malmquist indexes. Energy Econ. 2017, 66, 290–302. [Google Scholar] [CrossRef]
- Feng, C.; Wang, M. Analysis of energy efficiency and energy savings potential in China’s provincial industrial sectors. J. Clean. Prod. 2017, 164, 1531–1541. [Google Scholar] [CrossRef]
- Caves, D.W.; Christensen, L.R.; Diewert, W.E. The economic theory of index numbers and the measurement of input, output, and productivity. Econom. J. Econom. Soc. 1982, 50, 1393–1414. [Google Scholar] [CrossRef]
- China Securities Regulatory Commission Announced the Classification Results of Securities Companies in 2019. Available online: https://www.sac.net.cn/hyfw/hydt/201907/t20190729_139577.html (accessed on 26 July 2019).
- Wang, Y.R. Everbright Securities 2018 Net Profit of 103 Million Yuan, down 96.57%. Available online: http://news.cnstock.com/news,bwkx-201903-4355328.htm (accessed on 27 March 2019).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).