A New Kind of Parallel Natural Difference Method for Multi-Term Time Fractional Diffusion Model
Abstract
1. Introduction
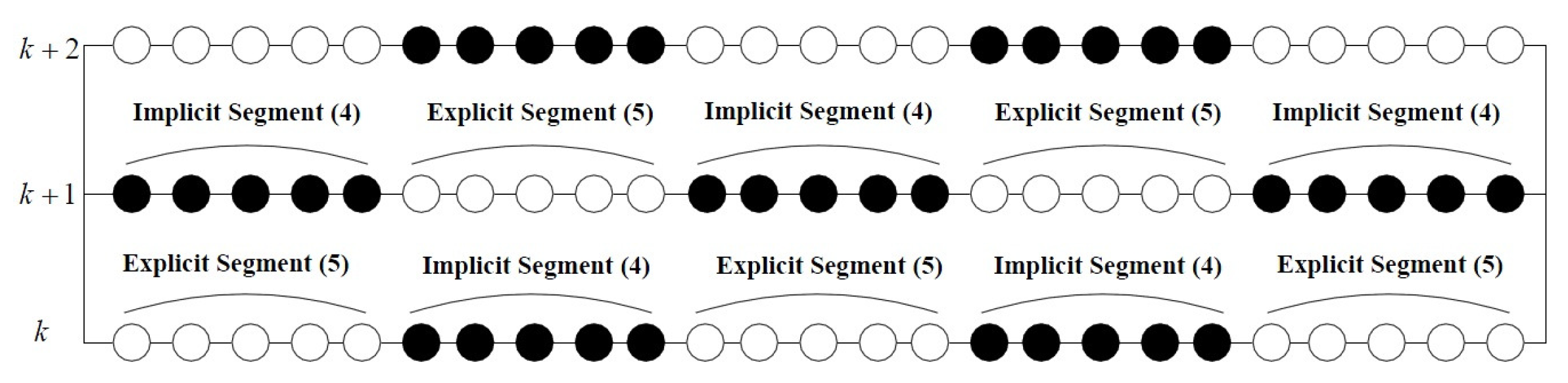
2. Construction of PASE-I Parallel Difference Scheme
3. Theoretical Analysis of PASE-I Difference Scheme
3.1. The Existence and Uniqueness of PASE-I Scheme’s Solution
3.2. Stability of PASE-I Scheme
3.3. Convergence of PASE-I Scheme
4. PASI-E Parallel Difference Scheme
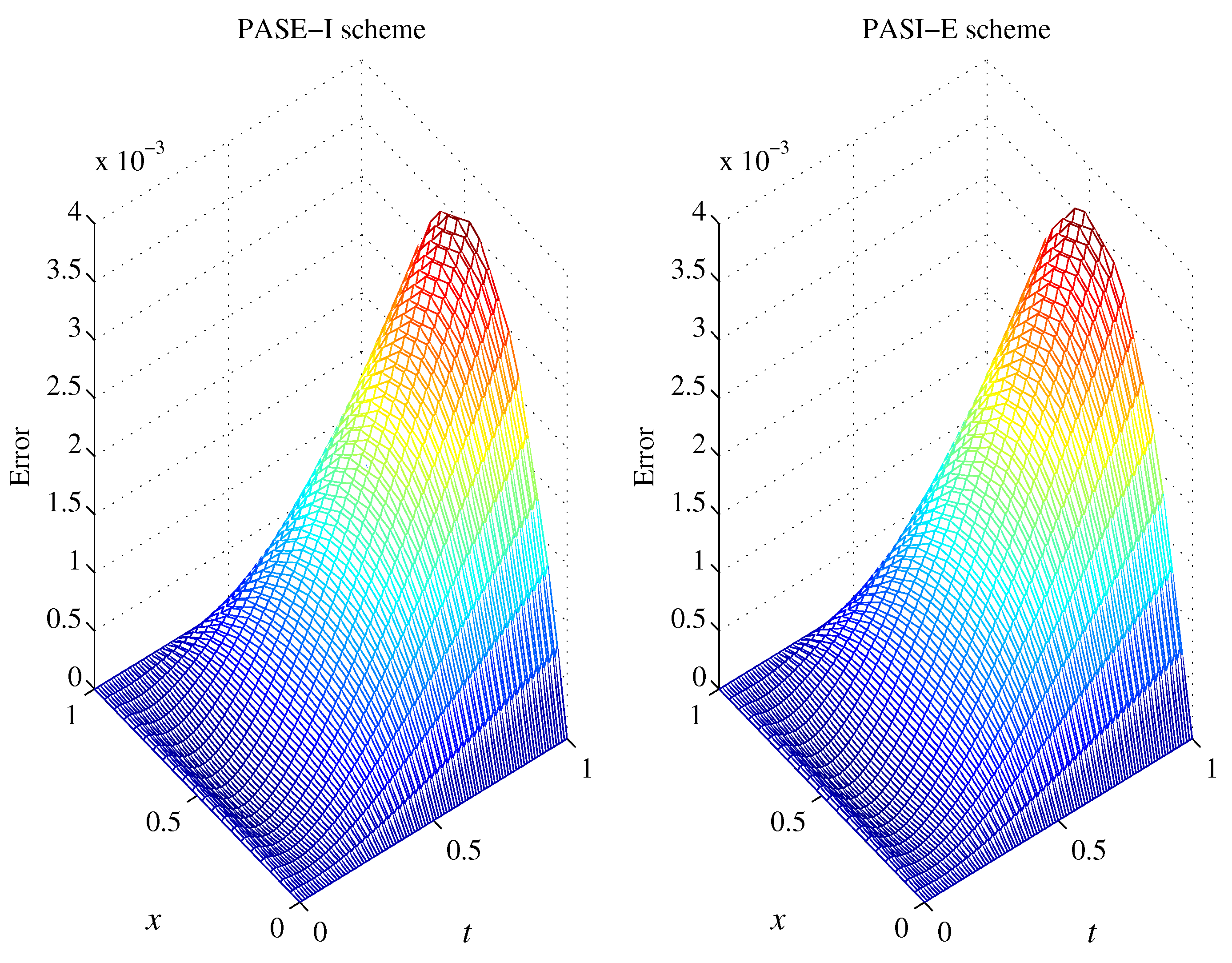
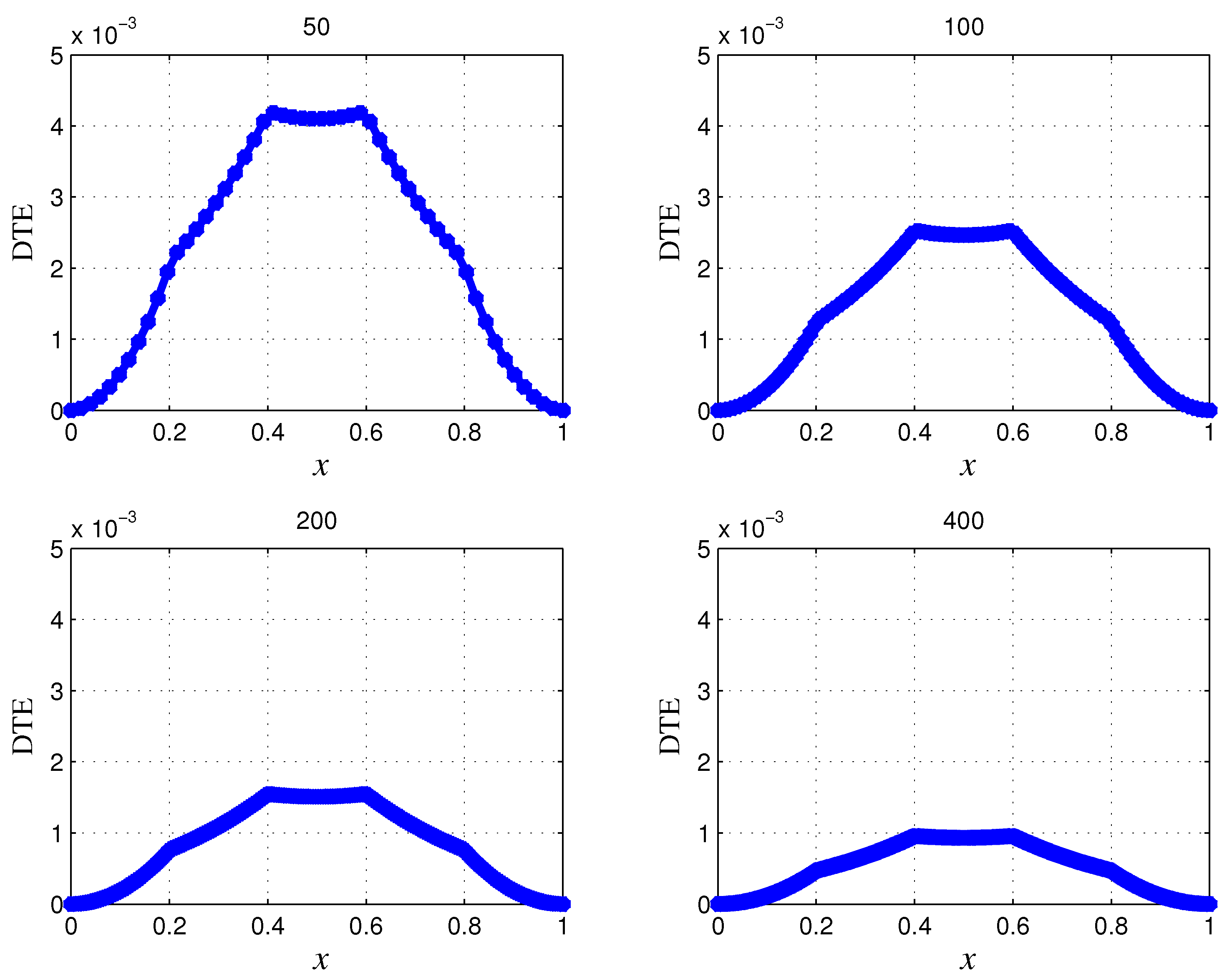
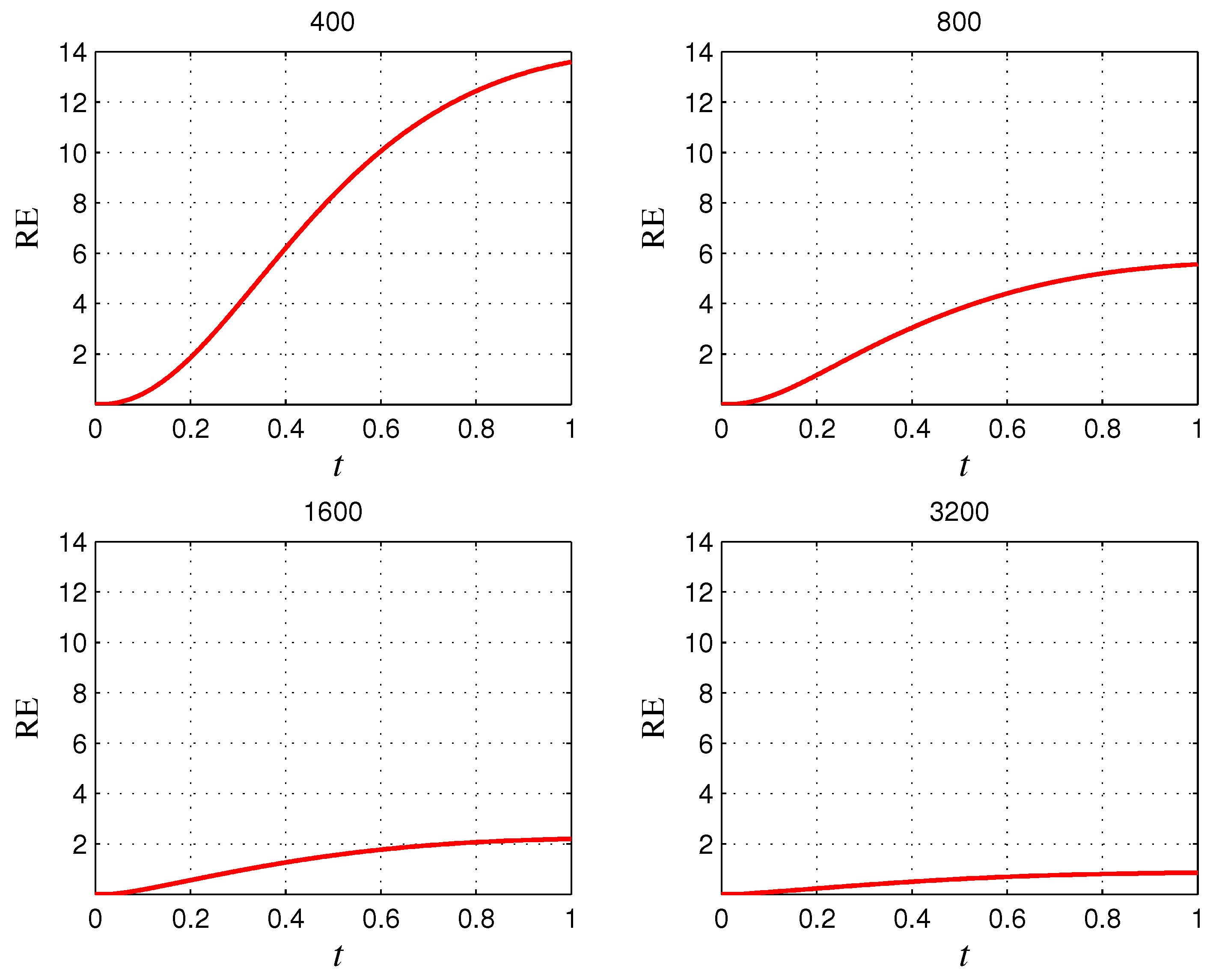
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers: Volume II: Applications; Higher Education Press: Beijing, China, 2013. [Google Scholar]
- Chen, W.; Sun, H.G. Fractional Differential Equations and Statistical Models of Anomalous Diffusion; Science Press: Beijing, China, 2017. (In Chinese) [Google Scholar]
- Sabatier, J.; Agrawal, O.P.; Machado, J.A.T. (Eds.) Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering; Beijing World Publishing Corporation: Beijing, China, 2014. [Google Scholar]
- Tejado, I.; Emiliano, P.; Duarte, V. Fractional Derivatives for Economic Growth Modelling of the Group of Twenty: Application to Prediction. Mathematics 2020, 8, 50. [Google Scholar] [CrossRef]
- Guo, B.L.; Pu, X.K.; Huang, F.H. Fractional Partial Differential Equations and Their Numerical Solutions; Science Press: Beijing, China, 2015. [Google Scholar]
- Liu, F.W.; Zhuang, P.H.; Liu, Q.X. Numerical Solutions of Fractional Partial Differential Equations and Their Application; Science Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Sun, Z.Z.; Gao, G.H. Finite Difference Methods for Fractional Differential Equations; Science Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Luchko, Y. Initial-boundary-value problems for the generalized multi-term time-fractional diffusion equation. Math. Anal. Appl. 2011, 374, 538–548. [Google Scholar] [CrossRef]
- Li, Z.Y.; Liu, Y.K.; Yamamoto, M. Initial-boundary value problems for multi-term time-fractional diffusion equations with positive constant coefficients. Appl. Math. Comput. 2015, 257, 381–397. [Google Scholar] [CrossRef]
- Sin, C.S.; Ri, G.I.; Kim, M.C. Analytical solutions to multi-term time-space Caputo-Riesz fractional diffusion equations on an infinite domain. Adv. Differ. Equ. 2017, 306. [Google Scholar] [CrossRef]
- Ye, H.; Liu, F.W.; Anh, V.; Turner, I. Maximum principle and numerical method for the multi-term time-space Riesz-Caputo fractional differential equations. Appl. Math. Comput. 2014, 227, 531–540. [Google Scholar] [CrossRef]
- Jin, B.; Lazarov, R.; Liu, Y.; Zhou, Z. The Galerkin finite element method for a multi-term time-fractional diffusion equation. J. Comput. Phys. 2015, 281, 825–843. [Google Scholar] [CrossRef]
- Shiralashetti, S.C.; Deshi, A.B. An efficient Haar wavelet collocation method for the numerical solution of multi-term fractional differential equations. Nonlinear Dynam. 2016, 83, 293–303. [Google Scholar] [CrossRef]
- Li, M.; Huang, C.M.; Ming, W.Y. Mixed finite-element method for multi-term time-fractional diffusion and diffusion-wave equations. Comp. Appl. Math. 2018, 37, 2309–2334. [Google Scholar] [CrossRef]
- Wang, F.L.; Fan, M.Z.; Zhan, Y.M.; Shi, Z.G.; Shi, D.Y. High accuracy analysis of anisotropic linear triangular element for multi-term time fractional diffusion equations. Math. Numer. Sin. 2018, 40, 299–312. (In Chinese) [Google Scholar]
- Wei, Y.B.; Zhao, Y.M.; Tang, Y.F.; Wang, F.; Shi, Z.; Li, K. High-accuracy analysis of finite-element method for two-term mixed time fractional diffusion-wave equations. Sci. Scinica Inform. 2018, 48, 871–887. (In Chinese) [Google Scholar] [CrossRef]
- Liu, F.W.; Meerschaert, M.M.; Mcgough, R.J.; Zhuang, P.; Liu, Q. Numerical methods for solving the multi-term time-fractional wave-diffusion equation. Fract. Calcul. Appl. Anal. 2013, 16, 9–25. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.H.; Sun, Z.Z. Efficient and stable numerical methods for multi-term time fractional sub-diffusion equations. East Asian J. Appl. Math. 2014, 4, 242–266. [Google Scholar] [CrossRef]
- Dehghan, M.; Safarpoor, M.; Abbaszadeh, M. Two high-order numerical algorithms for solving the multi-term time fractional diffusion-wave equations. Comp. Appl. Math. 2015, 290, 174–195. [Google Scholar] [CrossRef]
- Gao, G.H.; Alikhanov, A.A.; Sun, Z.Z. The temporal second order difference schemes based on the interpolation approximation for solving the time multi-term and distributed-order fractional sub-diffusion equations. J. Sci. Comput. 2017, 73, 93–121. [Google Scholar] [CrossRef]
- Yang, X.Z.; Shao, J.; Sun, S.Z. A class of efficient difference methods for the double-term time fractional sub-diffusion equation. Acta Math. Appl. Sin. 2019, 42, 492–505. (In Chinese) [Google Scholar]
- Zhou, Y.L. Difference schemes with intrinsic parallelism for quasi-linear parabolic systems. Sci. China (Ser. A) 1997, 40, 270–278. [Google Scholar] [CrossRef]
- Zhang, B.L.; Yuan, G.X.; Liu, X.P.; Chen, J. Parallel Finite Difference Methods for Partial Differential Equations; Science Press: Beijing, China, 1994. (In Chinese) [Google Scholar]
- Petter, B.; Mitchell, L. Parallel Solution of Partial Differential Equations; Springer: New York, NY, USA, 2000. [Google Scholar]
- Zhang, B.L.; Gu, T.X.; Mo, Z.Y. Principles and Methods of Numerical Parallel Computation; National Defense Industry Press: Beijing, China, 1999. (In Chinese) [Google Scholar]
- Yuan, G.W.; Sheng, Z.Q.; Hang, X.D. Calculation Methods of Diffusion Equations; Science Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Jiang, Y.L. New Methods for Engineering Mathematics; Higher Education Press: Beijing, China, 2013. (In Chinese) [Google Scholar]
- Wang, H.; Wang, K.; Sircar, T. A direct O(Nlog2N) finite difference method for fractional diffusion equations. J. Comput. Phys. 2010, 229, 8095–8104. [Google Scholar] [CrossRef]
- Diethelm, K. An efficient parallel algorithm for the numerical solution of fractional differential equations. Fract. Calcul. Appl. Anal. 2011, 14, 475–490. [Google Scholar] [CrossRef]
- Wang, H.; Basu, T.S. A fast finite difference method for two-dimensional space-fractional diffusion equations. SIAM J. Sci. Comput. 2012, 34, 2444–2458. [Google Scholar] [CrossRef]
- Gong, C.Y.; Bao, W.M.; Tang, G.J. A parallel algorithm for the Riesz fraction reaction-diffusion equation with explicit finite difference method. Fract. Calcul. Appl. Anal. 2013, 16, 654–669. [Google Scholar]
- Sweilam, N.H.; Moharram, H.; Moniem, N.K.A.; Ahmed, S. A parallel Crank-Nicolson finite difference method for time-fractional parabolic equation. J. Numer. Math. 2014, 22, 363–382. [Google Scholar] [CrossRef]
- Wang, Q.L.; Liu, J.; Gong, C.Y.; Tang, X.; Fu, G.; Xing, Z. An efficient parallel algorithm for Caputo fractional reaction-diffusion equation with implicit finite-difference method. Adv. Differ. Equ. 2016, 207. [Google Scholar] [CrossRef]
- Yang, X.Z.; Dang, X. A new parallel difference algorithm based on improved alternating segment Crank-Nicolson scheme for time fractional reaction-diffusion equation. Adv. Differ. Equ. 2019, 417. [Google Scholar] [CrossRef]
- Fu, H.F.; Wang, H. A preconditioned fast parareal finite difference method for space-time fractional partial differential equation. J. Sci. Comput. 2018, 78, 1724–1743. [Google Scholar] [CrossRef]
- Liu, W. Actual Combat Matlab Parallel Programming; Beihang University Press: Beijing, China, 2012. (In Chinese) [Google Scholar]
- Chi, X.B.; Wang, Y.W.; Wang, Y.; Liu, F. Parallel Computing and Implementation Technology; Science Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
| M | N | PASE-I Scheme | PASI-E Scheme | ||||
|---|---|---|---|---|---|---|---|
| 0.4 | 0.4 | 50 | 132 | 1.960988 | —— | 1.933065 | —— |
| 100 | 316 | 4.750145 | 2.045537 | 4.715343 | 2.035455 | ||
| 200 | 752 | 1.175639 | 2.014526 | 1.171268 | 2.009290 | ||
| 400 | 1788 | 2.927383 | 2.005761 | 2.921901 | 2.003092 | ||
| 800 | 4254 | 7.293185 | 2.004990 | 7.286329 | 2.003643 | ||
| 0.5 | 0.5 | 50 | 184 | 1.808959 | —— | 1.783177 | —— |
| 100 | 464 | 4.441176 | 2.026146 | 4.408679 | 2.016032 | ||
| 200 | 1169 | 1.093836 | 2.021544 | 1.097908 | 2.005589 | ||
| 400 | 2947 | 2.716023 | 2.009829 | 2.721104 | 2.012493 | ||
| 800 | 7426 | 6.763548 | 2.005643 | 6.757212 | 2.009691 | ||
| 0.6 | 0.6 | 50 | 267 | 1.344353 | —— | 1.345261 | —— |
| 100 | 719 | 3.270205 | 2.039459 | 3.271047 | 2.040061 | ||
| 200 | 1937 | 8.019243 | 2.027843 | 8.020099 | 2.028060 | ||
| 400 | 5214 | 1.979933 | 2.018014 | 1.979839 | 2.018236 | ||
| 800 | 14036 | 4.901814 | 2.014064 | 4.901704 | 2.014027 | ||
| N | PASE-I Scheme | PASI-E Scheme | ||||
|---|---|---|---|---|---|---|
| 0.35 | 0.35 | 200 | 1.540090 | —— | 1.541745 | —— |
| 400 | 4.981818 | 1.628270 | 4.986837 | 1.628367 | ||
| 800 | 1.579056 | 1.657609 | 1.580609 | 1.657643 | ||
| 1600 | 4.971665 | 1.667262 | 4.976502 | 1.667277 | ||
| 3200 | 1.561734 | 1.670579 | 1.563244 | 1.670588 | ||
| 0.4 | 0.2 | 200 | 1.641599 | —— | 1.643375 | —— |
| 400 | 5.320684 | 1.625418 | 5.326029 | 1.625530 | ||
| 800 | 1.681644 | 1.661739 | 1.683288 | 1.661777 | ||
| 1600 | 5.266880 | 1.674851 | 5.271969 | 1.674868 | ||
| 3200 | 1.643123 | 1.680508 | 1.644700 | 1.680517 | ||
| 0.8 | 0.2 | 200 | 6.070178 | —— | 6.075953 | —— |
| 400 | 2.349702 | 1.369260 | 2.351861 | 1.369307 | ||
| 800 | 9.139187 | 1.362340 | 9.147204 | 1.362400 | ||
| 1600 | 3.598744 | 1.344572 | 3.601678 | 1.344661 | ||
| 3200 | 1.445759 | 1.315666 | 1.446810 | 1.315793 | ||
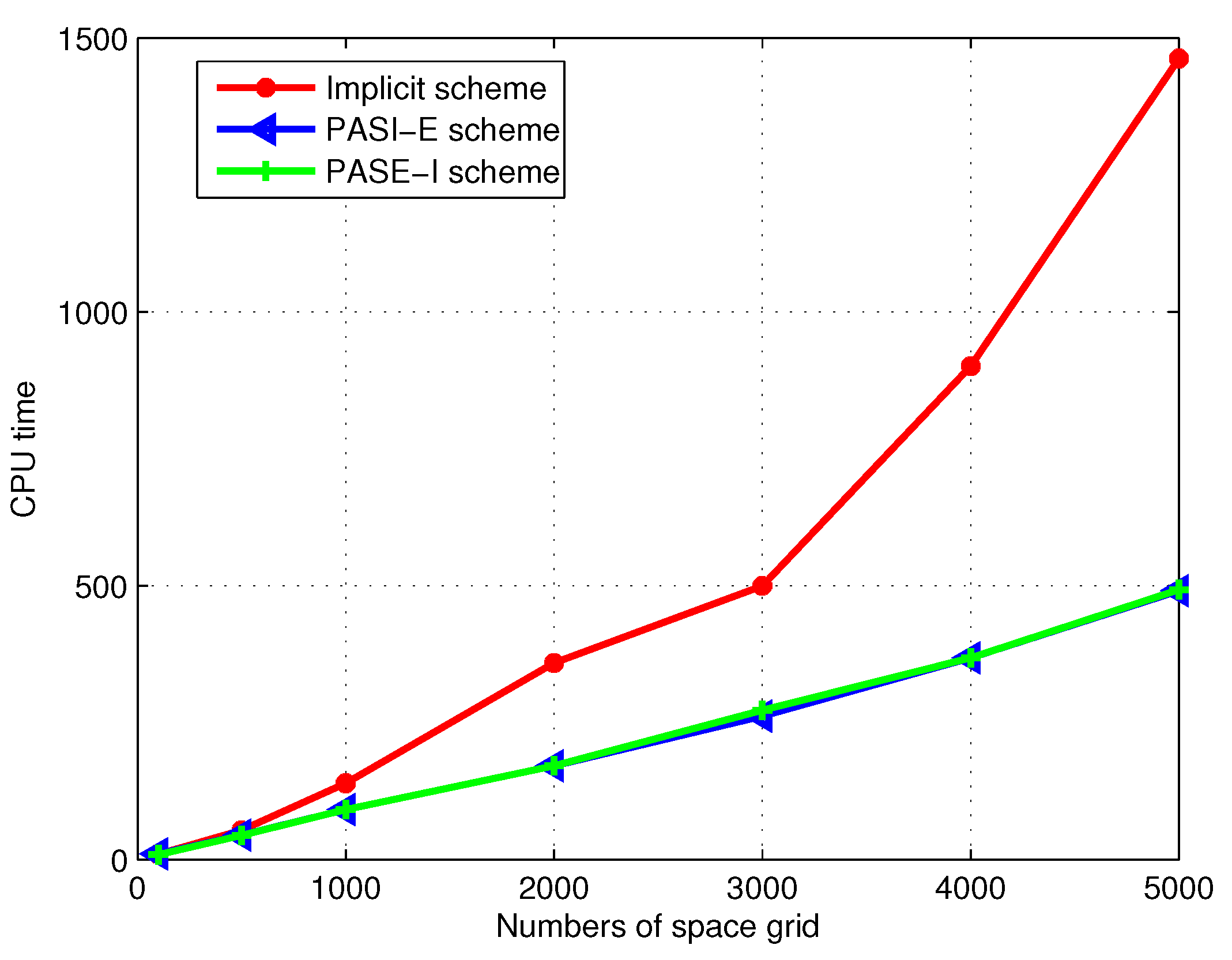
| 100 | 500 | 1000 | 2000 | 3000 | 4000 | 5000 | |
|---|---|---|---|---|---|---|---|
| Implicit | 9.90432 | 53.6988 | 139.582 | 359.223 | 499.958 | 900.628 | 1462.45 |
| PASE-I | 9.14516 | 44.5909 | 91.2816 | 171.389 | 272.927 | 368.622 | 493.003 |
| PASI-E | 10.5672 | 44.7052 | 91.4469 | 171.517 | 262.139 | 368.364 | 491.059 |
| of PASE-I | 1.08301 | 1.20425 | 1.52914 | 2.09594 | 1.83183 | 2.44322 | 2.96641 |
| of PASI-E | 0.93726 | 1.20117 | 1.52637 | 2.09437 | 1.90722 | 2.44494 | 2.97815 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Wu, L. A New Kind of Parallel Natural Difference Method for Multi-Term Time Fractional Diffusion Model. Mathematics 2020, 8, 596. https://doi.org/10.3390/math8040596
Yang X, Wu L. A New Kind of Parallel Natural Difference Method for Multi-Term Time Fractional Diffusion Model. Mathematics. 2020; 8(4):596. https://doi.org/10.3390/math8040596
Chicago/Turabian StyleYang, Xiaozhong, and Lifei Wu. 2020. "A New Kind of Parallel Natural Difference Method for Multi-Term Time Fractional Diffusion Model" Mathematics 8, no. 4: 596. https://doi.org/10.3390/math8040596
APA StyleYang, X., & Wu, L. (2020). A New Kind of Parallel Natural Difference Method for Multi-Term Time Fractional Diffusion Model. Mathematics, 8(4), 596. https://doi.org/10.3390/math8040596





