Abstract
Turbulence is the duality of chaotic dynamics and hierarchical organization of a field over a large range of scales due to advective nonlinearities. Quadratic nonlinearities (e.g., advection) in real space, translates into triadic interactions in Fourier space. Those interactions can be computed using fast Fourier transforms, or other methods of computing convolution integrals. However, more generally, they can be interpreted as a network of interacting nodes, where each interaction is between a node and a pair. In this formulation, each node interacts with a list of pairs that satisfy the triadic interaction condition with that node, and the convolution becomes a sum over this list. A regular wavenumber space mesh can be written in the form of such a network. Reducing the resolution of a regular mesh and combining the nearby nodes in order to obtain the reduced network corresponding to the low resolution mesh, we can deduce the reduction rules for such a network. This perspective allows us to develop network models as approximations of various types of turbulent dynamics. Various examples, such as shell models, nested polyhedra models, or predator–prey models, are briefly discussed. A prescription for setting up a small world variants of these models are given.
1. Introduction
Many fundamental concepts in nature are defined through dualities. A duality is an opposition/complementarity, represented by the canonical example of the wave-particle duality in modern physics, and commonly described through the principle of “yin and yang” in ancient Eastern tradition or through dialectics in modern Western thought. Turbulence is such a duality of chaotic disorder/hierarchical organization across a large range of scales. The mathematical idea of turbulence manifests itself as we approach the limit of an infinite range of scales. However, turbulence exists in the real world, where the ideal has to adjust itself to the constraints of the real, somewhat similar to real world fractals, manifesting fractal behavior only over a finite range of scales.
The archetypical example of turbulence is the Navier–Stokes equation, which describes the self-advection of a divergence-free velocity field that is dissipated at small scales due to kinematic viscosity as:
When we mix this system (via external forcing not shown in the above equation) with a spectrally localized large-scale forcing and have sufficiently small dissipation that is localized naturally at very small scales because of its form, it is well known to display universal behavior over a range of scales in between the scales of energy injection and those of dissipation. This particular setup due to Kolmogorov’s genius, where the energy is injected at large scales, cascades scale by scale towards small scales where it gets dissipated, gives rise to the so-called Kolmogorov spectrum, a power law where is the spectral energy density [1]. This flow of energy from one scale to another, in the wave-number space, requires a complicated hierarchical self-organization of its many elements.
Similarly, many fundamental problems in nature and in social systems can be formulated in terms of complex networks, which consist of structures made up of nodes connected by links or edges. Common examples are the Internet, the brain, ecological systems, and various parts of the global economy [2]. Studies on network theory, in particular formation of small-world [3] and scale-free networks [4] gave rise to a common understanding of these very different problems using similar conceptual abstractions, including understanding of the relations between network structure and dynamics such as synchronization [5] and percolation. Application of complex networks to turbulent flows is not a completely new idea. Application of directed percolation to turbulent transport [6] or various cellular automata or coupled map lattice [7] models are examples of this kind. Recent efforts include considering two dimensional turbulence as a network of vortices [8]. In this perspective, a network is a mathematical tool to model different aspects of a flow.
Multiscale evolution of “complexity” (that is, molecular competition with feedback loops leading to complexity in multicellular organisms at small scales, to ecosystems where diverse species compete at large scales) akin to the the idea of cascade in fluid turbulence (or rather “inverse cascade”, in this particular example) may take place in such networks. A detailed analysis of different levels of analogies of these systems is therefore likely to be beneficial to many fields including plasma turbulence or climate science where these models are not studied in as much detail as for example in the ecological setting.
This paper is an initial attempt at providing a bridge between the turbulence and network theories from the perspective of wave-number space evolution of turbulence. It poses many new questions without really trying to answer them, with a focus on laying out the foundation, and demonstrating the ideas with a few simple examples such as shell models.
Network approach can indeed provide an alternative perspective to the study of turbulence in the spectral domain; both in wave-number and in frequency. In particular, the context of wave turbulence provide a natural formulation in terms of a network of resonant triads [9]. Notice that, while our focus here is what is commonly called strong fluid turbulence (i.e., Kolmogorov turbulence), there is a whole host of real world problems where the turbulence is weak [10,11,12], wave-like and therefore relies on wave-resonances [13,14], or coexists with strong turbulence [15,16]. These problems are actually better suited for a formulation in terms of networks, since the resonant interactions can be seen as an actual constraint for the network connection, since the existence or not of resonances can lead to turning on and off of a connection. The role of wave-resonances on energy transfer [17,18] and dynamics of turbulence spectra [19,20] were studied in great detail for various physical problems. The fact that, especially in a quantized system, where such resonances are harder to satisfy, only a finite number of triads are activated is similarly well known [21]. However, it is worth re-iterating that the focus of the current paper is the strong Kolomogorov-like turbulence, and thus triad interactions and not three or four wave-interactions are the primary mechanism. It is imperative that the latter topic, already of interest [22] be similarly revisited in the future.
The rest of the paper is organized as follows. In Section 2, we describe the mathematical structure of the Fourier space formulation of the Navier–Stokes equation from a network theory perspective. We discuss energy transfer in Section 2.1, network reduction in Section 2.2, and modelization of transfer rates in Section 2.3. In Section 3, we discuss spectral reduction and beyond in Section 3.1 as an alternative strategy. In Section 4, we discuss various examples of regular network models, such as the nested polyhedra model in Section 4.1, predator–prey models in Section 4.2, and briefly talk about food webs in Section 4.3. Section 5 is the conclusion.
2. Fourier Space Formulation
In Fourier space, the Navier–Stokes equation becomes [1]:
with the Einstein summation convention. Note that this form of the equation actually implies a regular grid in a three dimensional wave-number space: with being integers going from 0 to , where is the number of points in the x direction. The basic idea of the network interpretation is to flatten this k-space grid into a list of wave-numbers, for example using:
so that the 3D grid turns into a vector, or a “list”, given by:
compute a list of all possible interactions such that , and thus write the equation in the form:
where
which for this example happens to be independent of and , but could in general depend on those as well. Note that we can symmetrize the interaction coefficient by using
In principle, the formulation in Equation (5) is equivalent to Equation (2), and since there are efficient methods for implementing Equation (2) numerically, using fast Fourier transforms and pseudo-spectral algorithms, it makes little sense to develop Equation (5) for numerical computations. It is nonetheless interesting, because it makes the network structure of the Fourier space evolution rather transparent. Furthermore, it can be generalized to irregular grids, or other systems rather easily. The main necessary ingredients are:
- a finite number of nodes in space (the grid in the above example);
- a list of node to pair couplings to be determined by the triadic interaction condition;
- the coefficient of interaction for each of these couplings; and
- a set of field variables (e.g., ) to evolve on each node of the network using Equation (5).
Note that many different problems in turbulence can be formulated in this form.
Once the abstraction of nodes (i.e., denoted by the node index ℓ) and links are introduced, we can put aside the regular grid, and use a generalization in terms of networks. However, an important obstacle in using the usual network formulation is the triadic nature of the interactions among wave-numbers. This effectively forces us to use links that are always between three nodes. This could have been avoided by introducing the triads themselves as different kinds of nodes in the network and constraining links to form only between triad nodes and wave-number nodes. However, this makes the analytical formulation rather cumbersome, thus here we opt for the former approach.
2.1. Energy Transfer
The energy of a given wave-number node can be defined as .
where
is the nonlinear transfer and is the production of energy (e.g., due to forcing) at node ℓ. It is clear that
since
and thus
where is the total production and is the total dissipation. The system can find a steady state with , even if P is a constant, since is a function of , which can adapt.
Consider a partition of the k space such that we can define a set of integers L, which divides the k space into an “inner” region and an “outer” region . The obvious example is which divides the k space into and regions that can naturally be called inner and outer regions.
The energy transfer among nodes that are all in the inner or outer regions is zero:
In addition, using Equation (11), we can relate:
which means that the total energy transfer (i.e., flux) from the inner to the outer region, can be written as:
where , and . Note that consists of two bits; first one is the energy gain to a node in the outer region due to a pair in the inner region, and the second one is the energy loss to a node in the inner region due to a pair in the outer region. Similarly, we can write:
where
2.2. Network Reduction
Now, consider a number of separate sets L which divide the k-space into distinct domains that cover it completely. In this case, we can write
where L, and are understood to be distinct groups of nodes (so the sum over excludes L and sum over excludes both L and ). Therefore, represents energy increase in group L, due to all the pairs with one element in and another in , which would vanish if no such interaction is possible. Similarly, is the energy increase in group L due to interactions with all the pairs that are both in Obviously, we have
and
as before.
2.3. Transfer Rates
The evolution of energy of a group of nodes as given in Equation (19) is a generalization of Equation (8), without any closure for the form of the transfer rates. In practice, if we want to use the transfer rates, we need to compute them by using the general form:
where and are are the two components of the interaction vector that appears initially in Equation (5).
computation of transfer rates, in general requires detailed knowledge of the full velocity field, which can not be obtained from the energies.
One can write down evolution equations for the energies of different components of the energy field, for example , using an helical decomposition , etc. However, the phase information is also needed to compute the transfer rates accurately as a function of time, and this means in practice that we need the full flow field at every sub-node ℓ.
The total transfer from outside to inside L can then be written as:
which is the net transfer from all other to L that is written as a sum over all such transfers that are mediated by a third group . The term is the self mediated transfer where the mediator is either L or itself. While here we do not intend to go into details of how one can propose a model for the transfer rate, a statistical closure such as the eddy damped quasi-normal Markovian approximation (EDQNM) for the network nodes could be use for such purpose [23].
3. Spectral Reduction
Using energy as the basis of a network formulation makes sense, but lacks certain important aspects such as phase evolution, synchronization, etc. The alternative, which is more straightforward and requires less modeling assumptions is the spectral reduction approximation [24,25] applied to networks. Unfortunately, spectral reduction has its own issues, in particular if one uses inhomogeneous partitions, which results in a different energy equipartition than the original one, however it can usually be formulated in such a way as to give back the original equations:
but in reduced nodes L, , and as in the previous section. We would in principle keep all the components of the vector field variable . In fact, there are only two independent variables, and , for the three-dimensional Navier–Stokes system [26]. The generic form given in Equation (25) can be interpreted either with running through physical components or helicity components , of course with corresponding interaction coefficients. Notice that, in Equation (25), we have implicitly defined:
and
where if there are no triadic interactions possible between any of the elements of the three node groups L, and .
3.1. Phase Dynamics: Synchronization vs. Random Phase
Spectral reduction approach allows us to keep track of phases. However, since they are also reduced, it is unclear what is exactly lost by removing the detailed internal phase evolution by a mean overall phase for each domain L. When Equation (25) is separated into phase and amplitude evolution, we get
One solution of this is so that we get back something similar to the model discussed in Section 2.1. However, this requires a rather complicated self-organization of the phases including a nonlinear synchronization of each triad evolution. This may or may not happen from Equation (29).
In fact, one can talk about two distinct limits of the phase evolution. (1) When the phases are relatively random, one can use a closure based on this approximation, such as the EDQNM closure discussed above. (2) When the phase evolution is in sync, we can use an expression for energy transfer based on Equation (28) where we replace by 1. During time evolution of real turbulence, one expects it to go through both of these cases for different triads. In principle, each triad chain will consist of a number of synchronized and unsynchronized oscillating phases.
Notice that here we wrote the amplitude and phase equations using the spectrally reduced forms. One can of course write them for the original Equation (5). In such a case, the phase evolution has many more degrees of freedom resulting in both synchronized an random phase transfer between the three domains L, , and .
3.2. Beyond Spectral Reduction
Assuming that in each group there are a large number of nodes, we can write an average variable, and a number of other variables defined in some form. For instance, if the number of nodes in the group is , this means we actually have internal variables in each group. Thus, if we want to obtain the exact distribution of energies and phases as in the original network, we would have to keep variables. These variables can be any orthogonal linear combinations of the original variables, for instance as in a discrete Fourier transform.
However, since we do not necessarily want all that information but rather a coarser version, it would make sense to transform these variables into some form where keeping only few of the terms would still give us the information we mostly need. For example, sorting the ’s according to their s, and using
and
where
gives us some additional information about the distribution of the field within the domain L. This could be used as a measure of which part of the reduced Fourier space volume does the interaction correspond to. It is unclear if by using cumulants, moments or some other representation, one can actually have a good enough representation with a low number of variables per volume. Nonetheless, we think that this perspective should be developed in the future.
4. Examples of Network Models
To use a particular network as the basis of a network model, there are some conditions. First, the network should be sufficiently connected, which means basically that every node should have more than one connection. The simplest examples are probably “shell models” [27], where each node represents the contribution from a range of wave-numbers, usually in the form of nearest neighbor interactions. For instance, the GOY model [28] can be written on a set of nodes, organized as , where g is the logarithmic scaling factor, with three links for each node:
The vector form of Equation (33) implies a sum over the connections (in this case three connections of the shell model). Note that the interaction coefficients are the ‘weights’ of these connections and therefore have the same length as the connections vector . As usual, one must have in order to conserve energy and different choices result in different secondary conservation laws, such as helicity or enstrophy. Finally, in the GOY model, all the amplitudes on the RHS are conjugated.
However, we could also write
where
for the GOY model with
In a similar spirit, spiral chain models [30] are also network models that can describe two-dimensional turbulence. However such models can be obtained from Fourier space decimation, and may impose exact triadic interaction conditions. In other words, while in a shell model, one does not necessarily have an exact matching condition , the spiral chain models can be constructed to have exact triadic matching among its nodes (e.g., ).
Note that shell models, as well as a majority of the examples given below are actually based on regular graphs (such as nearest neighbor interactions) instead of random or small world graphs. One interesting idea that needs to be explored in the future is the idea of using the Newman–Watts strategy [31] to go over the connections and update them with adding randomized connections. This has to be done at the level of triads, since the energy conservation can only be guaranteed if all three legs of the triad are in the list of interactions. In other words, one can add a few disparate scale interactions into the nearest neighbor formulation of the GOY system, without breaking energy conservation (see Figure 1).
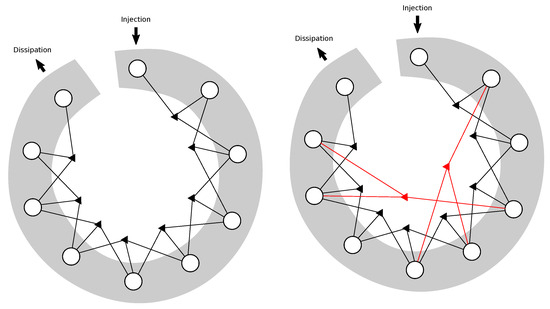
Figure 1.
The standard GOY model on the left (10 nodes, shown as an unclosed ring), and the small world version on the right, with some randomly added triads. Note that each triad enters an additional link to the list of connections for each of its three nodes. Note that the triangles for these disparate scale interactions are very elongated.
4.1. Nested Polyhedra Models
While spiral chain models are interesting examples of network formulation, they are better adapted to describing two-dimensional turbulence. Network models can of course be easily extended to two-dimensional turbulence as well as rotating or magnetohydrodynamic (MHD) turbulence. However, the focus here is still three-dimensional Navier–Stokes turbulence. While various possible networks can be constructed covering the wave-number domain, one particularly efficient one is the configuration of the nested polyhedra model (NPM).
This configuration, which consists of nested alternating icosahedron dodecahedron pairs, was recently introduced as a self-similar, spherically symmetric decimation of the wave-number domain whose vertices provide nodes that satisfy exact triadic matching conditions with neighboring scales [32]. This results in a network that can transfer energy from large to small scales, and since the connectivity of the network is constant as a function of scale, it can nicely handle a constant flux of energy. A similar model has also been developed for MHD [33].
The model can be written in the same form as Equation (35) but for a vector field:
where the Greek indices denote vector components. For the NPM, each node is connected to or other nodes, depending on if it is on a dodecahedron or an icosahedron. Keeping only half the vertices of each polyhedra (6 for icosahedron and 10 for dodecahedron) as in Figure 2 and obtaining the rest of the points by reflection with respect to the origin since , we can write the connection vector as described in Table 1 and Table 2. A python implementation of the nested polyhedra model can be found at [34].
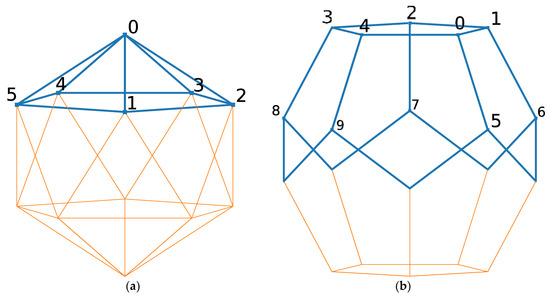

Table 1.
, where , which denotes the nth vertex of the mth polyhedron, is shown on the leftmost column, interacts with , and for an even m (i.e., an icosahedron node) where , and are to be taken from their corresponding columns. Note that a bar over the integer value indicates (i.e., not conjugated), whereas no bar means (i.e., conjugated).

Table 2.
where is shown on the leftmost column, interacts with , and for an odd m (i.e., a dodecahedron node) where , and are to be taken from their corresponding columns. As in Table 1, if the integer value has a bar over it (i.e., not conjugated), whereas no bar means (i.e., conjugated).
The results of such a model is interesting. It can cover a very large range of scales due to the extreme reduction but is nonetheless able to describe the cascade process by energy transfer from node to node. It is similar in this sense to a shell model, but, unlike a shell model, it is able to handle some anisotropy. An important weakness of the model is its inability to describe intermittency. In addition, similar to other models with non-uniform reduction, its statistical equipartition is different from a statistical equipartition on a regular grid.
To extend this formulation to a small world formulation, one has to somehow transform it from a Fourier space decimation procedure to a spectral reduction one. In the case of the usual interpretation of the nested polyhedra models, since the vertices can satisfy exact triadic matching conditions, all we have to do is to compute the interaction coefficients and the links that correspond to those exact triadic interactions. However, in a spectral reduction picture, one no longer needs exact triadic interactions between vertices, since each vertex represents a volume around that vertex, and therefore an approximate triadic matching of the vertices results in an interaction of the wave-numbers within those domains. Notice that, even when interpreted this way, the nonlinear interaction coefficient computed with the exact triadic interactions provide a good basis for the model. The strategy here would have to be a bit more subtle. Since there are many interactions that are probably completely forbidden in such a regular grid structure, one must go over all “possible” interactions [i.e., viable as an approximate interaction, for instance ], which is usually a very big list and randomly pick triads to add to the list of existing regular triad interactions.
4.2. Predator–Prey Models
Going back to energy budget of Section 2.1, one can construct simple models of evolution of energy of two separate domains. For example, the Equations (16) and (17), provide the basis for a competition for available energy. In particular, we can choose the domains such that the energy production (in this case, due to internal drive such as an instability source) so that is localized to the inner region and the dissipation is localized to the outer region . Now, if the transfer term is strictly from the inner to the outer region and is proportional to both energies so that (as would be the case for example in a random phase approximation), we obtain
which is basically the Lotka–Volterra system between the energies of the inner and outer regions. Notice that the inner region corresponds to the prey while the outer region corresponds to the predator. While the use of the terminology inner and outer may seem confusing, in particular from the picture of dissipation taking place at small scales in three-dimensional turbulence, it is clear that in 2D or quasi-2D turbulence where the picture is particularly more relevant, the instability drive would be at medium scales, whereas the role of predator would be played with anisotropic large-scale structures called zonal flows.
4.3. Food Webs
The predator–prey relations can be extended to include multiple species that feed on each other, or in this case each other’s energy, leading to the concept of the food web. For instance, a food web can represent the hierarchical predation relations between a large number of species found in an ecological system. It is also common to observe power-law behavior or scale-free distributions on a food web depending on network connectivity and network size. Another advantage of food webs as a template for turbulent systems is that they can be constructed either at a detail level where each species would be a separate node or at a coarser level where one would lump together various groups of species as would be the case, e.g., when we are talking about the whole ocean.
5. Conclusions
We show that wave-number space evolution of Navier–Stokes turbulence can be formulated as a network model where each node representing a wavenumber—or a collection of wavenumbers—is connected to a number of pairs of other such nodes through triadic interactions. The connection between a node and a pair represents a single triadic interaction—or the net effect of a number of such interactions over all the internal wavenumbers of the nodes. As a result, the cascade process can be described as a flow of energy across such a network through triadic interactions. It is not surprising that reduced cascade models, such as shell models, spiral chain models, or nested polyhedra models, can all be formulated as network models via either reduction or Fourier space decimation, where the network consists of a regular graph. We argue that, by adding some degree of randomness to those graphs, one may obtain small-world variations of these models. Spectral formulation over a regular grid, as well as spectral reduction, can also be interpreted as a transfer over a regular network structure. Finally, appearance of predator–prey models, with single or multiple predators, common in modeling of interactions between a low number of modes around marginal stability, for instance in plasma turbulence, is also a natural manifestation of the network picture. Extending the basic analogy, one can draw parallels between hierarchical network structures of Fourier modes in turbulence with those of food webs in ecosystems.
The network formulation of existing models that we have presented here is really only a reinterpretation. As such, it has no obvious, direct advantage over the original interpretation. However, it allows us to think and talk about turbulence using the language of networks, and this may allow us further understanding. For example, the idea that more triads are likely to attach themselves to a node that already has many connections, or the conception of a dynamical network model, starting from a finite number of nodes and extending as necessary—for example, as the nonlinear energy transfer to the candidate node exceeds a certain threshold—becomes possible. As discussed in the Introduction, such models may actually be more relevant to real world problems involving wave-turbulence or coexistence of strong and weak turbulence, since the number of activated modes are more likely to be sparser. We think that these issues should be addressed in future studies.
Author Contributions
Conceptualization, writing—original draft, and formal analysis, Ö.D.G.; and investigation, Y.L. and P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We would like to thank P. H. Diamond for valuable discussions, and Yang Li wishes to acknowledge the support of the China Scholarship Council.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Frisch, U. Turbulence: The Legacy of A. N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of small-world networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Arenas, A.; Díaz-Guilera, A.; Kurths, J.; Moreno, Y.; Zhou, C. Synchronization in complex networks. Phys. Rep. 2008, 469, 93–153. [Google Scholar] [CrossRef]
- Sipos, M.; Goldenfeld, N. Directed percolation describes lifetime and growth of turbulent puffs and slugs. Phys. Rev. E 2011, 84, 035304. [Google Scholar] [CrossRef] [PubMed]
- Kaneko, K. Overview of coupled map lattices. Chaos Interdiscip. J. Nonlinear Sci. 1992, 2, 279–282. [Google Scholar] [CrossRef] [PubMed]
- Taira, K.; Nair, A.G.; Brunton, S.L. Network structure of two-dimensional decaying isotropic turbulence. J. Fluid Mech. 2016, 795, R2. [Google Scholar] [CrossRef]
- Kartashova, E. (Ed.) Nonlinear Resonance Analysis. In Nonlinear Resonance Analysis; Cambridge University Press: Cambridge, UK, 2010; Volume 1. [Google Scholar]
- Newell, A. (Ed.) Nonlinear Wave Motion. Lectures in Applied Mathematics; Number 15; American Mathematical Society: Providence, RI, USA, 1974. [Google Scholar]
- Zakharov, V.E.; Kuznetsov, E.A. Hamiltonian formalism for nonlinear waves. Physics-Uspekhi 1997, 40, 1087. [Google Scholar] [CrossRef]
- Newell, A.C.; Rumpf, B. Wave Turbulence. Annu. Rev. Fluid Mech. 2011, 43, 59–78. [Google Scholar] [CrossRef]
- Thorpe, S.A. On wave interactions in a stratified fluid. J. Fluid Mech. 1966, 24, 737–751. [Google Scholar] [CrossRef]
- Kim, W.; West, B.J. Chaotic properties of internal wave triad interactions. Phys. Fluids 1997, 9, 632–647. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Korotkevich, A.O.; Pushkarev, A.; Resio, D. Coexistence of Weak and Strong Wave Turbulence in a Swell Propagation. Phys. Rev. Lett. 2007, 99, 164501. [Google Scholar] [CrossRef]
- Meyrand, R.; Kiyani, K.H.; Gürcan, Ö.D.; Galtier, S. Coexistence of Weak and Strong Wave Turbulence in Incompressible Hall Magnetohydrodynamics. Phys. Rev. X 2018, 8, 031066. [Google Scholar] [CrossRef]
- Furuichi, N.; Hibiya, T.; Niwa, Y. Bispectral Analysis of Energy Transfer within the Two-Dimensional Oceanic Internal Wave Field. J. Phys. Oceanogr. 2005, 35, 2104–2109. [Google Scholar] [CrossRef]
- Falcon, E.; Laroche, C.; Fauve, S. Observation of Gravity-Capillary Wave Turbulence. Phys. Rev. Lett. 2007, 98, 094503. [Google Scholar] [CrossRef]
- Connaughton, C.; Newell, A.C.; Pomeau, Y. Non-stationary spectra of local wave turbulence. Phys. D Nonlinear Phenom. 2003, 184, 64–85, Complexity and Nonlinearity in Physical Systems—A Special Issue to Honor Alan Newell. [Google Scholar] [CrossRef][Green Version]
- Buchhave, P.; Velte, C.M. Dynamic triad interactions and evolving turbulence spectra. arXiv 2019, arXiv:1906.04756. [Google Scholar]
- Kartashova, E.A. Weakly nonlinear theory of finite-size effects in resonators. Phys. Rev. Lett. 1994, 72, 2013–2016. [Google Scholar] [CrossRef]
- Pires, C.A.L.; Perdig ao, R.A.P. Non-Gaussian interaction information: Estimation, optimization and diagnostic application of triadic wave resonance. Nonlinear Process. Geophys. 2015, 22, 87–108. [Google Scholar] [CrossRef]
- Lesieur, M. Turbulence in Fluids, 3rd ed.; Kluwer: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Bowman, J.C.; Shadwick, B.A.; Morrison, P.J. Spectral Reduction: A Statistical Description of Turbulence. Phys. Rev. Lett. 1999, 83, 5491–5494. [Google Scholar] [CrossRef]
- Bowman, J.C.; Roberts, M. Pseudospectral reduction of incompressible two-dimensional turbulence. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2008–2013. [Google Scholar] [CrossRef]
- Waleffe, F. Inertial transfers in the helical decomposition. Phys. Fluids A Fluid Dyn. 1993, 5, 677–685. [Google Scholar] [CrossRef]
- Biferale, L. Shell models of energy cascade in turbulence. Ann. Rev. Fluid Mech. 2003, 35, 441–468. [Google Scholar] [CrossRef]
- Ohkitani, K.; Yamada, M. Temporal Intermittency in the Energy Cascade Process and Local Lyapunov Analysis in Fully-Developed Model Turbulence. Prog. Theor. Phys. 1989, 81, 329–341. [Google Scholar] [CrossRef]
- L’vov, V.S.; Podivilov, E.; Pomyalov, A.; Procaccia, I.; Vandembroucq, D. Improved shell model of turbulence. Phys. Rev. E 1998, 58, 1811–1822. [Google Scholar] [CrossRef]
- Gürcan, Ö.D.; Xu, S.; Morel, P. Spiral chain models of two-dimensional turbulence. Phys. Rev. E 2019, 100, 043113. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Watts, D.J. Scaling and percolation in the small-world network model. Phys. Rev. E 1999, 60, 7332–7342. [Google Scholar] [CrossRef]
- Gürcan, Ö.D. Nested polyhedra model of turbulence. Phys. Rev. E 2017, 95, 063102. [Google Scholar] [CrossRef]
- Gürcan, Ö.D. Nested polyhedra model of isotropic magnetohydrodynamic turbulence. Phys. Rev. E 2018, 97, 063111. [Google Scholar] [CrossRef]
- Gürcan, Ö.D. nestp3d. 2017. Available online: https://github.com/gurcani/nestp3d (accessed on 26 March 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).