Information Geometric Investigation of Solutions to the Fractional Fokker–Planck Equation
Abstract
1. Introduction
2. The Fokker–Planck and Langevin Equations
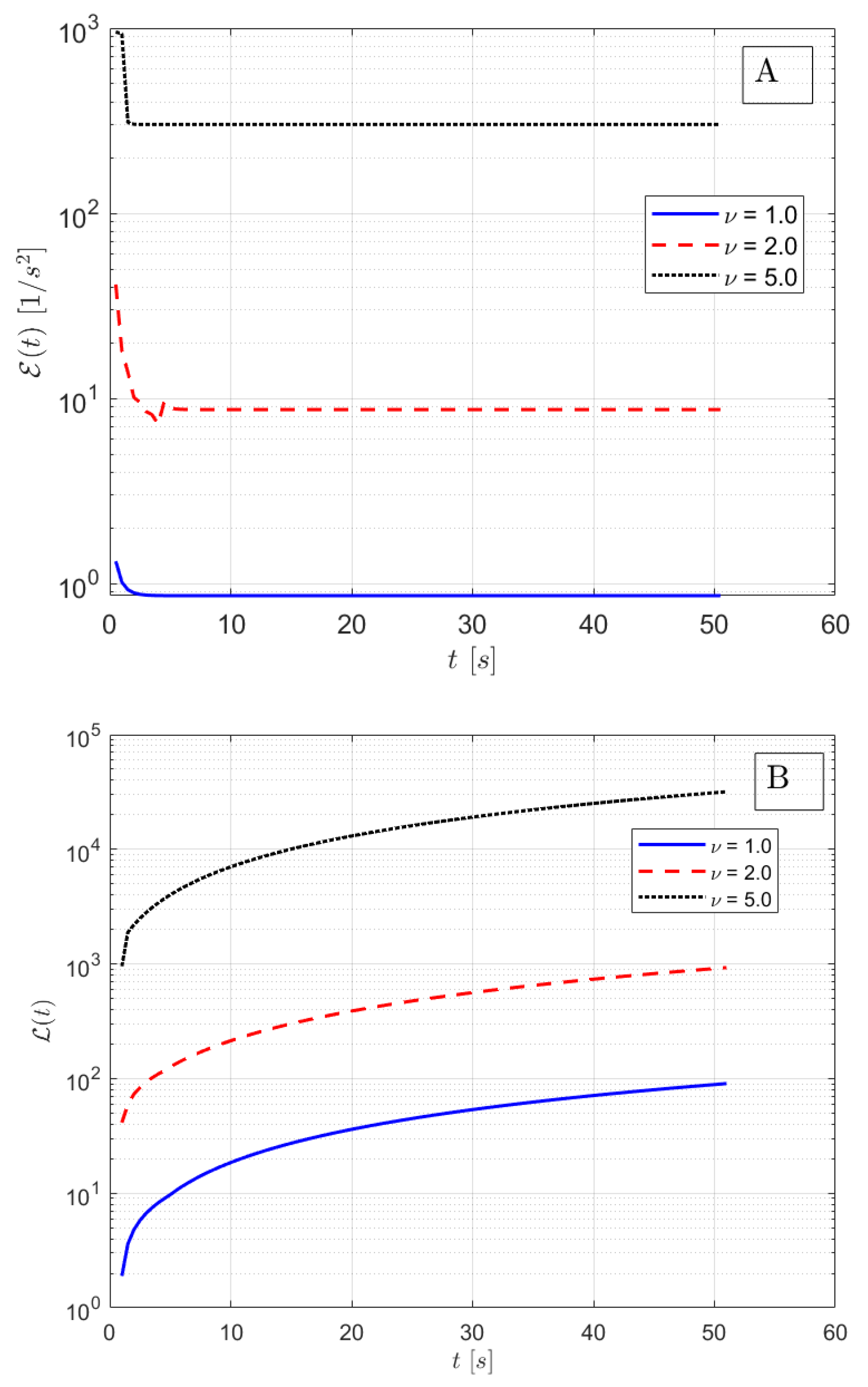
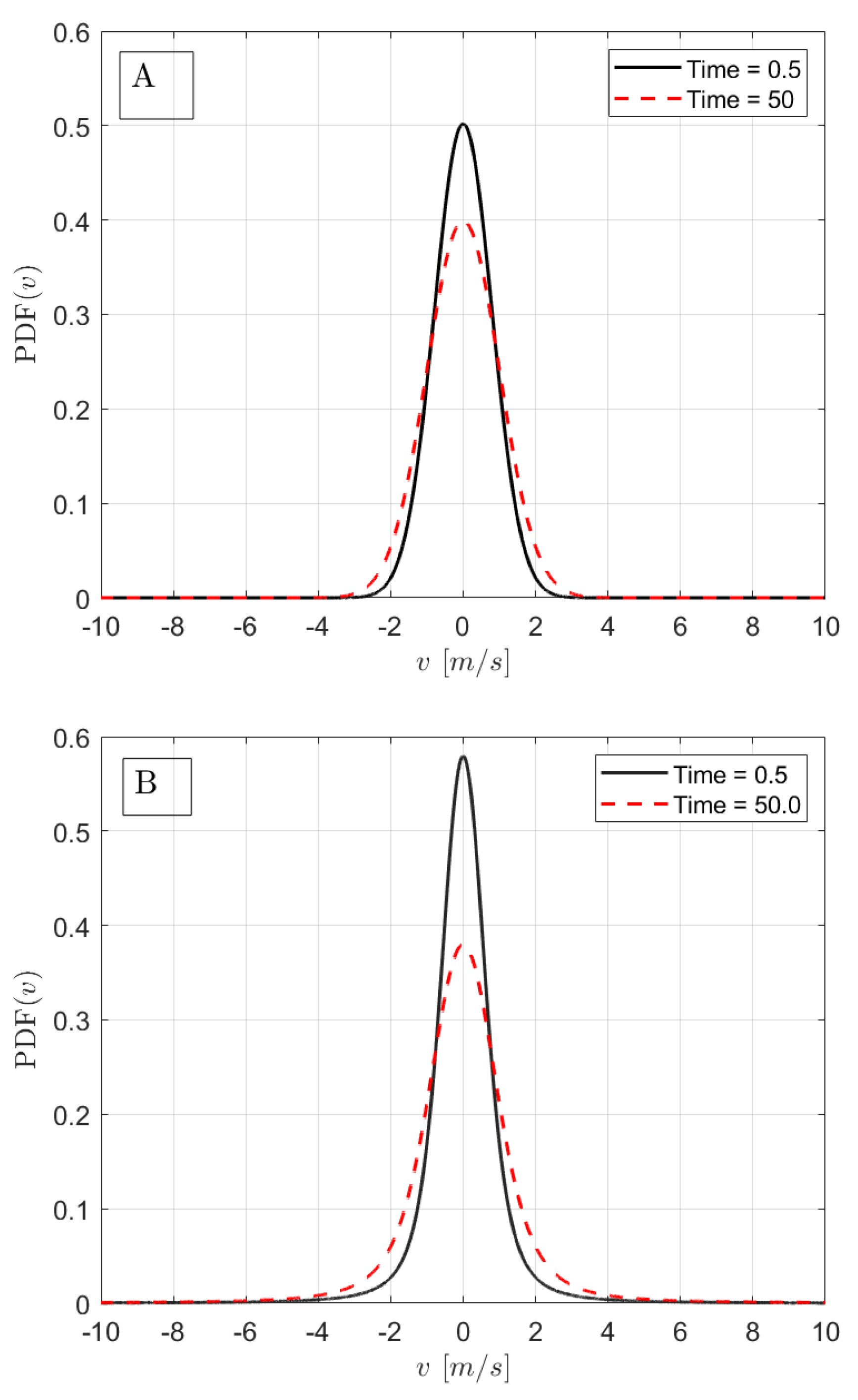
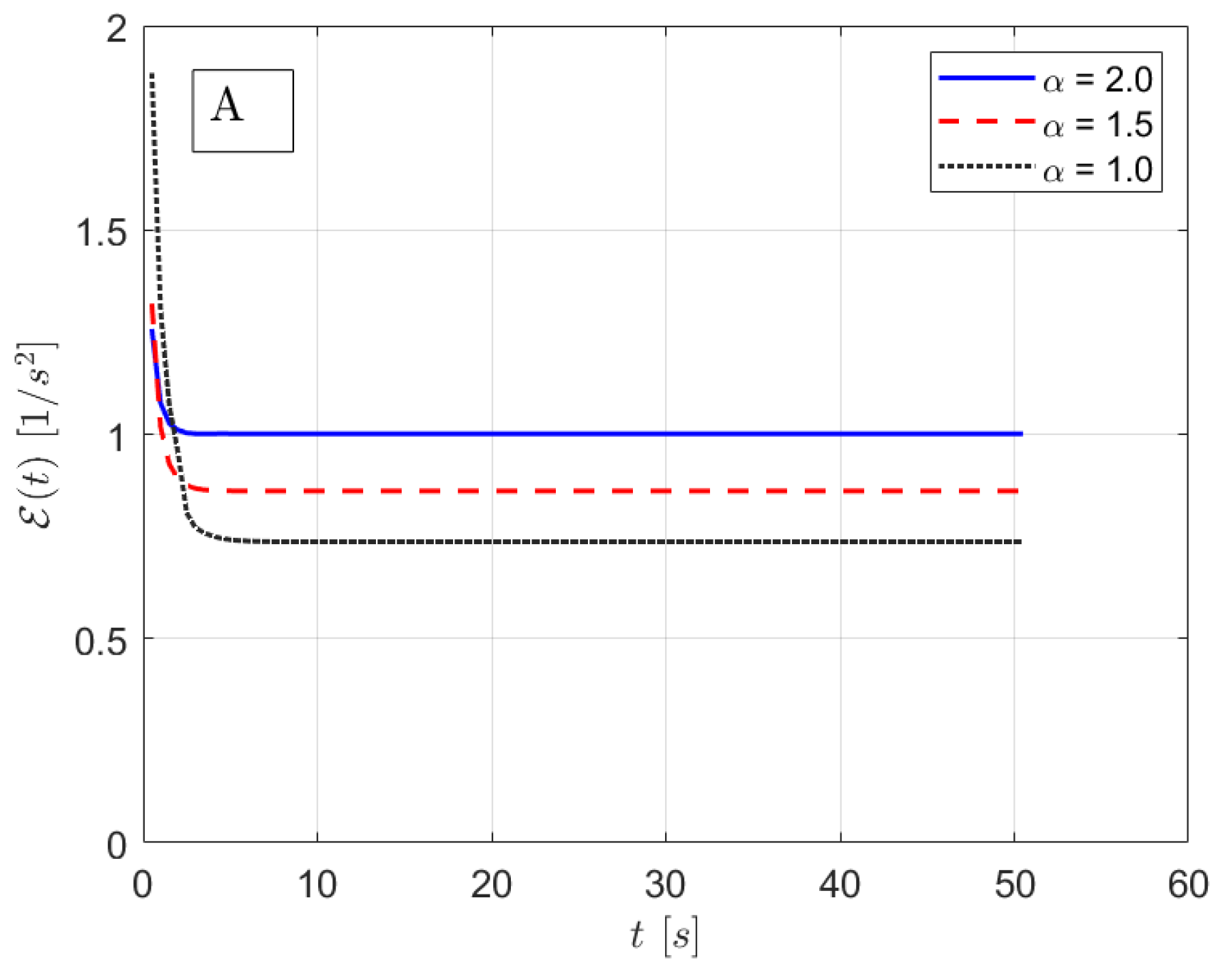
3. Results
4. Summary and Conclusions
Funding
Conflicts of Interest
References
- Carreras, B.A.; Hidalgo, C.; Sanchez, E.; Pedrosa, M.A.; Balbin, R.; Garcia, C.I.; van Milligen, B.; Newman, D.E.; Lynch, V.E. Fluctuation-induced flux at the plasma edge in toroidal devices. Phys. Plasmas 1996, 3, 2664. [Google Scholar] [CrossRef]
- Carreras, B.A.; van Milligen, B.; Pedrosa, M.A.; Balbin, R.; Hidalgo, C.; Newman, D.E.; Sanchez, E.; McKee, G.; Garcia-Cortes, J.; Bleuel, J.; et al. Experimental evidence of long-range correlations and self-similarity in plasma fluctuations. Phys. Plasmas 1999, 6, 1885. [Google Scholar] [CrossRef]
- Van Milligen, B.P.; Sanchez, R.; Carreras, B.A.; Lynch, V.E.; LaBombard, B.; Pedrosa, M.A.; Hidalgo, C.; Gonçalves, B.; Balbín, R.; The W7-AS Team. Additional evidence for the universality of the probability distribution of turbulent fluctuations and fluxes in the scrape-off layer region of fusion plasmas. Phys. Plasmas 2005, 12, 52501–52507. [Google Scholar] [CrossRef]
- Sanchez, R.; Newman, D.E.; Leboeuf, J.N.; Decyk, V.K.; Carreras, B.A. Nature of Transport across Sheared Zonal Flows in Electrostatic Ion-Temperature-Gradient Gyrokinetic Plasma Turbulence. Phys. Rev. Lett. 2008, 101, 205002–205004. [Google Scholar] [CrossRef]
- Del-Castillo-Negrete, D.; Carreras, B.A.; Lynch, V.E. Front Dynamics in Reaction-Diffusion Systems with Levy Flights: A Fractional Diffusion Approach. Phys. Rev. Lett. 2005, 94, 18302–18304. [Google Scholar] [CrossRef]
- Sanchez, R.; Carreras, B.A.; Newman, D.E.; Lynch, V.E.; van Milligen, B.P. Renormalization of tracer turbulence leading to fractional differential equations. Phys. Rev. E 2006, 74, 16305–16311. [Google Scholar] [CrossRef]
- Hahm, T.S. Nonlinear gyrokinetic equations for tokamak microturbulence. Phys. Fluids 1988, 31, 2670–2673. [Google Scholar] [CrossRef]
- Anderson, J.; Xanthopoulos, P. Signature of a universal statistical description for drift–wave plasma turbulence. Phys. Plasmas 2010, 17, 110702. [Google Scholar] [CrossRef]
- Zweben, S.J. Search for coherent structure within tokamak plasma turbulence. Phys. Fluids 2007, 28, 974–982. [Google Scholar] [CrossRef]
- Naulin, V. Turbulent transport and the plasma edge. J. Nuclear Mater. 2007, 363–365, 24–31. [Google Scholar] [CrossRef]
- Kaye, S.M.; Barnes, C.W.; Bell, M.G.; DeBoo, J.C.; Greenwald, M.; Riedel, K.; Sigmar, D.; Uckan, N.; Waltz, N. Status of global energy confinement studies. Phys. Plasmas 1990, 2, 2926–2940. [Google Scholar]
- Cardozo, N.J.L. Perturbative transport studies in fusion plasmas. Plasma Phys. Contr. Fusion 1995, 37, 799–852. [Google Scholar] [CrossRef]
- Gentle, K.W.; Bravenec, R.V.; Cima, G.; Gasquet, H.; Hallock, G.A.; Phillips, P.E.; Ross, D.W.; Rowan, W.L.; Wootton, A.J. An experimental counter-example to the local transport paradigm. Phys. Plasmas 1995, 2, 2292–2298. [Google Scholar] [CrossRef]
- Mantica, P.; Galli, P.; Gorini, G.; Hogeweij, G.M.D.; de Kloe, J.; Cardozo, N.J.L.; RTP Team. Nonlocal transient transport and thermal barriers in rijnhuizen tokamak project plasmas. Phys. Rev. Lett. 1999, 82, 5048–5051. [Google Scholar] [CrossRef]
- Van-Milligen, B.P.; de la Luna, E.; Tabars, F.L.; Ascasíbar, E.; Estrada, T.; Castejón, F.; Castellano, J.; Cortés, I.G.; Herranz, J.; Hidalgo, C.; et al. Ballistic transport phenomena in TJ-II. Nuclear Fusion 2002, 42, 787–795. [Google Scholar] [CrossRef]
- Kim, E.; Anderson, J. Structure based statistical theory of intermittency. Phys. Plasmas 2008, 15, 114506. [Google Scholar] [CrossRef]
- Carreras, B.A.; van Milligen, B.; Hidalgo, C.; Balbin, R.; Sanchez, E.; Cortes, I.G.; Pedrosa, M.A.; Bleuel, J.; Endler, M. Self–Similarity Properties of the Probability Distribution Function of Turbulence–Induced Particle Fluxes at the Plasma Edge. Phys. Rev. Lett. 1999, 83, 3653–3656. [Google Scholar] [CrossRef]
- Sokolov, I.M. Models of anomalous diffusion in crowded environments. Soft Matter 2012, 8, 9043–9052. [Google Scholar] [CrossRef]
- Metzler, R.; Jeon, J.-H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef]
- Meroz, Y.; Sokolov, I.M. A toolbox for determining subdiffusive mechanisms. Phys. Rep. 2015, 573, 1–29. [Google Scholar] [CrossRef]
- Weinhold, F. Metric geometry of equilibrium thermodynamics. J. Phys. Chem. 1975, 63, 2479. [Google Scholar] [CrossRef]
- Rupeiner, G. Thermodynamics: A Riemannian geometric model. Phys. Rev. Lett. 1979, 20, 1608. [Google Scholar] [CrossRef]
- Schlögl, F. Thermodynamic metric and stochastic measures. Z. Phys. B 1985, 59, 449–454. [Google Scholar] [CrossRef]
- Diósi, L.; Kulacsy, K.; Lukács, B.; Rácz, A. Thermodynamic length, time, speed, and optimum path to minimize entropy production. Z. Phys. Chem. 1996, 105, 11220. [Google Scholar] [CrossRef]
- Crooks, G.E. Measuring Thermodynamic Length. Phys. Rev. Lett. 2007, 99, 100602. [Google Scholar] [CrossRef]
- Feng, E.H.; Crooks, G.E. Far-from-equilibrium measurements of thermodynamic length. Phys. Rev. E 2009, 79, 012104. [Google Scholar] [CrossRef]
- Nicholson, S.B.; Kim, E. Investigation of the statistical distance to reach stationary distributions. Phys. Lett. A 2015, 379, 83. [Google Scholar] [CrossRef]
- Kim, E.; Hollerbach, R. Signature of nonlinear damping in geometric structure of a nonequilibrium process. Phys. Rev. E 2017, 95, 022137. [Google Scholar] [CrossRef]
- Kim, E.; Hollerbach, R. Geometric structure and information change in phase transitions. Phys. Rev. E 2017, 95, 062107. [Google Scholar]
- Kim, E.; Jacquet, Q.; Hollerbach, R. Information geometry in a reduced model of self–organised shear flows without the uniform coloured noise approximation. J. Stat. Mech. 2019, 2, 023204. [Google Scholar] [CrossRef]
- Kim, E. Investigating Information Geometry in Classical and Quantum Systems through Information Length. Entropy 2018, 20, 574. [Google Scholar] [CrossRef]
- Heseltine, J.; Kim, E. Comparing Information Metrics for a Coupled Ornstein–Uhlenbeck Process. Entropy 2019, 21, 775. [Google Scholar] [CrossRef]
- Montroll, E.W.; Scher, H. Random walks on lattices. IV. Continuous-time walks and influence of absorbing boundaries. J. Stat. Phys. 1973, 9, 101–135. [Google Scholar] [CrossRef]
- Kou, S.C.; Sunney, X. Generalized langevin equation with fractional Gaussian noise: Subdiffusion within a single protein molecule. Phys. Rev. Lett. 2004, 93, 1806031–1806034. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J.; Kim, E.; Moradi, S. A fractional Fokker–Planck model for anomalous diffusion. Phys. Plasmas 2014, 21, 122109. [Google Scholar] [CrossRef]
- Anderson, J.; Moradi, S.; Rafiq, T. Non–Linear Langevin and Fractional Fokker–Planck Equations for Anomalous Diffusion by Levy Stable Processes. Entropy 2018, 20, 760. [Google Scholar] [CrossRef]
- Anderson, J.; Kim, E.; Hnat, B.; Rafiq, T. Elucidating plasma dynamics in Hasegawa–Wakatani turbulence by information geometry. Phys. Plasmas 2020, 27, 022307. [Google Scholar] [CrossRef]
- Moradi, S.; Anderson, J.; Romanelli, M.; Kim, H.-T.; JET Contributors. Global scaling of the heat transport in fusion plasmas. Phys. Rev. Res. 2020, 2, 013027. [Google Scholar] [CrossRef]
- del Castillo, N.D.; Carreras, B.A.; Lynch, V.E. Fractional diffusion in plasma turbulence. Phys. Plasmas 2004, 11, 3854–3864. [Google Scholar] [CrossRef]
- del Castillo, N.D. Non-diffusive, non-local transport in fluids and plasmas. Nonlin. Process. Geophys. 2010, 17, 795–807. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anderson, J. Information Geometric Investigation of Solutions to the Fractional Fokker–Planck Equation. Mathematics 2020, 8, 668. https://doi.org/10.3390/math8050668
Anderson J. Information Geometric Investigation of Solutions to the Fractional Fokker–Planck Equation. Mathematics. 2020; 8(5):668. https://doi.org/10.3390/math8050668
Chicago/Turabian StyleAnderson, Johan. 2020. "Information Geometric Investigation of Solutions to the Fractional Fokker–Planck Equation" Mathematics 8, no. 5: 668. https://doi.org/10.3390/math8050668
APA StyleAnderson, J. (2020). Information Geometric Investigation of Solutions to the Fractional Fokker–Planck Equation. Mathematics, 8(5), 668. https://doi.org/10.3390/math8050668