1. Introduction
Fractional and classical calculations appeared simultaneously around 1695, when Leibniz and L’Höpital defined the semi-derivative. Additionally, Riemann, Liouville and Euler were interested in this idea. Since then, fractional calculus has suffered an evolution from theory to the real-world applications in medicine, economics and engineering, among others, as they can be modeled by means of differential equations with fractional order derivatives (see, [
1,
2,
3,
4], for example).
Fractional derivatives or partial derivatives are very suitable procedures for those problems whose hereditary properties must be preserved. Often, these kind of problems are related to systems of equations that are nonlinear if the differential equation is nonlinear also. Therefore, the idea of adapting iterative techniques to solve nonlinear equations by means of fractional derivatives is interesting. It was the aim of a recent manuscript by Brambila et al. [
5], who used the iterative expression of Newton’s, avoiding the proof of the order of convergence.
We deduced in [
6] a Newton-type fractional method for approximating the solution
of a nonlinear equation
, to achieve the order of convergence
and show good numerical performance. However, it is known (see for example Traub’s book [
7]) that in point-to-point methods, increasing their order implies adding functional evaluations of those derived from the higher orders of the nonlinear functions. Our initial question is: how does replacing derivatives with fractional ones affect the convergence order of the iterative method? At this point, we are interested in answering this question for both point-to-point and multipoint methods. A first result in this direction has been published in [
8], where a Chebyshev-type scheme is designed using fractional derivatives and the convergence order is demonstrated
. However, there are families of iterative methods of orders superior to two that use whole derivatives of second or greater order, on which we intend to work to achieve its extension to the fractional field.
In this section, we introduce some concepts related with fractional calculus. To deepen in this area, please refer to [
2,
9] and inside citations.
Given a function
,
,
) being,
,
, where
is the integer part of
, the fractional derivative of
, of Caputo-type, of order
is
where
is a gamma function with
.
The Caputo derivative holds the property of integer derivatives,
,
C being a constant, as we can see in [
9]. We will use
in this paper. To prove the convergence results in this paper, it is necessary to use Taylor power series expansion of a nonlinear function
by using Caputo derivatives. This is constructed in the following result.
Theorem 1 (Theorem 3, [
10])
. Let us suppose that for where , then we havewith , for all where (n times composition). On the other hand, Riemann–Liouville fractional derivative of first kind of
, being
an element of
(
) with
, is defined as
It is interesting to notice that Riemann–Liouville derivative satisfies
,
k being a constant. For the same reasons than in the case of Caputo fractional derivatives, a Taylor power series of function
by means of Riemann–Liouville derivatives must be provided (see [
11]).
Theorem 2 (Proposition 3.1, [
12])
. Let us assume the continuous function has fractional derivatives of order , for any positive integer k and any α, ; then the following equality holds,where is the Riemann–Liouville derivative of order of . Recently, two fractional variants of Newton’s method whose order of convergence was
were proposed in [
6]. They were designed by using Caputo and Riemann–Liouville derivatives. In the following iterative expression, we can see the Caputo-fractional Newton’s method
with
as a damping parameter. Let us denote this method by CFN
. Let us remark that, if
, the linear convergence of CFN
method is not guaranteed. Our first aim is to design a new fractional Newton-type method with Caputo or Riemann–Liouville derivatives that will be the seed for higher-order multipoint fractional iterative schemes discussed later on. These new methods will converge with, at least, linear convergence for any
.
In this manuscript,
Section 2 is devoted to the design and convergence analysis of the new point-to-point and multipoint methods, both using Caputo and Riemann–Liouville fractional derivatives. The numerical performance and dependence on initial estimations is analyzed in
Section 3, for all the iterative schemes. Finally, some conclusions are stated in
Section 4.
2. Design and Convergence Analysis
In order to construct a new fractional version of Newton’s method, we are going to use the Taylor development of the nonlinear function whose root we are looking for. Therefore, let
be a continuous function having a Caputo-type fractional derivative of order
, for any
,
. Then, by using Theorem 1,
can be estimated by a first-degree Taylor polynomial around its root
,
Therefore, the term
can be isolated as
and a new estimation
of
can be obtained, assuming
and
, for any
, by means of the iterative scheme
Let us denote this method by CFN. The following result states the conditions that assure its convergence.
Theorem 3. Let be a the continuous function with fractional derivatives of order , for any positive integer k and , in the open interval D holding the zero of , denoted by . Let us suppose is continuous and not null at . Additionally, let us consider an initial estimation , close enough to . Therefore, the local convergence order of the fractional Newton method of Caputo typeis at least , that being , and the error equation isbeing denoted by , where and , . Proof. By means of Theorem 1, the Taylor expansion of
and its Caputo-derivative
around
can be expressed by
and
respectively, being
for
.
Therefore,
that results, by the parameter
, in
Newton’s generalized binomial Theorem states that
where the generalized binomial coefficient is (see [
13])
, so simplifying:
Let
and
,
Now, the design of a fractional Newton method using Riemann–Liouville derivatives can be done in a similar way.
Theorem 4. Let be a the continuous function with fractional derivatives of order , for any positive integer k and , in the open interval D holding the zero of , denoted by . Let us suppose is continuous and not null at . Additionally, let us consider an initial estimation , close enough to . Therefore, the local convergence order of the fractional Newton method of Riemann–Liouville type (denoted by R-LFN),is at least , where , and again the error equation is It is then concluded that, not only both new fractional methods of Newton-type have the same order of convergence, , but also their error equations coincide. Moreover, as , it can be concluded that its order of convergence is at least linear and reaches quadratic convergence for (as then it coincides with classical Newton’s method).
Traub-Type Methods with Fractional Derivatives
Now, we introduce the design of a fractional multipoint method with Caputo derivative using CFN
as first step. The underlying idea is to adapt to the fractional context a common tool of the design of iterative methods: the composition. Traub proves in [
7] that the direct composition of two iterative methods whose orders of convergence are
p and
q, respectively, is another iterative scheme with order
. Therefore, by composing Newton’s method with itself,
that is fourth-order convergent. However, it is not an efficient procedure as it has four functional evaluations per iteration. Moreover, Traub shows that using the derivative of the first step at the second one, the order results to be incremented in one unit regarding Newton’s step and, therefore, its efficiency increases.
Our aim now is to apply this idea to proposed fractional Newton-type method CFN, in order to measure the increasing of the convergence with the composition (and later reduction of the number of functional evaluations) in the case of iterative schemes that use fractional derivatives. We call the resulting scheme fractional Traub-type method and denote it by CFT when Caputo fractional derivative is used.
Theorem 5. Let be a the continuous function with fractional derivatives of order , for any positive integer k and , in the open interval D holding the zero of , denoted by . Let us suppose is continuous and not null at . Additionally, let us consider an initial estimation , close enough to . Therefore, the local convergence order of the fractional Traub-type method with Caputo derivativesbeingis at least , where , and the error equation isbeing for and Proof. As the first step
of scheme (
8) is CFN
, whose order of convergence has been proven in Theorem 3, we omit the calculations and give the result with enough error terms to be used in this proof:
where
A has been already defined and
Let us develop
:
where Newton’s generalized binomial Theorem must be used to obtain the expansion of
and
Let us remark that, for all , and but and .
Then, the Taylor development of quotient
results
Furthermore, applying again Newton’s generalized binomial Theorem, we get
As
, after some algebraic manipulations, the error equation results in
☐
In what follows, we introduce the design of a fractional Traub method with Riemann–Liouville derivative using R-LFN as first step. Let us denote this method R-LFT. In the following results, the convergence conditions are stated and the resulting order is obtained to be the same as in case of Caputo fractional derivative.
Theorem 6. Let be a the continuous function with fractional derivatives of order , for any positive integer k and , in the open interval D holding the zero of , denoted by . Let us suppose is continuous and non zero at . Additionally, let us consider an initial estimation , close enough to . Therefore, the local convergence order of the fractional Traub method with Riemann–Liouville derivativesbeingis at least , being , and again the error equation isbeing In the next section, we are going to test the Newton and Traub-type methods shown before on some nonlinear functions. Moreover, we also analyze their dependence on the initial estimations used.
3. Numerical Stability
To get the results shown in this section, we have used Matlab R2018b with double precision arithmetics,
or
as stopping criteria, and a maximum of 500 iterations. For calculation of the gamma function,
, we use the program made in [
14]. For the Mittag–Leffler function,
, we use the program provided by Igor Podlubny in Mathworks. Regarding the precision of these functions, gamma function is calculated with 15 digits of accuracy along the real axis and 13 elsewhere in
; and
for computing the Mittag–Lefler function has 9 significant digits of precision. Moreover, in all the numerical tests, we used
, as in Caputo and as in Riemann–Liouville derivatives.
We are going to test three standard nonlinear functions in order to make a comparison between the designed methods. Our first function is
with roots
,
,
,
,
and
. The fractional derivatives used are:
In
Table 1, we can see that CFN
requires fewer iterations to converge than CFN
, for the same real value of
and the same values of
.
In the case of R-LFN
and R-LFN
, the same behavior as in the Caputo case can be observed. In
Table 2, R-LFN
requires fewer iterations than R-LFN
for a real value of
, while R-LFN
requires fewer iterations than R-LFN
for pure imaginary initial estimations with a large value for their imaginary part (see
Table 3 and
Table 4). Moreover, if we compare the Traub-type methods CFT and R-LFT with their first steps CFN
and R-LFN
respectively (for
), we can see that Traub method R-LFT requires fewer iterations than its first step. Indeed, it can be observed that, with the same initial estimation, to change the value of
, suppose a different root found.
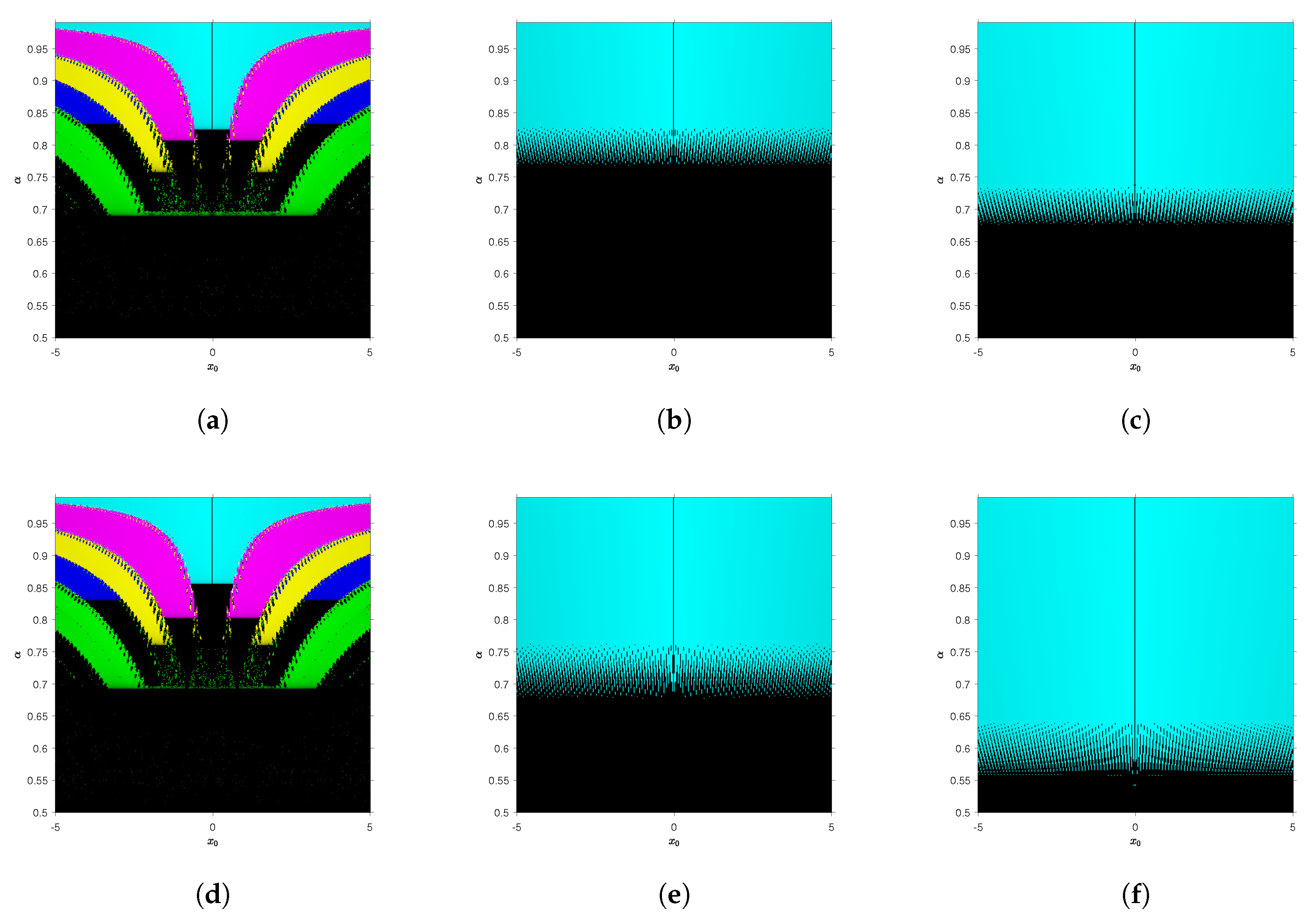
Now, we are going to analyze the dependence on the initial estimation of the Newton and Traub-type methods by using convergence planes defined in [
15]. In them (see, for example,
Figure 1) the abscissa axis corresponds to the starting guess and the fractional index
appears in the ordinate axis. A mesh of
points is used. Points that are not painted in black color correspond to those pairs of initial estimations and values of
that converge to one of the roots with a tolerance of
. Different colors mean convergence to different roots. Therefore, when a point is painted in black, this shows that no root is found in a maximum of 500 iterations. Moreover, for all convergence planes, the percentage of convergent pairs
is calculated, in order to compare the performance of the methods.
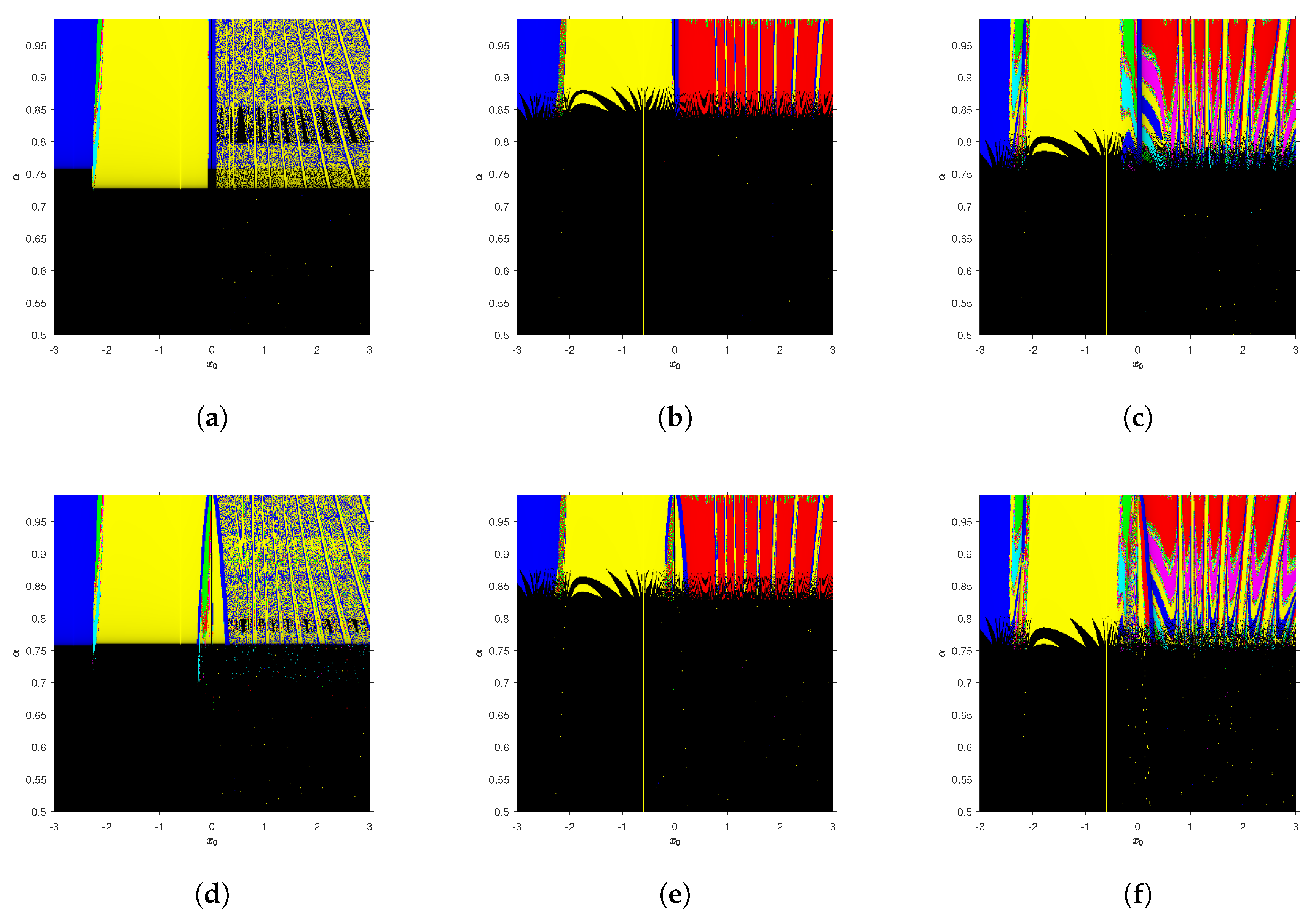
In
Figure 1 and
Figure 2, we see that CFN
and R-LFN
have a higher percentage of convergence than CFN
and R-LFN
respectively, not only with real or imaginary initial estimations, but also with Caputo or Riemann–Liouville derivatives. It can be also observed that Traub-type methods have a higher percentage of convergence than their first steps, with independence of the fractional derivative used. Moreover, the rate of convergent pairs
is almost the same in Traub-type and CFN
or R-LFN
, with higher convergence order.
Our second test function is
, which has an only real root,
. The fractional derivatives used in this case are:
In this case, is necessary to use a value of
closer to 1 to ensure the convergence. Now, there were no imaginary values used for the initial estimations due to erratic behavior of the results. For the real initial estimation used, see in
Table 5 that CFN
requires far fewer iterations than CFN
. However, methods using Riemann–Liouville fractional derivatives do not converge, in general. This is the reason why there is not a table for this case.
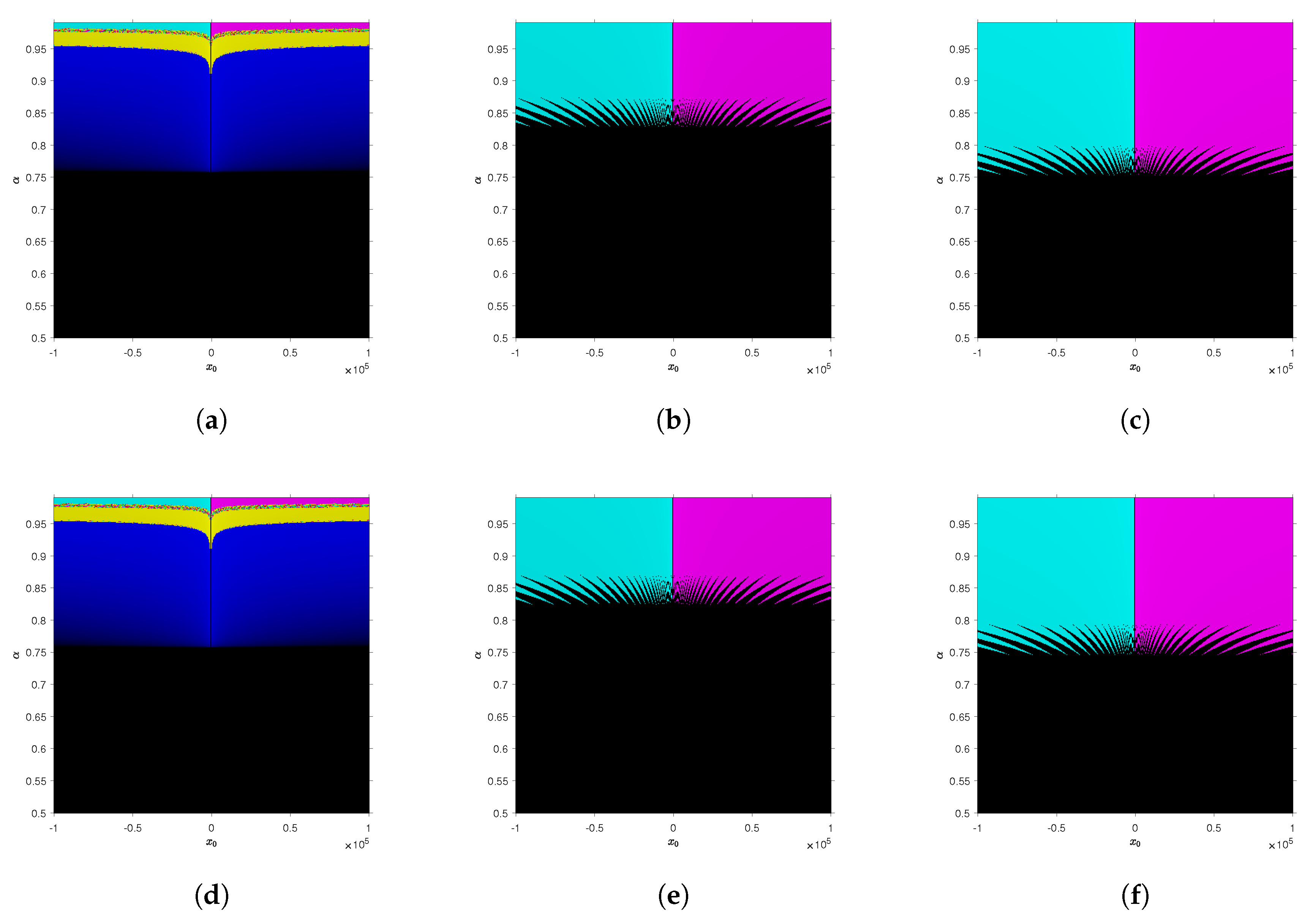
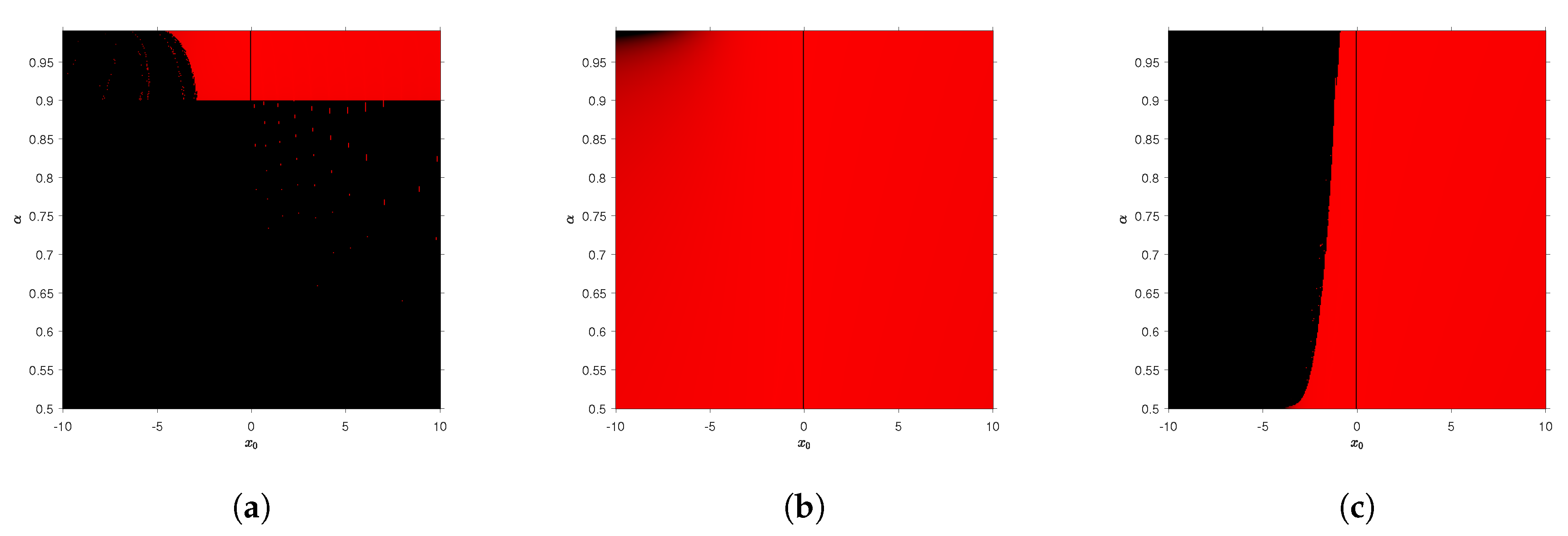
By changing the initial estimation, we see for test function
, different performances in the convergence planes than in the polynomial function
. In
Figure 3, we can see that CFN
highly improves the percentage of convergence of CFN
for real values of initial estimations. Moreover, the percentage of convergence of fractional methods using Riemann–Liouville derivative is lower than
, so they are omitted in the figure; meanwhile, there is convergence rate lower than
with both methods for imaginary values of initial estimations in Caputo-type methods and the low percentage, convergence holds for both Riemann–Liouville fractional methods.
Regarding Traub-type methods, it can be observed in
Figure 3 that it improves the percentage convergence of CFN
. This is not the case regarding CFN
, but it still has a high percentage of convergent points and a higher order of convergence than its first step.
Our last test function is
; some real roots are
,
,
,
,
,
,
,
,
,
,
,
and
. The fractional derivatives used in this case are:
In some cases, the methods can converge to the root
or
, that is far from the initial estimation used. It is observed in
Table 6 that the number of different roots that are reached by CFN
and CFT methods is higher than that of CFN
. This is a usual fact that has been observed in general in the numerical tests and can be considered as an advantage of these new methods. On the other hand, tests with pure imaginary initial estimations have not been included because there is no convergence for these cases with
.
We can also see that the number of iterations does not necessarily reduce when
increases, and also that all the methods converge to different roots. Additionally, in
Table 7 the observed performance is similar but the convergence in general is slower than in Caputo-type methods, the number of iterations required for satisfying the stopping criterion being higher.
Let us also remark that, in
Table 6 and
Table 7, the classical Newton and Traub’s methods (
) show the worst performances, as they do not converge to any of the solutions in the maximum number of iterations. On the contrary, proposed methods for
are able to reach different solutions within a reasonable number of iterations.
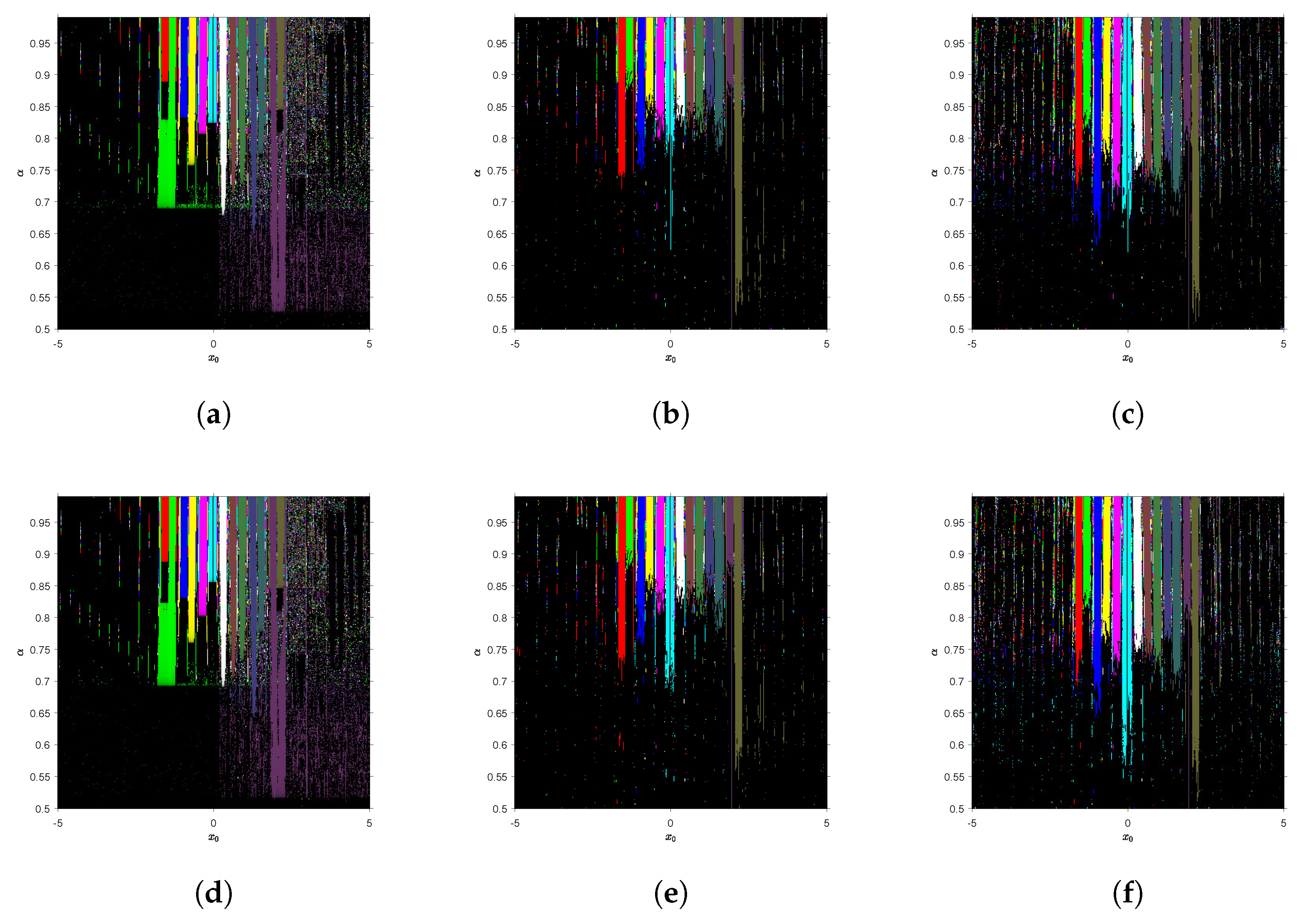
Regarding the wideness of the basins of attraction of the roots, in
Figure 4 and
Figure 5 we can see the convergence planes corresponding to all the methods applied on
for real and pure imaginary initial estimations. We notice that the percentage of converging initial pairs
is higher in case of imaginary initial guesses and is slightly better in case of methods using Riemann–Liouville fractional derivatives. Moreover, although many roots are found by using all the iterative schemes with real initial estimations, there is a clear difference when pure imaginary
is employed: only one root can be found by the proposed methods and several ones are obtained by scheme CFN
. Indeed, it can be stated that the wideness of the basins of attraction of the roots is higher when Traub-type methods are employed, compared with their first step. The rates of convergence are also higher or similar to Newton-type ones.
4. Concluding Remarks
Two new fractional Newton-type methods and two fractional Traub-type schemes have been designed by using Caputo and Riemann–Liouville derivatives. Improving the existing ones, the convergence properties of these procedures imply always (at least) linear convergence, reaching order and , respectively. Although the interest in this kind of method is mainly theoretical, some numerical tests have been done, and the dependence on the initial estimation has been analyzed.
It can be concluded that Traub-type procedures improve Newton-type ones, not only because they require fewer iterations, but also because they have higher percentages of convergence. Additionally, a better performance of iterative methods based on Caputo derivatives, with respect to Riemann–Liouville based schemes, has been observed.
The test made shows that, for some problems, the methods using fractional derivatives reach different solutions with the same initial approximation. In addition, in the case of example , the fractional iterative schemes work better than the classical Newton and Traub’s methods (), which do not converge within 500 iterations.