Least-Square-Based Three-Term Conjugate Gradient Projection Method for ℓ1-Norm Problems with Application to Compressed Sensing
Abstract
1. Introduction
2. Reformulation of the Model
3. Algorithm
| Algorithm 1 DF-LSTT |
Input. Choose any arbitrary initial point , the positive constants: , Step 0. Let and Step 1. Determine the step-size , where i is the smallest non-negative integer such that the following line search is satisfied: Step 2. Compute
Step 3. If and stop. Otherwise, compute the next iterate by
Step 4. If the stopping criterion is satisfied, that is, if stop. Otherwise, compute the next search direction by
Step 5. Finally, we set and return to step 1. |
4. Global Convergence
- 1.
- and are bounded.
- 2.
- 3.
5. Numerical Experiment
5.1. Experiments on the -Norm Regularization Problem in Compressive Sensing
5.2. Experiments on Some Large-Scaled Monotone Nonlinear Equations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Donoho, D.L. For most large underdetermined systems of linear equations the minimal ℓ1-norm solution is also the sparsest solution. Commun. Pure Appl. Math. 2006, 59, 797–829. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.L.; Santos, J.M.; Pauly, J.M. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar]
- Candes, E.; Romberg, J. Sparsity and incoherence in compressive sampling. Inverse Probl. 2007, 23, 969. [Google Scholar] [CrossRef]
- Daubechies, I.; Defrise, M.; De Mol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. J. Issued Courant Inst. Math. Sci. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Hale, E.T.; Yin, W.; Zhang, Y. A fixed-point continuation method for l1-regularized minimization with applications to compressed sensing. CAAM TR07-07 Rice Univ. 2007, 43, 44. [Google Scholar]
- Huang, S.; Wan, Z. A new nonmonotone spectral residual method for nonsmooth nonlinear equations. J. Comput. Appl. Math. 2017, 313, 82–101. [Google Scholar] [CrossRef]
- He, L.; Chang, T.C.; Osher, S. MR image reconstruction from sparse radial samples by using iterative refinement procedures. In Proceedings of the 13th Annual Meeting of ISMRM, Seattle, WA, USA, 6–12 May 2006; Volume 696. [Google Scholar]
- Moreau, J.J. Fonctions Convexes Duales et Points Proximaux dans un Espace Hilbertien. 1962. Available online: http://www.numdam.org/article/BSMF_1965__93__273_0.pdf (accessed on 26 February 2020).
- Figueiredo, M.A.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, Q.; Hu, Q. Non-smooth equations based method for ℓ1-norm problems with applications to compressed sensing. Nonlinear Anal. Theory Methods Appl. 2011, 74, 3570–3577. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhu, H. A conjugate gradient method to solve convex constrained monotone equations with applications in compressive sensing. J. Math. Anal. Appl. 2013, 405, 310–319. [Google Scholar] [CrossRef]
- Beale, E.M.L. A derivation of conjugate gradients. In Numerical Methods for Nonlinear Optimization; Lootsma, F.A., Ed.; Academic Press: London, UK, 1972. [Google Scholar]
- Nazareth, L. A conjugate direction algorithm without line searches. J. Optim. Theory Appl. 1977, 23, 373–387. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, W.; Li, D.H. A descent modified Polak–Ribière–Polyak conjugate gradient method and its global convergence. IMA J. Numer. Anal. 2006, 26, 629–640. [Google Scholar] [CrossRef]
- Andrei, N. On three-term conjugate gradient algorithms for unconstrained optimization. Appl. Math. Comput. 2013, 219, 6316–6327. [Google Scholar] [CrossRef]
- Liu, J.; Li, S. New three-term conjugate gradient method with guaranteed global convergence. Int. J. Comput. Math. 2014, 91, 1744–1754. [Google Scholar] [CrossRef]
- Tang, C.; Li, S.; Cui, Z. Least-squares-based three-term conjugate gradient methods. J. Inequalities Appl. 2020, 2020, 27. [Google Scholar] [CrossRef]
- Fletcher, R.; Reeves, C.M. Function minimization by conjugate gradients. Comput. J. 1964, 7, 149–154. [Google Scholar] [CrossRef]
- Solodov, M.V.; Svaiter, B.F. A new projection method for variational inequality problems. SIAM J. Control. Optim. 1999, 37, 765–776. [Google Scholar] [CrossRef]
- Liu, J.; Feng, Y. A derivative-free iterative method for nonlinear monotone equations with convex constraints. Numer. Algorithms 2018, 82, 245–262. [Google Scholar] [CrossRef]
- Liu, J.; Xu, J.; Zhang, L. Partially symmetrical derivative-free Liu–Storey projection method for convex constrained equations. Int. J. Comput. Math. 2019, 96, 1787–1798. [Google Scholar] [CrossRef]
- Ibrahim, A.H.; Garba, A.I.; Usman, H.; Abubakar, J.; Abubakar, A.B. Derivative-free RMIL conjugate gradient algorithm for convex constrained equations. Thai J. Math. 2019, 18, 212–232. [Google Scholar]
- Abubakar, A.B.; Rilwan, J.; Yimer, S.E.; Ibrahim, A.H.; Ahmed, I. Spectral three-term conjugate descent method for solving nonlinear monotone equations with convex constraints. Thai J. Math. 2020, 18, 501–517. [Google Scholar]
- Ibrahim, A.H.; Kumam, P.; Abubakar, A.B.; Jirakitpuwapat, W.; Abubakar, J. A hybrid conjugate gradient algorithm for constrained monotone equations with application in compressive sensing. Heliyon 2020, 6, e03466. [Google Scholar] [CrossRef] [PubMed]
- Abubakar, A.B.; Kumam, P.; Awwal, A.M. Global convergence via descent modified three-term conjugate gradient projection algorithm with applications to signal recovery. Results Appl. Math. 2019, 4, 100069. [Google Scholar] [CrossRef]
- Abubakar, A.B.; Kumam, P.; Awwal, A.M. An inexact conjugate gradient method for symmetric nonlinear equations. Comput. Math. Methods 2019, 1, e1065. [Google Scholar] [CrossRef]
- Pang, J.S. Inexact Newton methods for the nonlinear complementarity problem. Math. Program. 1986, 36, 54–71. [Google Scholar] [CrossRef]
- Zhou, W.; Li, D. Limited memory BFGS method for nonlinear monotone equations. J. Comput. Math. 2007, 25, 89–96. [Google Scholar]
- Liu, J.; Li, S. A projection method for convex constrained monotone nonlinear equations with applications. Comput. Math. Appl. 2015, 70, 2442–2453. [Google Scholar] [CrossRef]
- Wan, Z.; Guo, J.; Liu, J.; Liu, W. A modified spectral conjugate gradient projection method for signal recovery. Signal Image Video Process. 2018, 12, 1455–1462. [Google Scholar] [CrossRef]
- Kim, S.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. A method for large-scale ℓ1-regularized least squares. IEEE J. Sel. Top. Signal Process. 2007, 1, 606–617. [Google Scholar] [CrossRef]
- Abubakar, A.B.; Kumam, P.; Mohammad, H.; Awwal, A.M.; Sitthithakerngkiet, K. A Modified Fletcher–Reeves Conjugate Gradient Method for Monotone Nonlinear Equations with Some Applications. Mathematics 2019, 7, 745. [Google Scholar] [CrossRef]
- Bovik, A.C. Handbook of Image and Video Processing; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Lajevardi, S.M. Structural similarity classifier for facial expression recognition. Signal Image Video Process. 2014, 8, 1103–1110. [Google Scholar] [CrossRef]
- La Cruz, W.; Martínez, J.; Raydan, M. Spectral residual method without gradient information for solving large-scale nonlinear systems of equations. Math. Comput. 2006, 75, 1429–1448. [Google Scholar] [CrossRef]
- La Cruz, W. A spectral algorithm for large-scale systems of nonlinear monotone equations. Numer. Algorithms 2017, 76, 1109–1130. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Xu, C. A projection method for a system of nonlinear monotone equations with convex constraints. Math. Methods Oper. Res. 2007, 66, 33–46. [Google Scholar] [CrossRef]
- Bing, Y.; Lin, G. An efficient implementation of Merrill’s method for sparse or partially separable systems of nonlinear equations. SIAM J. Optim. 1991, 1, 206–221. [Google Scholar] [CrossRef]
- Yu, G.; Niu, S.; Ma, J. Multivariate spectral gradient projection method for nonlinear monotone equations with convex constraints. J. Ind. Manag. Optim. 2013, 9, 117–129. [Google Scholar] [CrossRef]
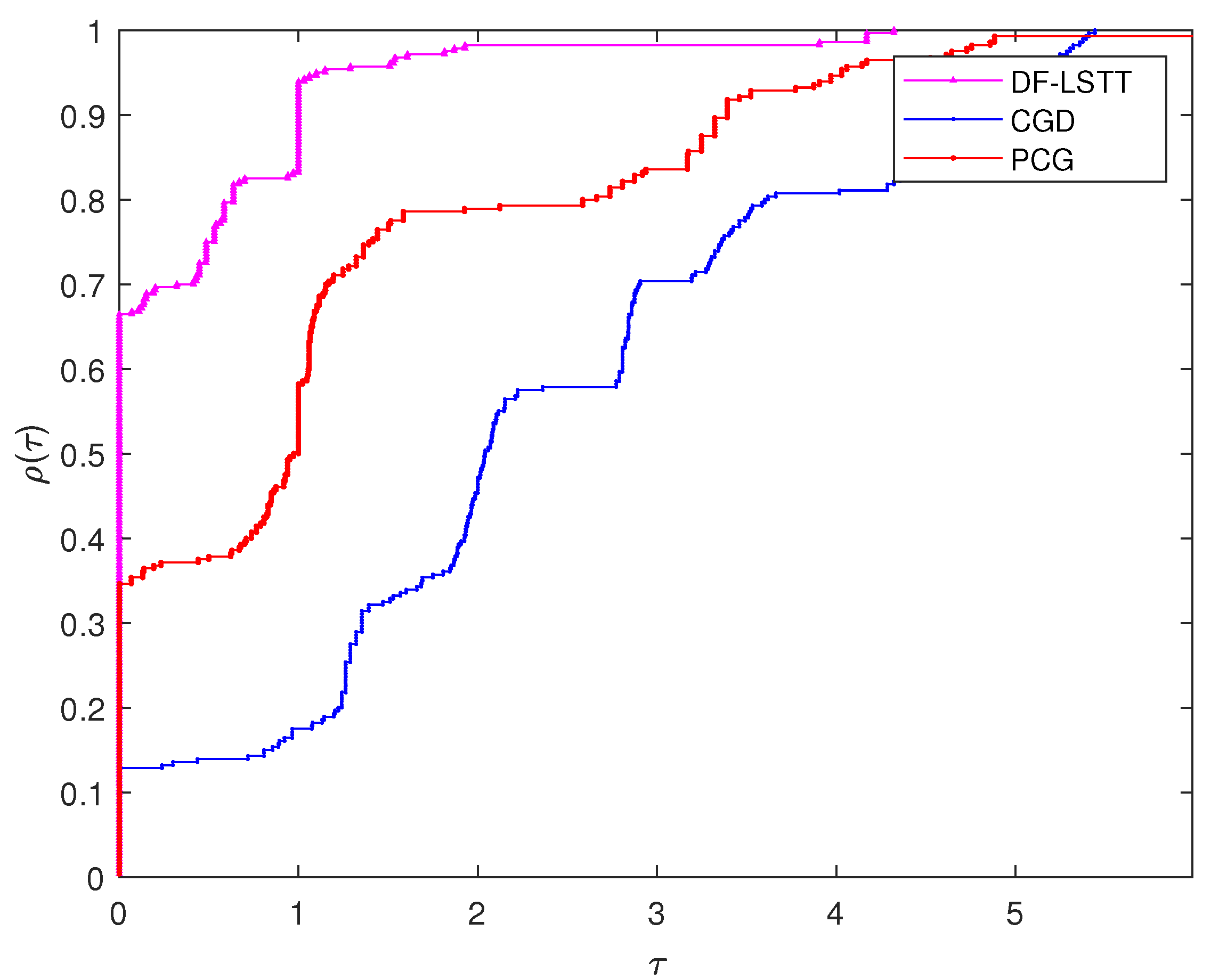
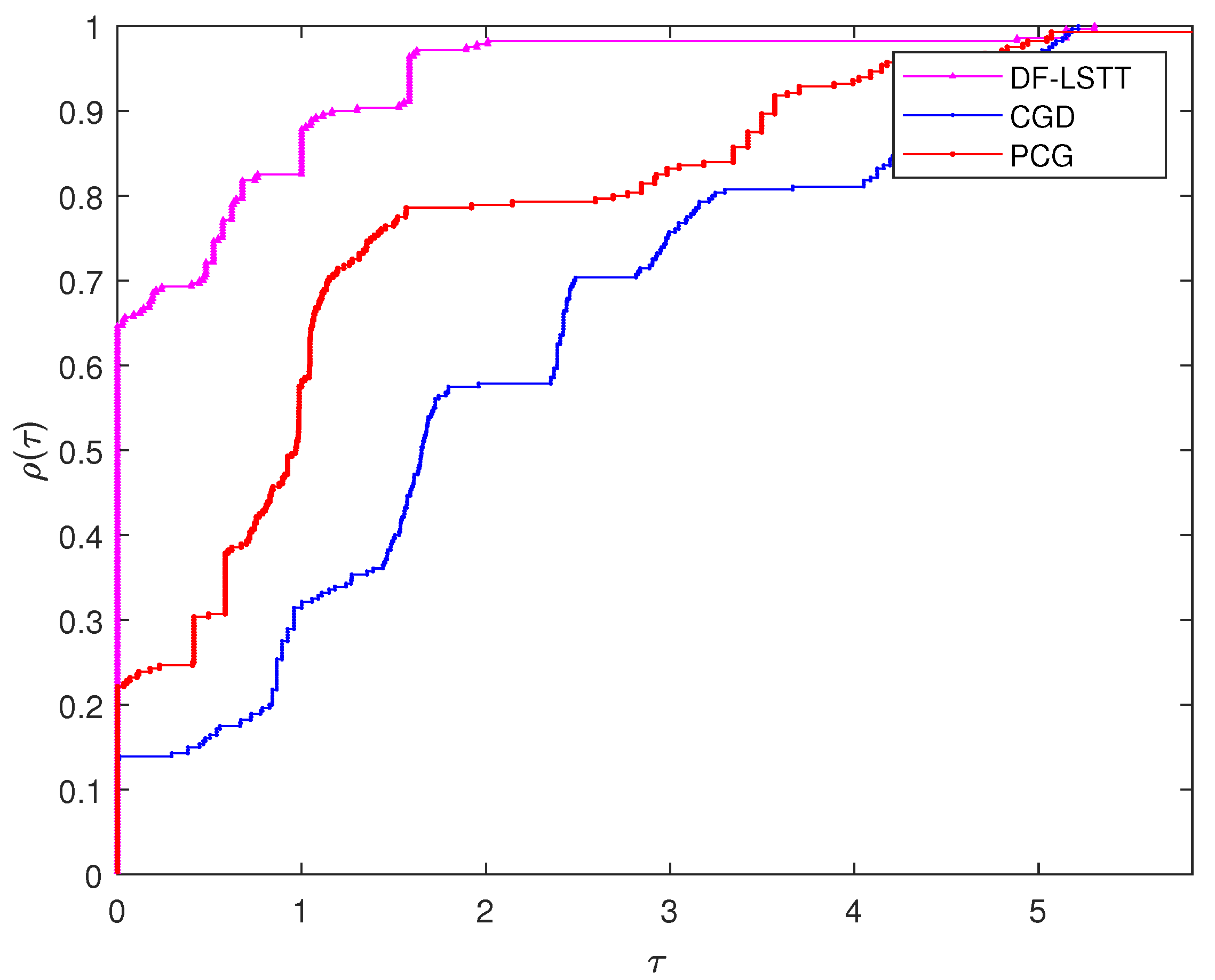
- Dolan, E.D.; Moré, J.J. Benchmarking optimization software with performance profiles. Math. Program. 2002, 91, 201–213. [Google Scholar] [CrossRef]
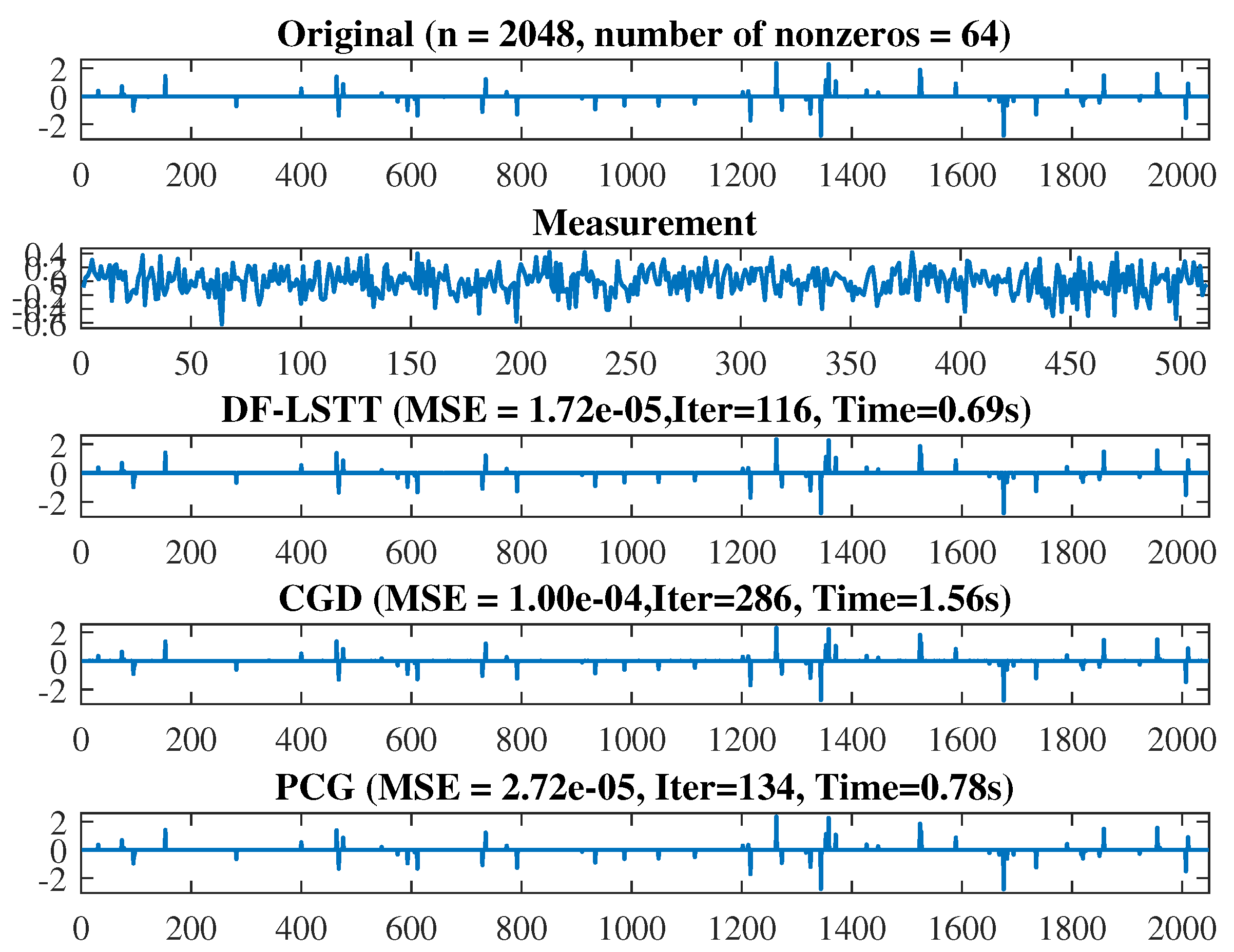
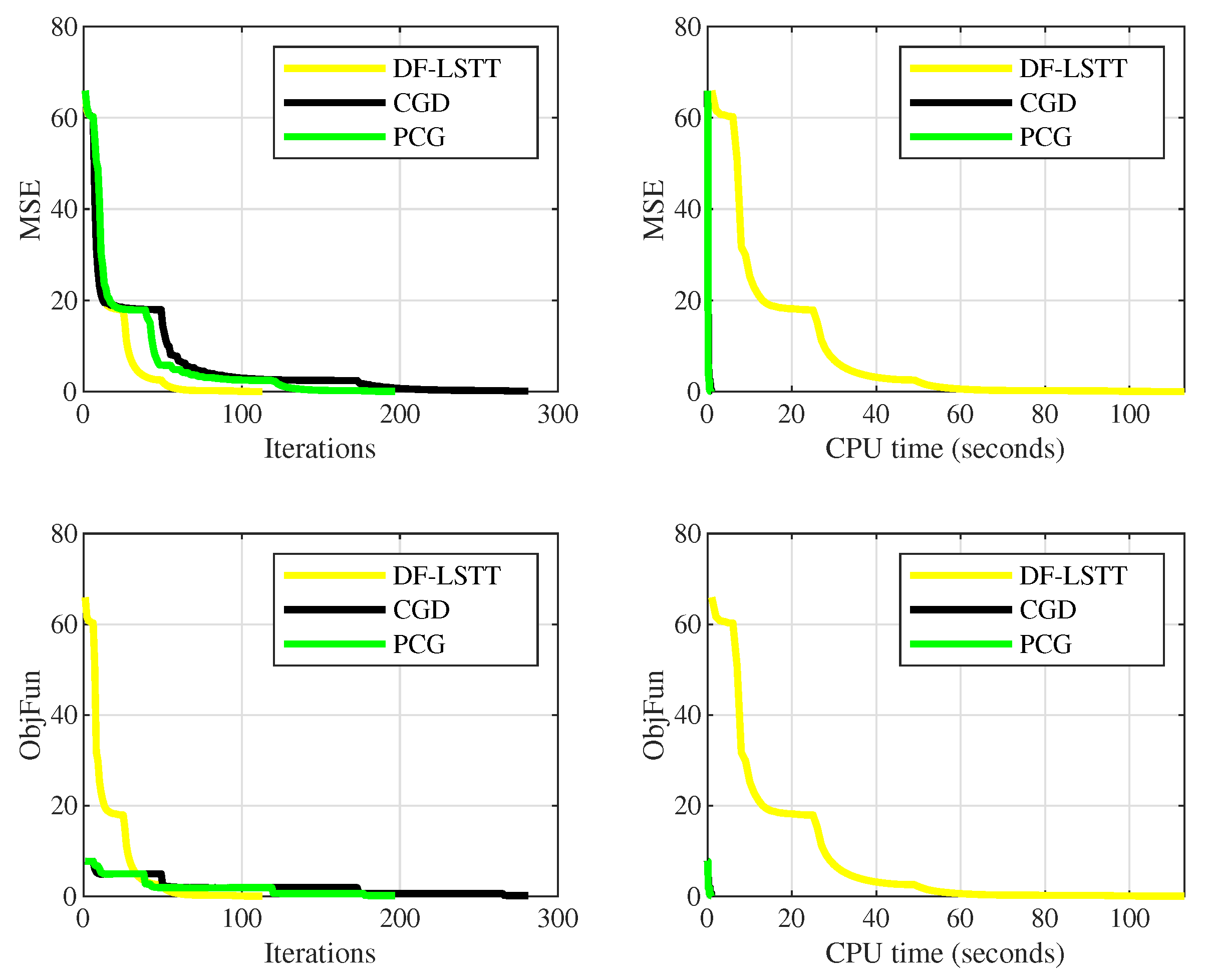



| DF-LSTT | CGD | PCG | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ITER | MSE | TIME | ITER | MSE | Time | ITER | MSE | Time | |
| 137 | 7.39 | 1.31 | 259 | 4.51 | 1.7 | 184 | 1.50 | 0.88 | |
| 88 | 9.18 | 0.73 | 187 | 7.04 | 1.38 | 144 | 1.63 | 1.42 | |
| 90 | 1.40 | 0.66 | 231 | 3.78 | 1.73 | 144 | 1.99 | 1.61 | |
| 86 | 1.26 | 0.78 | 228 | 2.15 | 1.41 | 82 | 5.32 | 0.78 | |
| 97 | 1.22 | 0.7 | 245 | 6.75 | 1.55 | 118 | 5.99 | 0.78 | |
| 87 | 9.72 | 0.64 | 199 | 5.13 | 1.33 | 82 | 4.50 | 0.83 | |
| 115 | 5.39 | 0.84 | 211 | 3.67 | 1.64 | 152 | 9.68 | 0.97 | |
| 89 | 1.31 | 1.27 | 158 | 1.56 | 3.14 | 150 | 1.16 | 1.59 | |
| 105 | 1.35 | 0.63 | 280 | 4.82 | 1.89 | 152 | 2.23 | 0.86 | |
| 97 | 5.22 | 0.63 | 228 | 3.89 | 1.45 | 154 | 8.00 | 2.3 | |
| Average | 99.1 | 1.02 | 0.819 | 222.6 | 5.73 | 1.722 | 136.2 | 1.14 | 1.202 |
| DF-LSTT | CGD | SGCS | MFRM | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Image | SNR | PSNR | SSIM | SNR | PSNR | SSIM | SNR | PSNR | SSIM | SNR | PSNR | SSIM |
| Tiffany | 21.25 | 23.08 | 0.9204 | 21.20 | 23.04 | 0.9193 | 21.24 | 23.07 | 0.9202 | 20.87 | 22.70 | 0.9128 |
| Lenna | 16.98 | 22.31 | 0.9176 | 16.93 | 22.26 | 0.9166 | 16.96 | 22.29 | 0.9173 | 16.60 | 21.94 | 0.9104 |
| Barbara | 13.81 | 20.23 | 0.6377 | 13.77 | 20.19 | 0.6355 | 13.80 | 20.22 | 0.6373 | 13.57 | 19.99 | 0.6231 |
| Average | 17.35 | 21.87 | 0.8252 | 17.30 | 21.83 | 0.8238 | 17.33 | 21.86 | 0.8249 | 17.01 | 21.54 | 0.8154 |
| DF-LSTT | CGD | PCG | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIM | INP | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM |
| 1000 | 2 | 7 | 0.011683 | 0.00 | 42 | 125 | 0.032606 | 9.97 | 18 | 71 | 0.020567 | 5.72 | |
| 2 | 7 | 0.007157 | 0.00 | 45 | 134 | 0.020408 | 9.45 | 18 | 71 | 0.017477 | 9.82 | ||
| 2 | 7 | 0.059349 | 0.00 | 48 | 143 | 0.025053 | 9.82 | 19 | 75 | 0.010401 | 7.10 | ||
| 2 | 7 | 0.010097 | 0.00 | 50 | 149 | 0.020462 | 9.70 | 18 | 71 | 0.014602 | 8.27 | ||
| 31 | 124 | 0.075653 | 7.60 | 51 | 152 | 0.022198 | 8.17 | 63 | 251 | 0.035587 | 9.58 | ||
| 14 | 55 | 0.041615 | 0.00 | 51 | 152 | 0.017499 | 8.56 | 61 | 243 | 0.070899 | 9.15 | ||
| 44 | 175 | 0.052359 | 1.83 | 38 | 113 | 0.013579 | 9.14 | 18 | 71 | 0.009228 | 9.24 | ||
| 5000 | 2 | 7 | 0.023049 | 0.00 | 41 | 122 | 0.045814 | 8.34 | 18 | 71 | 0.037294 | 7.42 | |
| 2 | 7 | 0.013178 | 0.00 | 43 | 128 | 0.051819 | 9.81 | 19 | 75 | 0.030883 | 6.53 | ||
| 2 | 7 | 0.008287 | 0.00 | 47 | 140 | 0.056948 | 8.05 | 20 | 79 | 0.040342 | 5.20 | ||
| 2 | 7 | 0.008819 | 0.00 | 48 | 143 | 0.060879 | 9.93 | 19 | 75 | 0.03691 | 8.10 | ||
| 28 | 112 | 0.14831 | 6.87 | 49 | 146 | 0.053006 | 8.36 | 62 | 247 | 0.0775 | 9.53 | ||
| 28 | 112 | 0.17661 | 3.38 | 49 | 146 | 0.061534 | 8.76 | 60 | 239 | 0.081647 | 9.10 | ||
| 19 | 75 | 0.10719 | 0.00 | 40 | 119 | 0.052358 | 7.70 | 19 | 75 | 0.042343 | 9.16 | ||
| 10,000 | 2 | 7 | 0.017941 | 0.00 | 40 | 119 | 0.082014 | 8.97 | 18 | 71 | 0.055224 | 9.50 | |
| 2 | 7 | 0.025597 | 0.00 | 43 | 128 | 0.074301 | 8.26 | 19 | 75 | 0.050823 | 8.15 | ||
| 2 | 7 | 0.015978 | 0.00 | 46 | 137 | 0.096062 | 8.46 | 20 | 79 | 0.046486 | 6.74 | ||
| 2 | 7 | 0.24659 | 0.00 | 48 | 143 | 0.097356 | 8.30 | 20 | 79 | 0.05297 | 5.11 | ||
| 39 | 156 | 0.86102 | 4.62 | 48 | 143 | 0.11071 | 8.75 | 62 | 247 | 0.19236 | 8.87 | ||
| 2 | 7 | 0.023214 | 0.00 | 48 | 143 | 0.087449 | 9.17 | 59 | 235 | 0.16649 | 9.96 | ||
| 11 | 43 | 0.089553 | 0.00 | 37 | 110 | 0.072561 | 7.58 | 20 | 79 | 0.055156 | 5.82 | ||
| 50,000 | 2 | 7 | 0.046111 | 0.00 | 39 | 116 | 0.29127 | 8.43 | 19 | 75 | 0.21501 | 8.80 | |
| 2 | 7 | 0.088396 | 0.00 | 41 | 122 | 0.32975 | 9.37 | 20 | 79 | 0.27646 | 7.39 | ||
| 2 | 7 | 0.050768 | 0.00 | 44 | 131 | 0.36349 | 9.16 | 21 | 83 | 0.28492 | 6.31 | ||
| 2 | 7 | 0.052953 | 0.00 | 46 | 137 | 0.34443 | 8.84 | 21 | 83 | 0.21931 | 5.10 | ||
| 34 | 136 | 1.336 | 2.22 | 46 | 137 | 0.41225 | 9.34 | 61 | 243 | 0.5975 | 8.85 | ||
| 2 | 7 | 0.10667 | 0.00 | 46 | 137 | 0.44581 | 9.78 | 59 | 235 | 0.59777 | 8.50 | ||
| 64 | 256 | 2.2443 | 4.32 | 46 | 137 | 0.44419 | 8.86 | 21 | 83 | 0.2052 | 5.79 | ||
| 100,000 | 2 | 7 | 0.092134 | 0.00 | 39 | 116 | 0.55718 | 7.72 | 20 | 79 | 0.37816 | 5.52 | |
| 2 | 7 | 0.14977 | 0.00 | 41 | 122 | 0.57738 | 8.33 | 21 | 83 | 0.45721 | 4.62 | ||
| 2 | 7 | 0.093678 | 0.00 | 44 | 131 | 0.62707 | 7.92 | 21 | 83 | 0.54042 | 8.78 | ||
| 2 | 7 | 0.10506 | 0.00 | 45 | 134 | 0.63408 | 9.66 | 21 | 83 | 0.53141 | 7.21 | ||
| 39 | 156 | 9.4738 | 9.14 | 46 | 137 | 0.66002 | 7.99 | 60 | 239 | 1.1271 | 9.73 | ||
| 2 | 7 | 0.32882 | 0.00 | 46 | 137 | 0.68921 | 8.38 | 58 | 231 | 1.1519 | 9.42 | ||
| 61 | 244 | 13.7075 | 7.48 | 41 | 122 | 0.58348 | 9.17 | 21 | 83 | 0.38529 | 8.20 | ||
| DF-LSTT | CGD | PCG | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIM | INP | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM |
| 1000 | 6 | 23 | 0.018184 | 1.73 | 55 | 163 | 0.032169 | 8.99 | 15 | 58 | 0.011849 | 8.59 | |
| 6 | 23 | 0.014572 | 2.51 | 61 | 181 | 0.0357 | 8.88 | 11 | 41 | 0.010006 | 9.07 | ||
| 6 | 23 | 0.019846 | 5.60 | 69 | 205 | 0.032634 | 8.33 | 17 | 65 | 0.012605 | 6.44 | ||
| 6 | 23 | 0.057022 | 1.19 | 76 | 226 | 0.028091 | 9.17 | 18 | 68 | 0.014979 | 6.00 | ||
| 8 | 31 | 0.030773 | 1.98 | 78 | 232 | 0.039636 | 9.18 | 13 | 47 | 0.009625 | 7.58 | ||
| 7 | 27 | 0.014646 | 2.53 | 81 | 241 | 0.03899 | 8.64 | 18 | 67 | 0.011159 | 5.40 | ||
| 14 | 55 | 0.026256 | 6.83 | 72 | 214 | 0.032568 | 8.68 | 19 | 73 | 0.016356 | 6.13 | ||
| 5000 | 6 | 23 | 0.046357 | 4.66 | 59 | 175 | 0.08852 | 8.02 | 16 | 62 | 0.037321 | 9.35 | |
| 6 | 23 | 0.07737 | 6.75 | 64 | 190 | 0.10686 | 9.97 | 12 | 45 | 0.030551 | 8.80 | ||
| 7 | 27 | 0.068471 | 2.49 | 72 | 214 | 0.12192 | 9.37 | 18 | 69 | 0.047498 | 6.98 | ||
| 7 | 27 | 0.1053 | 7.27 | 80 | 238 | 0.12654 | 8.26 | 19 | 72 | 0.039088 | 6.45 | ||
| 8 | 31 | 0.065362 | 5.25 | 82 | 244 | 0.11871 | 8.26 | 14 | 51 | 0.03502 | 6.71 | ||
| 7 | 27 | 0.062662 | 7.28 | 84 | 250 | 0.13106 | 9.71 | 19 | 71 | 0.040604 | 5.71 | ||
| 23 | 91 | 0.45265 | 1.77 | 75 | 223 | 0.16438 | 9.73 | 20 | 77 | 0.059424 | 6.86 | ||
| 10,000 | 6 | 23 | 0.081017 | 6.73 | 60 | 178 | 0.16239 | 9.04 | 17 | 66 | 0.075512 | 6.60 | |
| 6 | 23 | 0.15334 | 9.76 | 66 | 196 | 0.16906 | 9.00 | 13 | 49 | 0.041324 | 6.11 | ||
| 7 | 27 | 0.11084 | 3.61 | 74 | 220 | 0.19362 | 8.46 | 18 | 69 | 0.076734 | 9.83 | ||
| 5 | 19 | 0.076488 | 6.03 | 81 | 241 | 0.23663 | 9.32 | 19 | 72 | 0.064377 | 9.07 | ||
| 8 | 31 | 0.25185 | 7.57 | 83 | 247 | 0.21784 | 9.33 | 14 | 51 | 0.050394 | 9.18 | ||
| 8 | 31 | 0.15676 | 1.66 | 86 | 256 | 0.23307 | 8.77 | 19 | 71 | 0.075462 | 8.02 | ||
| 27 | 107 | 1.1061 | 4.66 | 77 | 229 | 0.27924 | 8.81 | 20 | 77 | 0.088795 | 9.69 | ||
| 50,000 | 7 | 27 | 0.5849 | 2.40 | 64 | 190 | 0.70165 | 8.26 | 18 | 70 | 0.25185 | 7.37 | |
| 7 | 27 | 0.48516 | 3.47 | 70 | 208 | 0.75749 | 8.23 | 14 | 53 | 0.27213 | 6.74 | ||
| 7 | 27 | 1.0522 | 8.23 | 77 | 229 | 0.81368 | 9.67 | 20 | 77 | 0.31128 | 5.50 | ||
| 7 | 27 | 0.34532 | 2.05 | 85 | 253 | 0.93153 | 8.52 | 21 | 80 | 0.28943 | 5.07 | ||
| 9 | 35 | 4.3347 | 2.69 | 87 | 259 | 0.94105 | 8.53 | 16 | 59 | 0.22366 | 5.02 | ||
| 8 | 31 | 0.92387 | 3.80 | 90 | 268 | 1.0832 | 8.02 | 20 | 75 | 0.27706 | 8.93 | ||
| 20 | 79 | 1.8206 | 8.21 | 81 | 241 | 1.4008 | 8.03 | 22 | 85 | 0.39411 | 5.41 | ||
| 100,000 | 7 | 27 | 0.73406 | 3.39 | 65 | 193 | 1.3721 | 9.34 | 19 | 74 | 0.52829 | 5.22 | |
| 7 | 27 | 0.49843 | 4.92 | 71 | 211 | 1.5287 | 9.30 | 14 | 53 | 0.37191 | 9.52 | ||
| 8 | 31 | 0.75063 | 1.82 | 79 | 235 | 1.6725 | 8.75 | 20 | 77 | 0.54637 | 7.78 | ||
| 7 | 27 | 0.50287 | 3.21 | 86 | 256 | 1.8409 | 9.64 | 21 | 80 | 0.57391 | 7.17 | ||
| 9 | 35 | 0.76034 | 3.81 | 88 | 262 | 1.9085 | 9.64 | 16 | 59 | 0.52223 | 7.07 | ||
| 8 | 31 | 0.48187 | 5.39 | 91 | 271 | 1.9642 | 9.07 | 21 | 79 | 0.72579 | 6.32 | ||
| 21 | 83 | 1.7606 | 1.06 | 82 | 244 | 2.5148 | 9.07 | 22 | 85 | 0.85567 | 7.66 | ||
| DF-LSTT | CGD | PCG | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIM | INP | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM |
| 1000 | 2 | 6 | 0.004359 | 0 | 1 | 2 | 0.029302 | 0 | 1 | 3 | 0.006887 | 0 | |
| 2 | 6 | 0.004097 | 0 | 1 | 2 | 0.003218 | 0 | 1 | 3 | 0.002975 | 0 | ||
| 2 | 6 | 0.002719 | 0 | 1 | 2 | 0.002851 | 0 | 1 | 3 | 0.007665 | 0 | ||
| 2 | 6 | 0.002236 | 0 | 1 | 3 | 0.003144 | 0 | 1 | 4 | 0.007096 | 0 | ||
| 2 | 6 | 0.002477 | 0 | 1 | 3 | 0.004593 | 0 | 1 | 4 | 0.005078 | 0 | ||
| 2 | 6 | 0.002744 | 0 | 1 | 3 | 0.003093 | 0 | 1 | 4 | 0.002427 | 0 | ||
| 15 | 59 | 0.056123 | 7.18 | 1 | 2 | 0.003046 | 0 | 1 | 3 | 0.006539 | 0 | ||
| 5000 | 2 | 6 | 0.008889 | 0 | 1 | 2 | 0.008198 | 0 | 1 | 3 | 0.008733 | 0 | |
| 2 | 6 | 0.012555 | 0 | 1 | 2 | 0.007947 | 0 | 1 | 3 | 0.008462 | 0 | ||
| 2 | 6 | 0.008658 | 0 | 1 | 2 | 0.007763 | 0 | 1 | 3 | 0.008092 | 0 | ||
| 2 | 6 | 0.00612 | 0 | 1 | 3 | 0.008812 | 0 | 1 | 4 | 0.009649 | 0 | ||
| 2 | 6 | 0.005853 | 0 | 1 | 3 | 0.009794 | 0 | 1 | 4 | 0.00889 | 0 | ||
| 2 | 6 | 0.006947 | 0 | 1 | 3 | 0.007755 | 0 | 1 | 4 | 0.007802 | 0 | ||
| 18 | 71 | 0.31812 | 7.95 | 1 | 2 | 0.010464 | 0 | 1 | 3 | 0.008169 | 0 | ||
| 10,000 | 2 | 6 | 0.015963 | 0 | 1 | 2 | 0.012685 | 0 | 1 | 3 | 0.012387 | 0 | |
| 2 | 6 | 0.016001 | 0 | 1 | 2 | 0.011649 | 0 | 1 | 3 | 0.01044 | 0 | ||
| 2 | 6 | 0.015956 | 0 | 1 | 2 | 0.010229 | 0 | 1 | 3 | 0.010306 | 0 | ||
| 2 | 6 | 0.018197 | 0 | 1 | 3 | 0.011267 | 0 | 1 | 4 | 0.01704 | 0 | ||
| 2 | 6 | 0.011355 | 0 | 1 | 3 | 0.01182 | 0 | 1 | 4 | 0.010001 | 0 | ||
| 2 | 6 | 0.018842 | 0 | 1 | 3 | 0.012149 | 0 | 1 | 4 | 0.012029 | 0 | ||
| 18 | 71 | 0.38333 | 8.40 | 1 | 2 | 0.010945 | 0 | 1 | 3 | 0.011036 | 0 | ||
| 50,000 | 2 | 6 | 0.069633 | 0 | 1 | 2 | 0.038998 | 0 | 1 | 3 | 0.038391 | 0 | |
| 2 | 6 | 0.058314 | 0 | 1 | 2 | 0.040189 | 0 | 1 | 3 | 0.04888 | 0 | ||
| 2 | 6 | 0.095231 | 0 | 1 | 2 | 0.038922 | 0 | 1 | 3 | 0.036443 | 0 | ||
| 2 | 6 | 0.046998 | 0 | 1 | 3 | 0.040942 | 0 | 1 | 4 | 0.043418 | 0 | ||
| 2 | 6 | 0.044827 | 0 | 1 | 3 | 0.053045 | 0 | 1 | 4 | 0.040382 | 0 | ||
| 2 | 6 | 0.091957 | 0 | 1 | 3 | 0.042239 | 0 | 1 | 4 | 0.041188 | 0 | ||
| 18 | 71 | 1.2966 | 5.49 | 1 | 2 | 0.046987 | 0 | 1 | 3 | 0.040932 | 0 | ||
| 100,000 | 2 | 6 | 0.11838 | 0 | 1 | 2 | 0.090727 | 0 | 1 | 3 | 0.077927 | 0 | |
| 2 | 6 | 0.11658 | 0 | 1 | 2 | 0.077024 | 0 | 1 | 3 | 0.074788 | 0 | ||
| 2 | 6 | 0.12338 | 0 | 1 | 2 | 0.10601 | 0 | 1 | 3 | 0.082006 | 0 | ||
| 2 | 6 | 0.16886 | 0 | 1 | 3 | 0.085545 | 0 | 1 | 4 | 0.08095 | 0 | ||
| 2 | 6 | 0.086942 | 0 | 1 | 3 | 0.090827 | 0 | 1 | 4 | 0.12206 | 0 | ||
| 2 | 6 | 0.11021 | 0 | 1 | 3 | 0.080531 | 0 | 1 | 4 | 0.080564 | 0 | ||
| 20 | 79 | 3.0379 | 3.93 | 1 | 2 | 0.078351 | 0 | 1 | 3 | 0.07851 | 0 | ||
| DF-LSTT | CGD | PCG | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIM | INP | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM |
| 1000 | 3 | 11 | 0.004591 | 0 | 68 | 203 | 0.029809 | 8.60 | 18 | 71 | 0.010585 | 9.93 | |
| 3 | 11 | 0.002489 | 0 | 71 | 212 | 0.036826 | 8.29 | 19 | 75 | 0.007156 | 8.75 | ||
| 2 | 7 | 0.002095 | 0 | 74 | 221 | 0.028185 | 8.89 | 20 | 79 | 0.009969 | 7.15 | ||
| 3 | 11 | 0.002705 | 0 | 76 | 227 | 0.034306 | 9.28 | 47 | 187 | 0.017485 | 7.83 | ||
| 2 | 7 | 0.002888 | 0 | 76 | 227 | 0.028661 | 9.95 | 46 | 183 | 0.019829 | 9.76 | ||
| 3 | 11 | 0.009778 | 0 | 77 | 230 | 0.035383 | 8.34 | 41 | 163 | 0.015464 | 8.77 | ||
| 57 | 228 | 0.088381 | 7.44 | 74 | 221 | 0.027205 | 8.89 | 20 | 79 | 0.010696 | 6.77 | ||
| 5000 | 3 | 11 | 0.01231 | 0 | 71 | 212 | 0.077834 | 9.85 | 20 | 79 | 0.024704 | 5.57 | |
| 3 | 11 | 0.009414 | 0 | 74 | 221 | 0.065757 | 9.49 | 20 | 79 | 0.029764 | 9.80 | ||
| 2 | 7 | 0.007662 | 0 | 78 | 233 | 0.10357 | 8.14 | 21 | 83 | 0.026368 | 8.01 | ||
| 3 | 11 | 0.016453 | 0 | 80 | 239 | 0.086417 | 8.50 | 49 | 195 | 0.057593 | 9.46 | ||
| 2 | 7 | 0.007345 | 0 | 80 | 239 | 0.07626 | 9.11 | 49 | 195 | 0.067517 | 8.68 | ||
| 3 | 11 | 0.011993 | 0 | 80 | 239 | 0.076816 | 9.55 | 44 | 175 | 0.07587 | 7.79 | ||
| 45 | 180 | 0.38386 | 2.35 | 78 | 233 | 0.066987 | 8.20 | 21 | 83 | 0.037799 | 7.86 | ||
| 10,000 | 3 | 11 | 0.011882 | 0 | 73 | 218 | 0.12965 | 8.91 | 20 | 79 | 0.076194 | 7.88 | |
| 3 | 11 | 0.029407 | 0 | 76 | 227 | 0.11801 | 8.59 | 21 | 83 | 0.053778 | 6.94 | ||
| 2 | 7 | 0.016882 | 0 | 79 | 236 | 0.13374 | 9.21 | 22 | 87 | 0.046575 | 5.67 | ||
| 3 | 11 | 0.018218 | 0 | 81 | 242 | 0.19064 | 9.62 | 50 | 199 | 0.11588 | 9.84 | ||
| 2 | 7 | 0.012436 | 0 | 82 | 245 | 0.12664 | 8.25 | 50 | 199 | 0.10082 | 9.03 | ||
| 3 | 11 | 0.049629 | 0 | 82 | 245 | 0.12031 | 8.64 | 45 | 179 | 0.088501 | 8.11 | ||
| 45 | 180 | 0.26301 | 3.61 | 79 | 236 | 0.13346 | 9.24 | 22 | 87 | 0.075082 | 5.55 | ||
| 50,000 | 3 | 11 | 0.059552 | 0 | 77 | 230 | 0.53026 | 8.16 | 21 | 83 | 0.17253 | 8.83 | |
| 3 | 11 | 0.05224 | 0 | 79 | 236 | 0.51796 | 9.84 | 22 | 87 | 0.16907 | 7.78 | ||
| 2 | 7 | 0.031386 | 0 | 83 | 248 | 0.55337 | 8.44 | 23 | 91 | 0.18569 | 6.36 | ||
| 3 | 11 | 0.089099 | 0 | 85 | 254 | 0.56858 | 8.81 | 53 | 211 | 0.46984 | 8.75 | ||
| 2 | 7 | 0.041153 | 0 | 85 | 254 | 0.63624 | 9.44 | 53 | 211 | 0.44157 | 8.02 | ||
| 3 | 11 | 0.068645 | 0 | 85 | 254 | 0.75653 | 9.89 | 47 | 187 | 0.5116 | 9.80 | ||
| 51 | 204 | 0.97251 | 2.43 | 83 | 248 | 0.59375 | 8.48 | 23 | 91 | 0.22912 | 6.16 | ||
| 100,000 | 3 | 11 | 0.23207 | 0 | 78 | 233 | 1.1907 | 9.24 | 22 | 87 | 0.32312 | 6.25 | |
| 3 | 11 | 0.096102 | 0 | 81 | 242 | 0.95676 | 8.90 | 23 | 91 | 0.36086 | 5.51 | ||
| 2 | 7 | 0.059522 | 0 | 84 | 251 | 0.99173 | 9.55 | 23 | 91 | 0.36819 | 8.99 | ||
| 3 | 11 | 0.18868 | 0 | 86 | 257 | 1.0274 | 9.97 | 54 | 215 | 0.82162 | 9.10 | ||
| 2 | 7 | 0.076178 | 0 | 87 | 260 | 1.3603 | 8.55 | 54 | 215 | 0.85533 | 8.34 | ||
| 3 | 11 | 0.13387 | 0 | 87 | 260 | 1.0415 | 8.95 | 49 | 195 | 0.7369 | 7.49 | ||
| 48 | 192 | 1.7777 | 7.92 | 84 | 251 | 0.99015 | 9.59 | 23 | 91 | 0.36125 | 8.67 | ||
| DF-LSTT | CGD | PCG | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIM | INP | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM |
| 1000 | 35 | 139 | 0.028177 | 4.01 | 90 | 268 | 0.024747 | 8.03 | 22 | 82 | 0.012429 | 7.48 | |
| 21 | 83 | 0.017203 | 6.42 | 89 | 265 | 0.02733 | 9.07 | 23 | 87 | 0.012966 | 7.31 | ||
| 31 | 123 | 0.02123 | 8.88 | 88 | 262 | 0.025983 | 8.96 | 23 | 89 | 0.011284 | 9.31 | ||
| 30 | 120 | 0.032095 | 3.98 | 89 | 266 | 0.040925 | 9.36 | 49 | 195 | 0.026429 | 8.45 | ||
| 27 | 108 | 0.048348 | 4.09 | 87 | 260 | 0.025181 | 9.16 | 53 | 211 | 0.019872 | 8.38 | ||
| 26 | 104 | 0.019389 | 4.97 | 84 | 251 | 0.031167 | 8.32 | 46 | 183 | 0.027704 | 8.80 | ||
| 28 | 111 | 0.066312 | 5.41 | 90 | 268 | 0.026267 | 9.86 | 168 | 670 | 0.05767 | 9.42 | ||
| 5000 | 30 | 119 | 0.099879 | 4.22 | 97 | 289 | 0.099454 | 8.47 | 24 | 90 | 0.036297 | 6.36 | |
| 49 | 195 | 0.20684 | 2.06 | 96 | 286 | 0.085712 | 9.58 | 25 | 94 | 0.03958 | 6.24 | ||
| 27 | 107 | 0.091189 | 6.71 | 95 | 283 | 0.12574 | 9.47 | 25 | 97 | 0.034165 | 5.86 | ||
| 25 | 100 | 0.11071 | 7.95 | 97 | 290 | 0.10252 | 8.05 | 53 | 211 | 0.076152 | 9.11 | ||
| 41 | 164 | 0.13125 | 8.90 | 94 | 281 | 0.092231 | 9.87 | 58 | 231 | 0.08755 | 8.56 | ||
| 30 | 120 | 0.10232 | 7.65 | 91 | 272 | 0.13952 | 8.88 | 50 | 199 | 0.07417 | 7.65 | ||
| 35 | 139 | 0.15239 | 4.54 | 97 | 289 | 0.094881 | 9.23 | 316 | 1262 | 0.39534 | 9.96 | ||
| 10,000 | 48 | 191 | 0.61255 | 5.75 | 100 | 298 | 0.30348 | 8.69 | 25 | 94 | 0.079057 | 5.40 | |
| 37 | 147 | 0.32599 | 2.23 | 99 | 295 | 0.18161 | 9.83 | 25 | 94 | 0.079123 | 8.90 | ||
| 25 | 99 | 0.17968 | 5.85 | 98 | 292 | 0.17487 | 9.72 | 25 | 97 | 0.072827 | 8.64 | ||
| 24 | 96 | 0.12434 | 8.81 | 100 | 299 | 0.18342 | 8.29 | 55 | 219 | 0.15362 | 9.11 | ||
| 31 | 124 | 0.17139 | 2.16 | 98 | 293 | 0.17674 | 8.14 | 60 | 239 | 0.13688 | 9.01 | ||
| 33 | 132 | 0.25773 | 7.87 | 94 | 281 | 0.16779 | 9.15 | 51 | 203 | 0.15962 | 9.62 | ||
| 43 | 171 | 0.35695 | 3.19 | 99 | 295 | 0.18399 | 8.84 | 325 | 1298 | 0.7484 | 9.67 | ||
| 50,000 | 99 | 395 | 6.631 | 5.43 | 107 | 319 | 0.77898 | 9.16 | 26 | 98 | 0.26672 | 6.75 | |
| 78 | 311 | 4.9202 | 6.69 | 107 | 319 | 0.79789 | 8.28 | 27 | 102 | 0.23943 | 5.16 | ||
| 36 | 143 | 0.81487 | 4.78 | 106 | 316 | 0.91174 | 8.19 | 27 | 105 | 0.30807 | 5.28 | ||
| 29 | 116 | 0.66459 | 7.02 | 107 | 320 | 1.1448 | 8.77 | 60 | 239 | 0.5978 | 8.66 | ||
| 30 | 120 | 0.7737 | 6.25 | 105 | 314 | 0.76987 | 8.61 | 65 | 259 | 0.61224 | 9.05 | ||
| 35 | 140 | 0.97053 | 3.67 | 101 | 302 | 0.75366 | 9.68 | 56 | 223 | 0.53722 | 8.19 | ||
| 48 | 191 | 2.2774 | 4.52 | 106 | 316 | 0.77381 | 8.74 | F | F | F | F | ||
| 100,000 | 95 | 379 | 11.9112 | 9.12 | 110 | 328 | 1.7098 | 9.39 | 26 | 98 | 0.4346 | 9.73 | |
| 95 | 379 | 10.7767 | 4.09 | 110 | 328 | 1.4604 | 8.50 | 27 | 102 | 0.44774 | 7.39 | ||
| 27 | 107 | 1.2642 | 4.65 | 109 | 325 | 1.4436 | 8.40 | 27 | 105 | 0.46265 | 7.77 | ||
| 30 | 120 | 1.5062 | 6.16 | 110 | 329 | 1.7956 | 9.00 | 62 | 247 | 1.0814 | 9.00 | ||
| 57 | 228 | 5.2267 | 9.73 | 108 | 323 | 1.4142 | 8.84 | 67 | 267 | 1.2447 | 9.50 | ||
| 27 | 107 | 1.4554 | 3.33 | 104 | 311 | 1.386 | 9.94 | 58 | 231 | 1.1897 | 8.32 | ||
| 119 | 475 | 16.6573 | 7.19 | 109 | 325 | 1.7025 | 9.46 | F | F | F | F | ||
| DF-LSTT | CGD | PCG | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIM | INP | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM |
| 1000 | 12 | 48 | 0.03188 | 2.30 | 83 | 248 | 0.031732 | 8.42 | 23 | 91 | 0.014183 | 9.28 | |
| 12 | 48 | 0.041971 | 2.23 | 83 | 248 | 0.031901 | 8.09 | 23 | 91 | 0.014925 | 8.92 | ||
| 12 | 48 | 0.040553 | 2.02 | 82 | 245 | 0.031622 | 8.91 | 23 | 91 | 0.020135 | 7.86 | ||
| 11 | 44 | 0.024141 | 6.97 | 80 | 239 | 0.031387 | 9.53 | 23 | 91 | 0.014473 | 5.38 | ||
| 11 | 44 | 0.038626 | 5.62 | 79 | 236 | 0.043836 | 9.56 | 22 | 87 | 0.016292 | 8.62 | ||
| 11 | 44 | 0.01937 | 3.35 | 77 | 230 | 0.029442 | 8.81 | 22 | 87 | 0.014627 | 5.08 | ||
| 12 | 48 | 0.041621 | 4.70 | 82 | 245 | 0.031674 | 9.04 | 23 | 91 | 0.026782 | 7.91 | ||
| 5000 | 12 | 48 | 0.096723 | 4.01 | 86 | 257 | 0.16263 | 9.65 | 25 | 99 | 0.062377 | 5.22 | |
| 12 | 48 | 0.14973 | 3.86 | 86 | 257 | 0.20647 | 9.28 | 25 | 99 | 0.063981 | 5.02 | ||
| 12 | 48 | 0.12093 | 3.40 | 86 | 257 | 0.17205 | 8.17 | 24 | 95 | 0.056084 | 8.82 | ||
| 12 | 48 | 0.10493 | 2.33 | 84 | 251 | 0.17167 | 8.74 | 24 | 95 | 0.059374 | 6.04 | ||
| 12 | 48 | 0.083136 | 1.87 | 83 | 248 | 0.15447 | 8.77 | 23 | 91 | 0.055294 | 9.67 | ||
| 11 | 44 | 0.082714 | 7.05 | 81 | 242 | 0.15192 | 8.08 | 23 | 91 | 0.055478 | 5.70 | ||
| 12 | 48 | 0.084104 | 3.48 | 86 | 257 | 0.16641 | 8.25 | 24 | 95 | 0.06338 | 8.87 | ||
| 10,000 | 12 | 48 | 0.158 | 5.68 | 88 | 263 | 0.34039 | 8.73 | 25 | 99 | 0.098299 | 7.38 | |
| 12 | 48 | 0.15694 | 5.46 | 88 | 263 | 0.35149 | 8.40 | 25 | 99 | 0.13644 | 7.09 | ||
| 12 | 48 | 0.2381 | 4.81 | 87 | 260 | 0.34294 | 9.25 | 25 | 99 | 0.11271 | 6.25 | ||
| 12 | 48 | 0.20746 | 3.29 | 85 | 254 | 0.26475 | 9.89 | 24 | 95 | 0.093885 | 8.54 | ||
| 12 | 48 | 0.15857 | 2.64 | 84 | 251 | 0.2461 | 9.92 | 24 | 95 | 0.10396 | 6.85 | ||
| 11 | 44 | 0.81101 | 9.97 | 82 | 245 | 0.24381 | 9.14 | 23 | 91 | 0.12403 | 8.06 | ||
| 12 | 48 | 0.16525 | 4.85 | 87 | 260 | 0.26637 | 9.35 | 25 | 99 | 0.10128 | 6.30 | ||
| 50,000 | 13 | 52 | 1.0506 | 1.98 | 91 | 272 | 1.2907 | 1.00 | 26 | 103 | 0.40761 | 8.26 | |
| 13 | 52 | 0.75114 | 1.91 | 91 | 272 | 1.1071 | 9.61 | 26 | 103 | 0.40356 | 7.95 | ||
| 13 | 52 | 0.98117 | 1.68 | 91 | 272 | 1.0738 | 8.47 | 26 | 103 | 0.41251 | 7.00 | ||
| 12 | 48 | 0.65997 | 7.36 | 89 | 266 | 1.0542 | 9.06 | 25 | 99 | 0.39262 | 9.56 | ||
| 12 | 48 | 0.46882 | 5.91 | 88 | 263 | 1.5109 | 9.08 | 25 | 99 | 0.39186 | 7.67 | ||
| 12 | 48 | 0.61393 | 3.48 | 86 | 257 | 1.0452 | 8.37 | 24 | 95 | 0.38423 | 9.03 | ||
| 13 | 52 | 0.54298 | 1.70 | 91 | 272 | 1.0556 | 8.54 | 26 | 103 | 0.4047 | 7.06 | ||
| 100,000 | 13 | 52 | 1.4092 | 2.81 | 93 | 278 | 2.7716 | 9.05 | 27 | 107 | 1.067 | 5.86 | |
| 13 | 52 | 1.3229 | 2.70 | 93 | 278 | 2.3812 | 8.70 | 27 | 107 | 1.2086 | 5.63 | ||
| 13 | 52 | 1.6913 | 2.38 | 92 | 275 | 2.6594 | 9.58 | 26 | 103 | 0.96952 | 9.90 | ||
| 13 | 52 | 1.3408 | 1.63 | 91 | 272 | 2.3237 | 8.20 | 26 | 103 | 0.94103 | 6.78 | ||
| 12 | 48 | 1.2425 | 8.35 | 90 | 269 | 3.1173 | 8.22 | 26 | 103 | 1.0502 | 5.44 | ||
| 12 | 48 | 1.3332 | 4.93 | 87 | 260 | 2.4359 | 9.47 | 25 | 99 | 0.88394 | 6.40 | ||
| 13 | 52 | 1.3846 | 2.40 | 92 | 275 | 2.6667 | 9.66 | 26 | 103 | 0.9198 | 9.98 | ||
| DF-LSTT | CGD | PCG | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIM | INP | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM |
| 1000 | 8 | 32 | 0.011558 | 5.30 | 37 | 110 | 0.013147 | 9.48 | 17 | 67 | 0.009313 | 6.98 | |
| 9 | 36 | 0.013381 | 9.70 | 37 | 110 | 0.013514 | 6.87 | 15 | 59 | 0.010714 | 9.89 | ||
| 7 | 28 | 0.011551 | 3.38 | 30 | 89 | 0.011236 | 6.51 | 16 | 63 | 0.008948 | 5.79 | ||
| 9 | 36 | 0.01024 | 2.83 | 38 | 113 | 0.013281 | 8.05 | 16 | 63 | 0.008965 | 5.21 | ||
| 9 | 36 | 0.00978 | 8.28 | 38 | 113 | 0.021489 | 8.05 | 19 | 75 | 0.014196 | 4.95 | ||
| 10 | 39 | 0.012021 | 1.26 | 37 | 109 | 0.011749 | 9.07 | 18 | 70 | 0.009389 | 8.93 | ||
| 21 | 84 | 0.035658 | 5.40 | 37 | 110 | 0.015765 | 6.61 | 20 | 79 | 0.019759 | 8.71 | ||
| 5000 | 9 | 36 | 0.042338 | 1.32 | 39 | 116 | 0.052548 | 8.30 | 18 | 71 | 0.037642 | 7.60 | |
| 10 | 40 | 0.081106 | 2.42 | 38 | 113 | 0.051834 | 9.60 | 17 | 67 | 0.027158 | 5.25 | ||
| 7 | 28 | 0.039851 | 7.55 | 31 | 92 | 0.041545 | 9.10 | 17 | 67 | 0.028917 | 6.31 | ||
| 9 | 36 | 0.039967 | 6.33 | 40 | 119 | 0.057437 | 7.05 | 17 | 67 | 0.037275 | 5.68 | ||
| 10 | 40 | 0.046165 | 2.06 | 40 | 119 | 0.052164 | 7.05 | 20 | 79 | 0.030917 | 5.39 | ||
| 10 | 39 | 0.044881 | 2.82 | 39 | 115 | 0.064438 | 7.94 | 19 | 74 | 0.046654 | 9.73 | ||
| 24 | 96 | 0.18701 | 6.38 | 38 | 113 | 0.074383 | 9.00 | 21 | 83 | 0.048626 | 9.52 | ||
| 10,000 | 9 | 36 | 0.084021 | 1.87 | 40 | 119 | 0.1459 | 7.34 | 19 | 75 | 0.060554 | 5.23 | |
| 10 | 40 | 0.091788 | 3.42 | 39 | 116 | 0.095325 | 8.50 | 17 | 67 | 0.057649 | 7.42 | ||
| 8 | 32 | 0.082144 | 1.19 | 32 | 95 | 0.074842 | 8.05 | 17 | 67 | 0.046905 | 8.92 | ||
| 9 | 36 | 0.065787 | 8.95 | 40 | 119 | 0.10024 | 9.96 | 17 | 67 | 0.05047 | 8.03 | ||
| 10 | 40 | 0.069698 | 2.92 | 40 | 119 | 0.10003 | 9.96 | 20 | 79 | 0.069303 | 7.62 | ||
| 10 | 39 | 0.1457 | 3.99 | 40 | 118 | 0.097749 | 7.02 | 20 | 78 | 0.055323 | 6.70 | ||
| 21 | 84 | 0.14332 | 3.62 | 39 | 116 | 0.12983 | 8.05 | 22 | 87 | 0.078308 | 6.51 | ||
| 50,000 | 9 | 36 | 0.25176 | 4.17 | 42 | 125 | 0.47157 | 6.42 | 20 | 79 | 0.29584 | 5.70 | |
| 10 | 40 | 0.76304 | 7.64 | 41 | 122 | 0.44664 | 7.43 | 18 | 71 | 0.21246 | 8.08 | ||
| 8 | 32 | 0.22903 | 2.66 | 34 | 101 | 0.30639 | 7.04 | 18 | 71 | 0.22024 | 9.71 | ||
| 10 | 40 | 0.46107 | 2.23 | 42 | 125 | 0.40534 | 8.72 | 18 | 71 | 0.19871 | 8.75 | ||
| 10 | 40 | 0.39956 | 6.52 | 42 | 125 | 0.46103 | 8.72 | 21 | 83 | 0.22027 | 8.30 | ||
| 10 | 39 | 0.30315 | 8.92 | 41 | 121 | 0.51651 | 9.82 | 21 | 82 | 0.23139 | 7.30 | ||
| 21 | 84 | 0.88881 | 4.14 | 41 | 122 | 0.73262 | 7.00 | 23 | 91 | 0.37248 | 7.08 | ||
| 100,000 | 9 | 36 | 0.49984 | 5.90 | 42 | 125 | 0.90106 | 9.08 | 20 | 79 | 0.57692 | 8.06 | |
| 11 | 44 | 0.83437 | 1.20 | 42 | 125 | 0.95004 | 6.58 | 19 | 75 | 0.51407 | 5.57 | ||
| 8 | 32 | 0.63611 | 3.76 | 34 | 101 | 0.74225 | 9.96 | 19 | 75 | 0.42249 | 6.69 | ||
| 10 | 40 | 0.80033 | 3.15 | 43 | 128 | 0.76591 | 7.71 | 19 | 75 | 0.41102 | 6.03 | ||
| 10 | 40 | 0.53766 | 9.23 | 43 | 128 | 0.79251 | 7.71 | 22 | 87 | 0.45205 | 5.72 | ||
| 11 | 43 | 0.69393 | 1.41 | 42 | 124 | 0.89477 | 8.69 | 22 | 86 | 0.50902 | 5.03 | ||
| 21 | 84 | 1.3381 | 8.09 | 41 | 122 | 1.451 | 9.90 | 24 | 95 | 0.74006 | 4.89 | ||
| DF-LSTT | CGD | PCG | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIM | INP | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM | ITER | FVAL | TIME | NORM |
| 1000 | 13 | 52 | 0.011502 | 4.53 | 21 | 62 | 0.007103 | 9.28 | 9 | 35 | 0.007659 | 2.15 | |
| 13 | 52 | 0.010497 | 2.74 | 21 | 62 | 0.007684 | 5.62 | 8 | 31 | 0.005796 | 7.72 | ||
| 12 | 48 | 0.018922 | 7.51 | 21 | 62 | 0.006208 | 5.36 | 8 | 31 | 0.004682 | 7.36 | ||
| 14 | 56 | 0.011298 | 2.60 | 23 | 68 | 0.00871 | 5.84 | 9 | 35 | 0.005209 | 7.18 | ||
| 14 | 56 | 0.0119 | 3.53 | 23 | 68 | 0.006241 | 7.91 | 9 | 35 | 0.004898 | 9.73 | ||
| 14 | 56 | 0.020175 | 5.07 | 24 | 71 | 0.006771 | 4.93 | 10 | 39 | 0.005248 | 2.36 | ||
| 9 | 36 | 0.007601 | 9.21 | 22 | 65 | 0.005934 | 5.11 | 9 | 35 | 0.004781 | 2.82 | ||
| 5000 | 14 | 56 | 0.044747 | 2.48 | 22 | 65 | 0.030281 | 9.01 | 9 | 35 | 0.014961 | 4.81 | |
| 13 | 52 | 0.039991 | 6.13 | 22 | 65 | 0.037367 | 5.46 | 9 | 35 | 0.019975 | 2.91 | ||
| 13 | 52 | 0.061786 | 4.11 | 22 | 65 | 0.024256 | 5.20 | 9 | 35 | 0.012236 | 2.78 | ||
| 14 | 56 | 0.037006 | 5.82 | 24 | 71 | 0.030963 | 5.67 | 10 | 39 | 0.012613 | 2.71 | ||
| 14 | 56 | 0.042827 | 7.89 | 24 | 71 | 0.027167 | 7.68 | 10 | 39 | 0.012167 | 3.67 | ||
| 15 | 60 | 0.040744 | 2.77 | 25 | 74 | 0.032369 | 4.79 | 10 | 39 | 0.014305 | 5.27 | ||
| 10 | 40 | 0.031693 | 5.07 | 23 | 68 | 0.017202 | 5.02 | 9 | 35 | 0.011532 | 6.18 | ||
| 10,000 | 14 | 56 | 0.1304 | 3.51 | 23 | 68 | 0.031436 | 5.53 | 9 | 35 | 0.015852 | 6.80 | |
| 13 | 52 | 0.082982 | 8.67 | 22 | 65 | 0.032629 | 7.71 | 9 | 35 | 0.01903 | 4.12 | ||
| 13 | 52 | 0.10124 | 5.82 | 22 | 65 | 0.031087 | 7.36 | 9 | 35 | 0.025673 | 3.93 | ||
| 14 | 56 | 0.084077 | 8.24 | 24 | 71 | 0.058121 | 8.02 | 10 | 39 | 0.015808 | 3.83 | ||
| 15 | 60 | 0.13836 | 2.73 | 25 | 74 | 0.034695 | 4.72 | 10 | 39 | 0.021954 | 5.19 | ||
| 15 | 60 | 0.09151 | 3.92 | 25 | 74 | 0.033872 | 6.78 | 10 | 39 | 0.017664 | 7.45 | ||
| 10 | 40 | 0.074314 | 7.22 | 23 | 68 | 0.04517 | 7.08 | 9 | 35 | 0.0245 | 8.64 | ||
| 50,000 | 14 | 56 | 0.48989 | 7.84 | 24 | 71 | 0.15209 | 5.37 | 10 | 39 | 0.070466 | 2.57 | |
| 14 | 56 | 0.39664 | 4.75 | 23 | 68 | 0.12867 | 7.49 | 9 | 35 | 0.059796 | 9.21 | ||
| 14 | 56 | 1.1025 | 3.19 | 23 | 68 | 0.26774 | 7.15 | 9 | 35 | 0.055552 | 8.79 | ||
| 15 | 60 | 0.37756 | 4.51 | 25 | 74 | 0.18066 | 7.79 | 10 | 39 | 0.063615 | 8.57 | ||
| 15 | 60 | 0.48364 | 6.11 | 26 | 77 | 0.20521 | 4.58 | 11 | 43 | 0.066811 | 1.96 | ||
| 15 | 60 | 0.38215 | 8.77 | 26 | 77 | 0.1468 | 6.58 | 11 | 43 | 0.070802 | 2.81 | ||
| 11 | 44 | 0.29749 | 3.97 | 24 | 71 | 0.15389 | 6.86 | 10 | 39 | 0.11456 | 3.27 | ||
| 100,000 | 15 | 60 | 0.76533 | 2.72 | 24 | 71 | 0.28556 | 7.60 | 10 | 39 | 0.15136 | 3.63 | |
| 14 | 56 | 0.96545 | 6.72 | 24 | 71 | 0.30656 | 4.60 | 10 | 39 | 0.15471 | 2.20 | ||
| 14 | 56 | 0.71691 | 4.51 | 24 | 71 | 0.27951 | 4.39 | 10 | 39 | 0.2006 | 2.10 | ||
| 15 | 60 | 0.76153 | 6.38 | 26 | 77 | 0.39044 | 4.78 | 11 | 43 | 0.18627 | 2.04 | ||
| 15 | 60 | 0.79539 | 8.64 | 26 | 77 | 0.57875 | 6.48 | 11 | 43 | 0.13307 | 2.77 | ||
| 16 | 64 | 0.82574 | 3.04 | 26 | 77 | 0.4141 | 9.31 | 11 | 43 | 0.142 | 3.98 | ||
| 11 | 44 | 0.52429 | 5.60 | 24 | 71 | 0.47424 | 9.71 | 10 | 39 | 0.15694 | 4.64 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan Ibrahim, A.; Kumam, P.; Abubakar, A.B.; Abubakar, J.; Muhammad, A.B. Least-Square-Based Three-Term Conjugate Gradient Projection Method for ℓ1-Norm Problems with Application to Compressed Sensing. Mathematics 2020, 8, 602. https://doi.org/10.3390/math8040602
Hassan Ibrahim A, Kumam P, Abubakar AB, Abubakar J, Muhammad AB. Least-Square-Based Three-Term Conjugate Gradient Projection Method for ℓ1-Norm Problems with Application to Compressed Sensing. Mathematics. 2020; 8(4):602. https://doi.org/10.3390/math8040602
Chicago/Turabian StyleHassan Ibrahim, Abdulkarim, Poom Kumam, Auwal Bala Abubakar, Jamilu Abubakar, and Abubakar Bakoji Muhammad. 2020. "Least-Square-Based Three-Term Conjugate Gradient Projection Method for ℓ1-Norm Problems with Application to Compressed Sensing" Mathematics 8, no. 4: 602. https://doi.org/10.3390/math8040602
APA StyleHassan Ibrahim, A., Kumam, P., Abubakar, A. B., Abubakar, J., & Muhammad, A. B. (2020). Least-Square-Based Three-Term Conjugate Gradient Projection Method for ℓ1-Norm Problems with Application to Compressed Sensing. Mathematics, 8(4), 602. https://doi.org/10.3390/math8040602






