Designing Developable C-Bézier Surface with Shape Parameters
Abstract
1. Introduction
- Rational curves and surfaces have weights for each control point. In general, the selection of the weight is not clear. Thus, the author in [12] concluded that “this added freedom of weights is potentially more a nuisance than a real help”.
- We know that the derivative of a degree n polynomial curve is a curve of degree ; this means that differential yields a simpler curve. However, the derivative of a degree n rational curve is a rational curve of degree . Thus, the derivative yields a curve with a high degree. If we repeat differentiation, we will get a curve of a high degree. It may not be dealt with in the CAD system.
- The rational model can not encompass transcendental curves, such as cycloid and helix. The curves are very important in technical application.
2. C-Bézier Curve with -Parameters
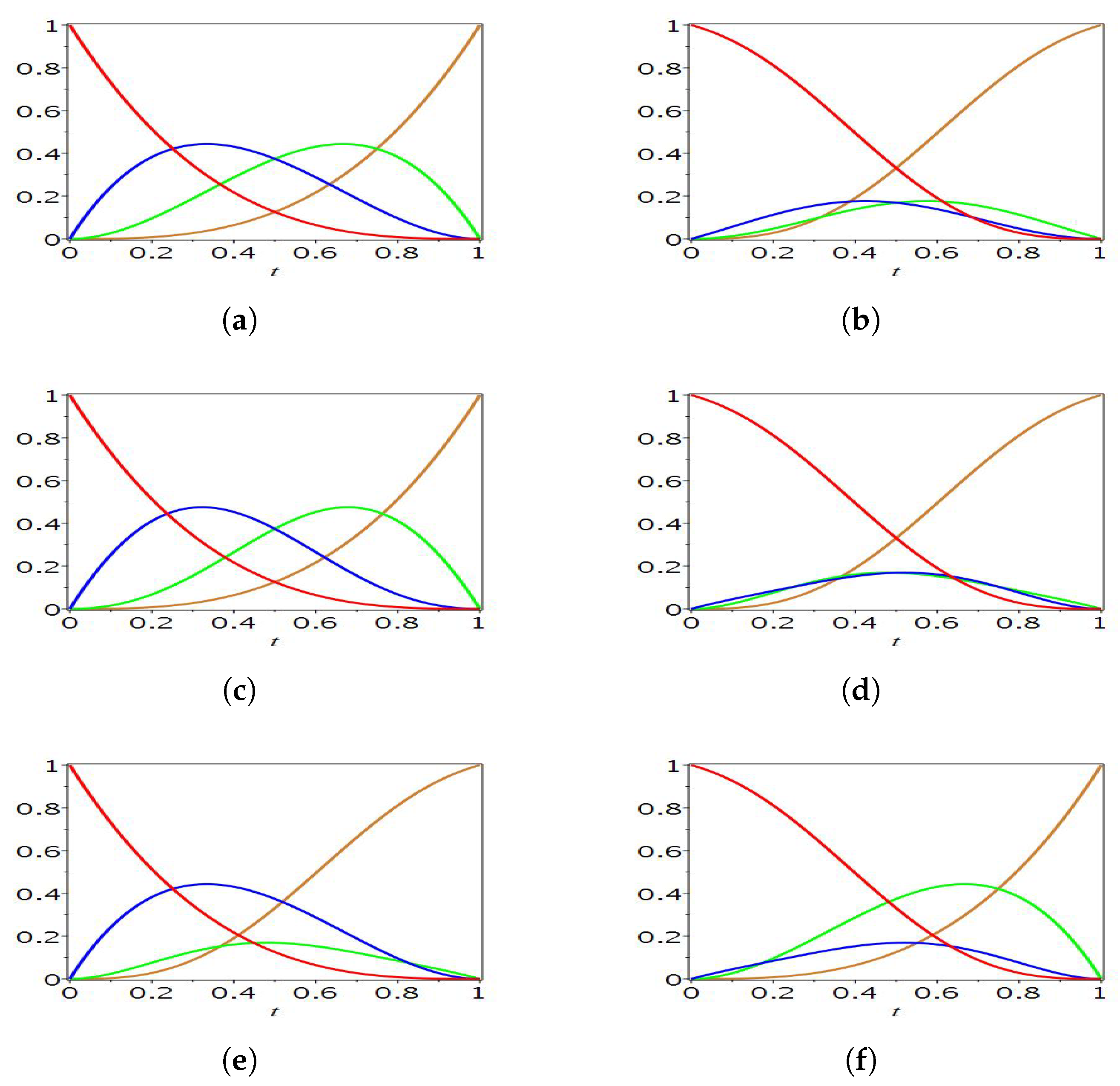
2.1. C-Bézier Basis Functions with n-Parameters
- (a).
- ;
- (b).
- ;
- (c).
- .
- (a).
- By Definition 1,
- (b).
- We prove this property by induction on n. When , we get . Assume holds on , that is,Then, for n, we haveAccording to Formula (2), it is easy to get
- (c).
- We prove this property by induction on n too. When , we haveAssume it holds for , that is, . On the left part of this equation, when we let , the term including is zero. Therefore, the right side of the equation only has parameter . Then, we haveAccording to , . Therefore,□
2.2. C-Bézier Curve with n-Parameters
- (a).
- (b).
- (c).
- .
- (a).
- Let ; then, Equation isBy Property 2 and 2, we have , then . In the similar way, .
- (b).
- When ,According to Property , , so we have
- (c).
- By using the above method, we can prove conclusion , so here we omit the process of the proof.
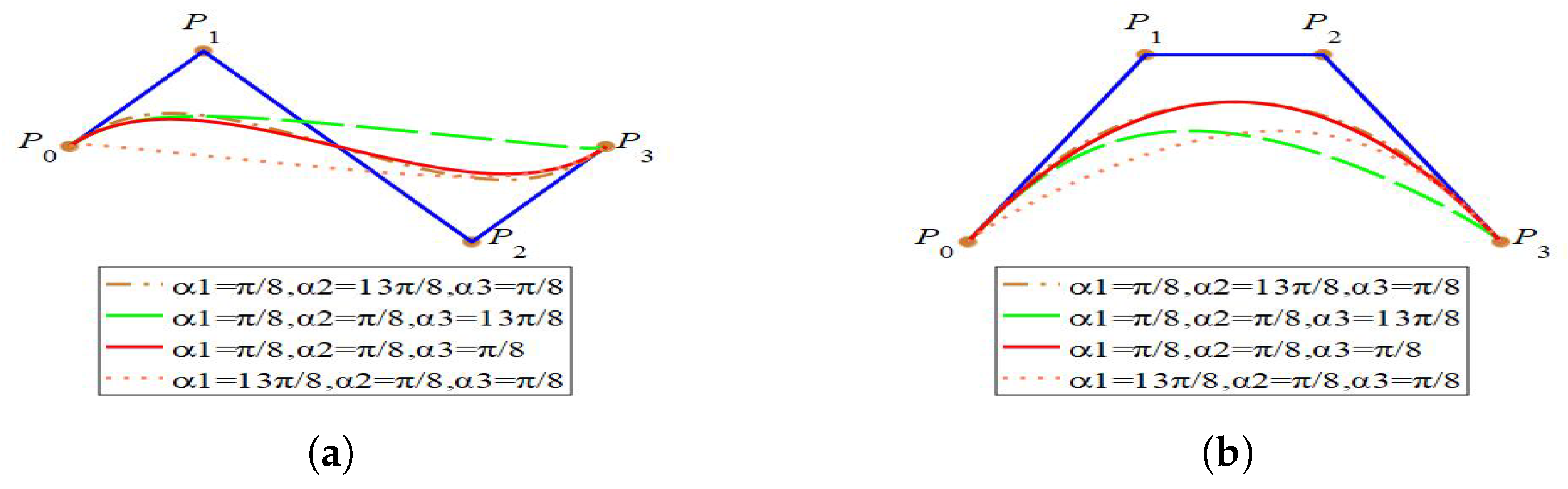
3. Developable Surface from Cubic C-Bézier Curve with Three Parameters
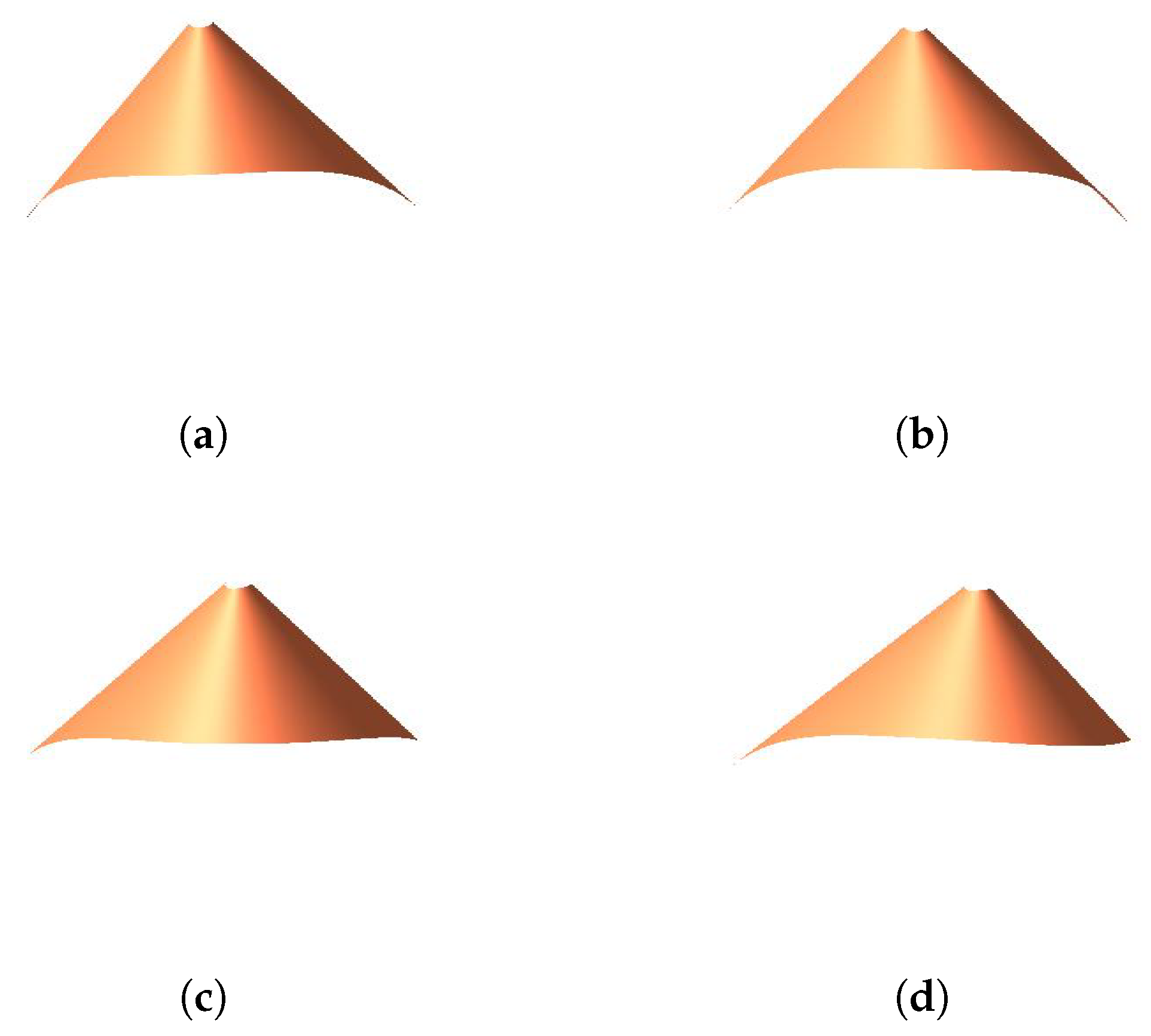
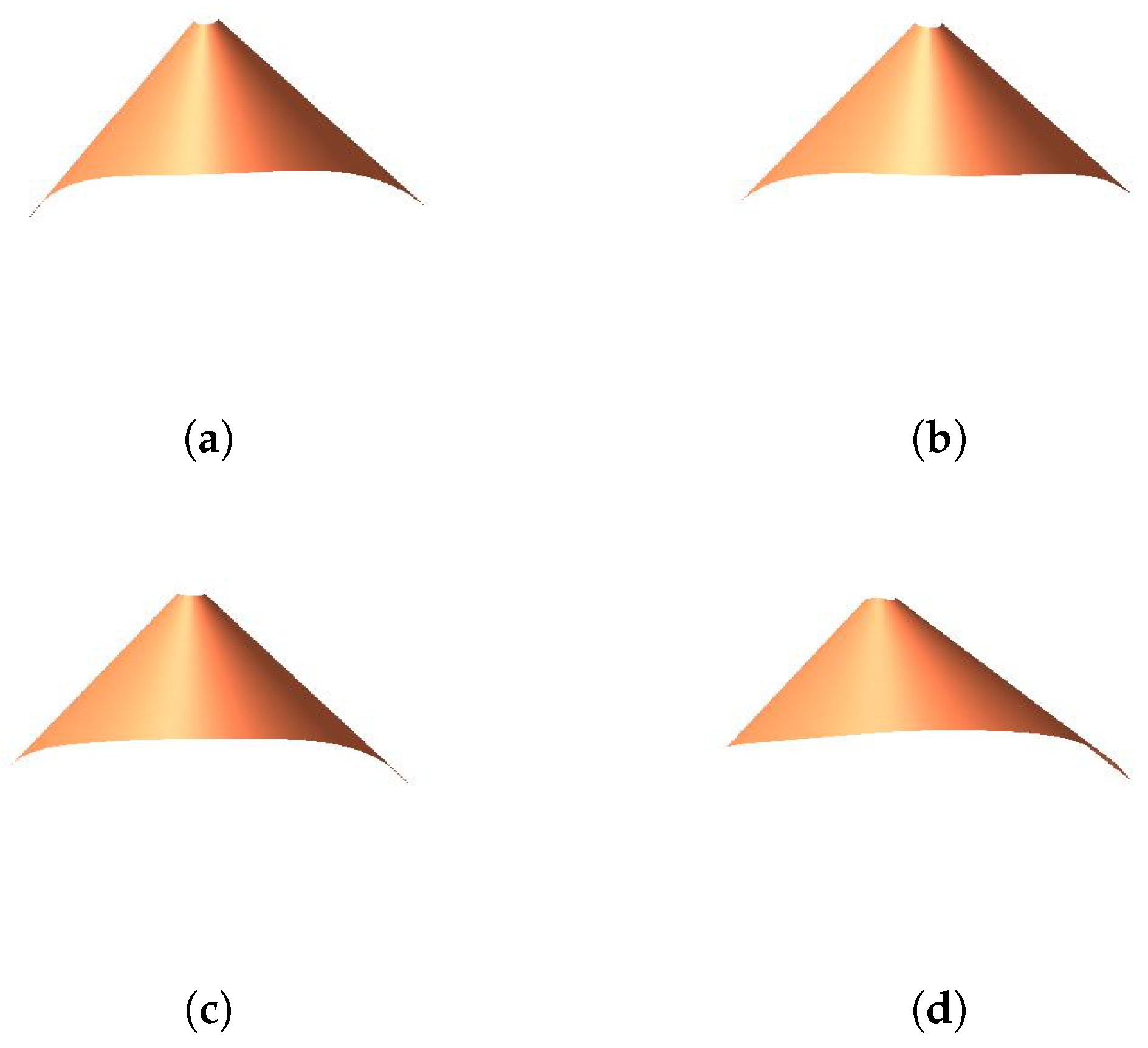
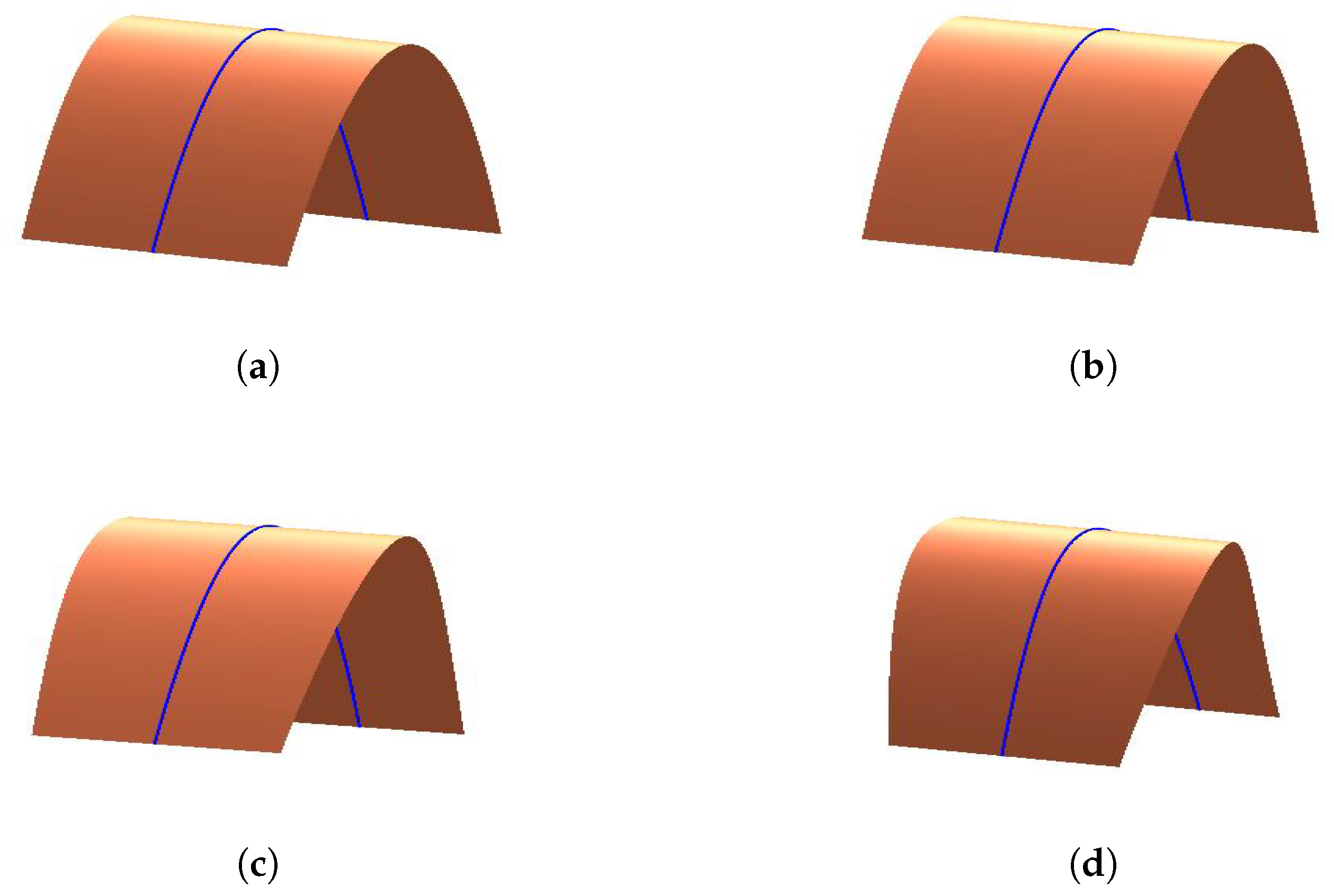
3.1. Enveloping Developable C-Bézier Surface
- When modifying the value of, and keepunchanged, the length and position of the generatorremain the same. The position of the generatorhas no change, but the length of it becomes longer when we increase the value of.
- When we change the value ofand keepunchanged, the generatorandhave no changes in position and length. However, the shape of the developable surfaces will be changed.
- If we keep the value ofunchanged and modify, the position and the length of the generatorkeep the same. The position of the generatoralso has no change, but the length of it will become longer when we increase the value of.
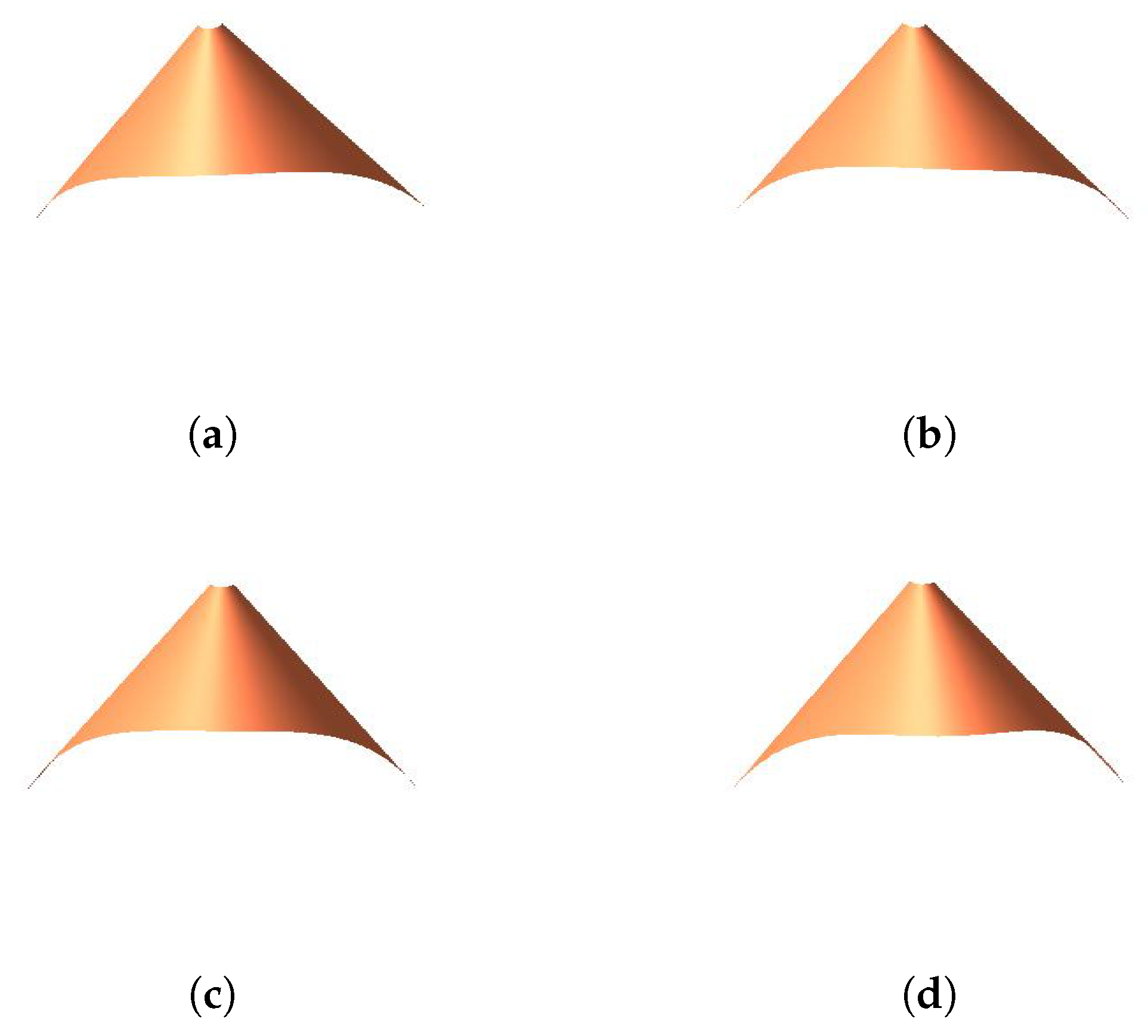
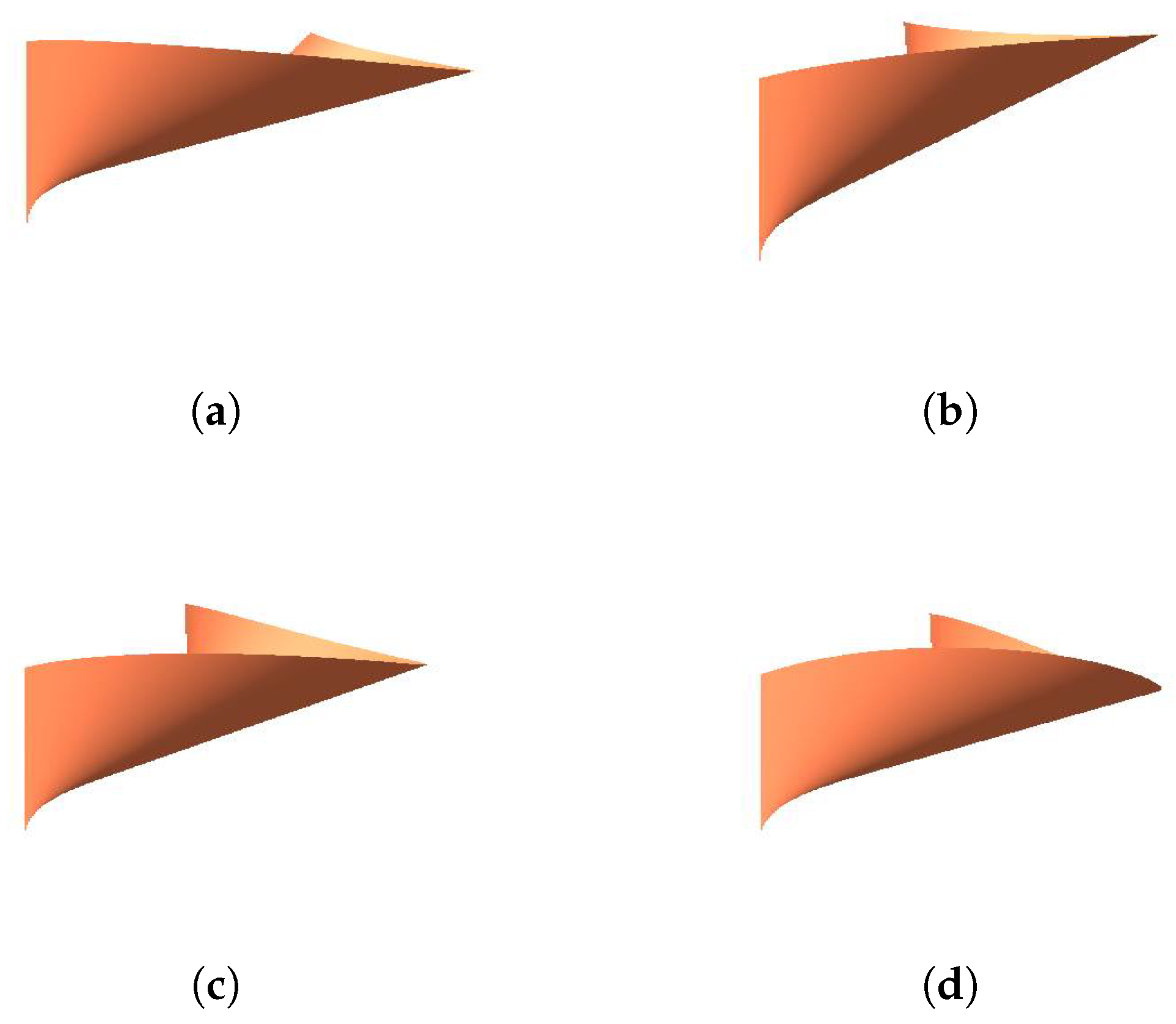
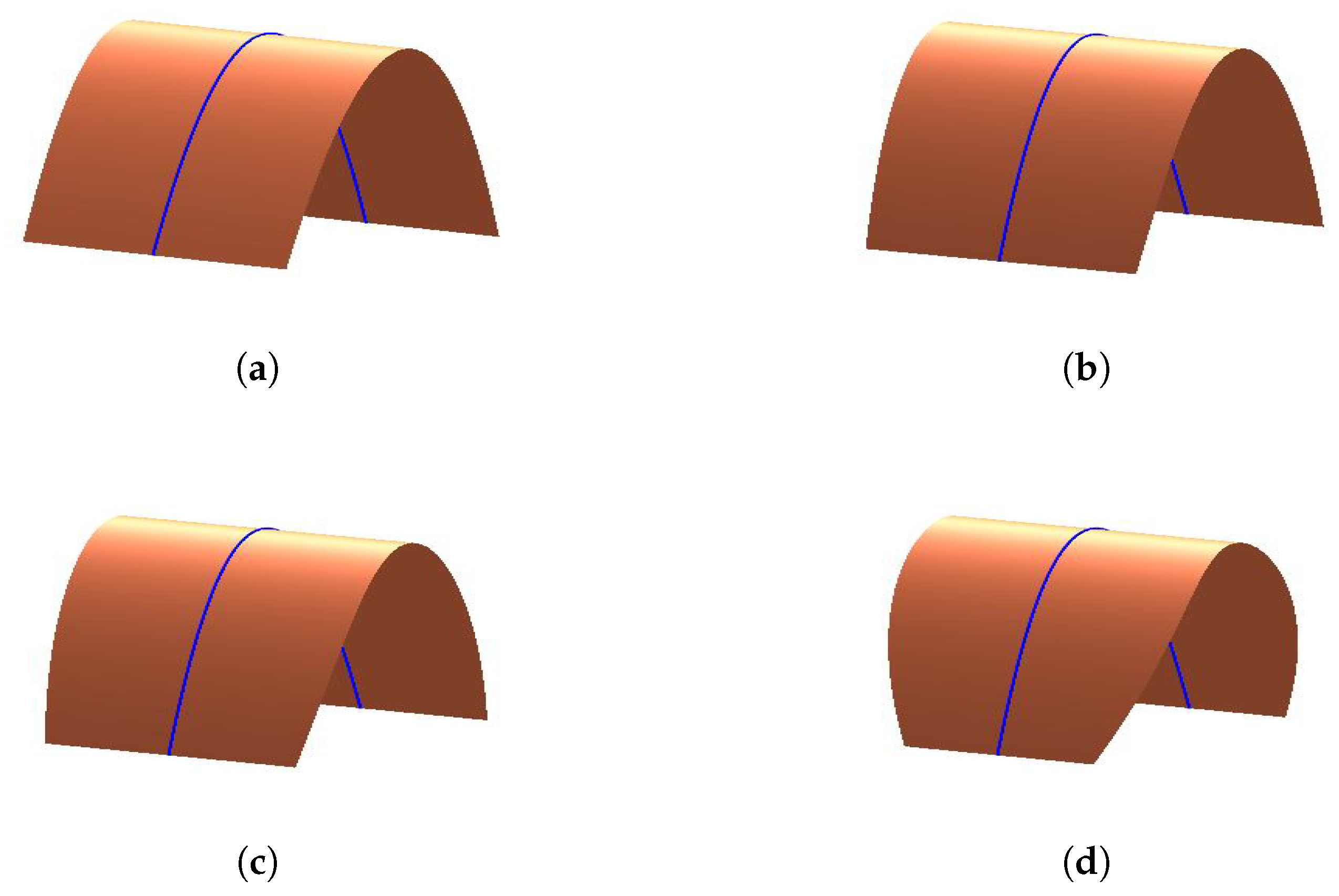
3.2. Developable Surface as the Tangent of Spine Curve
- When modifying the value ofand keepingunchanged, the length and position of the generatorremain the same. The position of the generatorremains unchanged, but the length of it becomes shorter when we increase the value of.
- When we only change the value of, the generatorandhave no changes in position and length. However, the lengths of the two generators become shorter when increasing the value of.
- We just modify the value of, the position and the length of the generatorremain unchanged. The position of the generatoralso has no change, but the length of it will become shorter when increasing the value of.
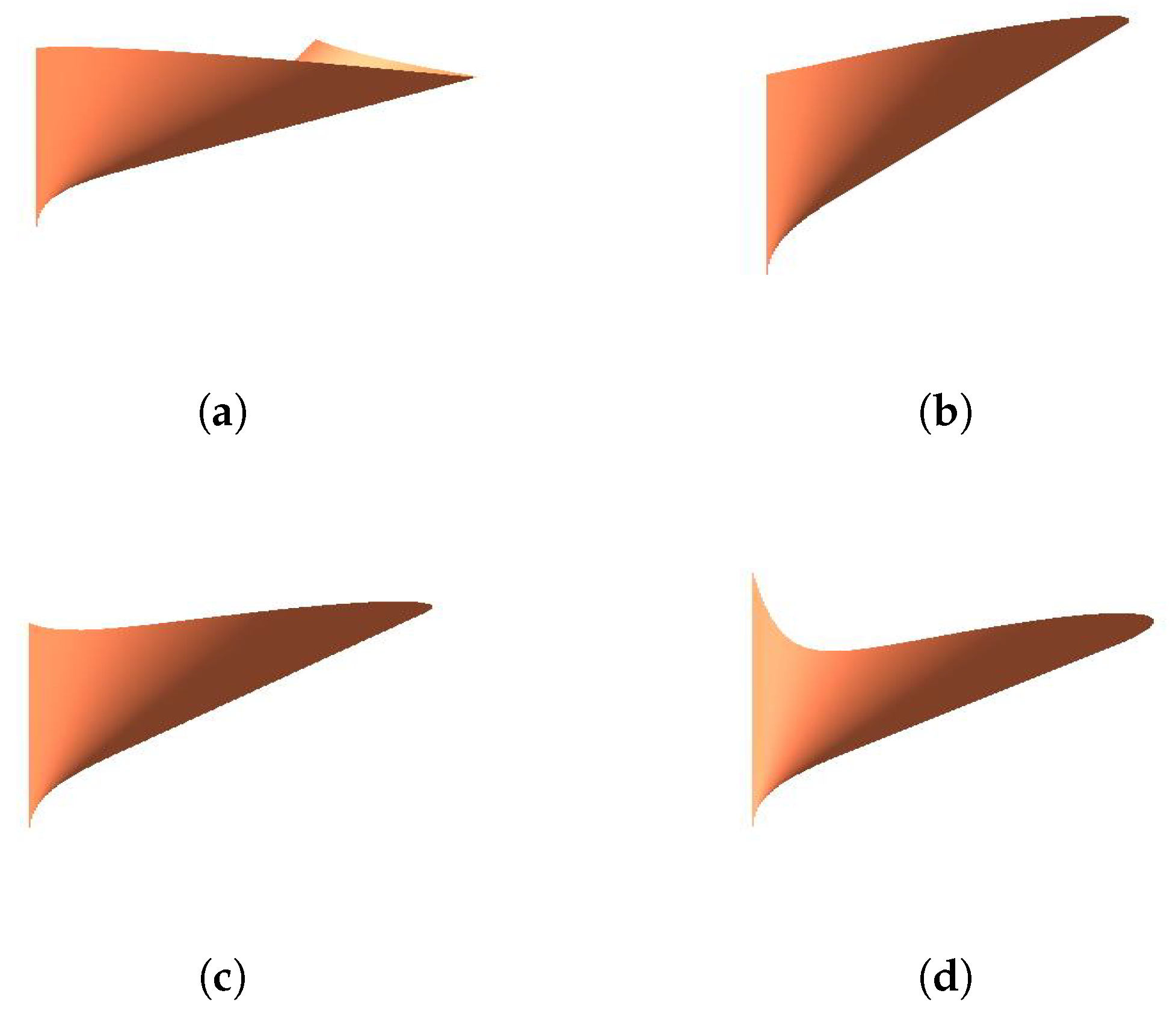
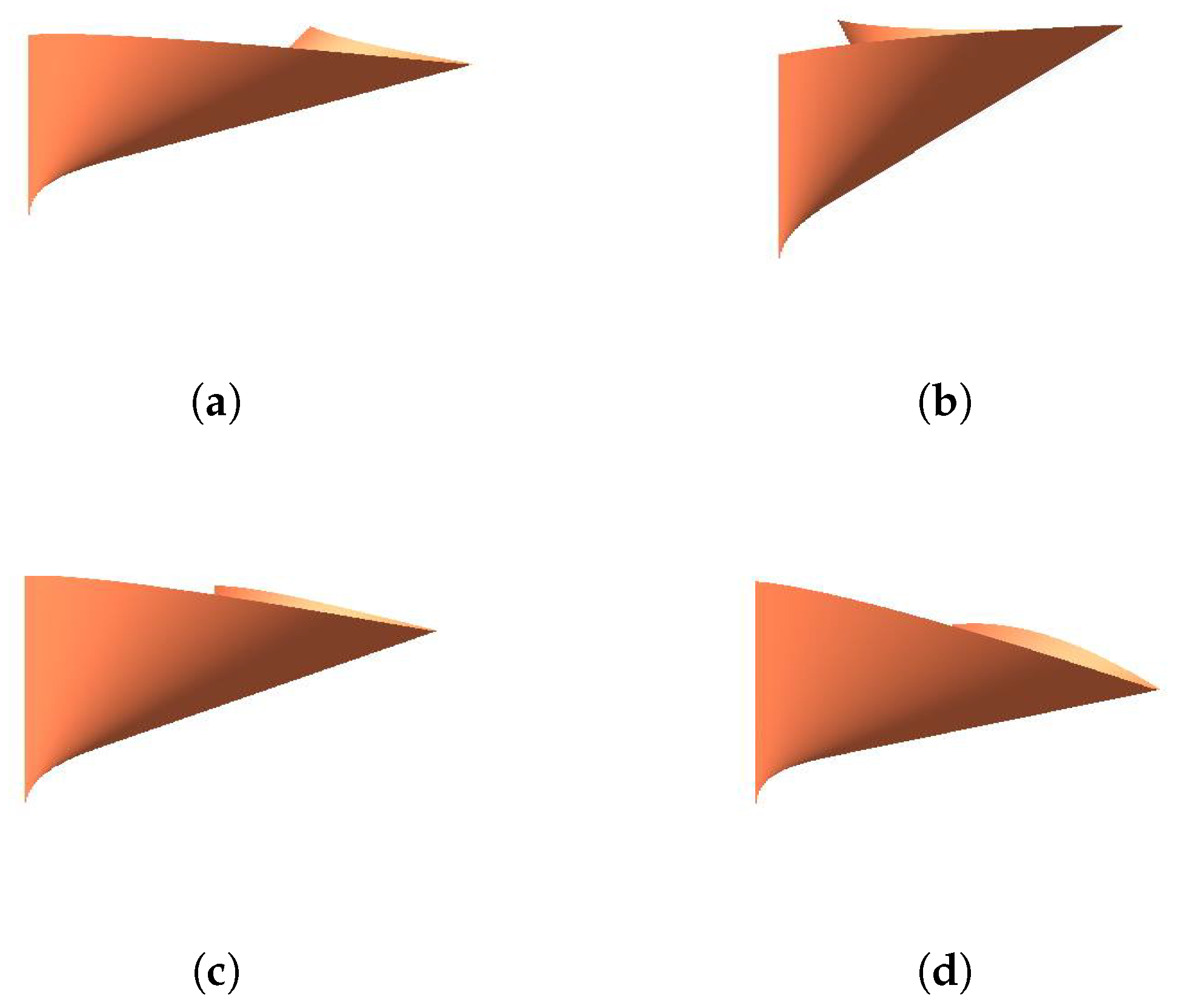
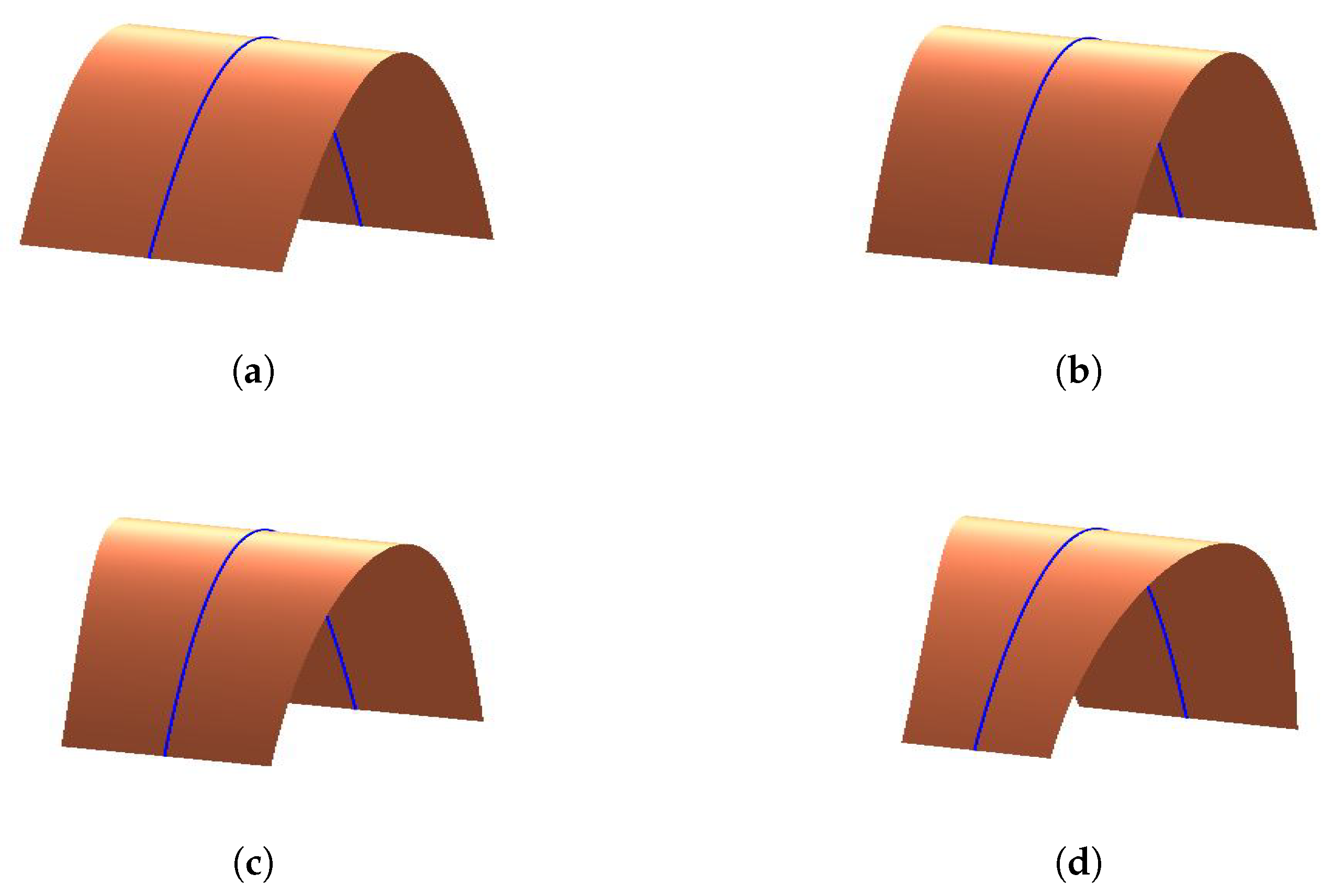
4. Developable Surface Interpolating Cubic Geodesic C-Bézier Curve with Parameters
5. Conclusions
- In the CAD/CAM field, the modeling of some products are often built by blending multiple developable patches together. Therefore, in the future, we will study the conditions of and Beta continuity of new C-Bézier developable surfaces and analyze the effects of shape parameters on the composite surface. We will try to apply the composite C-Bézier developable surface with parameters to design the car body, shoes, ship hull, etc. I think it will be a useful complement for CAD/CAM.
- Moreover, many researchers discussed the trigonometric curve and surface with some parameters; refer to [27,28,29]. We also want to extend our work to trigonometric curve and surface with some parameters, which can be controlled due to the freedom provided by these parameters. They can be efficient models in the fields of CAGD.
- Yang and Liang [23] presented a new kind of algebraic-trigonometric blended spline curve, called curves. The new curves can represent some conics and transcendental curves. We can extend our work to the C-B-spline curve and surface with n parameters. We will try to construct a spline curve to interpolate given points and to represent some conic curves. Because of more freedom, we may get more smooth and precise curves.
Author Contributions
Funding
Conflicts of Interest
References
- Aumann, G. Interpolation with developable Bézier patches. Comput. Aided Geom. Des. 1991, 8, 409–420. [Google Scholar] [CrossRef]
- Lang, J.; Ro¨schel, O. Developable (1,n)-Bézier surfaces. Comput. Aided Geom. Des. 1992, 9, 291–298. [Google Scholar] [CrossRef]
- Chalfant, J.S.; Maekawa, T. Design for manufacturing using B-Spline developable surfaces. J. Ship Prod. 1998, 42, 207–215. [Google Scholar]
- Pottmann, H.; Farin, G. Developable rational Bézier and B-spline surfaces. Comput. Aided Geom. Des. 1995, 12, 513–531. [Google Scholar] [CrossRef]
- Chu, C.H.; Séquin, C.H. Developable Bézier patches: Properties and design. Comput. Aided Des. 2002, 34, 511–527. [Google Scholar] [CrossRef]
- Bodduluri, R.M.C.; Ravani, B. Geometric design and fabrication of developable Bézier and B-spline surfaces. ASME Trans. J. Mech. Des. 1994, 116, 1024–1048. [Google Scholar] [CrossRef]
- Bodduluri, R.M.C.; Ravani, B. Design of developable surfaces using duality between plane and point geometies. Comput. Aided Des. 1993, 25, 621–632. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Wang, G.J. A new method for designing a developable surface utilizing the surface pencil through a given curve. Prog. Nat. Sci. 2008, 18, 105–110. [Google Scholar] [CrossRef]
- Li, C.Y.; Wang, R.H.; Zhu, C.G. An approach for designing a developable surface through a given line of curvature. Comput. Aided Des. 2013, 45, 621–627. [Google Scholar] [CrossRef]
- Farin, G. Rational curves and surfaces. In Mathematical Methods in Computer Aided Geometric Design; Lyche, T., Schumaker, I., Eds.; Academic Press: Boston, MA, USA, 1989. [Google Scholar]
- Piegl, I. On NURBS: A survey. IEEE Comput. Graph. Appl. 1991, 11, 55–71. [Google Scholar] [CrossRef]
- Farin, G. From conics to NURBS: A tutorial and survey. IEEE Comput. Graph. Appl. 1992, 1, 78–86. [Google Scholar] [CrossRef]
- Zhang, J.W. C-curves: An extension of cubic curves. Comput. Aided Geom. Des. 1996, 13, 199–217. [Google Scholar] [CrossRef]
- Zhang, J.W. Two different forms of C-B splines. Comput. Aided Geom. Des. 1997, 14, 31–41. [Google Scholar] [CrossRef]
- Zhang, J.W. C-Bézier Curves and Surfaces. Graph. Models Ima Process. 1999, 61, 2–15. [Google Scholar] [CrossRef]
- Han, X.A.; Ma, Y.C.; Huang, X.L. A novel generalization of Bezier curve and surface. J. Comput. Appl. Math. 2008, 217, 180–193. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Han, X.L. New cubic rational basis with tension shape parameters. Appl. Math. J. Chin. Univ. 2015, 30, 273–298. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Han, X.L.; Liu, S.J. Curve construction based on four αβ-Bernstein-like basis functions. J. Comput. Appl. Math. 2015, 273, 160–181. [Google Scholar] [CrossRef]
- Zhou, M.; Yang, J.Q.; Zheng, H.C.; Song, W.J. Design and shape adjustment of developable surfaces. Appl. Math. Model. 2013, 37, 3789–3801. [Google Scholar] [CrossRef]
- Hu, G.; Cao, H.X.; Qin, X.Q.; Wang, X. Geometric design and continuity conditions of developable λ-Bézier surfaces. Adv. Eng. Softw. 2017, 114, 235–245. [Google Scholar] [CrossRef]
- Hu, G.; Wu, J.L.; Qin, X.Q. A new approach in designing of local controlled developable H-Bézier surfaces. Adv. Eng. Softw. 2018, 121, 26–38. [Google Scholar] [CrossRef]
- Wang, C.W. Cubic trigonometric polynomial spline curves with shape parameter. J. Beijing Inst. Cloth. Technol. (Nat. Sci. Ed.) 2008, 28, 50–55. [Google Scholar]
- Yang, L.L.; Liang, J.F. A class of algebraic-trigonometric blended splines. J. Comput. Appl. Math. 2011, 235, 1713–1729. [Google Scholar]
- Chen, Q.Y.; Wang, G.Z. A class of Bézier-like curves. Comput. Aided Geom. Des. 2003, 20, 29–39. [Google Scholar] [CrossRef]
- Shang, Y.L. Consensus formation of two-level opinion dynamics. Acta Math. Sci. 2014, 34B, 1029–1040. [Google Scholar] [CrossRef]
- Carmo, M.D. Differential Geometry of Curves and Surfaces; Prentice Hall: Englewood Cliffs, NJ, USA, 1976. [Google Scholar]
- Sharma, R. Quartic Trigonometric Bézier Curves and Surfaces with Shape Parameter. Int. J. Innov. Res. Comput. Commun. Eng. 2016, 3297, 7712–7717. [Google Scholar]
- Bashir, U.; Abbas, M.; Awang, M.; Ali, J.M. A class of quasi-quintic trigonometric Bézier curve with two shape parameters. Sci. Asia 2013, 39S, 11–15. [Google Scholar] [CrossRef]
- Misro, M.Y.; Ramli, A.; Ali, J.M. Quintic trigonometric Bézier curve with two shape parameters. Sains Malays. 2017, 46, 825–831. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Zhu, C. Designing Developable C-Bézier Surface with Shape Parameters. Mathematics 2020, 8, 402. https://doi.org/10.3390/math8030402
Li C, Zhu C. Designing Developable C-Bézier Surface with Shape Parameters. Mathematics. 2020; 8(3):402. https://doi.org/10.3390/math8030402
Chicago/Turabian StyleLi, Caiyun, and Chungang Zhu. 2020. "Designing Developable C-Bézier Surface with Shape Parameters" Mathematics 8, no. 3: 402. https://doi.org/10.3390/math8030402
APA StyleLi, C., & Zhu, C. (2020). Designing Developable C-Bézier Surface with Shape Parameters. Mathematics, 8(3), 402. https://doi.org/10.3390/math8030402




