Point Orthogonal Projection onto a Spatial Algebraic Curve

Abstract

Point orthogonal projection onto a spatial algebraic curve plays an important role in computer graphics, computer-aided geometric design, etc. We propose an algorithm for point orthogonal projection onto a spatial algebraic curve based on Newton’s steepest gradient descent method and geometric correction method. The purpose of Algorithm 1 in the first step of Algorithm 4 is to let the initial iteration point fall on the spatial algebraic curve completely and successfully. On the basis of ensuring that the iteration point fallen on the spatial algebraic curve, the purpose of the intermediate for loop body including Step 2 and Step 3 is to let the iteration point gradually approach the orthogonal projection point (the closest point) such that the distance between them is very small. Algorithm 3 in the fourth step plays an important double acceleration and orthogonalization role. Numerical example shows that our algorithm is very robust and efficient which it achieves the expected and ideal result.

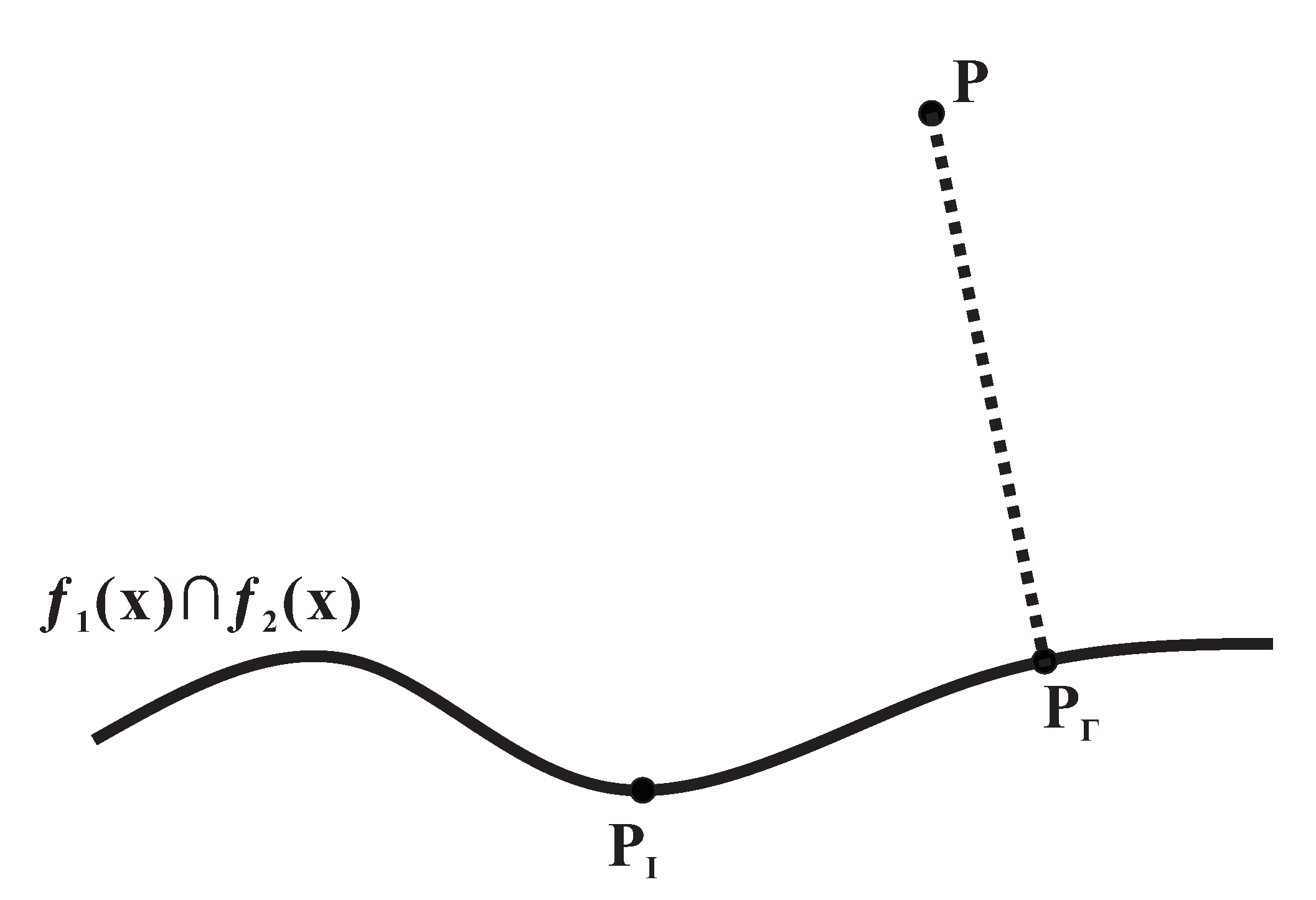
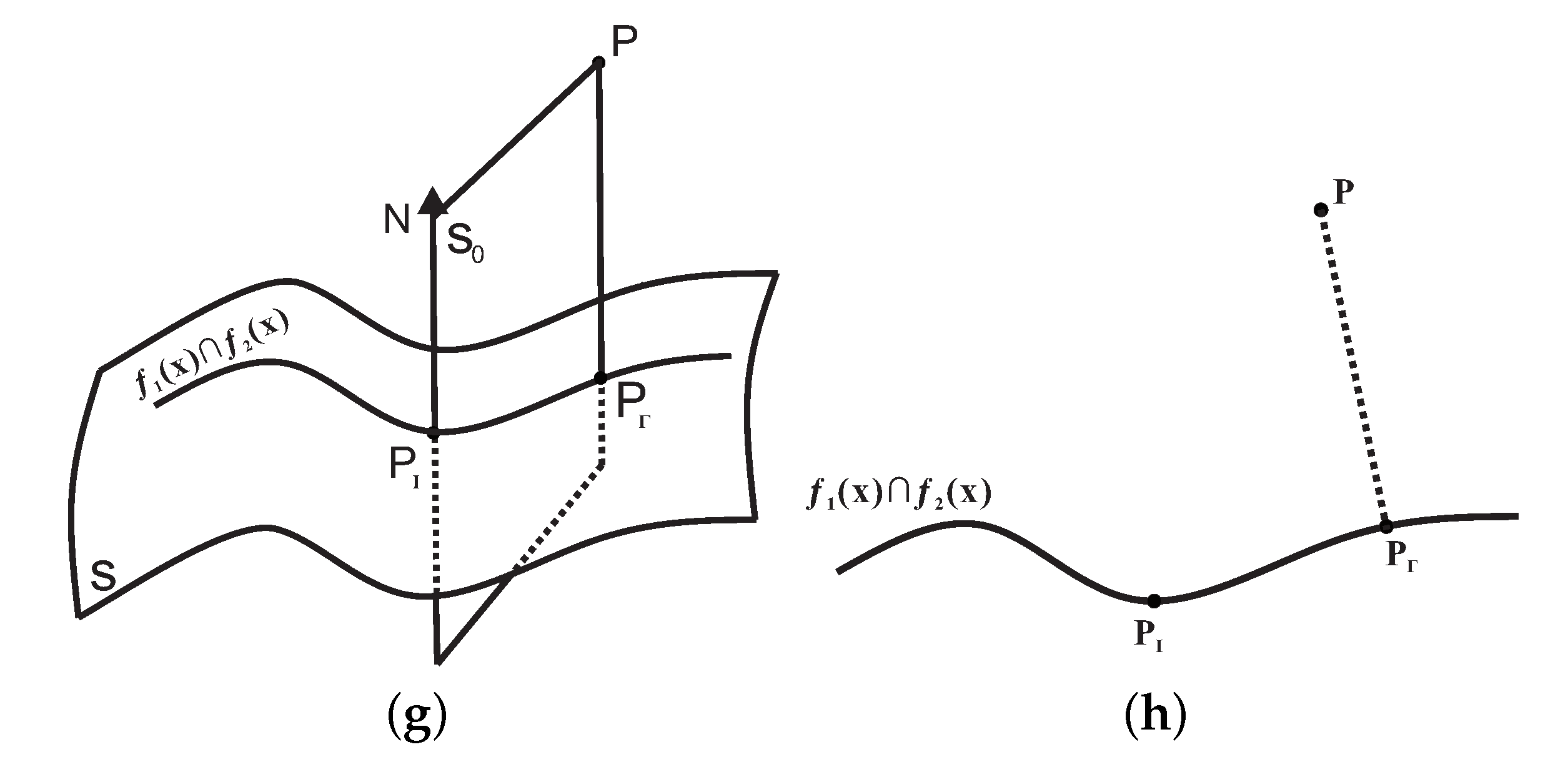
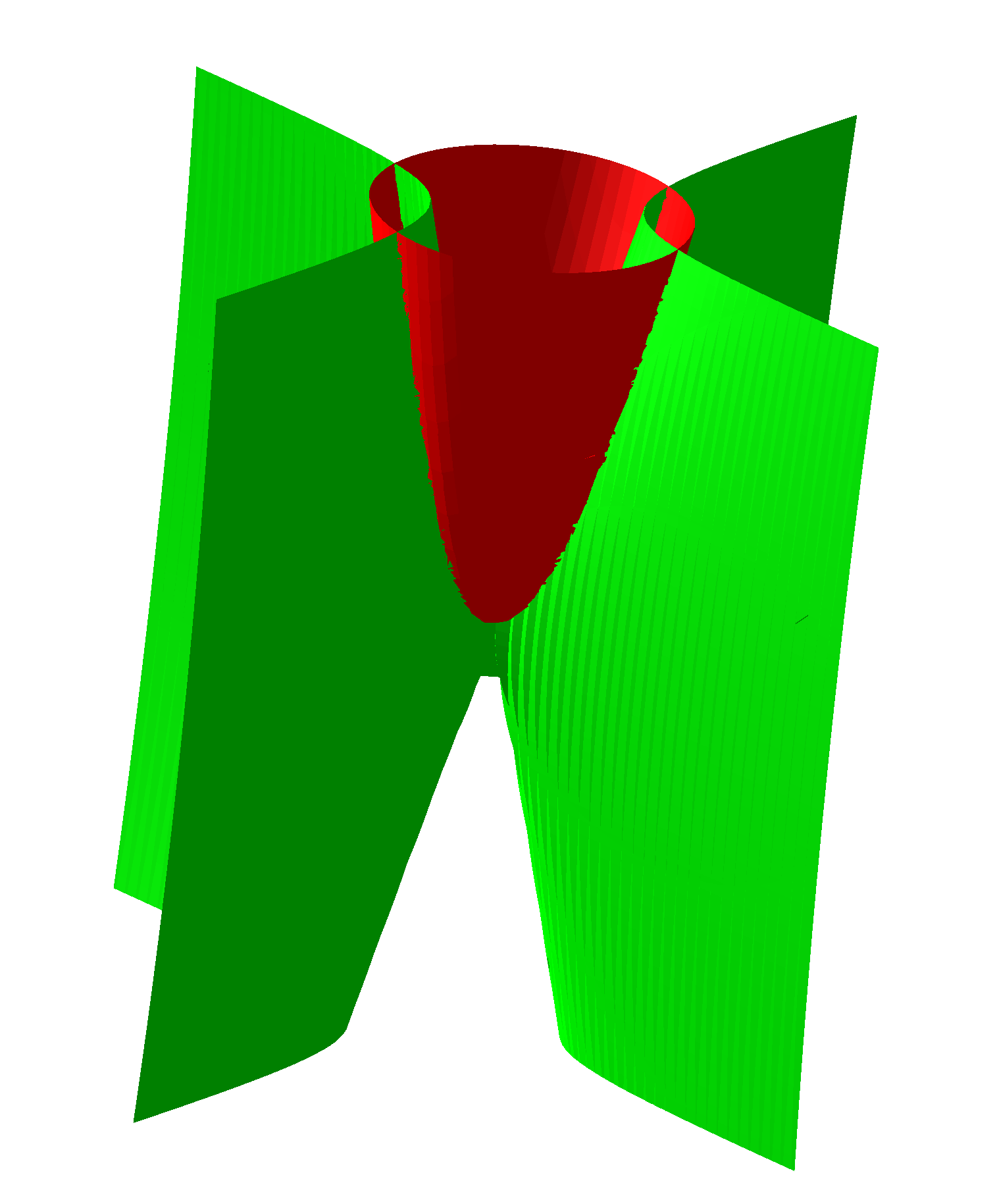
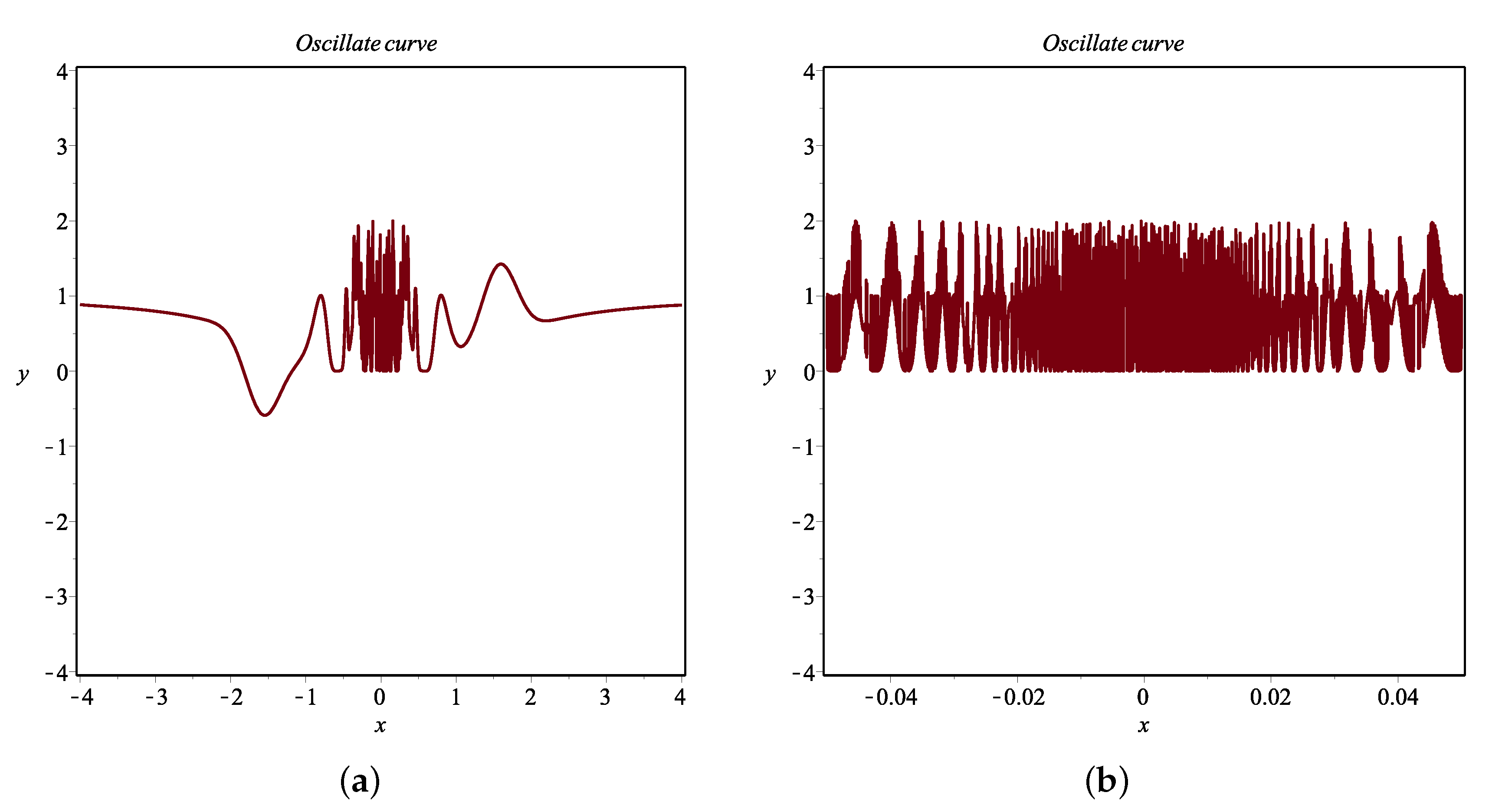
1. Introduction

Orthogonal projection is widely used and plays an important role in geometric modeling, computer graphics and computer aided geometric design. Pegna et al. [1] first proposed the concept of orthogonal projection, and discussed the calculation projecting problem of spatial parametric curve orthogonal projection onto a parametric surface and algebraic surface. The so-called orthogonal projection is to find a point on the curve such that the line segment connected to this point and the given point is perpendicular to the tangent line of the curve at this point. There is a close relationship between the orthogonal projection problem and distance projection problem [1]; therefore, the study of the distance projection problem is helpful for the study of the orthogonal projection problem to some extent.

Many scholars have done a lot of work in these two aspects. Hartmann [2] proposed a first-order tangent line method to calculate point orthogonal projection onto parametric curve and surface. For a few cases of non-convergence and as supplement and perfection of the first-order tangent line method [2], Liang et al. [3] and Li et al. [4] presented hybrid second-order method for orthogonal projection onto parametric curve and surface, respectively. Hu et al. [5] proposed a second-order geometric iterative algorithm with curvature information to approximate the orthogonal projection point of the given point on parametric curves and surfaces. Based on their work [5], Li et al. [6] provided an improved method for point orthogonal projection onto general parametric surface such that the efficiency in [6] is greatly improved compared with the existing methods. Ma et al. [7] studied the problem for point orthogonal projection onto NURBS curves and surfaces for which they adopted four-step technique: subdividing curve or surface into curve segments or surface patches, finding out the relationship between the control polygon of curve segment or surface patch and the test point, candidate curve segment or surface patch and approximate projection points being found out by comparison and the final projective point being obtained by comparing the distance between the test point and these approximate projective points. Since the minimum distance between two geometries occurred between a pair of special points, they studied the minimum distance between various specific geometry by using the property and obtained some satisfactory results [8,9,10].

Since the algebraic curve and surface are difficult to control accurately, it is difficult to find the orthogonal projection point on the algebraic curve and surface. At the same time, geometric modeling, computer graphics, computer aided geometric design and many other problems can come down to point orthogonal projection onto curve and surface problems. Therefore, it is of great significance to study point orthogonal projection onto algebraic curves and surfaces.

Up to the present day, the study of point orthogonal projection onto algebraic curves and surfaces is mainly divided into three types: orthogonal projection onto planar algebraic curve, spatial algebraic curve and algebraic surface. Since algebraic curves and algebraic surfaces have no parametric control, it is not easy to solve such problems directly. However, many scholars turned such problems into root-finding problems. There are three types for point orthogonal projection onto planar algebraic curve: local method, global method and compromise method between these two methods. According to the most basic geometric characteristics, the problem of point orthogonal projection onto planar algebraic curve can be understood as solving the equation which the cross product of gradient $\nabla f\left(\mathbf{X}\right)$ of the planar algebraic curve $f\left(\mathbf{X}\right)$ at point $\mathbf{X}$ and the vector $\overrightarrow{\mathbf{PX}}$ is zero. The equation can be specifically expressed as the following,

$$\nabla f\left(\mathbf{X}\right)\times (\mathbf{P}-\mathbf{X})=0$$

(1)

In fact, the geometric meaning is that the inner product of the tangent vector of the planar algebraic curve $f\left(\mathbf{X}\right)$ at point $\mathbf{X}$ and the vector $\overrightarrow{\mathbf{PX}}$ is zero. Equation (1) can be transformed into the corresponding iterative formula of Newton’s steepest gradient descent method.

$${\mathbf{X}}_{n+1}={\mathbf{X}}_n-(f\left({\mathbf{X}}_n\right)/〈\nabla f\left({\mathbf{X}}_n\right),\nabla f\left({\mathbf{X}}_n\right)〉)\nabla f\left({\mathbf{X}}_n\right).$$

(2)

William et al. [11] used composed method including Lagrange multiplier and Newton’s steepest gradient descent method to compute the orthogonal projection point on the planar algebraic curve for each test point. The characteristic of the method [11] is that it is fast but local and depends on the initial iterative point.

In addition to the Newton’s local iterative method to solve the equation for point orthogonal projection onto the planar algebraic curve, the first global method converting into solving system of nonlinear equations is the Homotopy continuous method [12,13]. They used the most classical Homotopy transformation method,

$$\mathbf{H}(\mathbf{X},t)=(1-t)\mathbf{P}\left(\mathbf{X}\right)+t\mathbf{Q}\left(\mathbf{X}\right),t\in [0,1],$$

(3)

where t is a continuous transformational parameter from 0 to 1, $\mathbf{P}\left(\mathbf{X}\right)=0$ and $\mathbf{Q}\left(\mathbf{X}\right)=0$ are original system of nonlinear equations to be solved and objective solution system of nonlinear equations, respectively. All isolated solutions of original system of nonlinear equations $\mathbf{P}\left(\mathbf{X}\right)=0$ can be obtained by the numerical continuous Homotopy method [12,13], where all the isolated solutions of $\mathbf{P}\left(\mathbf{X}\right)=0$ are exactly the same as the target solutions of system of nonlinear equations $\mathbf{Q}\left(\mathbf{X}\right)=0$. The robustness of the numerical continuous Homotopy methods [12,13] with global convergence is expounded and verified by [14] and their high time consumption property is summarized in [15]. The major difficulty of Homotopy method is how to find a very satisfactory objective solutions of system of nonlinear equations $\mathbf{Q}\left(\mathbf{X}\right)=0$.

Turning the projection problem into a resultant problem and then solving the resultants [16,17,18,19] is called the second global resultant method. Using the classical elimination theory, a system of two nonlinear equations with two variables can be transformed into a resultant polynomial with one variable being equivalent to the two original equations. The Sylvester’s resultant and Cayley’s statement of Bézout’s method are the most classical resultant methods [16,17,18,19]. If the degree of the planar algebraic curve is no more than 5, all roots of the nonlinear polynomial equation formed by the resultant methods can be solved. However, if the degree of the planar algebraic curve is more than 5, it is very difficult to directly solve all roots of two-polynomial system with the resultant method.

The third global method is Bézier clipping technique [20,21,22]. In the first step, the nonlinear system of Equation (1) is turned into Bézier form with convex hull property. The rest of the treatment is exactly the same as that of Ma et al. [7] so we do not give a detailed description here. The superiority of global Bézier clipping method is that all roots can be solved, or all orthogonal projection points can be obtained this way. There are two disadvantages of the global clipping method: the first disadvantage is that it needs a lot of time to subdivide, seek, judge and compare; the second disadvantage is that Equation (1) is difficult to directly convert into Bernstein-Bézier form for a small number of planar algebraic curves. Of course, an indirect solution to the difficulty which the idea is come from reviewer’s suggestion is that one can use a multivariate solver for this problem. Equation (7) gives a 3 × 3 algebraic system and its solution gives the stationary (candidate) points.

The first compromise method that is between local and global methods is proposed by Hartmann [2,23] which is composed of the geometric tangent property for computing orthogonal projection point. Continue to execute the iterative formula (2) until the iterative point falls on the planar algebra curve. Taking the iterative point fallen on the planar algebraic curve as being the initial iterative point, compute the foot point once by the iterative formula (4),

$$\mathbf{Q}=\mathbf{P}-(〈\mathbf{P}-{\mathbf{Y}}_n,\nabla f\left({\mathbf{Y}}_n\right)〉/〈\nabla f\left({\mathbf{Y}}_n\right),\nabla f\left({\mathbf{Y}}_n\right)〉)\nabla f\left({\mathbf{Y}}_n\right).$$

(4)

Repeat the above two steps until the foot point Q and the orthogonal projection point completely overlap. Unfortunately, for a small part of the planar algebraic curve, it is invalid to approach the orthogonal projective point with progressive tangent foot point. Based on Hartmann’s work in [2,23], Li et al. [24] proposed an improved method for calculating footpoint which the effect is good if the test point is not far away, but the effect is not ideal if the test point is particularly far away. In addition, on the important roles and applications of the algebraic curves and algebraic surfaces, some introduction and explanation are presented in these papers [2,9,10,23,24]. Here we will not explain and elaborate upon them in detail.

The second compromise method is proposed by Redding [25] who used the osculating circle technique to accomplish point orthogonal projection onto the planar algebraic curve. The osculating circle technique mainly includes three steps: (1) Compute curvature at point on the planar algebraic curve and the corresponding radius and center of the curvature circle determined by curvature. (2) Get the footpoint $\mathbf{Q}$ intersected with the line segment formed by the test point and the center of the curvature circle and curvature circle. (3) Take the footpoint $\mathbf{Q}$ approximately as the point fallen on the planar algebraic curve. Repeatedly execute the above three steps until the foorpoint $\mathbf{Q}$ and the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ completely coincide. Since there is a certain deviation in the third step of the osculating circle technique for footpoint $\mathbf{Q}$ approximating to the orthogonal projection point on the planar algebraic curve and the planar algebraic curve has no parametric control like parametric curve, the robustness of the osculating circle technique cannot be achieved very well. Greatly inspired by these works [2,23,25], Wu et al. [26] proposed an improved curvature circle algorithm for orthogonal projection onto a planar algebraic curve. Not only in robustness but also in efficiency, the Second Remedial Algorithm in [26] is very satisfactory and ideal.

The third compromise method is the circle shrinking method [27]. Repeatedly iterate the iterative formula (2) such that the iterative point can fall on the planar algebraic curve as much as possible. Draw a circle where the center and radius are the test point $\mathbf{P}$ and $∥\mathbf{P}-{\mathbf{P}}_{\mathtt{I}}∥$, respectively. Identify a point ${\mathbf{P}}^{+}$ on the circle by means of the mean value theorem and find the intersection named the current iterative point ${\mathbf{P}}_{\mathtt{I}}$ which is the intersection between the line segment $\overline{{\mathbf{PP}}^{+}}$ and the circle. Repeatedly run the above behavior until the distance between the current point ${\mathbf{P}}_{\mathtt{I}}$ and the previous point ${\mathbf{P}}_{\mathtt{I}}$ is almost zero. The circle shrinking technique [27] consumes more time to find point ${\mathbf{P}}^{+}$ each time and it is difficult to directly compute the intersection ${\mathbf{P}}_{\mathtt{I}}$ intersected of line segment $\overline{{\mathbf{PP}}^{+}}$ and the planar algebraic curve if the degree of the planar algebraic curve is more than 5.

The fourth compromise method with circle double-and-bisect algorithm is proposed by Hu et al. [28]. Starting with a very small circle with center being test point $\mathbf{P}$ and radius $r_1$ being arbitrarily small, draw a new circle with the same center being test point $\mathbf{P}$ and radius $r_2=2r_1$ (After that, the center of all circles is the test point $\mathbf{P}$). If the new circle does not intersect the planar algebraic curve, draw a new circle with radius twice of $r_2$. Keep repeating the above action, until the latest circle can intersect with the planar algebraic curve. The previous circle and the latest circle are tagged as the interior circle and the exterior circle, respectively. Furthermore, implement the rest of the process by adopting the bisecting technology. Continue to draw a new circle with new radius $r=(r_1+r_2)/2$. If the current circle with radius r intersects with the planar algebraic curve, substitute r for $r_2$, else for $r_1$. Repeatedly execute the above progress until the difference between the current radius and the previous radius is almost 0. However, with this method it is not easy to judge whether the exterior circle intersects the planar algebraic curve or not [28]. Moreover, the circle double-and-bisect algorithm [28] consumes more time to seek the intersection between the exterior circle and the planar algebraic curve.

On the problem of point orthogonal projection onto curve and surface, there exists a classical method which is transforming the problem of point orthogonal projection onto curve and surface into a specific solver problem. Barto$\check{n}$ M. [29] proposed two blending schemes solvers for solving the problem of point orthogonal projection onto curve and surface. As a system of nonlinear equations, throwing away no-root domain can be realized by a simple linear combination of functions and then determine all control points for its Bernstein-Bézier basis having the same sign, which must be in accord with the seeking function. It can continuously obtain these types of functions to get rid of the no-root domain through the continuous subdivision process. The efficiency of the geometric-based algorithm [29] is higher than that of the existing subdivision mode based GPU. Therefore, two blending schemes in [29] can efficiently reduce the number of subdivisions by using continuous eliminating no-root domains. Result from the consequence in [29], van Sosin and Elber [30] constructed a variety of complex piecewise polynomial systems having zero or inequality constraints in zero-dimensional or one-dimensional solution spaces. Finding out all the root solutions is the advantage of these methods [29,30]; however, more computation consume-time and the need for many subdivision steps are their disadvantages.

2. Algorithm Realization for Point Orthogonal Projection onto a Spatial Algebraic Curve

2.1. Newton’s Steepest Gradient Descent Method

Let us elaborate on the general idea. Let $\mathbf{P}$ be a test point. There is a spatial algebraic curve $\mathbf{C}$ which can be written as,

$$\left\{\begin{array}{c}{f}_1\left(\mathbf{X}\right)=0,\hfill \\ f_2\left(\mathbf{X}\right)=0.\hfill \end{array}\right.$$

(5)

where $\mathbf{X}$ is equal to $(x,y,z)$, and $f_1\left(\mathbf{X}\right)=0$ and $f_2\left(\mathbf{X}\right)=0$ are two algebraic surfaces, respectively. Their intersection set constitutes a spatial algebra curve $\mathbf{C}$. The aim of this paper is to seek a spatial point ${\mathbf{P}}_{\Gamma }$ on the spatial algebraic curve $\mathbf{C}$ to satisfy the basic relationship (See Figure 1),

$$∥\mathbf{P}-{\mathbf{P}}_{\Gamma }∥=\underset{\mathbf{X}\in \Gamma }{min}∥\mathbf{P}-\mathbf{X}∥.$$

(6)

On the other hand, the vector $\overrightarrow{\mathbf{PX}}$ determined by the test point $\mathbf{P}$ and point $\mathbf{X}$ on the spatial algebraic curve $\mathbf{C}$ is orthogonal to the tangent vector $\mathbf{T}$, where $\mathbf{T}=\nabla f_1\left(\mathbf{X}\right)\times \nabla f_2\left(\mathbf{X}\right)$. The corresponding equation formed by the inner product of the vector $\overrightarrow{\mathbf{PX}}$ and vector $\mathbf{T}$ can be expressed as,

$$\mathbf{F}\left(\mathbf{X}\right)=〈\mathbf{T},\mathbf{P}-\mathbf{X}〉=0.$$

(7)

The above two questions can be summed up as,

$$\left\{\begin{array}{c}{f}_1\left({\mathbf{P}}_{\Gamma }\right)=0,\hfill \\ f_2\left({\mathbf{P}}_{\Gamma }\right)=0,\hfill \\ \mathbf{F}\left({\mathbf{P}}_{\Gamma }\right)=0,\hfill \\ ∥\mathbf{P}-{\mathbf{P}}_{\Gamma }∥=\underset{\mathbf{X}\in \Gamma }{min}∥\mathbf{P}-\mathbf{X}∥,\hfill \end{array}\right.$$

(8)

where ${\displaystyle \nabla f=\left[\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}\right]}$ is Hamiltonian operator, symbol × is cross product and symbol $〈,〉$ is inner product. We take s as the arc length parameter of the spatial algebraic curve $\mathbf{C}$ and Let ${\displaystyle \mathbf{T}=\left[\frac{dx}{ds},\frac{dy}{ds},\frac{dz}{ds}\right]}$ be tangent vector along the spatial algebraic curve $\mathbf{C}$. There are many ways to construct the Newton’s steepest descent methods of the spatial algebraic curve with Equation (5). After many tests and comparisons, we find that the following model of Newton’s steepest descent method with Equation (9) is the best choice for the Newton’s steepest descent methods of the spatial algebraic curve.

$$\left\{\begin{array}{c}{\mathbf{Y}}_n={\mathbf{X}}_n-(f_1\left({\mathbf{X}}_n\right)/〈\nabla f_1\left({\mathbf{X}}_n\right),\nabla f_1\left({\mathbf{X}}_n\right)〉)/\nabla f_1\left({\mathbf{X}}_n\right),\hfill \\ {\mathbf{X}}_{n+1}={\mathbf{Y}}_n-(f_2\left({\mathbf{Y}}_n\right)/〈\nabla f_2\left({\mathbf{Y}}_n\right),\nabla f_2\left({\mathbf{Y}}_n\right)〉)/\nabla f_2\left({\mathbf{Y}}_n\right).\hfill \end{array}\right.$$

(9)

Repeatedly run Equation (9), called Newton’s steepest gradient descent method, until the iterative termination criteria are satisfied $\left|f_1\left({\mathbf{X}}_{n+1}\right)\right|<\epsilon$ and $\left|f_2\left({\mathbf{X}}_{n+1}\right)\right|<\epsilon$, where the initial iterative point is ${\mathbf{X}}_0=\mathbf{P}-(0.1,0.1,0.1)$ and the iterative point ${\mathbf{X}}_{n+1}$ fallen on the spatial algebraic curve $\mathbf{C}$ is called ${\mathbf{P}}_{\mathtt{I}}$. The Newton’s steepest gradient descent method (Algorithm 1) can be specifically described as (See Figure 2).

Algorithm 1: The Newton’s steepest gradient descent method

Input: The test point P and the spatial algebraic curve $\mathbf{C}$.

Output: The iterative point ${\mathbf{P}}_{\mathtt{I}}$ fallen on the spatial algebraic curve $\mathbf{C}$.

Description:

Step 1:

${\mathbf{X}}_{n+1}=\mathbf{P}-(0.1,0.1,0.1)$;

Do {

${\mathbf{X}}_n={\mathbf{X}}_{n+1}$;

Update ${\mathbf{X}}_{n+1}$ according to the iterative Equation (9);

}while ($\left|f_1\left({\mathbf{X}}_{n+1}\right)\right|>\epsilon \&\&\left|f_2\left({\mathbf{X}}_{n+1}\right)\right|>\epsilon \&\&∥{\mathbf{X}}_{n+1}-{\mathbf{X}}_n∥>\epsilon )$;

Step 2:

${\mathbf{P}}_{\mathtt{I}}={\mathbf{X}}_{n+1}$;

Return ${\mathbf{P}}_{\mathtt{I}}$;

Remark 1.

Starting from the initial iterative point ${\mathit{X}}_0$, the iterative point of the first equation of the Newton’s steepest gradient descent method with Equation (9) causes the iterative point to be closer to the first algebraic surface $f_1\left(\mathit{X}\right)$. Then through the iterating of the second equation with Equation (9), the iterative point of the second equation with Equation (9) causes the iterative point to be closer to the second algebraic surface $f_2\left(\mathit{X}\right)$. In this way, Equation (9) is iterated repeatedly such that the distance between the finally iterative point and every algebraic surface is almost zero. Namely, through alternating iteration of two sub-equations with Equation (9), the distance between the finally iterative point and the spatial algebraic curve determined by the intersection set of two algebraic surfaces is almost zero. The Newton’s steepest gradient descent method (9) has two advantages. The first advantage of the Newton’s steepest gradient descent method (9) is to promote the iterative point to fall on the spatial algebraic curve $\mathit{C}$ as much as possible. The second advantage of the Newton’s steepest gradient descent method (9) is that the iteration point fallen on the spatial algebraic curve is closer to the orthogonal projection point ${\mathit{P}}_{\Gamma }$, it is very convenient for implementation of the subsequent sub-algorithms.

2.2. Computing Foot-Point $\mathit{Q}$

Although the iterative point ${\mathbf{P}}_{\mathtt{I}}$ falls on the spatial algebraic curve, there is still a certain small distance between the iterative point ${\mathbf{P}}_{\mathtt{I}}$ and the orthogonal projection point ${\mathbf{P}}_{\Gamma }$. There is still a small certain gap between this and our ideal and goal. Our idea is to find a way to gradually reduce the distance between the iteration point ${\mathbf{P}}_{\mathtt{I}}$ and the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ to zero. In order to promote the iteration point ${\mathbf{P}}_{\mathtt{I}}$ and the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ closer, we use the tangent line perpendicular foot method to promote the iteration point ${\mathbf{P}}_{\mathtt{I}}$ and the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ being closer. The basic idea of this method can be realized as the following form. Draw a tangent line $\mathbf{L}$ of the spatial algebraic curve $\mathbf{C}$ at the iterative point ${\mathbf{P}}_{\mathtt{I}}$ fallen the the spatial algebraic curve $\mathbf{C}$. This tangent line $\mathbf{L}$ can be written as,

$$\mathbf{X}=t\times \mathbf{T}+{\mathbf{P}}_{\mathtt{I}},$$

(10)

where t is a tangent line parameter to be determined, and $\mathbf{T}$ is the tangent vector of the spatial algebraic curve $\mathbf{C}$ at the iterative point ${\mathbf{P}}_{\mathtt{I}}$. Through the test point $\mathbf{P}$, let us construct a plane such that the tangent line $\mathbf{L}$ is perpendicular to the plane. From primary geometric intuitiveness, it is not difficult to find that the intersection ${\mathbf{Q}}_0$ named the foot point intersected with the tangent line $\mathbf{L}$ and the plane can be expressed as

$${\mathbf{Q}}_0=t_0\times \mathbf{T}+{\mathbf{P}}_{\mathbf{I}},$$

(11)

where $t_0=〈\mathbf{P}-{\mathbf{P}}_{\mathtt{I}},\mathbf{T}〉/〈\mathbf{T},\mathbf{T}〉$. In this way, the position of the foot point ${\mathbf{Q}}_0$ is between the iteration point ${\mathbf{P}}_{\mathtt{I}}$ and the orthogonal projection ${\mathbf{P}}_{\Gamma }$. At this time, taking foot point ${\mathbf{Q}}_0$ as the initial iterative point of Algorithm 1, we obtain the new iterative point ${\mathbf{P}}_{\mathtt{I}}$ fallen on the spatial algebraic curve $\mathbf{C}$ which the new iterative point ${\mathbf{P}}_{\mathtt{I}}$ is called the current iterative point ${\mathbf{P}}_{\mathtt{I}}$. According to our observations and the basic geometry characteristic, we can also choose the foot point closer to the spatial algebraic curve. Let us choose a point $\mathbf{Q}$ on the line segment $\overline{{\mathbf{Q}}_0\mathbf{P}}$ such that $∥\overrightarrow{{\mathbf{Q}}_0\mathbf{Q}}∥=\frac{1}{2}\times ∥\overrightarrow{{\mathbf{Q}}_0{\mathbf{P}}_{\mathtt{I}}}∥$. Inspired by this, it is not difficult for us to establish the equation about foot-point $\mathbf{Q}$.

$$\frac{\overrightarrow{{\mathbf{Q}}_0\mathbf{Q}}}{\overrightarrow{{\mathbf{Q}}_0\mathbf{P}}}=d,$$

(12)

where $d=\frac{d_1}{d_2},d_1=\frac{∥\overrightarrow{{\mathbf{P}}_{\mathtt{I}}{\mathbf{Q}}_0}∥}{2},d_2=∥\overrightarrow{{\mathbf{Q}}_0\mathbf{P}}∥$. By solving Equation (12), foot-point $\mathbf{Q}$ can be specifically expressed as

$$\mathbf{Q}=d\times (\mathbf{P}-{\mathbf{Q}}_0)+{\mathbf{Q}}_0$$

(13)

The computation of the foot-point $\mathbf{Q}$ can be achieved via Algorithm 2 (See Figure 3).

Algorithm 2: Computing foot-point $\mathbf{Q}$

Input: The test point $\mathbf{P}$, the spatial algebraic curve $\mathbf{C}$ and the iterative point ${\mathbf{P}}_{\mathtt{I}}$ on the spatial algebraic curve $\mathbf{C}$.

Output: The foot-point $\mathbf{Q}$.

Description:

Step 1:

Compute the foot-point $\mathbf{Q}$ by the formula (13).

Return $\mathbf{Q}$;

2.3. Accelerating and Correcting Method

By Algorithm 1, the initial iteration point ${\mathbf{X}}_0$ can fall on the spatial algebraic curve $\mathbf{C}$ and a final iterative point ${\mathbf{P}}_{\mathtt{I}}$ is generated. Then the foot-point Q is obtained by Algorithm 2 derived from the final iterative point ${\mathbf{P}}_{\mathtt{I}}$. So the foot-point $\mathbf{Q}$ is taken as the initial iterative point of Algorithm 1, and a new current final iterative point ${\mathbf{P}}_{\mathtt{I}}$ fallen on the spatial algebraic curve $\mathbf{C}$ is generated. Run Algorithm 1 and Algorithm 2 alternately and repeatedly, the current iterative point ${\mathbf{P}}_{\mathtt{I}}$ is getting closer to the orthogonal projection point ${\mathbf{P}}_{\Gamma }$. However, the rate of the iterative point ${\mathbf{P}}_{\mathtt{I}}$ approaching the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ becomes slower and slower. And orthogonalization is hard to achieve. In other words, the first three sub-formulas of Formula (8) are difficult to satisfy which this process is not up to the ideal.

In order to overcome these two disadvantages, we add accelerating and correcting method after Algorithm 2 such that the first three sub-formulas of formula (8) can be satisfied as soon as possible. Since $\mathbf{T}=\nabla f_1\times \nabla f_2$ is the tangent vector of the spatial algebraic curve $\mathbf{C}$ at point $\mathbf{X}$, so the relationship between the tangent vector $\mathbf{T}=\nabla f_1\times \nabla f_2$ and the spatial algebraic curve $\mathbf{C}$ can be written as,

$$\left\{\begin{array}{c}〈\mathbf{T},\nabla f_1〉=0,\hfill \\ 〈\mathbf{T},\nabla f_2〉=0.\hfill \end{array}\right.$$

(14)

Furthermore, let $\mathbf{c}=\left[\frac{d^{2}x}{d{t}^2},\frac{d^{2}y}{d{t}^2},\frac{d^{2}z}{d{t}^2}\right]$ be the curvature vector of the spatial algebraic curve $\mathbf{C}$ at the point $\mathbf{X}$. Taking the first-order derivative of Equation (14) with respect to arc length parameter s, get the corresponding equation about curvature vector,

$$\left\{\begin{array}{c}\mathbf{T}{F}_2{\mathbf{T}}^{\mathtt{T}}+\nabla f_1{\mathbf{c}}^{\mathtt{T}}=0,\hfill \\ \mathbf{T}{G}_2{\mathbf{T}}^{\mathtt{T}}+\nabla f_2{\mathbf{c}}^{\mathtt{T}}=0,\hfill \\ \mathbf{T}{\mathbf{c}}^{\mathtt{T}}=0,\hfill \end{array}\right.$$

(15)

where $F_2=\left(\begin{array}{ccc}{f}_{1xx}\hfill & f_{1xy}\hfill & f_{1xz}\hfill \\ f_{1yx}\hfill & f_{1yy}\hfill & f_{1yz}\hfill \\ f_{1zx}\hfill & f_{1zy}\hfill & f_{1zz}\hfill \end{array}\right)$, $G_2=\left(\begin{array}{ccc}{f}_{2xx}\hfill & f_{2xy}\hfill & f_{2xz}\hfill \\ f_{2yx}\hfill & f_{2yy}\hfill & f_{2yz}\hfill \\ f_{2zx}\hfill & f_{2zy}\hfill & f_{2zz}\hfill \end{array}\right)$, $f_{1xx}=\frac{\partial {\cancel{f}}_1^2\left(X\right)}{\partial x^2},f_{1xy}=\frac{\partial {\cancel{f}}_1^2\left(X\right)}{\partial x\partial y}$, $f_{2xx}=\frac{\partial {\cancel{f}}_2^2\left(X\right)}{\partial x^2},f_{2xy}=\frac{\partial {\cancel{f}}_2^2\left(X\right)}{\partial x\partial y}$, etc. Solving Equation (15), the specific curvature vector $\mathbf{c}$ can be expressed as

$$\mathbf{c}=\left[-\mathbf{T}{F}_2{\mathbf{T}}^{\mathtt{T}},-\mathbf{T}{G}_2{\mathbf{T}}^{\mathtt{T}},0\right]W_2^{\mathtt{T}},$$

(16)

where $W_2=\left(\begin{array}{ccc}{f}_{1x}\hfill & f_{1y}\hfill & f_{1z}\hfill \\ f_{2x}\hfill & f_{2y}\hfill & f_{2z}\hfill \\ x_s\hfill & y_s\hfill & z_s\hfill \end{array}\right)$, $f_{1x}=\frac{\partial f_1\left(X\right)}{\partial x},f_{2x}=\frac{\partial f_2\left(X\right)}{\partial x},x_s=\frac{dx}{ds}$, etc. For the case of the spatial algebraic curve, the iterative point ${\mathbf{P}}_{\mathtt{I}}$ may deviate from the spatial algebraic curve $\mathbf{C}$. That is, the iterative point ${\mathbf{P}}_{\mathtt{I}}$ is not on two algebraic surfaces, $f_1\left({\mathbf{P}}_{\mathtt{I}}\right)=err1\ne 0$, $f_2\left({\mathbf{P}}_{\mathtt{I}}\right)=err2\ne 0$. The basic idea of error correcting can be described as follows. When the iterative point ${\mathbf{P}}_{\mathtt{I}}$ deviates from two algebraic surfaces, use correction vector $\delta \mathbf{V}=[\delta x,\delta y,\delta z]$ to correct iteration point ${\mathbf{P}}_{\mathtt{I}}$ such that $\left|f_1({\mathbf{P}}_{\mathtt{I}}\right|<Le$ and $\left|f_2\left({\mathbf{P}}_{\mathtt{I}}\right)\right|<Le$ ($Le$ is a particularly small value of the allowable error range). The corrected iteration point ${\mathbf{P}}_{\mathtt{I}}$ is guaranteed to be on the spatial algebraic curve and the deviations between the corrected iterative point ${\mathbf{P}}_{\mathtt{I}}$ and two algebraic surfaces are almost zero. $\Delta \mathbf{V}$ is on the plane formed by the tangent vector T and curvature vector c derived from the iteration point ${\mathbf{P}}_{\mathtt{I}}$ before correction and is perpendicular to the vector $\mathbf{T}\times \mathbf{c}$. Let $\delta \mathbf{V}$ be on the plane spanned by the vector $\Delta \mathbf{V}$ and $\mathbf{T}\times \mathbf{c}$, and $\delta \mathbf{V}$ points to two algebraic surfaces. From the above description, we can get the equation about the correction vector $\delta \mathbf{V}$,

$$\left\{\begin{array}{c}〈\nabla f_1,\delta \mathbf{V}〉=0,\hfill \\ 〈\nabla f_2,\delta \mathbf{V}〉=0,\hfill \\ 〈\left[(\mathbf{T}\times \mathbf{c})\times \Delta \mathbf{V}\right],\delta \mathbf{V}〉=0.\hfill \end{array}\right.$$

(17)

From Equation (17), it is not difficult to get the expression of the correction vector $\delta \mathbf{V}$,

$$\delta \mathbf{V}=[-err1,-err2,0]{[{(\nabla f_1)}^{\mathtt{T}},{(\nabla f_2)}^{\mathtt{T}},{\left[(\mathbf{T}\times \mathbf{c})\times \Delta \mathbf{V}\right]}^{\mathtt{T}}]}^{-1},$$

(18)

where $err1=f_1\left({\mathbf{P}}_{\mathtt{I}}\right)$, $err2=f_2\left({\mathbf{P}}_{\mathtt{I}}\right)$, at this moment, the iteration point ${\mathbf{P}}_{\mathtt{I}}$ is the iteration point before correction, $\Delta \mathbf{V}$ is the difference vector of the corrected iteration point ${\mathbf{P}}_{\mathtt{I}}$ subtracting the iteration point ${\mathbf{P}}_{\mathtt{I}}$ before correction. After a lot of testing, we have obtained a preliminary result. When the correction vector $\delta \mathbf{V}$ is added to the iteration point ${\mathbf{P}}_{\mathtt{I}}$ after iterating, it can promote the robustness and high efficiency of convergence from iteration point ${\mathbf{P}}_{\mathtt{I}}$ to orthogonal projection point ${\mathbf{P}}_{\Gamma }$. However, the rate which the iteration point ${\mathbf{P}}_{\mathtt{I}}$ converges to the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ is still very slow, at the same time, the rate of the orthogonalization of the tangent vector of the spatial algebraic curve at the iteration point ${\mathbf{P}}_{\mathtt{I}}$ and the vector connected to the test point $\mathbf{P}$ and the iteration point ${\mathbf{P}}_{\mathtt{I}}$ is also very slow. There is still a big gap between this situation and our expected goal. In order to accelerate the convergence of the iteration point to the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ and speed up the orthogonalization, we add three iterative formulas related to Newton’s steepest gradient descent method in front of the correction vector $\delta \mathbf{V}$. Therefore, the corresponding iterative formula for accelerating and orthogonalizing is as follows,

$$\left\{\begin{array}{c}{\mathbf{Y}}_n={\mathbf{X}}_n-(f_1\left({\mathbf{X}}_n\right)/〈\nabla f_1\left({\mathbf{X}}_n\right),\nabla f_1\left({\mathbf{X}}_n\right)〉)/\nabla f_1\left({\mathbf{X}}_n\right),\hfill \\ {\mathbf{Z}}_n={\mathbf{Y}}_n-(f_2\left({\mathbf{Y}}_n\right)/〈\nabla f_2\left({\mathbf{Y}}_n\right),\nabla f_2\left({\mathbf{Y}}_n\right)〉)/\nabla f_2\left({\mathbf{Y}}_n\right),\hfill \\ {\mathbf{U}}_n={\mathbf{Z}}_n-(F\left({\mathbf{Z}}_n\right)/〈\nabla F\left({\mathbf{Z}}_n\right),\nabla F\left({\mathbf{Z}}_n\right)〉)/\nabla F\left({\mathbf{Z}}_n\right),\hfill \\ {\mathbf{X}}_{n+1}={\mathbf{U}}_n+\delta \mathbf{V},\hfill \end{array}\right.$$

(19)

where $err1=f_1\left({\mathbf{Z}}_n\right)$, $err2=f_2\left({\mathbf{Z}}_n\right)$, $\nabla f_1,\nabla f_2,\mathbf{T},\mathbf{c}$ assigned by ${\mathbf{Z}}_n$, $\Delta \mathbf{V}={\mathbf{U}}_n-{\mathbf{Z}}_n$.

Remark 2.

We present a complete geometric interpretation for Equation (19). The first two formulas in Equation (19) that are not related to the test point $\mathit{P}$ are Newton’s steepest gradient descent method. The ultimate goal is to make the initial iteration point fall on the spatial algebraic curve $\mathit{C}$. Please refer to Remark 1 for the specific explanation of geometric meaning. The third formula of Equation (19) is the Newton’s steepest gradient descent method related to the test point $\mathit{P}$. This iterative formula is the iterative formula of Newton’s steepest gradient descent method formed by the direct deformation of the formula (7), which the formula (7) is the inner product of the vector $\overrightarrow{\mathit{PX}}$ formed by the test point $\mathit{P}$ and the point $\mathit{X}$ on the spatial algebra curve $\mathit{C}$ with the tangent vector $\mathit{T}$ at that point $\mathit{X}$ is zero. Therefore, the third iteration formula of Equation (19) is mainly used to accelerate the orthogonalization of the vector $\overrightarrow{\mathit{PX}}$ and the tangent vector $\mathit{T}$. The last formula of Equation (19) is to use the geometric correction vector $\delta \mathit{V}$ to promote the iteration point fall on the spatial algebraic curve $\mathit{C}$ as much as possible once again. Therefore, Equation (19) plays a dual roles of accelerating the iteration point to fall on the spatial algebraic curve $\mathit{C}$ and orthogonalization of the vector $\mathit{T}$ and the vector $\overrightarrow{{\mathit{PP}}_{\Gamma }}$. Then accelerating and correcting the method with Equation (19) makes the first three formulas of the formula (8) achieves very satisfactory result. This technique not only accelerates the convergence rate of the whole iteration process but also improves the iteration robustness. Furthermore, the accuracy of the whole iteration process can be improved by the accelerating and correcting method with Equation (19).

Based on the above illustration, we obtain the following Algorithm 3 (See Figure 4).

Algorithm 3: Accelerating and geometric correcting method for orthogonal projection onto a spatial algebraic curve

Input: The iterative point ${\mathbf{P}}_{\mathtt{I}}$ fallen on the spatial algebraic curve $\mathbf{C}$ and the spatial algebraic curve $\mathbf{C}$.

Output: The final orthogonal projection point ${\mathbf{P}}_{\Gamma }$ fallen on the spatial algebraic curve $\mathbf{C}$.

Description:

Step 1:

${\mathbf{x}}_{n+1}={\mathbf{P}}_{\mathtt{I}}$;

Do {

${\mathbf{X}}_n={\mathbf{X}}_{n+1}$;

Compute ${\mathbf{X}}_{n+1}$ according to Equation (19);

}while (${∥{\mathbf{X}}_{n+1}-{\mathbf{X}}_n∥}^2>\epsilon$&&$\left|f_1\left({\mathbf{X}}_{n+1}\right)\right|>\epsilon$&&$\left|f_2\left({\mathbf{X}}_{n+1}\right)\right|>\epsilon )$;

Step 2:

${\mathbf{P}}_{\Gamma }={\mathbf{X}}_{n+1}$;

Return ${\mathbf{P}}_{\Gamma }$;

Based on the above description, we give the complete algorithm for point orthogonal projection onto a spatial algebraic curve (Algorithm 4) (See Figure 5).

Algorithm 4: A complete algorithm for point orthogonal projection onto a spatial algebraic curve

Input: Test point $\mathbf{P}$ and the spatial algebraic curve $\mathbf{C}$.

Output: The final orthogonal projection point ${\mathbf{P}}_{\Gamma }$ of the test point $\mathbf{P}$.

Description:

Step 1: Starting from the neighbor point of the test point $\mathbf{P}$, calculate the iterative point ${\mathbf{P}}_{\mathtt{I}}$ fallen on the spatial algebraic $\mathbf{C}$ via Algorithm 1.

for(i = 0;i < 5;i + +) {

Step 2: Compute the foot-point $\mathbf{Q}$ via Algorithm 2.

Step 3: Project foot-point $\mathbf{Q}$ onto the spatial algebraic curve $\mathbf{C}$ via Algorithm 1, then get new point ${\mathbf{P}}_{\mathtt{I}}$ fallen on the spatial algebraic curve $\mathbf{C}$.

}

Step 4: The iterative point ${\mathbf{P}}_{\mathtt{I}}$ fallen on the spatial algebraic curve $\mathbf{C}$ being as the initial iterative point, calculate the finally orthogonal projection point ${\mathbf{P}}_{\Gamma }$ fallen on the spatial algebraic $\mathbf{C}$ via Algorithm 3.

Return ${\mathbf{P}}_{\Gamma }$;

Remark 3.

In this remark, we present a geometric interpretation for Algorithm 4. The purpose of the first step is to promote the initial iterative point completely iterate to the spatial algebraic curve. In Step 2, the foot-point $\mathit{Q}$ is derived from the iterative point ${\mathit{P}}_I$ fallen on the spatial algebraic curve of the first step. Now, the position of foot-point $\mathit{Q}$ is between the iteration point ${\mathit{P}}_I$ and the orthogonal projection point $\mathit{P}$. In other words, the foot-point $\mathit{Q}$ is closer to the orthogonal projection point than the test point $\mathit{P}$. Furthermore, by using Algorithm 1 of the third step, the foot-point $\mathit{Q}$ can be completely iterated to the spatial algebra curve, and the point at which this iteration point falls on the spatial algebraic curve is called the current iteration point and the last iteration point to fall on the spatial algebra curve is named the previous iteration point. It is obvious that the current iteration point is closer to the orthogonal projection point than the previous iterative point. After joint running Step 2 and Step 3 five times in this way, the distance between the latest current iterative point and the orthogonal projection point is very small. If we keep running in this way, the rate of the iteration point getting closer to the orthogonal projection point becomes slower and slower. Moreover, orthogonalization of the tangent vector $\mathit{T}$ and the vector $\overrightarrow{{\mathit{PP}}_{\Gamma }}$ is also difficult to realize. However, Algorithm 3 in the fourth step can make up for these two deficiencies. At this time, running Algorithm 3 plays double important roles for accelerating convergence and orthogonalization. Thus, Algorithm 4 is a robust and efficient algorithm which it achieves a very satisfactory result for point orthogonal projection onto the spatial algebraic curves. In addition, the five cycles of the intermediate $\mathit{for}$ loop body are an empirical value. When the distance between the test point and the spatial algebra curve is not very far, the intermediate $\mathit{for}$ loop body only needs 5 cycles. However, when the distance between the test point and the spatial algebraic curve is very large, the number of cycles of the $\mathit{for}$ loop body needs to be increased. The purpose is to promote the iterative point after the loop of $\mathit{for}$ loop body closer to the orthogonal projection point. Therefore, Algorithm 3 of the fourth step can conver the orthogonal projection point ${\mathit{P}}_{\Gamma }$ successfully and completely.

We have done a lot of tests for Algorithm 4. Whether the test point $\mathbf{P}$ is close to or far from the spatial algebra curve $\mathbf{C}$, the test point can be orthogonally projected to the spatial algebraic curve in a very robust and efficient way. We have another surprise and wonderful discovery. When the test point is not far from the spatial algebraic curve, Algorithm 4 can be expressed in simplified version form, where the $\mathbf{for}$ loop body in the middle can be omitted and the fourth formula with geometric correction method of Equation (19) can also be deleted. So Equation (19) naturally becomes Equation (20).

$$\left\{\begin{array}{c}{\mathbf{Y}}_n={\mathbf{X}}_n-(f_1\left({\mathbf{X}}_n\right)/〈\nabla f_1\left({\mathbf{X}}_n\right),\nabla f_1\left({\mathbf{X}}_n\right)〉)/\nabla f_1\left({\mathbf{X}}_n\right),\hfill \\ {\mathbf{Z}}_n={\mathbf{Y}}_n-(f_2\left({\mathbf{Y}}_n\right)/〈\nabla f_2\left({\mathbf{Y}}_n\right),\nabla f_2\left({\mathbf{Y}}_n\right)〉)/\nabla f_2\left({\mathbf{Y}}_n\right),\hfill \\ {\mathbf{X}}_{n+1}={\mathbf{Z}}_n-(F\left({\mathbf{Z}}_n\right)/〈\nabla F\left({\mathbf{Z}}_n\right),\nabla F\left({\mathbf{Z}}_n\right)〉)/\nabla F\left({\mathbf{Z}}_n\right),\hfill \end{array}\right.$$

(20)

The simplification version of Algorithm 4 can be described as the following Algorithm 5, where Algorithm 5 maintains the same robustness as Algorithm 4, and the time running efficiency of Algorithm 5 is much better than that of Algorithm 4.

Algorithm 5: A simplified version algorithm for point orthogonal projection onto a spatial algebraic curve

Input: Test point $\mathbf{P}$ and the spatial algebraic curve $\mathbf{C}$.

Output: Orthogonal projection point ${\mathbf{P}}_{\Gamma }$ of the test point $\mathbf{P}$ which orthogonally projects the test point $\mathbf{P}$ onto the spatial algebraic curve $\mathbf{C}$.

Description:

Step1: Calculate the iterative point ${\mathbf{P}}_{\mathtt{I}}$ fallen on the the spatial algebraic curve $\mathbf{C}$ via Algorithm 1.

Step 2:

${\mathbf{X}}_{n+1}={\mathbf{P}}_{\mathtt{I}}$;

Do {

${\mathbf{X}}_n={\mathbf{X}}_{n+1}$;

Compute ${\mathbf{X}}_{n+1}$ according to Equation (20);

}while (${∥{\mathbf{X}}_{n+1}-{\mathbf{X}}_n∥}^2>\epsilon$&&$\left|f_1\left({\mathbf{X}}_{n+1}\right)\right|>\epsilon$&&$\left|f_2\left({\mathbf{X}}_{n+1}\right)\right|>\epsilon )$;

Step 3: ${\mathbf{P}}_{\Gamma }$=${\mathbf{X}}_{n+1}$;

Return ${\mathbf{P}}_{\Gamma }$;

Remark 4.

In the actual algorithms implementation process, we take two optimized techniques. Firstly, if the test point $\mathit{P}$ is very far away from the spatial algebraic curveC, the initial iterative ${\mathit{X}}_0$ of Algorithm 1 is a very small proportion number of the test point $\mathit{P}$ which ensures that the initial iterative point ${\mathit{X}}_0$ converges to the spatial algebraic curve $\mathit{C}$ very robustly. However, the initial iterative point ${\mathit{X}}_0$ of Algorithm 1 in Step 3 of Algorithm 4 remains unchanged(${\mathit{X}}_0$=$\mathit{Q}$ ). Secondly, due to the spatial algebraic curve being composed of the intersection of two algebraic surfaces, the singularity of any algebraic surface may lead to the singularity of spatial algebraic curve. That is to say, the singularity of a spatial algebraic curve will cause the denominators of all formulas and iterative formulas to be zero. In order to avoid the degradation of all iterative formulas with zero denominators, we add a small perturbation number ε to the denominator of each iteration formula such that every iterative formula will not degenerate. Thus, every algorithm can run and iterate normally. Furthermore, no matter how far away the test point is from the spatial algebraic curve and whether there are singular points or not in the spatial algebra curve, Algorithm 4 can run very robustly and efficiently which it meets our expectations and ideals.

2.4. Finding out Initial Iterative Candidate Points

This subsection comes from the reviewer’s previous suggestion. In the field of practical computer graphics, computer-aided geometric design and other applications, it is necessary to solve not only a single orthogonal projection point but also all orthogonal projection points as much as possible. Our preliminary idea is to outline the spatial algebraic curve which the specific expression is presented by the formula (5). We try to find out several 3D bounding boxes within the specified region of the spatial algebraic curve such that every curve segment of the spatial algebraic curve is contained in one 3D bounding box. Randomly select a point in each 3D bounding box as the initial iteration point of Algorithm 4 or Algorithm 5. In this way, we can yield as many orthogonal projection points as possible by using Algorithm 4 or Algorithm 5. Then, through computing the distance between the test point $\mathbf{P}$ and each orthogonal projection point and by comparing with each distance one by one, the orthogonal projection point corresponding to the shortest distance is what we are looking for. However, it is very difficult to express the spatial algebraic curve directly. On the other hand, the geometric essence of point orthogonal projection onto the spatial algebraic curve is to find a point $\mathbf{X}$ on the spatial algebraic curve such that the vector $\overrightarrow{\mathbf{PX}}$ and the tangent vector $\mathbf{T}$($\mathbf{T}=\nabla f_1\left(\mathbf{X}\right)\times \nabla f_2\left(\mathbf{X}\right))$ on the spatial algebraic curve at point $\mathbf{X}$ are perpendicular to each other. Namely, the vector $\overrightarrow{\mathbf{PX}}$ is orthogonal to the tangent vector $\mathbf{T}$. The corresponding equation formed by the inner product of the vector $\overrightarrow{\mathbf{PX}}$ and the vector $\mathbf{T}$ is expressed as the form of Equation (7). The geometric meaning of Equation (7) is algebraic surface. So, outlining the spatial algebraic curve with Equation (5) is transforming into outlining the algebraic surface with Equation (7). We are gong to find several 3D bounding boxes within the specified region of the algebraic surface with Equation (7) such that every surface patch of the algebraic surface is contained in one 3D bounding box. Randomly select a point in each 3D bounding box as the initial iteration point of Algorithm 4 or Algorithm 5. In this way, we can yield as many orthogonal projection points as possible by using Algorithm 4 or Algorithm 5. Then through computing the distance between the test point $\mathbf{P}$ and each orthogonal projection point and by comparing with each distance one by one, the orthogonal projection point (the closest point) corresponding to the shortest distance is what we are looking for.Therefore, the orthogonal projection point (the closest point) satisfied the shortest distance completely conforms to every formula of Equation (8).

Let us suppose that the region $\Omega$ of the spatial algebraic curve with Equation (5) is $\Omega =\left[a_1,a_2\right]\times \left[b_1,b_2\right]\times \left[c_1,c_2\right]$. We may decide that the region of the algebraic surface is the same as that of the spatial algebraic curve. So the region of the algebraic surface is also $\Omega$. We adopt adaptive affine arithmetic method [31,32,33] to identify a series of 3D bounding boxes such that every algebraic surface patch is contained in every 3D bounding box. We orthogonally project the algebraic surface $\mathbf{F}\left(\mathbf{X}\right)=0$ onto $y-z$ plane, the $x-z$ plane and the $x-y$ plane at the point $(x_0,y_0,z_0)$, respectively, and we obtain the planar algebraic curves $\mathbf{F}(x_0,y,z)=0$, $\mathbf{F}(x,y_0,z)=0$ and $\mathbf{F}(x,y,z0)=0$. respectively. For the sake of convenience, the planar algebraic curves $\mathbf{F}(x_0,y,z)=0$, $\mathbf{F}(x,y_0,z)=0$ and $\mathbf{F}(x,y,z0)=0$ can be written as ${\mathbf{F}}_1(y,z)=0$, ${\mathbf{F}}_2(x,z)=0$, ${\mathbf{F}}_3(x,y)=0$, respectively. We set up a crucial judgment function for the planar algebraic curve ${\mathbf{F}}_1(y,z)=0$,

$${\Psi }_{yz}=\frac{2\left|{\mathbf{F}}_{1yz}\right|}{\sqrt{{(\frac{{\mathbf{F}}_{1y}}{y_2})}^2+{(\frac{{\mathbf{F}}_{1z}}{z_3})}^2}},$$

(21)

Similarly, we also set up two other crucial judgment functions for the planar algebraic curve ${\mathbf{F}}_2(x,z)=0$ and the planar algebraic curve ${\mathbf{F}}_3(x,y)=0$,

$${\Psi }_{xz}=\frac{2\left|{\mathbf{F}}_{2xz}\right|}{\sqrt{{(\frac{{\mathbf{F}}_{2x}}{x_1})}^2+{(\frac{{\mathbf{F}}_{2z}}{z_3})}^2}},$$

(22)

and

$${\Psi }_{xy}=\frac{2\left|{\mathbf{F}}_{3xy}\right|}{\sqrt{{(\frac{{\mathbf{F}}_{3x}}{x_1})}^2+{(\frac{{\mathbf{F}}_{3y}}{y_2})}^2}},$$

(23)

where ${\mathbf{F}}_{1y}=\frac{\partial {\mathbf{F}}_1(y,z)}{\partial y}$, ${\mathbf{F}}_{1z}=\frac{\partial {\mathbf{F}}_1(y,z)}{\partial z}$, ${\mathbf{F}}_{2x}=\frac{\partial {\mathbf{F}}_2(x,z)}{\partial x}$, ${\mathbf{F}}_{2z}=\frac{\partial {\mathbf{F}}_2(x,z)}{\partial z}$, ${\mathbf{F}}_{3x}=\frac{\partial {\mathbf{F}}_3(x,y)}{\partial x}$, ${\mathbf{F}}_{3y}=\frac{\partial {\mathbf{F}}_3(x,y)}{\partial y}$, ${\mathbf{F}}_{1yz}=\frac{{\partial }^2{\mathbf{F}}_1(y,z)}{\partial y\partial z}$, ${\mathbf{F}}_{2xz}=\frac{{\partial }^2{\mathbf{F}}_2(x,z)}{\partial x\partial z}$, ${\mathbf{F}}_{3xy}=\frac{{\partial }^2{\mathbf{F}}_3(x,y)}{\partial x\partial y}$, $x_0=\frac{a_1+a_2}{2}$, $x_1=\frac{a_2-a_1}{2}$, $y_0=\frac{b_1+b_2}{2}$, $y_2=\frac{b_2-b_1}{2}$, $z_0=\frac{c_1+c_2}{2}$, $z_3=\frac{c_2-c_1}{2}$. The each substitution value of variable $\mathbf{X}$ for nine partial derivative functions ${\mathbf{F}}_{1y}$, ${\mathbf{F}}_{1z}$, ${\mathbf{F}}_{2x}$, ${\mathbf{F}}_{2z}$, ${\mathbf{F}}_{3x}$, ${\mathbf{F}}_{3y}$, ${\mathbf{F}}_{1yz}$, ${\mathbf{F}}_{2xz}$, ${\mathbf{F}}_{3xy}$ is $(x_0,y_0,z_0)$. Afterwards, we will call this point $(x_0,y_0,z_0)$ as the center point of the 3D bounding box. Combining with Equation (21), Equation (22) and Equation (23), we get the crucial judgment function $\Psi$ with Equation (24),

$$\Psi =Max\{{\Psi }_{xy},{\Psi }_{yz},{\Psi }_{xz}\}.$$

(24)

We specify a threshold for the crucial judgment function $\Psi$ with Equation (24). The adaptive approach method which we have adopted for solving a series of 3D bounding boxes of the algebraic surface has absorbed the idea of the papers [31,32,33], which is for solving a series of 2D bounding boxes of the planar algebraic curve. The detailed explanation of Equation (24) is exactly similar to the explanation in [34]. On affine arithmetic, we mainly absorbed the ideas of this paper. As for the more complex topological structure of the algebraic surface, we have to absorb the idea of the paper [35] to solve a series of 3D bounding boxes of the algebraic surface. The specific description for solving a series of 3D bounding boxes of the algebraic surface can be expressed as Algorithm 6.

Algorithm 6: Finding out a series of 3D bounding boxes of the algebraic surface $\mathbf{F}\left(\mathbf{X}\right)=0$

Input: The algebraic surface $\mathbf{F}\left(\mathbf{X}\right)=0$ and the 3D bounding box containing or intersecting with the algebraic surface $\mathbf{F}\left(\mathbf{X}\right)=0$.

Output: A series of 3D bounding boxes of the algebraic surface $\mathbf{F}\left(\mathbf{X}\right)=0$.

Description:

Step 1: Subdivide this 3D bounding box into 8 3D sub-bounding boxes by dividing 2 on each axis.

Step 2: Evaluate the value $\Psi$ of each 3D sub-bounding box according to Equation (24).

Step 3: if($\Psi$ <= threshold and recursion times<10){

Run Algorithm 6 with the 3D sub-bounding box.

}

if($\Psi$ <= threshold and recursion times==10){

Store the sub-box to a set.

}

End Algorithm.

3. Convergence Analysis

This section proves that Algorithm 4 does not depend on the initial iteration point.

Theorem 1.

Algorithm 4 is independent of the initial iterative point.

Proof. 

According to Remark 4, if the test point $\mathbf{P}$ is very far away from the spatial algebraic curve $\mathbf{C}$, the initial iterative ${\mathbf{X}}_0$ of Algorithm 1 is a very small proportion number of the test point P. That is to say, as long as the distance between the initial iteration point ${\mathbf{X}}_0$ and the spatial algebraic curve is relatively near, the initial iteration point can converge to the spatial algebraic curve by using Algorithm 1, or the initial iteration point can successfully and completely iterate and fall on the spatial algebraic curve. Based on the iterative result of Algorithm 1, the general idea of the intermediate $\mathbf{for}$ loop body is to ensure that the iteration point falls on the spatial algebraic curve under the premise such that the iterative point ${\mathbf{P}}_{\mathtt{I}}$ can gradually move to a very close position of the orthogonal projection point. According to Remark 2, Algorithm 3 with Equation (19) plays a dual roles of accelerating the iteration point to fall on the spatial algebraic curve $\mathbf{C}$ and orthogonalization of the vector $\mathbf{T}$ and the vector $\overrightarrow{{\mathbf{PP}}_{\Gamma }}$. Then accelerating and correcting method with Equation (19) makes the first three formulas of the formula (8) achieve a very satisfactory result. This technique not only accelerates the convergence rate of the whole iteration process but also improves the iteration robustness. Furthermore, the accuracy of the whole iteration process can be improved by the accelerating and correcting the method with Equation (19). Therefore, for the initial iteration point ${\mathbf{X}}_0$ at any position, by using Algorithm 4, it can be finally iterated to spatial algebraic curve such that the finally iterative point fallen on the spatial algebraic curve is the orthogonal projection point. Namely, the final iteration point ${\mathbf{X}}_{n+1}$ that falls on the spatial algebraic curve satisfies the first three terms of the Formula (8). Specially, the test point P and the final iteration point ${\mathbf{X}}_{n+1}$ satisfy the relationship $〈\overrightarrow{{\mathbf{PX}}_{n+1}},\mathbf{T}〉=0$ or $〈\overrightarrow{{\mathbf{PP}}_{\Gamma }},\mathbf{T}〉=0$. It is possible that the orthogonal projection points obtained by Algorithm 4 may be different for different initial iteration points. Once the initial iteration point is determined, the orthogonal projection point is also uniquely determined accordingly. It can converge to the orthogonal projection point robustly and efficiently. It is demonstrated that Algorithm 4 is independent of the initial iterative point. ☐

In a similar way to the proof of Theorem 1, we can state the following result.

Theorem 2.

Algorithm 5 is independent of the initial iterative point.

4. Numerical Results

In this section, we present two examples to explain that Algorithm 4 is robust and efficient. All calculation were implemented by using Maple 18 environment with $\epsilon ={10}^{-20}$. In

Table 1. Test results of Algorithm 4 for Example 1.

P	(217,273,129)	(357, 263, 289)	(374,236,−389)	(274,336,−297)	(254,−356,287)
${\mathbf{P}}_{\Gamma }$	(1.347, 2.448,1.952)	(1.749, 2.095, 1.863)	(2.241, 1.357,1.715)	(−1.274,−2.498,1.966)	(−1.574,2.268,1.906)
$\left|f_1\left({\mathbf{P}}_{\Gamma }\right)\right|$	0.0	0.0	0.0	0.0	$2.0\times {10}^{-20}$
$\left|f_2\left({\mathbf{P}}_{\Gamma }\right)\right|$	$2.0\times {10}^{-19}$	$0.0$	$2.0\times {10}^{-19}$	$0.0$	$0.0$
$\left|\mathbf{F}\left({\mathbf{P}}_{\Gamma }\right)\right|$	$2.9\times {10}^{-17}$	$1.0\times {10}^{-17}$	$1.0\times {10}^{-17}$	$4.0\times {10}^{-17}$	$2.0\times {10}^{-17}$
$\mathbf{P}$	(354,−376,481)	(259,−276,−441)	(249,−386,−221)	(−369, 286, 317)	(−359, 686, 377)
${\mathbf{P}}_{\Gamma }$	(1.338, −2.454, 1.954)	(−1.266, 2.503, 1.967)	(−1.119, 2.591, 1.992 )	(−1.697, 2.150, 1.875)	(−0.946, 2.678, 2.017)
$\left|f_1\left({\mathbf{P}}_{\Gamma }\right)\right|$	$4.0\times {10}^{-20}$	$0.0$	$3.0\times {10}^{-20}$	$3.0\times {10}^{-20}$	$0.0$
$\left|f_2\left({\mathbf{P}}_{\Gamma }\right)\right|$	$3.0\times {10}^{-19}$	$1.0\times {10}^{-19}$	$1.0\times {10}^{-19}$	$1.0\times {10}^{-19}$	$1.0\times {10}^{-19}$
$\left|\mathbf{F}\left({\mathbf{P}}_{\Gamma }\right)\right|$	$0.0$	$2.0\times {10}^{-17}$	$4.0\times {10}^{-17}$	$1.0\times {10}^{-17}$	$0.0$
$\mathbf{P}$	( −348, 677,−397)	(−338, 357,−597)	(−368,−374, 497)	(−348,−324, 457)	(−385,−347,−467)
${\mathbf{P}}_{\Gamma }$	(−1.217, 2.534, 1.976)	(1.262,−2.505, 1.968)	(−1.373,−2.429, 1.947)	( −1.447,−2.373, 1.932)	(−2.031,−1.734, 1.783)
$\left|f_1\left({\mathbf{P}}_{\Gamma }\right)\right|$	0.0	$1.0\times {10}^{-20}$	$3.0\times {10}^{-20}$	0.0	0.0
$\left|f_2\left({\mathbf{P}}_{\Gamma }\right)\right|$	$1.0\times {10}^{-19}$	$1.0\times {10}^{-19}$	$1.0\times {10}^{-19}$	$1.0\times {10}^{-19}$	$0.0$
$\left|\mathbf{F}\left({\mathbf{P}}_{\Gamma }\right)\right|$	$1.0\times {10}^{-17}$	$2.0\times {10}^{-17}$	$3.0\times {10}^{-17}$	$3.0\times {10}^{-17}$	$8.0\times {10}^{-17}$
$\mathbf{P}$	(−355,−397,−492)
${\mathbf{P}}_{\Gamma }$	(1.290,2.487, 1.963)
$\left|f_1\left({\mathbf{P}}_{\Gamma }\right)\right|$	$4.0\times {10}^{-20}$
$\left|f_2\left({\mathbf{P}}_{\Gamma }\right)\right|$	$0.0$
$\left|\mathbf{F}\left({\mathbf{P}}_{\Gamma }\right)\right|$	$5.0\times {10}^{-17}$

and

Table 2. Test results of Algorithm 4 for Example 2.

P	(217,273,129)	(357, 263, 289)	(374,236,−289)	(254,310,−157)	(254,−356,287)
${\mathbf{P}}_{\Gamma }$	(0.515,0.461,0.248)	(0.410,0.580,0.229)	(0.360,0.661,0.231)	(0.675, 0.344,0.312)	(0.014,2.715, 1.847)
$\left|f_1\left({\mathbf{P}}_{\Gamma }\right)\right|$	0.0	0.0	$4.8\times {10}^{-15}$	$3.7\times {10}^{-11}$	$1.9\times {10}^{-11}$
$\left|f_2\left({\mathbf{P}}_{\Gamma }\right)\right|$	$2.7\times {10}^{-13}$	$7.4\times {10}^{-12}$	$6.1\times {10}^{-13}$	$2.5\times {10}^{-13}$	$3.5\times {10}^{-14}$
$\left|\mathbf{F}\left({\mathbf{P}}_{\Gamma }\right)\right|$	$3.5\times {10}^{-16}$	$2.2\times {10}^{-15}$	$4.2\times {10}^{-16}$	$3.7\times {10}^{-15}$	$7.3\times {10}^{-15}$
$\mathbf{P}$	(354,−376,481)	(259,−276,−441)	(249,−386,−221)	(−369, 286, 317)	(−359, 686, 377)
${\mathbf{P}}_{\Gamma }$	(0.099, 1.799,0.836)	(1.053,0.199,0.550)	(2.132,0.014, 1.664)	( 2.082,0.029,1.607)	(1.911,0.053,1.394)
$\left|f_1\left({\mathbf{P}}_{\Gamma }\right)\right|$	$4.6\times {10}^{-16}$	$3.5\times {10}^{-17}$	$2.7\times {10}^{-17}$	$7.6\times {10}^{-18}$	$5.7\times {10}^{-15}$
$\left|f_2\left({\mathbf{P}}_{\Gamma }\right)\right|$	$4.2\times {10}^{-16}$	$2.9\times {10}^{-15}$	$1.3\times {10}^{-15}$	$4.7\times {10}^{-16}$	$3.7\times {10}^{-15}$
$\left|\mathbf{F}\left({\mathbf{P}}_{\Gamma }\right)\right|$	$3.2\times {10}^{-16}$	$4.7\times {10}^{-15}$	$9.2\times {10}^{-15}$	$2.3\times {10}^{-16}$	$4.3\times {10}^{-17}$
$\mathbf{P}$	( −348, 477, −397)	(−338, 357, −597)	(−368, −374, 497)	(−348, −324, 457)	(−385, −347, −467)
${\mathbf{P}}_{\Gamma }$	(0.043, −0.042, 0.004)	(−1.771,−0.09,0.343)	(−0.559, −0.425,−0.016)	(−0.543, −0.439, −0.013)	(−0.255,−0.867,0.139)
$\left|f_1\left({\mathbf{P}}_{\Gamma }\right)\right|$	$4.7\times {10}^{-16}$	$5.3\times {10}^{-18}$	$5.8\times {10}^{-17}$	$2.3\times {10}^{-18}$	$8.2\times {10}^{-17}$
$\left|f_2\left({\mathbf{P}}_{\Gamma }\right)\right|$	$3.4\times {10}^{-18}$	$2.6\times {10}^{-17}$	$3.5\times {10}^{-18}$	$3.6\times {10}^{-16}$	$4.8\times {10}^{-17}$
$\left|\mathbf{F}\left({\mathbf{P}}_{\Gamma }\right)\right|$	$3.2\times {10}^{-16}$	$2.3\times {10}^{-15}$	$3.4\times {10}^{-16}$	$6.3\times {10}^{-15}$	$7.3\times {10}^{-16}$
$\mathbf{P}$	(−355, −397,−492)
${\mathbf{P}}_{\Gamma }$	(−0.388, −0.616,0.035)
$\left|f_1\left({\mathbf{P}}_{\Gamma }\right)\right|$	$7.5\times {10}^{-18}$
$\left|f_2\left({\mathbf{P}}_{\Gamma }\right)\right|$	$5.6\times {10}^{-17}$
$\left|\mathbf{F}\left({\mathbf{P}}_{\Gamma }\right)\right|$	$6.4\times {10}^{-18}$

, the five symbols $\mathbf{P}$, ${\mathbf{P}}_{\Gamma }$, $\left|f_1\left({\mathbf{P}}_{\Gamma }\right)\right|$, $\left|f_2\left({\mathbf{P}}_{\Gamma }\right)\right|$, $\left|\mathbf{F}\left({\mathbf{P}}_{\Gamma }\right)\right|$ are the test point, the orthogonal projection point of the test point, the absolute value of the deviation degree of the orthogonal projection point on the first algebraic surface, the absolute value of the deviation degree of the orthogonal projection point on the second algebraic surface and the absolute value of the expression of Equation (7), respectively.

Example 1.

Assume that there is a spatial algebraic curve $\left\{\begin{array}{c}{f}_1(x,y,z)=\frac{x^2}{9}+\frac{y^2}{16}+\frac{z^2}{9}-1\hfill \\ f_2(x,y,z)=x^2+y^2-4z\hfill \end{array}\right.$ (See Figure 6). In this area [−300, 300] × [−300, 300] × [−300, 300]. We randomly select a large number of test points, the probability of convergence can achieve 100% by Algorithm 4 which is verified to be very high robustness and efficiency for remote test points. In addition, in each of the eight quadrants, we randomly select two different test points. We calculate the corresponding orthogonal projection point, the absolute value of the deviation degree of the orthogonal projection point on the first algebraic surface, the absolute value of the deviation degree of the orthogonal projection point on the second algebraic surface and the absolute value of the expression of Equation (7) for each test point via Algorithm 4. The specific results are shown in Table 1.

Example 2.

Assume that there is a spatial algebraic curve $\left\{\begin{array}{c}{f}_1(x,y,z)=\frac{x^2}{9}+\frac{y^2}{16}+\frac{z^2}{9}+4xy-1\hfill \\ f_2(x,y,z)=x^2+y^2+x-4z\hfill \end{array}\right.$ (See Figure 7). In this area [−300, 300] × [−300, 300] × [−300, 300]. We randomly select a large number of test points, the probability of convergence can achieve 100% by Algorithm 4 which is verified to be very high robustness and efficiency for remote test points. In addition, in each of the eight quadrants, randomly select two different test points. We calculate the corresponding orthogonal projection point, the absolute value of the deviation degree of the orthogonal projection point on the first algebraic surface, the absolute value of the deviation degree of the orthogonal projection point on the second algebraic surface and the absolute value of the expression of Equation (7) for each test point via Algorithm 4. The specific results are shown in Table 2.

Remark 5.

If the test point is farther away from the spatial algebraic curve or if the spatial algebraic curve is smooth or if there are fewer singularities in the spatial algebraic curve or if the curvature of the spatial algebraic curve is locally non-high curvature, the algorithm provided by us has certain advantages. However, if the spatial algebraic curve has one of the following cases, any case will hinder and affect the normal operation of Algorithm 4. The robustness and the efficiency of Algorithm 4 are greatly reduced.

(1) 

The test point is particularly farther away from the spatial algebraic curve.

(2) 

The spatial algebraic curve is not smooth.

(3) 

There are many singularities in the spatial algebraic curve.

(4) 

The curvature of the spatial algebraic curve is locally high.

(5) 

There are many symmetries in spatial algebraic curves.

(6) 

The spatial algebraic curve are extremely or particularly oscillatory.

For example, there is a planar curve $f\left(x\right)={cos}^4\left(\frac{1}{x}\right)+{sin}^{19}\left(x\right)+{sin}^8(\frac{1}{x^2}),x\in [-4,4]$ (See Figure 8). From the graphic display results, this curve is particularly oscillatory. If the initial iteration point is slightly further away from the curve, it is difficult to implement by using Algorithm 1 because the inherent essence of the iterative formula (9) for Algorithm 1 is exactly the same as the classical Newton’s iterative method. In view of these non-convergent cases, we are going to take three approaches. The first approach is transforming the test point orthogonal projection onto the spatial algebraic curve problem into the root-finding problem [29,30,36,37]. The second approach is to explore a strategy such that the initial iteration point should be as close as possible to the spatial algebraic curve which the goal is to minimize the sensitivity of the initial iteration point. Absorb the very robust methods in the each part of the algorithm that we already have. Then optimize them to the maximum. The third approach is to explore a one or more brand new algorithms such that every algorithm could solve all or part of the above difficult situations. Of course, it is necessary to study the singularity, non-smoothness, local high curvature and oscillation of spatial algebraic curve. Then find out how they relate to each other. Finally, some ideal algorithms that can meet the requirements of robustness and high efficiency are explored based on their intrinsic relevance.

5. Conclusions and Future Work

In this paper, we have developed an algorithm for point orthogonal projection onto a spatial algebraic curve. Algorithm 4 mainly includes three core technologies: Newton’s steepest gradient descent method, computing foot-point method and geometric correction method. Algorithm 1 impels the iterative point to fall on the spatial algebraic curve. The middle for loop body is to let the iteration point move to the position closed to the orthogonal projection point. The algorithm 3 of the fourth step plays an important double accelerating and orthogonalization role. Numerical examples show that our algorithm is robust and efficient and it achieves our expected result. In future work, we will try to study the singularity, non-smoothness, local high curvature and oscillation of spatial algebraic curve. Then we will find out how they relate to each other. Finally, some ideal algorithms that can meet the requirements of robustness and high efficiency are explored based on their intrinsic relevance. We also try to extract and purify the idea of Algorithm 4. Moreover, the idea is applied to point orthogonal projecting onto algebraic surface.