The Existence of a Convex Polyhedron with Respect to the Constrained Vertex Norms

Abstract

Given a set of constrained vertex norms, we proved the existence of a convex configuration with respect to the set of distinct constrained vertex norms in the two-dimensional case when the constrained vertex norms are distinct or repeated for, at most, four points. However, we proved that there always exists a convex configuration in the three-dimensional case. In the application, we can imply the existence of the non-empty spherical Laguerre Voronoi diagram.

1. Introduction

Suppose that we are given a set of n points $\mathcal{V}=\{v_1,v_2,\dots ,v_n\}$ in two-dimensional and three-dimensional space. One of the fundamental questions in the discrete and computational geometry is to consider the convexity of the given set, such as computing the convex hull of $\mathcal{P}$. When $\mathcal{V}$ is finite, the convex hull of a set $\mathcal{V}$ is a polygon in the two-dimensional case and a polyhedron in the three-dimensional case. The problem of an algorithmic construction of a convex hull was initially addressed by Preperata [1].

The convex hull is a primitive object in computational geometry. For example, the construction of an ordinary spherical Voronoi diagram and spherical Laguerre Voronoi diagram, as defined in [2], uses the central projection of a 3D convex hull onto the sphere to generate Delaunay diagrams as presented in [3]. In the application viewpoint, Voronoi diagrams are widely used to model many natural phenomena displayed as tessellations. In the case of spherical tessellations, the spherical Laguerre Voronoi diagrams were used to model natural tessellations containing the weights of generators. For example, the research in [4] focused on the tessellation fitting of fruit skin patterns, and Chaidee et al. [5] proposed the dynamical model to generate spherical tessellations using the spherical Laguerre Voronoi diagrams.

In the case of the ordinary spherical Voronoi diagram, the points for computing a 3D convex hull are on the sphere. Therefore, the central projection of the 3D convex hull consists of a Delaunay triangulation of the diagram. However, the spherical Laguerre Delaunay diagram construction is different to the ordinary spherical Voronoi diagram in such a way that each generator contains its weight, and the points for generating the convex hull can be shifted over the sphere. Therefore, the convex hull of those points may include some points inside the constructed convex hull. As the diagram can be constructed from the central projection of the convex hull onto the sphere, the Laguerre cell corresponding to the hidden point is empty, which is a dilemma of the spherical Laguerre Voronoi diagram. Therefore, investigation on the non-emptiness properties of the diagram is theoretically important to model real-world phenomena using the spherical Laguerre Voronoi diagram.

Suppose that there is a set of weights of points of the spherical Laguerre Voronoi diagram $W=\{w_1,\dots ,w_n\}$. We would like to find the location of the generator position $\mathcal{P}=\{p_1,\dots ,p_n\}$ on the unit sphere $S^2$ in such a way that no cell of the generated spherical Laguerre Voronoi diagram is empty. This problem can be transformed into the following problem.

Given a set of scalars$\mathcal{R}=\{r_1,\dots ,r_n\}$and the origin O, we find a configuration of all points$\mathcal{V}=\{v_1,\dots ,v_n\}$under the norm constraint$r_i:=\parallel v_i\parallel$such that none of points lies strictly inside their convex polyhedron.

The illustration of this problem is shown in Figure 1 on the Euclidean plane. The left figure shows the points with respect to the given scalars regarded as the radii from the fixed point. In the right figure, the configuration of points with respect to the given scalars is a convex polygon.

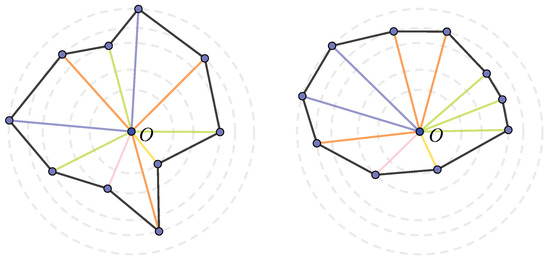
Figure 1. (Left) The general configuration of points on the concentric circles that forms a non-convex polygon; (right) the convex configuration of points with respect to the constrained vertex norms.

The mentioned problem can be considered as the convex configuration of points in the space. We first review the similar and related problems to our study.

1.1. Related Works

To consider the literature, we primarily focused on the problems of convexification and convex configuration in the two-dimensional case.

Suppose that there is a closed chain composed of the vertices and links. The reconfiguration problem considers whether the given configuration can be transformed into another configuration. Lenhart and Whitsides [6] considered the problem when the lengths of links were fixed, and the reconfiguration was allowed across other links. This result also proved that every polygon could be convexified in the standard triangular form, i.e., the edge lengths of resulting convex polygon were preserved.

The more specified problem to the reconfiguration problem is the polygon convexification problem, a problem to transform a configuration of the simple polygon in the initial stage to a convex polygon. Everett et al. [7] considered the polygon convexification problem in the case of star-shaped polygons and proved that every star-shaped polygon in the general position could be convexified. In this problem, it was not necessary to fix the lengths of the links.

One of the famous problems, called the carpenter’s rule problem, is to ask whether we can continuously move a simple polygon in such a way that all the vertices are in the convex position. Aichholzer et al. [8] and Connelly et al. [9] studied the problem of convexifying the polygonal cycle by employing a continuous motion as a convex closed curve such that no links cross each other during the motion. Especially, the study in [8] defined the term convex configuration as the configuration of a convex polygon where the edge links are fixed. Some results were compiled by Toussaint in [10].

In three-dimensional space, based on our observations, the configuration problem of points in 3D as a convex set has not been clearly identified yet. However, in the general dimension, the convex hull frame problem, known as the redundancy removal problem, is a problem to compute the vertex description of the given set of points. That is, to justify whether a point is in a convex hull of the given set. If it is inside the convex hull, we remove that point.

Clarkson [11] and Ottmann et al. [12] considered the algorithms for testing whether a given point is inside the convex hull. Dula and Helgason [13] studied the problem by identifying the extreme points (or vertices) of the convex hull of the given points using the linear programming viewpoint. Other similar problems included the vertex enumeration of the convex hull, as presented in [14].

With the basic problem of the convex hull frame problem, the closest issues to the Voronoi diagram in Laguerre geometry were first addressed by Aurenhammer [15] and Imai et al. [16]. In [16], the emptiness of the Laguerre Voronoi cell in Euclidean space ${\mathbb{R}}^d$ was identified so that the Voronoi polygon of the generating circle $c_k$ was empty if the center of circle $c_k$ was not on the boundary of the convex hull.

In the spherical case, they assumed that all points were on or close to a sphere. Carili et al. in [17] established the sufficient condition under which no point was hidden in other planes of the convex hull with respect to other points.

1.2. Problem Statement and Our Contribution

In this study, we investigated the modification of the previous convex configuration problem. Suppose that a set of constrained vertex norms is given with a fixed point. We would find the existence of a convex polyhedron whose vertices correspond to the given set of constrained vertex norms.

In the two dimensional case, the convex configuration of points is a polygon where the edge lengths of a polygon are allowed to be moved, and fixed for the constrained vertex norms, whereas the problems in [6,7,9] used fixed link lengths.

The problem in the two-dimensional case was generalized to the three-dimensional case, i.e., we find a convex polyhedron satisfying the given set of constrained vertex norms. The main motivation of this study was initiated from the non-empty property of the spherical Laguerre Voronoi diagram, where the problem can be simplified to the problem of the modified convex configuration problem in three-dimensional space. The existence of the convex configuration can guarantee that for any set of weights, and we can always find a spherical Laguerre Voronoi diagram whose Voronoi cells are nonempty, which is a different approach to the problems stated in [11,12,13,14].

This paper is organized as follows. In Section 2, the notation, definitions, and the formulation of the problems are provided. We discuss the existence of a convex polygon, which is a convex configuration in the two-dimensional case, in Section 3. In Section 4, the existence of the convex configuration in the three-dimensional is proved. The application of the problem to the spherical Laguerre Voronoi diagram, which answers the question from the motivation of the study, is described in Section 5. The concluding remarks and future studies are clarified in the last section.

2. Preliminaries

In this section, we define the notations and the necessary definitions. After that, we formulate the problem.

2.1. Notations and Definitions

First, we focus on the definitions in the two-dimensional case. The definitions in the three-dimensional case will be provided in the latter part. Let $V=\{v_1,\dots ,v_n\}$ be a set of vertices that are arranged counterclockwise on a plane with respect to a fixed point O by the lexicographical order, i.e., a vertex with a smaller angle is earlier than a vertex with a larger angle. If the two vertices have the same angle, a vertex with a shorter distance from O is earlier than a vertex with a longer distance from O.

An edge $e_i=(v_i,v_{i+1})$ is a segment joining the vertices $v_i$ and $v_{i+1}$ with the length $l_i:=d(v_i,v_{i+1})$, where $d(v_i,v_{i+1})$ denotes the Euclidean distance between $v_i$ and $v_{i+1}$. In this context, the norm $\parallel v_i\parallel$ of a vertex $v_i$ is the Euclidean distance $d(v_i,O)$ between $v_i$ and O. A chain is a straight line graph formed by the set of edges $\mathcal{E}=\{e_1,\dots ,e_{n-1}\}$. A polygon P is a closed region bounded by a closed chain generated from the set of edges $\{e_1,\dots ,e_n\}$, where $e_i=(v_i,v_{i+1})$ for all $1\le i<n-1$, except $e_n=(v_n,v_1)$. A polygon P is said to be simple if the chain does not intersect itself, except for the vertices of P.

Let $e_i=(v_i,v_{i+1})$ and $e_{i+1}=(v_{i+1},v_{i+2})$ be adjacent edges of a polygon P, whose common vertex is $v_{i+1}$. The angle between $e_i$ and $e_{i+1}$ is denoted by $\angle v_i{v}_{i+1}{v}_{i+2}$ and is measured clockwise from the segment $\overline{v_i{v}_{i+1}}$. A simple polygon P is said to be convex if, and only if, for any point $p,q$ in the polygon P, a segment joining p and q is in P. For each angle $\angle v_i{v}_{i+1}{v}_{i+2}$ of P, where $i=1,\dots ,n,v_{i+1}=v_1,v_{i+2}=v_2$, $\angle v_i{v}_{i+1}{v}_{i+2}\le \pi$ if, and only if, P is convex. It is impossible that $\angle v_i{v}_{i+1}{v}_{i+2}=\pi$ for all i. For the special case, a simple polygon P is said to be a strictly convex polygon if, and only if, $\angle v_i{v}_{i+1}{v}_{i+2}<\pi$ for all i.

For a given edge length set $L=\{l_1,\dots ,l_n\}$, a convex configuration of edge lengths is a convex polygon whose length of edges satisfies the set L with a counterclockwise order. The radius $r_i$ of a polygon vertex $v_i$ is defined as the Euclidean distance between the vertex $v_i$ and a given fixed point. Without a loss of generality, we assume that the origin O is such a fixed point. In this study, the radius $r_i$ will be regarded as the constrained vertex norms $\parallel v_i\parallel$ of the point $v_i$. For a given straight line ℓ, an arbitrary half-plane with respect to the line ℓ is denoted by $H\left(\ell \right)$. The half-plane containing the origin is written as $H^0\left(\ell \right)$.

Next, we generalize the mentioned definitions in three-dimensional space. We assume that $\mathcal{V}=\{v_1,\dots ,v_n\}$ is a set of points in the three-dimensional space. In our context, the convex polyhedron is a convex hull of a set $\mathcal{V}$. We can also construct a polyhedron from the intersection of a finite number of half-spaces. In this study, we focus on the polyhedron that is formed from the bounded intersection of half-spaces.

Similar to the two-dimensional case, without a loss of generality, the radius $r_i$ of a polyhedron vertex $v_i$ is defined by the Euclidean distance between $v_i$ and the origin O.

In spherical geometry, we consider a unit sphere $S^2$ where the center is located at the origin. We also define $S(O,r)$ as a sphere where the center is at O with radius r. For $p,q\in S^2$, let $\tilde{d}(p,q)$ be the geodesic distance between p and q defined by

$$\tilde{d}(p,q)=\arccos (p·q)\le \pi .$$

For a fixed point q on the surface of $S^2$, the spherical circle is defined as

$${\tilde{c}}_q=\{p\in S^2:\tilde{d}(p,q)\le r_i\},$$

which is the circle where the center is at the point q with radius $r_i$ and $0\le r_i<\pi /2$.

2.2. Problem Formulations

We assume that the set of constrained vertex norms $\mathcal{R}=\{r_1,r_2,\dots ,r_n\}$ is given. We place a point $v_i$ on the plane so that the distance between O and $v_i$ is the radius $r_i$. Therefore, a simple polygon P is formed from the counterclockwise sequence of vertices $\{v_1,\dots ,v_n\}$ generated by the sequence of constrained vertex norms $\mathcal{R}$.

In this study, we are interested in the following question. For a given set of constrained vertex norms $\mathcal{R}=\{r_1,r_2,\dots ,r_n\}$, does there exist a convex configuration of the vertices set $V=\{v_1,\dots ,v_n\}$ including O with respect to the set of constrained vertex norms $\mathcal{R}$? To avoid confusion with the problems in [6,8], the convex configuration in this context means that the radius $r_i$ is fixed for all i, and the length of edge $l_i:=d(v_i,v_{i+1})$ is allowed to be adjusted with respect to the position of $v_i$ and $r_i$.

In the three-dimensional case, the concept of convex configuration in our context can be considered similar to the two-dimensional case. We assume that a vertex $v_i$ is in ${\mathbb{R}}^3$ with the Euclidean distance between O and $v_i$, for instance, $r_i$. The convex configuration of the three-dimensional case is defined by the existence of a convex polyhedron whose points in the set $\mathcal{V}$ are vertices of the convex polyhedron. Therefore, the problem in three-dimensional space is to consider the existence of a convex configuration of $v_1,\dots ,v_n$ with respect to the given set of constrained vertex norms $\mathcal{R}$.

3. The Existence of a Convex Polygon in the Plane

For a set $V=\{v_1,v_2,\dots ,v_n\}$ of $n>3$ vertices in the plane, we investigated the convexity of the constructed polygon.

First, we proved the simple case when the constrained vertex norms were distinct. For a given sequence of distinct constrained vertex norms $\mathcal{R}$, the convex configuration can always exist by the following lemma.

Lemma 1.

Let$\mathcal{R}=\{r_1,\dots ,r_n\}$be a given set of constrained vertex norms, such that$r_i>0$and$r_i\ne r_j$for all$i,j$. We assume that$V=\{v_1,\dots ,v_n\}$is a set of vertices induced by$\mathcal{R}$. There exists a convex configuration of V with respect to the set of constrained vertex norms$\mathcal{R}$.

Proof. 

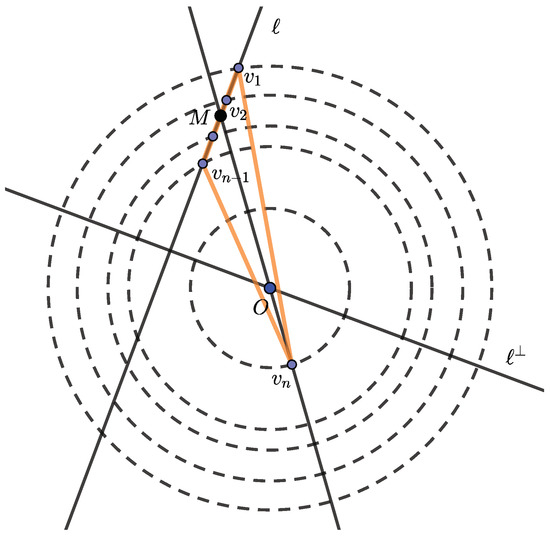
Without a loss of generality, we order the set $\mathcal{R}$ as the descending order, i.e., $r_1^{\prime }>r_2^{\prime }>\dots >r_n^{\prime }$. Therefore, the set $\{r_1^{\prime },r_2^{\prime },\dots ,r_n^{\prime }\}$ is a strictly decreasing sequence. We construct a sequence of concentric circles $\mathcal{C}=\{C_1,\dots ,C_n\}$, such that $C_i=C(O,r_i^{\prime })$ is a circle with radius $r_i^{\prime }$ where the center is O.

As $r_i$ are distinct positive numbers, there exists a line ℓ passing through all concentric circles $C_1,C_2,\dots ,C_{n-1}$, but which does not pass through the circle $C_n$. Let ${\ell }^{\perp }$ be a perpendicular line of ℓ at O. The circle $C_n$ is laid in a half-plane of $H\left(\ell \right)$. With the line ${\ell }^{\perp }$, we choose an arbitrary half-plane $H\left({\ell }^{\perp }\right)$. The vertices $v_1,v_2$$,\dots ,v_{n-1}$ are chosen by the the intersection of the circle $C_i$ for all $i=1,\dots ,n-1$, and the line ℓ, which are laid inside the half-plane $H\left({\ell }^{\perp }\right)$.

Let M be a midpoint of the segment $v_1$ and $v_{n-1}$. We draw a line $MO$. Then, the last vertex $v_n$ is chosen at the intersection of $MO$ and the circle $C_n$, which is in the other half-plane $H\left({\ell }^{\perp }\right)$, as shown in Figure 2. Hence, O is in the triangle $\Delta v_1{v}_{n-1}{v}_n$, which implies that O is laid inside the polygon constructed in the process of the vertices $\{v_1,v_2,\dots ,v_n\}$. This concludes the proof of the existence of the convex configuration. □

Figure 2. The construction of a convex polygon with respect to the given distinct constrained vertex norms.

In Lemma 1, the vertices $v_1,\dots ,v_n$ are allowed to be collinear. In the case of a strictly convex configuration, we can perturb the vertices to be non-collinear. Thereby, the following theorem is obtained.

Theorem 1.

For a given set of distinct positive constrained vertex norms$\mathcal{R}=\{r_1,\dots ,r_n\}$and with an induced vertices set$V=\{v_1,\dots ,v_n\}$, there exists a strictly convex configuration of V with respect to the constrained vertex norms set$\mathcal{R}$.

Proof. 

We assume that the vertices of a convex configuration are located by the processes in Theorem 1, as shown in Figure 2. The perturbation is done with the vertices $v_3,\dots ,v_{n-1}$ by the following processes.

We first consider the angular distance between vertices $v_1$ and $v_{n-1}$. For the triangle $\Delta v_1{v}_{n-1}{v}_n$, the angle $\gamma$ between $\overrightarrow{v_n{v}_1}$ and $\overrightarrow{v_n{v}_{n-1}}$ is $\gamma :=\arccos \left(\frac{r_1^2+r_{n-1}^2-d{(v_1,v_{n-1})}^2}{2r_1{r}_{n-1}}\right)$, and the angle $\zeta$ between $\overrightarrow{v_{n}M}$ and $\overrightarrow{v_n{v}_{n-1}}$ is $\zeta :=\arccos \left(\frac{d{(v_n,M)}^2+r_{n-1}^2-d{(M,v_{n-1})}^2}{2d(v_n,M)r_{n-1}}\right)$. For the vertex $v_{n-1}$, it should not be moved in the region of the region of $v_1{v}_{n}M$ to make a polygon P containing the origin O. Therefore, the angular movement of all vertices on the circle should be smaller than $\theta :=\gamma -\zeta$.

For the pair of vertices $v_1,v_2$, we draw a ray $\overrightarrow{v_1{v}_2}$. Therefore, the vertex $v_3$ should be perturbed on the left-handed side of the ray $\overrightarrow{v_1{v}_2}$ on the circle $C_{r_3^{\prime }}$ for a circular distance ${ϵ}_1$ with angle $\theta >{ϵ}_1/r_3^{\prime }>0$, and we move all vertices $v_4,\dots ,v_{n-1}$ along the ray $\overrightarrow{v_2{v}_3}$ to be $v_4^{\prime },\dots ,v_{n-1}^{\prime }$. Next, we fix a ray $\overrightarrow{v_2{v}_3}$ and perturb the vertex $v_4^{\prime }$ to the left side of the ray $\overrightarrow{v_2{v}_3}$ for a circular distance ${ϵ}_2$ on the circle $C_{r_4^{\prime }}$ with the angle $\theta -{ϵ}_1/r_3^{\prime }>{ϵ}_2/r_4^{\prime }>0$, to be $v_4^{\prime \prime }$, and move the other points $v_5^{\prime },\dots ,v_{n-1}^{\prime }$ along the ray $\overrightarrow{v_3{v}_4}$.

We continue these processes until all the vertices $v_3,\dots ,v_{n-1}$ are perturbed, such that

$$\frac{{ϵ}_1}{r_3^{\prime }}+\frac{{ϵ}_2}{r_4^{\prime }}+\dots +\frac{{ϵ}_{n-3}}{r_{n-1}^{\prime }}<\theta .$$

Hence, the resulting polygon is perturbed to be a strictly convex configuration, which concludes the proof of the existence. □

Before we prove the following lemma, we define the segment from the intersection between a line and all concentric circles. Let ℓ be a line, and $C_1$ be a circle with radius $r_1$, which is the largest circle among the concentric circles. $\overline{\ell }$ is the segment induced from the intersection between ℓ and $C_1$, whose initial and end points are on the circle $C_1$.

With a similar strategy to Lemma 1, we can extend to the case that some constrained vertex norms are same, and the repeated number of the constrained vertex norms is, at most, 4.

Lemma 2.

Let$\mathcal{R}=\{r_{(1,1)},\dots ,r_{(1,m_1)},r_{(2,1)},\dots ,r_{(2,m_2)},\dots ,r_{(k,1)},\dots ,r_{(k,m_k)}\}$be a set of constrained vertex norms, such that$r_{(i,1)}=\dots =r_{(i,m_i)}$for each$i=1,\dots ,k$and$1\le m_i\le 4$. Then, there exists a convex configuration V with respect to the set of constrained vertex norms$\mathcal{R}$.

Proof. 

Let V be a set of vertices, such that each vertex $v_{(i,j)}$ satisfies the radius $r_{(i,j)}$. We assume that the elements in $\mathcal{R}$ are sorted in such a way that

$$r_{(1,1)}=\dots =r_{(1,m_1)}>r_{(2,1)}=\dots =r_{(2,m_2)}>\dots >r_{(k,1)}=\dots =r_{(k,m_k)}.$$

We already proved the case $m_i=1$ for all i in Lemma 1. Similarly to Theorem 1, the proof relies on the location of points on concentric circles with constrained vertex norms $r_{(1,1)},r_{(2,1)},\dots ,r_{(k,1)}$. Hence, without a loss of generality, we assume that the center of the circles are at the origin O of the $XY$-plane.

To prove the convex configuration containing O with this assumption, the strategy of the proof is to distribute the points to all quadrants as much as possible. Therefore, it is necessary to separate into two cases when $\max \{m_1,\dots ,m_k\}=4$ and $\max \{m_1,\dots ,m_k\}=2$ or 3, as follows.

Case 1$\max \{m_1,\dots ,m_k\}=4$

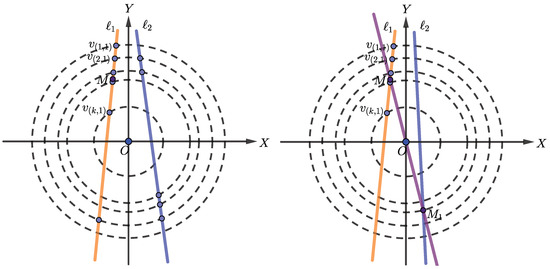
We construct lines ${\ell }_1$ and ${\ell }_2$ to intersect all concentric circles such that $\overline{{\ell }_1}$ and $\overline{{\ell }_2}$ are on the opposite half-plane with respect to the Y-axis as shown in Figure 3 (left). Then, we lay the points in the set V satisfying each circle radius on the intersection between ${\ell }_1,{\ell }_2$, and the concentric circles. This forms a convex quadrilateral containing the origin, which is a convex configuration of V with respect to the given constrained vertex norms.

Figure 3. The construction for the convex configuration of V when (left) $\max \{m_1,\dots ,m_k\}=4$ and (right) $\max \{m_1,\dots ,m_k\}=2$ or 3.

Case 2$\max \{m_1,\dots ,m_k\}=2$ or 3

We assume that $\max \{m_1,\dots ,m_k\}=m_p$ such that $r_{(m_p,1)}\ge r_{(m_j,1)}$ for all $j\ne p$.

We first draw a line ${\ell }_1$, such that $\overline{{\ell }_1}$ is on the side of a half-plane with respect to Y-axis. The first k points $v_{(1,1)},v_{(2,1)},\dots ,v_{(k,1)}$ are chosen from the intersection between ${\ell }_1$ and concentric circles in the same quadrant. After that, we find the midpoint M between $v_{(1,1)}$ and $v_{(k,1)}$ on the line ${\ell }_1$ and draw a line $\overline{MO}$. The intersection between $\overline{MO}$ and the circle $C_p$ with the radius $r_{(p,1)}$ is denoted as $M_1$. Then, we draw a line ${\ell }_2$ passing through $M_1$, where $\overline{{\ell }_2}$ is laid in the opposite half-plane of $\overline{{\ell }_1}$ with respect to the Y-axis, and ${\ell }_2$ intersects all concentric circles, which is shown in Figure 3 (right).

Hence, we place the remaining points on the intersections between ${\ell }_2$ and the concentric circles. As $M_1$ is the point on the largest circle that contains the maximum number of points, $v_{(1,1)}{v}_{(k,1)}{M}_1$ forms a triangle, or a convex quadrilateral $v_{(1,1)}{v}_{(k,1)}{M}_1{v}_{(q_1,q_2)}$ for some $q_1,q_2$, where $v_{(q_1,q_2)}$ is the point of the intersection between the circle ${\tilde{c}}_{q_1}$ and the line ${\ell }_2$. This forms a convex configuration of V with respect to the given constrained vertex norms $\mathcal{R}$ containing O.

With these cases, the proof is concluded as desired.

For the strictly convex configuration, we can employ a similar strategy to Theorem 1, as presented in the following theorem. □

Theorem 2.

For a given set of positive constrained vertex norms,$\mathcal{R}=\{r_{(1,1)},\dots$, $r_{(1,m_1)},r_{(2,1)},\dots$, $r_{(2,m_2)},\dots ,r_{(k,1)},\dots ,r_{(k,m_k)}\}$, such that$r_{(i,1)}=\dots =r_{(i,m_i)}$for each$i=1,\dots ,k$and$1\le m_i\le 4$, there exists a strictly convex configuration V with respect to the set of constrained vertex norms$\mathcal{R}$.

Proof. 

Suppose that the convex configuration is settled by Lemma 2. A proof relies on each case, as presented in Lemma 2.

Case 1$\max \{m_1,\dots ,m_k\}=4$

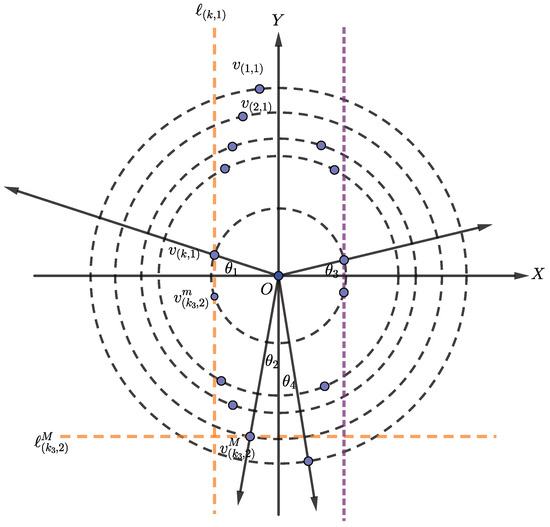
In this case, the construction in Lemma 2 yields a convex quadrilateral. Without a loss of generality, we assume that all points are separated into four quadrants, and we start from the points in the second quadrant.

We first move the $v_{(k,1)}$ to the position that is close to the negative side of the X-axis, i.e., the angle between $\overrightarrow{O{v}_{(k,1)}}$ and the negative side of the X-axis is ${\theta }_1$. Then we draw the line ${\ell }_{k,1}$ passing through $v_{(k,1)}$ and perpendicular to the X-axis. Suppose that $H^0\left({\ell }_{k,1}\right)$ is the half-plane including the origin. We perturb all vertices $v_{(2,1)},v_{(3,1)},\dots ,v_{(k-1,1)}$ by a technique similar to Theorem 1 in such a way that all the vertices are in the region $H^0\left({\ell }_{k,1}\right)\backslash {\ell }_{(k,1)}$. Therefore, there exists a line ${\ell }_1$ passing through $v_{(k-1,1)}$ and $v_{(k,1)}$, which is different to ${\ell }_{k,1}$.

Let $V_3=\{v_{(k_j,2)}:\mathrm{for}\mathrm{some}{k}_j=1,\dots ,k\}$ be a set of points in the third quadrant. We choose the point $v_{(k_3,2)}^m\in V_3$, such that $r_{(k_3,2)}=\min \{r_{(k_j,2)}:\mathrm{for}\mathrm{some}{k}_j=1,\dots ,k\}$, and $v_{(k_3,2)}^M\in V_3$, such that $r_{(k_3,2)}=\max \{r_{(k_j,2)}:\mathrm{for}\mathrm{some}{k}_j=1,\dots ,k\}$. We first move $v_{(k_3,2)}^m$ to the line ${\ell }_{k,1}$ and then move $v_{(k_3,2)}^M$ to the position that is close to the negative side of the Y-axis, i.e., the angle between $\overrightarrow{O{v}_{(k_3,1)}^M}$ and the negative side of the y-axis is ${\theta }_2$. After that, we construct a line ${\ell }_{k_3,2}^M$ passing through $v_{(k_3,2)}^M$ and perpendicular to the Y-axis. Then, we perturb all points in $V_3$ except $v_{(k_3,2)}^m$ and $v_{(k_3,2)}^M$ using the same technique in Theorem 1 such that all vertices lay in the region $(H^0\left({\ell }_{k,1}\right)\backslash {\ell }_{(k,1)})\cap (H^0\left({\ell }_{k_3,2}^M\right)\backslash {\ell }_{k_3,2}^M)\cap Q_3$, where $H^0\left({\ell }_{k_3,2}^M\right)$ is a half-plane of the line ${\ell }_{k_3,2}^M$ including the origin and $Q_3$ is the region of the third quadrant. The mentioned processes are shown in Figure 4.

Figure 4. The perturbation of the points to find the strictly convex configuration when $\max \{m_1,\dots ,m_k\}=4$.

Using a similar technique, we can perturb all vertices in the first quadrant and the fourth quadrant. Finally, the convex polygon can be closed by the point with the largest radius in the third quadrant and fourth quadrant, and the point with the largest radius in the first quadrant and the second quadrant. That is, there is a strictly convex configuration from the given set of constrained vertex norms.

Case 2$\max \{m_1,\dots ,m_k\}=2$ or 3

We can employ the same strategy of the first case to the points in the second, fourth, and the first quadrant to obtain the strictly convex configuration of the given set of constrained vertex norms.

Therefore, we can find the strictly convex configuration from the given set of constrained vertex norms in any case. □

4. Existence of a Convex Polyhedron in Three-Dimensional Space

Given a set of constrained vertex norms $\mathcal{R}=\{r_1,\dots ,r_n\}$, we assume that the constrained vertex norms are the Euclidean distance from the origin to the vertex $v_1,\dots ,v_n$ in three-dimensional space. The convex configuration, in this case, is the convex polyhedron containing the origin O.

In the three-dimensional case, the existence of the convex configuration can be proved. First, we consider the simple case where all of the constrained vertex norms are distinct.

Lemma 3.

For$n\ge 4$, given a set of positive constrained vertex norms,$\mathcal{R}=\{r_1,\dots ,r_n\}$, such that all of constrained vertex norms are distinct, there exists a convex configuration of$\mathcal{V}=\{v_1,\dots ,v_n\}$in three-dimensional space.

Proof. 

When $n=4$, we place the points $v_1,v_2,v_3,v_4$ with respect to $r_1,r_2,r_3,r_4$ as the vertices of the tetrahedron. Therefore, the convex configuration is obviously obtained.

Suppose that $n\ge 5$. We assume that the descending order of $\mathcal{R}=\{r_1,\dots ,r_n\}$ is ${\mathcal{R}}^{\prime }=\{r_1^{\prime },\dots ,r_n^{\prime }\}$, where $r_i^{\prime }=r_j$ for some $i,j$. We construct concentric spheres $S_1(O,r_1^{\prime }),S_2(O,r_2^{\prime })$ at the origin O with radius $r_1^{\prime }$ and $r_2^{\prime }$. Without a loss of generality, we place the vertex $v_1$ and $v_2$ on the north pole of sphere $S_1$ and the south pole of sphere $S_2$, respectively.

We consider the $XY$-plane and place the vertices $v_3,\dots ,v_n$ onto the $XY$-plane by the processes in Theorem 1 and Lemma 1 to obtain a convex polygon P of $\{v_3,\dots ,v_n\}$. Then, we join the edge $v_1$ from the north pole to the vertex set $\{v_3,\dots ,v_n\}$, and $v_2$ from the south pole to the same set. The obtained polyhedron is a polyhedron whose faces are triangles. As the polygon P is convex and contains the origin O, the constructed polyhedron is convex as desired. □

In general, the set of constrained vertex norms $\mathcal{R}$ is not necessarily distinct. We assume that the set of constrained vertex norms consists of n elements with distinct k elements. Let $\mathcal{R}=\{r_{(1,1)},\dots ,r_{(1,m_1)}$, $r_{(2,1)},\dots ,r_{(2,m_2)},\dots ,r_{(k,1)},\dots ,r_{(k,m_k)}\}$ be a set of constrained vertex norms such that

$$r_{(1,1)}=\dots =r_{(1,m_1)}>r_{(2,1)}=\dots =r_{(2,m_2)}>\dots >r_{(k,1)}=\dots =r_{(k,m_k)}$$

and $m_1+m_2+\dots +m_k=n$. That is, for the i-th layer, the radius of the i-th layer is $r_{(i,1)}$, and the i-th layer consists of $m_i$ points.

The following theorem shows the existence of a convex configuration in the three-dimensional case.

Theorem 3.

Let$\mathcal{R}$be a set of constrained vertex norms consisting of n elements with$m_i$repeated constrained vertex norms for each i distinct radius, such that the constrained vertex norms are arranged as

$$r_{(1,1)}=\dots =r_{(1,m_1)}>r_{(2,1)}=\dots =r_{(2,m_2)}>\dots >r_{(k,1)}=\dots =r_{(k,m_k)}$$

and$m_1+m_2+\dots +m_k=n$. Then, there exists a convex configuration of$\mathcal{V}=\{v_1,\dots ,v_n\}$induced by the set$\mathcal{R}$.

Proof. 

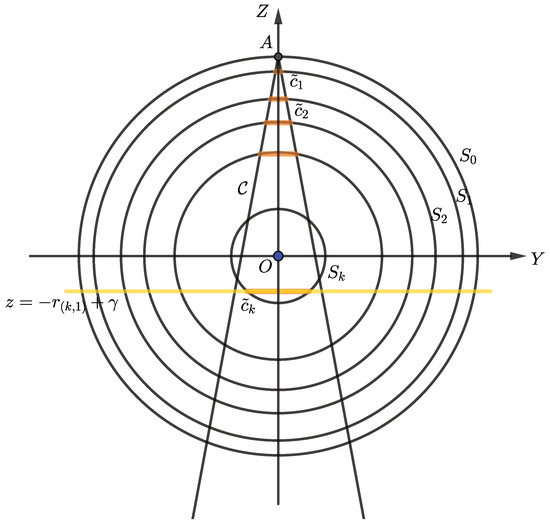
We first construct k concentric spheres $S_1,S_2,\dots ,S_k$ where the center is at O with constrained vertex norms $r_{(1,1)},r_{(2,1)}$, $\dots ,r_{(k,1)}$.

Let $S_0$ be a sphere where the radius is $r_{(1,1)}+ϵ$ for any $ϵ>0$. Therefore, there exists a circular cone $\mathcal{C}$ whose apex A is at the north pole of the sphere $S_0$, and the lateral area of the cone intersects all the concentric spheres, i.e., the apex angle $\theta$ satisfies $\theta <2\arctan \left(\frac{r_{(1,1)}+ϵ}{r_{(k,1)}}\right)$.

Hence, the cone $\mathcal{C}$ intersects the concentric spheres $S_1,S_2,\dots ,S_k$ such that the intersection between $\mathcal{C}$ and a sphere $S_j$ for all $j=1,2,\dots ,k-1$ is a spherical circle, ${\tilde{c}}_j$, where the centers are the north pole of each sphere. The distance from O to a point on the circle ${\tilde{c}}_j$ is $r_{(j,1)}$. Therefore, there are k circles from the largest sphere $S_1$ to the smallest sphere $S_k$ on the upper hemisphere, as shown in the cross section in Figure 5.

Figure 5. The cross section at the $YZ$-plane for the concentric spheres including a spherical circle of each layer and the cone $\mathcal{C}$.

We choose a line ℓ emanating from the apex A on the surface of $\mathcal{C}$. For each layer of circle ${\tilde{c}}_j$ over the upper hemisphere except the smallest layer ${\tilde{c}}_k$, we place a point on the line ℓ. Therefore, each layer has at least one point on its layer.

For the number of points of k layers $m_1,m_2,\dots ,m_k$, we assume that the p-th layer contains the maximum number of points, i.e., $m_p:=\max \{m_1,m_2,\dots ,m_k\}$. Therefore, we first distribute $m_p$ points on the spherical circle ${\tilde{c}}_p$ at the p-th layer in such a way that the angular distances $\beta$ between each vertex on the spherical circle ${\tilde{c}}_p$ are equal. We fix the point that is already placed on the line ℓ and distribute the other $m_p-1$ points, says $v_{p,1},v_{p,2},\dots ,v_{p,m_p}$.

For each $v_{p,i}$ on the p-level, we construct a plane $P_{v_{p,i}}$ passing through $v_{p,i}$ and the Z-axis to create a spherical grid. $P_{v_{p,i}}$ intersects all concentric spheres and generates longitude lines $L_{v_{p,i},{\tilde{c}}_p}$ on each sphere $S_i$, which are great circles.

Therefore, in each level $j=1,\dots ,p-1,p+1,\dots ,k$, the latitude is considered the spherical circle ${\tilde{c}}_j$, which intersects the longitude $L_{v_{p,j},{\tilde{c}}_p}$ to $m_p$ points. We can place $m_j$ points on those intersections arbitrarily since $m_j\le m_p$. As all vertices are laid on the convex surface, for each placed point on the intersections, there exists a plane tangent to the cone passing through that point, and all points are on the same side of the plane. Hence, there exist faces joining $v_{p_1,i_1},v_{p_2,i_2},v_{p_3,i_3}$ for some $p_1,i_1,p_2,i_2,p_3,i_3$, which form the faces of convex polyhedra.

With the exceptional case for the last smallest layer, for instance, the k-th level, we construct a plane $z=-r_{(k,1)}+\gamma$. Therefore, the parameter $\gamma$ can be considered in the following case.

If the k-th layer contains exactly one point, we choose $\gamma =0$. This means that the plane $z=-r_{m_1+\dots +m_{k-1}+1}$ is a tangent plane at $(0,0,-r_{(k,1)})$. Therefore, the polyhedron can be bounded by joining all of the vertices to that point.

Otherwise, we assume that there are $m_k$ points at the k-th layer. We choose a small $\gamma >0$, such that $\gamma <|r_{(k,1)}|$. Therefore, there exists a spherical circle in the k-th layer. Then, we distribute $m_k$ points, with the same angles and connecting the points in the k-th level to the above levels to construct a convex polyhedron.

Therefore, the convex configuration exists by the construction process, which concludes the proof. □

5. Applications

The main application of the existence of the convex configuration in the three-dimensional case is the confirmation regarding the non-emptiness properties of the spherical Laguerre Voronoi diagram, in which the details will be described soon.

We first recall the definitions and constructions of the spherical Laguerre Voronoi diagram, as presented in [2].

On the unit sphere $S^2$, let $P=\{p_1,\dots ,p_n\}$ be a set of points with the set of positive real numbers $W=\{w_1,\dots ,w_n\}$ and $\mathcal{G}=\{{\tilde{c}}_1,\dots ,{\tilde{c}}_n\}$ be a set of spherical circles whose center is each a point in P corresponding to each $w_i\in W$. The set W is regarded as the weight set, meaning that each center $p_i$ of the circle ${\tilde{c}}_i$ has its weight $w_i$. The spherical Laguerre Voronoi diagram $\mathcal{L}=\{L_1,\dots ,L_n\}$ is a Voronoi diagram generated from the set of spherical circles $\mathcal{G}$ with the Laguerre proximity ${\tilde{d}}_L(c_i,p)=\frac{\cos \left(\tilde{d}(p,p_i)\right)}{\cos \left(w_i\right)}$, for a point $p\in S^2$.

The algorithms for constructing the spherical Laguerre Voronoi diagram presented in [2] were based on the intersection of half-spaces of planes passing through the spherical circles containing the origin. The dual structure of the spherical Laguerre Voronoi diagram is the spherical Laguerre Delaunay diagram. Figure 6 shows the ordinary Voronoi diagram and spherical Laguerre Voronoi diagram with the same generators.

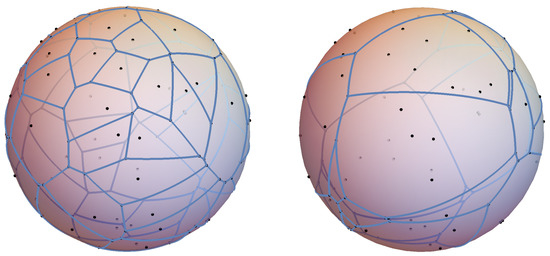
Figure 6. The Voronoi diagrams of 50 generators; (left) the ordinary spherical Voronoi diagram; (right) the spherical Laguerre Voronoi diagram with random weights. Certain cells lose in the case of the spherical Laguerre Voronoi diagram.

The spherical Laguerre Delaunay diagram can be constructed by the following procedures. For a set of generating circles $\mathcal{G}$, we suppose that $P_i$ is a plane passing through the spherical circle ${\tilde{c}}_i$. Therefore, the dual point of the plane $P_i$ can be considered as $P_i^{*}=\frac{1}{\cos w_i}{p}_i$, and the spherical Laguerre Delaunay diagram can be constructed from the central projection of the convex hull ${\mathcal{G}}^{*}=\{P_1^{*},\dots ,P_n^{*}\}$ onto the unit sphere $S^2$.

For a spherical Laguerre Voronoi diagram $\mathcal{L}$ generated by $\mathcal{G}$, the spherical Laguerre Voronoi cell $L_i$ is said to be empty if $L_i=\varnothing$. The spherical Laguerre Voronoi diagram $\mathcal{L}$ satisfies the non-emptiness property if for all i, $L_i\ne \varnothing$. A cell $L_i$ of the spherical Laguerre Voronoi diagram is empty if the dual point $P_i^{*}$ of the circle ${\tilde{c}}_i$ is inside of the convex hull of the set ${\mathcal{G}}^{*}$.

Instead of giving the spherical circles, we assume that the radii of the spherical circles are given. The interesting question is to consider whether or not we can find the location of the generators on the sphere in such a way that the generated spherical Laguerre Voronoi diagram satisfies the non-emptiness property.

The answer to the mentioned question is positive as follows.

Theorem 4.

Let$W=\{w_1,\dots ,w_n\}$be a set of spherical circle radii. Then, there exists a spherical Laguerre Voronoi diagram satisfying the non-emptiness property.

Proof. 

For the set of spherical circle radii $W=\{w_1,\dots ,w_n\}$, each radius corresponds to the radius $r_i=1/\cos \left(w_i\right)$. $r_i\ge 1$, by the assumption of the spherical circle radius. Thereby, we generated a set of constrained vertex norms $\mathcal{R}=\{r_1,\dots ,r_n\}$.

By Theorem 3, there exists a convex configuration of a set $\mathcal{P}=\{p_1,\dots ,p_n\}$ with respect to $\mathcal{R}$. Therefore, all dual points in ${\mathcal{G}}^{*}$ are on the corner of the convex hull of ${\mathcal{G}}^{*}$. That is, the spherical Laguerre Delaunay diagram with respect to ${\mathcal{G}}^{*}$ consists of all generators $\mathcal{P}=\{p_1,\dots ,p_n\}$.

Hence, this implies that there exists a spherical Laguerre Voronoi diagram satisfying the non-emptiness property with respect to a given set of radii as desired. □

6. Concluding Remarks

We consider the convex configuration problem of n points when the constrained vertex norms, which are measured from a fixed point, are given. In the two-dimensional case, we proved that the strictly convex configuration always exists when all constrained vertex norms are distinct or each radius is repeated for, at most, four points. However, the problem is still open when repeated constrained vertex norms are greater than or equal to five points. Therefore, we leave a conjecture to prove this interesting property.

Conjecture:For any set of given constrained vertex norms$\mathcal{R}$, it is not always possible to find the convex configuration with respect to the given set$\mathcal{R}$.

However, the existence of a convex configuration is guaranteed in the case of three-dimensional space. Using this fact, we can apply the existence of a convex configuration to the existence of the spherical Laguerre Voronoi diagram satisfying the non-emptiness property.