An Extended TOPSIS Method with Unknown Weight Information in Dynamic Neutrosophic Environment

Abstract

Decision-making activities are prevalent in human life. Many methods have been developed to address real-world decision problems. In some practical situations, decision-makers prefer to provide their evaluations over a set of criteria and weights. However, in many real-world situations, problems include a lack of weight information for the times, criteria, and decision-makers (DMs). To remedy such discrepancies, an optimization model has been proposed to determine the weights of attributes, times, and DMs. A new concept related to the correlation measure and some distance measures for the dynamic interval-valued neutrosophic set (DIVNS) are defined in this paper. An extend Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method in the interval-valued neutrosophic set with unknown weight information in dynamic neutrosophic environments is developed. Finally, a practical example is discussed to illustrate the feasibility and effectiveness of the proposed method.

1. Introduction

Multiple criteria decision-making (MCDM) problems have gained more attention to researchers in recent years. The purpose of the MCDM process is to make the best ideal choice reaching the highest standard of achievement from a set of alternatives. Existing studies of MCDM attempt to handle various kinds of multi-criteria decision-making problems. The MCDM’s evaluation is decided on the basis of alternative evaluations being withdrawn from to the weights of the criteria. They are completely unknown, based upon some diverse reasons, such as time pressure, partial knowledge, incomplete attribute information, and lack of decision-makers’ information, so that the overall evaluation cannot be derived. Especially, in real-world situations of group decisions, the exact appreciation of weights is important for handling MCDM problems and for making a decision. For solving such problems, several studies have attempted to develop the methods to handle the MCDM problems using various kinds of information, such as fuzzy set [1], interval fuzzy set [2,3], intuitionistic fuzzy set [4,5], hesitant fuzzy set [6], neutrosophic set [7,8,9,10], interval neutrosophic set [11,12,13,14,15], or single neutrosophic set [16], etc. [17,18,19], and various methods (e.g., maximizing deviation method, entropy, optimization method) [20,21,22] in which the information of criteria weights are incompletely known.

Yue et al. [23] presented a TOPSIS model to calculate the weights of the DMs under a group decision environment with individual information described as interval numbers. Sajjad Ali Khan et al. [6] introduced a study based on the combination of the maximizing deviation method and the TOPSIS method for resolving MCDM problems where the valuation information is depicted as Pythagorean hesitant fuzzy numbers and information about attribute weight is incomplete. Broumi et al. [24] proposed an extended TOPSIS method for solving multiple attribute decision-making based on two new concepts of complex neutrosophic sets. Gupta et al. [4] also extended the TOPSIS method under intuitionistic fuzzy sets and interval valued intuitionistic fuzzy sets. They considered different variations of weights of attributes depending on their subjective impression, cognitive thinking, and their psychology. Wang and Mendel [25] presented an optimization model to solve the decision-making (DM) problems on the Interval Type-2 (IT2) fuzzy set. All the DMs’ information is characterized by the IT2 fuzzy set and the attribute weights’ information is completely unknown. Maghrabie et al. [26] proposed a new model that used the maximizing deviation method and grey systems theory to estimate the unknown criteria weights. Peng [27] proposed a novel model for achieving unknown attribute weights and handling an IoT (Internet of Things) industry decision-making issue based on interval neutrosophic sets. Tian et al. [28] combined single-valued neutrosophic sets with completely unknown criteria weights and qualitative flexible multiple criteria method for MCDM problems. In addition, for handling multi attribute decision-making problems with interval neutrosophic information, Hong et al. [29] discussed some distance measure based on the TODIM (an acronym in Portuguese for Interactive and Multicriteria Decision Making) method.

According to above analyses, the motivations of this study are summarized as follows:

(1)

Many approaches attempted to handle the MCDM problem with unknown weight information, but there is little research on discovering the weights of the DMs, the attributes, and the time in the group decision-making problems, and these methods are approximately complex.

(2)

Another reason is that the TOPIS model in [13] could not work efficiently without determining the evaluation information of decision-makers and this issue was not considered in [13].

(3)

In real application situations, many MCDM problems reflect a lack of weight information for the times, criteria, and decision-makers.

Therefore, we focus on the issue of multiple attribute group decision-making model based on an interval-valued neutrosophic fuzzy environment, and DMs’ information is characterized by interval-valued neutrosophic fuzzy sets, and the information is completely and partially unknown. We study multiple attribute group decision-making methods with incompletely known weights of DMs, attributes, and time in the neutrosophic setting and the interval-valued neutrosophic setting.

In this paper, our aim is to propose a novel decision-making approach based on DIVNS for unknown weight information to effectively solve the above deficits. The main contributions of this paper can be summarized as follows:

• We define a new correlation measure and some distance measures for DIVNS.
• An optimization model is proposed to determine the weight information for the times, criteria, and decision-makers.
• An extend TOPSIS method under interval-valued neutrosophic set with unknown weight information in the dynamic neutrosophic environment is established.

To do that, the rest of this work is organized as follows. In Section 2, we review some basis concepts. In Section 3, we develop a TOPSIS approach to handle the MCDM problems under DIVNS in dynamic neutrosophic environments where all information of attributes, DMs, and time is completely and partially unknown. Section 4 presents the numerical results of applying our proposed method in a practical problem to demonstrate the feasibility of this method. Some comparative analyses with existing algorithms are presented in Section 5. Finally, this paper ends with some conclusions of this study in Section 6.

2. Preliminary

In this section, we review some basic knowledge, such as dynamic interval-valued neutrosophic sets and MCDM.

2.1. Dynamic Interval-Valued Neutrosophic Sets

Neutrosophic sets are characterized by truth membership (T), indeterminacy membership (I), and falsity membership (F) with the conditions as 0 <= T <= 1; 0 <= I <= 1; 0 <= F <= 1. Moreover, three membership functions have to satisfy 0 <= T + I + F <= 3. Some other concepts were designed based on neutrosophic sets such as the neutrosophic probability and neutrosophic statistics, that refer to both randomness and indeterminacy with no such contraints of memberships [30]. Herein, we extend the neutrosophic set and logic to the dynamic interval-valued neutrosophic set where each element in the new neutrosophic set is expressed by the interval-valued neutrosophic number and time sequence.

Definition 1

[31]. Let $U$ be a universe of discourse. $A$ is an interval neutrosophic set expressed by:

$$A=\left\{x,⟨\left[T_A^L\left(x\right),T_A^U\left(x\right)\right],\left[I_A^L\left(x\right),I_A^U\left(x\right)\right],\left[F_A^L\left(x\right),F_A^U\left(x\right)\right]⟩|x\in U\right\}$$

(1)

where $\left[T_A^L\left(x\right),T_A^U\left(x\right)\right]\subseteq \left[0,1\right]$; $\left[I_A^L\left(x\right),I_A^U\left(x\right)\right]\subseteq \left[0,1\right]$; $\left[F_A^L\left(x\right),F_A^U\left(x\right)\right]\subseteq \left[0,1\right]$ represents truth, indeterminacy, and falsity membership functions of an element.

Thong et al. [13] introduced the concept of a DIVNS, which is shown as follows.

Definition 2

[13]. Let $U$ be a universe of discourse. $A$ is a dynamic–valued neutrosophic set (DIVNS) expressed by,

$$A=\left\{x,⟨\left[T_x^L\left(t\right),T_x^U\left(t\right)\right],\left[I_x^L\left(t\right),I_x^U\left(t\right)\right],\left[F_x^L\left(t\right),F_x^U\left(t\right)\right]⟩|x\in U\right\}$$

(2)

where $t=\left\{t_1,t_2,\dots ,t_k\right\}$; $\left[T_x^L\left(t\right),T_x^U\left(t\right)\right]\subseteq \left[0,1\right];$ $\left[I_x^L\left(t\right),I_x^U\left(t\right)\right]\subseteq \left[0,1\right];$ $\left[F_x^L\left(t\right),F_x^U\left(t\right)\right]\subseteq \left[0,1\right]$ and for convenience, we call $\tilde{n}=⟨\left[T_x^L\left(t\right),T_x^U\left(t\right)\right],\left[I_x^L\left(t\right),I_x^U\left(t\right)\right],\left[F_x^L\left(t\right),F_x^U\left(t\right)\right]⟩$ a dynamic interval–valued neutrosophic element (DIVNE).

2.2. MCDM Problems in a Dynamic Neutrosophic Environment

Thong et al. [13] expressed MCDM problems in the dynamic neutrosophic environment as follows:

Consider a MCDM problem containing $A=\left\{A_1,A_2,\dots ,A_v\right\}$ and $C=\left\{C_1,C_2,\dots ,C_n\right\}$ and $D=\left\{D_1,D_2,\dots ,D_h\right\}$ are sets of alternatives, criteria, and decision-makers. For a decision-maker $D_q(q=1,2,3,\dots ,h)$ the evaluation characteristic of an alternatives $A_m(m=1,2,3,\dots ,v)$ on a criteria $C_p(p=1,2,3,\dots ,n)$ in time sequence $t=\left\{t_1,t_2,\dots ,t_k\right\}$ is represented by the decision matrix where $d_{mp}^q\left(t\right)=⟨x_{d_{mp}}^q\left(t\right),\left(T^q\left(d_{mp},t\right),I^q\left(d_{mp},t\right),F^q\left(d_{mp},t\right)\right)⟩;t=\left\{t_1,t_2,\dots ,t_k\right\}$ taken by DIVNSs evaluated by decision-maker $D_q$.

3. An Extended TOPSIS Method for Unknown Weight Information

This section proposes the method to handle the MCDM problem that include a lack of the weight information for the times, criteria, and DMs in dynamic netrosophic environments.

3.1. Correlation Coefficient Measure for Dynamic Interval-Valued Neutrosophic Sets

We propose a novel correlation coefficient measure for DIVNSs based on the idea in [32].

Definition 3.

Let$Y\left(t\right)=\left\{\left(x\left(t\right),⟨T_{}^Y\left(x,t_l\right),I_{}^Y\left(x,t_l\right),F_{}^Y\left(x,t_l\right)⟩\right),\forall t_l\in t,x\in U\right\}$and$Z\left(t\right)=\left\{\left(x\left(t\right),⟨T_{}^Z\left(x,t_l\right),I_{}^Z\left(x,t_l\right),F_{}^Z\left(x,t_l\right)⟩\right),\forall t_l\in t,x\in U\right\}$be two DIVNs in$t=\left\{t_1,t_2,\dots ,t_k\right\}$and$U=\left(x_1,x_2,\dots ,x_n\right)$. A correlation coefficient measure between$A$and$B$ is:

$$K\left(Y,Z\right)=\frac{C\left(Y,Z\right)}{max\left(T\left(Y\right),T\left(Z\right)\right)}=\frac{{\displaystyle {\sum }_{i=1}^{n}C\left(Y\left(x_i\right),Z\left(x_i\right)\right)}}{max\left({\displaystyle {\sum }_{i=1}^{n}T\left(Y\left(x_i\right)\right)},{\displaystyle {\sum }_{i=1}^{n}T\left(Z\left(x_i\right)\right)}\right)}$$

(3)

where $C\left(Y,Z\right)$ is considered the correlation between two DIVNSs $Y$ and $Z$; $T\left(Y\right)$ and $T\left(Z\right)$ refer to the information energies if the two DIVNSs, respectively. These components are provided by:

$$\begin{array}{l}C\left(Y,Z\right)=\frac{1}{k}{\displaystyle \sum _{l=1}^k{\displaystyle \sum _{i=1}^{n}C\left(Y\left(x_i,t_l\right),Z\left(x_i,t_l\right)\right)}}\\ =\frac{1}{k}{\displaystyle \sum _{l=1}^k{\displaystyle \sum _{i=1}^n\frac{1}{2}\left[\begin{array}{l}\inf T_Y\left(x_i,t_l\right)\times \inf T_Z\left(x_i,t_l\right)+\sup T_Y\left(x_i,t_l\right)\times \sup T_Z\left(x_i,t_l\right)\\ +\inf I_Y\left(x_i,t_l\right)\times \inf I_Z\left(x_i,t_l\right)+\sup I_Y\left(x_i,t_l\right)\times \sup I_Z\left(x_i,t_l\right)\\ +\inf F_Y\left(x_i,t_l\right)\times \inf F_Z\left(x_i,t_l\right)+\sup F_Y\left(x_i,t_l\right)\times \sup F_Z\left(x_i,t_l\right)\end{array}\right]}}\\ T\left(Y\right)=\frac{1}{k}{\displaystyle \sum _{l=1}^k{\displaystyle \sum _{i=1}^{n}T\left(Y\left(x_i,t_l\right)\right)}}\\ =\frac{1}{k}{\displaystyle \sum _{l=1}^k{\displaystyle \sum _{i=1}^n\frac{1}{2}\left[\begin{array}{l}{\left(\inf T_Y\left(x_i,t_l\right)\right)}^2+{\left(\sup T_Y\left(x_i,t_l\right)\right)}^2+{\left(\inf I_Y\left(x_i,t_l\right)\right)}^2+{\left(\sup I_Y\left(x_i,t_l\right)\right)}^2\\ +{\left(\inf F_Y\left(x_i,t_l\right)\right)}^2+{\left(\sup F_Y\left(x_i,t_l\right)\right)}^2\end{array}\right]}}\\ T\left(Z\right)=\frac{1}{k}{\displaystyle \sum _{l=1}^k{\displaystyle \sum _{i=1}^{n}T\left(Z\left(x_i,t_l\right)\right)}}\\ =\frac{1}{k}{\displaystyle \sum _{l=1}^k{\displaystyle \sum _{i=1}^n\frac{1}{2}\left[\begin{array}{l}{\left(\inf T_Z\left(x_i,t_l\right)\right)}^2+{\left(\sup T_Z\left(x_i,t_l\right)\right)}^2+{\left(\inf I_Z\left(x_i,t_l\right)\right)}^2+{\left(\sup I_Z\left(x_i,t_l\right)\right)}^2\\ +{\left(\inf F_Z\left(x_i,t_l\right)\right)}^2+{\left(\sup F_Z\left(x_i,t_l\right)\right)}^2\end{array}\right]}}\end{array}$$

Theorem 1.

The correlation coefficient$K$between$Y$and$Z$satisfies the follow properties:

(i)

$0\le K\left(Y,Z\right)\le 1$

(ii)

$K\left(Y,Z\right)=K\left(Z,Y\right)$

(iii)

$K\left(Y,Z\right)=1\iff Y=Z$

Proof. 

(i) for any $i=1,2,3,\dots ,n$, the values of $\left[\inf T_Y\left(x_i,t_l\right),\sup T_Y\left(x_i,t_l\right)\right]$; $\left[\inf I_Y\left(x_i,t_l\right),\sup I_Y\left(x_i,t_l\right)\right]$; $\left[\inf F_Y\left(x_i,t_l\right),\sup F_Y\left(x_i,t_l\right)\right]$; $\left[\inf T_Z\left(x_i,t_l\right),\sup T_Z\left(x_i,t_l\right)\right]$; $\left[\inf I_Z\left(x_i,t_l\right),\sup I_Z\left(x_i,t_l\right)\right]$;$\left[\inf F_Z\left(x_i,t_l\right),\sup F_Z\left(x_i,t_l\right)\right]\subseteq \left[0,1\right]$ exist for any $i=1,2,3,\dots ,n$. Thus, it is hold that $C\left(Y,Z\right)\ge 0;T\left(Y\right)\ge 0;T\left(Z\right)\ge 0$. Therefore

$$K\left(Y,Z\right)=\frac{C\left(Y,Z\right)}{max\left(T\left(Y\right),T\left(Z\right)\right)}\ge 0$$

and according to the Cauchy–Schwarz inequality, it holds that:

$$K\left(Y,Z\right)=\frac{C\left(Y,Z\right)}{max\left(T\left(Y\right),T\left(Z\right)\right)}\le 1$$

Therefore, $0\le K\left(Y,Z\right)\le 1$.

(ii) It is obvious that if $Y\left(t\right)=Z\left(t\right)$, $\forall l\in \left\{1,2,\dots ,k\right\}$. We have:

$\inf T_Y^{}\left(x_i,t_l\right)=\inf T_Z^{}\left(x_i,t_l\right)$; $\sup T_Y^{}\left(x_i,t_l\right)=\sup T_Z^{}\left(x_i,t_l\right)$; $\inf I_Y^{}\left(x_i,t_l\right)=\inf I_Z^{}\left(x_i,t_l\right)$; $\sup I_Y^{}\left(x_i,t_l\right)=\sup I_Z^{}\left(x_i,t_l\right)$; $\inf F_Y^{}\left(x_i,t_l\right)=\inf F_Z^{}\left(x_i,t_l\right)$; $\sup F_Y^{}\left(x_i,t_l\right)=\sup F_Z^{}\left(x_i,t_l\right)$;

Thus, $K\left(Y,Z\right)=K\left(Z,Y\right)$. Theorem 1 is proved.

(iii) It is easily observed. □

3.2. Distance Measures for Dynamic Interval-Valued Neutrosophic Sets

In this section, we present the definitions of the Hamming and Euclidean distances between DIVNEs and distance of two dynamic interval-valued neutrosophic matrices.

Definition 4.

Let$n_1$and$n_2$be two DIVNEs. The dynamic interval-valued neutrosophic distance between$n_1$and$n_2$ is determined as follows:

(i) 

The Hamming distance:

$$d_1\left(n_1,n_2\right)=\frac{1}{6\times k}{\displaystyle \sum _{l=1}^k\left(\begin{array}{l}\left|T_{n_1}^L\left(t_l\right)-T_{n_2}^L\left(t_l\right)\right|+\left|T_{n_1}^U\left(t_l\right)-T_{n_2}^U\left(t_l\right)\right|+\left|I_{n_1}^L\left(t_l\right)-I_{n_2}^L\left(t_l\right)\right|\\ +\left|I_{n_1}^U\left(t_l\right)-I_{n_2}^U\left(t_l\right)\right|+\left|F_{n_1}^L\left(t_l\right)-F_{n_2}^L\left(t_l\right)\right|+\left|F_{n_1}^U\left(t_l\right)-F_{n_2}^U\left(t_l\right)\right|\end{array}\right)}$$

(4)

(ii) 

The Euclidean distance:

$$d_2\left(n_1,n_2\right)=\sqrt{\frac{1}{6\times k}{\displaystyle \sum _{l=1}^k\left(\begin{array}{l}{\left(T_{n_1}^L\left(t_l\right)-T_{n_2}^L\left(t_l\right)\right)}^2+{\left(T_{n_1}^U\left(t_l\right)-T_{n_2}^U\left(t_l\right)\right)}^2+{\left(I_{n_1}^L\left(t_l\right)-I_{n_2}^L\left(t_l\right)\right)}^2\\ +{\left(I_{n_1}^L\left(t_l\right)-I_{n_2}^L\left(t_l\right)\right)}^2+{\left(F_{n_1}^L\left(t_l\right)-F_{n_2}^L\left(t_l\right)\right)}^2+{\left(F_{n_1}^U\left(t_l\right)-F_{n_2}^U\left(t_l\right)\right)}^2\end{array}\right)}}$$

(5)

(iii) 

The geometry distance:

$$d_3\left(n_1,n_2\right)={\left(\frac{1}{6\times k}{\displaystyle \sum _{l=1}^k}\left(\begin{array}{l}{\left(T_{n_1}^L\left(t_l\right)-T_{n_2}^L\left(t_l\right)\right)}^{\alpha }+{\left(T_{n_1}^U\left(t_l\right)-T_{n_2}^U\left(t_l\right)\right)}^{\alpha }+{\left(I_{n_1}^L\left(t_l\right)-I_{n_2}^L\left(t_l\right)\right)}^{\alpha }\\ +{\left(I_{n_1}^L\left(t_l\right)-I_{n_2}^L\left(t_l\right)\right)}^{\alpha }+{\left(F_{n_1}^L\left(t_l\right)-F_{n_2}^L\left(t_l\right)\right)}^{\alpha }+{\left(F_{n_1}^U\left(t_l\right)-F_{n_2}^U\left(t_l\right)\right)}^{\alpha }\end{array}\right)\right)}^{\frac{1}{\alpha }}$$

(6)

where$\alpha >0$and

• If$\alpha =1$, then equation (6) refers to the Hamming distance.
• If$\alpha =2$, then equation (6) refers to the Euclidean distance.

Therefore, the distance in Equation (6) is a generalization of distances in Equation (5) and Equation (4).

Definition 5.

Given two dynamic interval-valued neutrosophic matrices$A_1={\left[\alpha \left(t_l\right)\right]}_{h\times n}$and$A_2={\left[\beta \left(t_l\right)\right]}_{h\times n}$, the elements of both$A_1$and$A_2$are described by DIVNS. After that the distance between$A_1$and$A_2$ is defined by:

$$d\left(A_1,A_2\right)=\frac{1}{hn}{\displaystyle \sum _p^n{\displaystyle \sum _q^{h}d\left({\alpha }_{qp},{\beta }_{qp}\right)}}$$

(7)

where $d\left({\alpha }_{qp},{\beta }_{qp}\right)$ is the distance between two DIVNEs.

3.3. Unknown Weight Information in Dynamic Neutrosophic Environment

3.3.1. Determining the Weight of Time

It is common knowledge that the weights of time periods have an important role in MCDM problems practical application. In the followings, we present how to determine the weights of time periods in dynamic neutrosophic environments.

Definition 6.

Given a basic unit-interval monotonic (BUM) function$g:[0,1]\to [0,1]$, the time weight can be determined as follows:

$$\lambda \left(t_l\right)=g\left(\frac{R_l}{TV}\right)-g\left(\frac{R_{l-1}}{TV}\right),$$

(8)

where$R_l={\displaystyle \sum _{j=1}^l{V}_j};TV={\displaystyle \sum _{i=1}^k{V}_i};V_i=1+T\left(M{D}_i\right)$;$T\left(M{D}_i\right)$denotes the support of$i^{th}$largest argument by all the other arguments:

$$T\left(M{D}_i\right)={\displaystyle \sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^{k}Sup\left(M{D}_i,M{D}_j\right)}$$

$$\begin{array}{l}sup\left(M{D}_i,M{D}_j\right)=1-d\left(M{D}_i,M{D}_j\right)\\ =1-\frac{1}{hn}{\displaystyle \sum _q^h{\displaystyle \sum _{p=1}^n}}\sqrt{\frac{1}{6}\left(\begin{array}{l}{\left(T^L\left(x_{pq}^i\right)-T^L\left(x_{pq}^j\right)\right)}^2+{\left(T^U\left(x_{pq}^i\right)-T^U\left(x_{pq}^j\right)\right)}^2+{\left(I^L\left(x_{pq}^i\right)-I^L\left(x_{pq}^j\right)\right)}^2+\\ {\left(I^U\left(x_{pq}^i\right)-I^U\left(x_{pq}^j\right)\right)}^2+{\left(F^L\left(x_{pq}^i\right)-F^L\left(x_{pq}^j\right)\right)}^2+{\left(F^U\left(x_{pq}^i\right)-F^U\left(x_{pq}^j\right)\right)}^2\end{array}\right)}\end{array}$$

(9)

3.3.2. Determining the Weights of Decision-Makers

The weights of DMs play a critical role in MCDM problems. In this section, we present how to determine the weights of DMs in dynamic neutrosophic environment.

Definition 7.

Let$D_1={\left[\alpha \left(t_l\right)\right]}_{v\times n}$and$D_2={\left[\beta \left(t_l\right)\right]}_{v\times n}$be two dynamic interval-valued neutrosophic matrices, in which the elements of both$D_1$and$D_2$are expressed by DIVNS. Then the correlation coefficient between$D_1$and$D_2$is defined by:

$$C\left(D_1,D_2\right)=\frac{1}{nv}{\displaystyle \sum _p^n{\displaystyle \sum _m^{v}K\left({\alpha }_{mp},{\beta }_{mp}\right)}}$$

(10)

where$K\left({\alpha }_{mp},{\beta }_{mp}\right)$is correlation coefficient measure between two DIVNEs.

Theorem 2.

For two Dynamic interval-valued neutrosophic matrices$D_1={\left[\alpha \left(t_l\right)\right]}_{v\times n}$and$D_2={\left[\beta \left(t_l\right)\right]}_{v\times n}$where the elements of both$D_1$and$D_2$are expressed by DIVNSs,$C\left(D_1,D_2\right)$satisfies the three conditions:

(i) 

$0\le C\left(D_1,D_2\right)\le 1$

(ii) 

$C\left(D_1,D_2\right)=C\left(D_2,D_1\right)$

(iii) 

$D_1=D_2$if and only if$C\left(D_1,D_2\right)=1$

Proof. 

(i) According to Theorem 1, we have $0\le K\left({\alpha }_{mp},{\beta }_{mp}\right)\le 1$; $m=1,2,3,\dots ,v;p=1,2,3,\dots ,n$, Thus,

$$0\le \frac{1}{nv}{\displaystyle \sum _p^n{\displaystyle \sum _m^{v}K\left({\alpha }_{mp},{\beta }_{mp}\right)}}\le 1$$

(ii) According to Definition 3 and Theorem 1 it is easily observed.

(iii) According to Theorem 1 we obtain $C\left(D_1,D_2\right)=1\iff D_1=D_2$

Thus, Theorem 2 is proved. □

Definition 8.

For the decision-maker$D_q$, the weights of decision-makers can be defined as follows:

$${\omega }_q=\frac{{\delta }_q}{{\displaystyle \sum _{q=1}^h{\delta }_q}}$$

(11)

where${\delta }_q$has the form:

$${\delta }_q={\displaystyle \sum _{\begin{array}{l}{q}^{\prime }=1;\\ q^{\prime }\ne q\end{array}}^{h}C\left(D_q,D_{q^{\prime }}\right)}$$

(12)

$C\left(D_q,D_{q^{\prime }}\right)$is the correlation coefficient between two decision-makers$q$ and $q^{\prime }$.

3.3.3. Determining the Weights of the Criteria

In real life applications, the attribute information may be completely unknown. Thus, we need to develop an integrated programming model for MCDM problems under the dynamic neutrosophic environment.

Definition 9.

Let$C_p$be the$p^{th}$criterion and$A_m$be the$m^{th}$alternative, the deviation value between$A_m$and all the other alternatives in dynamic neutrosophic environment can be calculated as:

$$O_{mp}\left(w\right)={\displaystyle \sum _{\begin{array}{l}k=1;\\ k\ne i\end{array}}^{v}d\left(n_{mp},n_{kp}\right)}{w}_p$$

(13)

where$w_p$is weight of the$p^{th}$criterion.$d\left(n_{mp},n_{kp}\right)$is the distance between two DIVNEs.

Definition 10.

The deviation among all the alternatives to the others can be computed by the global deviation function as follows:

$$\begin{array}{c}{O}_p\left(w\right)={\displaystyle \sum _{m=1}^v{O}_{mp}\left(w\right)}={\displaystyle \sum _{m=1}^v{\displaystyle \sum _{\begin{array}{l}k=1;\\ k\ne m\end{array}}^{v}d\left(n_{mp},n_{kp}\right)}}{w}_p\\ \mathrm{s}.\mathrm{t}.{\displaystyle \sum _{p=1}^n{w}_p}=1;w_{p\ge 0};\end{array}$$

(14)

By using the deviation degree between evaluations [33], the criteria weights can be calculated. Then, we construct optimization decision making model with the purpose of maximizing the decision space in the following:

$$\max O\left(w\right)={\displaystyle \sum _{p=1}^n{O}_p\left(w\right)}={\displaystyle \sum _{p=1}^n{\displaystyle \sum _{m=1}^v{\displaystyle \sum _{\begin{array}{l}k=1;\\ k\ne m\end{array}}^{v}d\left(n_{mp},n_{kp}\right)}}{w}_p^{\ast }}\to \max$$

(15)

where $d\left(n_{mp},n_{kp}\right)$ is the distance between two elements. The optimization model can be solved based on the Lagrange function. Let $\xi$ be the Lagrange multiplier. We have:

$$\begin{gathered} L\left(w_p^{\ast },\xi \right)=O\left(w\right)-\frac{1}{2}\xi \left({\displaystyle \sum _{p=1}^n{\left(w_p^{\ast }\right)}^2-1}\right) \\ L\left(w_p^{\ast },\xi \right)={\displaystyle \sum _{p=1}^n{\displaystyle \sum _{m=1}^v{\displaystyle \sum _{\begin{array}{l}k=1;\\ k\ne m\end{array}}^{v}d\left(n_{mp},n_{kp}\right)}}{w}_p^{\ast }}-\frac{1}{2}\xi \left({\displaystyle \sum _{p=1}^n{\left(w_p^{\ast }\right)}^2-1}\right) \\ \{\begin{array}{l}\frac{\partial L}{\partial w_p}={\displaystyle \sum _{m=1}^v{\displaystyle \sum _{\begin{array}{l}k=1;\\ k\ne m\end{array}}^{v}d\left(n_{mp},n_{kp}\right)}}-\xi w_p^{\ast }=0\\ \frac{\partial L}{\partial \xi }=\frac{1}{2}\left({\displaystyle \sum _{p=1}^n{\left(w_p^{\ast }\right)}^2-1}\right)=0\end{array}\Rightarrow w_p^{\ast }=\frac{{\displaystyle \sum _{m=1}^v{\displaystyle \sum _{\begin{array}{l}k=1;\\ k\ne m\end{array}}^{v}d\left(n_{mp},n_{kp}\right)}}}{\xi } \end{gathered}$$

Since ${\displaystyle \sum _{m=p}^n{\left(w_p^{\ast }\right)}^2=1}$, the value of $\xi$ can be calculated as follows:

$${\displaystyle \sum _{p=1}^n{\left(\frac{{\displaystyle \sum _{m=1}^v{\displaystyle \sum _{\begin{array}{l}k=1;\\ k\ne m\end{array}}^{v}d\left(n_{mp},n_{kp}\right)}}}{\xi }\right)}^2}=1,\mathrm{thus},\xi =\sqrt{{\displaystyle \sum _{p=1}^n{\left[{\displaystyle \sum _{m=1}^v{\displaystyle \sum _{\begin{array}{l}k=1;\\ k\ne m\end{array}}^{v}d\left(n_{mp},n_{kp}\right)}}\right]}^2}}$$

From the above equations, a formula to calculate the criteria weights can be obtained as follows:

$$w_p^{\ast }=\frac{{\displaystyle \sum _{m=1}^v{\displaystyle \sum _{\begin{array}{l}k=1;\\ k\ne m\end{array}}^{v}d\left(n_{mp},n_{kp}\right)}}}{\sqrt{{\displaystyle \sum _{p=1}^n{\left[{\displaystyle \sum _{m=1}^v{\displaystyle \sum _{\begin{array}{l}k=1;\\ k\ne m\end{array}}^{v}d\left(n_{mp},n_{kp}\right)}}\right]}^2}}}$$

(16)

3.4. TOPSIS Method with Unknown Weight Information in Dynamic Neutrosophic Environments

In this section, we develop a MCDM approach based on the TOPSIS model with unknown weight information in dynamic neutrosophic environments. The scheme of the proposed MCDM technique is given in Figure 1. The detailed method is constructed as follows:

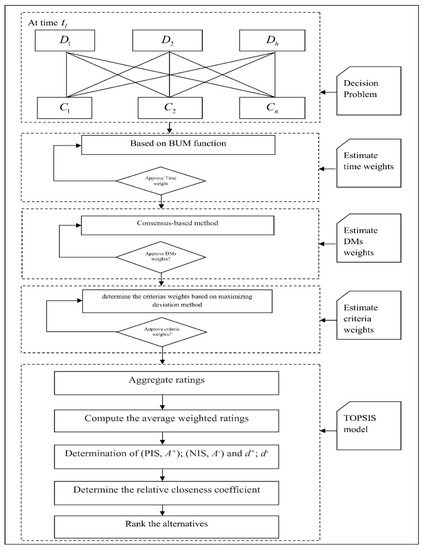
Figure 1. TOPSIS method with unknown weight information.

Step 1. Construct the dynamic interval-valued neutrosophic decision matrix as MCDM problems expressed in Section 2.2.

Step 2. Using Equation (8) to determine the time weights $\lambda =\left({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_k\right)$ of $k$ time sequence:

$$g\left(x\right)=\frac{e^{\alpha x}-1}{e^{\alpha }-1}$$

(17)

Step 3. Using Equations (10)–(12) to determine the DMs’ weights $\omega =\left({\omega }_1,{\omega }_2,\dots ,{\omega }_h\right)$ of $h$ decision-makers.

Step 4. I the criteria weight information is completely unknown, we determine the criteria weights $w={\left(w_1,w_2,\dots ,w_n\right)}^T$ of $n$ criteria by using Equation (16), otherwise go to Step 5.

Step 5. Suppose $W={\left[\psi \left(t_l\right)\right]}_{p\times q};p=1,2,3,\dots ,n;q=1,2,3,\dots ,h;l=1,2,3,\dots ,k$ be dynamic interval-valued neutrosophic matrix of important criteria weights. ${\psi }_{pq}\left(t_l\right)$ is the weight of decision-maker $q^{th}$ to criterion $p^{th}$ in time sequence $t_l$. The criteria weights $w={\left(w_1,w_2,\dots ,w_n\right)}^T$ can be calculated by:

$$w_p=⟨\begin{array}{l}\left[⟨1-{\left\{1-{\left(1-{\displaystyle \sum _{q=1}^h{T}_{pq}^L\left({\psi }_{t_l}\right)}\right)}^{\frac{1}{h}}\right\}}^{\frac{1}{k}}⟩,⟨1-{\left\{1-{\left(1-{\displaystyle \sum _{q=1}^h{T}_{pq}^U\left({\psi }_{t_l}\right)}\right)}^{\frac{1}{h}}\right\}}^{\frac{1}{k}}⟩\right],\\ \left[{\left({\displaystyle \sum _{q=1}^h{I}_{pq}^L\left({\psi }_{t_l}\right)}\right)}^{\frac{1}{h\ast k}},{\left({\displaystyle \sum _{q=1}^h{I}_{pq}^U\left({\psi }_{t_l}\right)}\right)}^{\frac{1}{h\ast k}}\right],\left[{\left({\displaystyle \sum _{q=1}^h{F}_{pq}^L\left({\psi }_{t_l}\right)}\right)}^{\frac{1}{h\ast k}},{\left({\displaystyle \sum _{q=1}^h{F}_{pq}^U\left({\psi }_{t_l}\right)}\right)}^{\frac{1}{h\ast k}}\right]\end{array}⟩$$

(18)

Step 6. The aggregate ratings of alternative $m$ and criteria $p$ can be estimated as:

$$x_{mp}=\frac{1}{h\ast k}\otimes ⟨\begin{array}{l}\left[⟨1-{\left\{1-{\left(1-{\displaystyle \sum _{q=1}^h{T}_{pmq}^L\left(x_{t_l}\right)}\right)}^{\frac{1}{h}}\right\}}^{\frac{1}{k}}⟩,⟨1-{\left\{1-{\left(1-{\displaystyle \sum _{q=1}^h{T}_{pmq}^U\left(x_{t_l}\right)}\right)}^{\frac{1}{h}}\right\}}^{\frac{1}{k}}⟩\right]\\ \left[{\left({\displaystyle \sum _{q=1}^h{I}_{pmq}^L\left(x_{t_l}\right)}\right)}^{\frac{1}{h\ast k}},{\left({\displaystyle \sum _{q=1}^h{I}_{pmq}^U\left(x_{t_l}\right)}\right)}^{\frac{1}{h\ast k}}\right],\overline{F_{mp}\left(x\right)}=\left[{\left({\displaystyle \sum _{q=1}^h{F}_{pmq}^L\left(x_{t_l}\right)}\right)}^{\frac{1}{h\ast k}},{\left({\displaystyle \sum _{q=1}^h{F}_{pmq}^U\left(x_{t_l}\right)}\right)}^{\frac{1}{h\ast k}}\right]\end{array}⟩,$$

(19)

Step 7: Average weighted ratings of alternatives can be calculated as follows:

Case 1: If the information about the criteria weights is known, the criteria weights is a collection of DIVNEs and the average weighted ratings of alternatives in $t_l,$ calculated by:

$$G_m=\frac{1}{p}{\displaystyle \sum _{p=1}^n\begin{array}{l}\left(⟨\begin{array}{l}\left[T_{{}_{mp}}^L\left(x\right)\times T_{{}_p}^L\left(w\right),T_{{}_{mp}}^U\left(x\right)\times T_{{}_p}^U\left(w\right)\right],\\ \left[I_{{}_{mp}}^L\left(x\right)+I_{{}_p}^L\left(w\right)-I_{{}_{mp}}^L\left(x\right)\times I_{{}_p}^L\left(w\right),I_{{}_{mp}}^U\left(x\right)+I_{{}_p}^U\left(w\right)-I_{{}_{mp}}^U\left(x\right)\times I_{{}_p}^U\left(w\right)\right],\\ \left[F_{{}_{mp}}^L\left(x\right)+F_{{}_p}^L\left(w\right)-F_{{}_{mp}}^L\left(x\right)\times F_{{}_p}^L\left(w\right),F_{{}_{mp}}^U\left(x\right)+F_{{}_p}^U\left(w\right)-F_{{}_{mp}}^U\left(x\right)\times F_{{}_p}^U\left(w\right)\right]\end{array}⟩\right);\\ m=1,2,3,\dots ,v;p=1,2,3,\dots ,n;\end{array}}$$

(20)

Case 2: If the information about the criteria weights is unknown, the criteria weights is a collection of DIVNEs and average weighted ratings of alternatives in $t_l,$ calculated by:

$$G_m=\frac{1}{p}{\displaystyle \sum _{p=1}^n\begin{array}{l}\left(⟨\begin{array}{l}\left[1-{\left(1-T_{{}_{mp}}^L\left(x\right)\right)}^{w_p},1-{\left(1-T_{{}_{mp}}^U\left(x\right)\right)}^{w_p}\right],\\ \left[{\left(I_{{}_{mp}}^L\left(x\right)\right)}^{w_p},{\left(I_{{}_{mp}}^U\left(x\right)\right)}^{w_p}\right],\left[{\left(F_{{}_{mp}}^L\left(x\right)\right)}^{w_p},{\left(F_{{}_{mp}}^U\left(x\right)\right)}^{w_p}\right]\end{array}⟩\right);\\ m=1,2,3,\dots ,v;p=1,2,3,\dots ,n;\end{array}}$$

(21)

Step 8: Determine the interval neutrosophic positive ideal solution (PIS, $A^{+}$) and the interval neutrosophic negative ideal solution (NIS, $A^{-}$):

$$A^{+}=\left\{x,\left(\left[1,1\right],\left[0,0\right],\left[0,0\right]\right)\right\}$$

(22)

$$A^{-}=\left\{x,\left(\left[0,0\right],\left[1,1\right],\left[1,1\right]\right)\right\}$$

(23)

Step 9: Compute the distance of alternatives.

The distances of each alternative in time sequence $t_l,$ are calculated:

$$d_m^{+}=\sqrt{{\left(G_m-A^{+}\right)}^2}$$

(24)

$$d_m^{-}=\sqrt{{\left(G_m-A^{-}\right)}^2}$$

(25)

where $d_m^{+}$ and $d_m^{-}$ represent the shortest and farthest distances of alternative $A_m.$

Step 10: Determine the relative closeness coefficient.

The closeness coefficient values are calculated below:

$$C{C}_m=\frac{d_m^{-}}{d_m^{+}+d_m^{-}}$$

(26)

Step 11: Rank the alternatives based on the relative closeness coefficients.

4. Experiments

This section applies the proposed method with dataset in [17] to evaluate lecturers’ performances from ULIS, Vietnam National University, Hanoi, Vietnam. The hierarchical structure of the constructed multi-criteria decision-making problem is depicted in Figure 2 for the dataset.

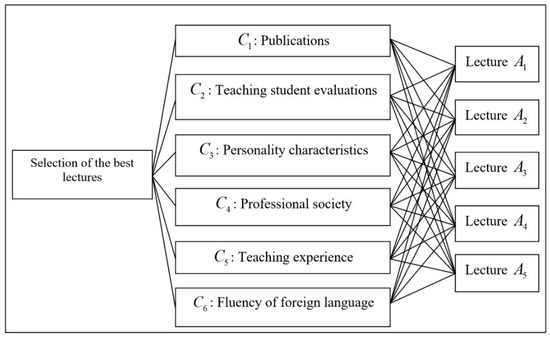
Figure 2. Evaluation lecturer’s performance problem.

According to the language labels in Table 1 below, the rating of lectures through criteria sets are done by decision-makers.

Table 1. Language variables.

Language Labels	Short Labels	Values
Very-Poor	Vr	([0.1, 0.2], [0.6, 0.7], [0.7, 0.8])
Poor	Pr	([0.2, 0.3], [0.5, 0.6], [0.6, 0.7])
Medium	Mm	([0.3, 0.5], [0.4, 0.6], [0.4, 0.5])
Good	Gd	([0.5, 0.6], [0.4, 0.5], [0.3, 0.4])
Very-Good	Vd	([0.6, 0.7], [0.2, 0.3], [0.2, 0.3])

Step 1: Dynamic interval-valued neutrosophic decision matrix shown in Table 2.

Table 2. Dynamic interval-valued neutrosophic decision matrix.

Criteria	Lecturers	Decision Makers
		t1			t2			t3
		${\mathit{D}}_1$	${\mathit{D}}_2$	${\mathit{D}}_3$	${\mathit{D}}_1$	${\mathit{D}}_2$	${\mathit{D}}_3$	${\mathit{D}}_1$	${\mathit{D}}_2$	${\mathit{D}}_3$
C1	A1	Mm	Gd	Gd	Gd	Gd	Gd	Gd	Vd	Gd
	A2	Gd	Gd	Vd	Vd	Gd	Vd	Vd	Gd	Vd
	A3	Mm	Gd	Gd	Gd	Gd	Gd	Gd	Gd	Vd
	A4	Go	Mm	Gd	Gd	Gd	Gd	Gd	Gd	Gd
	A5	Mm	Gd	Mm	Go	Go	Mm	Gd	Gd	Gd
C2	A1	Gd	Gd	Gd	Vd	Gd	Gd	Gd	Gd	Gd
	A2	Vd	Gd	Vd	Mm	Gd	Gd	Vd	Gd	Gd
	A3	Vd	Gd	Gd	Gd	Mm	Gd	Gd	Mm	Gd
	A4	Gd	Gd	Gd	Gd	Vd	Gd	Gd	Gd	Vd
	A5	Vd	Gd	Gd	Gd	Vd	Gd	Gd	Gd	Mm
C3	A1	Vd	Vd	Gd	Gd	Vd	Gd	Gd	Mm	Gd
	A2	Gd	Vd	Gd	Vd	Gd	Vd	Gd	Gd	Vd
	A3	Gd	Vd	Vd	Gd	Gd	Gd	Gd	Vd	Gd
	A4	Gd	Gd	Gd	Vd	Gd	Gd	Vd	Gd	Gd
	A5	Vd	Gd	Gd	Gd	Vd	Gd	Gd	Gd	Gd
C4	A1	Mm	Gd	Mm	Gd	Gd	Mm	Mm	Gd	Mm
	A2	Gd	Mm	Gd	Gd	Mm	Gd	Gd	Mm	Gd
	A3	Gd	Gd	Gd	Gd	Gd	Mm	Gd	Gd	Vd
	A4	Mm	Poo	Mm	Gd	Mm	Mm	Gd	Gd	Mm
	A5	Mm	Mm	Poo	Mm	Mm	Mm	Mm	Gd	Mm
C5	A1	Mm	Gd	Mm	Mm	Gd	Gd	Gd	Mm	Gd
	A2	Gd	Vd	Go	Vd	Gd	Gd	Gd	Vd	Gd
	A3	Gd	Gd	Mm	Gd	Gd	Gd	Gd	Vd	Gd
	A4	Vd	Gd	Gd	Vd	Gd	Gd	Vd	Gd	Gd
	A5	Gd	Gd	Gd	Gd	Gd	Gd	Gd	Vd	Gd
C6	A1	Vd	Gd	Gd	Vd	Gd	Vd	Vd	Gd	Vd
	A2	Gd	Gd	Gd	Gd	Vd	Gd	Gd	Gd	Vd
	A3	Vd	Gd	Vd	Vd	Gd	Vd	Vd	Gd	Vd
	A4	Gd	Vd	Gd	Gd	Vd	Gd	Gd	Gd	Gd
	A5	Gd	Gd	Gd	Vd	Gd	Gd	Gd	Vd	Gd

Step 2: Bases on Equation (8) and BUM function in Equation (17), we receive the weights of the time periods:

$${\lambda }_1=0.280;{\lambda }_2=0.330;{\lambda }_3=0.390$$

Step 3: Using Equations (10)–(12) to calculate weights of the DMs, we receive the weights of the DMs as follows:

$${\omega }_1=0.330;{\omega }_2=0.337;{\omega }_3=0.333$$

Step 4: Based on the basic of maximizing deviation method and Equation (16), we receive the weights of the criteria as follows:

$$w_1=0.160;w_2=0.165;w_3=0.171;w_4=0.166;w_5=0.175;w_6=0.163$$

Step 5: Average weighted ratings are shown in Table 3.

Table 3. Average weighted ratings of lectures.

Lecturers	Weighted Ratings
A1	([0.072, 0.102], [0.871, 0.906], [0.848, 0.883])
A2	([0.083, 0.112], [0.852, 0.889], [0.833, 0.871])
A3	([0.082, 0.110], [0.867, 0.900], [0.842, 0.878])
A4	([0.077, 0.105], [0.867, 0.901], [0.844, 0.880])
A5	([0.073, 0.102], [0.871, 0.907], [0.850, 0.884])

Step 6: Compute the distance of each lecture from (PIS, $A^{+}$) and (NIS, $A^{-}$). The results are shown in Table 4 below.

Table 4. The distance of each lecture.

Lecturers	${\mathit{d}}^{+}$	${\mathit{d}}^{-}$
A1	0.113845	0.889443
A2	0.128101	0.875218
A3	0.120105	0.882727
A4	0.117807	0.885273
A5	0.113326	0.889768

Step 7: Calculate the closeness coefficient for lectures. Table 5 shows the values of the closeness coefficient.

Table 5. The closeness coefficient of lectures.

Lecturers	Proposed Model
A1	0.11355
A2	0.12778
A3	0.11983
A4	0.11752
A5	0.11301

Step 8: Rank the lectures based on the values of the closeness coefficients.

Table 5 shows the ranking order is $A_2\succ A_3\succ A_4\succ A_1\succ A_5$ and $A_2$ is the best lecture.

5. Comparison with the Related Methods

In this section, we compare the proposed method with those in Thong et al. [17] and Peng [29] to demonstrate the advantages for unknown weight information in dynamic neutrosophic environments. Data used to prove the performance of the method are in [17]. Table 6 shows that the rankings of lectures by Thong et al. [17] as $A_2\succ A_3\succ A_4\succ A_1\succ A_5$ and Peng [29] as $A_2\succ A_3\succ A_1\succ A_4\succ A_5$. Thus, $A_2$ is still the best option. These results are the same as our proposed method. However, the proposed method can be solved with unknown weight information in a dynamic neutrosophic environment. Moreover, it is more generalized and flexible than Thong et al. [17]’s method with unknown weight information in a dynamic neutrosophic environment.

Table 6. A comparison study with some existing methods.

Methods	Ranking Values					Ranking Order
	${\mathit{A}}_1$	${\mathit{A}}_2$	${\mathit{A}}_3$	${\mathit{A}}_4$	${\mathit{A}}_5$
Proposed method	0.11355	0.12778	0.11983	0.11752	0.11301	$A_2\succ A_3\succ A_4\succ A_1\succ A_5$
Thong et al. [17] (Topsis Model)	0.33916	0.36694	0.35124	0.34526	0.33778	$A_2\succ A_3\succ A_4\succ A_1\succ A_5$
Peng [29] (Similarity measure)	0.92735	0.94145	0.92949	0.90850	0.89896	$A_2\succ A_3\succ A_1\succ A_4\succ A_5$

6. Conclusions

In this paper, we proposed a novel approach to solve MCDM problems in dynamic neutrosophic environments where all the information supplied by the DMs is described as interval-valued neutrosophic sets and the information about the weight of attributes, DMs, and time may be incompletely known. A new concept related to the correlation measure and some distance measures for dynamic interval-valued neutrosophic sets are defined. Then, we have proposed an extended TOPSIS method to solve MCDM problems, are is expressed with the interval-valued neutrosophic setting in dynamic neutrosophic environments. Finally, the effectiveness of the proposed method has been demonstrated with the purpose of evaluating lecturers’ performance in ULIS, Vietnam National University, Hanoi, Vietnam. We considered in this situation that all the weight information about the criteria, DMs, and time is expressed with various conditions is unknown.

Since the proposed method has not demonstrated its practicality and effectiveness with more real applications and the weight information about the criteria and DMs that change over time is not mentioned in our method, in the future, we will conduct further studies to handle unknown weight information in which the criteria and DMs vary with time periods and with more real decision-making data.