Asymptotic Approximations of Ratio Moments Based on Dependent Sequences
Abstract
1. Introduction
1.1. Inverse Moment Models and Ratio Models
1.2. Definitions of WOD and m-WOD
1.3. Our Models
2. Results
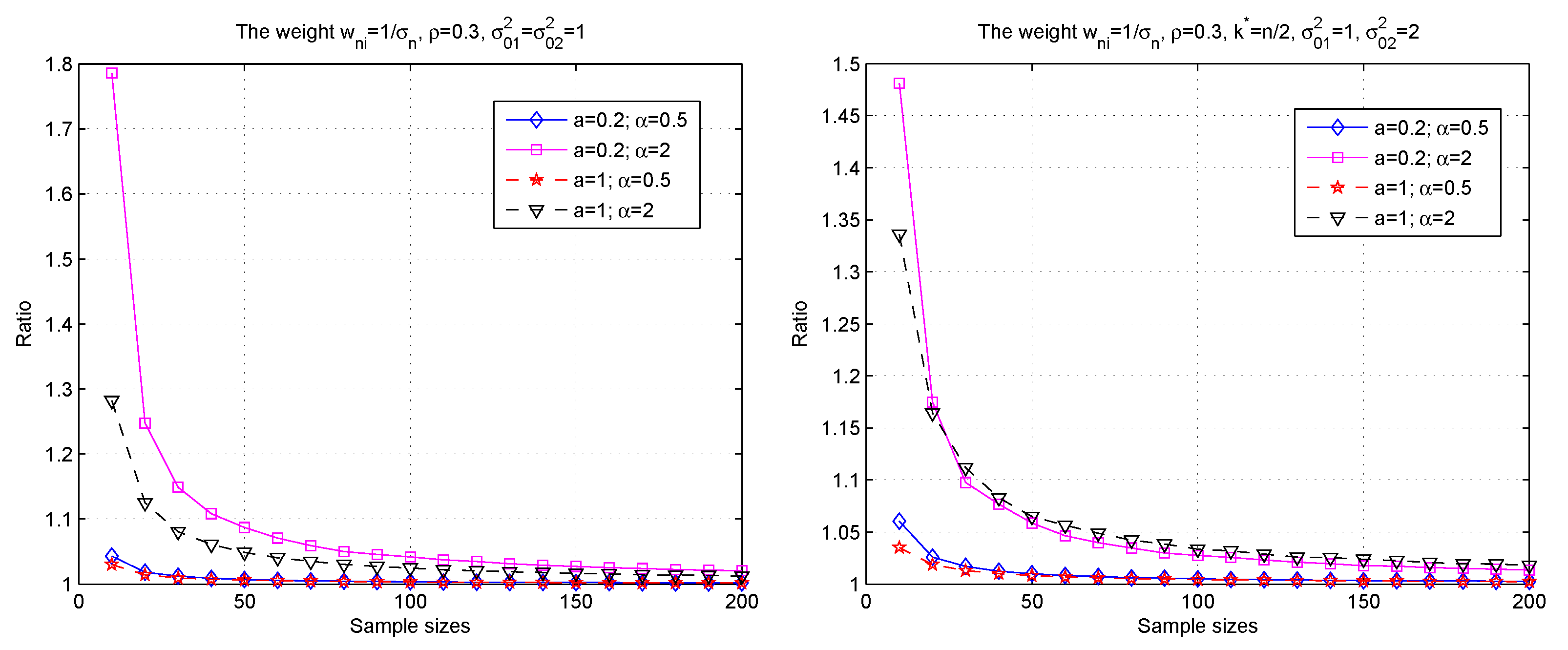
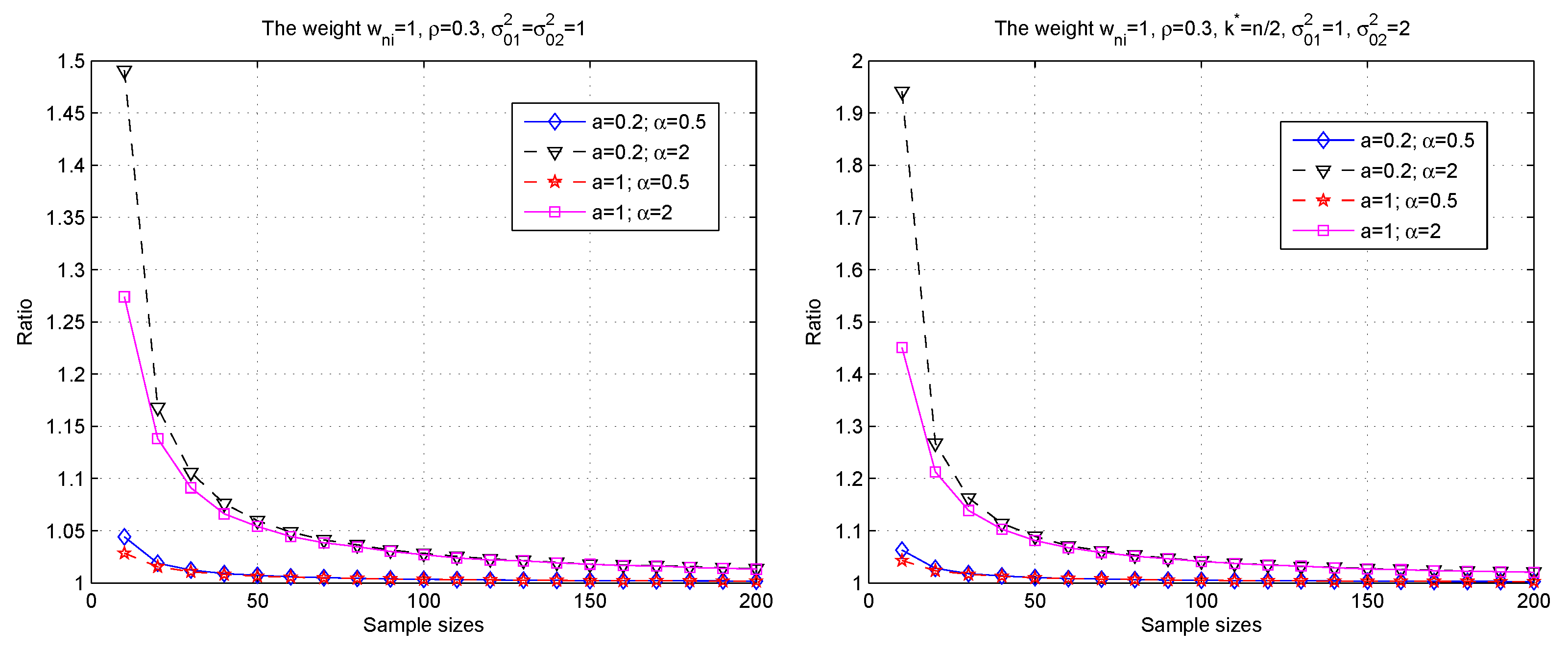
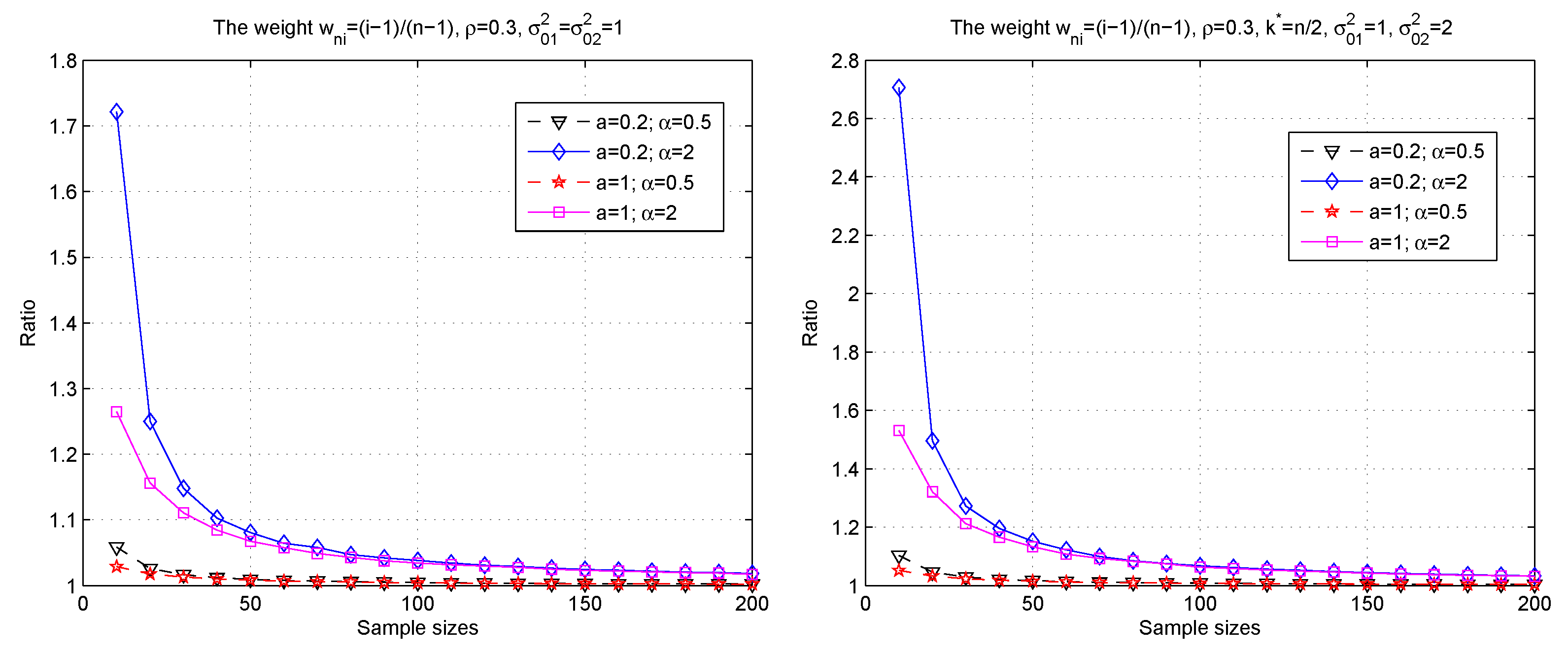
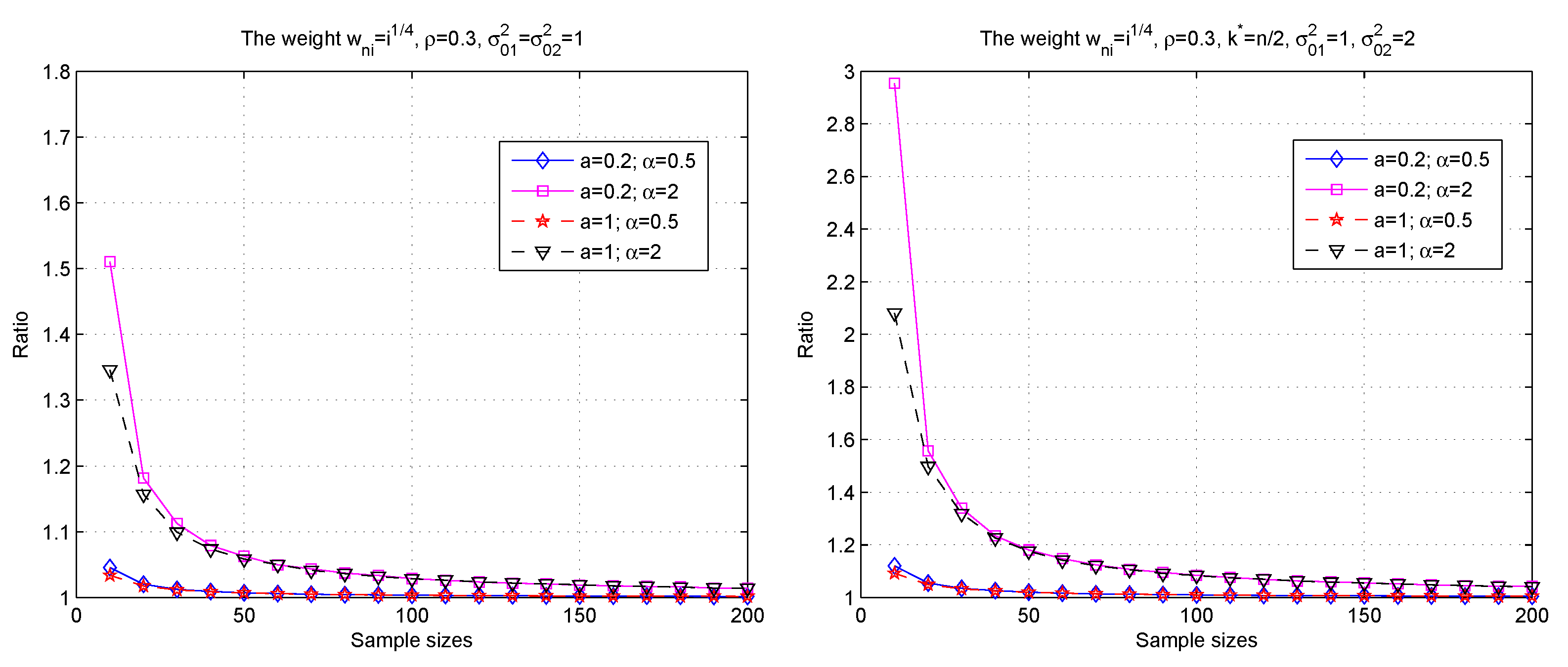
3. Simulations
4. Conclusions
5. Proofs of Main Results
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, T.J.; Shi, X.P.; Miao, B.Q. Asymptotic approximation of inverse moments of nonnegative random variables. Statist. Probab. Lett. 2009, 79, 1366–1371. [Google Scholar] [CrossRef]
- Garcia, N.L.; Palacios, J.L. On inverse moments of nonnegative random variables. Statist. Probab. Lett. 2001, 53, 235–239. [Google Scholar] [CrossRef]
- Kaluszka, M.; Okolewski, A. On Fatou-type lemma for monotone moments of weakly convergent random variables. Statist. Probab. Lett. 2004, 66, 45–50. [Google Scholar] [CrossRef]
- Jäntschi, L. Detecting extreme values with order statistics in samples from continuous distributions. Mathematics 2020, 8, 216. [Google Scholar] [CrossRef]
- Wang, X.J.; Hu, S.H.; Yang, W.Z.; Ling, N.X. Exponential inequalities and inverse moment for NOD sequence. Statist. Probab. Lett. 2010, 80, 452–461. [Google Scholar] [CrossRef]
- Sung, S.H. On inverse moments for a class of nonnegative random variables. J. Inequal. Appl. 2010, 2010, 823767. [Google Scholar] [CrossRef][Green Version]
- Xu, M.; Chen, P.Y. On inverse moments for nonnegative NOD sequence. Acta Math. Sin. (Chin. Ser.) 2013, 55, 201–206. [Google Scholar]
- Horng, W.J.; Chen, P.Y.; Hu, T.C. On approximation for inverse moments of nonnegative random variables. J. Math. Stat. Oper. Res. (JMSOR) 2012, 1, 38–42. [Google Scholar] [CrossRef]
- Hu, S.H.; Wang, X.H.; Yang, W.Z.; Wang, X.J. A note on the inverse moment for the nonnegative random variables. Commun. Statist.-Theory Methods 2014, 43, 1750–1757. [Google Scholar] [CrossRef]
- Shi, X.P.; Wu, Y.H.; Liu, Y. A note on asymptotic approximations of inverse moments of nonnegative random variables. Statist. Probab. Lett. 2010, 80, 1260–1264. [Google Scholar] [CrossRef]
- Yang, W.Z.; Hu, S.H.; Wang, X.J. On the asymptotic approximation of inverse moment for nonnegative random variables. Commun. Statist.-Theory Methods 2017, 46, 7787–7797. [Google Scholar] [CrossRef]
- Yang, W.Z.; Shi, X.P.; Li, X.Q.; Hu, S.H. Approximations to inverse moments of double-indexed weighted sums. J. Math. Anal. Appl. 2016, 440, 833–852. [Google Scholar] [CrossRef]
- Li, X.Q.; Liu, X.; Yang, W.Z.; Hu, S.H. The inverse moment for widely orthant dependent random variables. J. Inequal. Appl. 2016, 2016, 161. [Google Scholar] [CrossRef][Green Version]
- Shi, X.P.; Reid, N.; Wu, Y.H. Approximation to the moments of ratios of cumulative sums. Canad. J. Statist. 2014, 42, 325–336. [Google Scholar] [CrossRef]
- Wang, Y.B.; Cheng, D.Y. Basic renewal theorems for random walks with widely dependent increments. J. Math. Anal. Appl. 2011, 384, 597–606. [Google Scholar] [CrossRef]
- Hu, T.C.; Chiang, C.Y.; Taylor, R.L. On complete convergence for arrays of rowwise m-negatively associated random variables. Nonlinear Anal. 2009, 71, e1075–e1081. [Google Scholar] [CrossRef]
- Liu, L. Precise large deviations for dependent random variables with heavy tails. Statist. Probab. Lett. 2009, 79, 1290–1298. [Google Scholar] [CrossRef]
- Lehmann, E.L. Some concepts of dependence. Ann. Math. Stat. 1966, 37, 1137–1153. [Google Scholar] [CrossRef]
- Hu, T.Z. Negatively superadditive dependence of random variables with applications. Chin. J. Appl. Probab. Statist. 2000, 16, 133–144. [Google Scholar]
- Joag-Dev, K.; Proschan, F. Negative association of random variables with applications. Ann. Statist. 1983, 11, 286–295. [Google Scholar] [CrossRef]
- Bulinski, A.V.; Shaskin, A. Limit Theorems for Associated Random Fields and Related Systems; World Scientific: Singapore, 2007; pp. 1–20. [Google Scholar]
- Davidian, M.; Giltinan, D.M. Nonlinear Models for Repeated Measurement Data; Chapman and Hall: New York, NY, USA, 1995; pp. 16–60. [Google Scholar]
- Tomasz, J.; Kozubowskia, T.J.; Podgórski, K.; Rychlik, I. Multivariate generalized Laplace distribution and related random fields. J. Multivar. Anal. 2013, 113, 59–72. [Google Scholar]
- Ko, B.; Tang, Q. Sums of dependent nonnegative random variables with subexponential tails. J. Appl. Probab. 2008, 45, 85–94. [Google Scholar] [CrossRef]
- Yang, W.Z.; Zhao, Z.R.; Wang, X.H.; Hu, S.H. The large deviation results for the nonlinear regression model with dependent errors. TEST 2017, 26, 261–283. [Google Scholar]
- Wang, Y.B.; Cui, Z.L.; Wang, K.Y.; Ma, X.L. Uniform asymptotics of the fnite-time ruin probability for all times. J. Math. Anal. Appl. 2012, 390, 208–223. [Google Scholar] [CrossRef]
- Wang, K.Y.; Wang, Y.B.; Gao, Q.W. Uniform asymptotics of the fnite-time ruin probability of dependent risk model with a constant interest rate. Methodol. Comput. Appl. Probab. 2013, 15, 109–124. [Google Scholar] [CrossRef]
- Wang, X.J.; Xu, C.; Hu, T.C.; Volodin, A.I.; Hu, S.H. On complete convergence for widely orthant-dependent random variables and its applications in nonparametric regression models. TEST 2014, 23, 607–629. [Google Scholar]
- Yang, W.Z.; Liu, T.T.; Wang, X.J.; Hu, S.H. On the Bahadur Representation of sample quantiles for widely orthant dependent sequences. Filomat 2014, 28, 1333–1343. [Google Scholar] [CrossRef]
- Wang, X.J.; Hu, S.H. The consistency of the nearest neighbor estimator of the density function based on WOD samples. J. Math. Anal. Appl. 2015, 429, 497–512. [Google Scholar] [CrossRef]
- Shen, A.T.; Zhang, Y.; Xiao, B.Q.; Volodin, A. Moment inequalities for m-negatively associated random variables and their applications. Statist. Pap. 2017, 58, 911–928. [Google Scholar] [CrossRef]
- Wang, X.J.; Wu, Y.; Hu, S.H. Exponential probability inequality for m-END random variables and its applications. Metrika 2016, 79, 127–147. [Google Scholar] [CrossRef]
- Wu, Y.F.; Rosalsky, A.; Volodin, A. Some mean convergence and complete convergence theorems for sequences of m-linearly negative quadrant dependent random variables. Appl. Math. 2013, 58, 511–529. [Google Scholar] [CrossRef][Green Version]
- Wu, Y.F.; Rosalsky, A.; Volodin, A. Erratum to Some mean convergence and complete convergence theorems for sequences of m-linearly negative quadrant dependent random variables. Appl. Math. 2017, 62, 209–211. [Google Scholar] [CrossRef]
- Ye, R.Y.; Xinsheng Liu, X.S.; Yu, Y.C. Pointwise optimality of wavelet density estimation for negatively associated biased sample. Mathematics 2020, 8, 176. [Google Scholar] [CrossRef]
- Hsu, D.A. Detecting shifts of parameter in gamma sequences with applications to stock price and air traffic flow analysis. J. Am. Statist. Assoc. 1979, 74, 31–40. [Google Scholar] [CrossRef]
- Inclán, C.; Tiao, G.C. Use of cumulative sums of squares for retrospective detection of changes of variance. J. Am. Statist. Assoc. 1994, 89, 913–923. [Google Scholar]
- Abbas, N.; Abujiya, M.A.R.; Riaz, M.; Mahmood, T. Cumulative sum chart modeled under the presence of outliers. Mathematics 2020, 8, 269. [Google Scholar] [CrossRef]
- Doukhan, P.; Lang, G. Evaluation for moments of a ratio with application to regression estimation. Bernoulli 2009, 15, 1259–1286. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, H.; Ding, S.; Li, X.; Yang, W. Asymptotic Approximations of Ratio Moments Based on Dependent Sequences. Mathematics 2020, 8, 361. https://doi.org/10.3390/math8030361
Fang H, Ding S, Li X, Yang W. Asymptotic Approximations of Ratio Moments Based on Dependent Sequences. Mathematics. 2020; 8(3):361. https://doi.org/10.3390/math8030361
Chicago/Turabian StyleFang, Hongyan, Saisai Ding, Xiaoqin Li, and Wenzhi Yang. 2020. "Asymptotic Approximations of Ratio Moments Based on Dependent Sequences" Mathematics 8, no. 3: 361. https://doi.org/10.3390/math8030361
APA StyleFang, H., Ding, S., Li, X., & Yang, W. (2020). Asymptotic Approximations of Ratio Moments Based on Dependent Sequences. Mathematics, 8(3), 361. https://doi.org/10.3390/math8030361




