Further Results on the Total Roman Domination in Graphs

Abstract

Let G be a graph without isolated vertices. A function $f:V\left(G\right)\to \{0,1,2\}$ is a total Roman dominating function on G if every vertex $v\in V\left(G\right)$ for which $f\left(v\right)=0$ is adjacent to at least one vertex $u\in V\left(G\right)$ such that $f\left(u\right)=2$, and if the subgraph induced by the set $\{v\in V(G):f(v)\ge 1\}$ has no isolated vertices. The total Roman domination number of G, denoted ${\gamma }_{tR}\left(G\right)$, is the minimum weight $\omega \left(f\right)={\sum }_{v\in V\left(G\right)}f\left(v\right)$ among all total Roman dominating functions f on G. In this article we obtain new tight lower and upper bounds for ${\gamma }_{tR}\left(G\right)$ which improve the well-known bounds $2\gamma \left(G\right)\le {\gamma }_{tR}\left(G\right)\le 3\gamma \left(G\right)$, where $\gamma \left(G\right)$ represents the classical domination number. In addition, we characterize the graphs that achieve equality in the previous lower bound and we give necessary conditions for the graphs which satisfy the equality in the upper bound above.

1. Introduction

Domination theory is a classical and interesting topic in theory of graphs, as well as one of the most active areas of research in this topic. The increasing interest in this area is partly explained by the diversity of applications to both theoretical and real-world problems, such as facility location problems, monitoring communication, coding theory, algorithm design, complex ecosystems, electrical networks, among others. A set $D\subseteq V\left(G\right)$ of vertices of a graph G is a dominating set if every vertex in $V\left(G\right)\backslash D$ is adjacent to at least one vertex in D. The domination number of G, denoted by $\gamma \left(G\right)$, is the minimum cardinality among all dominating sets of G. Many variants of the previous concept have appeared in the literature. We refer to [1,2] for numerous results on this issue.

A remarkable variant of the parameter above, and one of the most studied, is as follows. A dominating set D of a graph G without isolated vertices is a total dominating set if the subgraph induced by the vertices of D has no isolated vertex. Notice that any graph with no isolated vertex has a total dominating set, since $D=V\left(G\right)$ is such a set. The total domination number of G, denoted by ${\gamma }_t\left(G\right)$, is the minimum cardinality among all total dominating sets of G. More information on total domination in graphs can be found in the survey [3] and the book [4].

Next, we consider another variant of the concept of domination. A semitotal dominating set of a graph G without isolated vertices, is a dominating set D of G such that every vertex in D is within distance two of another vertex of D. The semitotal domination number, denoted by ${\gamma }_{t2}\left(G\right)$, is the minimum cardinality among all semitotal dominating sets of G. This parameter was introduced by Goddard et al. in [5], and was also further studied in [6,7,8].

For any graph without isolated vertices, we have that every semitotal dominating set is also a dominating set. Similarly, every total dominating set is a semitotal dominating set. Hence, the next inequality chain, given in [5], relates the parameters above.

$$\gamma \left(G\right)\le {\gamma }_{t2}\left(G\right)\le {\gamma }_t\left(G\right)$$

(1)

In the last decades, functions defined on graphs have received much attention in domination theory. This fact may be because the classical (total) domination problem can be studied using functions defined on graphs. Based on this approach, we consider the following concepts, which are also variants of the domination in graphs.

Let $f:V\left(G\right)\to \{0,1,2\}$ be a function on a graph G. Notice that f generates three sets $V_0$, $V_1$ and $V_2$, where $V_i=\{v\in V\left(G\right):f\left(v\right)=i\}$ for $i=0,1,2$. In this sense, from now on, we will write $f(V_0^f,V_1^f,V_2^f)$ so as to refer to the function f. Given a set $S\subseteq V\left(G\right)$, $f\left(S\right)={\sum }_{v\in S}f\left(v\right)$. We define the weight of f as $\omega \left(f\right)=f\left(V\left(G\right)\right)=|V_1^f|+2|V_2^f|$. In this sense, by an $f\left(V\right(G\left)\right)$-function, we mean a function of weight $f\left(V\right(G\left)\right)$. If the function f is clear from the context, then we will simply write $f(V_0,V_1,V_2)$. We shall also use the following notations: $V_{1,2}=\{v\in V_1:N\left(v\right)\cap V_2\ne \varnothing \}$ and $V_{1,1}=V_1\backslash V_{1,2}$.

Roman domination in graphs was formally defined by Cockayne, Dreyer, Hedetniemi, and Hedetniemi [9] motivated, in part, by an article in Scientific American of Ian Stewart entitled “Defend the Roman Empire" [10]. A Roman dominating function (RDF) on a graph G is a function $f(V_0,V_1,V_2)$ satisfying that every vertex $u\in V_0$ is adjacent to at least one vertex $v\in V_2$. The Roman domination number of G, denoted by ${\gamma }_R\left(G\right)$, is the minimum weight among all RDFs on G. Further results on Roman domination can be found for example, in [11,12,13,14].

Another kind of functions defined on graphs are the total Roman dominating functions, which were introduced by Liu and Chang [15] and later, studied by Abdollahzadeh Ahangar et al. in [16]. A total Roman dominating function (TRDF) on a graph G without isolated vertices, is an RDF $f(V_0,V_1,V_2)$ such that the set $V_1\cup V_2$ is a total dominating set of G. The minimum weight among all TRDFs on G is the total Roman domination number of G and it is denoted by ${\gamma }_{tR}\left(G\right)$.

Abdollahzadeh Ahangar et al. [16] give the next relationship between the total Roman domination number and the domination number of a graph: If G is a graph with no isolated vertex, then

$$2\gamma \left(G\right)\le {\gamma }_{tR}\left(G\right)\le 3\gamma \left(G\right).$$

(2)

Also, the authors of [16] proposed open problems concerning characterizing the graphs that satisfy the equalities in the inequality chain above. While the families of trees which satisfy these equalities has been characterized in [17], it remains an open problem to characterize graphs in general. In that sense, in this article we study the open problems above. In the next section we first give new lower and upper bounds for this parameter, which improve the bounds given in the Inequality chain (2). Also, in Section 3 we give a characterization for the graphs G that satisfy the equality ${\gamma }_{tR}\left(G\right)=2\gamma \left(G\right)$; and finally, in Section 4 we give some necessary conditions that satisfy the graphs G for which ${\gamma }_{tR}\left(G\right)=3\gamma \left(G\right)$.

Notation

Throughout this article we consider $G=\left(V\right(G),E(G\left)\right)$ as a simple graph of order $n=\left|V\right(G\left)\right|$. Given a vertex v of G, $N\left(v\right)$ and $N\left[v\right]$ represent the open neighbourhood and the closed neighbourhood of v, respectively. For a set $D\subseteq V\left(G\right)$, its open neighbourhood and closed neighbourhood are $N\left(D\right)={\cup }_{v\in D}N\left(v\right)$ and $N\left[D\right]=N\left(D\right)\cup D$, respectively. The boundary of the set D is defined as $\partial \left(D\right)=N\left(D\right)\backslash D$. The private neighbourhood of a vertex v with respect to a set $D\subseteq V\left(G\right)$ ($v\in D$), denoted by $pn(v,D)$, is defined by $pn(v,D)=\{u\in V(G):N(u)\cap D=\{v\left\}\right\}$. The vertices of $pn(v,D)$ will be called private neighbours of v with respect to D. Given a vertex $v\in D\subseteq V\left(G\right)$, $epn(v,D)=pn(v,D)\cap \left(V\right(G)\backslash D)$ represent the external private neighbourhood of v with respect to D. Also, and as is commonly defined, $G-D$ denotes the graph obtained from G such that $V(G-D)=V\left(G\right)\backslash D$ and $E(G-D)=E\left(G\right)\backslash \{uv\in E(G):u\in D\mathrm{or}v\in D\}$. The subgraph induced by $D\subseteq V\left(G\right)$ is denoted by $G\left[D\right]$. For any two vertices u and v, the distance $d(u,v)$ between u and v is the length of a shortest $u-v$ path.

A set X of vertices of G is a packing in G if the closed neighbourhoods of vertices in X are pairwise disjoint, that is, if $N\left[u\right]\cap N\left[v\right]=\varnothing$, for every pair of different vertices $u,v\in X$.

A leaf vertex of a graph G is a vertex of degree one, and a support vertex of G is a vertex adjacent to a leaf. The set of leaves and support vertices are denoted by $L\left(G\right)$ and $S\left(G\right)$, respectively. Also, given a set $D\subseteq V\left(G\right)$ we denote $I\left(D\right)$ as an independent set of maximum cardinality in $G\left[D\right]$ such that $\left|I\right(D)\cap S(G\left)\right|$ is maximum.

Other definitions will be introduced as needed.

2. Main Result

We begin this section with the following useful result of total Roman dominating functions given in [16].

Lemma 1

([16]). If G is a graph with no isolated vertex, then there exists a ${\gamma }_{tR}\left(G\right)$-function $f(V_0,V_1,V_2)$ such that either $V_2$ is a dominating set of G, or the set S of vertices not dominated by $V_2$ satisfies $G\left[S\right]=k{K}_2$ for some $k\ge 1$, where $S\subseteq V_1$ and $\partial \left(S\right)\subseteq V_0$.

It is known from [9] that for any graph G, ${\gamma }_R\left(G\right)\le 2\gamma \left(G\right)$ and also, from Inequality chain (1) that $\gamma \left(G\right)\le {\gamma }_{t2}\left(G\right)$. Hence, and as consequence of both inequalities above, we deduce that the following result improves the lower and upper bounds given in Inequality chain (2) for the total Roman domination number of graphs.

Theorem 1.

For any graph G with neither isolated vertex nor components isomorphic to $K_2$,

$${\gamma }_{t2}\left(G\right)+\gamma \left(G\right)\le {\gamma }_{tR}\left(G\right)\le {\gamma }_R\left(G\right)+\gamma \left(G\right).$$

Proof. 

We first prove the lower bound. By Lemma 1, there exists a ${\gamma }_{tR}\left(G\right)$-function $g(V_0^g,V_1^g,V_2^g)$ such that either $V_2^g$ is a dominating set of G, or $V_{1,1}^g$ satisfies $G\left[V_{1,1}^g\right]\cong k{K}_2$ for some $k\ge 1$. Hence, $V_2^g$ is a dominating set of $G-V_{1,1}^g$ and can be extended to a dominating set of G by adding to it the set $I\left(V_{1,1}^g\right)$. So $\gamma \left(G\right)\le |V_2^g\cup I\left(V_{1,1}^g\right)| = |V_2^g| + |V_{1,1}^g|/2$. Moreover, $V_2^g\cup V_{1,2}^g$ is a total dominating set of $G-V_{1,1}^g$ and it is easy to check that $V_2^g\cup V_{1,2}^g\cup I\left(V_{1,1}^g\right)$ is a semitotal dominating set of G. Therefore ${\gamma }_{t2}\left(G\right)\le |V_2^g\cup V_{1,2}^g\cup I\left(V_{1,1}^g\right)| = |V_2^g| + |V_{1,2}^g| + |I\left(V_{1,1}^g\right)| = |V_2^g| + |V_{1,2}^g| + |V_{1,1}^g|/2$ and so,

$${\gamma }_{t2}\left(G\right)+\gamma \left(G\right)\le \left(\right|V_2^g| + |V_{1,2}^g| + |V_{1,1}^g|/2)+\left(\right|V_2^g| + |V_{1,1}^g|/2)=2|V_2^g| + |V_1^g| ={\gamma }_{tR}\left(G\right),$$

which completes the proof of the lower bound.

Now, in order to prove the upper bound, let D be a $\gamma \left(G\right)$-set and $f(V_0,V_1,V_2)$ be a ${\gamma }_R\left(G\right)$-function. Also, we consider $V_{1,0}=\{v\in V_1:N\left(v\right)\subseteq V_0\}$ and let $f^{\prime }(V_0^{\prime },V_1^{\prime },V_2^{\prime })$ be a function defined as follows.

(a)

For every vertex $x\in (V_{1,0}\cup V_2)\cap D$, choose a vertex $u\in (V_0\cap N\left(x\right))\backslash D$ (if it exists), and label it as $f^{\prime }\left(u\right)=1$.

(b)

For every vertex $x\in V_0\cap D$, $f^{\prime }\left(x\right)=1$.

(c)

For any other vertex u not previously labelled, $f^{\prime }\left(u\right)=f\left(u\right)$.

Since f is an RDF on G, by construction we have that $f^{\prime }$ is a TRDF on G. Therefore,

$$\begin{array}{ccc}\hfill {\gamma }_{tR}\left(G\right)& \le & \omega \left(f^{\prime }\right)\hfill \\ & \le & |V_1|+2|V_2|+|(V_{1,0}\cup V_2)\cap D|+|V_0\cap D|\hfill \\ & \le & \left(\right|V_1|+2|V_2\left|\right)+\left|D\right|\hfill \\ & =& {\gamma }_R\left(G\right)+\gamma \left(G\right),\hfill \end{array}$$

which completes the proof. □

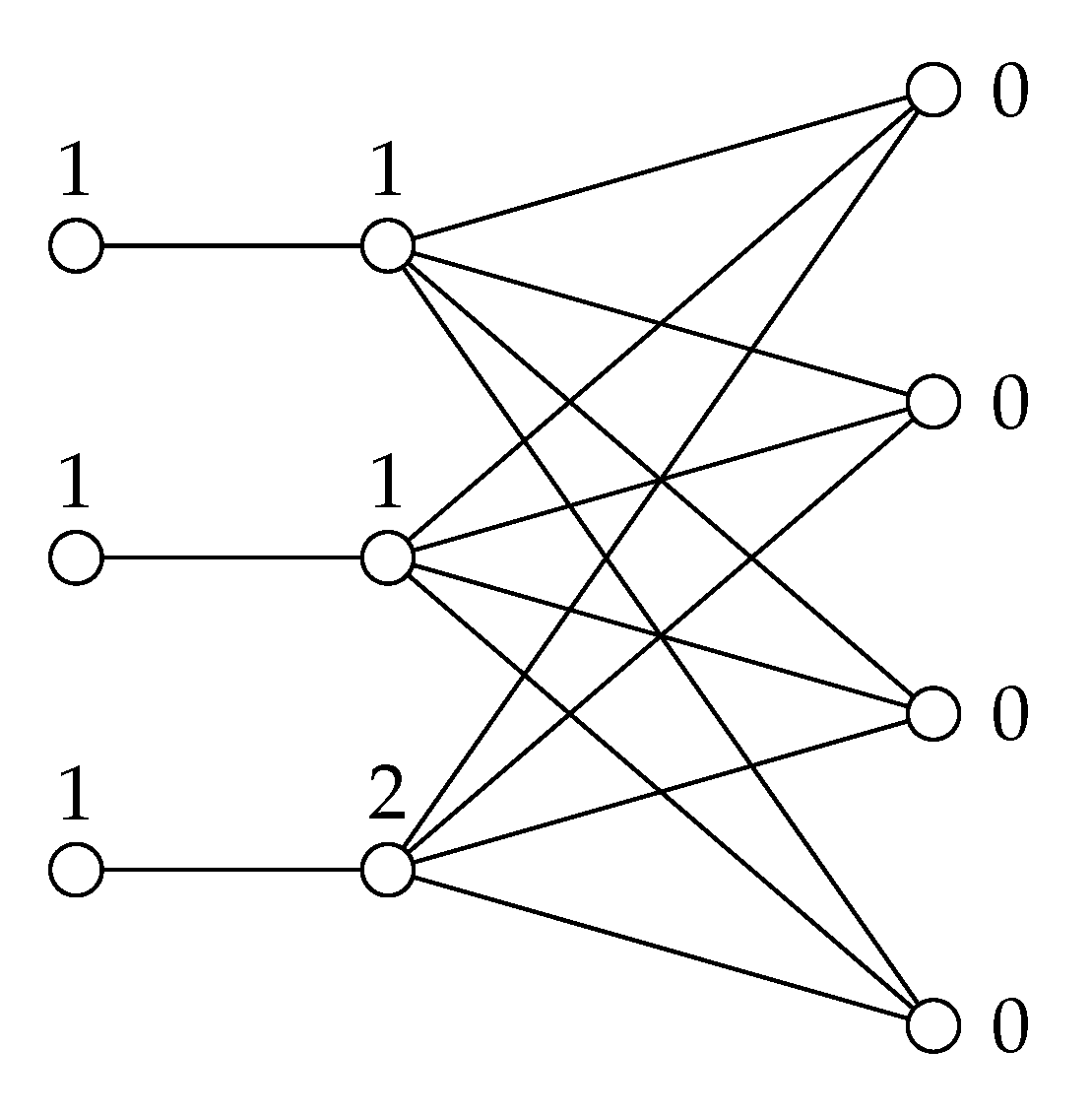
Now, we show a family of graphs $G_{p,q}$ given by Cabrera et al. in [18], which satisfy that ${\gamma }_{tR}\left(G_{p,q}\right)={\gamma }_{t2}\left(G_{p,q}\right)+\gamma \left(G_{p,q}\right)$ (observe that $\gamma \left(G_{p,q}\right)=p$, ${\gamma }_{t2}\left(G_{p,q}\right)=p+1$ and ${\gamma }_{tR}\left(G_{p,q}\right)=2p+1$). Let $p,q$ be two integers such that $q\ge p\ge 2$. From the complete bipartite graph $K_{p,q}$ and the empty graph $N_p$, we construct the graph $G_{p,q}$ as follows. We add p new edges which form a matching between the vertices of $N_p$ and the vertices of degree q in $K_{p,q}$. Figure 1 shows the graph $G_{3,4}$ and a ${\gamma }_{tR}\left(G_{3,4}\right)$-function $g(V_0,V_1,V_2)$.

Next, we provide some useful properties that satisfies a specific TRDF for the graphs G with ${\gamma }_{tR}\left(G\right)={\gamma }_{t2}\left(G\right)+\gamma \left(G\right)$.

Theorem 2.

For any graph G such that ${\gamma }_{tR}\left(G\right)={\gamma }_{t2}\left(G\right)+\gamma \left(G\right)$, there exists a ${\gamma }_{tR}\left(G\right)$-function $f(V_0,V_1,V_2)$ satisfying the following conditions.

(i)

Either $V_2$ is a dominating set of G, or the set $V_{1,1}$ satisfies $G\left[V_{1,1}\right]=k{K}_2$ for some $k\ge 1$, where $\partial \left(V_{1,1}\right)\subseteq V_0$.

(ii)

$V_2\cup I\left(V_{1,1}\right)$ is a $\gamma \left(G\right)$-set and $V_2\cup V_{1,2}\cup I\left(V_{1,1}\right)$ is a ${\gamma }_{t2}\left(G\right)$-set.

(iii)

$G\left[V_{1,2}\right]$ is isomorphic to an empty graph. Furthermore, if $v\in V_{1,2}$, then $|N\left(v\right)\cap V_2| =1$.

Proof. 

Let $f(V_0,V_1,V_2)$ be a ${\gamma }_{tR}\left(G\right)$-function that satisfies Lemma 1. Hence, condition (i) holds.

Now, we proceed to prove (ii). First, we notice that $A=V_2\cup I\left(V_{1,1}\right)$ and $B=V_2\cup V_{1,2}\cup I\left(V_{1,1}\right)$ are a dominating set and a semitotal dominating set, respectively. Hence, $\gamma \left(G\right)\le \left|A\right|$ and ${\gamma }_{t2}\left(G\right)\le \left|B\right|$. Since $\left|A\right|+\left|B\right|={\gamma }_{tR}\left(G\right)$ and ${\gamma }_{tR}\left(G\right)={\gamma }_{t2}\left(G\right)+\gamma \left(G\right)$, we obtain that $\left|B\right|+\left|A\right|={\gamma }_{t2}\left(G\right)+\gamma \left(G\right)$. If $\left|A\right|>\gamma \left(G\right)$, then $\left|B\right|<{\gamma }_{t2}\left(G\right)$, which is a contradiction. Therefore, $\left|A\right|=\gamma \left(G\right)$ and so, $\left|B\right|={\gamma }_{t2}\left(G\right)$, which completes the proof of (ii).

Finally, we proceed to prove (iii). Let $v\in V_{1,2}$. Clearly, $N\left(v\right)\cap V_2\ne \varnothing$. If $N\left(v\right)\cap V_{1,2}\ne \varnothing$ or $|N\left(v\right)\cap V_2|>1$, then $(V_2\cup V_{1,2}\cup I\left(V_{1,1}\right))\backslash \left\{v\right\}$ is a semitotal dominating set of G, which is a contradiction with the fact that $V_2\cup V_{1,2}\cup I\left(V_{1,1}\right)$ is a ${\gamma }_{t2}\left(G\right)$-set by (ii). Therefore, $N\left(v\right)\cap V_{1,2}=\varnothing$ and $|N\left(v\right)\cap V_2| =1$, which implies that $G\left[V_{1,2}\right]$ is isomorphic to an empty graph, and that $|N\left(v\right)\cap V_2| =1$, which completes the proof. □

We consider again the family of graphs $G_{p,q}$. Let $g(V_0,V_1,V_2)$ be a ${\gamma }_{tR}\left(G_{p,q}\right)$-function defined as $V_2=\left\{v\right\}$ and $V_1=(S\left(G_{p,q}\right)\cup L\left(G_{p,q}\right))\backslash \left\{v\right\}$, for some $v\in S\left(G\right)$. Notice that g satisfies the conditions given in Theorem 2. For an example, see the ${\gamma }_{tR}\left(G_{3,4}\right)$-function g showed in the Figure 1.

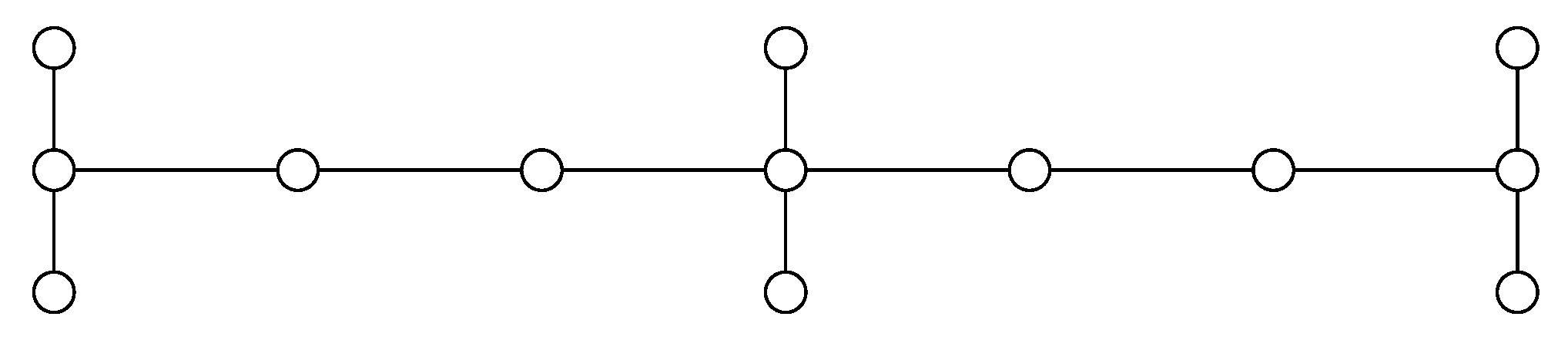
Next, we will show a family of graphs $G_r$ that satisfy the upper bound in the Theorem 1. In this case we have that $\gamma \left(G_r\right)=r$, ${\gamma }_R\left(G_r\right)=2r$ and ${\gamma }_{tR}\left(G_r\right)=3r$, where $r\ge 2$ is an integer. The graph $G_r$ is constructed from the path graph $P_{3r-2}=v_1{v}_2\cdots v_{3r-2}$ and the empty graph $N_2$ by taking one copy of $P_{3r-2}$ and r copies of $N_2$ and adding edges between the vertex $v_{3i-2}$ and the i-th copy of $N_2$, for $i\in \{1,\dots ,r\}$. Figure 2 shows the graph $G_3$.

3. Graphs $\mathbf{G}$ with ${\mathbf{\gamma }}_{\mathbf{tR}}\left(\mathbf{G}\right)=\mathbf{2}\mathbf{\gamma }\left(\mathbf{G}\right)$

We begin this section with a simple characterization, which is a direct consequence of Theorem 1 and the Inequality chains (1) and (2).

Theorem 3.

Let G be a graph with no isolated vertex. Then ${\gamma }_{tR}\left(G\right)=2\gamma \left(G\right)$ if and only if ${\gamma }_{tR}\left(G\right)={\gamma }_{t2}\left(G\right)+\gamma \left(G\right)$ and ${\gamma }_{t2}\left(G\right)=\gamma \left(G\right)$.

We observe that the condition ${\gamma }_{tR}\left(G\right)={\gamma }_{t2}\left(G\right)+\gamma \left(G\right)$ is a necessary condition but is not sufficient to satisfy the equality ${\gamma }_{tR}\left(G\right)=2\gamma \left(G\right)$. For instance, see the graph $G_{3,4}$ shown in Figure 1.

Next, we give another characterization for the graphs G satisfying ${\gamma }_{tR}\left(G\right)=2\gamma \left(G\right)$. It is important to emphasize that this characterization depends only of the existence of a $\gamma \left(G\right)$-set which satisfies some specific conditions.

Theorem 4.

Let G be a graph with no isolated vertex. Then ${\gamma }_{tR}\left(G\right)=2\gamma \left(G\right)$ if and only if there exist a $\gamma \left(G\right)$-set S and a set $D\subseteq S$ such that

(a)

$G\left[D\right]$ is isomorphic to an empty graph.

(b)

$\left|epn\right(v,S\left)\right|=1$, for every vertex $v\in D$.

(c)

$\gamma (G-D^{*})={\gamma }_t(G-D^{*})$, where $D^{*}={\bigcup }_{v\in D}epn(v,S)\cup D$.

Proof. 

First, we suppose that ${\gamma }_{tR}\left(G\right)=2\gamma \left(G\right)$. By Lemma 1, there exists a ${\gamma }_{tR}\left(G\right)$-function $g(V_0^g,V_1^g,V_2^g)$ such that either $V_2^g$ is a dominating set of G, or $V_{1,1}^g$ satisfies $G\left[V_{1,1}^g\right]\cong k{K}_2$ for some $k\ge 1$. By proceeding analogously as the proof of the lower bound of Theorem 1 and since ${\gamma }_{tR}\left(G\right)=2\gamma \left(G\right)={\gamma }_{t2}\left(G\right)+\gamma \left(G\right)$, we obtain $\gamma \left(G\right)= |V_2^g| + |V_{1,1}^g|/2$ and ${\gamma }_{t2}\left(G\right)= |V_2^g| + |V_{1,2}^g| + |V_{1,1}^g|/2$. Therefore $V_{1,2}^g=\varnothing$.

Let D be the set formed by taking one vertex from each $K_2$-component of $G\left[V_{1,1}^g\right]$. Notice that $D\cup V_2^g$ is a dominating set of G. Hence $2\gamma \left(G\right)={\gamma }_{tR}\left(G\right)= |V_1^g|+2|V_2^g| =2|D|+2|V_2^g|$, which implies that $S=D\cup V_2^g$ is a $\gamma \left(G\right)$-set. Thus, by construction of sets S and D, it is easy to see that Statements (a) and (b) hold.

Next, we prove Statement (c). Let $D^{*}={\bigcup }_{v\in D}epn(v,S)\cup D$. It is readily seen that from D and any $\gamma (G-D^{*})$-set we can construct a dominating set of G, and as $V_{1,2}^g=\varnothing$, we obtain $\frac{1}{2}{\gamma }_{tR}\left(G\right)=\gamma \left(G\right)\le \gamma (G-D^{*})+\left|D\right|\le |V_2^g|+\frac{1}{2}\left|V_{1,1}^g\right|=\frac{1}{2}{\gamma }_{tR}\left(G\right)$. Thus, we have equalities in the inequality chain above. In particular, $\gamma (G-D^{*})=\left|V_2^g\right|$. Also, notice that $V_2^g$ is a total dominating set of $G-D^{*}$ since $V_{1,2}^g=\varnothing$. Hence, we deduce ${\gamma }_t(G-D^{*})\le \left|V_2^g\right|=\gamma (G-D^{*})$, which implies ${\gamma }_t(G-D^{*})=\gamma (G-D^{*})$, and Statement (c) holds, as desired.

Conversely, we suppose there exist a $\gamma \left(G\right)$-set S and a set $D\subseteq S$ such that Statements (a), (b) and (c) hold. Let $A_D$ be a ${\gamma }_t(G-D^{*})$-set. By Statements (a) and (b) we have that $S\backslash D$ is a dominating set of $G-D^{*}$ and so, by using Statement (c), we deduce that $|A_D| =\gamma (G-D^{*})\le |S\backslash D|$. Moreover, we observe that the function $f(V_0,V_1,V_2)$, defined by $V_1=D^{*}$ and $V_2=A_D$, is a TRDF on G. Therefore, by Inequality chain (2) and statements above, we obtain $2\gamma \left(G\right)\le {\gamma }_{tR}\left(G\right)\le \omega \left(f\right)= |D^{*}|+2|A_D|\le 2|D|+2|S\backslash D| =2|S| =2\gamma \left(G\right)$. Thus, we have equalities in the previous inequality chain. In particular, ${\gamma }_{tR}\left(G\right)=2\gamma \left(G\right)$, which completes the proof. □

4. Some Necessary Conditions for the Graphs $\mathbf{G}$ satisfying ${\mathbf{\gamma }}_{\mathbf{tR}}\left(\mathbf{G}\right)=\mathbf{3}\mathbf{\gamma }\left(\mathbf{G}\right)$

Analogously to the section above, we continue now with a simple characterization, which is a direct consequence of Theorem 1 and the well-know inequality ${\gamma }_R\left(G\right)\le 2\gamma \left(G\right)$.

Theorem 5.

Let G be a graph without isolated vertices. Then ${\gamma }_{tR}\left(G\right)=3\gamma \left(G\right)$ if and only if ${\gamma }_{tR}\left(G\right)={\gamma }_R\left(G\right)+\gamma \left(G\right)$ and ${\gamma }_R\left(G\right)=2\gamma \left(G\right)$.

We want to accentuate that in all the examples in which we have observed that the upper bound of Theorem 1 is achieved, we also have that ${\gamma }_R\left(G\right)=2\gamma \left(G\right)$. In such a sense, we propose the following conjecture, which we could not prove.

Conjecture 1. Let G be a graph with no isolated vertex. Then ${\gamma }_{tR}\left(G\right)=3\gamma \left(G\right)$ if and only if ${\gamma }_{tR}\left(G\right)={\gamma }_R\left(G\right)+\gamma \left(G\right)$.

In order to give some necessary conditions for the graphs G satisfying ${\gamma }_{tR}\left(G\right)=3\gamma \left(G\right)$, we shall need the following definition and useful results.

Definition 1.

A graph G satisfies Property $\mathcal{P}$ if for every $\gamma \left(G\right)$-set S, there exist no three vertices $x,y,z\in S$ such that

• There exists a vertex $y^{\prime }\in epn(y,S)$ such that $d(x,y^{\prime })=d(y^{\prime },z)=2$.
• $\left|epn\right(x,S\left)\right|=\left|epn\right(z,S\left)\right|=2$.

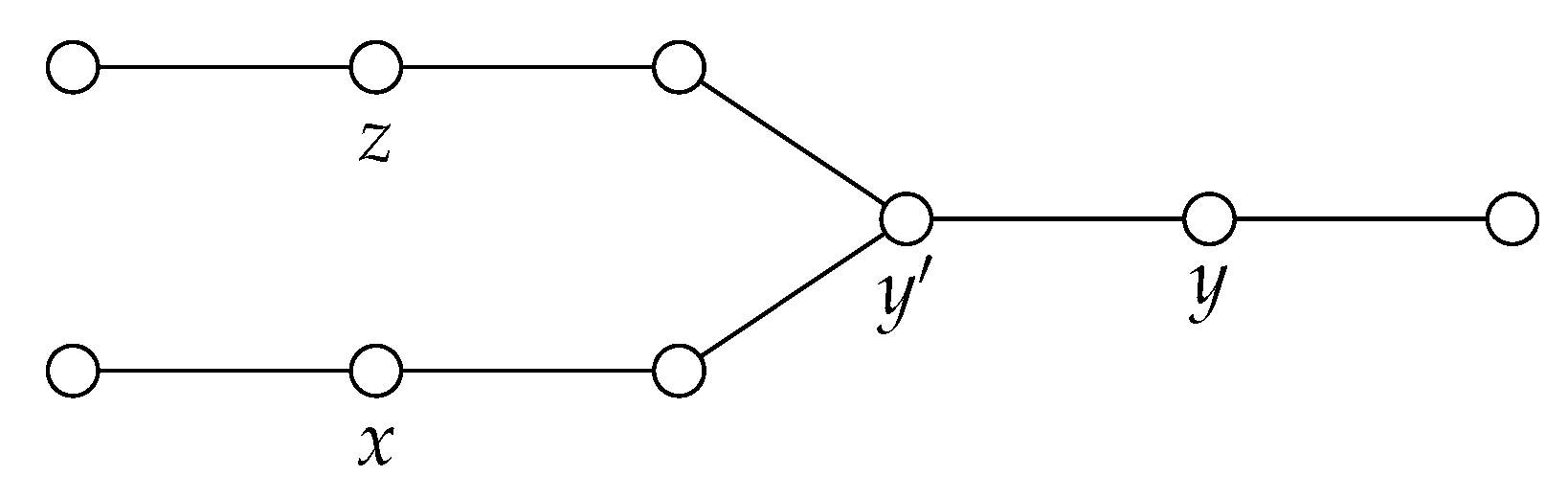
Notice that the families of graphs $G_{p,q}$ and $G_r$ given in Section 2 satisfy the Property $\mathcal{P}$. Moreover, the Figure 3 shows a graph G that does not satisfy Property $\mathcal{P}$. Observe that the set $S=\{x,y,z\}$ is a $\gamma \left(G\right)$-set and also, it is easy to see that $\left|epn\right(x,S\left)\right|=\left|epn\right(z,S\left)\right|=2$ and that the vertex $y^{\prime }\in epn(y,S)$ satisfies the condition $d(x,y^{\prime })=d(y^{\prime },z)=2$.

Lemma 2.

Let G be a graph and let S be a $\gamma \left(G\right)$-set. If S is a packing, then for all $v\in S$ there exists $v^{\prime }\in S$ such that $d(v,v^{\prime })=3$.

Proof. 

Suppose there exists a vertex $v\in S$ such that for all vertex $v^{\prime }\in S\backslash \left\{v\right\}$, it is satisfied that $d(v,v^{\prime })>3$ (notice that $d(v,v^{\prime })\ge 3$ because S is a packing). Hence, every vertex at distance two of v is not dominated by S, which is a contradiction. This completes the proof. □

Proposition 1.

If G is a graph such that every $\gamma \left(G\right)$-set is a packing, then for every $\gamma \left(G\right)$-set S and for every $v\in S$ it is satisfied that $\left|epn\right(v,S\left)\right|\ge 2$.

Proof. 

Let S be a $\gamma \left(G\right)$-set and let $v\in S$. Since S is a packing, we have that $epn(v,S)\ne \varnothing$. If $epn(v,S)=\left\{u\right\}$, then v is a vertex of degree one. By using Lemma 2, we have that $S^{\prime }=(S\backslash \left\{v\right\})\cup \left\{u\right\}$ is a $\gamma \left(G\right)$-set, but is not a packing, contradicting the hypothesis. So $\left|epn\right(v,S\left)\right|\ge 2$, as desired. □

Theorem 6.

Let G be a graph. If ${\gamma }_{tR}\left(G\right)=3\gamma \left(G\right)$, then the following statements hold.

(i)

${\gamma }_R\left(G\right)=2\gamma \left(G\right)$.

(ii)

S is a packing, for every $\gamma \left(G\right)$-set S.

(iii)

G satisfies Property $\mathcal{P}$.

Proof. 

By Theorem 5, Statement (i) follows. Moreover, Abdollahzadeh Ahangar et al. showed in [16] that every $\gamma \left(G\right)$-set is a packing, which implies that Statement (ii) holds.

Next we prove Statement (iii). In that sense, we suppose that G does not satisfy Property $\mathcal{P}$. Hence there exist a $\gamma \left(G\right)$-set S and three vertices $x,y,z\in S$ satisfying the conditions given in Definition 1. By Statement (ii) and Proposition 1 we have $\left|epn\right(v,S\left)\right|\ge 2$, for every $v\in S$. Let $x^{\prime }\in epn(x,S)\backslash N\left(y^{\prime }\right)$ and $z^{\prime }\in epn(z,S)\backslash N\left(y^{\prime }\right)$. Now, we consider the function f defined as follows.

(a)

For every vertex $u\in (S\backslash \{x,z\})\cup \left\{y^{\prime }\right\}$, set $f\left(u\right)=2$.

(b)

For every vertex $v\in S\backslash \{x,y,z\}$, choose a vertex $v^{\prime }\in N\left(v\right)$, and label it as $f\left(v^{\prime }\right)=1$.

(c)

For $u\in \{x,z,x^{\prime },z^{\prime }\}$, set $f\left(u\right)=1$.

(d)

For any other vertex u not previously labelled, set $f\left(u\right)=0$.

Notice that, by construction, f is a TRDF on G. Therefore,

$$\begin{array}{ccc}\hfill {\gamma }_{tR}\left(G\right)& \le & \omega \left(f\right)\hfill \\ & \le & 2|(S\backslash \{x,z\})\cup \left\{y^{\prime }\right\}|+|S\backslash \{x,y,z\}|+|\{x,z,x^{\prime },z^{\prime }\}|\hfill \\ & =& 2\left(\right|S|-1)+\left(\right|S|-3)+4\hfill \\ & =& 3\left|S\right|-1\hfill \\ & <& 3\gamma \left(G\right),\hfill \end{array}$$

which is a contradiction. Hence G satisfies Property $\mathcal{P}$ and the proof is complete. □

5. Conclusions and Open Problems

New results concerning the study of total Roman domination in graphs have been presented in this article. Among the main contributions, the following should be highlighted.

• As the main result, we have provided new lower and upper bounds for the total Roman domination number of graphs, which improve other well-known bounds.
• We have shown a theoretical characterization for the graphs G satisfying ${\gamma }_{tR}\left(G\right)=2\gamma \left(G\right)$.
• We have shown some necessary conditions for the graphs G that satisfy ${\gamma }_{tR}\left(G\right)=3\gamma \left(G\right)$.

On the other hand, and as a consequence of this study, some open problems have arisen. Next, we expose some of the most interesting.

(a)

Characterize the graphs G satisfying ${\gamma }_{tR}\left(G\right)={\gamma }_{t2}\left(G\right)+\gamma \left(G\right)$.

(b)

Characterize the graphs G satisfying ${\gamma }_{tR}\left(G\right)={\gamma }_R\left(G\right)+\gamma \left(G\right)$.

(c)

Settle Conjecture 1.