Optimization of the Solution of a Dispersion Model
Abstract
1. Introduction
2. Dispersion Model and Its Solutions
2.1. Solution of the Dispersion Model for Closed Vessels
2.2. An Improved Solution for the Boundary Value Problem (1)–(3)
2.3. A New Iterative Method for Estimating the Vessel Dispersion Number
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mac Mullin, R.B. The Theory of Short Circuiting in Continuous-Flow Mixing Vessels in Series and the Kinetics of Chemical Reactions in Such Systems. Trans. Am. Inst. Chem. Eng. 1935, 31, 409–458. [Google Scholar]
- Danckwerts, P.V. Continuous flow systems: Distribution of residence times. Chem. Eng. Sci. 1953, 2, 1–13. [Google Scholar] [CrossRef]
- Fogler, H.S. Elements of Chemical Reaction Engineering, 5th ed.; Prentice Hall: Boston, MA, USA, 2016. [Google Scholar]
- Levenspiel, O. Chemical Reaction Engineering, 3rd ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Nauman, E.B. Chemical Reactor Design, Optimization, and Scaleup, 2nd ed.; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Froment, G.F.; Bischoff, K.B.; De Wilde, J. Chemical Reactor Analysis and Design, 3rd ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Nauman, E.B. Residence Time Theory. Ind. Eng. Chem. Res. 2008, 47, 3752–3766. [Google Scholar] [CrossRef]
- Matko, T.; Fawcett, N.; Sharp, A.; Stephenson, T. A numerical model of flow in circular sedimentation tanks. Process Saf. Environ. 1996, 74, 197–204. [Google Scholar] [CrossRef]
- Nauman, E.B. Residence time distribution theory for unsteady stirred tank reactors. Chem. Eng. Sci. 1969, 24, 1461–1470. [Google Scholar] [CrossRef]
- Niemi, A.J.; Zenger, K.; Thereska, J.; Martinez, J.G. Tracer testing of processes under variable flow and volume. Nukleonika 1998, 43, 73–94. [Google Scholar]
- Fernandez-Sempere, J.; Font-Montesinos, R.; Espejo-Alcaraz, O. Residence time distribution for unsteady-state systems. Chem. Eng. Sci. 1995, 50, 223–230. [Google Scholar] [CrossRef]
- Claudel, S.; Leclerc, J.P.; Tétar, L.; Lintz, H.G.; Bernard, A. Recent extensions of the residence time distribution concept: Unsteady state conditions and hydrodynamic model developments. Braz. J. Chem. Eng. 2000, 17, 947–954. [Google Scholar] [CrossRef]
- Bogatykh, I.; Osterland, T. Characterization of Residence Time Distribution in a Plug Flow Reactor. ChemIngTech 2019, 91, 668–672. [Google Scholar] [CrossRef]
- Hohmann, L.; Schmalenberg, M.; Prasanna, M.; Matuschek, M.; Kockmann, N. Suspension flow behavior and particle residence time distribution in helical tube devices. Chem. Eng. J. 2019, 360, 1371–1389. [Google Scholar] [CrossRef]
- Chen, K.; Bachmann, P.; Bück, A.; Jacob, M.; Tsotsas, E. CFD simulation of particle residence time distribution in industrial scale horizontal fluidized bed. J. Powder Technol. 2019, 345, 129–139. [Google Scholar] [CrossRef]
- Deshmukh, S.S.; Sathe, M.J.; Joshi, J.B.; Koganti, S.B. Residence time distribution and flow patterns in the single-phase annular region of annular centrifugal extractor. Ind. Eng. Chem. Res. 2009, 48, 37–46. [Google Scholar] [CrossRef]
- Kolhe, N.S.; Mirage, Y.H.; Patwardhan, A.V.; Rathod, V.K.; Pandey, N.K.; Mudali, U.K.; Natarajan, R. CFD and experimental studies of single phase axial dispersion coefficient in pulsed sieve plate column. Chem. Eng. Res. Des. 2011, 89, 1909–1918. [Google Scholar] [CrossRef]
- Fazli-Abukheyli, R.; Darvishi, P. Combination of axial dispersion and velocity profile in parallel tanks-in-series compartment model for prediction of residence time distribution in a wide range of non-ideal laminar flow regimes. Chem. Eng. Sci. 2019, 195, 531–540. [Google Scholar] [CrossRef]
- Ding, S.; Liu, L.; Xu, J. A study of the determination of dimensionless number and its influence on the performance of a combination wastewater reactor. Procedia Environ. Sci. 2013, 18, 579–584. [Google Scholar] [CrossRef][Green Version]
- Elias, Y.; von Rohr, P.R. Axial dispersion, pressure drop and mass transfer comparison of small-scale structured reaction devices for hydrogenations. Chem. Eng. Process. 2016, 106, 1–12. [Google Scholar] [CrossRef]
- Makinia, J.; Wells, S.A. Evaluation of empirical formulae for estimation of the longitudinal dispersion in activated sludge reactors. Water Res. 2005, 39, 1533–1542. [Google Scholar] [CrossRef]
- Sharma, L.; Nigam, K.D.P.; Roy, S. Axial dispersion in single and multiphase flows in coiled geometries: Radioactive particle tracking experiments. Chem. Eng. Sci. 2017, 157, 116–126. [Google Scholar] [CrossRef]
- Murphy, K.L.; Timpany, P.L. Design and analysis of mixing for an aeration tank. J. Sanit. Eng. Div. 1967, 93, 1–15. [Google Scholar]
- Courant, R.; Hilbert, D. Methods of Mathematical Physics Volume II; Wiley-Interscience: Hoboken, NJ, USA, 1989. [Google Scholar]
- Thomas, H.A.; McKee, J.E. Longitudinal Mixing in Aeration Tank. Sew. Works J. 1944, 16, 42–55. [Google Scholar]
- Borkowski, P. Adaptive system for steering a ship along the desired route. Mathematics 2018, 6, 196. [Google Scholar] [CrossRef]
- Van der Laan, E.T. Notes on diffusion-type model for longitudinal mixing in flow. Chem. Eng. Sci. 1958, 7, 187. [Google Scholar]
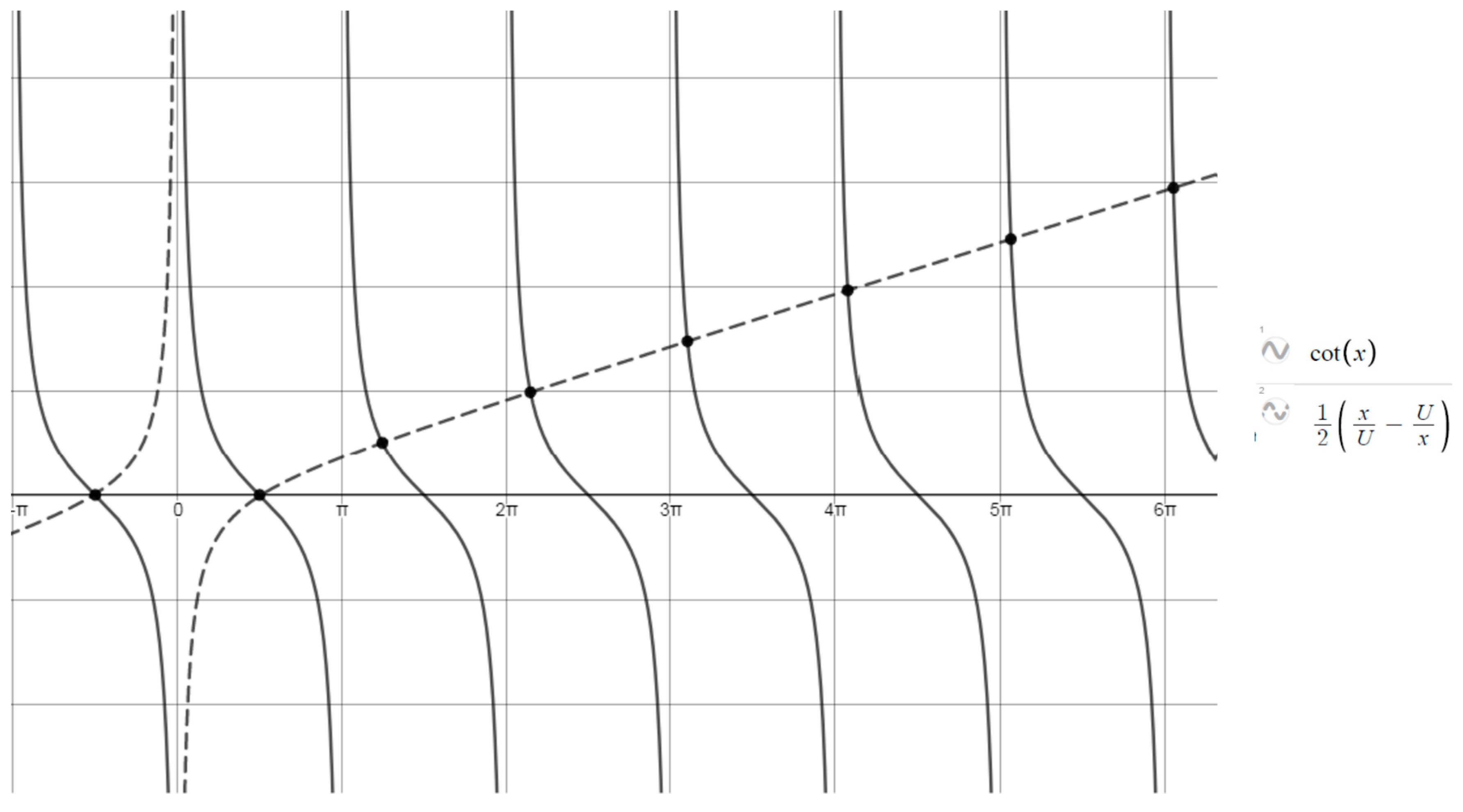
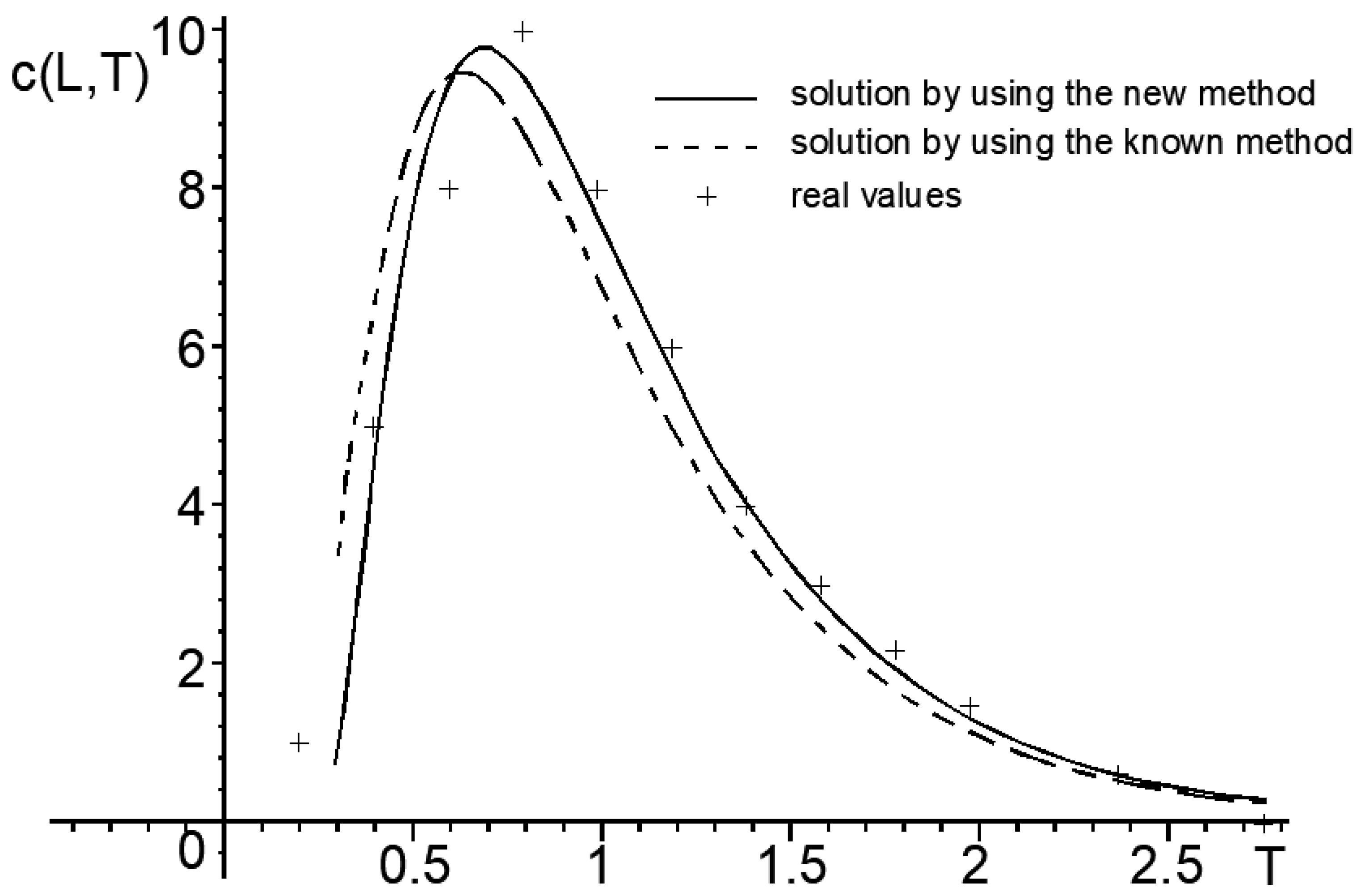

| ti (min) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 14 |
| ci (mg/L) | 0 | 1 | 5 | 8 | 10 | 8 | 6 | 4 | 3 | 2.2 | 1.5 | 0.6 | 0 |
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 0 | 0.1979 | 0.3957 | 0.5936 | 0.7914 | 0.9893 | 1.1871 | 1.3850 | 1.5829 | 1.7807 | 1.9786 | 2.3743 | 2.77 |
| i | βi | γi | |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| 0.13 | 0.14 | 0.15 | 0.16 | 0.17 | 0.18 | 0.19 | 0.2 | 0.21 | |
| 4.4090 | 3.9981 | 3.5411 | 3.2279 | 3.0203 | 2.8912 | 2.8213 | 2.7965 | 2.8061 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimache, A.-N.; Groza, G.; Jianu, M.; Perju, S.; Rece, L.; Harničárová, M.; Valíček, J. Optimization of the Solution of a Dispersion Model. Mathematics 2020, 8, 318. https://doi.org/10.3390/math8030318
Dimache A-N, Groza G, Jianu M, Perju S, Rece L, Harničárová M, Valíček J. Optimization of the Solution of a Dispersion Model. Mathematics. 2020; 8(3):318. https://doi.org/10.3390/math8030318
Chicago/Turabian StyleDimache, Alexandru-Nicolae, Ghiocel Groza, Marilena Jianu, Sorin Perju, Laurențiu Rece, Marta Harničárová, and Jan Valíček. 2020. "Optimization of the Solution of a Dispersion Model" Mathematics 8, no. 3: 318. https://doi.org/10.3390/math8030318
APA StyleDimache, A.-N., Groza, G., Jianu, M., Perju, S., Rece, L., Harničárová, M., & Valíček, J. (2020). Optimization of the Solution of a Dispersion Model. Mathematics, 8(3), 318. https://doi.org/10.3390/math8030318







