Modified Inertial Hybrid and Shrinking Projection Algorithms for Solving Fixed Point Problems
Abstract
1. Introduction
- (C1)
- and ;
- (C2)
- .
- (D1)
- is nondecreasing with and , ;
- (D2)
- Exists such that and ;
- (D3)
- defined in (4) assume that is bounded and is bounded for any .
2. Preliminaries
- (1)
- The Euclidean projection of onto an Euclidean ball is given by
- (2)
- The Euclidean projection of onto a box is given by
- (3)
- The Euclidean projection of onto a halfspace is given by
3. Modified Inertial Hybrid and Shrinking Projection Algorithms
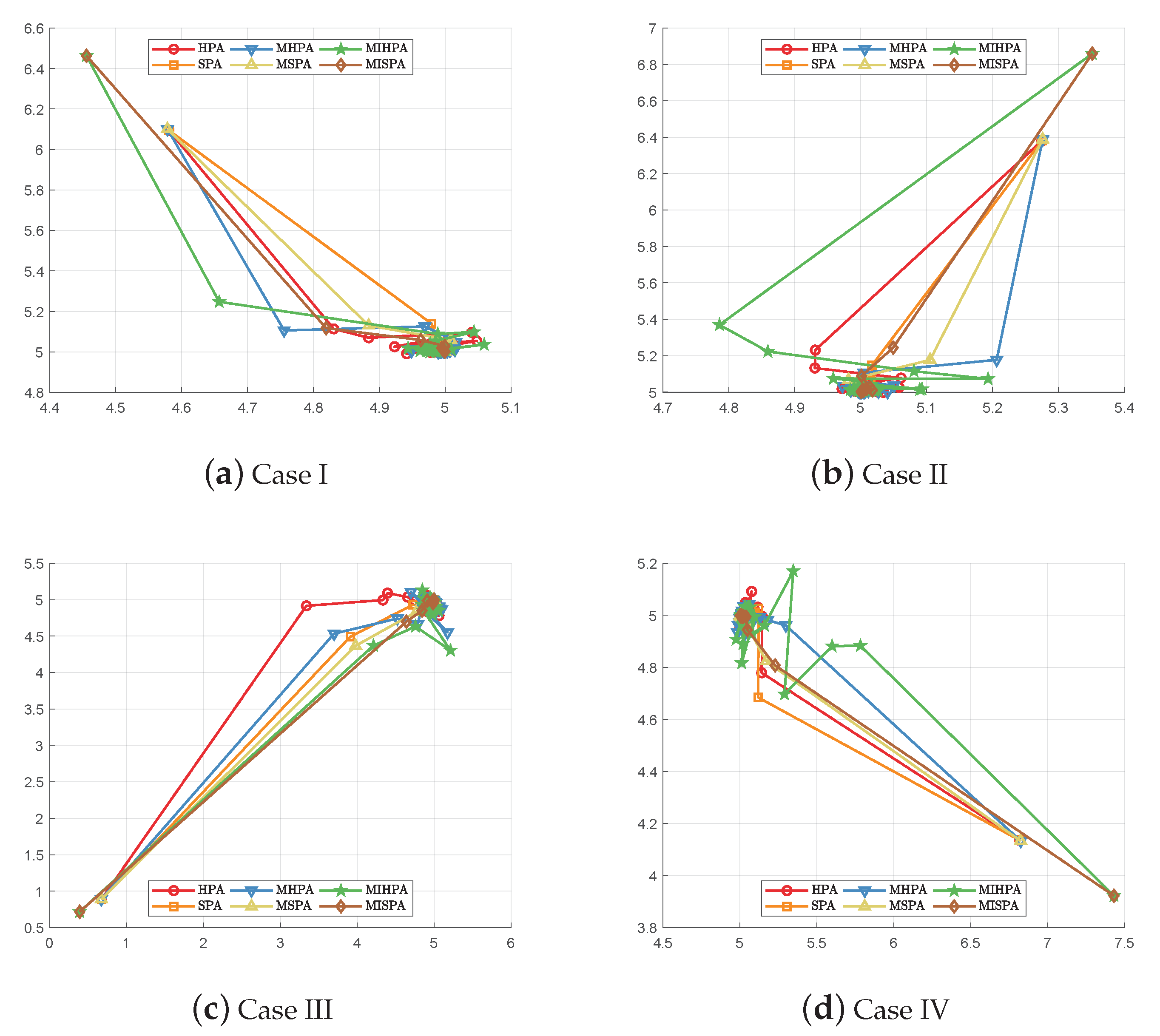
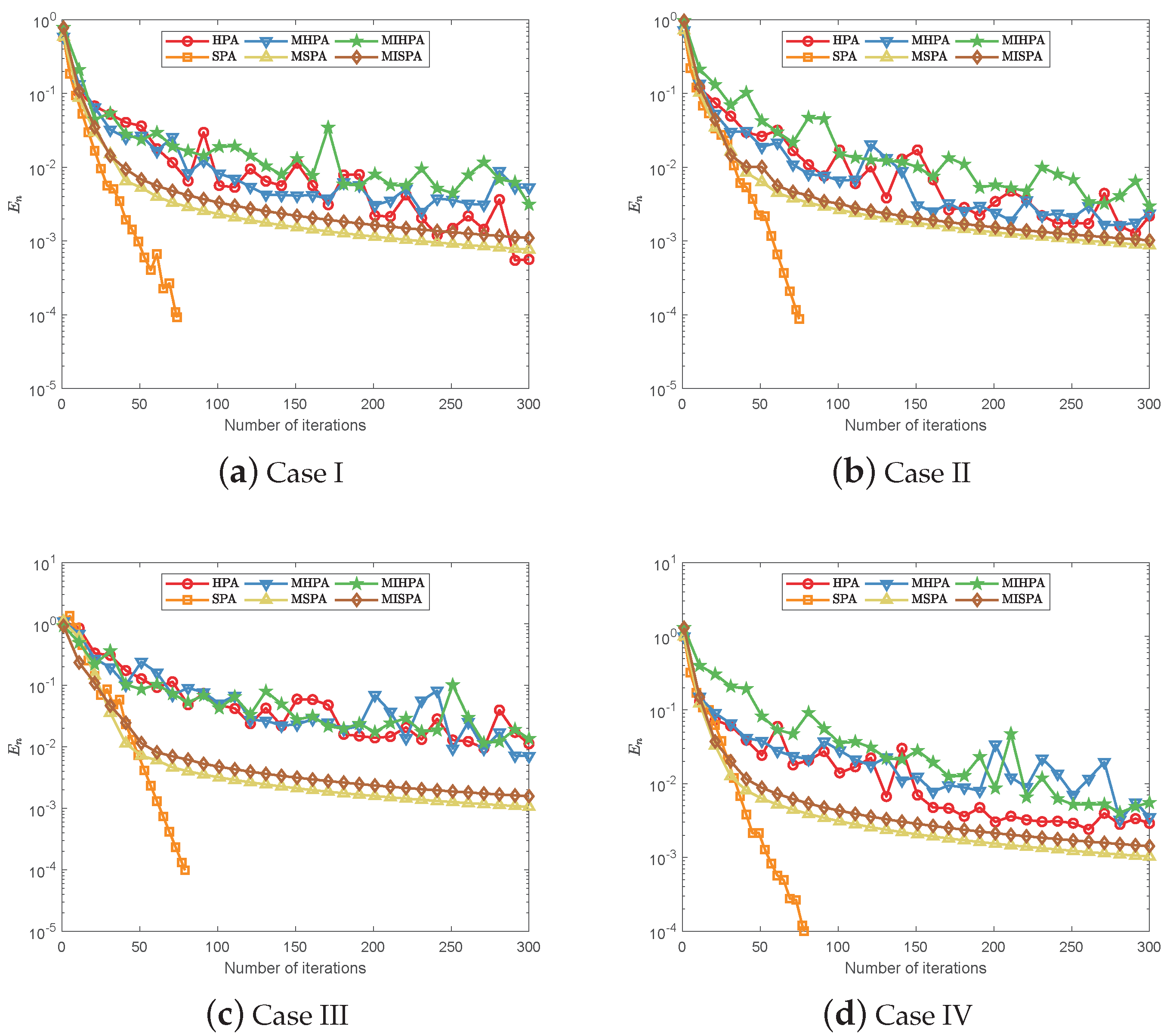
4. Numerical Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qin, X.; Yao, J.C. A viscosity iterative method for a split feasibility problem. J. Nonlinear Convex Anal. 2019, 20, 1497–1506. [Google Scholar]
- Cho, S.Y. Generalized mixed equilibrium and fixed point problems in a Banach space. J. Nonlinear Sci. Appl. 2016, 9, 1083–1092. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Ansari, Q.H.; Qin, X. Linear conditioning, weak sharpness and finite convergence for equilibrium problems. J. Glob. Optim. 2020. [Google Scholar] [CrossRef]
- Dehaish, B.A.B. A regularization projection algorithm for various problems with nonlinear mappings in Hilbert spaces. J. Inequal. Appl. 2015, 2015, 1–14. [Google Scholar] [CrossRef]
- Dehaish, B.A.B. Weak and strong convergence of algorithms for the sum of two accretive operators with applications. J. Nonlinear Convex Anal. 2015, 16, 1321–1336. [Google Scholar]
- Qin, X.; An, N.T. Smoothing algorithms for computing the projection onto a Minkowski sum of convex sets. Comput. Optim. Appl. 2019, 74, 821–850. [Google Scholar] [CrossRef]
- Takahahsi, W.; Yao, J.C. The split common fixed point problem for two finite families of nonlinear mappings in Hilbert spaces. J. Nonlinear Convex Anal. 2019, 20, 173–195. [Google Scholar]
- An, N.T.; Qin, X. Solving k-center problems involving sets based on optimization techniques. J. Glob. Optim. 2020, 76, 189–209. [Google Scholar] [CrossRef]
- Cho, S.Y.; Kang, S.M. Approximation of common solutions of variational inequalities via strict pseudocontractions. Acta Math. Sci. 2012, 32, 1607–1618. [Google Scholar] [CrossRef]
- Takahashi, W. The shrinking projection method for a finite family of demimetric mappings with variational inequality problems in a Hilbert space. Fixed Point Theory 2018, 19, 407–419. [Google Scholar] [CrossRef]
- Qin, X.; Cho, S.Y.; Wang, L. A regularization method for treating zero points of the sum of two monotone operators. Fixed Point Theory Appl. 2014, 2014, 75. [Google Scholar] [CrossRef]
- Chang, S.S.; Wen, C.F.; Yao, J.C. Zero point problem of accretive operators in Banach spaces. Bull. Malays. Math. Sci. Soc. 2019, 42, 105–118. [Google Scholar] [CrossRef]
- Tan, K.K.; Xu, H.K. Approximating fixed points of non-expansive mappings by the Ishikawa iteration process. J. Math. Anal. Appl. 1993, 178, 301. [Google Scholar] [CrossRef]
- Sharma, S.; Deshpande, B. Approximation of fixed points and convergence of generalized Ishikawa iteration. Indian J. Pure Appl. Math. 2002, 33, 185–191. [Google Scholar]
- Singh, A.; Dimri, R.C. On the convergence of Ishikawa iterates to a common fixed point for a pair of nonexpansive mappings in Banach spaces. Math. Morav. 2010, 14, 113–119. [Google Scholar] [CrossRef]
- De la Sen, M.; Abbas, M. On best proximity results for a generalized modified Ishikawa’s iterative scheme driven by perturbed 2-cyclic like-contractive self-maps in uniformly convex Banach spaces. J. Math. 2019, 2019, 1356918. [Google Scholar] [CrossRef]
- Nakajo, K.; Takahashi, W. Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups. J. Math. Anal. Appl. 2003, 279, 372–379. [Google Scholar] [CrossRef]
- Takahashi, W.; Takeuchi, Y.; Kubota, R. Strong convergence theorems by hybrid methods for families of nonexpansive mappings in Hilbert spaces. J. Math. Anal. Appl. 2008, 341, 276–286. [Google Scholar] [CrossRef]
- Cho, S.Y. Strong convergence analysis of a hybrid algorithm for nonlinear operators in a Banach space. J. Appl. Anal. Comput. 2018, 8, 19–31. [Google Scholar]
- Qin, X.; Cho, S.Y.; Wang, L. Iterative algorithms with errors for zero points of m-accretive operators. Fixed Point Theory Appl. 2013, 2013, 148. [Google Scholar] [CrossRef]
- Chang, S.S.; Wen, C.F.; Yao, J.C. Common zero point for a finite family of inclusion problems of accretive mappings in Banach spaces. Optimization 2018, 67, 1183–1196. [Google Scholar] [CrossRef]
- Qin, X.; Cho, S.Y. Convergence analysis of a monotone projection algorithm in reflexive Banach spaces. Acta Math. Sci. 2017, 37, 488–502. [Google Scholar] [CrossRef]
- He, S.; Dong, Q.-L. The combination projection method for solving convex feasibility problems. Mathematics 2018, 6, 249. [Google Scholar] [CrossRef]
- Polyak, B.T. Some methods of speeding up the convergence of iteration methods. Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Maingé, P.E. Convergence theorems for inertial KM-type algorithms. J. Comput. Appl. Math. 2008, 219, 223–236. [Google Scholar] [CrossRef]
- Lorenz, D.; Pock, T. An inertial forward-backward algorithm for monotone inclusions. J. Math. Imaging Vis. 2015, 51, 311–325. [Google Scholar] [CrossRef]
- Qin, X.; Wang, L.; Yao, J.C. Inertial splitting method for maximal monotone mappings. J. Nonlinear Convex Anal. 2020, in press. [Google Scholar]
- Thong, D.V.; Hieu, D.V. Inertial extragradient algorithms for strongly pseudomonotone variational inequalities. J. Comput. Appl. Math. 2018, 341, 80–98. [Google Scholar] [CrossRef]
- Luo, Y.L.; Tan, B. A self-adaptive inertial extragradient algorithm for solving pseudo-monotone variational inequality in Hilbert spaces. J. Nonlinear Convex Anal. 2020, in press. [Google Scholar]
- Liu, L.; Qin, X. On the strong convergence of a projection-based algorithm in Hilbert spaces. J. Appl. Anal. Comput. 2020, 10, 104–117. [Google Scholar]
- Tan, B.; Xu, S.S.; Li, S. Inertial shrinking projection algorithms for solving hierarchical variational inequality problems. J. Nonlinear Convex Anal. 2020, in press. [Google Scholar]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Boţ, R.I.; Csetnek, E.R.; Hendrich, C. Inertial Douglas–Rachford splitting for monotone inclusion problems. Appl. Math. Comput. 2015, 256, 472–487. [Google Scholar] [CrossRef]
- Sakurai, K.; Iiduka, H. Acceleration of the Halpern algorithm to search for a fixed point of a nonexpansive mapping. Fixed Point Theory Appl. 2014, 2014, 202. [Google Scholar] [CrossRef]
- Dong, Q.-L.; Yuan, H.B.; Cho, Y.J.; Rassias, T.M. Modified inertial Mann algorithm and inertial CQ-algorithm for nonexpansive mappings. Optim. Lett. 2018, 12, 87–102. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; Springer: New York, NY, USA, 2011; Volume 48. [Google Scholar]
- Kim, T.H.; Xu, H.K. Strong convergence of modified Mann iterations for asymptotically nonexpansive mappings and semigroups. Nonlinear Anal. 2006, 64, 1140–1152. [Google Scholar] [CrossRef]
- Martinez-Yanes, C.; Xu, H.K. Strong convergence of the CQ method for fixed point iteration processes. Nonlinear Anal. 2006, 64, 2400–2411. [Google Scholar] [CrossRef]
- Xu, H.K. Averaged mappings and the gradient-projection algorithm. J. Optim. Theory Appl. 2011, 150, 360–378. [Google Scholar] [CrossRef]
- Dong, Q.-L.; Cho, Y.J.; Zhong, L.L.; Rassias, T.M. Inertial projection and contraction algorithms for variational inequalities. J. Glob. Optim. 2018, 70, 687–704. [Google Scholar] [CrossRef]
- Beck, A.; Sabach, S. Weiszfeld’s method: Old and new results. J. Optim. Theory Appl. 2015, 164, 1–40. [Google Scholar] [CrossRef]
| Algorithm | Initial Value | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MIHPA | rand(N,1) | Iter. | 223 | 248 | 218 | 239 | 283 | 245 | 258 | 249 | 248 | 247 |
| MISPA | 127 | 137 | 148 | 159 | 169 | 163 | 167 | 187 | 186 | 190 | ||
| MIHPA | ones(N,1) | Iter. | 327 | 315 | 407 | 354 | 342 | 356 | 377 | 391 | 348 | 349 |
| MISPA | 174 | 189 | 181 | 199 | 217 | 208 | 279 | 250 | 243 | 256 | ||
| MIHPA | 10rand(N,1) | Iter. | 1057 | 1377 | 1522 | 1494 | 1307 | 1119 | 1261 | 1098 | 1005 | 1070 |
| MISPA | 549 | 570 | 704 | 698 | 845 | 852 | 987 | 856 | 1003 | 975 | ||
| MIHPA | −10rand(N,1) | Iter. | 445 | 410 | 574 | 504 | 657 | 716 | 729 | 730 | 659 | 682 |
| MISPA | 316 | 313 | 350 | 416 | 423 | 386 | 427 | 392 | 516 | 556 |
| Iter. | HPA | SPA | MHPA | MSPA | MIHPA | MISPA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | (0.2944,0.8061) | 0.8582 | (0.2944,0.8061) | 0.8582 | (0.4607,0.8706) | 0.9850 | (0.4607,0.8706) | 0.9850 | (0.4607,0.8706) | 0.9850 | (0.4607,0.8706) | 0.9850 |
| 50 | (0.0049,0.0164) | 0.0171 | (0.0000,0.0001) | 0.0001 | (0.0142,0.0357) | 0.0384 | (0.0142,0.0264) | 0.0300 | (0.0094,0.0357) | 0.0369 | (0.0142,0.0278) | 0.0312 |
| 100 | (0.0006,0.0017) | 0.0018 | (0.0000,0.0000) | 0.0000 | (0.0116,0.0110) | 0.0159 | (0.0072,0.0133) | 0.0151 | (0.0096,0.0144) | 0.0173 | (0.0067,0.0137) | 0.0153 |
| 200 | (−0.0003,0.0013) | 0.0014 | (0.0000,0.0000) | 0.0000 | (0.0059,0.0053) | 0.0080 | (0.0034,0.0068) | 0.0076 | (0.0061,0.0047) | 0.0077 | (0.0036,0.0060) | 0.0070 |
| 300 | (0.0007,0.0003) | 0.0008 | (0.0000,0.0000) | 0.0000 | (0.0043,0.0030) | 0.0053 | (0.0021,0.0045) | 0.0049 | (0.0045,0.0038) | 0.0058 | (0.0018,0.0053) | 0.0056 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, B.; Xu, S.; Li, S. Modified Inertial Hybrid and Shrinking Projection Algorithms for Solving Fixed Point Problems. Mathematics 2020, 8, 236. https://doi.org/10.3390/math8020236
Tan B, Xu S, Li S. Modified Inertial Hybrid and Shrinking Projection Algorithms for Solving Fixed Point Problems. Mathematics. 2020; 8(2):236. https://doi.org/10.3390/math8020236
Chicago/Turabian StyleTan, Bing, Shanshan Xu, and Songxiao Li. 2020. "Modified Inertial Hybrid and Shrinking Projection Algorithms for Solving Fixed Point Problems" Mathematics 8, no. 2: 236. https://doi.org/10.3390/math8020236
APA StyleTan, B., Xu, S., & Li, S. (2020). Modified Inertial Hybrid and Shrinking Projection Algorithms for Solving Fixed Point Problems. Mathematics, 8(2), 236. https://doi.org/10.3390/math8020236







