A New Vision on the Prosumers Energy Surplus Trading Considering Smart Peer-to-Peer Contracts
Abstract
1. Introduction
2. Literature Review
3. A New Vision for Prosumer Energy Surplus Trading Algorithm
- Transactions are settled by the local non-profit μG manager or aggregator using the consumer or prosumer merit order derived from the priority mechanism agreed for trading and data from the metering system.
- The prosumer-consumer acquisition priority rules are the same for the entire μG.
- To be able to acquire electricity from a prosumer Pk, a consumer Cj must have previously signed a P2P contract that includes the bilateral trading agreement, price, and other supplemental information, such as trading priority.
- By default, any prosumer and prosumers in the μG have signed bilateral P2P trading contracts. In other words, any prosumer who has a generation surplus can theoretically sell electricity to any consumer in the microgrid. This setting is changeable to exclude any consumer from the trading process.
- When a consumer is awarded a P2P contract, the power supplied by the prosumer will try to match the entire load of the consumer, within the limit of the available surplus, as in Equation (1). This setting is changeable to allow specified quantity requirements for each consumer.
- The selling price of a prosumer is considered fixed for all trading intervals of a day. This assumption is made because only PV panels are used at this point as generation sources, and no storage capabilities are present in the μG. Thus, the local generation does not cover evening peak load or low consumption night hours, which would favor the application of differentiated tariffs.
- The consumers in the network are generally one-phase, supplied through a four-wire three-phase network. Prosumers are supplying their surplus generation in the μG using a three-phase balanced connection point, as required by technical regulations for LV distribution systems [35].
- When transactions take place between certain prosumers and consumers, the prosumers will deliver and the consumer will receive electricity from the same grid.
- If the surplus exceeds the local demand traded via P2P contracts, the μG market administrator will sell the untraded electricity back to the grid, at regulated tariffs.
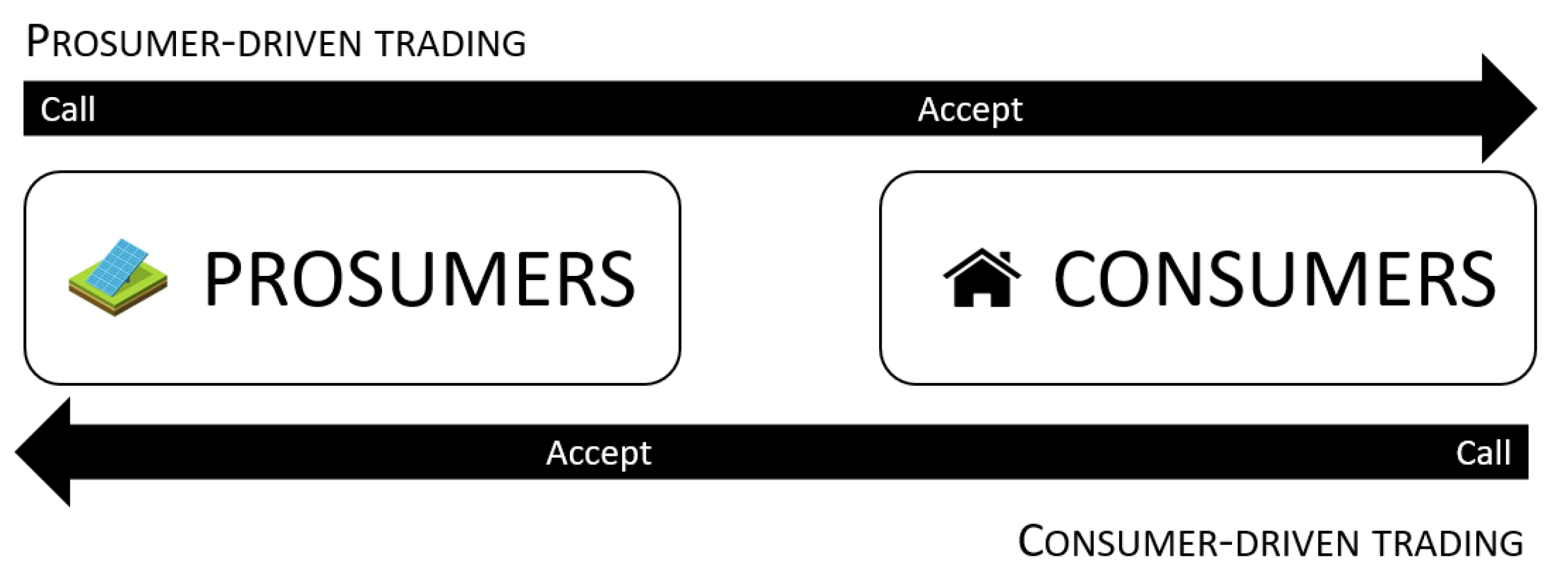
- Prosumer-driven
- ○
- Scenario 1: Path of supply length
- ○
- Scenario 2: Instantaneous power demand
- ○
- Scenario 3: Daily energy consumption-based clustering
- ○
- Scenario 4: Blockchain offers
- Consumer-driven:
- ○
- Scenario 5: Minimum price for consumers
3.1. Trading Priority Based on the Length of the Supply Path—Scenario 1 (Prosumer-Driven)
3.2. Trading Priority Based on Consumer Hourly Demand—Scenario 2 (Prosumer-Driven)
3.3. Trading Priority Based on Consumer Daily Demand—Scenario 3
3.4. Trading Priority Based on the Blockchain Technology—Scenario 4
3.5. Trading Priority Based on the Minimum Price for Consumers—Scenario 5
| Algorithm 1: The proposed trading algorithm |
| Step 1. Specify trading scenario: 1—network length; 2—instantaneous demand; 3—daily demand; 4—blockchain trading; 5—prosumer minimum price with blockchain. Step 2. Load input data: the consumer load profile matrix C, the prosumer generation matrix G, the supply path lengths of the network, the prosumer price matrix PR. Step 3. According to the selected scenario, compute priority matrices M1, M2, M3. Step 4. Initialize the acquisition matrix A and financial settlement matrix F. Step 5. Initialize the unsold surplus us = 0. Step 6. Trading: for prosumer-driven scenarios for each hour h, h = 1..24 for each prosumer k, k = 1, …, np compute surplus S (h, k); if S (h, k) > 0 srp = S (h, k); find ix, the row index corresponding to prosumer k in matrix M1 case Scenario 1—network length build a temporary consumer priority matrix MTC with two rows: row 1: line ix from matrix M1; row 2: line h from matrix C; (MTC, A, F, srp) = Subroutine 1 (MTC, A, F, srp, h, ix, nc). case Scenario 2—instantaneous demand build a temporary consumer priority matrix MTC with two rows: row 1: line h from matrix C; row 2: line ix from matrix M1; (MTC, A, F, srp) = Subroutine 2 (MTC, A, F, srp, h, ix, nc) case Scenario 3—daily demand build a temporary consumer priority matrix MTC with two rows: row 1: line ix from matrix M2; row 2: line h from matrix C; (MTC, A, F, srp) = Subroutine 1 (MTC, A, F, srp, h, ix, nc) case Scenario 4—blockchain trading build a temporary consumer priority matrix MTC with two rows: row 1: line ix from matrix M3; row 2: line h from matrix C; (MTC, A, F, srp) = Subroutine 1 (MTC, A, F, srp, h, ix, nc) Update line h from C using the modified matrix MTC Update the unsold surplus: us = us + srp; for consumer-driven scenarios—prosumer minimum price with blockchain for each hour h, h = 1, …, 24 compute the total surplus for hour h, srph; if srph > 0 build a temporary consumer priority matrix MTC with two rows: row 1: line h from matrix M3; row 2: line h from matrix C; build a temporary prosumer priority matrix MTP with two rows: row 1: line h from matrix PR; row 2: line h from matrix S; (MTC, MTP, A, F, srp) = Subroutine 3 (MTC, MTP, A, F, h) Step 7. Compute the hourly and total electricity sold by prosumers to each consumer and the electricity traded hourly and daily by all prosumers, using matrices A and F. |
| Subroutine 1 |
| Step 1. Read input data: the priority matrix MTC, acquisition matrix A, the financial settlement matrix F, the surplus to be distributed between consumers srp, the current prosumer index ix, the current hour h. Step 2. Transpose matrix MTC into matrix MC. Step 3. Sort matrix MC ascending by column 1, and for equal values in column 1, sort descending the corresponding values in column 2. Step 4. Distribute the surplus srp: set initial consumer index: k = 0; while srp > 0 or (k < nc) k = k + 1; if the consumer has a P2P contract subtract the available surplus from its trading offer MC (k, 2) = MC (k, 2) − srp; if the surplus exceeds the consumer contract quantity: MC (k, 2) < 0 update remaining surplus: srp = − MC (k, 2); the contract from consumer k is fulfilled: MC (k, 2) = 0; else the contract from consumer k is partially fulfilled and the surplus is depleted: srp = 0; update matrix MTC for by subtracting from the served consumer demand the fulfilled contract; update acquisition matrix A for hour h according to the served consumer k, serving prosumer ix and traded quantity |
| Subroutine 2 |
| Step 1. Read input data: the priority matrix MTC, the acquisition matrix A, the financial settlement matrix F, the surplus to be distributed between consumers srp, the current prosumer index ix, the number of consumers nc, the current hour h. Step 2. Transpose matrix MTC into matrix MC. Step 3. Sort matrix MC descending by column 1, and for equal values in column 1, sort ascending the corresponding values in column 2. Step 4. Distribute the surplus srp: set initial consumer index: k = 0; while srp > 0 or (k < nc) k = k + 1; if the consumer has a P2P contract subtract the available surplus from its trading offer MC (k, 1) = MC (k, 1) − srp; if the surplus exceeds the consumer contract quantity: MC (k, 1) < 0 update remaining surplus: srp = − MC (k, 1); the contract from consumer k is fulfilled: MC (k, 1) = 0; else the contract from consumer k is partially fulfilled and the surplus is depleted: srp = 0; update matrix MTC for by subtracting from the served consumer demand the fulfilled contract; update acquisition matrix A and financial settlement matrix F for hour h according to the served consumer k, serving prosumer ix and traded quantity. |
| Subroutine 3 |
| Step 1. Read input data: the priority matrix for consumers MTC, the priority matrix for prosumers MTP, the acquisition matrix A, the financial settlement matrix F, hour h. Step 2. Transpose matrix MTC into matrix MC, and matrix MTP into matrix MP Step 3. Sort matrix MC in ascending order of consumer priority (column 1). Keep original consumer order in vector idxk. Step 4. Sort matrix MT ascending by column 1, and for equal values in column 1, sort descending the corresponding values in column 2. Keep original prosumer order in vector idxp. Step 5. Compute the total surplus and consumption (st, ct). Step 6. Distribute the surplus srp: set initial consumer index: kc = 0 and prosumer index kp = 0; while (st > 0) & (ct > 0) increase consumer index: kc = kc + 1; read consumption to be traded c_crt = MC (kc, 2); if c_crt > 0, if consumption exists while (c_crt > 0) & (st > 0) increase consumer index: kp = kp + 1; read prosumer surplus p_crt = MP (kp, 2); if p_crt > 0 subtract the surplus from the consumption c_crt = c_crt − p_crt; if the surplus exceeds the consumer contract quantity: c_crt < 0 update remaining surplus: t_crt = c_crt; p_crt = − c_crt; the contract from consumer k is fulfilled c_crt = 0; else the contract from consumer k is partially fulfilled and the surplus is depleted: p_crt = 0; compute traded consumption ctz = abs (t_crt − abs (c_crt); update transposed consumption and generation priority matrices MC (kc, 2) = c_crt; MP (kp, 2) = p_crt; update consumption and generation priority matrices MTC (2, idxc (kc)) = MC (kc, 2); MTP (2, idxp (kp)) = MP (kp, 2); identify price pr = MP (kp, 1); update st and ct; update acquisition matrix A and financial settlement matrix F. |
4. Results
5. Discussion
6. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a, b, X | Clusters |
| A | The acquisition matrix |
| A(h,j,k) | The electricity sold at hour h to consumer j by prosumer k |
| ANRE | Regulation National Agency in Energy Domain |
| C | Matrix of consumptions |
| Cj | Consumer j |
| ct | Total consumption |
| The mean of cluster X | |
| dab | the distance between cluster A and cluster B |
| DER | Distributed Energy Resources |
| DG | Distributed Generation |
| DR | Demand Response |
| DSM | Demand Side Management |
| EC | European Commission |
| EDN | Electricity Distribution Network |
| ESS | Energy Storage System |
| EU | European Union |
| F | The financial settlement matrix |
| F(h,j,k) | The payment made by consumer j to prosumer k at hour h |
| FCFS | First Came—First Served |
| G | Matrix of generations |
| ICT | Information and Communication Technologies |
| ix | index |
| h | The current hour (h, …, 1, …, H) |
| j | The index for consumers |
| k | The index for prosumers |
| l | The consumer (l, …, 1, … , nc) |
| p | The number of priority matrix. |
| Lj,k | The length between consumer j and prosumer k |
| LV | Low Voltage |
| Mp | Matrix of priorities, (p, …, 1, … , 3) |
| MC | The Transposed Temporary Consumer Priority Matrix |
| MP | The Transposed Temporary Prosumer Priority Matrix |
| MPC | Model Productive Control |
| MTC | Temporary Consumer Priority Matrix |
| MTP | Temporary Prosumer Priority Matrix |
| MU | Monetary unit |
| MV | Medium Voltage |
| nc | total number of consumers (j, …, 1, …, nc) |
| nh | total number of hour (h, …, 1, …, nh) |
| np | total number of prosumers (k, …, 1, …, np) |
| nx | number of elements grouped in cluster X |
| P2P | Peer-to-Peer |
| PEST | Prosumers Energy Surplus Trading |
| Ph,j | Maximum active power at hour h, of consumers j |
| Pk | Prosumer k |
| PR | Vector of prices |
| Psurplus | Power surplus of prosumers |
| Ptrade | Power traded by prosumers |
| PV | Photovoltaic |
| S | Matrix of surplus |
| Scny | Scenarios (y, …, 1, …, 5) |
| srp | Surplus |
| srph | Total surplus for hour h |
| SSRES | Small-Scale Renewable Energy Sources |
| st | Total surplus |
| us | Unsold surplus |
| Wj | The total active energy for consumer j, in kWh |
| μG | Micro-grid |
| μM | Micro-market |
| ℝ | Set of reals |
| ℤ | Set of integers |
Appendix A
| - | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 |
| h1 | 0.616 | 2.010 | 0.273 | 0.000 | 1.370 | 2.418 | 1.152 | 1.936 | 0.310 |
| h2 | 0.608 | 1.908 | 0.078 | 0.020 | 1.520 | 2.210 | 1.664 | 1.368 | 0.678 |
| h3 | 0.557 | 2.004 | 0.048 | 0.260 | 1.910 | 2.149 | 2.056 | 1.376 | 0.300 |
| h4 | 0.522 | 2.010 | 0.306 | 0.040 | 1.770 | 2.151 | 2.048 | 2.048 | 0.640 |
| h5 | 0.522 | 1.902 | 0.063 | 0.050 | 1.990 | 2.192 | 1.816 | 1.528 | 0.360 |
| h6 | 0.571 | 2.004 | 0.165 | 0.250 | 2.070 | 2.299 | 1.168 | 2.992 | 0.468 |
| h7 | 0.529 | 1.836 | 0.213 | 0.125 | 2.280 | 2.364 | 0.720 | 3.352 | 0.748 |
| h8 | 0.592 | 1.236 | 0.060 | 4.710 | 2.530 | 2.543 | 1.704 | 2.240 | 3.208 |
| h9 | 0.562 | 1.302 | 0.312 | 1.290 | 1.850 | 2.382 | 1.976 | 2.112 | 2.815 |
| h10 | 0.616 | 1.200 | 0.258 | 0.525 | 1.850 | 2.549 | 1.944 | 2.192 | 1.483 |
| h11 | 0.860 | 1.188 | 0.243 | 2.985 | 1.460 | 2.426 | 1.904 | 2.232 | 4.538 |
| h12 | 0.535 | 1.146 | 0.423 | 1.895 | 1.180 | 2.414 | 1.872 | 2.144 | 3.295 |
| h13 | 0.641 | 1.140 | 0.198 | 4.595 | 1.650 | 2.450 | 2.456 | 2.048 | 3.650 |
| h14 | 0.322 | 1.374 | 0.378 | 0.930 | 1.950 | 2.418 | 2.632 | 2.176 | 5.230 |
| h15 | 0.181 | 1.944 | 0.321 | 0.260 | 1.810 | 2.444 | 1.896 | 2.256 | 4.293 |
| h16 | 0.214 | 1.542 | 0.207 | 0.535 | 2.640 | 2.467 | 2.072 | 2.328 | 3.895 |
| h17 | 0.781 | 2.148 | 0.495 | 2.125 | 2.810 | 2.553 | 2.080 | 2.288 | 3.028 |
| h18 | 0.764 | 1.902 | 0.282 | 1.025 | 2.720 | 2.757 | 2.016 | 2.336 | 1.980 |
| h19 | 0.426 | 1.968 | 0.336 | 0.140 | 3.580 | 3.042 | 2.720 | 2.464 | 1.768 |
| h20 | 0.426 | 1.968 | 0.336 | 0.140 | 3.580 | 3.042 | 2.720 | 2.464 | 1.768 |
| h21 | 0.496 | 1.956 | 0.207 | 0.210 | 5.310 | 3.515 | 2.672 | 3.136 | 3.033 |
| h22 | 0.561 | 1.986 | 0.405 | 0.480 | 5.390 | 3.248 | 2.488 | 1.312 | 5.695 |
| h23 | 0.554 | 1.872 | 0.246 | 0.195 | 4.750 | 3.075 | 2.432 | 1.336 | 4.033 |
| h24 | 0.578 | 1.986 | 0.045 | 0.100 | 3.170 | 2.713 | 2.088 | 1.184 | 1.180 |
| - | C11 | C12 | C13 | C14 | C15 | C16 | C17 | C18 | C19 |
| h1 | 0.230 | 0.585 | 0.142 | 0.910 | 2.783 | 2.220 | 0.210 | 0.360 | 0.345 |
| h2 | 0.220 | 0.765 | 0.078 | 0.920 | 2.411 | 1.320 | 0.000 | 0.525 | 0.286 |
| h3 | 0.200 | 0.585 | 0.352 | 0.925 | 2.548 | 0.942 | 0.000 | 0.534 | 0.243 |
| h4 | 0.200 | 0.675 | 0.440 | 1.225 | 2.313 | 0.972 | 0.045 | 0.636 | 0.213 |
| h5 | 0.200 | 0.660 | 0.062 | 1.345 | 2.288 | 0.954 | 0.000 | 0.444 | 0.237 |
| h6 | 1.240 | 0.570 | 1.416 | 1.290 | 2.426 | 1.044 | 0.115 | 0.462 | 0.242 |
| h7 | 1.400 | 0.900 | 0.482 | 1.325 | 3.239 | 1.374 | 0.075 | 0.477 | 0.281 |
| h8 | 1.440 | 0.630 | 0.182 | 1.520 | 3.798 | 3.984 | 0.475 | 0.450 | 0.287 |
| h9 | 1.170 | 0.765 | 0.502 | 1.430 | 3.097 | 2.184 | 0.380 | 0.504 | 0.278 |
| h10 | 1.130 | 0.645 | 1.046 | 1.120 | 4.371 | 1.986 | 0.495 | 0.579 | 0.268 |
| h11 | 1.390 | 0.555 | 0.150 | 1.170 | 2.994 | 1.986 | 1.130 | 0.573 | 0.285 |
| h12 | 1.740 | 0.630 | 1.032 | 1.265 | 3.763 | 2.844 | 0.630 | 0.498 | 0.315 |
| h13 | 1.760 | 0.615 | 0.056 | 1.760 | 2.999 | 1.566 | 0.420 | 0.600 | 0.301 |
| h14 | 1.200 | 0.570 | 0.056 | 2.000 | 2.759 | 0.930 | 0.980 | 0.540 | 0.329 |
| h15 | 0.280 | 0.750 | 0.236 | 1.840 | 3.807 | 0.798 | 0.955 | 0.357 | 0.312 |
| h16 | 0.460 | 0.555 | 1.024 | 1.815 | 3.317 | 1.152 | 0.965 | 0.423 | 0.350 |
| h17 | 3.180 | 0.825 | 0.232 | 2.015 | 3.214 | 1.944 | 0.970 | 0.588 | 0.366 |
| h18 | 2.570 | 0.780 | 0.890 | 2.365 | 2.940 | 2.046 | 0.960 | 0.570 | 0.468 |
| h19 | 2.890 | 0.780 | 0.458 | 2.480 | 3.445 | 2.460 | 1.450 | 0.678 | 0.443 |
| h20 | 2.890 | 0.780 | 0.458 | 2.480 | 3.445 | 2.460 | 1.450 | 0.678 | 0.443 |
| h21 | 3.210 | 0.630 | 0.864 | 2.580 | 3.278 | 1.884 | 1.385 | 0.753 | 0.454 |
| h22 | 3.260 | 0.570 | 1.326 | 2.365 | 2.475 | 1.374 | 1.660 | 0.621 | 0.482 |
| h23 | 2.815 | 0.720 | 0.376 | 2.060 | 2.073 | 1.380 | 1.235 | 0.750 | 0.509 |
| h24 | 1.780 | 0.570 | 0.200 | 1.495 | 2.769 | 1.158 | 0.880 | 0.390 | 0.328 |
| - | C20 | C21 | C22 | C23 | C24 | C25 | C26 | C27 | C28 |
| h1 | 1.010 | 0.973 | 0.636 | 0.790 | 0.049 | 1.266 | 0.384 | 0.248 | 0.006 |
| h2 | 1.100 | 1.013 | 0.484 | 0.780 | 0.056 | 1.194 | 0.384 | 0.296 | 0.000 |
| h3 | 0.990 | 0.733 | 0.448 | 0.730 | 0.749 | 1.056 | 0.388 | 0.260 | 0.000 |
| h4 | 1.090 | 0.453 | 0.460 | 0.920 | 1.148 | 1.032 | 0.392 | 0.292 | 0.000 |
| h5 | 1.070 | 0.680 | 0.520 | 0.800 | 1.148 | 1.014 | 0.400 | 0.208 | 0.000 |
| h6 | 1.450 | 0.773 | 0.512 | 1.340 | 1.148 | 1.020 | 0.396 | 0.356 | 0.048 |
| h7 | 2.260 | 0.980 | 0.428 | 0.960 | 1.946 | 1.122 | 0.376 | 0.700 | 0.035 |
| h8 | 0.610 | 1.560 | 0.368 | 0.270 | 1.393 | 1.116 | 0.352 | 0.336 | 0.038 |
| h9 | 0.310 | 1.580 | 0.408 | 0.420 | 1.596 | 1.110 | 0.356 | 0.144 | 0.000 |
| h10 | 0.400 | 1.347 | 0.408 | 1.000 | 2.975 | 1.110 | 0.360 | 0.128 | 0.001 |
| h11 | 0.310 | 1.713 | 0.668 | 0.930 | 1.519 | 1.242 | 0.620 | 0.204 | 0.019 |
| h12 | 0.500 | 1.913 | 0.412 | 1.050 | 2.492 | 1.260 | 0.344 | 0.320 | 0.127 |
| h13 | 0.760 | 3.127 | 0.344 | 1.020 | 1.974 | 1.266 | 0.324 | 0.476 | 0.014 |
| h14 | 0.630 | 2.560 | 0.428 | 0.970 | 1.974 | 1.260 | 0.332 | 0.384 | 0.005 |
| h15 | 1.260 | 1.433 | 1.068 | 1.010 | 2.240 | 1.206 | 0.940 | 0.456 | 0.061 |
| h16 | 1.170 | 2.013 | 0.424 | 1.110 | 2.296 | 1.134 | 2.500 | 0.352 | 0.022 |
| h17 | 1.620 | 4.000 | 0.448 | 1.540 | 1.778 | 1.140 | 2.544 | 2.000 | 0.020 |
| h18 | 1.620 | 1.067 | 0.468 | 1.630 | 1.939 | 1.260 | 2.820 | 0.876 | 0.057 |
| h19 | 1.620 | 1.907 | 0.436 | 1.570 | 1.750 | 1.296 | 2.104 | 1.824 | 0.000 |
| h20 | 1.620 | 1.907 | 0.436 | 1.570 | 1.750 | 1.296 | 2.104 | 1.824 | 0.000 |
| h21 | 2.440 | 2.473 | 1.092 | 1.280 | 1.106 | 1.212 | 2.144 | 0.728 | 0.102 |
| h22 | 2.570 | 2.253 | 1.484 | 1.110 | 1.092 | 1.194 | 2.084 | 0.688 | 0.103 |
| h23 | 1.450 | 1.933 | 1.364 | 0.710 | 1.092 | 1.194 | 2.248 | 0.256 | 0.133 |
| h24 | 1.010 | 1.260 | 0.880 | 0.840 | 0.763 | 1.176 | 2.008 | 0.324 | 0.036 |
| - | C11 | C12 | C13 | C14 | |
|---|---|---|---|---|---|
| h1 | P6 | P7 | P15 | P21 | P27 |
| h2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| h3 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| h4 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| h5 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| h6 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| h7 | 2.070 | 2.299 | 4.375 | 2.361 | 0.356 |
| h8 | 2.280 | 2.627 | 4.824 | 2.785 | 0.700 |
| h9 | 2.530 | 3.247 | 5.385 | 3.286 | 1.004 |
| h10 | 2.592 | 3.438 | 5.325 | 3.329 | 1.581 |
| h11 | 2.966 | 3.642 | 5.673 | 3.639 | 1.735 |
| h12 | 3.346 | 3.826 | 5.769 | 3.751 | 1.859 |
| h13 | 3.509 | 3.639 | 5.643 | 3.735 | 1.915 |
| h14 | 3.945 | 3.863 | 5.825 | 3.812 | 1.984 |
| h15 | 3.297 | 3.803 | 5.704 | 3.742 | 1.756 |
| h16 | 2.994 | 3.492 | 5.353 | 3.461 | 1.562 |
| h17 | 2.640 | 2.877 | 4.642 | 2.832 | 0.915 |
| h18 | 2.810 | 2.553 | 4.276 | 4.000 | 2.000 |
| h19 | 2.720 | 2.757 | 4.101 | 2.237 | 0.876 |
| h20 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| h21 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| h22 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| h23 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| h24 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
References
- Huang, J.; Jiang, C.; Xu, R. A review on distributed energy resources and MicroGrid. Renew. Sustain. Energy Rev. 2008, 12, 2472–2483. [Google Scholar]
- Pudjianto, D.; Ramsay, C.; Strbac, G. Virtual power plant and system integration of distributed energy resources. IET Renew. Power Gener. 2007, 1, 10–16. [Google Scholar] [CrossRef]
- Hierzinger, R.; Albu, M.; van Elburg, H.; Scott, A.; Lazicki, A.; Penttinen, L.; Puente, F.; Saele, H. European Smart Metering Landscape Report 2012—Update May 2013; ÖSTERREICHISCHE ENERGIEAGENTUR–AUSTRIAN ENERGY AGENCY: Vienna, Austria, 2013. [Google Scholar]
- Kohlhepp, P.; Harb, H.; Wolisz, H.; Waczowicz, S.; Müller, D.; Hagenmeyer, V. Large-scale grid integration of residential thermal energy storages as demand-side flexibility resource: A review of international field studies. In Renewable and Sustainable Energy Reviews; Elsevier: Amsterdam, The Netherlands, 2019; Volume 101, pp. 527–547. [Google Scholar]
- Pitì, A.; Verticale, G.; Rottondi, C.; Capone, A.; Lo Schiavo, L. The role of smart meters in enabling real-time energy services for households: The Italian case. Energies 2017, 10, 199. [Google Scholar] [CrossRef]
- Mengelkamp, E.; Notheisen, B.; Beer, C.; Dauer, D.; Weinhardt, C. A blockchain-based smart grid: Towards sustainable local energy markets. Comput. Sci.-Res. Dev. 2018, 33, 207–214. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Cheng, M.; Zhou, Y.; Long, C. A Bidding System for Peer-to-Peer Energy Trading in a Grid connected Microgrid. Energy Procedia 2016, 103, 147–152. [Google Scholar] [CrossRef]
- Espe, E.; Potdar, V.; Chang, E. Prosumer Communities and Relationships in Smart Grids: A Literature Review, Evolution and Future Directions. Energies 2018, 11, 2528. [Google Scholar] [CrossRef]
- Andoni, M.; Robu, V.; Flynn, D.; Abram, S.; Geach, D.; Jenkins, D.; McCallum, P.; Peacock, A. Blockchain technology in the energy sector: A systematic review of challenges and opportunities. Renew. Sustain. Energy Rev. 2019, 100, 143–174. [Google Scholar] [CrossRef]
- Wu, J.; Tran, N. Application of blockchain technology in sustainable energy systems: An overview. Sustainability 2018, 10, 3067. [Google Scholar] [CrossRef]
- Kim, H.J.; Song, Y.H.; Kim, S.W.; Yoon, Y.T. Implementation of peer-to-peer energy auction based on transaction zoning considering network constraints. J. Int. Counc. Electr. Eng. 2019, 9, 53–60. [Google Scholar] [CrossRef]
- Liu, T.; Tan, X.; Sun, B.; Wu, Y.; Guan, X.; Tsang, D.H.K. Energy Management of Cooperative Microgrids with P2P Energy Sharing in Distribution Networks. In Proceedings of the IEEE International Conference on Smart Grid Communications (SmartGridComm), Miami, FL, USA, 2–5 November 2015; pp. 410–415. [Google Scholar]
- Di Silvestre, M.L.; Gallo, P.; Ippolito, M.G.; Musca, R.; Sanseverino, E.R.; Tran, Q.T.T.; Zizzo, G. Ancillary Services in the Energy Blockchain for Microgrids. IEEE Trans. Ind. Appl. 2019, 55, 7310–7319. [Google Scholar] [CrossRef]
- Wang, N.; Xu, W.; Xu, Z.; Shao, W. Peer-to-Peer Energy Trading among Microgrids with Multidimensional Willingness. Energies 2018, 11, 3312. [Google Scholar] [CrossRef]
- Kang, J.; Yu, R.; Huang, X.; Maharjan, S.; Zhang, Y.; Hossain, E. Enabling localized peer-to-peer electricity trading among plug-in hybrid electric vehicles using consortium blockchains. IEEE Trans. Ind. Inform. 2017, 13, 3154–3164. [Google Scholar] [CrossRef]
- Thakur, S.; Hayes, B.P.; Breslin, J.G. Distributed Double Auction for Peer to Peer Energy Trade Using Blockchains. In Proceedings of the 2018 5th International Symposium on Environment-Friendly Energies and Applications (EFEA), Rome, Italy, 24–26 September 2018; pp. 1–8. [Google Scholar]
- Khorasany, M.; Mishra, Y.; Ledwich, G. Design of auction-based approach for market clearing in peer-to-peer market platform. J. Eng. 2019, 2019, 4813–4818. [Google Scholar] [CrossRef]
- Islam, S.N. A New Pricing Scheme for Intra-Microgrid and Inter-Microgrid Local Energy Trading. Electronics 2019, 8, 898. [Google Scholar] [CrossRef]
- Leal-Arcas, R.; Lesniewska, F.; Proedrou, F. Prosumers as New Energy Actors. In Africa-EU Renewable Energy Research and Innovation Symposium; Springer: Berlin/Heidelberg, Germany, 2018; pp. 139–151. [Google Scholar]
- Zhang, C.; Wu, J.; Zhou, Y.; Cheng, M.; Long, C. Peer-to-Peer energy trading in a Microgrid. Appl. Energy 2018, 220, 1–12. [Google Scholar] [CrossRef]
- El Rahi, G.; Etesami, S.R.; Saad, W.; Mandayam, N.B.; Poor, H.V. Managing Price Uncertainty in Prosumer-Centric Energy Trading: A Prospect-Theoretic Stackelberg Game Approach. IEEE Trans. Smart Grid 2019, 10, 702–713. [Google Scholar] [CrossRef]
- Bremdal, B.A.; Olivella, P.; Rajasekharan, J. EMPOWER: A network market approach for local energy trade. In IEEE Manchester PowerTech; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Cali, U.; Fifield, A. Towards the decentralized revolution in energy systems using blockchain technology. Int. J. Smart Grid Clean Energy 2019, 8, 245–256. [Google Scholar]
- Uslar, M.; Rohjans, S.; Neureiter, C.; Pröstl Andrén, F.; Velasquez, J.; Steinbrink, C.; Efthymiou, V.; Migliavacca, G.; Horsmanheimo, S.; Brunner, H.; et al. Applying the Smart Grid Architecture Model for Designing and Validating System-of-Systems in the Power and Energy Domain: A European Perspective. Energies 2019, 12, 258. [Google Scholar] [CrossRef]
- Jogunola, O.; Ikpehai, A.; Anoh, K.; Adebisi, B.; Hammoudeh, M.; Gacanin, H.; Harris, G. Comparative Analysis of P2P Architectures for Energy Trading and Sharing. Energies 2018, 11, 62. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.; Zhang, C.; Cheng, M.; Al-Wakeel, A. Feasibility of peer-to-peer energy trading in low voltage electrical distribution networks. Energy Procedia 2017, 105, 2227–2232. [Google Scholar] [CrossRef]
- Yu, Q.; Meeuw, A.; Wortmann, F. Design and implementation of a blockchain multi-energy system. Energy Inform. 2018, 1, 17. [Google Scholar] [CrossRef]
- Paudel, A.; Chaudhari, K.; Long, C.; Gooi, H.B. Peer-to-Peer Energy Trading in a Prosumer-Based Community Microgrid: A Game-Theoretic Model. IEEE Trans. Ind. Electron. 2018, 66, 6087–6097. [Google Scholar] [CrossRef]
- Aldaouab, I.; Daniels, M.; Ordóñez, R. MPC for Optimized Energy Exchange between Two Renewable-Energy Prosumers. Appl. Sci. 2019, 9, 3709. [Google Scholar] [CrossRef]
- Hou, P.; Yang, G.; Hu, J.; Douglass, P.J.; Xue, Y. An Interactive Transactive Energy Mechanism Integrating Grid Operators, Aggregators and Prosumers. arXiv 2019, arXiv:1912.07139. [Google Scholar]
- Amanbek, Y.; Tabarak, Y.; Nunna, H.K.; Doolla, S. Decentralized Transactive Energy Management System for Distribution Systems with Prosumer Microgrids. In Proceedings of the 19th International Carpathian Control Conference (ICCC), Szilvasvarad, Hungary, 28–31 May 2018; pp. 553–558. [Google Scholar]
- Nizami, M.S.H.; Hossain, M.J.; Amin, B.M.R.; Kashif, M.; Fernandez, E.; Mahmud, K. Transactive Energy Trading of Residential Prosumers Using Battery Energy Storage Systems. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Le Cadre, H.; Jacquot, P.; Wan, C.; Alasseur, C. Peer-to-Peer Electricity Market Analysis: From Variational to Generalized Nash Equilibrium. Eur. J. Oper. Res. 2020, 282, 753–771. [Google Scholar] [CrossRef]
- Neagu, B.C.; Grigoras, G.; Ivanov, O. An Efficient Peer-to-Peer Based Blokchain Approach for Prosumers Energy Trading in Microgrids. In Proceedings of the International Conference on Modern Power Systems (MPS), Cluj Napoca, Romania, 21–23 May 2019; pp. 1–4. [Google Scholar]
- Barrero-González, F.; Pires, V.F.; Sousa, J.L.; Martins, J.F.; Milanés-Montero, M.I.; González-Romera, E.; Romero-Cadaval, E. Photovoltaic Power Converter Management in Unbalanced Low Voltage Networks with Ancillary Services Support. Energies 2019, 12, 972. [Google Scholar] [CrossRef]
- All You Need to Know to Become a prosumer. Available online: https://energyindustryreview.com/renewables/all-you-need-to-know-to-become-a-prosumer/ (accessed on 18 December 2019).
- National Regulatory Authority for Energy. The 228 Order for the Approval of the Technical Norm Technical Conditions for Connection to the Public Electrical Networks of the Prosumers; National Regulatory Authority for Energy: Bucharest, Romania, 2018.
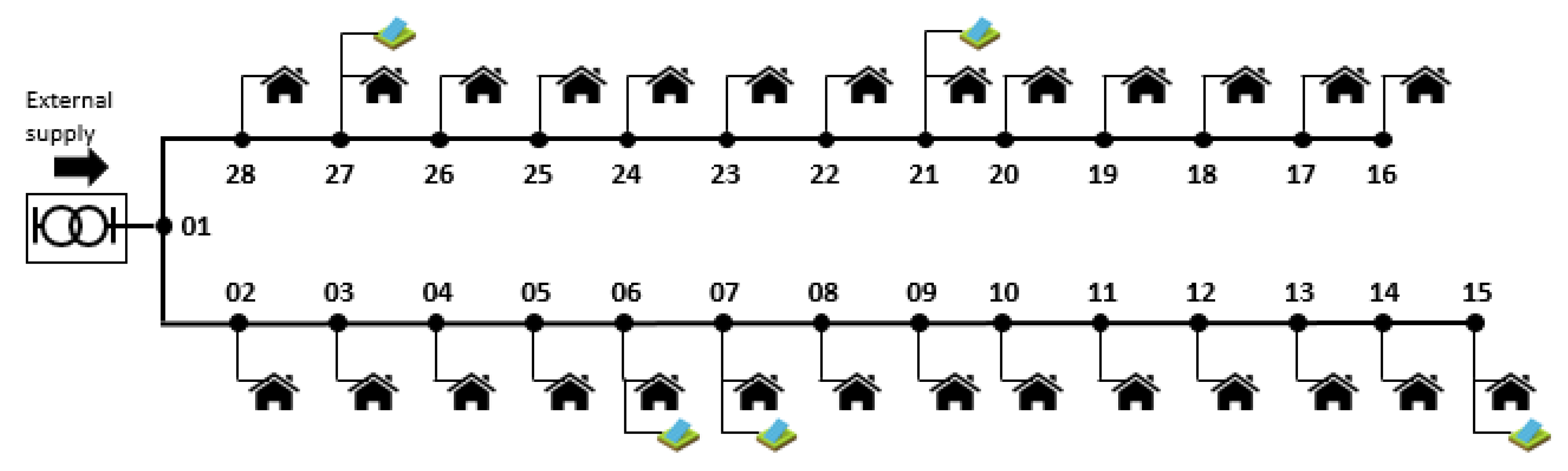
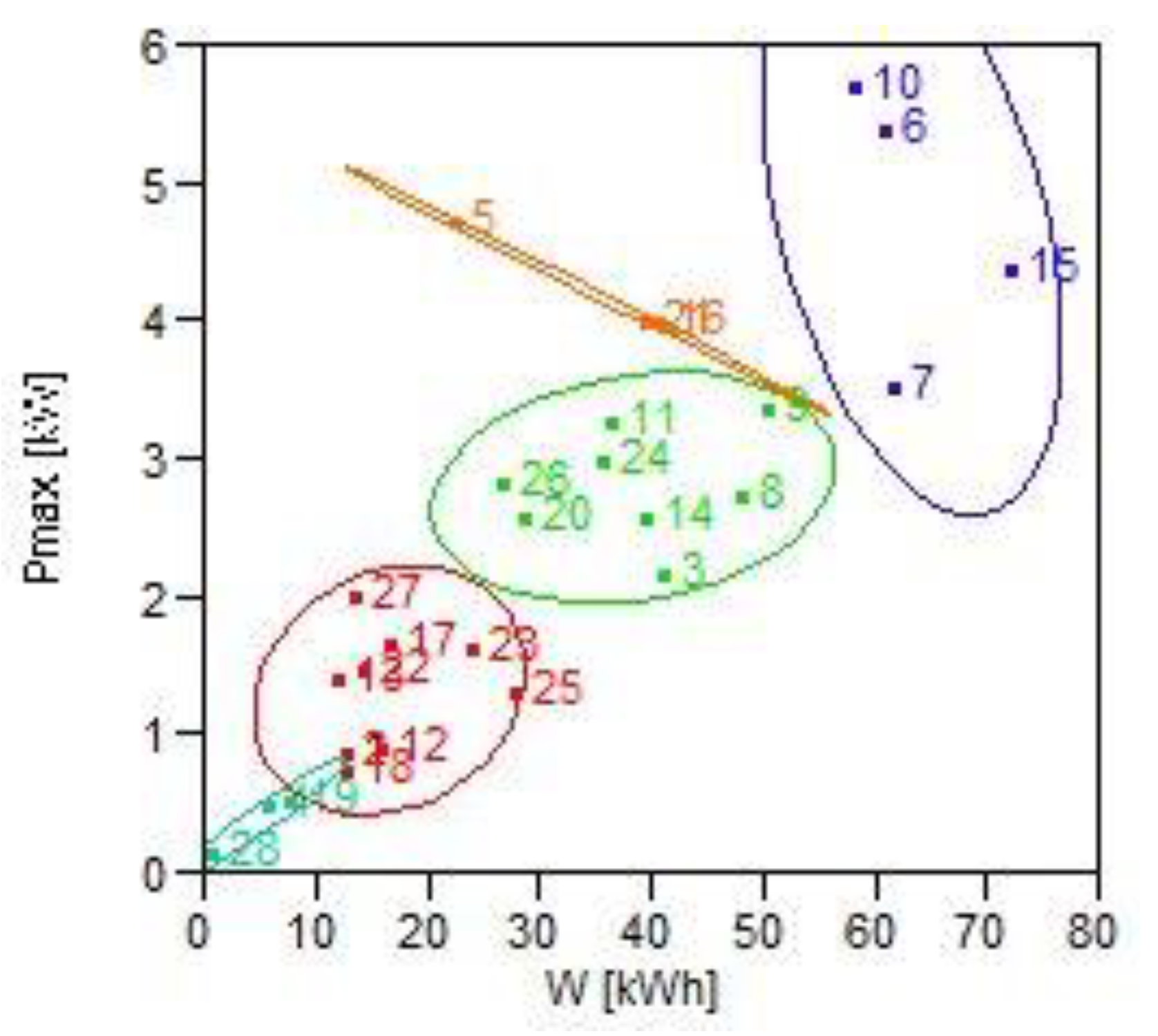
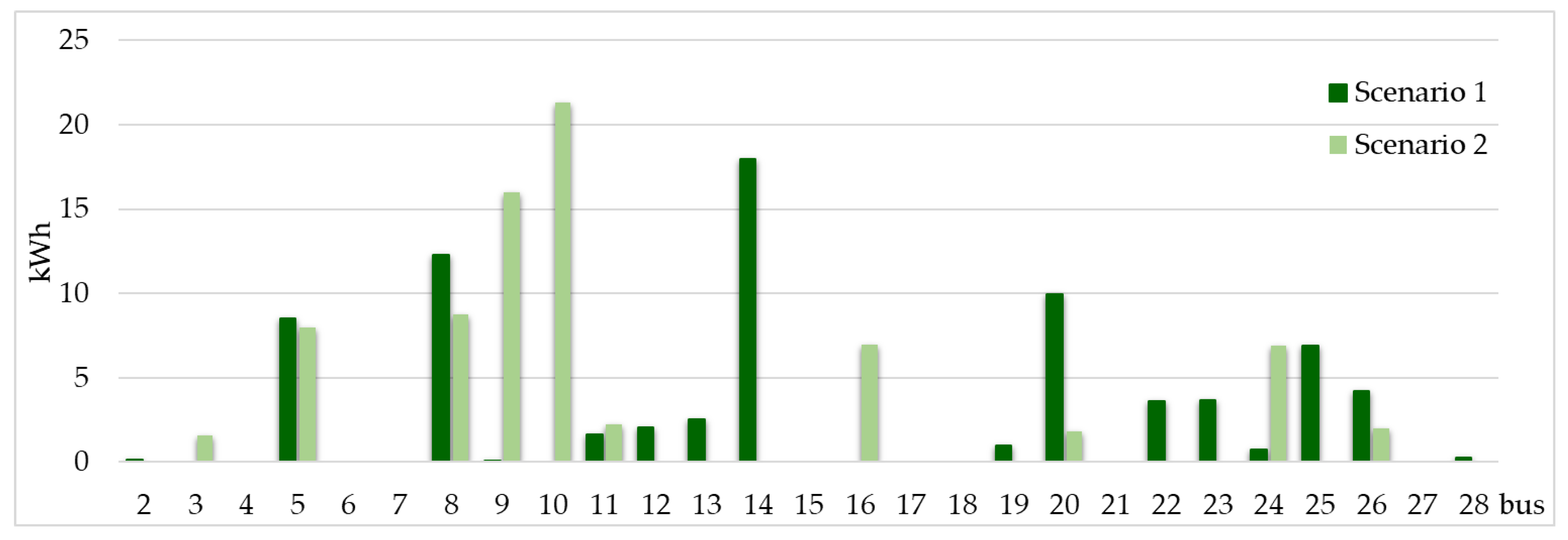
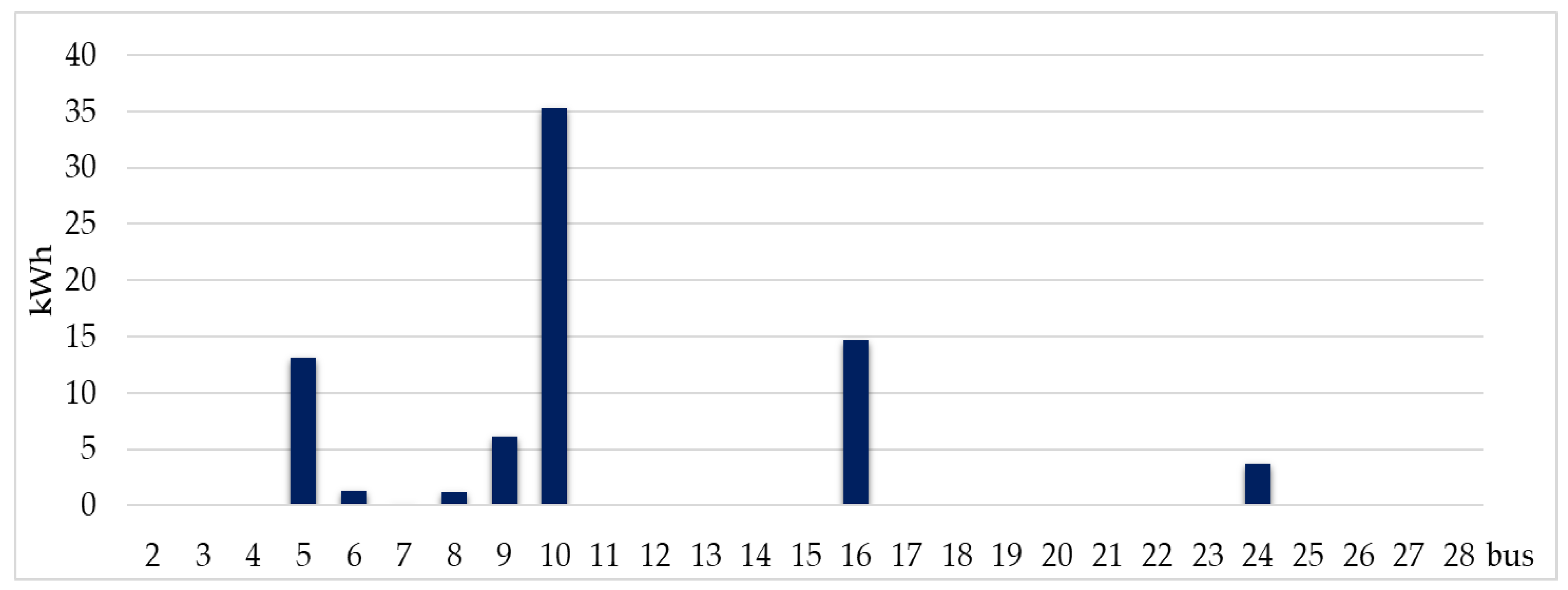
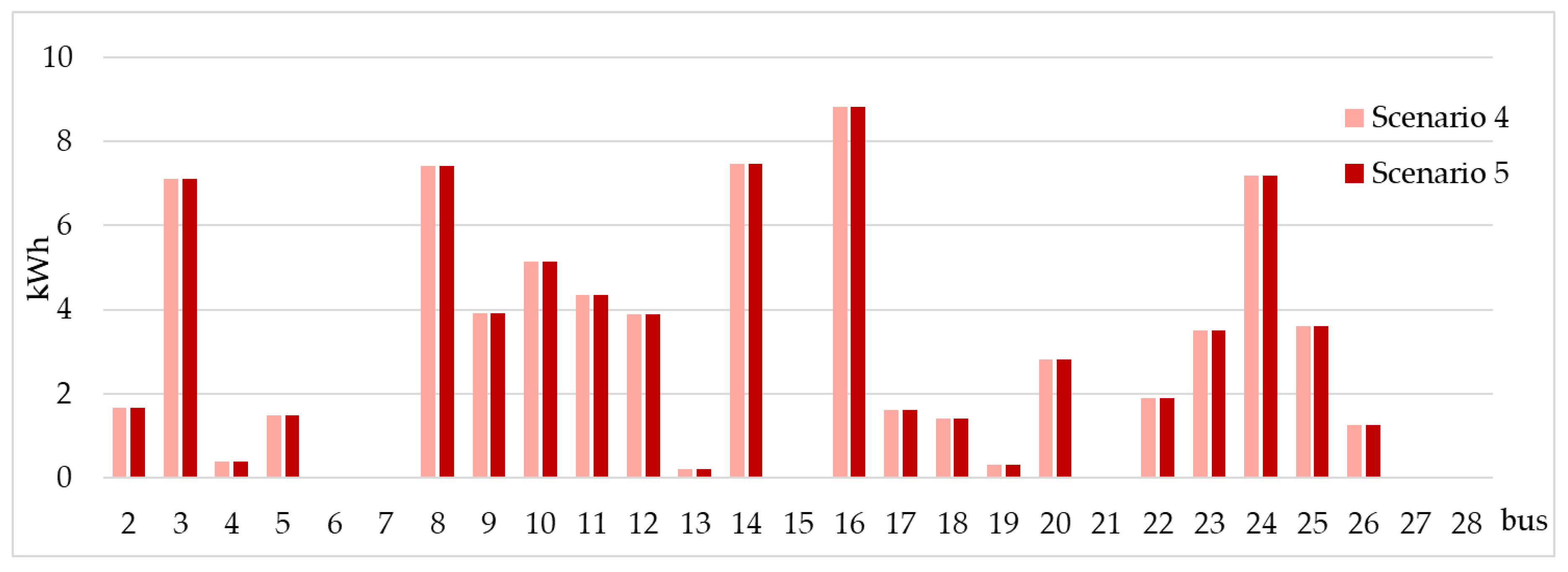
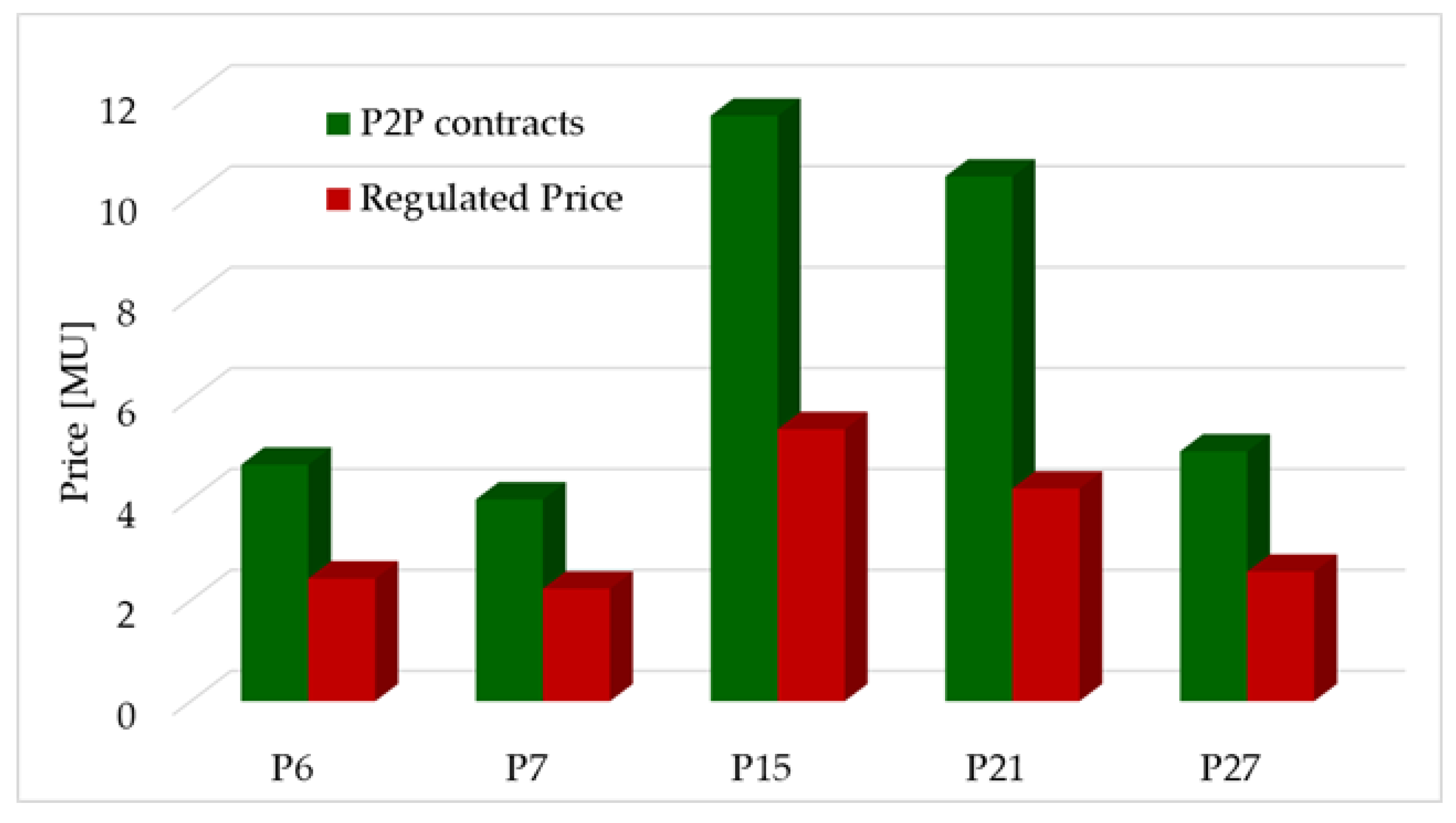
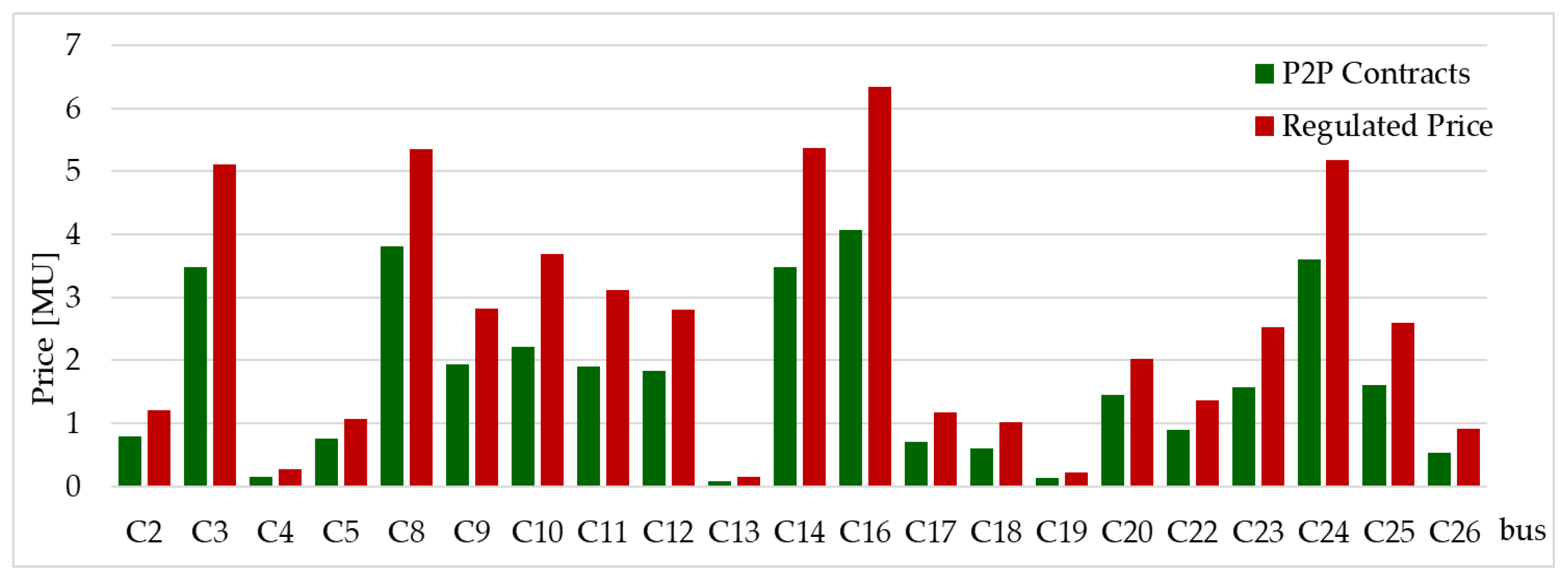
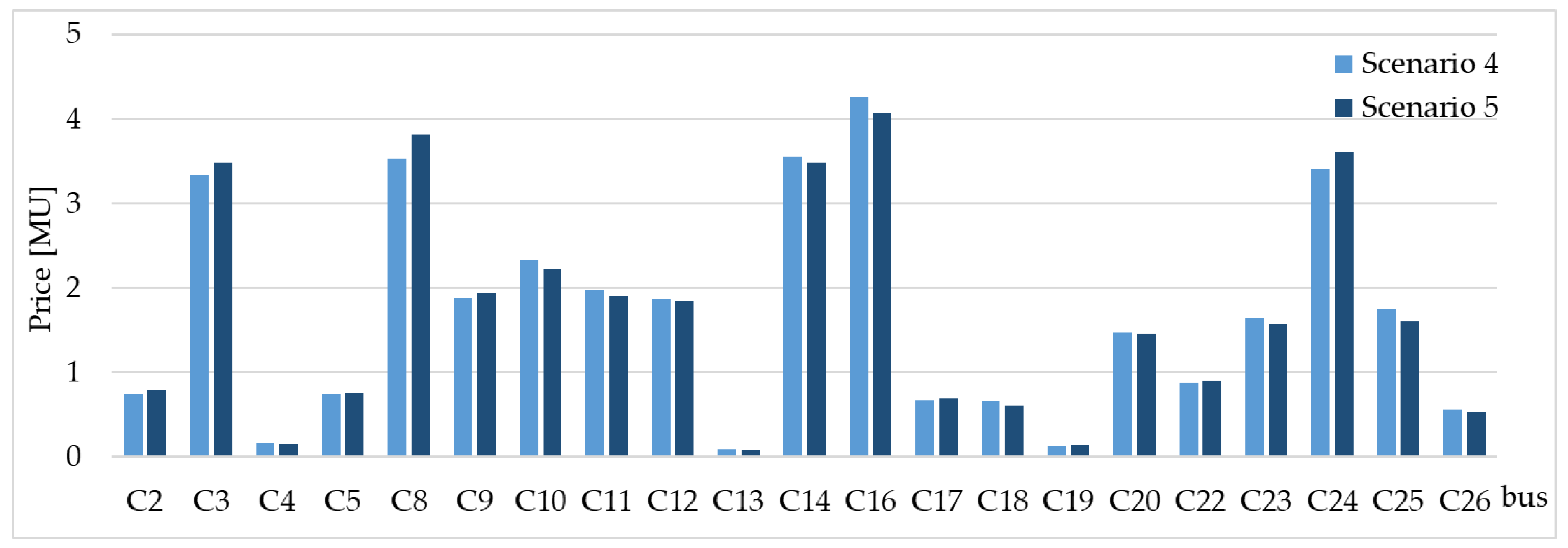
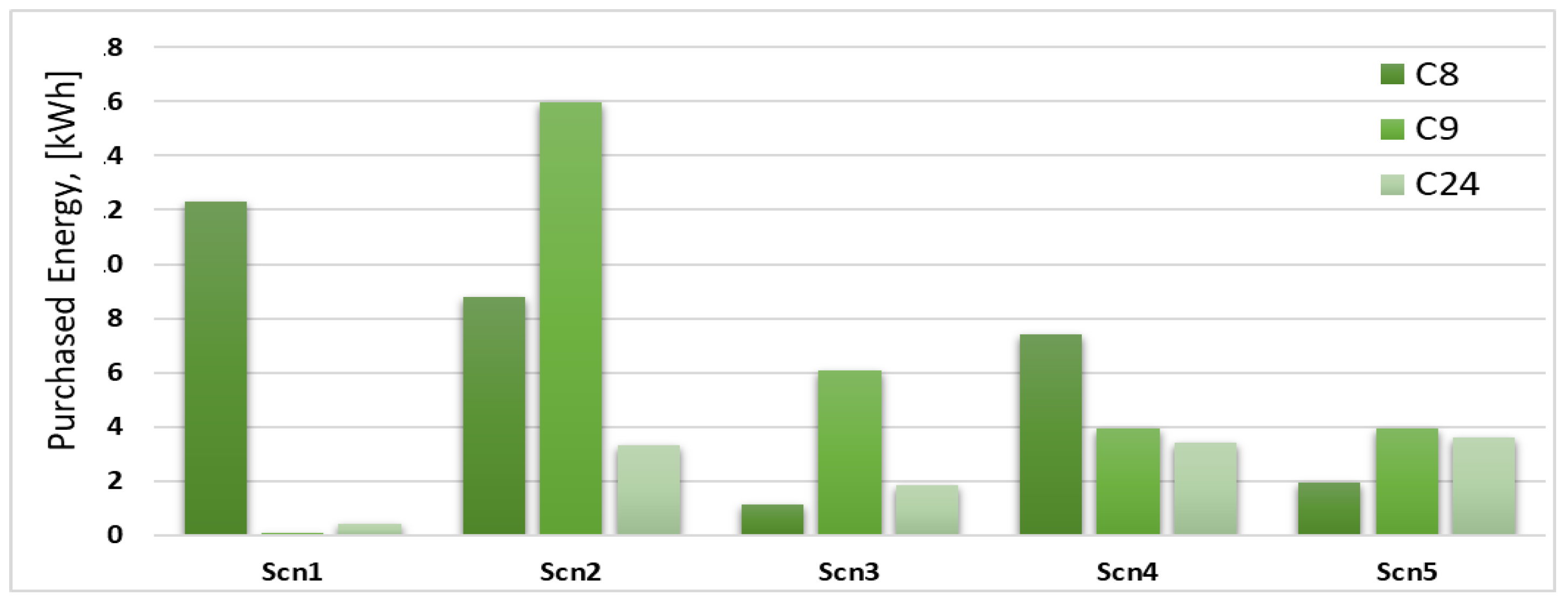
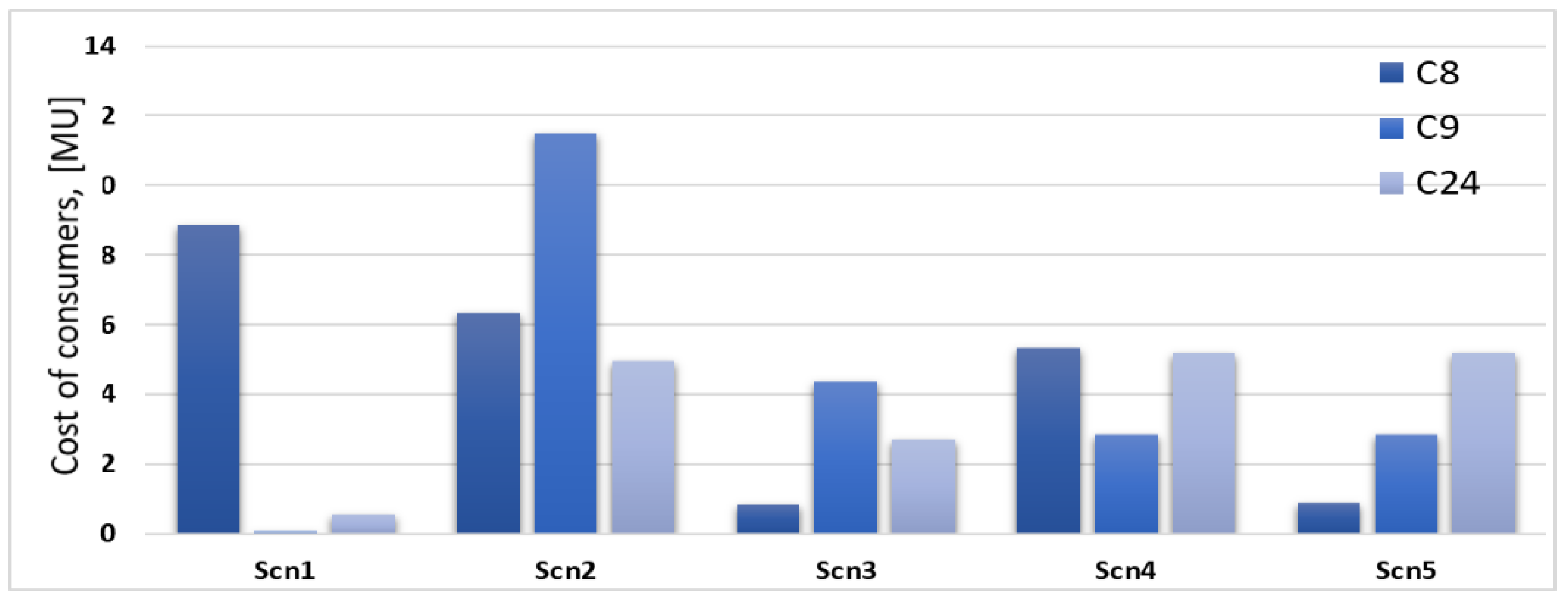
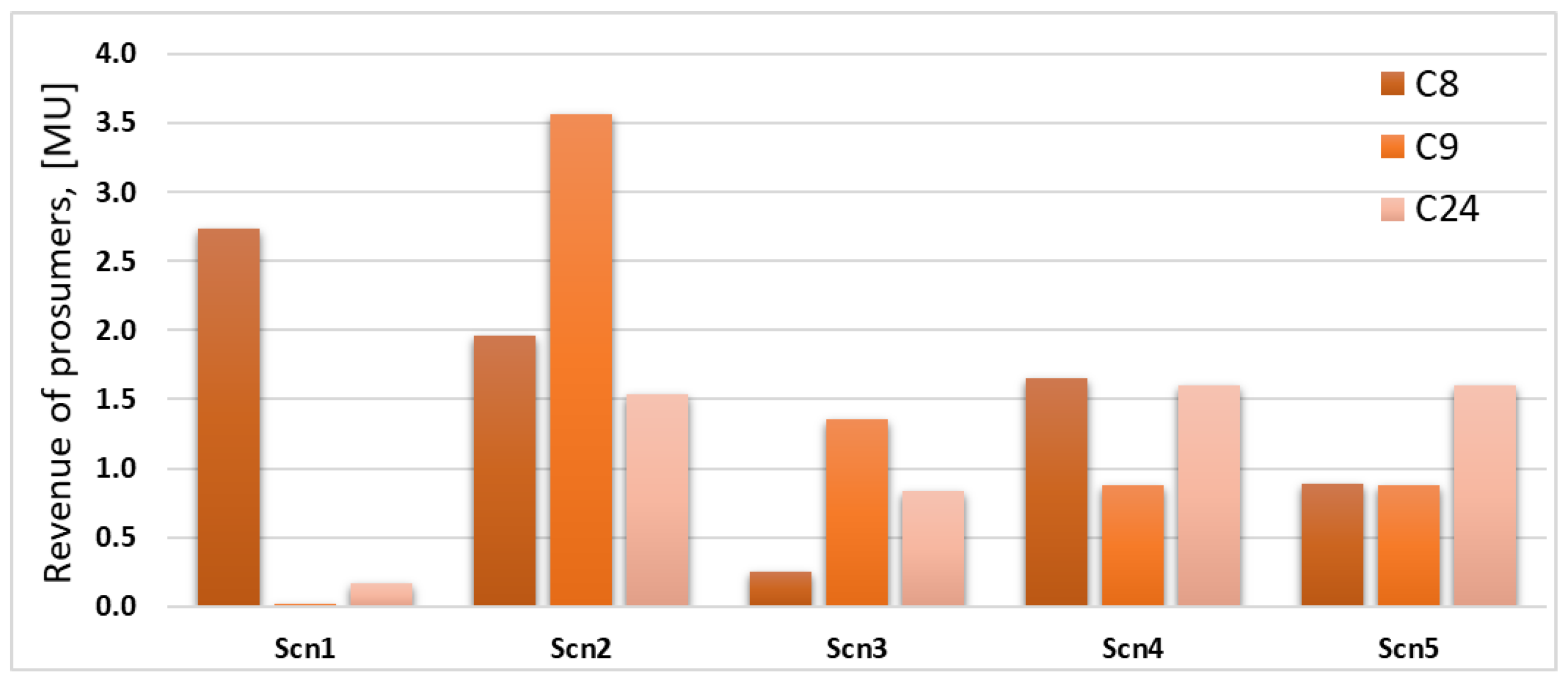
| References | Path of Supply (S1) | Instantaneous Power Demand (S2) | Daily Energy Consumption (S3) | Blockchain Technologies (S4) | Minimum Price for Consumers (S5) | P2P Contracts |
|---|---|---|---|---|---|---|
| [7,17] | no | no | no | no | yes | yes |
| [11,12,25] | yes | no | no | no | no | yes |
| [13] | no | no | yes | yes | no | yes |
| [14,15] | no | no | yes | yes | yes | yes |
| [16,23] | yes | no | no | yes | no | yes |
| [18] | no | no | yes | no | no | no |
| [20,26] | no | no | yes | no | no | yes |
| [21,22,30] | no | no | no | no | yes | no |
| [27] | no | no | no | yes | yes | no |
| [28] | no | no | yes | no | yes | yes |
| [29] | no | yes | no | no | no | yes |
| [31] | no | yes | no | yes | no | no |
| [32,33] | no | no | no | no | yes | yes |
| Proposed approach | yes | yes | yes | yes | yes | yes |
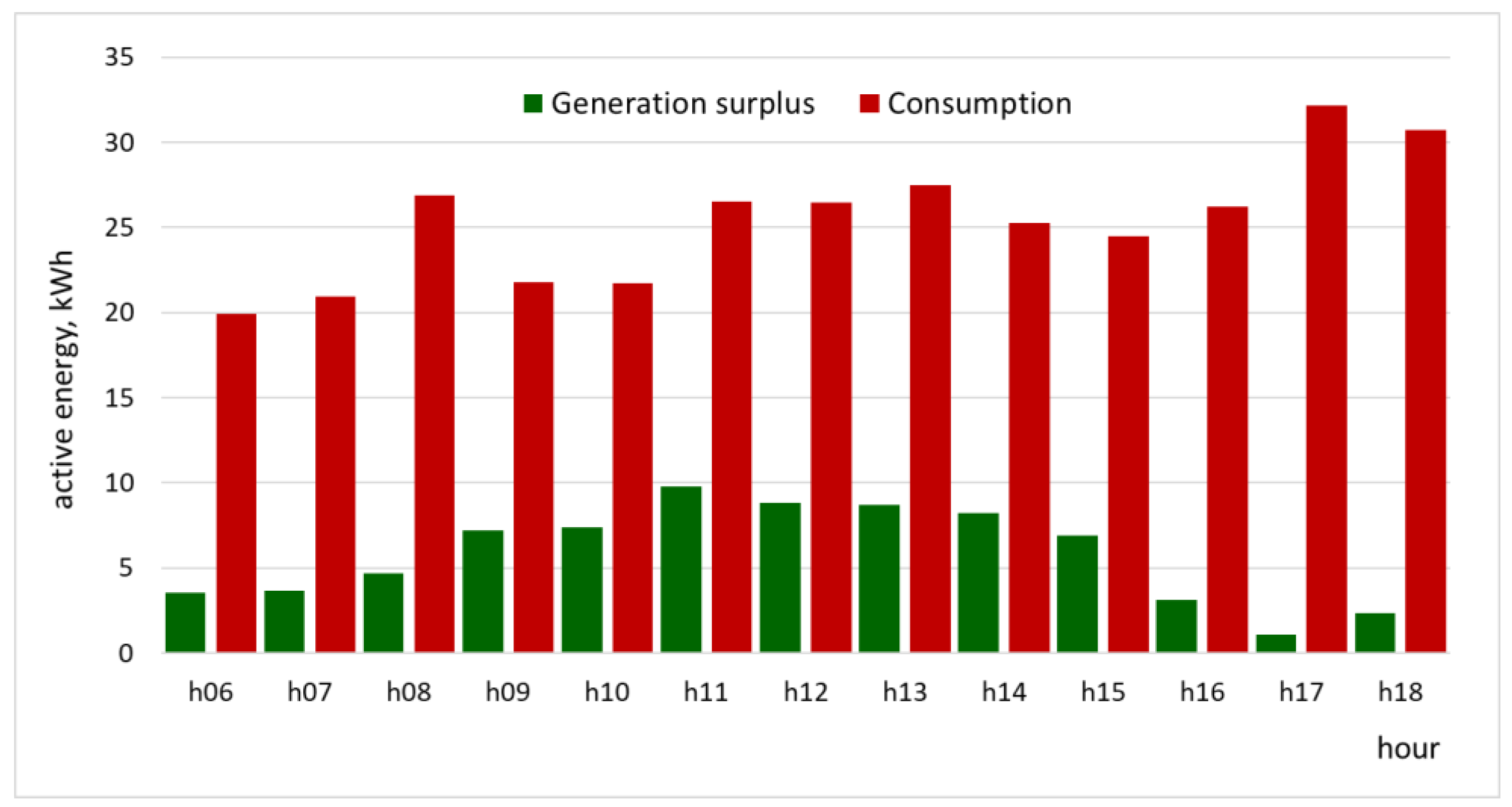
| Hour | Bus with Prosumers | Total Surplus | Total Consumption | ||||
|---|---|---|---|---|---|---|---|
| 6 | 7 | 15 | 21 | 27 | |||
| h06 | 0 | 0 | 1.95 | 1.59 | 0 | 3.54 | 19.91 |
| h07 | 0 | 0.26 | 1.59 | 1.81 | 0 | 3.65 | 20.96 |
| h08 | 0 | 0.70 | 1.59 | 1.73 | 0.67 | 4.68 | 26.86 |
| h09 | 0.74 | 1.06 | 2.23 | 1.75 | 1.44 | 7.21 | 21.78 |
| h10 | 1.12 | 1.09 | 1.30 | 2.29 | 1.61 | 7.41 | 21.74 |
| h11 | 1.89 | 1.40 | 2.78 | 2.04 | 1.66 | 9.75 | 26.50 |
| h12 | 2.33 | 1.23 | 1.88 | 1.82 | 1.60 | 8.85 | 26.45 |
| h13 | 2.29 | 1.41 | 2.83 | 0.69 | 1.51 | 8.73 | 27.51 |
| h14 | 1.35 | 1.39 | 2.95 | 1.18 | 1.37 | 8.23 | 25.25 |
| h15 | 1.18 | 1.05 | 1.55 | 2.03 | 1.11 | 6.91 | 24.46 |
| h16 | 0 | 0.41 | 1.32 | 0.82 | 0.56 | 3.12 | 26.19 |
| h17 | 0 | 0 | 1.06 | 0 | 0 | 1.06 | 32.15 |
| h18 | 0 | 0 | 1.16 | 1.17 | 0 | 2.33 | 30.75 |
| total | 10.90 | 9.99 | 24.17 | 18.90 | 11.51 | 75.48 | 330.52 |
| Selling price | 0.43 | 0.40 | 0.48 | 0.55 | 0.43 | - | - |
| Prosumer | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | Scenario 3 | |||||||||
| Cons. | 6 | 7 | 15 | 21 | 27 | 6 | 7 | 15 | 21 | 27 |
| 1 | X | X | X | X | X | X | X | X | X | X |
| 2 | 4 | 5 | 13 | 8 | 2 | 4 | 4 | 4 | 4 | 4 |
| 3 | 3 | 4 | 12 | 9 | 3 | 3 | 3 | 3 | 3 | 3 |
| 4 | 2 | 3 | 11 | 10 | 4 | 5 | 5 | 5 | 5 | 5 |
| 5 | 1 | 2 | 10 | 11 | 5 | 2 | 2 | 2 | 2 | 2 |
| 6 | X | 1 | 9 | 12 | 6 | X | 1 | 1 | 1 | 1 |
| 7 | 1 | X | 8 | 13 | 7 | 1 | X | 1 | 1 | 1 |
| 8 | 2 | 1 | 7 | 14 | 8 | 3 | 3 | 3 | 3 | 3 |
| 9 | 3 | 2 | 6 | 15 | 9 | 3 | 3 | 3 | 3 | 3 |
| 10 | 4 | 3 | 5 | 16 | 10 | 1 | 1 | 1 | 1 | 1 |
| 11 | 5 | 4 | 4 | 17 | 11 | 3 | 3 | 3 | 3 | 3 |
| 12 | 6 | 5 | 3 | 18 | 12 | 4 | 4 | 4 | 4 | 4 |
| 13 | 7 | 6 | 2 | 19 | 13 | 4 | 4 | 4 | 4 | 4 |
| 14 | 8 | 7 | 1 | 20 | 14 | 3 | 3 | 3 | 3 | 3 |
| 15 | 9 | 8 | X | 21 | 15 | 1 | 1 | X | 1 | 1 |
| 16 | 17 | 18 | 26 | 5 | 11 | 2 | 2 | 2 | 2 | 2 |
| 17 | 16 | 17 | 25 | 4 | 10 | 4 | 4 | 4 | 4 | 4 |
| 18 | 15 | 16 | 24 | 3 | 9 | 4 | 4 | 4 | 4 | 4 |
| 19 | 14 | 15 | 23 | 2 | 8 | 5 | 5 | 5 | 5 | 5 |
| 20 | 13 | 14 | 22 | 1 | 7 | 3 | 3 | 3 | 3 | 3 |
| 21 | 12 | 13 | 21 | X | 6 | 2 | 2 | 2 | X | 2 |
| 22 | 11 | 12 | 20 | 1 | 5 | 4 | 4 | 4 | 4 | 4 |
| 23 | 10 | 11 | 19 | 2 | 4 | 4 | 4 | 4 | 4 | 4 |
| 24 | 9 | 10 | 18 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 25 | 8 | 9 | 17 | 4 | 2 | 4 | 4 | 4 | 4 | 4 |
| 26 | 7 | 8 | 16 | 5 | 1 | 3 | 3 | 3 | 3 | 3 |
| 27 | 6 | 7 | 15 | 6 | X | 4 | 4 | 4 | 4 | X |
| 28 | 5 | 6 | 14 | 7 | 1 | 5 | 5 | 5 | 5 | 5 |
| Scenarios/Bus | Scn1 | Scn2 | Scn3 | Scn4 | Scn5 |
|---|---|---|---|---|---|
| Bus 6 | 10.899 | 10.899 | 10.899 | 10.899 | 10.899 |
| Bus 7 | 9.998 | 9.998 | 9.998 | 9.998 | 9.998 |
| Bus 15 | 24.170 | 24.170 | 24.170 | 24.170 | 24.170 |
| Bus 21 | 18.903 | 18.903 | 18.903 | 18.903 | 18.903 |
| Bus 27 | 11.511 | 11.511 | 11.511 | 11.511 | 11.511 |
| Scn./Cons. | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 |
| Scn1 | 0.136 | 0.000 | 0.000 | 8.532 | 0.000 | 0.000 | 12.287 | 0.077 | 0.000 |
| Scn2 | 0.000 | 1.588 | 0.000 | 7.951 | 0.000 | 0.000 | 8.781 | 15.973 | 21.325 |
| Scn3 | 0.000 | 0.000 | 0.000 | 13.134 | 1.310 | 0.116 | 1.141 | 6.088 | 35.305 |
| Scn4 | 1.678 | 7.109 | 0.378 | 1.489 | 0.000 | 0.000 | 7.430 | 3.927 | 5.133 |
| Scn5 | 1.678 | 7.109 | 0.378 | 1.489 | 0.000 | 0.000 | 7.430 | 3.927 | 5.133 |
| Scn./Cons. | C11 | C12 | C13 | C14 | C15 | C16 | C17 | C18 | C19 |
| Scn1 | 1.615 | 2.036 | 2.546 | 17.973 | 0.000 | 0.000 | 0.000 | 0.000 | 0.963 |
| Scn2 | 2.232 | 0.000 | 0.000 | 0.000 | 0.000 | 6.964 | 0.000 | 0.000 | 0.000 |
| Scn3 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 14.654 | 0.000 | 0.000 | 0.000 |
| Scn4 | 4.340 | 3.885 | 0.206 | 7.460 | 0.000 | 8.814 | 1.625 | 1.407 | 0.315 |
| Scn5 | 4.340 | 3.885 | 0.206 | 7.460 | 0.000 | 8.814 | 1.625 | 1.407 | 0.315 |
| Scn./Cons. | C20 | C21 | C22 | C23 | C24 | C25 | C26 | C27 | C28 |
| Scn1 | 9.949 | 0.000 | 3.597 | 3.654 | 0.740 | 6.919 | 4.191 | 0.000 | 0.265 |
| Scn2 | 1.805 | 0.000 | 0.000 | 0.000 | 6.882 | 0.000 | 1.980 | 0.000 | 0.000 |
| Scn3 | 0.000 | 0.000 | 0.000 | 0.000 | 3.733 | 0.000 | 0.000 | 0.000 | 0.000 |
| Scn4 | 2.822 | 0.000 | 1.901 | 3.500 | 7.187 | 3.612 | 1.264 | 0.000 | 0.001 |
| Scn5 | 2.822 | 0.000 | 1.901 | 3.500 | 7.187 | 3.612 | 1.264 | 0.000 | 0.001 |
| Bus | The Active Energy Surplus | Total kWh | P2P Price | Total Cost/Revenue | |||||
|---|---|---|---|---|---|---|---|---|---|
| P6 | P7 | P15 | P21 | P27 | for Cj | for Pk | |||
| 2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.136 | 0.136 | 0.058 | 0.098 | 0.030 |
| 5 | 8.532 | 0.000 | 0.000 | 0.000 | 0.000 | 8.532 | 3.669 | 6.143 | 1.903 |
| 8 | 2.366 | 9.921 | 0.000 | 0.000 | 0.000 | 12.287 | 4.986 | 8.847 | 2.740 |
| 9 | 0.000 | 0.077 | 0.000 | 0.000 | 0.000 | 0.077 | 0.031 | 0.055 | 0.017 |
| 11 | 0.000 | 0.000 | 1.615 | 0.000 | 0.000 | 1.615 | 0.775 | 1.163 | 0.360 |
| 12 | 0.000 | 0.000 | 2.036 | 0.000 | 0.000 | 2.036 | 0.977 | 1.466 | 0.454 |
| 13 | 0.000 | 0.000 | 2.546 | 0.000 | 0.000 | 2.546 | 1.222 | 1.833 | 0.568 |
| 14 | 0.000 | 0.000 | 17.973 | 0.000 | 0.000 | 17.973 | 8.627 | 12.941 | 4.008 |
| 19 | 0.000 | 0.000 | 0.000 | 0.963 | 0.000 | 0.963 | 0.529 | 0.693 | 0.215 |
| 20 | 0.000 | 0.000 | 0.000 | 9.949 | 0.000 | 9.949 | 5.472 | 7.164 | 2.219 |
| 22 | 0.000 | 0.000 | 0.000 | 3.597 | 0.000 | 3.597 | 1.979 | 2.590 | 0.802 |
| 23 | 0.000 | 0.000 | 0.000 | 3.654 | 0.000 | 3.654 | 2.010 | 2.631 | 0.815 |
| 24 | 0.000 | 0.000 | 0.000 | 0.740 | 0.000 | 0.740 | 0.407 | 0.533 | 0.165 |
| 25 | 0.000 | 0.000 | 0.000 | 0.000 | 6.919 | 6.919 | 2.975 | 4.982 | 1.543 |
| 26 | 0.000 | 0.000 | 0.000 | 0.000 | 4.191 | 4.191 | 1.802 | 3.018 | 0.935 |
| 28 | 0.000 | 0.000 | 0.000 | 0.000 | 0.265 | 0.265 | 0.114 | 0.191 | 0.059 |
| Bus | The Active Energy Surplus, in kWh | Total kWh | P2P Price | Total Cost/Revenue | |||||
|---|---|---|---|---|---|---|---|---|---|
| P6 | P7 | P15 | P21 | P27 | for Cj | for Pk | |||
| 3 | 0.000 | 0.000 | 0.000 | 1.588 | 0.000 | 1.588 | 0.873 | 1.143 | 0.354 |
| 5 | 2.295 | 2.105 | 1.957 | 0.000 | 1.595 | 7.951 | 3.454 | 5.725 | 1.773 |
| 8 | 0.000 | 0.000 | 5.088 | 3.693 | 0.000 | 8.781 | 4.473 | 6.322 | 1.958 |
| 9 | 0.000 | 1.356 | 7.315 | 3.859 | 3.443 | 15.973 | 7.657 | 11.501 | 3.562 |
| 10 | 7.488 | 4.256 | 4.406 | 1.867 | 3.308 | 21.325 | 9.486 | 15.354 | 4.755 |
| 11 | 0.000 | 0.000 | 1.062 | 1.170 | 0.000 | 2.232 | 1.153 | 1.607 | 0.498 |
| 16 | 0.000 | 2.281 | 1.302 | 1.726 | 1.655 | 6.964 | 3.198 | 5.014 | 1.553 |
| 20 | 0.000 | 0.000 | 0.000 | 1.805 | 0.000 | 1.805 | 0.993 | 1.300 | 0.403 |
| 24 | 1.116 | 0.000 | 1.880 | 2.376 | 1.510 | 6.882 | 3.339 | 4.955 | 1.535 |
| 26 | 0.000 | 0.000 | 1.161 | 0.819 | 0.000 | 1.980 | 1.008 | 1.425 | 0.441 |
| Bus | The Active Energy Surplus, in kWh | Total kWh | P2P Price | Total Cost/Revenue | |||||
|---|---|---|---|---|---|---|---|---|---|
| P6 | P7 | P15 | P21 | P27 | for Cj | for Pk | |||
| 5 | 0.000 | 0.058 | 5.091 | 5.604 | 2.381 | 13.134 | 6.573 | 9.456 | 2.929 |
| 6 | 0.000 | 0.000 | 0.208 | 1.102 | 0.000 | 1.310 | 0.706 | 0.943 | 0.292 |
| 7 | 0.000 | 0.000 | 0.116 | 0.000 | 0.000 | 0.116 | 0.056 | 0.084 | 0.026 |
| 8 | 0.000 | 0.000 | 0.000 | 0.000 | 1.141 | 1.141 | 0.491 | 0.822 | 0.255 |
| 9 | 0.000 | 0.000 | 0.012 | 3.301 | 2.775 | 6.088 | 3.014 | 4.383 | 1.358 |
| 10 | 10.899 | 8.954 | 12.399 | 2.491 | 0.563 | 35.305 | 15.831 | 25.420 | 7.873 |
| 16 | 0.000 | 0.986 | 6.345 | 4.595 | 2.728 | 14.654 | 7.140 | 10.551 | 3.268 |
| 24 | 0.000 | 0.000 | 0.000 | 1.811 | 1.922 | 3.733 | 1.822 | 2.688 | 0.832 |
| Bus | The Active Energy Surplus, in kWh | Total kWh | P2P Price | Total Cost/Revenue | |||||
|---|---|---|---|---|---|---|---|---|---|
| P6 | P7 | P15 | P21 | P27 | for Cj | for Pk | |||
| 2 | 0.860 | 0.000 | 0.000 | 0.176 | 0.641 | 1.678 | 0.743 | 1.208 | 0.374 |
| 3 | 0.000 | 1.154 | 2.962 | 1.394 | 1.599 | 7.109 | 3.338 | 5.118 | 1.585 |
| 4 | 0.378 | 0.000 | 0.000 | 0.000 | 0.000 | 0.378 | 0.163 | 0.272 | 0.084 |
| 5 | 0.000 | 0.000 | 0.181 | 0.749 | 0.559 | 1.489 | 0.739 | 1.072 | 0.332 |
| 8 | 0.244 | 1.048 | 0.603 | 2.761 | 2.773 | 7.430 | 3.525 | 5.350 | 1.657 |
| 9 | 0.000 | 0.002 | 2.046 | 0.773 | 1.106 | 3.927 | 1.884 | 2.827 | 0.876 |
| 10 | 2.295 | 1.356 | 0.122 | 1.361 | 0.000 | 5.133 | 2.336 | 3.695 | 1.145 |
| 11 | 1.845 | 0.745 | 1.130 | 0.620 | 0.000 | 4.340 | 1.975 | 3.125 | 0.968 |
| 12 | 0.000 | 0.645 | 2.572 | 0.668 | 0.000 | 3.885 | 1.860 | 2.797 | 0.866 |
| 13 | 0.150 | 0.056 | 0.000 | 0.000 | 0.000 | 0.206 | 0.087 | 0.148 | 0.046 |
| 14 | 1.116 | 0.691 | 2.141 | 2.140 | 1.372 | 7.460 | 3.551 | 5.371 | 1.664 |
| 16 | 1.917 | 1.632 | 1.634 | 3.631 | 0.000 | 8.814 | 4.259 | 6.346 | 1.966 |
| 17 | 0.000 | 1.331 | 0.294 | 0.000 | 0.000 | 1.625 | 0.674 | 1.170 | 0.362 |
| 18 | 0.000 | 0.263 | 1.144 | 0.000 | 0.000 | 1.407 | 0.654 | 1.013 | 0.314 |
| 19 | 0.000 | 0.298 | 0.017 | 0.000 | 0.000 | 0.315 | 0.127 | 0.227 | 0.070 |
| 20 | 0.000 | 0.000 | 1.100 | 1.722 | 0.000 | 2.822 | 1.475 | 2.032 | 0.629 |
| 22 | 0.412 | 0.000 | 1.136 | 0.000 | 0.353 | 1.901 | 0.874 | 1.369 | 0.424 |
| 23 | 0.000 | 0.410 | 3.090 | 0.000 | 0.000 | 3.500 | 1.647 | 2.520 | 0.781 |
| 24 | 0.000 | 0.000 | 2.430 | 1.649 | 3.108 | 7.187 | 3.410 | 5.174 | 1.603 |
| 25 | 0.742 | 0.368 | 1.242 | 1.260 | 0.000 | 3.612 | 1.755 | 2.601 | 0.805 |
| 26 | 0.940 | 0.000 | 0.324 | 0.000 | 0.000 | 1.264 | 0.560 | 0.910 | 0.282 |
| Bus | The Active Energy Surplus, in kWh | Total kWh | P2P Price | Total Cost/Revenue | |||||
|---|---|---|---|---|---|---|---|---|---|
| P6 | P7 | P15 | P21 | P27 | for Cj | for Pk | |||
| 2 | 0.000 | 0.860 | 0.000 | 0.817 | 0.000 | 1.678 | 0.794 | 1.208 | 0.374 |
| 3 | 0.889 | 0.000 | 2.610 | 2.430 | 1.179 | 7.109 | 3.479 | 5.118 | 1.585 |
| 4 | 0.000 | 0.378 | 0.000 | 0.000 | 0.000 | 0.378 | 0.151 | 0.272 | 0.084 |
| 5 | 0.000 | 0.000 | 0.930 | 0.559 | 0.000 | 1.489 | 0.754 | 1.072 | 0.332 |
| 8 | 1.184 | 0.108 | 0.546 | 4.988 | 0.603 | 7.430 | 3.818 | 5.350 | 1.657 |
| 9 | 0.002 | 0.000 | 0.538 | 1.879 | 1.508 | 3.927 | 1.941 | 2.827 | 0.876 |
| 10 | 2.663 | 1.413 | 1.056 | 0.000 | 0.000 | 5.133 | 2.217 | 3.695 | 1.145 |
| 11 | 1.690 | 1.397 | 0.000 | 0.620 | 0.633 | 4.340 | 1.899 | 3.125 | 0.968 |
| 12 | 0.000 | 0.000 | 3.153 | 0.087 | 0.645 | 3.885 | 1.839 | 2.797 | 0.866 |
| 13 | 0.056 | 0.150 | 0.000 | 0.000 | 0.000 | 0.206 | 0.084 | 0.148 | 0.046 |
| 14 | 0.047 | 1.093 | 2.906 | 1.331 | 2.083 | 7.460 | 3.480 | 5.371 | 1.664 |
| 16 | 2.031 | 1.517 | 3.289 | 1.308 | 0.668 | 8.814 | 4.066 | 6.346 | 1.966 |
| 17 | 0.886 | 0.000 | 0.000 | 0.000 | 0.739 | 1.625 | 0.699 | 1.170 | 0.362 |
| 18 | 0.000 | 0.263 | 0.214 | 0.000 | 0.930 | 1.407 | 0.608 | 1.013 | 0.314 |
| 19 | 0.298 | 0.000 | 0.000 | 0.000 | 0.017 | 0.315 | 0.135 | 0.227 | 0.070 |
| 20 | 0.000 | 0.000 | 1.410 | 1.412 | 0.000 | 2.822 | 1.453 | 2.032 | 0.629 |
| 22 | 0.000 | 0.412 | 1.136 | 0.353 | 0.000 | 1.901 | 0.904 | 1.369 | 0.424 |
| 23 | 0.000 | 0.410 | 1.477 | 0.000 | 1.613 | 3.500 | 1.567 | 2.520 | 0.781 |
| 24 | 1.152 | 0.000 | 3.031 | 3.003 | 0.000 | 7.187 | 3.602 | 5.174 | 1.603 |
| 25 | 0.000 | 1.056 | 1.547 | 0.117 | 0.892 | 3.612 | 1.613 | 2.601 | 0.805 |
| 26 | 0.000 | 0.940 | 0.324 | 0.000 | 0.000 | 1.264 | 0.532 | 0.910 | 0.282 |
| No. of. Scenarios | No. of Consumers | Diff. of Common Consumers |
|---|---|---|
| Scn1 | 16 | 13 |
| Scn2 | 10 | 7 |
| Scn3 | 8 | 5 |
| Scn4 | 21 | 18 |
| Scn5 | 23 | 20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neagu, B.-C.; Ivanov, O.; Grigoras, G.; Gavrilas, M. A New Vision on the Prosumers Energy Surplus Trading Considering Smart Peer-to-Peer Contracts. Mathematics 2020, 8, 235. https://doi.org/10.3390/math8020235
Neagu B-C, Ivanov O, Grigoras G, Gavrilas M. A New Vision on the Prosumers Energy Surplus Trading Considering Smart Peer-to-Peer Contracts. Mathematics. 2020; 8(2):235. https://doi.org/10.3390/math8020235
Chicago/Turabian StyleNeagu, Bogdan-Constantin, Ovidiu Ivanov, Gheorghe Grigoras, and Mihai Gavrilas. 2020. "A New Vision on the Prosumers Energy Surplus Trading Considering Smart Peer-to-Peer Contracts" Mathematics 8, no. 2: 235. https://doi.org/10.3390/math8020235
APA StyleNeagu, B.-C., Ivanov, O., Grigoras, G., & Gavrilas, M. (2020). A New Vision on the Prosumers Energy Surplus Trading Considering Smart Peer-to-Peer Contracts. Mathematics, 8(2), 235. https://doi.org/10.3390/math8020235








