Comparing Groups of Decision-Making Units in Efficiency Based on Semiparametric Regression

Abstract

We consider a stochastic frontier model in which a deviation of output from the production frontier consists of two components, a one-sided technical inefficiency and a two-sided random noise. In such a situation, we develop a semiparametric regression-based test and compare the technical efficiencies of the different decision-making unit groups, assuming that the production frontier function is the same for all the groups. Our test performs better than the previously proposed ones for the same purpose in numerical studies, and also has the theoretical advantage of working under more general assumptions. To illustrate our method, we apply the proposed test to Program for International Student Assessment (PISA) 2015 data and investigate whether an efficiency difference exists between male and female student groups at a specific age in terms of learning time and achievement in mathematics.

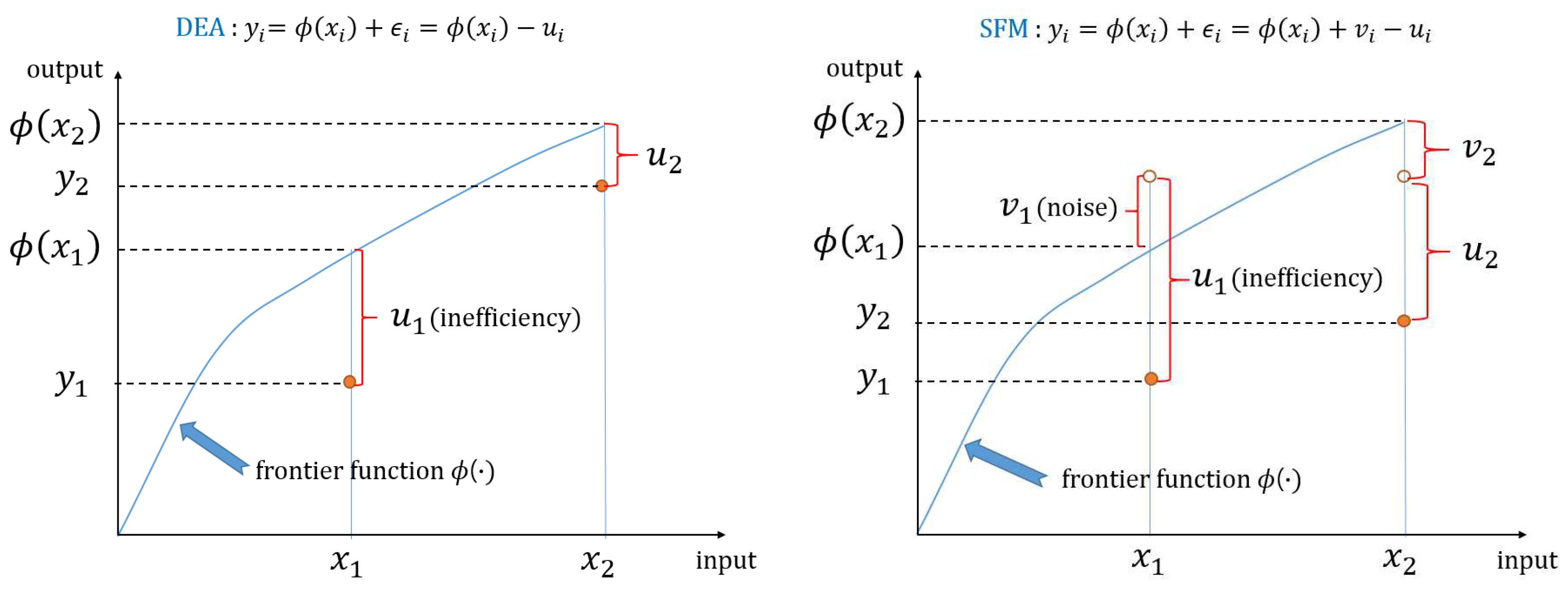
1. Introduction

Efficiency comparison between groups is currently used in various fields such as banking, insurance, sports, and R&D investment evaluation. Numerous empirical studies frequently analyze group efficiency using so-called Data Envelopment Analysis (DEA). DEA is a body of techniques for measuring relative efficiency by comparing it with the possible frontiers of decision-making units (DMUs) with multiple inputs and outputs. Here, the term DMU is used to collectively refer to all the units in which the production activity takes place. In the DEA framework, the DMU efficiency scores of each group can be obtained after specifying some assumptions appropriate to the situation, and then the comparison of the efficiency distributions of the groups is made on the basis of their obtained scores. For example, Golany and Storberg [1] and Lee et al. [2] applied non-parametric tests, such as the Mann–Whitney (MW) and Kruskal–Wallis tests, to the efficiency scores. Cummins et al. [3] introduced a dummy variable to indicate the groups, and then regressed the efficiency scores on the dummy variable. Simar and Zelenyuk [4] adapted the test developed in Li [5] to the DEA context and applied it to the obtained scores, to test the equality of efficiency distributions. O’Donnell et al. [6] used the concept of a meta-frontier to compare the technical efficiencies of firms that may be classified into different groups.

However, this stream of research under the DEA framework has a limitation in that it does not consider the noise factor in the production process. DEA typically assumes that the inefficiency of the DMU is the only cause of its production not reaching its maximum output, but obviously there are many uncontrolled factors which need to be considered as the cause. From this recognition, Aigner and Chu [7] and Meeusen and van den Broeck [8] first proposed the stochastic frontier model (SFM), which allows for both unobserved variation in output: the technical inefficiency of the production unit and the noise which represents the effect of innumerable uncontrollable factors. For illustrative comparison between DEA and SFM frameworks, see Figure 1.

Nowadays, the stochastic frontier model is used in a large literature of studies of production. Hence, we feel the need to develop a method and compare the efficiency difference between groups under SFM framework. One pioneering work in this direction is Banker et al. [9]. They developed five DEA-based hypothesis tests to compare the efficiency of groups under SFM. Although the paper referred above is an important development toward group efficiency comparison under SFM, their tests need to improve further.

First, their rather strong assumptions might limit the applicability of the proposed methods. For their parametric tests, they assumed the equality of both noise variance and inefficiency variance across groups. Second, their theoretical justification of the proposed methods needs to be checked. As regards their ordinary least squares (OLS) test of the mean difference in inefficiency, they provided its asymptotic normality as theoretical basis, but to our knowledge, such asymptotic normality is difficult to obtain because of the slow convergence rate of the DEA estimator when the number of input variables is greater than or equal to 2. The same comment is given in Section 3.2 of Simar and Wilson [10] on a similar type of asymptotic normality result as proof of Proposition 1 in Banker and Natarajan [11]. Finally, because they used the DEA methods for SFM, the tests they developed were based not directly on inefficiency itself, but on the inefficiency contaminated by positive measurement error due to noise. This indirect approach can lower the performance of their tests.

This observation has motivated us to develop a theoretically sound tool for comparison of group inefficiencies in the presence of noise. We develop such a methodology using a semi-parametric regression technique instead of DEA methods. The newly developed test performs better than the tests of Banker et al. [9] in numerical studies. It also has the theoretical advantage of working under more general assumptions compared to Banker et al. [9].

The rest of this paper is organized as follows. Section 2 describes our proposed test for group inefficiency comparison. We then perform some simulation studies and compare our test with the tests proposed by Banker et al. [9] in Section 3. We illustrate our method by applying the proposed test to Program for International Student Assessment (PISA) 2015 data and investigate whether an efficiency difference exists between male and female student groups at a specific age in terms of learning time and achievement in mathematics in Section 4. Section 5 provides some discussion and future research topics.

2. Group Efficiency Comparison under SFM

Assume that we have observations on n DMUs, where each observation consists of a vector of p inputs ${\mathbf{X}}_i={(X_{1,i},\dots ,X_{p,i})}^{\top }$ and the corresponding output $Y_i$. We consider the case where n DMUs can be divided into two distinct groups with $n_l$ observations $(n=n_1+n_2)$. We assume the following stochastic frontier model for two groups of DMUs:

$$\begin{array}{ccc}\hfill (\mathrm{The}\mathrm{first}\mathrm{group})Y_i& =& \varphi ({\mathbf{X}}_i)+{\epsilon }_{1,i},i\in \{1,\dots ,n_1\};\hfill \\ \hfill (\mathrm{The}\mathrm{second}\mathrm{group})Y_i& =& \varphi ({\mathbf{X}}_i)+{\epsilon }_{2,i},i\in \{n_1+1,\dots ,n_1+n_2\},\hfill \end{array}$$

(1)

where ${\epsilon }_{l,i}=V_{l,i}-U_{l,i}$, $V_{l,i}$ is a random noise term of the lth group with $E(V_{l,i}|{\mathbf{X}}_i)=0$, and $U_{l,i}$ is an inefficiency term of the lth group with $U_{l,i}\ge 0$ for $l=1,2$. We assume that the same production technology is applied to both DMU groups. Hence, the production frontier function $\varphi (·)$ is the same throughout the groups, as in Banker et al. [9]. Under this model, we need to estimate the difference $E(U_1)-E(U_2)$ and test the hypothesis

$$\begin{array}{c}\hfill H_0:E(U_1)-E(U_2)=0\mathrm{vs}.H_1:E(U_1)-E(U_2)>0(<0)\end{array}$$

(2)

to know which DMU group is more efficient. A novelty of our approach in developing the test is to implement the test without imposing any parametric assumption on the frontier function $\varphi (·)$, and with minimal assumptions on inefficiency and random noise. Banker et al. [9] also implemented the test without any parametric assumption on $\varphi (·)$, but with additional restrictive parametric assumptions on noise and inefficiency. In the following sections, we first review the work of Banker et al. [9] and then explain the development of our semiparametric regression-based test.

2.1. The Previous Work

To apply the DEA methods to SFM, Banker et al. [9] assumed that the random noise variables $V_{1,i},V_{2,i}$ are bounded above by $V^{max}$, that is, $V_{1,i},V_{2,i}\le V^{max}$. Under this assumption, they transformed model (1) as

$$\begin{array}{c}\hfill Y_i=(\varphi ({\mathbf{X}}_i)+V^{max})-(V^{max}-V_{l,i}+U_{l,i})\equiv \tilde{\varphi }({\mathbf{X}}_i)-{\tilde{U}}_{l,i},l=1,2.\end{array}$$

(3)

Since ${\tilde{U}}_{l,i}=(V^{max}-V_{1,i})+U_{l,i}\ge 0$, they considered the translated production function $\tilde{\varphi }(·)=\varphi (·)+V^{max}$ as a new production function, and ${\tilde{U}}_{l,i}$ as the inefficiency of the DEA framework. The new inefficiency ${\tilde{U}}_i^l$ can be estimated as $\widehat{\tilde{\varphi }}({\mathbf{X}}_i)-Y_i$ after $\tilde{\varphi }(·)$ is estimated using the conventional DEA methods. After estimating ${\tilde{U}}_{l,i}$ using DEA methods, they used it for group efficiency comparison. This approach is advantageous in that we use the strength of the existing well-developed DEA techniques. However, the approach has one disadvantage in that the tests developed are based not on inefficiency ($U_{l,i}$) itself, but on the inefficiency contaminated by the positive measurement error ($V^{max}-V_{l,i}$) due to random noise. Additionally, the distributional property of the inefficiency estimated using DEA methods is generally hard to derive or quite complicated, making it very difficult to develop a statistical test theory based on estimated inefficiency (estimate of ${\tilde{U}}_{l,i}$). Hence, we are motivated to develop a test for (2) directly based on inefficiency $U_{l,i}$. We will explain this in the following section.

2.2. The Proposed Test

This section introduces our approach to testing the hypothesis in (2). Unlike Banker et al. [9], we do not require that neither the noise variance nor inefficiency should be equal across groups. Moreover, we allow for distributional difference in the composite error $\epsilon$ and input vector ${\mathbf{X}}_i$ from the production environmental factors of each group. Specifically, the variance of $V_l$ and mean of inefficiency $U_l$ can differ by the group as well as conditional distribution of ${\mathbf{X}}_i$, given group l.

First, model (1) can be written as two nonparametric mean regression models as follows:

$$\begin{array}{ccc}\hfill Y_i& =& [\varphi ({\mathbf{X}}_i)-E(U_1)]+[V_{1,i}-(U_{1,i}-E(U_1))]\hfill \\ & \equiv & {\varphi }^{*}({\mathbf{X}}_i)+{\epsilon }_{1,i}^{*},i\in \{1,\dots ,n_1\};\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill Y_i& =& [E(U_1)-E(U_2)]+[\varphi ({\mathbf{X}}_i)-E(U_1)]+[V_{2,i}-(U_{2,i}-E(U_2))]\hfill \\ & \equiv & {\beta }_0+{\varphi }^{*}({\mathbf{X}}_i)+{\epsilon }_{2,i}^{*},i\in \{n_1+1,\dots ,n_1+n_2\},\hfill \end{array}$$

(5)

where $E({\epsilon }_{1,i}^{*})=E({\epsilon }_{2,i}^{*})=0$, and ${\beta }_0=E(U_1)-E(U_2)$. If a dummy variable is defined for groups letting $T_i=0$ for $i\in \{1,\dots ,n_1\}$ and $T_i=1$ for $i\in \{n_1+1,\dots ,n_1+n_2\}$, the two models (4) and (5) can be integrated into a single partial linear semiparametric regression model as follows:

$$Y_i={\beta }_0{T}_i+{\varphi }^{*}({\mathbf{X}}_i)+{\epsilon }_i^{*},i\in \{1,\dots ,n\},$$

(6)

where ${\epsilon }_i^{*}=(1-I(T_i=1)){\epsilon }_{1,i}^{*}+I(T_i=1){\epsilon }_{2,i}^{*}$ and $E({\epsilon }_i^{*}|T_i,{\mathbf{X}}_i)=0$. Using this model (6), we can test hypothesis (2) by testing hypothesis

$$H_0:{\beta }_0=0\mathrm{vs}.H_1:{\beta }_0>0(<0).$$

(7)

Note that $Var({\epsilon }_i^{*}|T_i,{\mathbf{X}}_i)=(1-I(T_i=1))Var({\epsilon }_{1,i}^{*})+I(T_i=1)Var({\epsilon }_{2,i}^{*})$. Thus, model (6) is a heteroscedastic partial linear model. Liang [12] and Ma et al. [13] studied model (6) when ${\mathbf{X}}_i$ is univariate. By extending the theory from there to the case where ${\mathbf{X}}_i$ is multivariate, we can test hypothesis (7). In Appendix A, we prove the asymptotic normality of the kernel-based profile estimator of ${\beta }_0$ based on a local linear model smoother when ${\mathbf{X}}_i$ is multivariate, and provide the necessary assumptions for it. As with the estimator in Liang [12], the kernel-based profile estimator of ${\beta }_0$ when ${\mathbf{X}}_i$ is multivariate is given as

$$\begin{array}{c}\hfill {\widehat{\beta }}_0={({\mathbf{T}}^{\top }{(\mathbf{I}-\mathbf{S})}^{\top }(\mathbf{I}-\mathbf{S})\mathbf{T})}^{-1}{\mathbf{T}}^{\top }{(\mathbf{I}-\mathbf{S})}^{\top }(\mathbf{I}-\mathbf{S})\mathbf{Y}\equiv \mathbf{H}\mathbf{Y},\end{array}$$

(8)

where $\mathbf{T}={(T_1,\dots ,T_n)}^{\top }$, $\mathbf{Y}={(Y_1,\dots ,Y_n)}^{\top }$, and $\mathbf{S}$ the smoother matrix for estimating the vector ${(E(·|{\mathbf{X}}_1),\dots ,E(·|{\mathbf{X}}_n))}^{\top }$. If we choose local linear regression as the smoothing method, the smoothing matrix $\mathbf{S}={[{\mathbf{s}}_{{\mathbf{X}}_1}\cdots {\mathbf{s}}_{{\mathbf{X}}_n}]}^{\top }$ will be a collection of row vectors, each of which is the smoother vector

$${\mathbf{s}}_{\mathbf{x}}^{\top }={\mathbf{e}}_1^{\top }{({\mathbf{X}}_{\mathbf{x}}^{\top }{\mathbf{W}}_{\mathbf{x}}{\mathbf{X}}_{\mathbf{x}})}^{-1}{\mathbf{X}}_{\mathbf{x}}^{\top }{\mathbf{W}}_{\mathbf{x}},$$

(9)

where ${\mathbf{e}}_1^{\top }=(1,0,\dots ,0)$ is a $(p+1)\times 1$ vector; ${\mathbf{W}}_{\mathbf{x}}=\mathrm{diag}\left\{K_{\mathbf{h}}({\mathbf{X}}_1-\mathbf{x}),\cdots ,K_{\mathbf{h}}({\mathbf{X}}_n-\mathbf{x})\right\}$ for some kernel function K and bandwidth vector $\mathbf{h}={(h_1,\dots ,h_p)}^{\top }$; and

$${\mathbf{X}}_{\mathbf{x}}=\left[\begin{array}{cc}1& {({\mathbf{X}}_1-\mathbf{x})}^{\top }\\ ⋮& ⋮\\ 1& {({\mathbf{X}}_n-\mathbf{x})}^{\top }\end{array}\right].$$

(10)

Here, $K_{\mathbf{h}}({\mathbf{X}}_i-\mathbf{x})={\prod }_{j=1}^p{h}_j^{-1}K((X_{j,i}-x_j)/h_j)$. From the theorem in Appendix A, under some regularity conditions, $\sqrt{n}({\widehat{\beta }}_0-{\beta }_0)$ is asymptotically normal with mean zero and variance ${\sigma }^2=E{({\tilde{T}}^2)}^{-2}E{({\epsilon }^{*}\tilde{T})}^2$, where $\tilde{T}=T-E(T|\mathbf{X})$. Using a consistent estimator of ${\sigma }^2$, we can test (7) with significance level $\alpha$ by rejecting $H_0$ if $Z={\widehat{\beta }}_0/(\widehat{\sigma }/\sqrt{n})\ge z_{\alpha }(\mathrm{or}\le -z_{\alpha }$), where $z_{\alpha }$ is the $(1-\alpha )$-quantile of the standard normal distribution.

As regards the estimation of ${\sigma }^2$, we can first directly estimate variance ${\sigma }^2$ using the estimates ${\widehat{\epsilon }}_i^{*}$ and $\widehat{E}(T|{\mathbf{X}}_i)$, where ${\widehat{\epsilon }}_i^{*}=Y_i-{\widehat{\beta }}_0{T}_i-\widehat{{\varphi }^{*}}({\mathbf{X}}_i)$ and $\widehat{{\varphi }^{*}}(·)$ is the local linear estimator of ${\varphi }^{*}(·)$ based on $Y_i-{\widehat{\beta }}_0{T}_i,i=1,\dots n$. We can also estimate it using the sandwich covariance estimate based on (8),

$$\widehat{Var}({\widehat{\beta }}_0|\mathbf{T},{\mathbf{X}}_1,\dots ,{\mathbf{X}}_n)=\mathbf{H}\widehat{Var}(\mathbf{Y}|\mathbf{T},{\mathbf{X}}_1,\dots ,{\mathbf{X}}_n){\mathbf{H}}^{\top }.$$

(11)

Matrix $\widehat{Var}(\mathbf{Y}|\mathbf{T},{\mathbf{X}}_1,\dots ,{\mathbf{X}}_n)$ is diagonal, with the ith diagonal element equal to

$$\widehat{E}(\widehat{{{\epsilon }^{*}}^2}|T_i,{\mathbf{X}}_i)=(1-I(T_i=1))\widehat{Var}({\epsilon }_1^{*})+I(T_i=1)\widehat{Var}({\epsilon }_2^{*}),$$

(12)

where

$$\begin{array}{c}\hfill \widehat{Var}({\epsilon }_1^{*})=n_1^{-1}\sum _{i:T_i=0}{({\widehat{\epsilon }}_i^{*})}^2-{\left(n_1^{-1}\sum _{i:T_i=0}{\widehat{\epsilon }}_i^{*}\right)}^2,\end{array}$$

(13)

$$\begin{array}{c}\hfill \widehat{Var}({\epsilon }_2^{*})=n_2^{-1}\sum _{i:T_i=1}{({\widehat{\epsilon }}_i^{*})}^2-{\left(n_2^{-1}\sum _{i:T_i=1}{\widehat{\epsilon }}_i^{*}\right)}^2.\end{array}$$

(14)

Since the frontier function is generally (coordinatewise) non-decreasing with respect to the input variables, one might consider it necessary to impose such a monotonicity on ${\varphi }^{*}(·)$. However, from Theorem 2.1 in Huang [14], such imposition will not decrease the asymptotic variance of ${\widehat{\beta }}_0$; that is, it shows no theoretical improvement in performance. We therefore choose to develop the test without the monotonicity assumption for simplicity.

Note that our test directly estimates the mean difference in inefficiency $E(U_1)-E(U_2)$ using the semiparametric regression technique. Thus, the proposed test can work under assumptions that are more general than those in Banker et al. [9]. Additionally, we do not have to assume that noise has a finite upper support bound ($V_{max}$). However, the tests in Banker et al. [9] need such assumptions because they estimate ${\tilde{U}}_{l,i}=(V_{max}-V_{l,i})+U_{l,i}$ and use it as a surrogate estimate of $U_{l,i}$. However, $V_{max}-V_{l,i}$ may hamper the tests and degrade their performance.

3. Numerical Studies

In this section, we compare the performance of our test with those of Banker et al. [9]. We consider single and multiple input cases and use sandwich formulas to estimate the variance in estimators.

3.1. Single Input Case

We first consider a single input case using the following model:

$$\begin{array}{ccc}\hfill Y_i& =& \varphi (X_i)+V_{1,i}-U_{1,i},i\in \{1,\dots ,n_1\}\hfill \\ \hfill Y_i& =& \varphi (X_i)+V_{2,i}-U_{2,i},i\in \{n_1+1,\dots ,n_1+n_2\},\hfill \end{array}$$

where $\varphi (x)=30x-9x^2$, $X\sim U(0,1)$, $U_{l,i}\sim N_{+}(0,{\sigma }_{l,u}^2)$, and $V_{l,i}$ follow the truncated normal distribution with mean 0 and variance ${\sigma }_{l,v}^2$, which lies within $(-6{\sigma }_{l,v},6{\sigma }_{l,v})$, $l=1,2$. Here, $N_{+}$ stands for a normal distribution limited to the domain $[0,\infty )$. As for $V_{l,i}$, we try two cases to reflect both the equal and unequal error variances between groups. We set ${\sigma }_{1,v}={\sigma }_{2,v}=1$ for the equal error variance case and ${\sigma }_{1,v}=\sqrt{2},{\sigma }_{2,v}=1$ for the unequal variance case. To evaluate the type I error rate and power, we again consider two cases based on whether a mean difference (${\beta }_0$) exists or does not exist between group inefficiencies: ${\sigma }_{1,u}={\sigma }_{2,u}=1$ $({\beta }_0=0)$ and ${\sigma }_{1,u}=\sqrt{2},{\sigma }_{2,u}=1$ $({\beta }_0=0.3305)$. Here, the type I error rate implies the rate of supporting group difference in mean inefficiency when there is no difference and the power means the rate of supporting group difference in mean inefficiency when there are really inefficiency differences between groups.

We consider three sample sizes, $n=100$, 200, and 400; the proportion of each group is approximately 50% and number of replications is 1000. For a comparison, we report the type I error and power of the following five tests with significance level $\alpha =0.05$: our proposed test (PT), the OLS test, the T-test, the Mann-Whitney (MW) test, the Kolmogorov-Smirnov (KS) test, and the F-test. The last five tests are from Banker et al. [9]. We used a plug-in principle (see Ruppert et al. [15]) to find the bandwidth for our PT.

The test results are depicted in

Table 1. Type I error and power of the single input case with equal and unequal error variances.

		Type I Error						Power
		(Rejection Rate When ${\mathit{\beta }}_0$ = 0)						(Rejection Rate When ${\mathit{\beta }}_0$ = 0.3305)
Variances	$\mathbf{n}$	PT	OLS	T	MW	KS	F	PT	OLS	T	MW	KS	F
Equal	100	0.052	0.050	0.050	0.050	0.037	0.013	0.377	0.336	0.320	0.283	0.200	0.152
(${\sigma }_{1,v}={\sigma }_{2,v}$)	200	0.062	0.058	0.056	0.062	0.047	0.006	0.595	0.555	0.547	0.483	0.397	0.300
	400	0.063	0.064	0.062	0.061	0.052	0.003	0.848	0.822	0.818	0.761	0.665	0.533
Unequal	100	0.047	0.065	0.060	0.050	0.062	0.037	0.337	0.337	0.328	0.276	0.277	0.279
(${\sigma }_{1,v}\ne {\sigma }_{2,v}$)	200	0.053	0.064	0.063	0.052	0.099	0.029	0.505	0.468	0.463	0.388	0.521	0.401
	400	0.044	0.051	0.050	0.048	0.179	0.026	0.738	0.722	0.712	0.645	0.836	0.650

. Four of these tests, that is, except the KS test and the F-test, seem to respect the significance level in both the equal and unequal variance cases. However, the KS test obviously shows a larger type I error rate than expected for unequal error variances and the F-test seems to be a conservative test, which gives much smaller type I error probabilities than expected. As regards the power, our PT performs best, with the largest power among all the tests. In unequal variance cases where $n=200,400$, the KS test has larger power than our PT. However, the KS test is not reliable since it tends to reject the null hypothesis too easily in those cases. Finally, all tests tend to show higher power with larger sample sizes.

3.2. Multiple Input Case

We next consider a multiple input case with $p=3$. All the components in the simulation, except for the frontier function $\varphi$, are the same as in the single input case. As regards the frontier function, we consider two scenarios: the production function has an additive form, and the production function does not have an additive form. The additive assumption on the production function is used in Ferrara and Vidoli [16], but it may not be satisfied in some cases. However, in case of multiple covariates, the practical applicability of our proposed method may become worse since it requires multivariate smoothing and therefore suffers from the well-known “curse of dimensionality” problem as the dimension of the covariates becomes higher. In this case, additive modeling can be a meaningful alternative. For this, we try to estimate the difference in group efficiencies and test whether it is zero with an alternative estimating strategy, where we employ a backfitting procedure, which is a well-known estimating approach under the additive assumption. See Appendix B for details of the alternative method. Considering these two scenarios (additive and non-additive production functions), we examine how our PT(n) and its alternative based on the additive assumption, PT(a), behave depending on the validity of the assumption. The model considered here is

$$\begin{array}{ccc}\hfill Y_i& =& \varphi ({\mathbf{X}}_i)+V_{1,i}-U_{1,i},i\in \{1,\dots ,n_1\}\hfill \\ \hfill Y_i& =& \varphi ({\mathbf{X}}_i)+V_{2,i}-U_{2,i},i\in \{n_1+1,\dots ,n_1+n_2\},\hfill \end{array}$$

where $X_{j,i},j=1,2,3$, are generated from $U(0,1)$ independently. For the first scenario, we set $\varphi (\mathbf{x})=(30x_1-9x_1^2)+(5+2arctan(10(x_2-0.5)))+(4\sqrt{x_3})$; this has an additive structure. For the second scenario, we consider $\varphi (\mathbf{x})={\left(4\sqrt{x_1}+7\sqrt{x_2}+5\sqrt{x_3}+8\sqrt{x_1{x}_2}+10\sqrt{x_2{x}_3}+9\sqrt{x_1{x}_3}\right)}^{1.1}$. Note that both these production functions are concave. For PT(n), we select bandwidths by a generalized cross validation method (see Hastie and Tibshirani [17]), and for PT(a), we adopt a plug-in principle, as in the single input case.

The performances of PT(n) and PT(a) as well as the other five tests are reported in

Table 2. Type I error and power of the multiple input case with equal and unequal error variances when the true production function is not additive.

		Type I Error							Power
		(Rejection Rate When ${\mathit{\beta }}_0$ = 0)							(Rejection Rate When ${\mathit{\beta }}_0$ = 0.3305)
Variances	$\mathbf{n}$	PT(a)	PT(n)	OLS	T	MW	KS	F	PT(a)	PT(n)	OLS	T	MW	KS	F
Equal	100	0.066	0.053	0.044	0.043	0.054	0.040	0.141	0.220	0.294	0.234	0.235	0.170	0.133	0.492
(${\sigma }_{1,v}={\sigma }_{2,v}$)	200	0.059	0.077	0.049	0.050	0.044	0.035	0.113	0.328	0.488	0.473	0.471	0.356	0.268	0.644
	400	0.048	0.056	0.039	0.039	0.037	0.031	0.064	0.509	0.765	0.705	0.706	0.580	0.517	0.815
Unequal	100	0.061	0.063	0.101	0.099	0.054	0.046	0.316	0.199	0.258	0.346	0.340	0.173	0.143	0.649
(${\sigma }_{1,v}\ne {\sigma }_{2,v}$)	200	0.058	0.074	0.139	0.137	0.062	0.053	0.381	0.302	0.433	0.583	0.580	0.347	0.331	0.849
	400	0.048	0.060	0.128	0.130	0.046	0.093	0.385	0.468	0.682	0.793	0.792	0.530	0.650	0.947

and

Table 3. Type I error and power of the multiple input case with equal and unequal error variances when the true production function is additive.

		Type I Error							Power
		(Rejection Rate When ${\mathit{\beta }}_0$ = 0)							(Rejection Rate When ${\mathit{\beta }}_0$ = 0.3305)
Variances	$\mathbf{n}$	PT(a)	PT(n)	OLS	T	MW	KS	F	PT(a)	PT(n)	OLS	T	MW	KS	F
Equal	100	0.054	0.072	0.046	0.045	0.041	0.034	0.065	0.364	0.328	0.213	0.208	0.170	0.132	0.279
(${\sigma }_{1,v}={\sigma }_{2,v}$)	200	0.066	0.060	0.063	0.061	0.056	0.045	0.045	0.578	0.551	0.387	0.384	0.318	0.258	0.403
	400	0.054	0.055	0.034	0.034	0.033	0.033	0.018	0.820	0.801	0.572	0.571	0.503	0.419	0.517
Unequal	100	0.057	0.070	0.066	0.062	0.044	0.048	0.144	0.301	0.295	0.236	0.228	0.153	0.121	0.381
(${\sigma }_{1,v}\ne {\sigma }_{2,v}$)	200	0.068	0.060	0.089	0.089	0.054	0.060	0.137	0.501	0.481	0.415	0.414	0.281	0.290	0.566
	400	0.057	0.054	0.058	0.058	0.032	0.056	0.096	0.719	0.695	0.588	0.586	0.446	0.535	0.720

. From Table 2, our PT(n) outperforms the competitors overall, especially in the unequal variances case. Note that its type I error rates do not deviate much from 0.05, which means that the type I error rate is under control as desired; those of other competitors such as the OLS, T and KS tests tend to be a bit smaller than this level in case of equal variances, and considerably larger in case of unequal variances. The MW test seems to respect the level like PT(n) but PT(n) turns to be more powerful than MW. Note that PT(a) shows good results in terms of type I error rate, with comparable power to the MW test. Its power is lower than that of PT(n), but this is natural since the true production function is not additive. The F-test seems to be anticonservative leading to too high of a type I error probability, especially in the unequal variances case. However, in the equal variance case, the F-test shows shows very good performance in terms of type I error rate and power in large samples, as reported in Banker et al. [9]. From Table 3, our proposed two tests outperform their competitors when the additive assumption is true. Note that under the additive assumption, both PT(a) and PT(n) correctly specify the model. From our simulation, PT(a) slightly outperforms PT(n), since their type I error rates are close to 0.05 and the power of PT(a) is larger than that of PT(n). In case of equal variances, the type I error rates of the five competitors tend to be below 0.05, but when the variances are unequal, their power becomes much lower than our proposed tests although overall they show satisfactory type I errors. The only exception is the F-test. It shows the largest power in the unequal variances case but such merit is dimmed by considerably larger type I errors than other tests.

4. Application to PISA 2015 Data

In this section, we applied our PT to PISA 2015 data and test the efficiency difference between male and female student groups at a specific age in terms of learning time ($X_i$) and achievement ($Y_i$) in mathematics. The data can be downloaded from http://www.oecd.org/pisa/data/. PISA is a worldwide study to evaluate educational systems by measuring the scholastic performance of 15-year-old school students in mathematics, science, and reading. We considered the regional averages of the students’ learning time and achievement in mathematics based on test results of the 2015 version as production data. Out of the 103 regions in the data, two regions, Nova Scotia in Canada and Chile, were excluded from our analysis in view of their outlier characteristics in efficiency analysis.

Usually, international large-scale assessments data include measurement errors at the individual as well as group level. Therefore, we considered the following stochastic frontier model for such data:

$$\begin{array}{ccc}\hfill (\mathrm{Male}\mathrm{Students})Y_i& =& \varphi (X_i)+V_i^{male}-U_i^{male},i\in \{1,\dots ,101\}\hfill \\ \hfill (\mathrm{Female}\mathrm{Students})Y_i& =& \varphi (X_i)+V_i^{female}-U_i^{female},i\in \{102,\dots ,202\}.\hfill \end{array}$$

In this model, we assumed that there would be no gender difference in learning ability from a biological point of view and use the same production frontier for both gender group. It means that all the socio-economic characteristics of differentiation between the gender groups were in the random error terms and not introduced in the frontier function.

Table 4. Summary statistics of our PISA 2015 data.

		min	${\mathit{Q}}_1$	median	mean	${\mathit{Q}}_3$	max
male	$X_i$	27.89	39.52	41.72	43.10	47.81	56.70
	$Y_i$	338.5	470.6	499.7	483.9	513.8	565.6
female	$X_i$	25.23	38.99	41.49	41.98	45.26	56.67
	$Y_i$	339.0	456.9	487.9	474.8	501.9	565.0

shows summary statistics of each student group data. We applied the six tests in Section 3 to the data and calculated the p-values for the following hypothesis testing:

$$\begin{array}{c}\hfill H_0:E(U^{male})=E(U^{female})\mathrm{vs}.H_1:E(U^{male})<E(U^{female})\end{array}$$

From Samuelsson and Samuelsson [18], it is known that male students are often more involved in mathematics classes than female students. Additionally, since women are more involved in domestic chores than men and for men time is often made free by their families and relatives for the learning activity, male students are likely to be in an environment where they can focus more on studying than female students. Hence, we expected the results of the test to indicate that the effectiveness of male students was greater than that of female students in average.

Table 5. P-values of the six tests to detect efficiency difference in groups of male and female students in terms of learning time and achievement in mathematics.

test	PT	OLS	T	MW	KS	F
p-value	0.049	0.150	0.150	0.044	0.057	0.322

gives the test results. At a significance level of around $\alpha =0.05$, our PT, the MW test, and the KS test (with p-value slightly higher that $\alpha =0.05$) supported the hypothesis that on average male students are more efficient in mathematics than female students. However, the OLS test, the T-test and the F-test reported no significant difference in learning efficiency between the two groups. The reason for this could be the somewhat restrictive assumptions for test validity. Thus, the three tests seem to face the risk of unreasonable results if the assumptions are not satisfied in practice, but our PT does not seem to suffer from this problem.

5. Discussion and Conclusions

In this study, we developed tests with sound statistical theory for group efficiency comparison under SFM with considerably better performance than the previous tests proposed in numerical simulations. However, there is still room for improvement in our methods.

First, since we perform full nonparametric modeling for the frontier function $\varphi (·)$, which can be multivariate, our test might suffer from the “curse of dimensionality” and require high-order kernels for implementation with four or more input variables. In such a situation, we can consider an alternative test with spirit as in our test when the frontier function $\varphi (\mathbf{X})$ has an additive structure, that is, $\varphi (\mathbf{X})={\sum }_{j=1}^p{\varphi }_j(X_j)$, or could be well-approximated by it.

Second, we only deal with one output case, which limits practical applications. Our methods should be extended to cover the case of multi-output production frontiers, which DEA methods cover.

Third, we assume the same production frontier for both group, which is a clear limitation in practice since such situation is not frequently observed. If it is important to assume separate production frontier functions for different groups, one can use the meta-frontier approach. O’Donnell et al. [6] proposed a meta-frontier approach to compare the group technical efficiencies under stochastic frontier framework. The proposed method has the advantage that it can be used without assuming a common frontier function. However, the use of their method sometimes can be restricted by their assumption that the frontier production function is log-linear.

Finally, if one is interested in estimating the mean inefficiency of each group, we refer to Noh and Van Keiligom [19], which is a recent work along that direction.