Partial Key Attack Given MSBs of CRT-RSA Private Keys

Abstract

The CRT-RSA cryptosystem is the most widely adopted RSA variant in digital applications. It exploits the properties of the Chinese remainder theorem (CRT) to elegantly reduce the size of the private keys. This significantly increases the efficiency of the RSA decryption algorithm. Nevertheless, an attack on RSA may also be applied to this RSA variant. One of the attacks is called partially known private key attack, that relies on the assumption that the adversary has knowledge of partial bits regarding RSA private keys. In this paper, we mount this type of attack on CRT-RSA. By using partial most significant bits (MSBs) of one of the RSA primes, p or q and its corresponding private exponent, d, we obtain an RSA intermediate. The intermediate is derived from $p-1$ and RSA public key, e. The analytical and novel reason on the success of our attack is that once the adversary has obtained the parameters: approximation of private exponent ${\tilde{d}}_p$, approximation of p, $\tilde{p}$ and the public exponent e where ${\tilde{d}}_p,\tilde{p},e=N^{\alpha /2}$ where $0<\alpha \le 1/4$ such that $|d_p-{\tilde{d}}_p|,|p-\tilde{p}|<N^{\frac{1-\alpha }{2}}$ and has determined the largest prime of $⌊\frac{p-1}{e}⌋$, it will enable the adversary to factor the RSA modulus $N=pq$. Although the parameter space to find the prime factor is large, we show that one can adjust its “success appetite” by applying prime-counting function properties. By comparing our method with contemporary partial key attacks on CRT-RSA, upon determining a suitable predetermined “success appetite” value, we found out that our method required fewer bits of the private keys in order to factor N.

1. Introduction

RSA algorithm is known as one of the earliest public-key cryptosystems, introduced in 1977 [1]. However, its practical applications multiply in numbers with the coming of the digital age that requires swift key transportation mechanism to establish secure communication, either by encrypting a key or verifying a digital certificate. To ensure the encryption (or signing) and decryption (or verification) of RSA works, an RSA modulus $N=pq$ is introduced where $p\ne q$ and $p<q<2p$. To encrypt or sign, an RSA public exponent, e is required such that it satisfies $gcd(e,\varphi (N\left)\right)=1$ where $\varphi \left(N\right)$ is Euler’s totient function. To decrypt or verify, an RSA private exponent, d is required such that it satisfies the RSA key equation,

$$ed\equiv 1(mod\varphi (N\left)\right).$$

One of the hard mathematical problems that become the sources of security for RSA is embedded in N and called an integer factorization problem. Since p and q are very large n-bit primes (typically $n=1024$), the best current algorithm to factor N is still running in sub-exponential times using a method called general number field sieve [2]. Therefore, no modern computers yet can threaten the security of RSA.

As RSA algorithms need to be flexible and meet the demands of their applications, a lot of RSA variants have been introduced over the years. In this paper, we focus on a variant of RSA called Chinese remainder theorem (CRT) RSA cryptosystem [3]. This variant applies the result from the Chinese remainder theorem by utilizing two private exponents, $d_p$ and $d_q$, instead of a single private exponent in standard RSA. These private exponents are derived from the original d with respect to its corresponding RSA primes, p and q. The addition in numbers of private exponents in CRT-RSA may require additional modular exponentiations, but the computations in CRT-RSA are significantly faster compared to the computations in standard RSA, since $d_p$ and $d_q$ are significantly smaller in size compared to the original d [4]. Due to this speed up, CRT-RSA is ubiquitous in many cryptographic implementations today.

For the past attacks on RSA and its variants to be successful, an adversary needs to gain certain advantages. One of the advantages is that the adversary knows partial bits of RSA private parameters, d and p and/or q. The bits may be derived from their most significant bits (MSBs) or least significant bits (LSBs). This assumption is realistic since there is a method called side-channel attacks that is helpful to retrieve certain bits of parameters from cryptographic devices [5].

Using the partially known bits, an adversary can conduct an attack called partial key exposure attack. This kind of attack initially was executed on a standard RSA cryptosystem by [6], where they showed that $2/3$ bits of p or q are required to factor N using an integer programming technique. Then, Ref. [7] reduced the required value of bits to $1/2$ using the LLL algorithm. This method utilizes a lattice-based approach to find the small solution of polynomials modulo N that consequently results in the factorization of N. It then proliferated other partial key exposure attacks on standard RSA cryptosystem [8,9,10]. For the collection of this type of attack on standard RSA cryptosystem, refer to [11].

In 2003, Ref. [12] showed that partial key exposure attack can also be conducted on CRT-RSA. Given an approximation $d_p$, called ${\tilde{d}}_p$, that has half of the MSBs of $d_p$, they showed that factorization of N can be solved easily. Particularly, $d_p$ satisfies $e{d}_p\equiv 1(modp-1)$ within the CRT-RSA key equation, and given $\widetilde{d_p}$ such that $|d_p-{\tilde{d}}_p|<N^{1/4-\alpha }$ for some $\alpha$ that satisfy $e=N^{\alpha }<N^{1/4}$ where e is the public exponent of CRT-RSA, then N can be factored in polynomial time. It then can be generalized to $|d_p-{\tilde{d}}_p|<N^{1/4}$ if e is very small, which occurs greatly in most implementations. This result utilized an approach using lattice-based approximation which has been extended in [13,14,15].

Another method of attacking CRT-RSA is using a key reconstruction algorithm by [16]. The method is motivated by the capability of a newly introduced side-channel attack called cold boot attacks [17]. It systematically constructs bits of RSA private keys namely RSA private exponent and RSA primes from any random bit positions as its initial point. The method only requires at least 0.27 bits from any bit position of $p,q,d,d_p,d_q$. If this condition is fulfilled, then the adversary can solve the factorization of N in polynomial time using the lattice-based method. In more recent work, Ref. [18] proposed an improvement of past attacks by showing an attack that requires less amount of leaked MSBs for all $e<N^{0.375}$. The attack can be conducted by selecting better lattice constructions of the underlying polynomials created from the obtained partial information.

Our contribution. We take a novel approach in conducting partial key exposure attack on CRT-RSA by proving that by knowing the largest prime factor of $⌊\frac{p-1}{e}⌋$ called $a_1$, N can be factored in polynomial time if the conditions on the approximations of $d_p$ and p are satisfied. We also extend this result by showing the difficulties of finding $a_1$ can be reduced by having sufficient combinations of computing power and success appetites.

Organization of the article. In Section 2, we show the CRT-RSA key generation algorithm in its full form. We also introduce a certain theorem, definition and lemmas that will be utilized in our attack. In Section 3, we introduce our attack by parts. First, we show the conditions required to conduct our attack. Then, we proceed with the attack by proving that by knowing the largest prime factor of $⌊\frac{p-1}{e}⌋$ called $a_1$, our attack can factor N in polynomial time using conditions from the first part of the attack. In Section 4, we estimate the number of primes that can be the candidates for the largest prime factor of $⌊\frac{p-1}{e}⌋$ using a theorem provided before. Then, in Section 5, we estimate the number of primes that can be the candidates for the largest prime factor of $⌊\frac{p-1}{e}⌋$ if based on various success appetites which have been pre-defined. By using this estimation, we discuss our method compared to other methods that attacked CRT-RSA in Section 6 before we finally conclude our paper in Section 7.

2. Preliminaries

One of the earliest variations of the RSA cryptosystem is to decrypt the plaintext using Chinese remainder theorem or CRT (more on CRT can be read here [19]). This variant, called CRT-RSA, is proposed by the creators of RSA in their patent application [3]. The rationale of using the concept is to utilize much smaller parameter size in the decryption algorithm specifically during computing the modular exponentiation computation. As we shall see, in Algorithm 1, the key generation algorithm of CRT-RSA employs almost similar computations compared to the standard process. However, the difference lies in additional computations of

$$d_p\equiv e^{-1}(modp-1)$$

and

$$d_q\equiv e^{-1}(modq-1)$$

which we called CRT exponents as in Algorithm 1 (line 5 and line 6). The CRT-RSA key generation algorithm is as follows:

Algorithm 1 Chinese remainder theorem (CRT)-RSA Key Generation Algorithm

Input: Security parameter, n

Output: RSA public keys $(N,e)$, and RSA private keys $(p,q,\varphi \left(N\right),d_p,d_q)$

1: Generate randomly two distinct of n-bit primes p and q, where $p<q<2p$.   2: Compute $N=pq$.   3: Compute $\varphi \left(N\right)=(p-1)(q-1)$.   4: Choose e such that $e<\varphi \left(N\right)$ and $gcd(e,\varphi (N\left)\right)=1$.   5: Compute $d_p$ such that $e{d}_p\equiv 1(modp-1)$.   6: Compute $d_q$ such that $e{d}_q\equiv 1(modq-1)$.   7: Output $(N,e)$ as RSA public keys and $(p,q,\varphi \left(N\right),d_p,d_q)$ as RSA private keys.

In this paper, supposing $e=N^{\frac{\alpha }{2}}$, we assume that the adversary is given a fraction $\alpha$ of the MSBs of $d_p$ and p (or q). We shall see that by having this information, the adversary can derive an important intermediate that allows us to find d in polynomial time, thus factoring N in polynomial time. However, to find the greatest prime factor of the intermediate that can enable our attack, we need to count the number of primes that can be the suitable candidates for our greatest prime factor. To achieve that, we need to utilize the prime counting function as follows: (See [20], (Theorem 6.9)).

Theorem 1.

Let $\pi \left(X\right)$ be a function estimating number of primes $\le X$. Then

$$\pi \left(X\right)\le \frac{X}{lnX}\left(1+\frac{1}{lnX}+\frac{2.334}{{ln}^{2}X}\right)$$

for $X\ge 2953652287$.

After the adversary can count the number of primes that can be the suitable candidates for our greatest prime factor, the adversary need to know the probability of finding the prime in a known parameter space. This probability will help the adversary to adjust the success appetite of the attack and consequently determine whether the attack is feasible, based on the computational ability of the adversary. To estimate the probability, we require an application of the prime number theorem called Dickman’s function. Given a real number value, this function computes the probability of the greatest prime factor of an integer to be less than the given value. We call this function a Dickman’s function [21,22] and it is defined as below:

Definition 1

(Dickman’s function). The probability function that a random integer between 1 and N will have its greatest prime factor less than $N^{\zeta }$ is defined through the integral equation

$$F\left(\zeta \right)={\int }_0^{\zeta }F(t/(1-t))\frac{dt}{t}$$

for $0\le \zeta \le 1$.

Dickman’s function is defined in a form of cumulative distribution function. It is important to determine the distribution of the greatest prime factor of a given value. For example, let $\zeta =1/2$ then

$$\begin{array}{ccc}F(1/2)\hfill & =\hfill & {\int }_0^{1/2}F(t/(1-t))\frac{dt}{t}=1-{\int }_{1/2}^{1}F(t/(1-t))\frac{dt}{t}\hfill \\ \hfill & =\hfill & 1-{\int }_{1/2}^1\frac{dt}{t}=1+ln(1/2)=0.3068.\hfill \end{array}$$

(1)

This means that for any random integer N, there is a probability of 0.3068 that its greatest prime factor is less than $N^{1/2}$. Next, we require these two lemmas to help us in the attack.

Lemma 1.

Let $u,v,w\in \mathbb{Z}$ where $v<u<v+w$. If $⌊\frac{u}{w}⌋=\frac{u}{w}-{ϵ}_1$ and $⌊\frac{v}{w}⌋=\frac{v}{w}-{ϵ}_2$ such that ${ϵ}_2-{ϵ}_1<0$, then $⌊\frac{u}{w}⌋=⌊\frac{v}{w}⌋$.

Proof. 

Observe that

$$0<u-v<w\Rightarrow 0<\frac{u}{w}-\frac{v}{w}<1.$$

Since

$$0<\frac{u}{w}\Rightarrow 0\le ⌊\frac{u}{w}⌋<\frac{u}{w}$$

(2)

and

$$0<\frac{v}{w}\Rightarrow 0\le ⌊\frac{v}{w}⌋<\frac{v}{w}.$$

(3)

If $⌊\frac{u}{w}⌋=\frac{u}{w}-{ϵ}_1$ and $⌊\frac{v}{w}⌋=\frac{v}{w}-{ϵ}_2$ for ${ϵ}_2-{ϵ}_1<0$, computing (2) and (3) will get

$$\begin{array}{ccc}0\le ⌊{\displaystyle \frac{u}{w}}⌋-⌊{\displaystyle \frac{v}{w}}⌋\hfill & =\hfill & \left({\displaystyle \frac{u}{w}}-{ϵ}_1\right)-\left({\displaystyle \frac{v}{w}}-{ϵ}_2\right)\hfill \\ \hfill & =\hfill & \left({\displaystyle \frac{u}{w}}-{\displaystyle \frac{v}{w}}\right)+\left({ϵ}_2-{ϵ}_1\right)\hfill \\ \hfill & <\hfill & 1+({ϵ}_2-{ϵ}_1)<1+0=1\hfill \end{array}$$

(4)

Since $⌊\frac{u}{w}⌋$ and $⌊\frac{v}{w}⌋$ are integers, $⌊\frac{u}{w}⌋-⌊\frac{v}{w}⌋=0\Rightarrow ⌊\frac{u}{w}⌋=⌊\frac{v}{w}⌋$. □

This result will help us to enable the attack later presented in Theorem 2.

Lemma 2.

If an integer H divides $⌊\frac{rs}{t}⌋$ then $⌊\frac{rs}{t}⌋·\frac{1}{H}=⌊\frac{rs}{tH}⌋$.

Proof. 

Let $\frac{rs}{t}=z_1+\frac{r^{\prime }}{t}$ for some integer $z_1$ and $r^{\prime }$ where $r^{\prime }<t$. Then

$$\begin{array}{ccc}\hfill ⌊\frac{rs}{t}⌋·\frac{1}{H}& =& ⌊z_1+\frac{r^{\prime }}{t}⌋·\frac{1}{H}\hfill \\ & =& ⌊z_1⌋·\frac{1}{H}\hfill \\ & =& \frac{z_1}{H}\hfill \end{array}$$

If H divides $⌊\frac{rs}{t}⌋$ then H will also divides $z_1$. Hence $\frac{z_1}{H}=z_2$ for some integer $z_2\in \mathbb{Z}$. That is,

$$⌊\frac{rs}{t}⌋·\frac{1}{H}=z_2.$$

(5)

Then

$$\begin{array}{ccc}⌊{\displaystyle \frac{rs}{tH}}⌋\hfill & =\hfill & ⌊{\displaystyle \frac{z_1}{H}}+{\displaystyle \frac{r^{\prime }}{tH}}⌋\hfill \\ \hfill & =\hfill & ⌊{\displaystyle \frac{z_1}{H}}⌋\hfill \\ \hfill & =\hfill & ⌊z_2⌋\hfill \\ \hfill & =\hfill & z_2.\hfill \end{array}$$

(6)

Comparing (5) and (6), This completes the proof. □

The above results will help us to enable the attack later presented in Theorem 2.

3. The Attack

The initial strategy in our attack is to find the conditions on the approximations of $d_p$ and p to enable our attack. By using these conditions, we shall prove mathematically that there exists an unknown intermediate that will help us to find the factorization of N in polynomial time.

First, to find the conditions on the approximations of $d_p$ and p, we need the following lemma regarding an approximation of p.

Lemma 3.

Let $N=pq$ with $p<q<2p$. If there exists $\tilde{p}$ where $|p-\tilde{p}|<p^{1-\alpha }$ then $(p-1)\tilde{p}>\frac{1}{8}N$.

Proof. 

From $p<q<2p$ we know

$$p^2<pq<2p^2\Rightarrow p<N^{1/2}<\sqrt{2}p$$

(7)

and

$$pq<q^2<2pq\Rightarrow N^{1/2}<q<2N^{1/2}$$

(8)

Combining (7) and (8), we get $p<N^{1/2}<q$. Since p and q are of the same bit length, observe

$$p>p-1>\frac{q}{2}>\frac{N^{1/2}}{2}.$$

(9)

Suppose $|p-\tilde{p}|<p^{1-\alpha }$. This implies $\tilde{p}$ shares the same a fraction $\alpha$ of the MSBs with p and subsequently $\tilde{p}>\frac{p}{2}$. Thus

$$\begin{array}{ccc}\hfill (p-1)\tilde{p}& >& \frac{N^{1/2}}{2}\tilde{p}>\frac{N^{1/2}}{2}\frac{p}{2}>\frac{N^{1/2}}{2}\frac{N^{1/2}}{4}\hfill \\ & =& \frac{1}{8}N.\hfill \end{array}$$

This completes the proof. □

The next lemma assumes that $p<q<2p$, then we show that, by having a fraction $\alpha$ of the MSBs of p and q of CRT-RSA modulus, we can get an approximation of p to a certain bound.

Lemma 4.

Let $N=pq$ be an CRT-RSA modulus with $p<q<2p$. If a fraction α of the MSBs of p or q are known then we can find $\tilde{p}$ such that $|p-\tilde{p}|<N^{\frac{1-\alpha }{2}}$.

Proof. 

We know that if $p<q<2p$ then $p^2<N<2p^2$. Observe $p<N^{1/2}<\sqrt{2}p$. If a fraction $\alpha$ of the MSBs of p are known then we can find $\tilde{p}$ which consists of a fraction $\alpha$ of the MSBs of p such that

$$|p-\tilde{p}|<p^{1-\alpha }<N^{\frac{1-\alpha }{2}}.$$

On the side of q, since $N^{1/2}<q^2<2pq\Rightarrow N^{1/2}<q<{\left(2N\right)}^{1/2}$, if a fraction $\alpha$ of the MSBs of q are known, then

$$|q-\tilde{q}|<q^{1-\alpha }<{\left(2N\right)}^{\frac{1-\alpha }{2}}.$$

Since q and $\tilde{q}$ shares the same a fraction $\alpha$ of the MSBs, then $\tilde{q}<{\left(2N\right)}^{1/2}$. Given $\tilde{q}$, we can compute $\tilde{p}=\frac{N}{\tilde{q}}$ which satisfies

$$|p-\tilde{p}|=\left|\frac{N}{q}-\frac{N}{\tilde{q}}\right|=\left|\frac{N(\tilde{q}-q)}{q\tilde{q}}\right|<\frac{N\left({\left(2N\right)}^{\frac{1-\alpha }{2}}\right)}{2N}<N^{\frac{1-\alpha }{2}}.$$

This completes the proof. □

From Lemma 4, we know that by having a fraction $\alpha$ of MSBs of p or q, we can obtain an approximation of p called $\tilde{p}$ where $|p-\tilde{p}|<N^{\frac{1-\alpha }{2}}$. This approximation of p will enable the next lemma to find $k_p$ given a fraction $\alpha$ of the MSBs of $d_p$ and $\tilde{p}$ where $e{d}_p=1+k_p(p-1)$ and $|p-\tilde{p}|<N^{\frac{1}{2}-\alpha }$.

Lemma 5.

Let $N=pq$ be an CRT-RSA modulus with $p<q<2p$. Suppose $e=N^{\frac{\alpha }{2}}$ be a valid public exponent with $0<\alpha \le 1/4$ and $d_p$ be its corresponding private exponent which satisfies CRT-RSA key equation $e{d}_p=1+k_p(p-1)$. If a fraction α of the MSBs of $d_p$ and p (or q) are known, then the constant $k_p$ in the key equation can be determined, up to a small constant additive error, in time polynomial in $log\left(N\right)$.

Proof. 

Recall that one of the private exponent of CRT-RSA satisfies $e{d}_p=1+k_p(p-1)$. So, we can write

$$k_p=\frac{e{d}_p-1}{p-1}$$

(10)

If a fraction $\alpha$ of the MSBs of $d_p$ are known, then we have $\widetilde{d_p}$ such that $|d_p-\widetilde{d_p}|<d_p^{1-\alpha }<N^{\frac{1}{2}(1-\alpha )}$. From Lemma 4, if we have a fraction $\alpha$ of the MSBs of p (or q) are known then we have $\tilde{p}$ such that $|p-\tilde{p}|<p^{1-\alpha }<N^{\frac{1}{2}(1-\alpha )}$. ${\tilde{k}}_p$ is given by

$${\tilde{k}}_p=⌈\frac{e{\tilde{d}}_p-1}{\tilde{p}}⌋=\frac{e{\tilde{d}}_p-1}{\tilde{p}}+ϵ,$$

for some $\left|ϵ\right|\le 1/2$, reveals some of the most significant bits of $k_p$. In particular, notice that

$$\begin{array}{ccc}\left|k_p-{\tilde{k}}_p\right|\hfill & =\hfill & \left|{\displaystyle \frac{e{d}_p-1}{p-1}}-⌈{\displaystyle \frac{e\widetilde{d_p}-1}{\tilde{p}}}⌋\right|=\left|{\displaystyle \frac{e{d}_p-1}{p-1}}-{\displaystyle \frac{e\widetilde{d_p}-1}{\tilde{p}}}+ϵ\right|\hfill \\ \hfill & =\hfill & \left|{\displaystyle \frac{\tilde{p}(e{d}_p-1)}{(p-1)\tilde{p}}}-{\displaystyle \frac{(p-1)(e\widetilde{d_p}-1)}{(p-1)\tilde{p}}}+ϵ\right|\hfill \\ \hfill & =\hfill & \left|{\displaystyle \frac{\tilde{p}e{d}_p-\tilde{p}-pe\widetilde{d_p}+p+e\widetilde{d_p}-1}{(p-1)\tilde{p}}}+ϵ\right|\hfill \\ \hfill & =\hfill & \left|{\displaystyle \frac{\tilde{p}e{d}_p-\tilde{p}-\tilde{p}e\widetilde{d_p}+\tilde{p}e\widetilde{d_p}-pe\widetilde{d_p}+p+e\widetilde{d_p}-1}{(p-1)\tilde{p}}}+ϵ\right|\hfill \\ \hfill & <\hfill & \left|{\displaystyle \frac{\tilde{p}e(d_p-\widetilde{d_p})}{(p-1)\tilde{p}}}+{\displaystyle \frac{(\tilde{p}-p)(e\widetilde{d_p}-1)}{(p-1)\tilde{p}}}+ϵ\right|\hfill \\ \hfill & <\hfill & \left|{\displaystyle \frac{e(d_p-\widetilde{d_p})}{(p-1)}}+{\displaystyle \frac{(\tilde{p}-p)\left(e\widetilde{d_p}\right)}{(p-1)\tilde{p}}}+ϵ\right|.\hfill \end{array}$$

(11)

If $(p-1)\tilde{p}>\frac{1}{8}N$ as in Lemma 3, then (11) will be

$$\left|k_p-{\tilde{k}}_p\right|<\left|N^{\frac{\alpha }{2}+\frac{1}{2}(1-\alpha )-\frac{1}{2}}+8N^{\frac{1}{2}(1-\alpha )+\frac{\alpha }{2}+\frac{1}{2}-1}+ϵ\right|<10$$

for large N. Hence, the constant $k_p$ will be in the range $\left\{{\tilde{k}}_p-10,{\tilde{k}}_p+10\right\}$. Since $k_p$ can be computed in time polynomial in $log\left(N\right)$. This completes the proof. □

Lemma 5 shows the significance of knowing a fraction $\alpha$ of the MSBs of d and p, in order to find $k_p$. It also shows that the conditions presented in Lemma 5 must be carried throughout the attack since it enables the attack. The value of $k_p$ obtained in Lemma 5 is utilized in the next proposition.

Proposition 1.

Let $N=pq$ be an CRT-RSA modulus with $p<q<2p$ and $|p-\tilde{p}|<N^{\frac{1}{2}-\alpha }$. Suppose $e=N^{\frac{\alpha }{2}}$ be a valid public exponent with $0<\alpha \le 1/4$ and $d_p$ be its corresponding private exponent, which satisfies $e{d}_p=1+k_p(p-1)$. Let $e{d}_p^{\prime }=1(mod{k}_p)$ for some $d_p^{\prime }\in \mathbb{Z}$ then $d_p=k_p⌊\frac{(p-1)}{e}⌋+d_p^{\prime }$.

Proof. 

Observe that

$$\begin{array}{ccc}\hfill e{d}_p& =& 1+k_p(p-1)\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill e{d}_p^{\prime }& =& 1+k_p^{\prime }{k}_p.\hfill \end{array}$$

(13)

for some $k_p^{\prime }\in \mathbb{Z}$. Substitute value of e in (12) into (13), we obtain

$$\begin{array}{ccc}\hfill \left({\displaystyle \frac{1+k_p(p-1)}{d_p}}\right)d_p^{\prime }& =& 1+k_p^{\prime }{k}_p\hfill \\ \hfill d_p^{\prime }+d_p^{\prime }{k}_p(p-1)& =& d_p+d_p{k}_p^{\prime }{k}_p\hfill \end{array}$$

(14)

Rearranging (14), we have

$$\begin{array}{ccc}{d}_p\hfill & =\hfill & d_p^{\prime }{k}_p(p-1)-d_p{k}_p^{\prime }{k}_p+d_p^{\prime }\hfill \\ \hfill & =\hfill & k_p(d_p^{\prime }(p-1)-d_p{k}_p^{\prime })+d_p^{\prime }.\hfill \end{array}$$

(15)

The term $d_p^{\prime }(p-1)-d{k}_p^{\prime }$ can become

$$\begin{array}{ccc}\hfill d_p^{\prime }(p-1)-d_p{k}_p^{\prime }& =& {\displaystyle \frac{1+k_p^{\prime }k}{e}}(p-1)-d_p{\displaystyle \frac{d_p^{\prime }e-1}{k_p}}\hfill \\ \hfill & =& {\displaystyle \frac{(p-1)k_p(1+k_p^{\prime }{k}_p)-e{d}_p(d_p^{\prime }e-1)}{k_{p}e}}\hfill \\ \hfill & =& {\displaystyle \frac{(p-1)k_p(1+k_p^{\prime }{k}_p)-((p-1)k_p+1)(d_p^{\prime }e-1)}{k_{p}e}}\hfill \\ \hfill & =& {\displaystyle \frac{(p-1)k_p(1+k_p^{\prime }{k}_p)-\left((p-1)k_p\right)(d_p^{\prime }e-1)+1}{k_{p}e}}-{\displaystyle \frac{d_p^{\prime }}{k_p}}\hfill \\ \hfill & =& {\displaystyle \frac{(p-1)k_p(1+k_p^{\prime }{k}_p)-\left((p-1)k_p\right)(d_p^{\prime }e-1)}{k_{p}e}}+{\displaystyle \frac{1-e{d}_p^{\prime }}{k_{p}e}}\hfill \\ \hfill & =& {\displaystyle \frac{(p-1)k_p(1+k_p^{\prime }{k}_p)-\left((p-1)k_p\right)(d_p^{\prime }e-1)}{k_{p}e}}-{\displaystyle \frac{k_p^{\prime }{k}_p}{k_{p}e}}\hfill \\ \hfill & =& {\displaystyle \frac{(p-1)k_p(1+k_p^{\prime }{k}_p)-\left((p-1)k_p\right)(d_p^{\prime }e-1)}{k_{p}e}}-{\displaystyle \frac{k_p^{\prime }}{e}}\hfill \\ \hfill & >& \left({\displaystyle \frac{(p-1)}{e}}\left(k_p^{\prime }{k}_p-d_p^{\prime }e+2\right)\right)-1\hfill \end{array}$$

(16)

since $\frac{k_p^{\prime }}{e}<1$. If $e{d}_p^{\prime }=1+k_p^{\prime }{k}_p$ then $k_p^{\prime }{k}_p-d_p^{\prime }e=-1$. Thus, (16) become

$$\begin{array}{ccc}\hfill d_p^{\prime }(p-1)-d_p{k}_p^{\prime }& >& \left({\displaystyle \frac{(p-1)}{e}}\left(-1+2\right)\right)-1\hfill \\ \hfill & =& {\displaystyle \frac{(p-1)}{e}}-1.\hfill \end{array}$$

(17)

This implies that $\frac{(p-1)}{e}-(d_p^{\prime }(p-1)-d_p{k}_p^{\prime })<1$. Since $d_p^{\prime }(p-1)-d_p{k}_p^{\prime }$ is always an integer, $d_p^{\prime }(p-1)-d_p{k}_p^{\prime }=⌊\frac{(p-1)}{e}⌋$. Now, we can see that

$$d_p=k_p⌊\frac{(p-1)}{e}⌋+d_p^{\prime }.$$

(18)

This completes the proof. □

Remark 1.

Equation (18) shows that under assumption of Proposition 1, which values $d_p^{\prime }$ and $k_p^{\prime }$ are known, it is crucial that $⌊\frac{(p-1)}{e}⌋$ is kept secret.

The next theorem shows the implication of the results from Proposition 1 in our aim to factor CRT-RSA modulus in polynomial time.

Theorem 2.

Let $N=pq$ be a CRT-RSA modulus with $p<q<2p$. Suppose $e=N^{\frac{\alpha }{2}}$ be a valid public exponent with $0<\alpha \le 1/4$ and $d_p$ be its corresponding private exponent which satisfies $e{d}_p=1+k_p(p-1)$. Let $e{d}_p^{\prime }=1+k_p^{\prime }{k}_p$ for some $k_p,k_p^{\prime },d_p^{\prime }\in \mathbb{Z}$. Let $a_1$ be one of the prime factor of $⌊\frac{(p-1)}{e}⌋=a_1^{b_1}·a_2^{b_2}·\dots ·a_n^{b_n}=\prod _{i=1}^n{a}_i^{b_i}$ such that $\left|(p-1)-\tilde{p}\right|<e{a}_1$. Suppose $⌊\frac{\tilde{p}}{e{a}_1}⌋=\frac{\tilde{p}}{e{a}_1}-{ϵ}_1$ and $⌊\frac{p-1}{e{a}_1}⌋=\frac{p-1}{e{a}_1}-{ϵ}_2$ such that ${ϵ}_2-{ϵ}_1<0$. If $a_1$ and a fraction α of the MSBs of $d_p$ and p (or q) are known then N can be factored in polynomial time.

Proof. 

If $a_1$ satisfies $\left|(p-1)-\tilde{p}\right|<e{a}_1$, and $⌊\frac{\tilde{p}}{e{a}_1}⌋=\frac{\tilde{p}}{e{a}_1}-{ϵ}_1$ and $⌊\frac{p-1}{e{a}_1}⌋=\frac{p-1}{e{a}_1}-{ϵ}_2$ such that ${ϵ}_2-{ϵ}_1<0$, from Lemma 1, we obtain

$$⌊\frac{\tilde{p}}{e{a}_1}⌋=⌊\frac{(p-1)}{e{a}_1}⌋$$

(19)

Lemma 2 implies if $a_1$ divides $⌊\frac{(p-1)}{e}⌋$ then $⌊\frac{(p-1)}{e}⌋·\frac{1}{a_1}=⌊\frac{(p-1)}{e·a_1}⌋$. This also implies

$$⌊\frac{(p-1)}{e}⌋·\frac{a_1}{a_1}=⌊\frac{(p-1)}{e·a_1}⌋a_1$$

(20)

From Proposition 1,

$$\begin{array}{ccc}\hfill d_p& =& k_p⌊{\displaystyle \frac{(p-1)}{e}}⌋+d_p^{\prime }\hfill \\ \hfill & =& k_p{\displaystyle \frac{a_1}{a_1}}⌊{\displaystyle \frac{(p-1)}{e}}⌋+d_p^{\prime }\hfill \\ \hfill & =& k_p{a}_1⌊{\displaystyle \frac{(p-1)}{e{a}_1}}⌋+d_p^{\prime }\hfill \\ \hfill & =& k_p{a}_1⌊{\displaystyle \frac{\tilde{p}}{e{a}_1}}⌋+d_p^{\prime }.\hfill \end{array}$$

(21)

If $\tilde{p}$ and a fraction $\alpha$ of the MSBs of $d_p$ are known, based on Lemma 5, we can find $k_p$ in polynomial time. Then, we can compute $d_p^{\prime }$ as $d_p^{\prime }\equiv 1/e(mod{k}_p)$. If $a_1$ is known, we can compute $d_p$ in (21). Using the value of $d_p$, we can obtain p by computing $p=\frac{e{d}_p-1}{k_p}+1$ and factorizes N. This completes the proof. □

Remark 2.

We have shown that given α most significant bits of $d_p$ and p, the complexity of factoring N depends on knowing the factor of $⌊\frac{(p-1)}{e{a}_1}⌋$. This demonstrates that we have reduced one of the hard problems of RSA from factoring N to factoring $⌊\frac{(p-1)}{e{a}_1}⌋$. However, the complexity of factorization is still sub-exponential according to the current factorization technique.

We construct an algorithm based on our attack. The parameters used in the algorithm are described in Table 1:

Table 1. List of Parameters Used in the Attack.

Parameters known before the attack:	•  RSA public keys, $(\mathit{N},\mathit{e})$ •  approximation of d, ${\tilde{\mathit{d}}}_{\mathit{p}}$ •  approximation of p, $\tilde{\mathit{p}}$ •  a prime factor of $⌊\frac{(\mathit{p}-1)}{\mathit{e}}⌋,{\mathit{a}}_1$
Parameters known during the attack:	•  Constant from CRT-RSA    key Equation (10), $k_p$ •  Intermediate of (13), ${\tilde{k}}_p$ •  Intermediate of (13), $d_p^{\prime }$
Parameters known after the attack:	•  CRT-RSA private exponent, $d_p$ •  CRT-RSA private key, p •  CRT-RSA private key, q

The algorithm takes the input of RSA public keys $(N,e)$ and a prime factor of $⌊\frac{(p-1)}{e}⌋,a_1$ that satisfies $\left|(p-1)-\tilde{p}\right|<e{a}_1$, given a fraction $\alpha$ of the MSBs of $d_p$ and $\tilde{p}$. The algorithm is as follows:

Remark 3.

Since we assume that the value of $a_1$ is already known in Algorithm 2, the algorithm runs in polynomial time.

The following is an example to illustrate Algorithm 2.

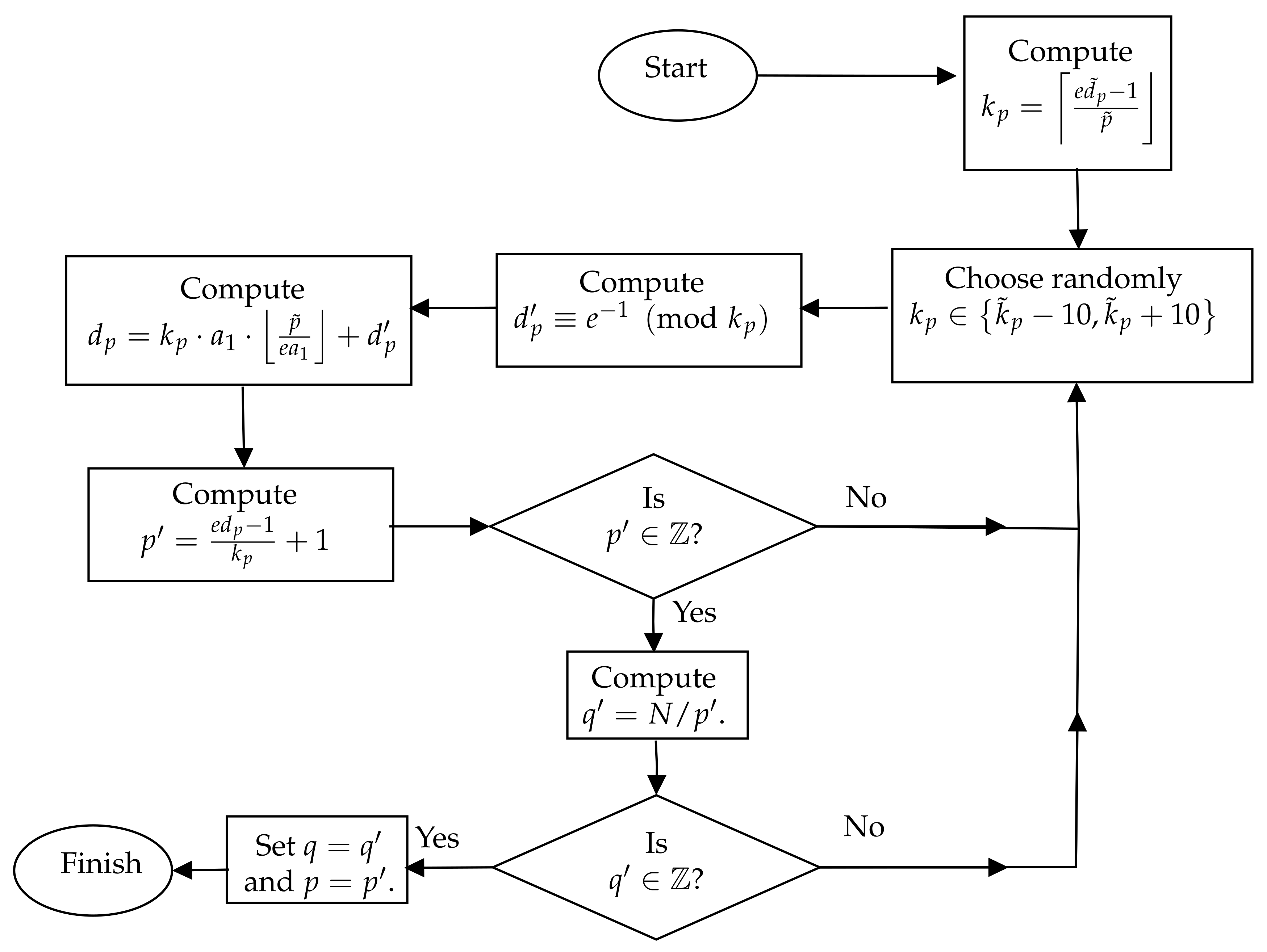
Algorithm 2 Factoring N of CRT-RSA via Theorem 2

Input: CRT-RSA public keys $(N,e)$, ${\tilde{d}}_p,\tilde{p}$ and prime factor of $⌊\frac{(p-1)}{e}⌋,a_1$

Output:$p,q$

1: Compute ${\tilde{k}}_p=⌈\frac{e{\tilde{d}}_p-1}{\tilde{p}}⌋$.   2: Set $k_p\in \{{\tilde{k}}_p-10,{\tilde{k}}_p+10\}$.             ▹ Step 1 until 2 are based on Lemma 5   3: for each $k_p$ do   4:     Compute $d_p^{\prime }\equiv e^{-1}(mod{k}_p)$   5:     Compute $d_p=k_p·a_1·⌊\frac{\tilde{p}}{e{a}_1}⌋+d_p^{\prime }$.   6:     Compute $p^{\prime }=\frac{e{d}_p-1}{k_p}+1$.   7:     if $p^{\prime }\in \mathbb{Z}$ then   8:         Compute $q^{\prime }=N/p^{\prime }$.   9:         if $q^{\prime }\in \mathbb{Z}$ then   10:            Set $q=q^{\prime }$.   11:         end if   12:         Set $p=p^{\prime }$.   13:     end if   14: end for   15: Output p and q

Example 1.

We use RSA-2048 in this example. Specifically, we are given

$$\begin{array}{ccc}\hfill N& =& 26854041985238375212475778164676011572680663430940658107484164678\hfill \\ & & 81881009475246975164803757355184419648595055886375159003247478439\hfill \\ & & 92143741255730632610827884401657509117670049123360590970470225653\hfill \\ & & 67370191193688936329713163878893198502800751634549138639730928812\hfill \\ & & 40142505876139322063065708976736945544675563231857474829753757364\hfill \\ & & 89461162692635457445662945510534745278831004328830299446277566122\hfill \\ & & 87687169004926239194650447064129592636966022464572301245637234770\hfill \\ & & 50294647480922968543256342945263036346158795045888810801423391916\hfill \\ & & 97736283477365028685949028278325146903748790144455033008532116417\hfill \\ & & 89895820938922463256886051224441\hfill \end{array}$$

and $e=2588040962967479019863275440499$ which is about $N^{0.05}$. Let

$$\begin{array}{ccc}\hfill {\tilde{d}}_p& =& 36055607231202775283080802009652619678848579202676835359522337232\hfill \\ & & 45304648210382882262903480159927251198134217538338417610010663688\hfill \\ & & 39077835797132043978282412016850688884540907420868648185609637754\hfill \\ & & 11063506013449129456265445743931127981044130978483361430857693084\hfill \\ & & 40916227786667499669328426663847808738852591212\hfill \end{array}$$

where a fraction α of the MSBs of $d_p$ are given such that $|d_p-\widetilde{d_p}|<d_p^{1-\alpha }$. In this case, $\alpha =0.1$ or about 10% (103-bits) bits of its original, $d_p$. Then, let

$$\begin{array}{ccc}\hfill \tilde{p}& =& 14367613307214246903591926069142770099295123891127829274068843132\hfill \\ & & 84507873128193703874025274483229621351740372731847216208987451381\hfill \\ & & 22600446098472260720529957802520996016314325569094216775717168908\hfill \\ & & 41782721517081770370921396206536643264683692385497895745823983436\hfill \\ & & 0770156094067408884861977891020041626737366980204\hfill \end{array}$$

where a fraction α of the MSBs of p (or q) are also given, such that $|p-\tilde{p}|<p^{1-\alpha }$. From Lemma 5, given ${\tilde{d}}_p$ and $\tilde{p}$, we obtain ${\tilde{k}}_p$ and proceed to recover $k_p=64947035018102022468569402425$ in polynomial time. Then, we compute

$$\begin{array}{ccc}\hfill d_p^{\prime }& \equiv & e^{-1}(mod{k}_p)\hfill \\ & \equiv & 14291832328785630096514471874(mod64947035018102022468569402425)\hfill \end{array}$$

Given that we also know one of the prime factor of $⌊\frac{p}{e}⌋$,

$$\begin{array}{ccc}\hfill a_1& =& 43185843225970563415154944273587881760667418641821175935878843801\hfill \\ & & 62779147404915309140284507695180396733831689901698607027115346112\hfill \\ & & 71569728695701943263595028176276635021689474779238127599104918615\hfill \\ & & 72151376677546400416324969826940325349800202462521919212154035625\hfill \\ & & 31983030526947\hfill \end{array}$$

such that $|\tilde{p}-p|<e{a}_1$. Then

$$\begin{array}{ccc}\hfill d_p& =& k_p·a_1·⌊\frac{\tilde{p}}{e{a}_1}⌋+d_p^{\prime }\hfill \\ & =& 36055607231202775283080802009649108834176664752875840471779128853\hfill \\ & & 65479408662427699263008533084770049815277792852591783505517277427\hfill \\ & & 76754417366858919379167907800491269897943246773311982875789843868\hfill \\ & & 49579557361199476994871376824209224903108180826295016253816460096\hfill \\ & & 02016637714750590649460512253997299687719907999.\hfill \end{array}$$

By knowing $d_p$, we can get

$$\begin{array}{ccc}\hfill p& =& \frac{e{d}_p-1}{k_p}+1\hfill \\ & =& 14367613307214246903591926069142452203848898341656376495846139272\hfill \\ & & 96888354084505142420920972987941360124023642545598929784435347521\hfill \\ & & 29827893551421260667238347559758806433514905636985352008519026850\hfill \\ & & 47195482010956044783038279094608638461799318081089013845804738749\hfill \\ & & 4897239865723803413293355621434998234772291243981.\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill q& =& N/p\hfill \\ & =& 18690677018537559979968031085225887816085307412051352387412281562\hfill \\ & & 63664879599722127409077204025890837680223683840960510872264130729\hfill \\ & & 19499428723542093381211298664979433605748124826497957558030353615\hfill \\ & & 18738757121243839997910925158423130594718234233298178099345593794\hfill \\ & & 9142322870446532378712921531570515925370391213661.\hfill \end{array}$$

N has been successfully factored.

Figure 1 shows the flowchart based on Algorithm 2:

Figure 1. Flowchart of Algorithm 2.

Our Attack in RSA Implementation

In most RSA implementations, RSA public exponent e is a small integer. The reason for this choice is to optimize the computing time of the RSA encryption algorithm. In this part, we investigate the implication of the size of e in our attack. Typically, $e=2^{16}+1$. Since we set $e=N^{\frac{\alpha }{2}}$ in our attack, observe that

$$\alpha =2{log}_{N}e\approx 2{log}_{2^{2048}}{2}^{16}+1\approx 0.01562$$

in the implementation of RSA-2048.

This implicates that our attack requires $0.01562·2048=31.98976$ or about 32 bits of $d_p$ and p to be exposed since $|d_p-{\tilde{d}}_p|<N^{1-\alpha }$ and $|p-\tilde{p}|<p^{1-\alpha }$. The exposed bits may come from the side-channel attack or a brute-force method, since the number of bits that are required are quite small. The number of exposed bits that are required can be reduced, if the size of N or e is smaller.

4. Estimating Number of Candidates for ${\mathit{a}}_{\mathbf{1}}$

To find an $a_1$ that satisfy $\left|(p-1)-\tilde{p}\right|<e{a}_1$ posed in Theorem 2, we can anticipate that $a_1$ to be the largest prime factor of $⌊\frac{(p-1)}{e}⌋$. We need to estimate the number of primes that are eligible to be $a_1$. However, first, the next lemma modifies the result by [20] and applies it to show an estimation of the number of primes between two bounds.

Lemma 6.

Let $N^{\zeta }$ and $N^{\theta }$ respectively be the upper and lower bounds of $a_1$ where $0<\theta <\zeta <1$. Then, the number of primes between $N^{\zeta }$ and $N^{\theta }$ will be less than $N^{\zeta }\left(\frac{1}{ln{N}^{\zeta }}\right)\left(1+\frac{1}{ln{N}^{\theta }}+\frac{2.334}{{ln}^2{N}^{\theta }}\right)$.

Proof. 

Let F be the number of primes less than the upper bound of $a_1$ and G be the number of primes less than the lower bound of $a_1$. Then, according to Theorem 1,

$$F=\frac{N^{\zeta }}{ln{N}^{\zeta }}\left(1+\frac{1}{ln{N}^{\zeta }}+\frac{2.334}{{ln}^2{N}^{\zeta }}\right)$$

and

$$G=\frac{N^{\theta }}{ln{N}^{\theta }}\left(1+\frac{1}{ln{N}^{\theta }}+\frac{2.334}{{ln}^2{N}^{\theta }}\right).$$

To estimate the number of candidates of $a_1$, we need to calculate

$$\begin{array}{ccc}\hfill F-G& =& {\displaystyle \frac{N^{\zeta }}{ln{N}^{\zeta }}}\left(1+{\displaystyle \frac{1}{ln{N}^{\zeta }}}+{\displaystyle \frac{2.334}{{ln}^2{N}^{\zeta }}}\right)-{\displaystyle \frac{N^{\theta }}{ln{N}^{\theta }}}\left(1+{\displaystyle \frac{1}{ln{N}^{\theta }}}+{\displaystyle \frac{2.334}{{ln}^2{N}^{\theta }}}\right)\hfill \\ \hfill & <& {\displaystyle \frac{N^{\zeta }}{ln{N}^{\zeta }}}\left(1+{\displaystyle \frac{1}{ln{N}^{\theta }}}+{\displaystyle \frac{2.334}{{ln}^2{N}^{\theta }}}\right)-{\displaystyle \frac{N^{\theta }}{ln{N}^{\theta }}}\left(1+{\displaystyle \frac{1}{ln{N}^{\theta }}}+{\displaystyle \frac{2.334}{{ln}^2{N}^{\theta }}}\right)\hfill \\ \hfill & =& \left({\displaystyle \frac{N^{\zeta }}{ln{N}^{\zeta }}}-{\displaystyle \frac{N^{\theta }}{ln{N}^{\theta }}}\right)\left(1+{\displaystyle \frac{1}{ln{N}^{\theta }}}+{\displaystyle \frac{2.334}{{ln}^2{N}^{\theta }}}\right)\hfill \\ \hfill & <& \left({\displaystyle \frac{N^{\zeta }}{ln{N}^{\zeta }}}\right)\left(1+{\displaystyle \frac{1}{ln{N}^{\theta }}}+{\displaystyle \frac{2.334}{{ln}^2{N}^{\theta }}}\right)\hfill \\ \hfill & =& N^{\zeta }\left({\displaystyle \frac{1}{ln{N}^{\zeta }}}\right)\left(1+{\displaystyle \frac{1}{ln{N}^{\theta }}}+{\displaystyle \frac{2.334}{{ln}^2{N}^{\theta }}}\right)\hfill \end{array}$$

(22)

as $N^{\theta }<N^{\zeta }$. This completes the proof. □

Then, we need to find the upper and lower bounds of $a_1$ that satisfy the condition posed in Theorem 2.

Proposition 2.

Let $N=pq$ be a CRT-RSA modulus with $p<q<2p$. Suppose $e=N^{\frac{\alpha }{2}}$ is a valid public exponent with $0<\alpha \le 1/4$ and $d_p$ be its corresponding private exponent which satisfies $e{d}_p=1+k_p(p-1)$. Let $e{d}_p^{\prime }=1+k_p^{\prime }{k}_p$ for some $k_p,k_p^{\prime },d_p^{\prime }\in \mathbb{Z}$. Let a fraction α of the MSBs of $d_p$ and p (or q) are known. If $a_1$ be one of the prime factor of $⌊\frac{(p-1)}{e}⌋=a_1^{b_1}·a_2^{b_2}·\dots ·a_n^{b_n}=\prod _{i=1}^n{a}_i^{b_i}$ such that $\left|(p-1)-\tilde{p}\right|<e{a}_1$ then $a_1$ will be bounded as $N^{\frac{1-3\alpha }{2}}<a_1<N^{\frac{1-\alpha }{2}}$.

Proof. 

We know that $\left|(p-1)-\tilde{p}\right|<e{a}_1$ where $|p-\tilde{p}|<N^{\frac{1}{2}-\alpha }$. Then

$$\begin{array}{ccc}\hfill a_1& >& \frac{\left|(p-1)-\tilde{p}\right|}{e}\hfill \\ & \approx & \frac{N^{\frac{1}{2}-\alpha }}{N^{\frac{\alpha }{2}}}\hfill \\ & =& N^{\frac{1}{2}-\alpha -\frac{\alpha }{2}}=N^{\frac{1-3\alpha }{2}}.\hfill \end{array}$$

Thus, $N^{\frac{1-3\alpha }{2}}$ is the lower bound for $a_1$. For the upper bound, we know that $a_1<⌊\frac{(p-1)}{e}⌋$ as $a_1$ is a factor of $⌊\frac{(p-1)}{e}⌋$. Then

$$\begin{array}{ccc}\hfill a_1& <& ⌊\frac{(p-1)}{e}⌋\hfill \\ & <& \frac{N^{\frac{1}{2}}}{N^{\frac{\alpha }{2}}}\hfill \\ & =& N^{\frac{1-\alpha }{2}}\hfill \end{array}$$

Thus, $a_1<N^{\frac{1-\alpha }{2}}$. This follows the result. □

After we know the upper and lower bounds of $a_1$, we can estimate the number of primes between the bounds. To achieve that, we use the estimation in Lemma 6. The estimation is as follows in the next proposition.

Proposition 3.

Let $N=pq$ be an CRT-RSA modulus with $p<q<2p$. Suppose $e=N^{\frac{\alpha }{2}}$ be a valid public exponent with $0<\alpha \le 1/4$ and $d_p$ be its corresponding private exponent which satisfies $e{d}_p=1+k_p(p-1)$. Let $e{d}_p^{\prime }=1+k_p^{\prime }{k}_p$ for some $k_p,k_p^{\prime },d_p^{\prime }\in \mathbb{Z}$. Let a fraction α of the MSBs of $d_p$ and p (or q) are known. If $a_1$ be one of the prime factor of $⌊\frac{(p-1)}{e}⌋=a_1^{b_1}·a_2^{b_2}·\dots ·a_n^{b_n}=\prod _{i=1}^n{a}_i^{b_i}$ such that $\left|(p-1)-\tilde{p}\right|<e{a}_1$ then the number of candidates of $a_1$ that satisfies Theorem 2. will be less than

$$\frac{N^{\frac{1-\alpha }{2}}\left({ln}^2\left(N^{\frac{1-3\alpha }{2}}\right)+ln\left(N^{\frac{1-3\alpha }{2}}\right)+2.334\right)}{ln\left(N^{\frac{1-\alpha }{2}}\right){ln}^2\left(N^{\frac{1-3\alpha }{2}}\right)}.$$

Proof. 

We use results from Lemma 6 to count the sum of primes that satisfy Theorem 2. Thus, we changes $H_1$ and $H_2$ in Lemma 6 to $N^{\frac{1-\alpha }{2}}$ and $N^{\frac{1-3\alpha }{2}}$ respectively based on the bounds in Proposition 2. Equation (22) will become

$$\begin{array}{cc}\hfill & \frac{N^{\frac{1-\alpha }{2}}}{ln{N}^{\frac{1-\alpha }{2}}}\left(1+\frac{1}{\left(\frac{1-3\alpha }{2}\right)lnN}+\frac{2.334}{{\left(\frac{1-3\alpha }{2}\right)}^2{ln}^{2}N}\right)\hfill \\ \hfill & =\frac{N^{\frac{1-\alpha }{2}}}{ln\left(N^{\frac{1-\alpha }{2}}\right)}+\frac{N^{\frac{1-\alpha }{2}}}{ln\left(N^{\frac{1-\alpha }{2}}\right)ln\left(N^{\frac{1-3\alpha }{2}}\right)}+\frac{N^{\frac{1-\alpha }{2}}\left(2.334\right)}{ln\left(N^{\frac{1-\alpha }{2}}\right){ln}^2\left(N^{\frac{1-3\alpha }{2}}\right)}\hfill \\ \hfill & =\frac{N^{\frac{1-\alpha }{2}}\left({ln}^2\left(N^{\frac{1-3\alpha }{2}}\right)+ln\left(N^{\frac{1-3\alpha }{2}}\right)+2.334\right)}{ln\left(N^{\frac{1-\alpha }{2}}\right){ln}^2\left(N^{\frac{1-3\alpha }{2}}\right)}.\hfill \end{array}$$

(23)

This completes the proof. □

The following is an example to illustrate the result from Proposition 3.

Example 2.

In this example, we try to illustrate the number of primes that are eligible to be the candidates of $a_1$.To do that, we set $\alpha =\frac{1}{4}$ to imitate the lowest possible estimation of the number of primes. We also substitute the value of N from Example 1 into (23) which approximates to

$$2.736665\times {10}^{228}\approx N^{0.3705816}.$$

This is the approximation of the amount of primes that are eligible to be the candidates of $a_1$.

5. Estimating the Number of Candidates for ${\mathit{a}}_{\mathbf{1}}$ with Various Success Appetite

To reduce the number of the candidates of $a_1$ to be manipulated by an adversary, we define the “success appetite” terminology to best describe our findings.

Definition 2.

CRT-RSA Success Appetite, $G\left({\delta }_h\right)$ is the conditional probability of successfully finding the largest prime factor of $⌊\frac{p}{e}⌋$, $a_1$; where $a_1$ is less than $N^{y_1}$, given that $a_1$ is greater than $N^{y_2}$ where $N=pq$ and $y_1>y_2$ for suitable $y_1,y_2\in (0,1)$.

Remark 4.

Success appetite as described in this paper relates to the success probability of the adversary to find the actual value of $a_1$ from a certain set of primes. The adversary can choose his success appetite, depending on computing resources available to the adversary. The probability of success for the adversary depends on the size of the set of prime candidates where $a_1$ resides. As such, success appetite and probability of success are two different concepts.

Since further experiment and analysis must be completed to be corroborated with the independent nature of Dickman’s function and randomized values of $⌊\frac{p_i}{e_i}⌋$, we put forward the next conjecture that defines CRT-RSA success appetite quantitatively.

Conjecture 1.

Given i different RSA moduli, $N_i=p_i{q}_i$ that are randomly generated in RSA key generation algorithm, then the largest number of RSA moduli of which the greatest prime factor of $⌊\frac{p_i}{e_i}⌋$ is between its intended success-dependent upper and lower bound is $G\left({\delta }_h\right)·i$.

By having the CRT-RSA success appetite, an adversary can evaluate it using the next corollary.

Proposition 4.

Let $N=pq$ be an RSA modulus. Let $e=N^{\frac{\alpha }{2}}$ be an RSA public exponent and d be an RSA private exponent where $0<\alpha \le 1/4$. Let $a_1$ be one of the prime factors of $⌊\frac{p}{e}⌋=a_1^{b_1}·a_2^{b_2}·\dots ·a_n^{b_n}=\prod _{i=1}^n{a}_i^{b_i}$. Suppose B is a known integer larger than $\rho \varphi \left(N\right)$ and $B-\rho \varphi \left(N\right)<e{a}_1$. Let $F_X\left(y\right)$ be the Dickman’s function. If ${\delta }_h$ is the CRT-RSA success appetite, then the number of candidates of $a_1$ that satisfies Theorem 2 will be less than

$$\frac{N^{\frac{1-\alpha }{2}}\left({ln}^2\left(N^{\frac{1-3\alpha }{2}}\right)+ln\left(N^{\frac{1-3\alpha }{2}}\right)+2.334\right)}{ln\left(N^{\frac{1-\alpha }{2}}\right){ln}^2\left(N^{\frac{1-3\alpha }{2}}\right)}.$$

where $y_1=F^{-1}\left({\delta }_h·F_X\left(\overline{\frac{1-3\alpha }{2}}\right)+F_X\left(\frac{1-3\alpha }{2}\right)\right)$.

Proof. 

Let $F_X\left(y\right)$ or $F\left(y\right)$ be the probability function for a random integer between 1 and X to have the greatest prime factor less than $X^y$ as defined in Definition 1 (Dickman’s function). Let $X^{y_1}$ be the upper bound of $a_1$ and $X^{y_2}$ to be the lower bound of $a_1$, then (23) can also be written as

$$\frac{N^{y_1}\left({ln}^2\left(N^{y_2}\right)+ln\left(N^{y_2}\right)+2.334\right)}{ln\left(N^{y_1}\right){ln}^2\left(N^{y_2}\right)}$$

(24)

Next, we define

• $F\left(y_1\right)$ to be the probability of X having its greatest prime factor less than $X^{y_1}$;
• $F\left(y_2\right)$ to be the probability of X having its greatest prime factor less than $X^{y_2}$; and
• $F\left(\overline{y_2}\right)$ to be the probability of X not having its greatest prime factor less than $X^{y_2}$.

Let ${\delta }_h$ be the success appetite as defined in Definition 2, we can rewrite ${\delta }_h$ as the probability of $⌊\frac{p-1}{e}⌋$ having its largest prime factor less than $N^{y_1}$, given that it has no largest prime factor less than $N^{y_2}$. Using the definition of conditional probability, observe that

$$\begin{array}{ccc}\hfill {\delta }_h=F\left(y_1\right|\overline{y_2})& =& {\displaystyle \frac{F(y_1\cap \overline{y_2})}{F\left(\overline{y_2}\right)}}\hfill \\ \hfill & =& {\displaystyle \frac{F\left(y_1\right)-F\left(y_2\right)}{F\left(\overline{y_2}\right)}}.\hfill \end{array}$$

(25)

From (25),

$$\begin{array}{ccc}\hfill F\left(y_1\right)-F\left(y_2\right)& =& {\delta }_h·F\left(\overline{y_2}\right)\hfill \\ \hfill F\left(y_1\right)& =& {\delta }_h·F\left(\overline{y_2}\right)+F\left(y_2\right)\hfill \\ \hfill y_1& =& F^{-1}\left({\delta }_h·F\left(\overline{y_2}\right)+F\left(y_2\right)\right).\hfill \end{array}$$

According to Proposition 2, $y_2=\frac{1-3\alpha }{2}$. Substitute values of $y_1$ and $y_2$ into (24), we obtain

$$\frac{N^{y_1}\left({ln}^2\left(N^{\frac{1-3\alpha }{2}}\right)+ln\left(N^{\frac{1-3\alpha }{2}}\right)+2.334\right)}{ln\left(N^{y_1}\right){ln}^2\left(N^{\frac{1-3\alpha }{2}}\right)}.$$

(26)

where $y_1=F^{-1}\left({\delta }_h·F\left(\overline{\frac{1-3\alpha }{2}}\right)+F\left(\frac{1-3\alpha }{2}\right)\right)$ □

Proposition 4 shows that an adversary can adjust the upper bound of $a_1$ according to the success appetite preferred by the adversary. In the next section, we can see how this adjustment can reduce the number of primes eligible to be the significant candidates of $a_1$.

6. Comparative Analysis

In this section, we show two comparisons. In the first comparison, we compare the changes of the number of candidates of $a_1$, $\pi \left(a_1\right)$ in terms of $\beta$ (where $\pi \left(a_1\right)=N^{\beta }$) when the success appetite, ${\delta }_h$ changes. We also set $\alpha =0.05,0.1,0.15,0.2$ and $0.25$ to see the changes in $\pi \left(a_1\right)$. The full details of the values are shown in Table 2.

Table 2. Comparison in Number of Candidates of $a_1$ In Terms of Logarithm to Base N with Respect to ${\delta }_h$ and $\alpha$.

Intended Success Probability, ${\mathit{\delta }}_{\mathit{h}}$	$\mathit{\beta }$, $\mathit{\pi }\left({\mathit{a}}_1\right)={\mathit{N}}^{\mathit{\beta }}$
	$\mathbf{\alpha }=\mathbf{0}.\mathbf{05}$	$\mathbf{\alpha }=\mathbf{0}.\mathbf{1}$	$\mathbf{\alpha }=\mathbf{0}.\mathbf{15}$	$\mathbf{\alpha }=\mathbf{0}.\mathbf{2}$	$\mathbf{\alpha }=\mathbf{0}.\mathbf{25}$
0.01	0.4208	0.3464	0.2719	0.1973	0.1250
0.25	0.4324	0.3682	0.3023	0.2337	0.1796
0.50	0.4448	0.3925	0.3375	0.2785	0.2289
0.75	0.4575	0.4182	0.3768	0.3318	0.2913
1.00	0.4706	0.4457	0.4205	0.3952	0.3704

Based on Table 2, when ${\delta }_h$ progressively reduces from 1 to 0.01, for $\alpha =0.05$, the number of candidates also slowly reduces from $N^{0.4706}$ to $N^{0.4208}$, $N^{0.4457}$ to $N^{0.3464}$ for $\alpha =0.1$, $N^{0.4205}$ to $N^{0.2719}$ for $\alpha =0.15$, $N^{0.3952}$ to $N^{0.1973}$ for $\alpha =0.2$ and $N^{0.3704}$ to $N^{0.125}$ for $\alpha =0.25$. In general, the number of candidates decreases as the values of the success appetites decrease. A similar pattern occurs when the values of $\alpha$ increases. This means that the best situation for an adversary to conduct an attack against CRT-RSA using our method is when $0.25$ MSBs of d and p (or q) are known with a consideration of a success appetite that is as small as possible.

In the second comparison, we intend to compare our attack with results from [12,13,14,15,16]. All of these results require some bits of $d_p$ to be known beforehand. In [15], Takayatsu et al. provided a result which includes bits of $d_q$. A comparison with our results is shown in Table 3.

Table 3. Comparison of Our Method Against Existing Methods to Conduct Partial-Key Exposure Attack Against CRT-RSA.

Attacks	Exposed Information about Private Keys for the Attack to be Successful	Methodology
Heninger and Shacham (2009)	Given 0.27 of the bits of $p,q,d,d_p,d_q$	Using random reconstruction algorithm
Blömer and May (2003)	Given $\widetilde{d_p},e=N^{\alpha }$ such that $|d_p-{\tilde{d}}_p|<N^{\frac{1}{4}-\alpha }$ where $0<\alpha \le 1/4$	Using lattice-based method
Lu et al. (2014)	Given $\widetilde{d_p}\approx N^{\gamma }$, $e\approx N^{\alpha }$ where $|d_p-{\tilde{d}}_p|<N^{{\gamma }_1}$ such that $\gamma ,{\gamma }_1,\alpha$ satisfy conditions in Theorem 6 of [13]
Sarkar and Venkateswarlu (2014)	Given $e\approx N^{\alpha }$ and bits of $d_p$ except for n many blocks with sizes ${\gamma }_{i}logN$ bits for $1\le i\le n$, such that $\gamma ,{\gamma }_1,\alpha$ satisfy inequality in Theorem 1 of [14]
Takayatsu and Kunihiro (2015)	Given $\widetilde{d_p}\approx N^{\gamma }$, $e\approx N^{\alpha }$ where $d_p\approx N^{{\gamma }_1}$ such that $\alpha ,\gamma ,{\gamma }_1$ satisfy conditions in Theorem 6 of [15]
Our method	Given ${\tilde{d}}_p,\tilde{p},e=N^{\alpha /2}$ where $0<\alpha \le 1/4$ such that $|d_p-{\tilde{d}}_p|,|p-\tilde{p}|<N^{\frac{1-\alpha }{2}}$	Need to determine the largest prime factor of $⌊\frac{p-1}{e}⌋$

Based on Table 3, Ref. [16] requires at least 0.27 random bits of all $p,q,d,d_p,d_q$. The attack also used random reconstruction algorithm. On another hand, attack by [12] requires an approximation of $d_p$ called ${\tilde{d}}_p$ to be given, such that $|d_p-{\tilde{d}}_p|<N^{\frac{1}{4}-\alpha }$ where $e=N^{\alpha }$. The suitable size of e used in the attack is $1<e<N^{1/4}$. The methodology used in [12] can also be applied in many conditions, since we can see that the extension of the results in [13,14,15] are also using the similar lattice-based approach.

Meanwhile, our attack requires an approximation of $d_p$ and p called ${\tilde{d}}_p$ and $\tilde{p}$ to be given, such that $|d_p-{\tilde{d}}_p|,|p-\tilde{p}|<N^{\frac{1-\alpha }{2}}$. As $0<\alpha \le 1/4$, this means that the suitable range for e in our case is $0<e<N^{1/8}$. based on Table 3, Ref. [12] needs the approximation of $d_p$ to be between 0 and $<N^{1/4}$ from the actual $d_p$. Meanwhile, in our case, we need the approximation of $d_p$ and p to be between $N^{3/8}$ and $N^{1/2}$ from the actual values of $d_p$ and p. This means that our attack is less stringent and requires less MSBs of private keys to be known than [12] (although our attack needs two approximations of private keys). In addition, our method takes a different approach compared to other results, since we detach our method from the common approach of partial key attack on CRT-RSA by using the lattice-based method to finding the largest prime factor of $⌊\frac{p-1}{e}⌋$ with versatile success appetites.

7. Conclusions

We have successfully factored the modulus of CRT-RSA in polynomial time using our new method under specific conditions. Given $e=N^{\frac{\alpha }{2}}$, where $0<\alpha \le 1/4$, the method requires an approximation of private exponent called ${\tilde{d}}_p$ and approximation of p called $\tilde{p}$ to be known, such that $|d_p-{\tilde{d}}_p|,|p-\tilde{p}|<N^{\frac{1-\alpha }{2}}$. Our attack also requires the largest prime factor of $⌊\frac{p-1}{e}⌋$. By utilizing Dickman’s theorem, we showed a practical approach to identify the prime from a set of primes that the factor most likely resides in. The approach manipulates a versatile self-defined value known as the success appetite value that can be referred to by the adversary based on the computational power at hand. This makes our attack less stringent and requires fewer MSBs of private keys to be known than existing attacks. For a future extension of this work, one may develop a new method to find $a_1$ from a smaller set of primes. The method should include a marked up algorithm that identifies $a_1$, where its respective success appetite is compared with the number of candidates of $a_1$ in terms of the logarithm to base N, as shown in Table 2. Another interesting future approach to tackle the problem of finding $a_1$ is by using synchronized machine learning with the aid of cloud systems for its storage space, as shown in [23].