1. Introduction
The analysis of portfolio risk requires statistical models and techniques that accurately capture the (time-varying) dependence between prices or returns of individual assets and account for salient characteristics of the individual (marginal) distributions. For this purpose, in the last decades, there is abundant literature devoted to extending the risk modeling to the multivariate context. One of the most successful approaches are the multivariate GARCH-family models that parameterize the variance–covariance matrix through different specifications, e.g., the Vech model [
1], the factor GARCH [
2], the constant conditional correlation (CCC) model [
3], the BEKK model [
4], the dynamic conditional correlation (DCC) model [
5] or the dynamic equicorrelation model (DECO) [
6], among others—see [
7], for a comprehensive survey. All of these models, parsimoniously feature the dependence structure, thus (partially) tackling the “curse of dimensionality”, but their extension beyond the normality assumption is far from trivial.
Different solutions have been provided to model the multivariate non-Gaussian distribution of asset returns. On the one hand, [
8] showed that under correct specification of the conditional mean-variance model, maximum likelihood (ML) estimation under the Gaussian distribution provides consistent estimates even when normality is violated, which is the basis of the quasi ML (QML) estimation. On the other hand, many non-Gaussian distributions straightforwardly admit a multivariate GARCH-family structure, particularly the class of elliptical distributions [
9]. However, these extensions are developed at the cost of losing the consistency of the two-step estimation (i.e., with a higher computational burden), which is feasible under Gaussianity [
10], and their capacity to account for tail dependence is rather limited.
Within the methods to define multivariate distributions [
11], a particularly appealing solution to all these problems is the use of copulas, which allow deriving a multivariate distribution with a dependence measure from a group of arbitrary marginal distributions, in virtue of the Sklar’s theorem—see, e.g., [
12]. However, the moment computation of the applications that involve integration (e.g., providing risk measures) becomes analytically intractable and requires numerical algorithms [
13].
Another interesting approach is the semi-nonparametric (SNP) extension of the multivariate Gaussian through Gram–Charlier (GC) series. As a matter of fact, GC series have been proved, under regularity conditions, to be a valid asymptotic expansion of any distribution, see [
14] or [
15]. A multivariate extension of the GC distribution was explored by [
16,
17,
18]. In particular, the two latter showed the utility of these distributions to capture the distribution of portfolios of financial returns. Since then, alternative versions have been proposed to tackle different problems: positivity [
19], two-step estimation [
20], approximation properties [
21], generalizations to other distributions [
22], method of moments estimation [
23], time-varying conditional moments [
24], specifications in vector notation [
25], or risk forecasting [
26]. These models not only preserve the asymptotic approximation property, but also are very tractable from both the theoretical and empirical viewpoint. Although the curse of dimensionality is a little more serious than in other models, it can be smoothed through the implementation of two-step or recursive estimation methods. Furthermore, this approach naturally admits the incorporation of multivariate GARCH-family models as CCC, DCC, or DECO.
This research is focused on assessing the performance of the multivariate positive GC distribution [
27], that implies a symmetric distribution being positive in the whole domain for capturing the risk of highly volatile assets. To this end, we analyze portfolios of cryptocurrencies, which are modeled as AR-GJR-GARCH [
28] (i.e., considering asymmetric conditional variances) and a covariance structure consistent to either DCC or DECO. The former is estimated through a simplifying method based on the estimation of bivariate models and the latter is jointly estimated but assuming equal correlation among the crypto assets. The comparison of both methods sheds light on the gains of simplifying the estimation method or the correlation dynamics when dealing with the computational burden of multivariate SNP modeling.
The performance will be evaluated in terms of three alternative risk measures: value-at-risk (VaR), median shortfall (MS), and expected shortfall (ES). Each of them has supporters and opponents, but VaR and ES have been the most used in the financial industry for the last years. In addition to these traditional measures, we consider MS, which can be easily computed as a higher level of VaR and, to the best of our knowledge, is barely used related to cryptocurrencies [
29], despite being a more robust measure in the presence of extreme events.
In order to assess the model validation, we consider backtesting techniques applying the conditional coverage (CC) test [
30] and dynamic quantile (DQ) test [
31] for both VaR and MS. For ES we apply recently developed tests for backtesting: multinomial test [
32] and ES regression test [
33], the latter being the first ES test that only requires ES forecasts as input parameters regardless of VaR.
Our findings indicate that SNP-DCC and SNP-DECO show small differences between both methodologies in all portfolios selected. The results support our new proposal of implementing SNP-DCC as an acceptable alternative to model larger portfolios tackling the curse of dimensionality considering a two-step method. In general, there is hardly any difference between 97.5%-MS and 99%-VaR, but for 97.5%-VaR the best results are for SNP-DCC model, especially with portfolios less volatile and with higher correlations. On the other hand, for the far-end tail, the results are slightly better for the SNP-DECO model. For ES, the empirical application shows excellent results for both models being slightly better for portfolios with higher volatile and less correlated assets.
The remaining of the article is structured as follows:
Section 2 revises the multivariate GC model specified with either DCC or DECO structures and portfolio risk performance measures.
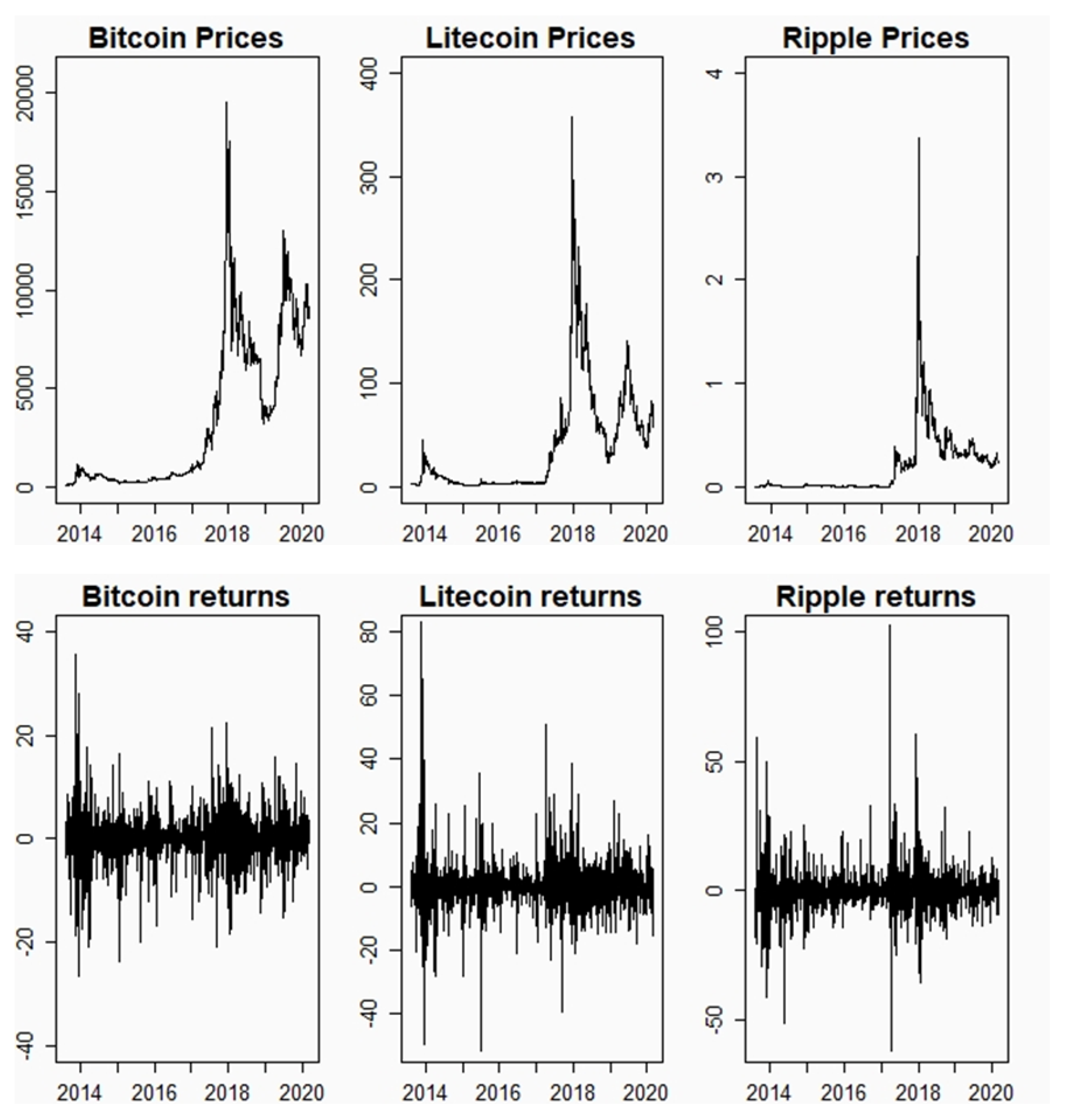
Section 3 introduces cryptocurrencies and performs an application of the models described in
Section 2 for a three-variate portfolio on three salient crypto assets: Bitcoin, Litecoin, and Ripple. Finally,
Section 4 summaries what we have learned from the two methods for computing portfolio risk with GC distributions.
2. The Model
2.1. Multivariate Gram–Charlier Model
A multivariate GC expansion of a given pdf
,
, can be expressed as the following infinite series of the derivatives of order
of the multivariate normal pdf,
, as shown in Equations (1)–(5)—see [
34]:
where, for convenient purposes, we consider the standard multivariate normal pdf—i.e., vector
has
0 mean and
(identity or order
n) matrix,
and
being the joint cumulants of the vector
, which are related to the derivatives of the natural logarithm of the characteristic function
:
where
the symbol
representing the scalar product of two vectors and
This is a nice definition, but, unfortunately, for empirical purposes becomes intractable unless small (finite) orders for the expansions and the vector dimension
n are considered. For this reason, Ref. [
20] provided a feasible expression for the multivariate Gram–Charlier density (referred to as SNP density), which is directly formulated in terms of the product of
n independent (univariate) marginal Gram–Charlier expansions, as given in Equations (6)–(8):
where ϕ
and
is a
m-order Gram–Charlier expansion (without loss of generalization we consider the same
m for all
n dimensions) expressed in terms of Hermite polynomials, i.e.,
In order to solve potential positivity problems of the truncated GC series, which is particularly important when applying backtesting techniques, positive transformations can be directly implemented. For instance, the transformation provided by [
27] may be considered by replacing Equation (7) by Equation (9):
This extension of the multivariate GC density is a well-defined density although its statistical properties are slightly different to the original multivariate GC distribution (see [
19]).
The Hermite polynomials satisfy well-known orthogonality properties—Equations (10) and (11),
which are the basis of
being a density when expansions are truncated at a finite
n. Furthermore, the first six Hermite polynomials are
,
,
,
,
,
,
The higher-order parameters account for extreme values and jumps at the distribution tails, and, if necessary, make the semi-nonparametric Gram–Charlier expansion approximate any “regular” pdf.
In addition, the ability of the (multivariate) Gram–Charlier family to adopt a wide variety of shapes with a flexible number of parameters, including fat tails with non-monotonic decay, this distribution presents three interesting properties:
(i) Marginals are also Gram–Charlier distributed, the univariate marginals being described in Equation (12).
(ii) Both linear transformations and linear combinations are also Gram–Charlier distributed [
35]. As a consequence, the pdf of the vector
can be expressed as in Equation (13).
Note that the (positive definite) variance and covariance matrix can be expressed as where is a diagonal matrix containing conditional volatilities and a correlation matrix that can be decomposed as (e.g., spectral decomposition).
Furthermore, if then, is a univariate Gram–Charlier with conditional mean and conditional variance .
(iii) The Log-likelihood of conditional mean-variance and the rest of the distribution is separable, and thus the two-step estimation procedures may be implemented—see [
20] for further details. Particularly, in the first step conditional mean and variance can be estimated by quasi maximum likelihood (QML) and in the second step the rest of the parameters of the Gram–Charlier density, including the conditional correlations, should be jointly estimated.
2.2. The Dynamic Conditional Correlation Model
The property (ii) in the above section allows the consideration of the dynamic nature of conditional variance and covariance matrix by alternative multivariate GARCH models. In this paper we focus on the SNP-DCC and the SNP-DECO models, for returns filtered through standard ARMA models for conditional mean (particularly we use an AR(1)) and a version of the GJR model [
28] for conditional variance—see [
36] or [
37]. This model allows asymmetric responses of conditional variances to negative and positive shocks. The asymmetric response of conditional correlation might also be included, but the implementation of the AGDCC [
38] model with SNP distributions is left for further research. All in all, the final model can be parameterized as in Equations (14)–(21)—note that the correlation matrix of DCC and DECO are represented by Equations (19) and (20), respectively:
where
,
,
,
and
;
;
is the unconditional correlation matrix;
is a vector of ones; A, B, and ii′ − A − B positive definite matrices;
(a diagonal matrix with the same diagonal as
) and
the Hadamard product of two identically sized matrices (computed by element-by-element multiplication). For the DECO model,
is an identity matrix of order one,
is a
matrix of ones and
is set equal to the average pairwise DCC correlations as in Equation (20), where
is the ith row and jth column element of
.
These models were originally defined for the Gaussian distribution. In this research, we assume a Gram–Charlier conditioned on the information set
, as stated in Equation (15). This involves a non-trivial evaluation of the polynomial terms in Equation (9) on
, which for the bivariate DCC model results in Equation (22)—see [
20]:
where
and
.
Likewise, for the DECO model,
may be written as in Equation (23)—see [
22]:
where
.
The DECO model greatly simplifies the estimation, but at the cost of imposing the same correlation among all variables. In addition, the DCC considers a richer time-varying correlation structure but is more dependent on the “curse of dimensionality” of multivariate modeling. As an intermediate solution, we propose a procedure that implements the DCC model estimation by exploiting the properties of the Gram–Charlier and, particularly, the independent estimation of the conditional correlation parameters in the bivariate Gram–Charlier marginal densities defined in Equation (24). It is noteworthy that if marginals are defined in terms of
the bivariate marginal distribution is dependent on the dimension
n of the original vector for which the marginal is computed, e.g., the bivariate distribution becomes the Equation (24)—see the proof in
Appendix A:
For the returns series of the portfolio defined in Equation (26) and such that = 1, 2, …, n and , our procedure can be described in the following four stages.
Stage 1: Independent estimation of portfolio conditional mean and variance for each univariate pdfs (QML).
Stage 2: Using the standardized variables filtered through the estimates obtained in stage 1, conditional correlations for each pairwise variables are estimated under a bivariate Gram–Charlier density for DCC and with joint estimation for DECO (since the latter requires imposing the same structure for all dimensions).
Stage 3: The portfolio’s Gram–Charlier distribution is estimated for the univariate series standardized by the forecasted portfolio mean-variance model according to the estimates in stages 1 and 2.
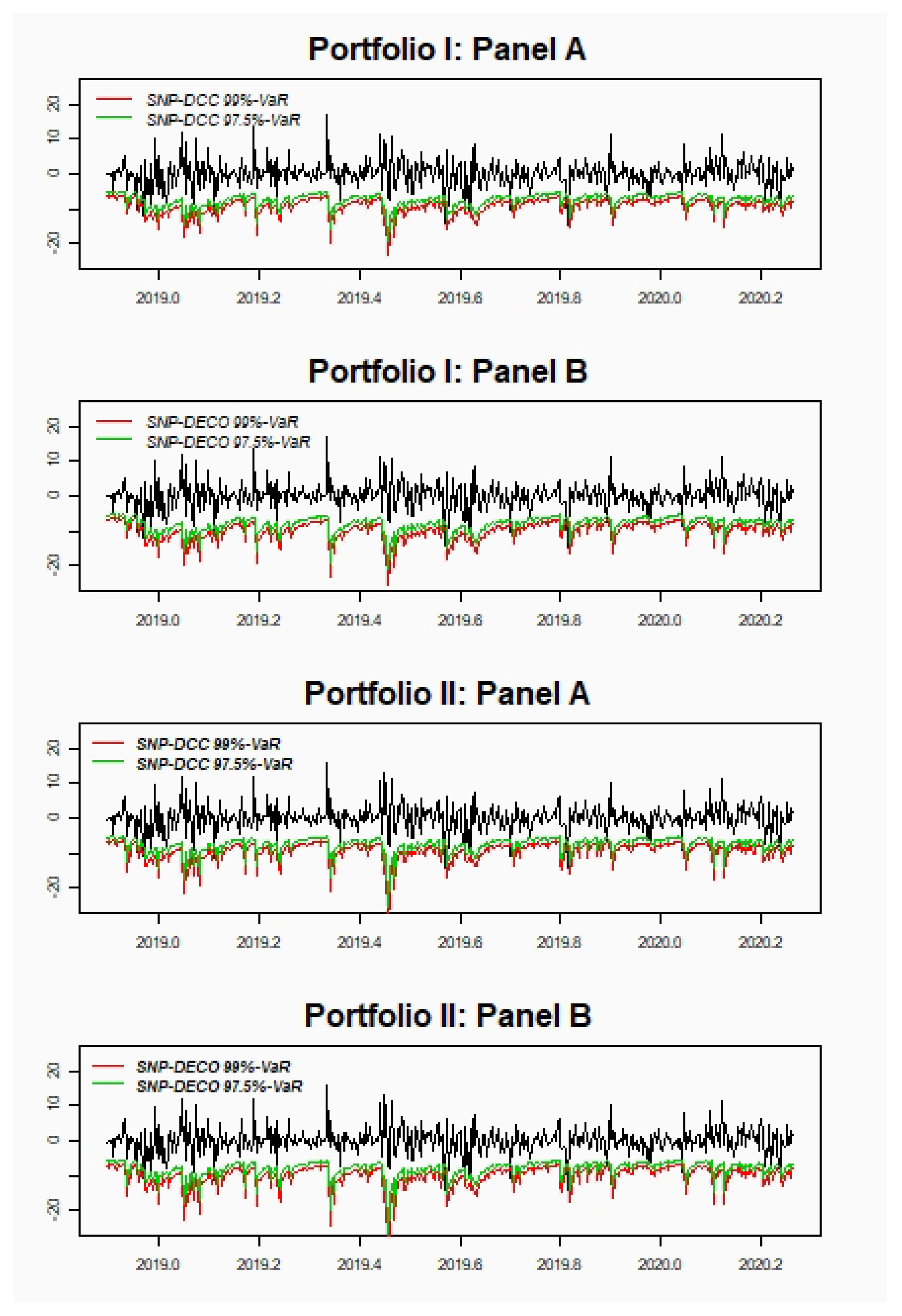
Stage 4: Given the quantiles of the portfolio distribution (Stage 3) and the estimates for its mean-variance model (stages 1 and 2) risk assessment in terms of value at risk (VaR) and expected shortfall (ES) of the Gram–Charlier under DECO and DCC is tested.
2.3. Risk Performance Model
Risk forecasting methods provide an excellent approach to assess the level of risk for portfolios on the basis of the accurate estimation of both the correlation matrix and distribution tails. To compare the best model validation, we have chosen three major risk measures: value-at-risk (VaR), expected shortfall (ES), and median shortfall (MS).
VaR is the best-known measure in the risk management industry. It started employing as capital adequacy measures for banks and it is widely used in the global financial industry [
39]. It can be defined as the maximum potential loss for the portfolio (P) return with a confidence level for a time horizon and it is represented in Equation (25)
where
and
are the one-step ahead forecasted conditional mean and conditional standard deviation for the portfolio
in Equation (26), and
the estimated α-quantile of the assumed (
n-asset) conditional portfolio distribution.
Given the weight
of the return of every, the
portfolio mean and variance can be straightforwardly obtained as in Equations (27) and (28), respectively,
where
and
are the conditional mean and standard deviation of asset i, and
is the conditional correlation of every (i and j) asset pairwise.
The portfolio quantile
, where
depicts the cumulative distribution function (cdf) that, for the case of the GC distribution, can be computed from Equation (29),
or, alternatively, for the positive version in Equations (6) and (9)—see [
27], as in Equation (30),
It is noteworthy that these quantiles require the estimation of portfolio density parameters (). Alternatively, the quantiles can be directly obtained evaluating the standardized GC density in Equation (6) (i.e., with identity variance and covariance matrix) on the transformed values according to Equations (22) and (23), since these values incorporate the information of the conditional variance and covariance structure.
However, one of the major drawbacks in VaR computation is using only a quantile, disregarding the rest of the values in the tail of the distribution and thus being more sensitive to extreme values. For the purpose of robustness, we consider the MS, which is the median of the tail given a significance level
. The performance of this latter measure has been studied in other areas [
40,
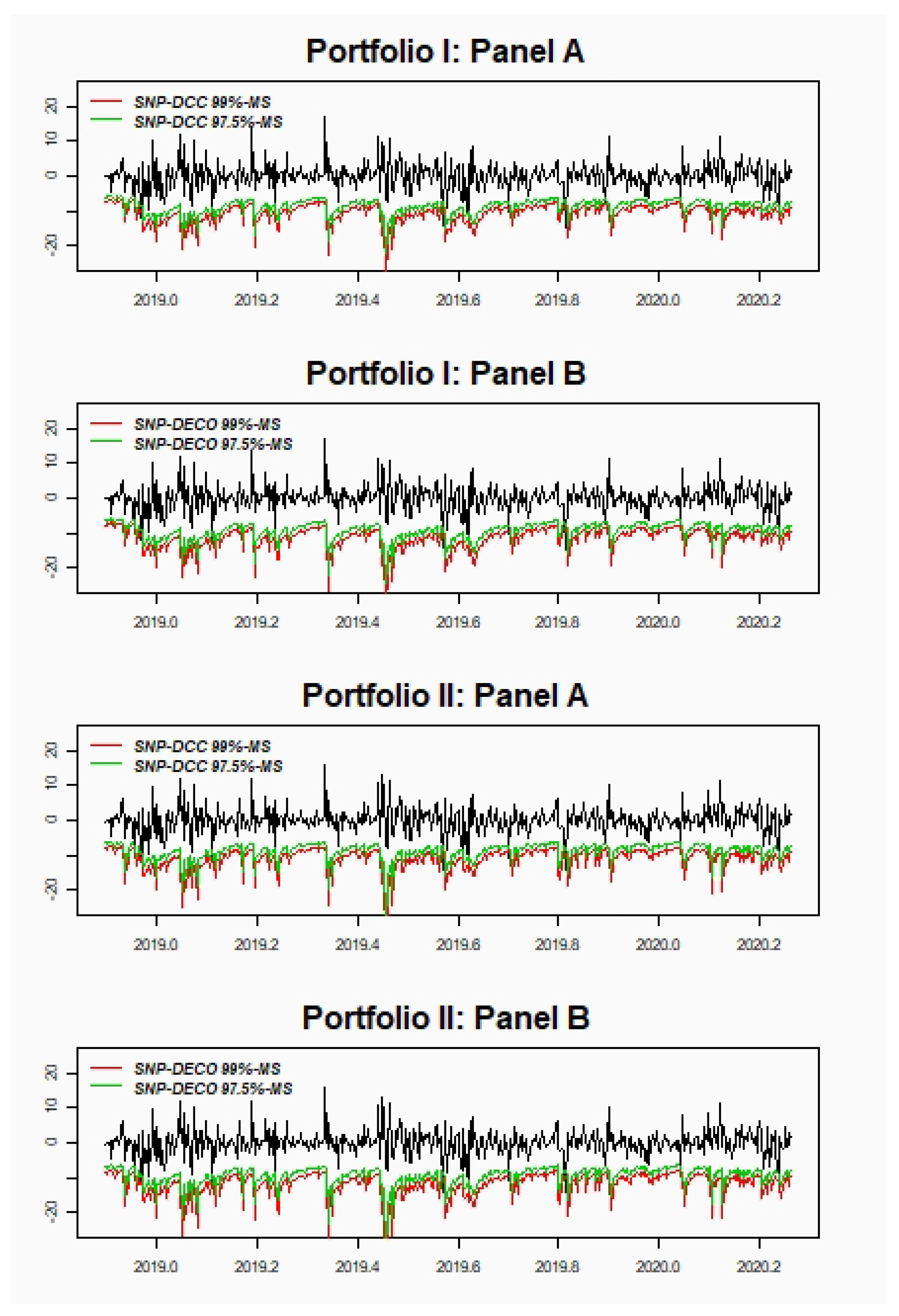
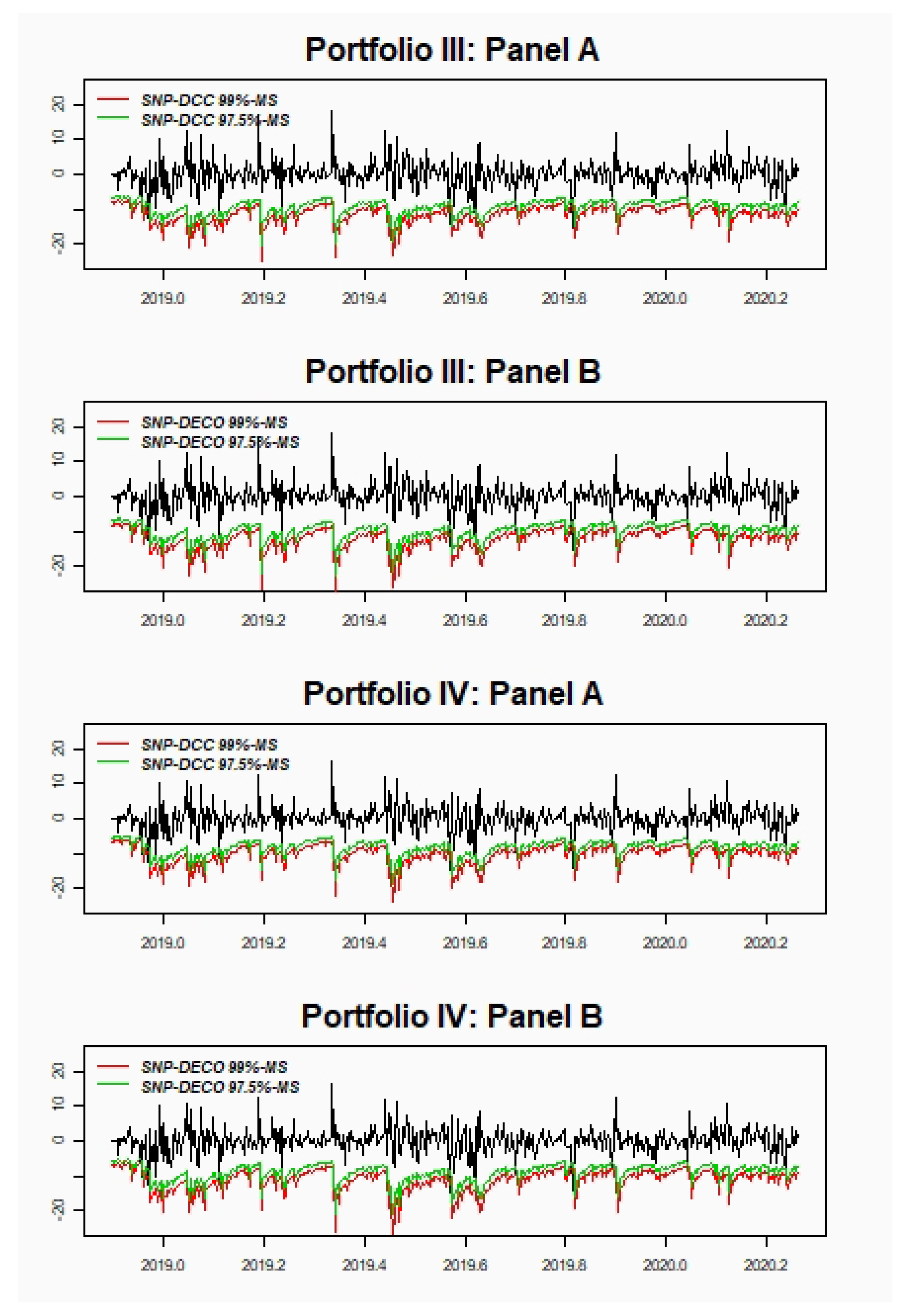
41], but to the best of our knowledge, it is not commonly used with cryptocurrencies. It may be directly computed from VaR as in Equation (31),
provided that the loss exceeds the VaR at level
α [
42] and it is based on the equivalence with VaR where the 99%-MS and 97.5%-MS are estimated as 99.5%-VaR and 98.75%-VaR, respectively.
Finally, the third risk measure is the ES, defined in Equation (32), which is more sensitive to events in the tail end of a distribution beyond VaR,
For convenience, an approximation to ES can be obtained by averaging
N quantiles with different confidence levels [
43], e.g., for
N = 8, in Equation (33)
Model performance is assessed through backtesting techniques, which evaluate any forecasted risk measure through the out-of-sample (backtesting) period on the basis of the information of a (usually rolling) in-sample window. This method seems appropriate for stationary series, and provided that the moments of the distribution exist, condition that is satisfied for the SNP modeling. Appropriate tests for backtesting risk measures are also selected. Particularly, for VaR and MS backtesting, the CC test is implemented where the null hypothesis is the correct model specification, and the exceptions satisfy the unconditional coverage and independence test. Results are complemented by the DQ test (with 4 lags) and the actual over expected (AE) ratio, the latter comparing the number of observed over expected exceptions, i.e., the closer to one the better the model.
Regarding ES, we apply the ES regression [
33], ESR hereafter, a brand-new backtesting ES forecast and, to the best of our knowledge, barely used in cryptos [
29]. We propose one of its specifications which consists in testing one-sided (such as most of the VaR backtest) beside two-sided alternatives: Intercept ESR which is the first test for ES stand-alone and consists of a regression framework for the forecast errors on an intercept term in the ES regression equation. It only requires ES forecasts as input parameters regardless of VaR, fixing the slope parameter to one in the regression and only estimating the intercept term.
4. Conclusions
In the last decades, there have been proposed a vast literature on methodologies and models to improve portfolio risk measures. This paper focuses on the multivariate SNP modeling of the return distribution based on the GC series approximation, which has been scarcely used despite its advantages in terms of flexibility and accuracy. However, the curse of dimensionality is even more severe in this framework, which calls for solutions that make portfolio estimation tractable. Based on the properties of the SNP distribution we propose a very simple and consistent method of estimation that consists of estimating the DCC model on bivariate marginal SNP distributions and plugging these dynamic correlations on the univariate portfolio SNP distribution. We argue that this method is feasible even for large portfolios although at the cost of an increase in the number of correlations/distributions to estimate. However, such a procedure is even more appealing than the DECO model, a straightforward alternative, since DECO requires a joint estimation of the SNP distribution, which is very computationally demanding even when it considers a very naive correlation structure.
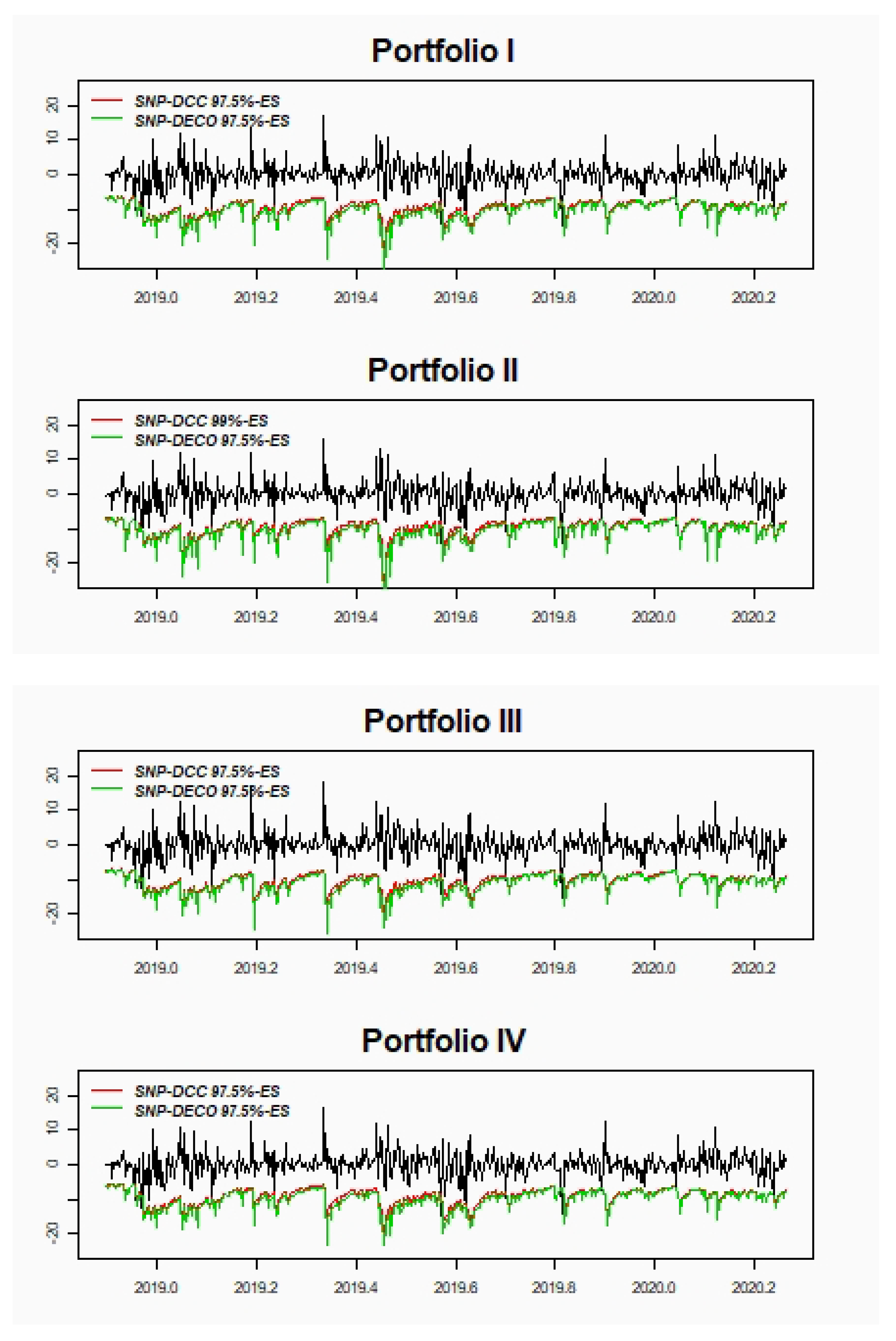
The performance of both the SNP-DCC (stepwise procedure) and the (jointly estimating) SNP-DECO are tested for several portfolios of major cryptocurrencies including Bitcoin, Litecoin, and Ripple. The model incorporates also a multivariate AR-GJR-GARCH structure and positivity transformations of the SNP density. Performance is compared through backtesting procedures for different risk measures 97.5% and 99% VaR and MS and 97.5%-ES. The implemented tests find small differences between both methodologies, supporting our proposal to implement the SNP-DCC model estimation with the bivariate Gram–Charlier marginal densities. Furthermore, the SNP-DCC model seems to provide lower risk portfolio measures since it exploits the more flexible correlation structure than the SNP-DECO, thus being preferable for diversification and hedging.
All of this suggests that the stepwise procedure for estimating SNP-DCC seems to be a very simple and accurate method for risk management, particularly useful for large portfolios where assets feature different characteristics in terms of volatility and correlation (i.e., more diversified) and when risk measures are computed at 97.5% confidence level.