The Geometry of a Randers Rotational Surface with an Arbitrary Direction Wind
Abstract
1. Introduction
- the geodesic foliation on , that is the leaves are curves in tangent to the geodesic spray ;
- the indicatrix foliation of , that is the leaves are indicatrix curves in tangent .
2. Finsler Metrics. The Randers Case
2.1. An Ubiquitous Family of Finsler Structures: The Randers Metrics
- (i)
- is strongly convex, and
- (ii)
- the indicatrix of includes the origin .
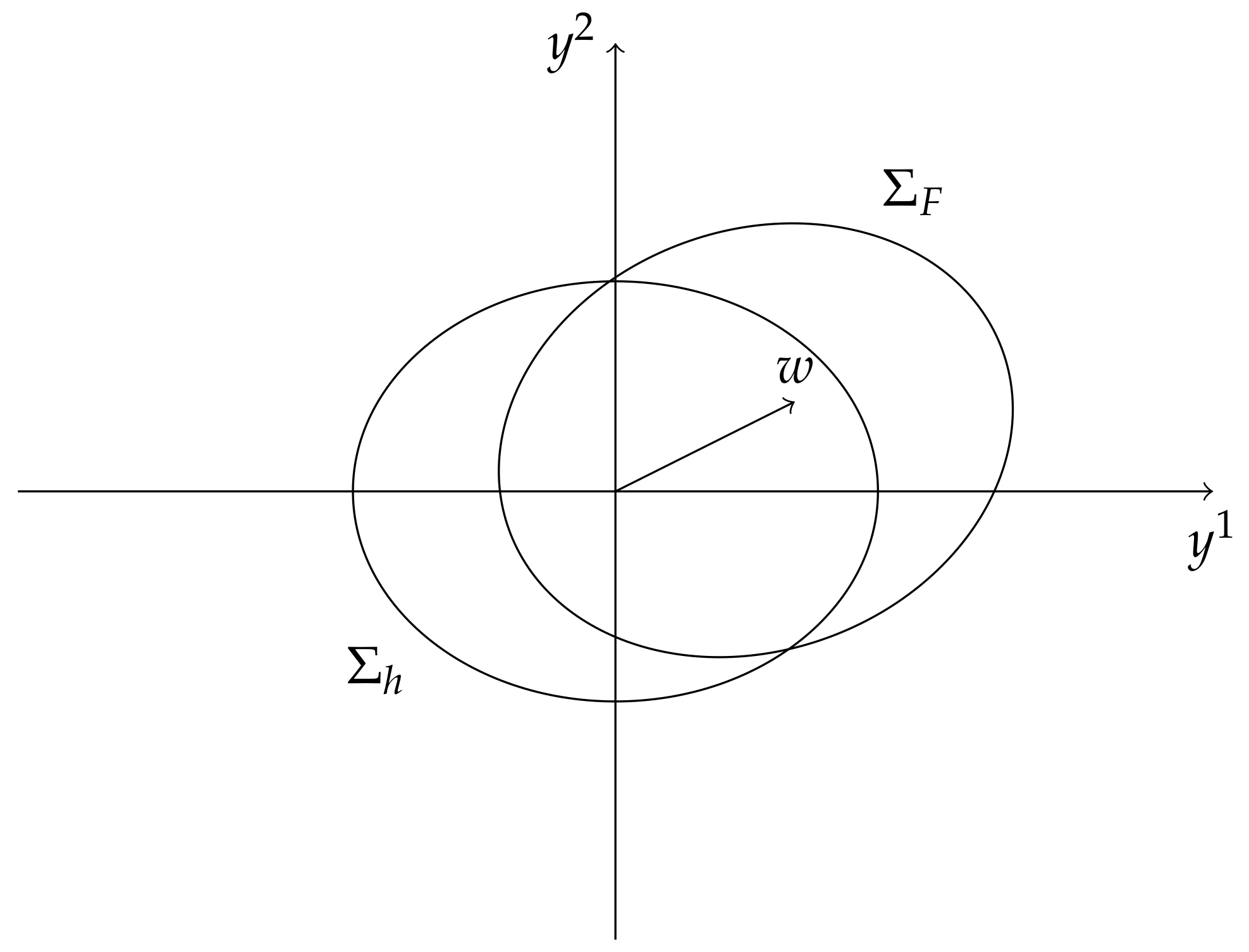
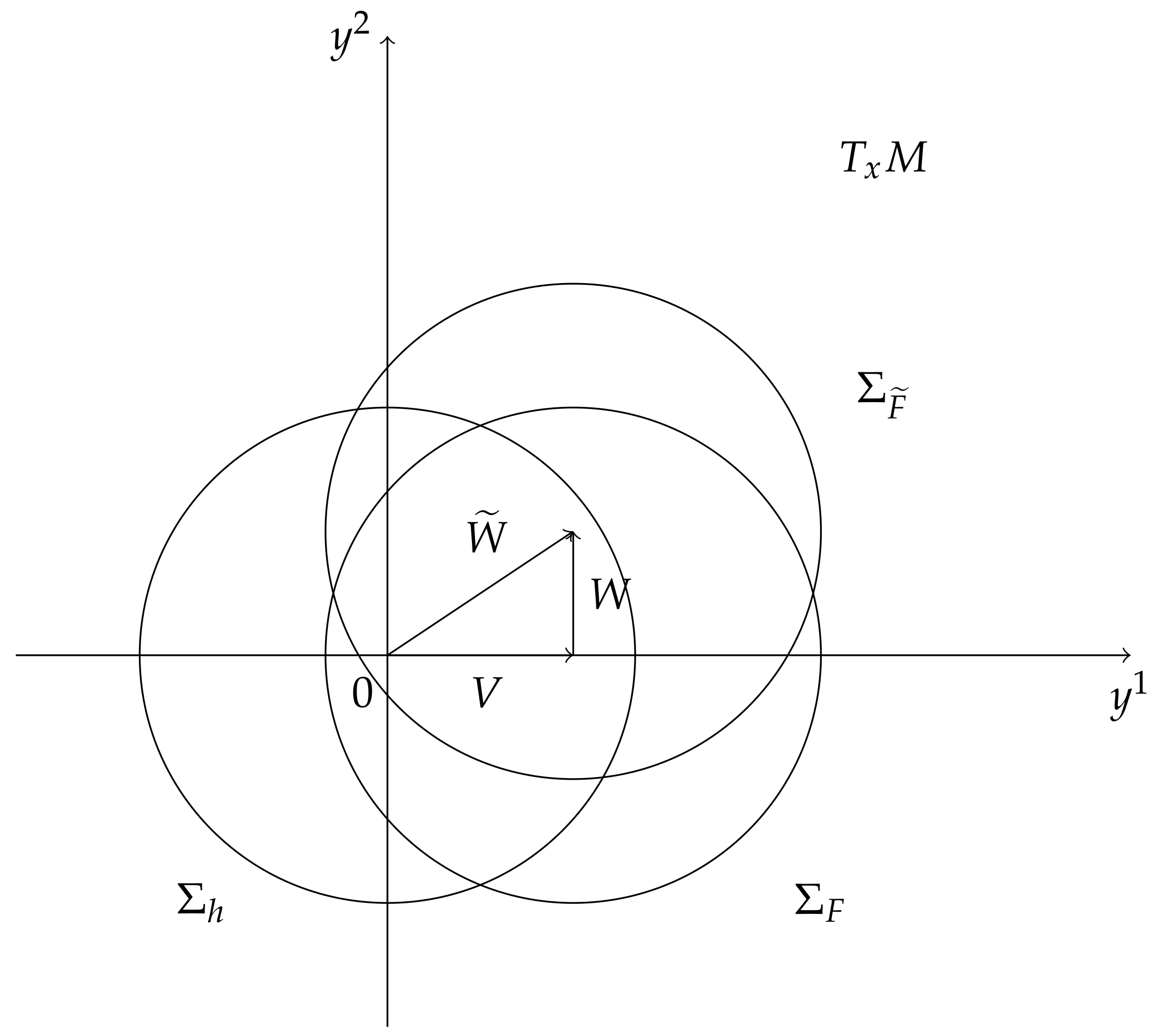
2.2. A Two Steps Zermelo’s Navigation
- (I)
- Riemannian metric with wind and assume condition ;
- (II)
- Finsler metric with wind W and assume W satisfies condition , where is the solution of the Zermelo’ s navigation problem for the navigation data with wind V, such that ,
3. Geodesics, the Conjugate and Cut Loci
3.1. The Case Closed
- (i)
- There exists a smooth function such that .
- (ii)
- The Randers metric F is projectively equivalent to α, i.e., the geodesics of coincide with the geodesics of the Riemannian metric α as non-parameterized curve.
- (iii)
- The Finslerian length of any piecewise curve on M joining the points p and q is given bywhere is the Riemannian length with respect to α of γ.
- (iv)
- The geodesic γ is minimizing with respect to α if and only if it is minimizing with respect to F.
- (v)
- For any two points p and q, we havewhere is the Riemannian distance between p and q with respect to α of γ.
- (vi)
- For an F-unit speed geodesic γ, if we put and , then q is conjugate to p along γ with respect to F if and only if q is conjugate to p along γ with respect to α.
- (vii)
- The cut locus of p with respect to F coincide with the cut locus of p with respect to α.
- (i)
- Using Proposition 3, it is clear that the differential Equation (15) is equivalent to closed 1-form, i.e., .On the other hand, since M is simply connected manifold, any closed 1-form is exact, hence in this case (15) is equivalent to .
- (ii)
- Follows immediately from the classical result in Finsler geometry that a Randers metric is projectively equivalent to its Riemannian part if and only if (see for instance [1], p. 298).
- (iii)
- The length of the curve , given by is given bywhere we use(see [19] for more details).
- (iv)
- It follows from (iii).
- (v)
- It follows immediately from (ii) and (iii) (see [19] for a detailed discussion on this type of distance).
- (vi)
- From (ii), we know that and are projectively equivalent, i.e., their non-parameterized geodesics coincide as set points. More precisely, if , is an -unit speed geodesic, and , is an F-unit speed geodesic, then there exists a parameter changing , such that with the inverse function such that .Observe that if then , where .Let us consider a Jacobi field along such thatand construct the geodesic variation , such thatSince the variation vector field is a Jacobi field, it follows that all geodesics in the variation are -geodesics for any .Similarly with the case of base manifold, every curve in the variation can be reparametrized as an F-geodesic. In other words, for each it exists a parameter changing , such thatWe will compute the variation vector field of the variation as followsIf we evaluate this relation for we getthat isFor a point , this formula readsi.e., the Jacobi field is linear combination of the tangent vector and .Let us assume is conjugate point to p along the F-geodesic , i.e., . It results cannot be linear independent, hence , i.e., is conjugate to p along the -geodesic .Conversely, if is conjugate to p along the -geodesic then (18) can be written asand the conclusion follows from the same linearly independence argument as above.
- (vii)
- Observe that .Indeed, if all -geodesics from p are globally minimizing. Assume and we can consider q end point of , i.e., q must be F-conjugate to p along the geodesic from p to q. This implies the corresponding point on is conjugate to p, this is a contradiction.Converse argument is identical.Let us assume and are not empty sets.If , then we have two cases:
- (I)
- q is an end point of , i.e., it is conjugate to p along a minimizing geodesic from p to q. Therefore q is the closest conjugate to p along the F-geodesic which is the reparameterization of (see (vi)).
- (II)
- q is an interior point of . Since the set of points in founded at the intersection of exactly minimizing two geodesics of same length is dense in the closed set , it is enough to consider this kind of cut point. In the case such that there are two -geodesics , of same length from p to , then from the statement (iv) it is clear that the point has the same property with respect to F.Hence, . This inverse conclusion follows from the same argument as above by changing roles of with F.
3.2. The Case W Is F-Killing Field
- (i)
- X is Killing field for ;
- (ii)
- , where L is the symbol for the Lie derivative, and is the canonical lift of X to ;
- (iii)
- (iv)
- , where “ | ” is the h-covariant derivative with respect to the Chern connection.
- (i)
- The -unit speed geodesics can be written aswhere is the 1-parameter flow of W and ρ is an F-unit speed geodesic.
- (ii)
- For any Jacobi field along such that , the vector field is a Jacobi field along and .
- (iii)
- For any and any flag with flag pole and transverse edge , the flag curvatures K and of F and , respectively, are related byprovided and V are linearly independent.
- (i)
- The point is -conjugate to along the -geodesic if and only if the corresponding point is the F-conjugate point to along ρ.
- (ii)
- is (forward) complete if and only if is (forward) complete.
- (iii)
- If ρ is a F-global minimizing geodesic from to a point , then is an -global minimizing geodesic from to , where .
- (iv)
- If is a F-cut point of p, then , i.e., it is a -cut point of p, where .
- (i)
- Since is a diffeomorphism on M (see Lemma 3), it is clear that its tangent map is a regular linear mapping (Jacobian of is non-vanishing). Then, Lemma 5 shows that vanishes if and only if J vanishes, and the conclusion follow easily.
- (ii)
- Let us denote by and the exponential maps of F and , respectively. Then, impliesIf is complete, Hopf–Rinow theorem for Finsler manifolds implies that for any , the exponential map is defined on all of M. Taking into account Lemma 3, from (22) it follows is defined on all of , and again by Hopf–Rinow theorem we obtain that is complete. The converse proof is similar.
- (iii)
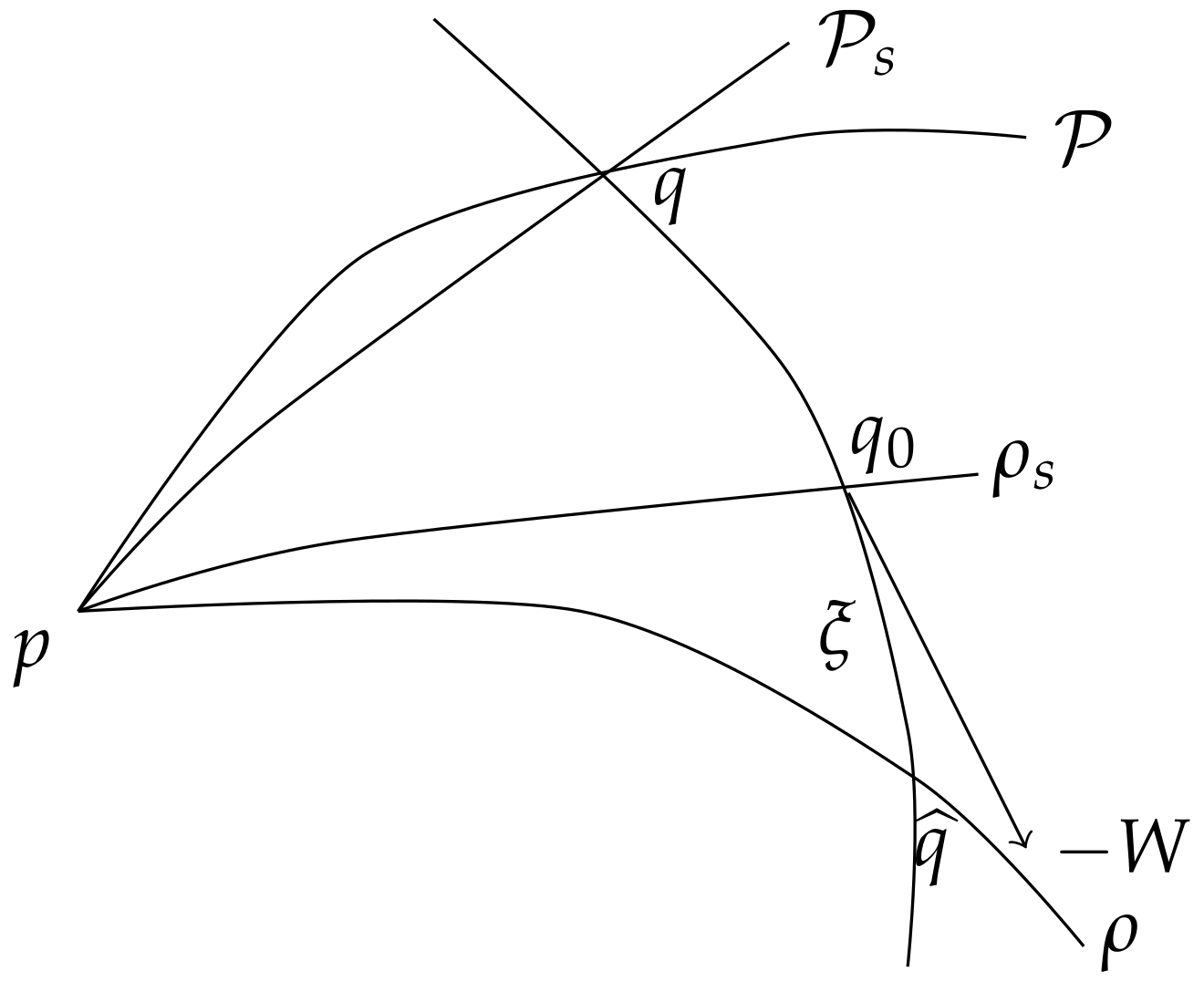
- Firstly observe that , since and .We will proof this statement by contradiction (see Figure 4).For this, let us assume that, even though is globally minimizing, the flow-corresponding geodesic from p to q is not minimizing anymore. In other words, there must exist a shorter minimizing geodesic from p to such that . (We use the subscript s for short).We consider next, the F-geodesic obtained from by flow deviation, i.e., , and denote . Then, triangle inequality in shows thatwhere we denote by the flow orbit from W through q oriented from to . In other words , and using the hypothesis , it follows
- (iv)
- It follows from (iii) and the definition of cut locus.
- (I)
- V satisfies the differential relationwhere , ;
- (II)
- W is Killing with respect to h and the Lie bracket .
- (i)
- The -unit speed geodesics are given bywhere φ is the flow of W and is an F-unit speed geodesic.Equivalently,where is an α-unit speed geodesic and is the parameter change .
- (ii)
- The point is conjugate to along the -geodesic if and only if the corresponding point on the F-geodesic ρ is conjugate to p, or equivalently, is conjugate to p along the α-geodesic from p to .
- (iii)
- If , then , where .
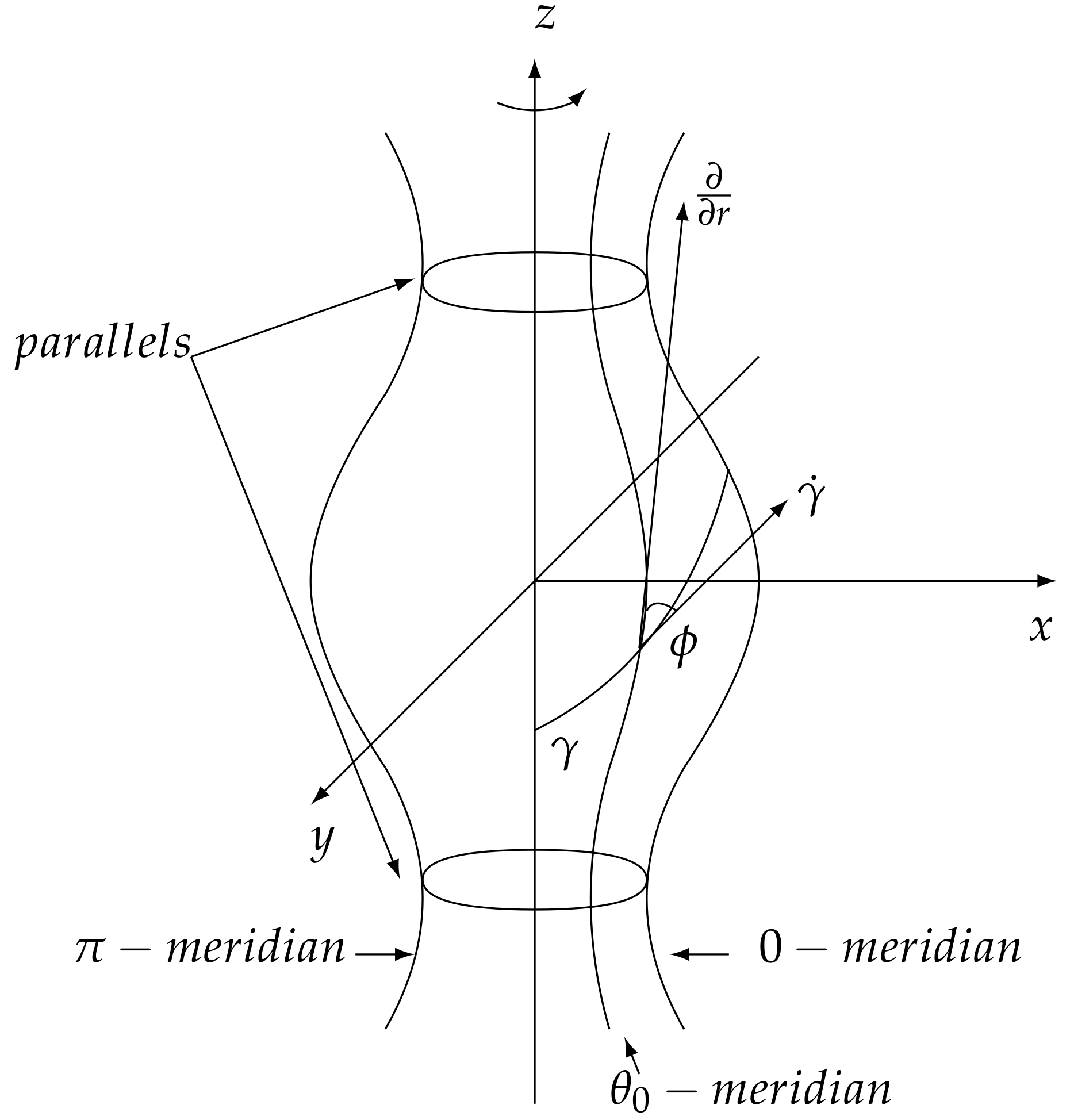
4. Surfaces of Revolution
4.1. Finsler Surfaces of Revolution
4.2. The Riemannian Case
- The cut locus is the union of a subarc of the parallel opposite to q and the meridian opposite to q if and , i.e.,
- The cut locus is the meridian opposite to q if or if .
- It is easy to see that if the Gauss curvature everywhere, then h-geodesics cannot have conjugate points. It follows that in the case the h-cut locus of a point is the opposite meridian to the point.
- See [14] for a more general class of Riemannian cylinders of revolution whose cut locus can be determined.
4.3. Randers Rotational Metrics, the Case
- (i)
- The solution of the Zermelo’s navigation problem for and wind is the Randers metric , whereand .
- (ii)
- The solution of Zermelo’s navigation problem for the data and wind , such that , is the Randers metric , whereand .
- (iii)
- (i)
- The solution of Zermelo’s navigation problem with and is obtained from (9) with .Taking into account that , it follows and a straightforward computation leads to (29).
- (ii)
- Similar with (i) using and , hence and .
- (iii)
- Follows from Theorem 1. We observe that is actually equivalent to and .Indeed,andwhere we use .
- Observe that we actually perform a rigid translation of the Riemannian indicatrix by , which is actually equivalent to translating by V followed by the translation of by W (see Remark 2).
- Observe that the Randers metric given by (29) on the topological cylinder is rotational invariant, hence is a Finslerian surface of revolution. This type of Randers metrics are called Randers rotational metrics. Indeed, let us denote . Observe that in the case is an odd or even function, the function is an even function such that .
- (i)
- The -unit speed geodesics are given bywhere is α-unit speed geodesic and is the parametric change .
- (ii)
- The point is conjugate to along the -geodesic if and only if is conjugate to p with respect to α along the α-geodesic from p to .
- (iii)
- The point is an α-cut point of p if and only if , where .
- (i)
- With notations in Theorem 6, if there exist a smooth function and a constant B such that and if everywhere, then the α-cut locus and the cut locus of a point is the opposite meridian to the point p.Moreover, the cut locus of is the deformed opposite meridian by the flow of the vector field .
- (ii)
- With the notations in Theorem 6, if there exist a smooth function and a constant B such that , is decreasing along any half meridian and , then the α-cut locus and the F-cut locus of a point are given as in Theorem 5.
- (i)
- It follows from Proposition 6 and Theorem 6.
- (ii)
- Likewise, it follows by combining Proposition 6 and Remark 8, part 1.
4.4. The Case Special
- (i)
- The Gauss curvatures and of and , respectively, are proportional, i.e.,where α is the Riemannian metric obtained in the solution of the Zermelo’s navigation problem for and .
- (ii)
- The geodesic flows and of and , respectively, satisfywhere is the difference vector field on endowed with the canonical coordinates .
- (I)
- If everywhere, then
- (i)
- the α-cut locus of a point p is the opposite meridian.
- (ii)
- the F-cut locus of a point p is the opposite meridian, where ,and ,
- (iii)
- the -cut locus of a point p is the twisted opposite meridian by the flow action .
- (II)
- With the notations in Theorem 6 let us assume that has Gaussian curvature satisfying is decreasing along any half meridian and . Then, in this case, the cut locus of is a subarc of the opposite meridian is of the opposite parallel deformed by the flow of .
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bao, D.; Chern, S.S.; Shen, Z. An Introduction to Riemann Finsler Geometry; Graduate Texts in Mathematics; Springer: New York, NY, USA, 2000. [Google Scholar]
- Bao, D. On two curvature-driven problems in Riemann-Finsler geometry. Adv. Stud. Pure Math. 2007, 48, 19–71. [Google Scholar]
- Bryant, R. Projectively flat Finsler 2-spheres of constant flag curvature. Sel. Math. 1997, 3, 161–203. [Google Scholar] [CrossRef]
- Myers, S.B. Connections between differential geometry and topology I. Duke Math. J. 1935, 1, 376–391. [Google Scholar] [CrossRef]
- Buchner, M. Simplicial structure of the real analytic cut locus. Proc. Am. Math. Soc. 1977, 64, 118–121. [Google Scholar] [CrossRef]
- Buchner, M. The structure of the cut locus in dimension less than or equal to six. Compos. Math. 1978, 37, 103–119. [Google Scholar]
- Gluck, H.; Singer, D. Scattering of geodesic fields I. Ann. Math. 1978, 108, 347–372. [Google Scholar] [CrossRef]
- Shiohama, K.; Shioya, T.; Tanaka, M. The Geometry of Total Curvature on Complete Open Surfaces; Cambridge Tracts in Mathematics 159; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Itoh, J.; Sabau, S.V. Riemannian and Finslerian spheres with fractal cut loci. Diff. Geom. Its Appl. 2016, 49, 43–64. [Google Scholar] [CrossRef][Green Version]
- Hama, R.; Chitsakul, P.; Sabau, S.V. The geometry of a Randers rotational surface. Publ. Math. Debr. 2015, 87, 473–502. [Google Scholar] [CrossRef][Green Version]
- Hama, R.; Kasemsuwan, J.; Sabau, S.V. The cut locus of a Randers rotational 2-sphere of revolution. Publ. Math. Debr. 2018, 93, 387–412. [Google Scholar] [CrossRef]
- Kopacz, P. On generalization of Zermelo navigation problem on Riemannian manifolds. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950058. [Google Scholar] [CrossRef]
- Chitsakul, P. The structure theorem for the cut locus of a certain class of cylinders of revolution I. Tokyo J. Math. 2014, 37, 473–484. [Google Scholar] [CrossRef][Green Version]
- Chitsakul, P. The structure theorem for the cut locus of a certain class of cylinders of revolution II. Tokyo J. Math. 2015, 38, 239–248. [Google Scholar] [CrossRef][Green Version]
- Zermelo, E. Über das Navigationsproblem bei ruhender oder veränderlicher Windverteilung. Z. Angew. Math. Mech. 1931, 11, 114–124. [Google Scholar] [CrossRef]
- Shen, Z. Finsler metrics with K=0 and S=0. Canad. J. Math. 2003, 55, 112–132. [Google Scholar] [CrossRef]
- Bao, D.; Robles, C.; Shen, Z. Zermelo navigation on Riemannian manifolds. J. Differ. Geom. 2004, 66, 377–435. [Google Scholar] [CrossRef]
- Robles, C. Geodesics in Randers spaces of constant curvature. Trans. Amer. Math. Soc. 2007, 359, 1633–1651. [Google Scholar]
- Sabau, S.V.; Shibuya, K.; Shimada, H. Metric structures associated to Finsler metrics. Publ. Math. Debr. 2014, 84, 89–103. [Google Scholar] [CrossRef]
- Innami, N.; Nagano, T.; Shiohama, K. Geodesics in a Finsler surface with one-parameter group of motions. Publ. Math. Debr. 2016, 89, 137–160. [Google Scholar] [CrossRef]
- Hrimiuc, D.; Shimada, H. On the L-duality between Lagrange and Hamilton manifolds. Nonlinear World 1996, 3, 613–641. [Google Scholar]
- Miron, R.; Hrimiuc, D.; Shimada, H.; Sabau, S.V. The Geometry of Hamilton and Lagrange Spaces; Fundamental Theories of Physics; Kluwer Academic Publishers Group: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Foulon, P.; Matveev, V.S. Zermelo deformation of Finsler metrics by Killing vector fields. Electron. Res. Announc. Math. Sci. 2018, 25, 1–7. [Google Scholar] [CrossRef]
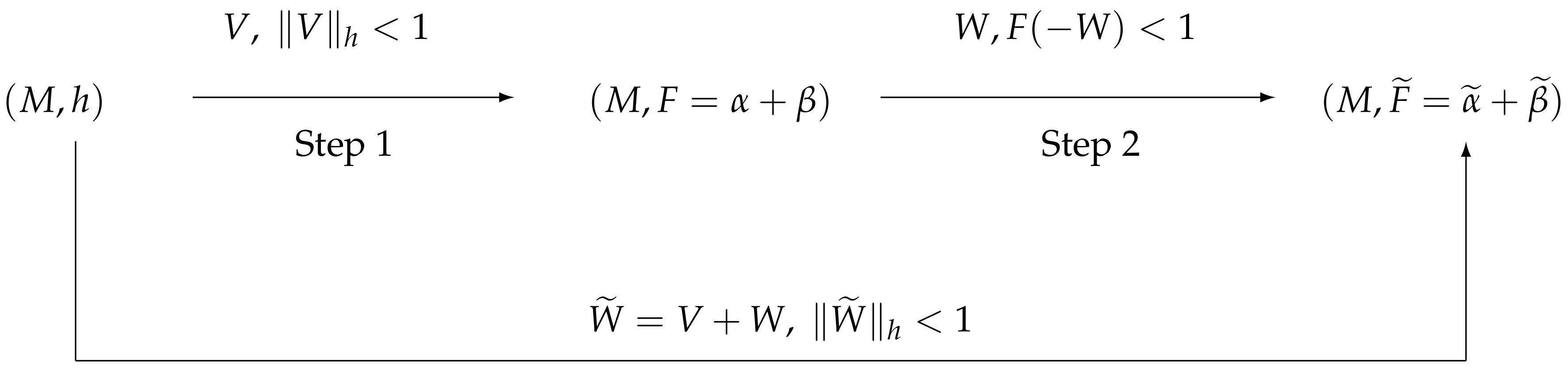
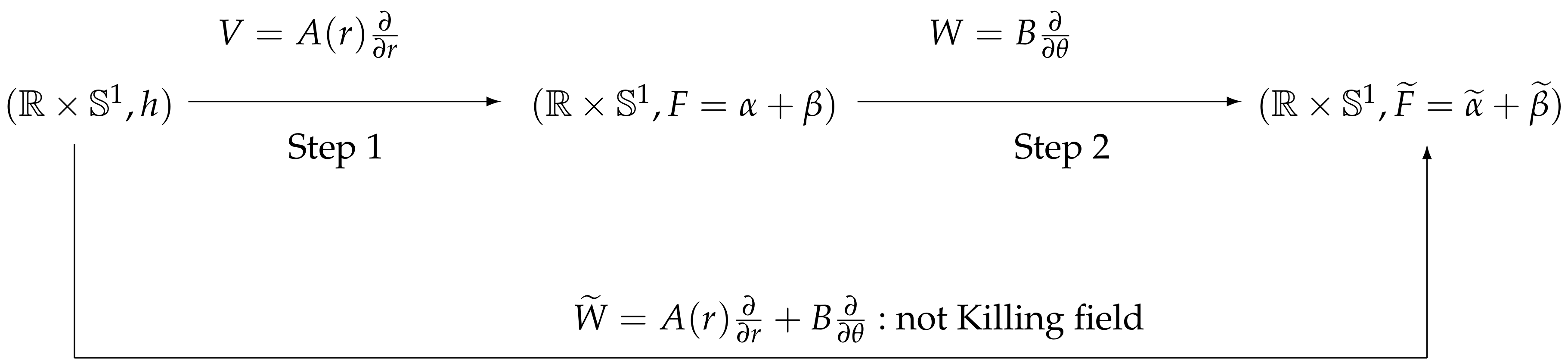
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hama, R.; Sabau, S.V. The Geometry of a Randers Rotational Surface with an Arbitrary Direction Wind. Mathematics 2020, 8, 2047. https://doi.org/10.3390/math8112047
Hama R, Sabau SV. The Geometry of a Randers Rotational Surface with an Arbitrary Direction Wind. Mathematics. 2020; 8(11):2047. https://doi.org/10.3390/math8112047
Chicago/Turabian StyleHama, Rattanasak, and Sorin V. Sabau. 2020. "The Geometry of a Randers Rotational Surface with an Arbitrary Direction Wind" Mathematics 8, no. 11: 2047. https://doi.org/10.3390/math8112047
APA StyleHama, R., & Sabau, S. V. (2020). The Geometry of a Randers Rotational Surface with an Arbitrary Direction Wind. Mathematics, 8(11), 2047. https://doi.org/10.3390/math8112047



