Abstract
Real-world complex systems are often modeled by networks such that the elements are represented by vertices and their interactions are represented by edges. An important characteristic of these networks is that they contain clusters of vertices densely linked amongst themselves and more sparsely connected to nodes outside the cluster. Community detection in networks has become an emerging area of investigation in recent years, but most papers aim to solve single-objective formulations, often focused on optimizing structural metrics, including the modularity measure. However, several studies have highlighted that considering modularityas a unique objective often involves resolution limit and imbalance inconveniences. This paper opens a new avenue of research in the study of multi-objective variants of the classical community detection problem by applying multi-objective evolutionary algorithms that simultaneously optimize different objectives. In particular, they analyzed two multi-objective variants involving not only modularity but also the conductance metric and the imbalance in the number of nodes of the communities. With this aim, a new Pareto-based multi-objective evolutionary algorithm is presented that includes advanced initialization strategies and search operators. The results obtained when solving large-scale networks representing real-life power systems show the good performance of these methods and demonstrate that it is possible to obtain a balanced number of nodes in the clusters formed while also having high modularity and conductance values.
1. Introduction
Graph theory is one of the most important branches of mathematics. Graphs are often used to model networks such that nodes (vertices) are the elements and links (edges) denote interactions between these elements. In practice, graph theory is used to model real-life complex systems using graphs and to understand the role of the nodes within a given network. Some applications of graph theory are found in the study of transportation networks, computer and interconnection networks, telecommunication networks, electrical networks, biological systems, social networks, etc. [1].
Community detection is an emerging area of research that is attracting interest among scientists studying complex networks. The aim here is to detect community structures, that is, groups of densely interconnected nodes such that connections between the nodes are denser than connections with the rest of the network. The interest in detecting these groups or communities comes from the fact that the elements of each community potentially share similar features. Most research papers dealing with community detection consider single-objective formulations in which only one objective, usually modularity [2], is optimized. However, recent investigations have shown some drawbacks derived from the only use of modularity. For example, in [3], the existence of resolution limit problems is demonstrated, while other authors have detected the existence of imbalance problems [4], which implies that classical measures tend to overestimate either the exterior or the interior of a community. Some approaches have been proposed to mitigate the latter inconvenience, including symmetric frameworks to maintain a balance between the interior and the exterior of a community [5].
Given the above, it seems suitable to design algorithms to detect communities that consider not only modularity but also other objective functions. A large number of methods have been proposed for solving multi-objective optimization problems (MOPs). Among these approaches, Multi-objective Evolutionary Algorithms (MOEAs) are probably the most widely applied strategies. This paper proposes a new MOEA, called Multi-objective Generational Genetic Algorithm+ (MOGGA+), which extends the features of the Generational Genetic Algorithm+ (GGA+) [6] that has successfully been applied to the classical single-objective formulation of the community detection problem. MOGGA+ uses different strategies to obtain a set of non-dominated solutions as an approximation to the Pareto-optimal front [7]. This method is compared with a high-performance MOEA often used in the literature for solving large-scale benchmarks and network data taken from large-scale power grids.
The rest of the paper is organized as follows: Section 2 describes the problem of community detection in graphs, including an overview of some multi-objective formulations applied to this problem. Section 3 includes a formal description of the bi-objective formulations proposed in the paper. Section 4 presents in detail the algorithm proposed to solve these bi-objective problems. Section 5 presents the empirical study, which compares the proposed method with other approaches in several case studies of different sizes and topologies. Finally, Section 6 provides the conclusions of this investigation.
2. Multi-Objective Community Detection: An Overview
Community detection is a problem closely related to graph partitioning [8]. In fact, graph partitioning is often used for community detection in different areas of application [9]. However, while the goal of graph partitioning is to minimize the number of edges connecting nodes from different graphs, community detection consists of finding community structures [10], that is, groups of densely interconnected nodes such that connections between the nodes are denser than connections with the rest of the network. The interest in detecting these groups or communities comes from the fact that the elements of each community potentially share similar features [11,12]. It is important to remark that, in some real-world situations, the number of community structures of the network is known beforehand while, in many other cases, the number of communities is initially unknown and the algorithms must obtain several solutions featuring different numbers of community structures.
Most research papers dealing with community detection consider single-objective formulations in which only one objective (usually modularity [2]) is optimized. However, modularity maximization (see Equation (1)) is an nondeterministic polynomial-time hard (NP-hard) problem [13], which means it is not possible to guarantee that the optimum solution will be found within a limited execution time [14]. Despite the generalized use of modularity to find community structures, some authors have detected resolution limit [3] and imbalance problems [4].
Many problems in science and engineering are multi-objective since they involve the simultaneous optimization of two or more conflicting objectives, that is, the improvement of an objective often involves the deterioration of another or others. Typically, these MOPs have been addressed using scalarization techniques that combine the different objective functions into a single one that can then be solved by single-objective algorithms. Two typical scalarization techniques are linear weighting and -constrained methods [15]. On the one hand, the idea behind weighting methods is to assign weights to each objective function and then to maximize (or minimize) the weighted sum of the objectives. On the other hand, -constrained methods establish a rank among objectives according to their importance, such that each objective function is optimized individually, subject to the restriction that the higher ranked functions cannot exceed a certain percentage of the optimal values reached in previous generations (iterations). Despite their popularity, scalarization methods have certain drawbacks; for example, the assignment of weights or rankings to the objectives is often arbitrary. Furthermore, these methods only obtain a single (global) trade-off solution. A method to overcome these difficulties is to use Pareto-based optimization techniques. Pareto-based multi-objective algorithms aim to obtain not one but a set of solutions that are evaluated in terms of Pareto-dominance relations [16]. A solution A is said to be non-dominated or Pareto-optimal if no other feasible solution B dominates it, i.e., B is not better than A in at least one objective. The set of all non-dominated solutions found in the solution space forms the so-called Pareto-optimal front that represents the optimal trade-off between all objectives considered. This approach is very useful in decision-making processes since it provides a set of solutions to experts who will choose the one that best suits their preferences. It is important to remark that it is very difficult to obtain the Pareto-optimal front in complex optimization problems, which is why the aim is to obtain a set of non-dominated solutions as an approximation to that set [17]. Many authors have also considered decomposition algorithms that decompose the task of approximating the Pareto-optimal front into a set of subtasks such that each task is a subproblem which can be single-objective or multi-objective. This strategy becomes useful when dealing with many objectives, but it seems to be more accurate for obtaining the entire Pareto-optimal front in bi-objective formulations since it provides a set of possible solutions to the decision-maker.
In recent years, some researchers have proposed solving the community detection problem by considering several objectives simultaneously. For example, [18] proposed the Multi-objective Genetic Algorithm for Networks (MOGA-Net), which maximizes the intra-connections inside each community and minimizes interconnections between different communities. These objectives were also considered in [19], which proposed a MOEA with decomposition (MOEA/D-Net). Other authors have proposed decomposing modularity into two terms that represent the intra-link strength and the interlink strength of a partition [20]. Similarly, [21,22] proposed multi-objective evolutionary frameworks for solving multi-objective community detection approaches that consider the intra-neighbour score and the inter-neighbour score as objectives to optimize. In [23], a multi-objective algorithm was presented to optimize the community score and the community fitness. A MOEA based on Affinity Propagation (APMOEA) was presented in [3] to optimize the ratio association and the ratio cut, obtaining good results in comparison with MOEA/D-Net. In [24], the label-based dynamic multi-objective genetic algorithm (L-DMGA) was proposed for maximizing the snapshot quality and for minimizing the temporal cost. In [25], a Multi-objective Genetic Algorithm (MOGA-OCD) was proposed for detecting overlapping communities such that the internal connectivity of the communities is maximized, whereas the number of external connections to the rest of the graph is minimized. In [26], the negative ratio association and ratio cut were optimized using the Discrete Inverse Modelling-based MOEA with Decomposition algortihm (DIM-MOEA/D), which obtains a similar or better performance than other approaches, including MOCD [20], MOGA-Net [18], MOEA/D-net [19], and MODPSO/D [27].
In addition to MOEAs, other meta-heuristic approaches for solving multi-objective community detection problems have been proposed. This is the case of the Particle Swarm Optimization (PSO) algorithm with decomposition (MOPSO/D) proposed in [27] for minimizing the kernel k-means and ratio cut. These objectives were also considered years later in [28], which proposed the so-called MOPSO-Net, also based on PSO. In [29], the researchers presented the so-called Multi-objective Immune Algorithm for Multi-Resolution Community Detection (MICD), which aims to optimize the modified ratio association and the ratio cut. In [30], a Multi-objective Biogeography-based Optimization Algorithm with Decomposition (MBBOD) was presented to simultaneously optimize modularity and a metric that measures the similarity of attributes of the nodes of a community. Another MBBOD implementation was introduced in [31], where the two objectives optimized were modularity and the normalized mutual information. This pair of objectives were also considered in [32] and were optimized by the Multi-objective Discrete Teaching–Learning-based Optimization with Decomposition (MODTLBO/D), which obtained good results in comparison with MOCD [20], MOGA-Net [18], MOEA/D-Net [19], and MODPSO/D [27] in different problem instances. Other researchers proposed a multi-objective optimization community detection algorithm with attribute information (MOCDA) to simultaneously optimize modularity and homogeneity [33]. This pair of objectives has also been considered in [34], which proposed the so-called Multi-objective Attributed Community Detection Algorithm with Node Importance Analysis (MANIA). Another investigation [35] proposed a local information-based MOEA (L-MOEA) that adopts a decomposition strategy to optimize the negative ratio association and ratio cut.
Therefore, taking into account these and other previous studies, it is obvious that it is possible to create a large number of multi-objective community detection formulations by combining different objectives [36]. The overview of the state of the art in this field shows that most papers dealing with community detection from a multi-objective perspective still currently use scalarization or decomposition approaches. Only a few approaches have solved multi-objective community detection approaches considering Pareto-based methods, for example, as in [37], which proposed the Multi-objective Adaptive Fast Evolutionary Algorithm for community detection (F-SGCD) that optimizes community score and community fitness using Pareto-dominance comparisons. The novelty and contributions of this investigation are as follows: (1) For the first time, a Pareto-based MOEA was designed to reduce the imbalance in the number of nodes of the communities in addition to structural metrics [38], such as modularity and conductance. (2) The new Pareto-based MOEA include advanced initialization strategies and search operators. (3) For the first time, multi-objective community detection was evaluated in graphs that represent the topological structure of real power systems.
3. Problem Formulation
This paper proposes the analysis of two bi-objective formulations of the community detection problem based on some previous studies that have highlighted that most papers related to community detection aim to optimize structural metrics such as modularity (internal connectedness) and conductance (normalized edge cut) while ignoring an important dimension: community size [38]. This is the reason that has led us to analyze two multi-objective formulations that try to optimize the following objectives: (a) maximize the modularity (Equation (1)) and minimize the imbalance (Equation (3)), and (b) maximize the conductance (Equation (2)) and minimize the imbalance (Equation (3)).
- Modularity (Q) [2]: Modularity considers that a solution is good if there are many edges within communities and only a few between them. A solution with a Q value close to 1 indicates strong community structure from a topological perspective [30].where M is the number of edges, and are the degrees of two given nodes of the network (i and j), is the element of the adjacency matrix that is located in the ith row and the jth column, and indicates if node i and node j are in the same community () or not (). The aim is, therefore, to maximize the modularity (Q) value.
- Conductance (CON) [39,40]: Conductance is a measure of the fraction of total edge volume that points outside the community. The aim here is to minimize the conductance (CON) value.where is the number of edges of the ith community that are linked to nodes from other communities, is the number of edges of the ith community that are not linked to nodes from other communities, and N is the number of communities considered.
- Imbalance (IMB): Imbalance represents the difference in the number of nodes included in the communities detected. The aim is, therefore, to minimize the imbalance value.where is the number of nodes of the ith community, is the number of nodes of the network divided by the number of communities considered, and N is the number of communities considered.
4. Multi-Objective Generational Genetic Algorithm: MOGGA+
This section presents MOGGA+, a Pareto-based MOEA that solves the multi-objective formulations described above. MOGGA+ extends the single-objective algorithm GGA+ [6] by including some strategies such as radial initialization, the use of n sets of non-dominated solutions, and the dynamic modification of the probability of applying evolutionary operators in runtime. In particular, it incorporates a new data structure that assigns some probabilities of executing a genetic operator that can be dynamically adjusted (within a given range) according to the evolution of the operator during successive generations of the algorithm.
Figure 1 shows the operation of MOGGA+. The input data required by MOGGA+ is a graph G modelling a given network, the number of communities to be detected, the population size, crossover rate, mutation rate, and the termination criterion (maximum number of generations). With this information, MOGGA+ creates a new population initialized based on the radial initialization process and initializes the migration vector between boundaries. Then, the algorithm evaluates the individuals through the objective functions and creates a set of non-dominated solutions that will store all the individuals that satisfy the constraints. After that, the individuals of the population are sorted by assigning a rank according to Pareto-dominance comparisons. Then, a new population is generated by applying the dynamically selected genetic operator (crossover and/or mutation) and the individuals are checked in order to update the non-dominated set. Finally, the replacement operator is applied to the new population. At the end of the execution, the algorithm returns the set of non-dominated solutions.
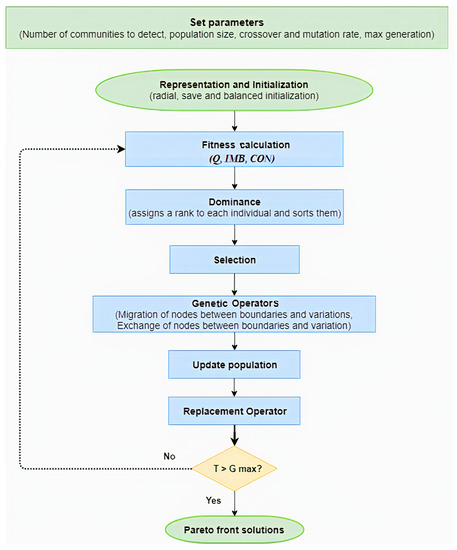
Figure 1.
Multi-objective Generational Genetic Algorithm+ (MOGGA+) operation.
4.1. Genetic Representation
The genetic representation used by MOGGA+ is based in the following notation:
where vector represents the mth individual of the population and indicates the community to which the ith node belongs. All the nodes in this individual contain a positive integer value, where N is the total number of nodes of the network.
4.2. Initialisation of the Population
Random initialisation can generate unfeasible solutions, that is, isolated nodes or groups of nodes that are not interconnected with nodes of the same community. To guarantee that the individuals generated during the initialization process are feasible, the initialization process used by MOGGA+ is based on the concept of safe initialization [41]. In addition, to avoid the generation of unbalanced size communities, the concept of balanced initialization used in [6] is incorporated to establish the community size. Moreover, MOGGA+ allows each individual of the population to search for a different number of communities (degree of abstraction), such that the network can be analyzed from a global perspective (a few communities) to a higher detail (many communities).
Furthermore, to improve the quality of the initial communities, a radial initialization is used, which functions as follows: Given a set of communities , where C is the number of communities to detect, each community is created by including that node not previously assigned to another community having a higher degree of connectivity with other nodes. Then, those neighbouring nodes of node not previously assigned to community are incorporated until it reaches the community size previously established. If the community size is not reached after including node and its neighbours , the process is repeated with the first neighbour node, . If this criteria is not reached, the process is then repeated with the second neighbour node, , and so on. In the hypothetical case that the community does not reach the preestablished size, the process would be repeated considering the neighbour nodes located at the next level of distance, that is, using concentric ratios where the neighbour nodes are added within that distance. This process can be observed in the example shown in Figure 2. Here, the maximum number of communities to be detected is 2 and the number of nodes is 27. The initialization vector will establish the size of the communities at = 13 and = 14. Next, a non-assigned node is selected considering the concept of node with a higher degree. In this case, node 1 (degree 5) is selected and then included in community . As has not been completed (current size 1 with respect to = 13), the neighbouring nodes to node 1 are included, that is, community now contains nodes 1 to 6, but the maximum size = 13 has still not been reached, which is the reason why the next level is analyzed, until the community is completed ( contains nodes 1 to 13). Once community is completed, this process is repeated to complete community .
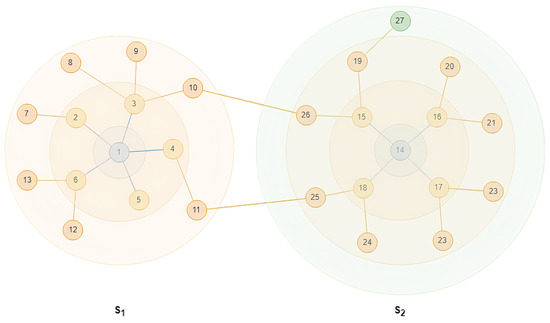
Figure 2.
Radial initialisation.
4.3. Migration Vector and Genetic Operators
MOGGA+ uses a migration vector between boundaries [6]. This vector determines the most attractive destination of each boundary node between different communities, such that the destination community for a certain node will be the one that contains the highest number of nodes connected to the former node. Based on this migration vector, the algorithm herein proposed (MOGGA+) applies several genetic search operators that have been especially designed to obtain the maximum performance of the proposed data structure.
4.3.1. Mutation Operator
MOGGA+ uses three mutation operators that consist of the migration of boundary nodes to a different community. These operators are randomly applied.
- Migration of a boundary node to the best destination community (M1): moves boundary node j located at community to the best neighbouring community [6].
- Migration of N nodes to the best destination community (M2): moves boundary node j located at community to the best destination community . Furthermore, a random number of neighbouring nodes of node j are also moved to community .
- Migration of N nodes to a random destination community (M3): moves boundary node j located at community to a random destination community . Furthermore, a random number of neighbouring nodes of node j are also moved to community .
4.3.2. Crossover Operator
Some studies have shown that typical crossover operators are not suitable for community detection problems since they lead to the disruption of good communities or may even cause the generated communities to be disconnected, thus significantly degrading the search capability of the algorithms [42]. Our implementation consists of the exchange of communities between boundary nodes of different communities. Two crossover/exchange operators are considered by MOGGA+:
- Best exchange of boundary nodes (EX1): moves boundary node j located at community to the best neighbouring community , and then moves from to the node k which obtains the best result from moving to the community.
- Random exchange of boundary nodes (EX2): moves the boundary node j located at the community to a random community , and then moves from to the node k that gets the best result from moving to the community.
4.3.3. Selection Operator
MOGGA+ uses an elitist replacement procedure for substituting a percentage of individuals of the main population for some individuals of the non-dominated set. The number of individuals to replace in each generation is a random number calculated in the range ((( + ) × ), ( × )), where
- : minimum number of individuals to replace;
- : maximum number of individuals to replace;
- : parameter that dynamically increases the number of individuals to replace, that is, the algorithm becomes more elistist when the number of generations performed increases. Let be the number of generations that the population will evolve; then, the value of is calculated as follows: = ()/.
4.4. Termination Criteria
The termination criteria used here is to perform a maximum number of generations ().
5. Empirical Study
This section analyzes the performance of MOGGA+ in several networks. The algorithms have been developed in C#. Net Framework 4. C# is an object-oriented language that allows for the development of graphic interfaces to visualize the results of the optimization algorithms. Furthermore, not only managed code is used, but it is also possible to call external unmanaged code and to utilize reference types and user-defined value types, which are key aspects in the development of optimisation algorithms. The computer used to execute the codes is a personal computer with an Intel Core i7 3630QM processor (4 cores and 2 threads per core) at 2.4 GHz, 8 GB DDR3 RAM.
5.1. Algorithms
Experimental analysis involving optimization algorithms often involve the comparison between algorithms in order to determine the most efficient in terms of solution quality and/or runtime. In this case, MOGGA+ is compared with MOGA-Net [18] for two reasons. This algorithm has been used for two reasons: MOGA-Net is a multi-objective algorithm developed by Clara Pizzuti which is often used in the context of multi-objective community detection, and MOGA-Net adapts the well-known Non-dominated Sorting Genetic Algorithm (NSGA-II) proposed by Deb et al. [43] to the problem of community detection. The genetic representation of MOGA-Net is based on the locus-based adjacency representation [44]. The initialization process is based on random generation of individuals but taking into account the effective connections of the nodes in the network. MOGA-Net uses a standard uniform crossover operator, while the mutation operator is implemented in order to guarantee that each node is linked only to one of its neighbours in the mutated child. The operation of MOGA-Net consists of creating a new population initialized at random and repaired to produce safe individuals. After that, the algorithm evaluates the individuals through the objective functions and then applies NSGA-II to each one. NSGA-II assigns a rank according to Pareto dominance and sorts the individuals. Then, a new population is generated by applying the genetic operators (uniform crossover and mutation). Finally, once the termination criterion is achieved, the set of non-dominated solutions obtained is returned as an output of the algorithm. It is worth noting that it was necessary to implement a new version of MOGA-Net that considers the objectives of modularity, imbalance, and conductance since the original MOGA-Net implementation maximizes the intra-connections inside each community and minimizes interconnections between different communities.
5.2. Test Problems
To conduct performance analysis of the different algorithms herein presented, networks representing five national-scale power grids proposed in [45] are utilized. Four graphs correspond to European areas: Italy, including Sardinia and Sicily; Germany, the continental territory of France; and the Iberian peninsula, including the Balearic islands. The fifth network is the Texas power grid. Table 1 describes some graph characteristics of these five networks. Some previous studies have shown that community detection in national-scale high-voltage transmission networks provides topological information about the physical layout of these grids [45].

Table 1.
Description of the graphs used to model the five power grids.
5.3. Parameter Settings
Table 2 shows the parameters settings used by MOGGA+. Some of these parameters, including population size and the number of generations, are the same than those used in [6], which applied a sensitivity analysis to determine accurate values for the population size and probabilities of applying the evolutionary operators. In the present study, the probabilities of applying different variants of the mutation, crossover, and selection operators are established within a range of values, such that each mutation operator (M1, M2, and M3) and crossover operator (EX1 and EX2) has a certain probability of being executed according to the results obtained in previous generations, that is, the probability of applying an operator is increased if its use improves the quality of the solutions or is reduced if it deteriorates these solutions. The population size and the number of generations (termination criterion) is the same for MOGA-Net.

Table 2.
MOGGA+ parameters.
5.4. Performance Metrics
As commented above, the aim of multi-objective optimization algorithms is to obtain the true Pareto-optimal front or, alternatively, an approximation to it. However, an important issue here is the intrinsic trade-off between the goals of proximity and diversity preservation [46], that is, the selection mechanisms should select a diverse set of solutions close to the set of non–dominated solutions. A large number of performance metrics have been proposed in the past [47]. Two widely used metrics have been used in our study: the hyper-volume and the Schott’s spacing metrics. The Hyper-volume (HV) metric is the only unary indicator that is Pareto-compliant [48] and often used as a measure of convergence towards the Pareto front as well as the maximum spread of the solutions obtained. The Schott’s Spacing (SS) metric [49] measures the spread of solutions in a non-dominated set according to the relative distance between the nearest solutions in the non-dominated set.
5.5. Results and Discussion
To conduct the performance analysis, a total of 30 independent runs have been performed for each algorithm on the five networks representing the power grids of Italy, France, Germany, the Iberian peninsula, and Texas. The accuracy of the algorithms has been evaluated according to the HV and SS metrics described above. Table 3 shows the results obtained by both algorithms in these five networks when optimizing modularity and imbalance, while Table 4 shows the same comparison when optimizing conductance and imbalance. As can be observed, in both multi-objective formulations, MOGGA+ clearly outperforms the results obtained by MOGA-Net in all these networks in terms of the HV metric, that is, the former provides a better approximation to the (unknown) true Pareto-optimal front than the latter.

Table 3.
Results obtained by Multi-objective Genetic Algorithm for Networks (MOGA-Net) and MOGGA+ considering the modularity and imbalance objectives.

Table 4.
Results obtained by MOGA-Net and MOGGA+ considering the conductance and imbalance objectives.
Analysis of the results in terms of the SS metric indicates, however, that MOGA-Net outperforms MOGGA+. These results are due to the characteristics of spacing metrics. In particular, some previous studies have highlighted that, if the solutions of the non-dominated set are clustered in small groups, the distance between the groups is not considered since only the shortest distances are computed [50]. Our results denote that MOGGA+ obtains a better approximation to the true Pareto-optimal front but that these solutions are relatively dispersed in the solution space, while MOGA-Net often obtains a set of non-dominated solutions distant from the Pareto-optimal front but more concentrated so that the spacing between solutions is smaller, thus obtaining a better result in the SS metric. Figure 3 shows the non-dominated fronts obtained by MOGA-Net and MOGGA+ in the Italian network when optimizing both formulations. It is important to remark that the non-dominated fronts shown in both figures are concave because minimization of the conductance and imbalance objectives has been implemented as the maximization of the inverse values of CON (Equation (2)) and IMB (Equation (3)). These figures show that MOGGA obtains fronts of non-dominated solutions that are closer to the (unknown) Pareto-optimal front but that there are several solutions which are far from the others, which is why the SS metric obtained by MOGA-Net is better.
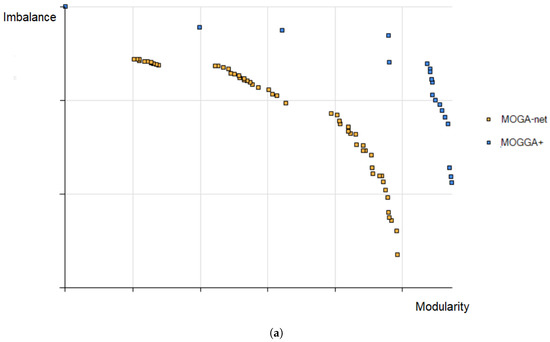
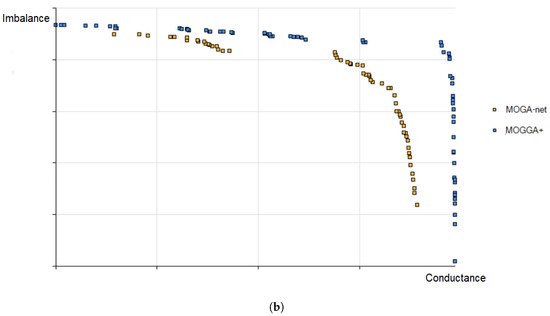
Figure 3.
Comparison between MOGA-Net and MOGGA+ in the Italian network considering (a) modularity and imbalance, and (b) conductance and imbalance.
Finally, Figure 4 and Figure 5 display some examples of communities detected by MOGGA+ in the five networks representing power grids considering different levels of resolution (2 and 10 communities). These figures are useful to understand how the implemented algorithms could provide high-quality solutions considering different objectives, such that the decision-maker could later decide which one is the best option according to the particular characteristics of the study at hand. In this case, it is observed that solutions with only two communities return balanced solutions while augmenting the number of communities often increases the imbalance.

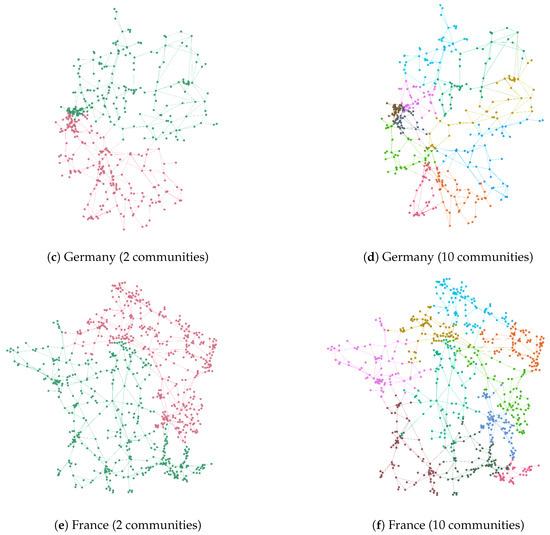
Figure 4.
Communities detected in the networks representing the power grids of Italy, Germany, and France considering 2 and 10 communities.
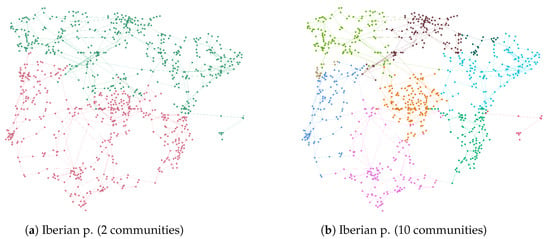
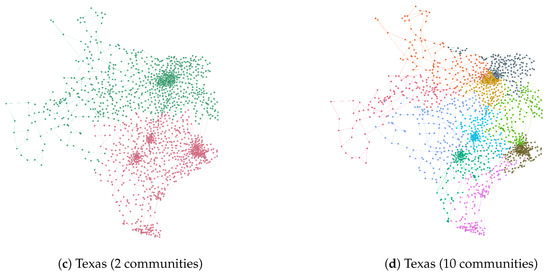
Figure 5.
Communities detected in the networks representing the power grids of the Iberian Peninsula and Texas considering 2 and 10 communities.
6. Conclusions
Community detection is a relevant area of investigation in the field of complex networks. An overview of the state-of-the-art in this field shows that most published papers aim to maximize the modularity value. However, considering modularity as a lone objective can involve resolution limit and imbalance inconveniences. This paper is the first to propose the use of Pareto-based MOEAs for solving two different multi-objective formulations: (a) maximization of modularity and minimization of imbalance, and (b) maximization of conductance and minimization of imbalance. More specifically, a new MOEA that includes effective initialization methods and search operators to obtain high-quality non-dominated sets is presented. The empirical study compares MOGGA+ with MOGA-Net for solving these multi-objective formulations in graphs having hundreds of vertices and edges that represent the topological structure of real power systems. The numerical and graphical results show the high performance of these Pareto-based MOEAs for solving both formulations. This paper opens a new line of research in the detection of community structures considering different objectives simultaneously. Moreover, the results obtained in a set of graphs representing high-voltage transmission networks can be used to obtain information on the physical layout of these grids. As future work, these approaches will be also compared with other methods different from genetic algorithms.
Author Contributions
Conceptualization, M.G. and C.G.; methodology, C.G. and R.B.; software, M.G. and R.B.; validation, M.G. and F.G.M.; formal analysis, A.A. and R.B.; investigation, M.G., A.A. and R.B.; resources, C.G.; data curation, M.G. and A.A.; writing—original draft preparation, F-G.M. and R.B.; writing—review and editing, F.G.M. and R.B.; visualization, M.G. and F.G.M.; supervision, C.G. and A.A.; project administration, C.G.; funding acquisition, F.G.M. and R.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish Ministry of Science, Innovation, and Universities, grant number PGC2018-098813-B-33.
Acknowledgments
This research was supported by the Spanish Ministry of Science, Innovation, and Universities (project PGC2018-098813-B-33) and by the Regional Government of Andalusia (ceiA3 project) at the University of Almeria.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arumugam, S.; Brandstädt, A.; Nishizeki, T. Handbook of Graph Theory, Combinatorial Optimization, and Algorithms; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Shang, R.; Luo, S.; Zhang, W.; Stolkin, R.; Jiao, L. A multiobjective evolutionary algorithm to find community structures based on affinity propagation. Phys. A Stat. Mech. Appl. 2016, 453, 203–227. [Google Scholar] [CrossRef]
- Sun, P.G. Imbalance problem in community detection. Phys. A Stat. Mech. Appl. 2016, 457, 364–376. [Google Scholar] [CrossRef]
- Sun, P.G.; Sun, X. Complete graph model for community detection. Phys. A Stat. Mech. Appl. 2017, 471, 88–97. [Google Scholar] [CrossRef]
- Guerrero, M.; Montoya, F.G.; Baños, R.; Alcayde, A.; Gil, C. Adaptive community detection in complex networks using genetic algorithms. Neurocomputing 2017, 266, 101–113. [Google Scholar] [CrossRef]
- Wang, L.; Ng, A.H.; Deb, K. Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Gil, C.; Ortega, J.; Montoya, M.; Baños, R. A mixed heuristic for circuit partitioning. Comput. Optim. Appl. 2002, 23, 321–340. [Google Scholar] [CrossRef]
- Tripathy, B. De-Anonymization Techniques for Social Networks; Academic Press an Imprint of Elsevier: London, UK, 2019. [Google Scholar]
- Newman, M.E. Communities, modules and large-scale structure in networks. Nat. Phys. 2012, 8, 25–31. [Google Scholar] [CrossRef]
- Rossi, F.; Villa-Vialaneix, N. Optimizing an organized modularity measure for topographic graph clustering: A deterministic annealing approach. Neurocomputing 2010, 73, 1142–1163. [Google Scholar] [CrossRef]
- Wang, R.S.; Zhang, S.; Wang, Y.; Zhang, X.S.; Chen, L. Clustering complex networks and biological networks by nonnegative matrix factorization with various similarity measures. Neurocomputing 2008, 72, 134–141. [Google Scholar] [CrossRef]
- Brandes, U.; Delling, D.; Gaertler, M.; Gorke, R.; Hoefer, M.; Nikoloski, Z.; Wagner, D. On modularity clustering. IEEE Trans. Knowl. Data Eng. 2008, 20, 172–188. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W. H. Freeman & Co.: New York, NY, USA, 1979. [Google Scholar]
- Emmerich, M.T.; Deutz, A.H. A tutorial on multiobjective optimization: Fundamentals and evolutionary methods. Nat. Comput. 2018, 17, 585–609. [Google Scholar] [CrossRef] [PubMed]
- Coello, C.A.C.; Lamont, G.B.; Van Veldhuizen, D.A. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: Berlin/Heidelberg, Germany, 2007; Volume 5. [Google Scholar]
- Baños, R.; Gil, C.; Paechter, B.; Ortega, J. A hybrid meta-heuristic for multi-objective optimization: MOSATS. J. Math. Model. Algorithms 2007, 6, 213–230. [Google Scholar] [CrossRef]
- Pizzuti, C. A multiobjective genetic algorithm to find communities in complex networks. IEEE Trans. Evol. Comput. 2011, 16, 418–430. [Google Scholar] [CrossRef]
- Gong, M.; Ma, L.; Zhang, Q.; Jiao, L. Community detection in networks by using multiobjective evolutionary algorithm with decomposition. Phys. A Stat. Mech. Appl. 2012, 391, 4050–4060. [Google Scholar] [CrossRef]
- Shi, C.; Yan, Z.; Cai, Y.; Wu, B. Multi-objective community detection in complex networks. Appl. Soft Comput. 2012, 12, 850–859. [Google Scholar] [CrossRef]
- Bara’a, A.A.; Khoder, H.S. A new multi-objective evolutionary framework for community mining in dynamic social networks. Swarm Evol. Comput. 2016, 31, 90–109. [Google Scholar]
- Hariz, W.A.; Abdulhalim, M.F. Improving the performance of evolutionary multi-objective co-clustering models for community detection in complex social networks. Swarm Evol. Comput. 2016, 26, 137–156. [Google Scholar]
- Amiri, B.; Hossain, L.; Crawford, J.W.; Wigand, R.T. Community detection in complex networks: Multi–objective enhanced firefly algorithm. Knowl.-Based Syst. 2013, 46, 1–11. [Google Scholar] [CrossRef]
- Niu, X.; Si, W.; Wu, C.Q. A label-based evolutionary computing approach to dynamic community detection. Comput. Commun. 2017, 108, 110–122. [Google Scholar] [CrossRef]
- Bello-Orgaz, G.; Salcedo-Sanz, S.; Camacho, D. A multi-objective genetic algorithm for overlapping community detection based on edge encoding. Inf. Sci. 2018, 462, 290–314. [Google Scholar] [CrossRef]
- Zou, F.; Chen, D.; Huang, D.S.; Lu, R.; Wang, X. Inverse modelling-based multi-objective evolutionary algorithm with decomposition for community detection in complex networks. Phys. A Stat. Mech. Appl. 2019, 513, 662–674. [Google Scholar] [CrossRef]
- Gong, M.; Cai, Q.; Chen, X.; Ma, L. Complex network clustering by multiobjective discrete particle swarm optimization based on decomposition. IEEE Trans. Evol. Comput. 2013, 18, 82–97. [Google Scholar] [CrossRef]
- Rahimi, S.; Abdollahpouri, A.; Moradi, P. A multi-objective particle swarm optimization algorithm for community detection in complex networks. Swarm Evol. Comput. 2018, 39, 297–309. [Google Scholar] [CrossRef]
- Gong, M.; Chen, X.; Ma, L.; Zhang, Q.; Jiao, L. Identification of multi-resolution network structures with multi-objective immune algorithm. Appl. Soft Comput. 2013, 13, 1705–1717. [Google Scholar] [CrossRef]
- Reihanian, A.; Feizi-Derakhshi, M.R.; Aghdasi, H.S. Community detection in social networks with node attributes based on multi-objective biogeography based optimization. Eng. Appl. Artif. Intell. 2017, 62, 51–67. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, Y.; Li, B.; Sun, G. Multiobjective biogeography based optimization algorithm with decomposition for community detection in dynamic networks. Phys. A Stat. Mech. Appl. 2015, 436, 430–442. [Google Scholar] [CrossRef]
- Chen, D.; Zou, F.; Lu, R.; Yu, L.; Li, Z.; Wang, J. Multi-objective optimization of community detection using discrete teaching-learning-based optimization with decomposition. Inf. Sci. 2016, 369, 402–418. [Google Scholar] [CrossRef]
- Wu, P.; Pan, L. Multi-objective community detection method by integrating users’ behavior attributes. Neurocomputing 2016, 210, 13–25. [Google Scholar] [CrossRef]
- Moayedikia, A. Multi-objective community detection algorithm with node importance analysis in attributed networks. Appl. Soft Comput. 2018, 67, 434–451. [Google Scholar] [CrossRef]
- Cheng, F.; Cui, T.; Su, Y.; Niu, Y.; Zhang, X. A local information based multi-objective evolutionary algorithm for community detection in complex networks. Appl. Soft Comput. 2018, 69, 357–367. [Google Scholar] [CrossRef]
- Osaba, E.; Del Ser, J.; Camacho, D.; Bilbao, M.N.; Yang, X.S. Community detection in networks using bio-inspired optimization: Latest developments, new results and perspectives with a selection of recent meta-heuristics. Appl. Soft Comput. 2020, 87, 106010. [Google Scholar] [CrossRef]
- Li, Q.; Cao, Z.; Ding, W.; Li, Q. A multi-objective adaptive evolutionary algorithm to extract communities in networks. Swarm Evol. Comput. 2020, 52, 100629. [Google Scholar] [CrossRef]
- Wagenseller, P.; Wang, F.; Wu, W. Size matters: A comparative analysis of community detection algorithms. IEEE Trans. Comput. Soc. Syst. 2018, 5, 951–960. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, H.; Zhang, Y. Overlapping community detection based on conductance optimization in large-scale networks. Phys. A Stat. Mech. Appl. 2019, 522, 69–79. [Google Scholar] [CrossRef]
- Pattanayak, H.S.; Sangal, A.L.; Verma, H.K. Community detection in social networks based on fire propagation. Swarm Evol. Comput. 2019, 44, 31–48. [Google Scholar] [CrossRef]
- Pizzuti, C. Ga-net: A genetic algorithm for community detection in social networks. In Parallel Problem Solving from Nature–PPSN X; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1081–1090. [Google Scholar]
- He, D.; Wang, Z.; Yang, B.; Zhou, C. Genetic algorithm with ensemble learning for detecting community structure in complex networks. In Proceedings of the 2009 Fourth International Conference on Computer Sciences and Convergence Information Technology, Seoul, Korea, 24–26 November 2009; pp. 702–707. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Park, Y.; Song, M. A genetic algorithm for clustering problems. In Proceedings of the Third Annual Conference on Genetic Programming, San Francisco, CA, USA, 22–25 July 1998; Volume 1998, pp. 568–575. [Google Scholar]
- Guerrero, M.; Montoya, F.G.; Baños, R.; Alcayde, A.; Gil, C. Community detection in national-scale high voltage transmission networks using genetic algorithms. Adv. Eng. Inform. 2018, 38, 232–241. [Google Scholar] [CrossRef]
- Bosman, P.A.; Thierens, D. The balance between proximity and diversity in multiobjective evolutionary algorithms. IEEE Trans. Evol. Comput. 2003, 7, 174–188. [Google Scholar] [CrossRef]
- Menchaca-Mendez, A.; Coello, C.A.C. Selection mechanisms based on the maximin fitness function to solve multi-objective optimization problems. Inf. Sci. 2016, 332, 131–152. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; Da Fonseca, V.G. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Schott, J.R. Fault Tolerant Design Using Single and Multicriteria Genetic Algorithm Optimization; Technical Report; Air Force Institute of Technology: Wright-Patterson Air Force Base, OH, USA, 1995. [Google Scholar]
- Taghavi, T.; Pimentel, A.D. Design metrics and visualization techniques for analyzing the performance of moeas in dse. In Proceedings of the 2011 International Conference on Embedded Computer Systems: Architectures, Modeling and Simulation, Samos, Greece, 18–21 July 2011; pp. 67–76. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).