A Meshless Method Based on the Laplace Transform for the 2D Multi-Term Time Fractional Partial Integro-Differential Equation
Abstract
1. Introduction
2. Proposed Numerical Scheme
2.1. Localized Meshless Method
3. Numerical Inversion of the Laplace Transform
4. Convergence and Accuracy
| Algorithm 1. |
|
5. Stability Analysis
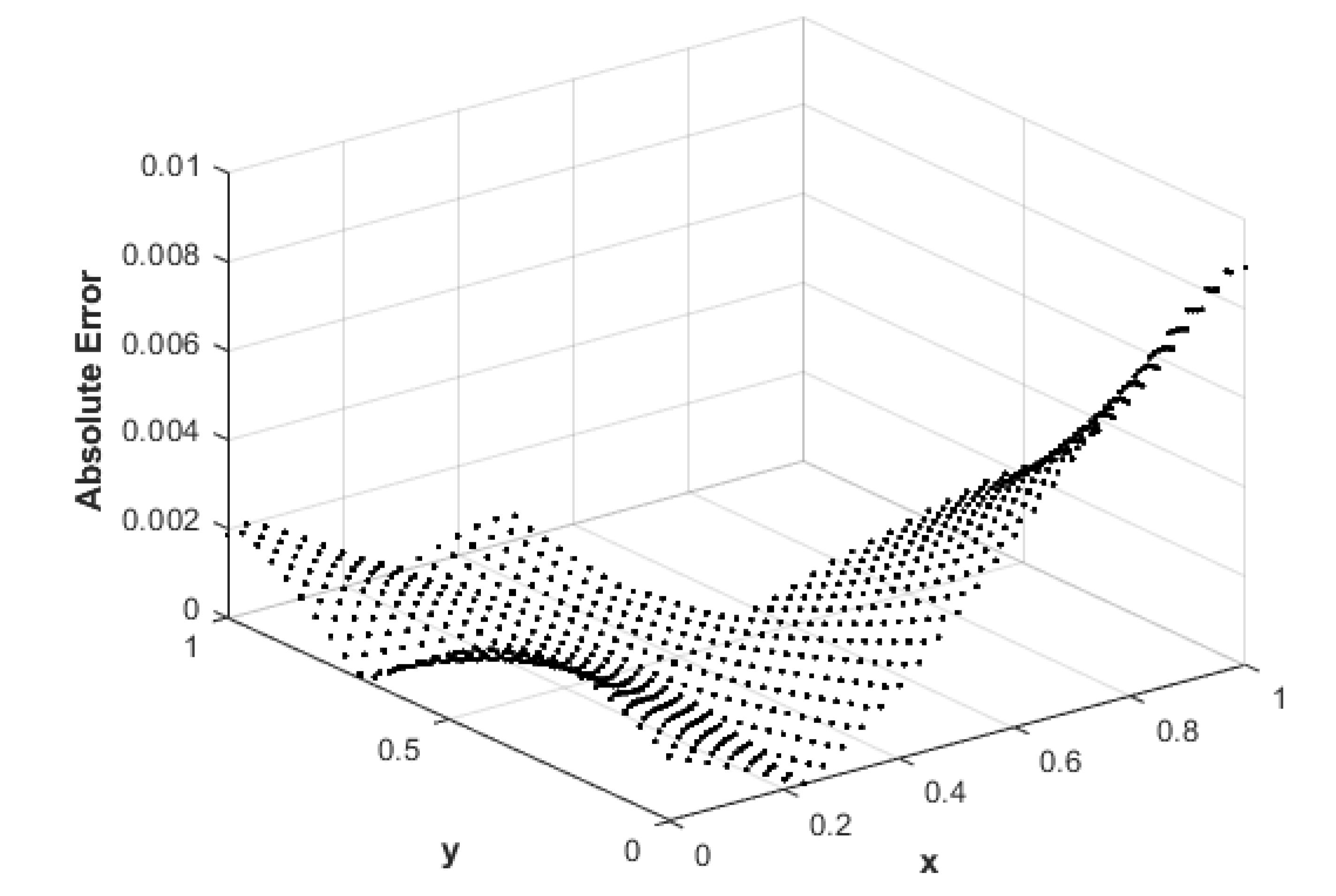
6. Numerical Results and Discussion
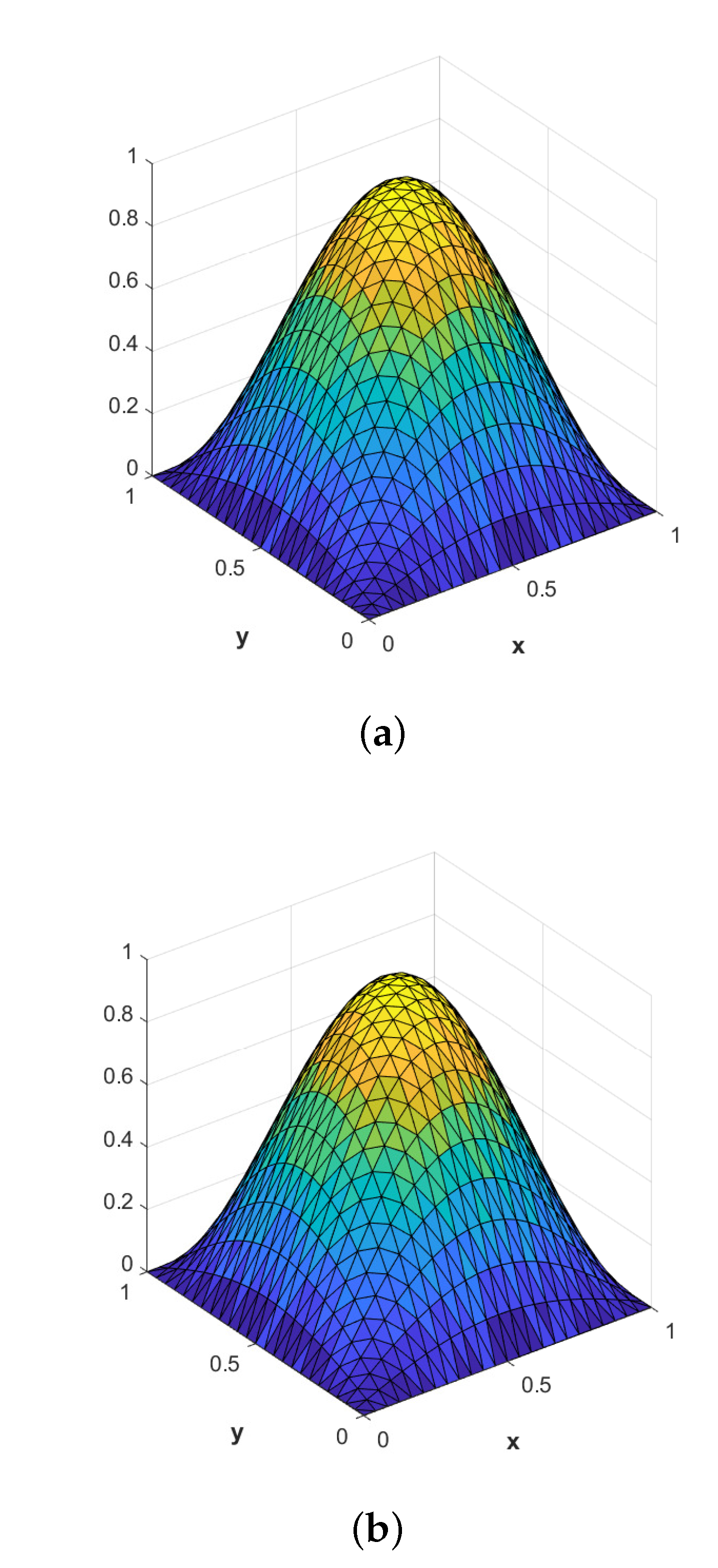
6.1. Square Domain
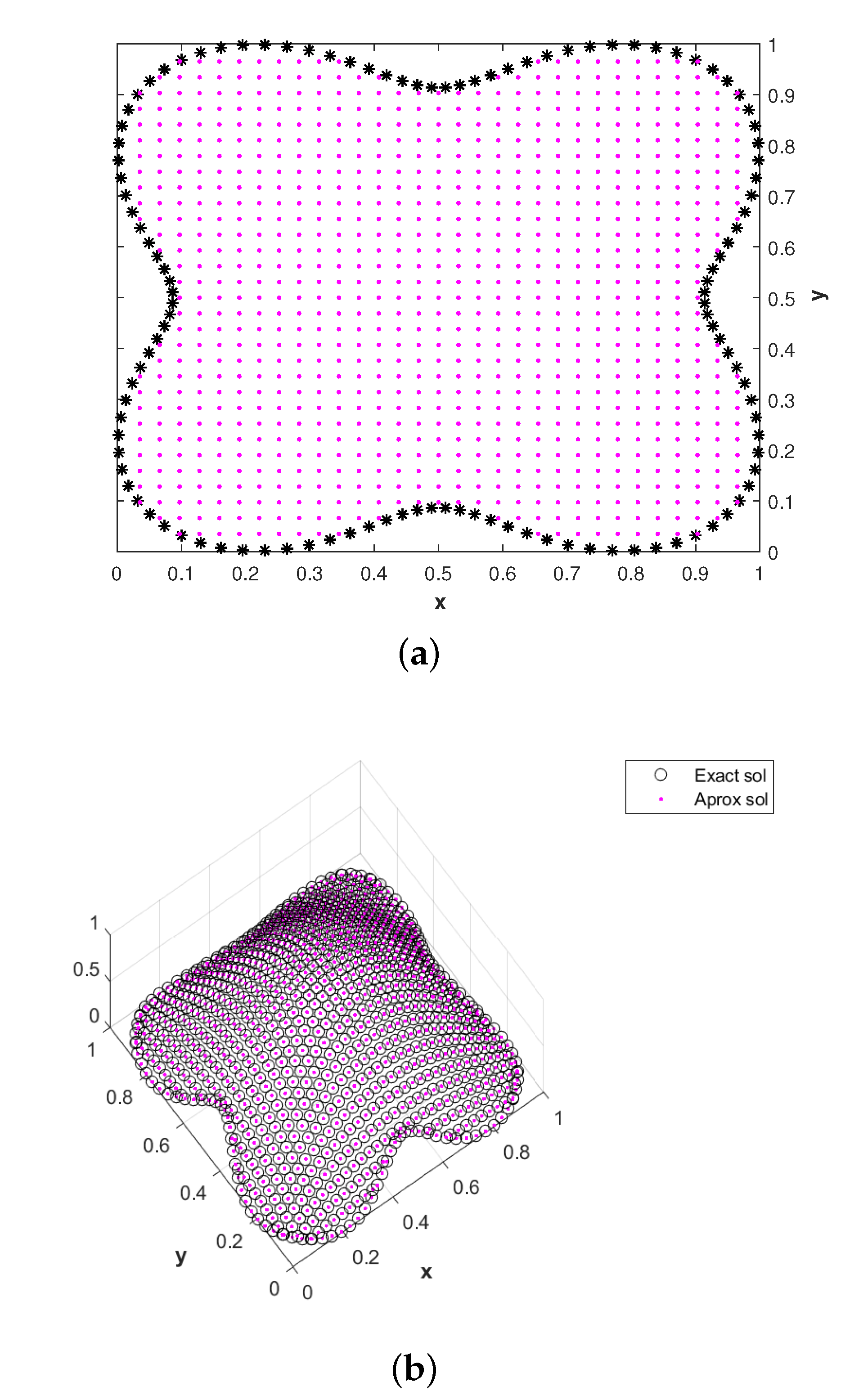
6.2. Nut-Shaped Domain
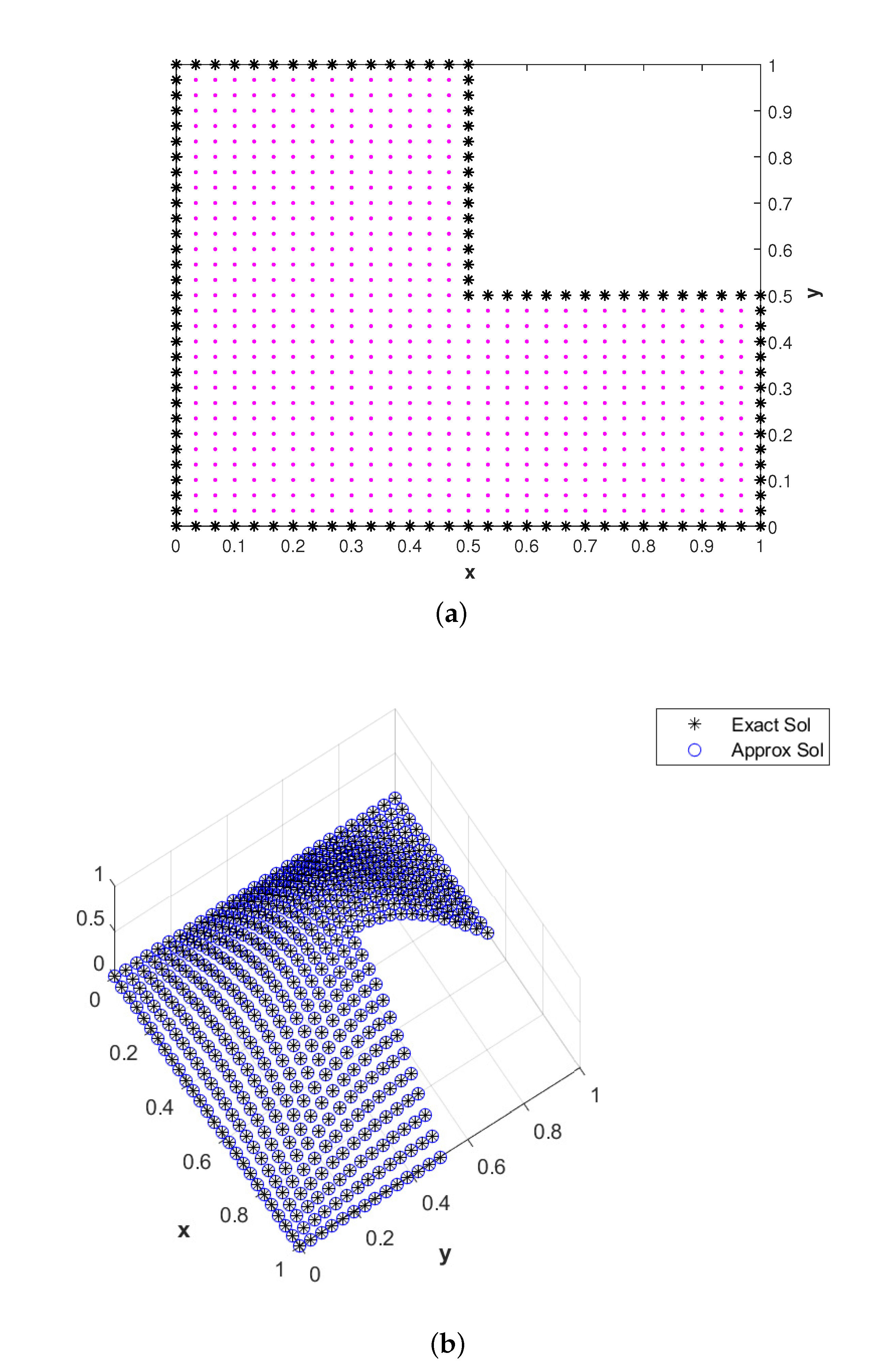
6.3. L-Shaped Domain
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Renardy, M. Mathematical analysis of viscoelastic flows. Ann. Rev. Fluid Mech. 1989, 21, 21–36. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Arqub, O.A. Computational algorithm for solving Fredholm time-fractional partial integro-differential equations of Dirichlet functions type with error estimates. Appl. Math. Comput. 2019, 342, 280–294. [Google Scholar]
- Arshed, S. B-spline solution of fractional integro partial differential equation with a weakly singular kernel. Numer. Methods Partial Differ. Equ. 2017, 33, 1565–1581. [Google Scholar] [CrossRef]
- Arqub, O.A.; Al-Smadi, M. Numerical algorithm for solving time-fractional partial integro-differential equations subject to initial and Dirichlet boundary conditions. Numer. Methods Partial Differ. Equ. 2018, 34, 1577–1597. [Google Scholar] [CrossRef]
- Tang, T. A finite difference scheme for partial integro-differential equations with a weakly singular kernel. Appl. Numer. Math. 1993, 11, 309–319. [Google Scholar] [CrossRef]
- Long, W.; Xu, D.; Zeng, X. Quasi wavelet based numerical method for a class of partial integro-differential equation. Appl. Math. Comput. 2012, 218, 11842–11850. [Google Scholar] [CrossRef]
- Chen, C.; Thome, V.; Wahlbin, L.B. Finite element approximation of a parabolic integro-differential equation with a weakly singular kernel. Math. Comput. 1992, 58, 587–602. [Google Scholar] [CrossRef]
- Xu, D. On the discretization in time for a parabolic integro-differential equation with a weakly singular kernel I: Smooth initial data. Appl. Math. Comput. 1993, 58, 1–27. [Google Scholar]
- Wulan, L.; Xu, D. Finite central difference/finite element approximations for parabolic integro-differential equations. Computing 2010, 90, 89–111. [Google Scholar]
- EL-Asyed, A.M.A.; Soliman, A.F.; El-Azab, M.S. On the numerical solution of partial integro-differential equations. Math. Sci. Lett. 2012, 1, 71–80. [Google Scholar]
- Fairweather, G. Spline collocation methods for a class of hyperbolic partial integro-differential equations. SIAM J. Numer. Anal. 1994, 31, 444–460. [Google Scholar] [CrossRef]
- Siddiqi, S.S.; Arshed, S. Cubic B-spline for the Numerical Solution of Parabolic Integro-differential Equation with a Weakly Singular Kernel. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 2065–2073. [Google Scholar] [CrossRef]
- Huang, Y.Q. Time discretization scheme for an integro-differential equation of parabolic type. J. Comput. Math. 1994, 12, 259–263. [Google Scholar]
- Hu, S.; Qiu, W.; Chen, H. A backward Euler difference scheme for the integro-differential equations with the multi-term kernels. Int. J. Comput. Math. 2020, 97, 1254–1267. [Google Scholar] [CrossRef]
- Kılıçman, A.; Ahmood, W.A. Solving multi-dimensional fractional integro-differential equations with the initial and boundary conditions by using multi-dimensional Laplace Transform method. Tbilisi Math. J. 2017, 10, 105–115. [Google Scholar] [CrossRef]
- Gu, X.M.; Wu, S.L. A parallel-in-time iterative algorithm for Volterra partial integral-differential problems with weakly singular kernel. J. Comput. Phys. 2020, 417, 109576. [Google Scholar] [CrossRef]
- Saadatmandi, A.; Khani, A.; Azizi, M.R. A sinc-Gauss-Jacobi collocation method for solving Volterra’s population growth model with fractional order. Tbilisi Math. J. 2018, 11, 123–137. [Google Scholar] [CrossRef]
- Moradi, L.; Mohammadi, F.; Conte, D. A discrete orthogonal polynomials approach for coupled systems of nonlinear fractional order integro-differential equations. Tbilisi Math. J. 2019, 12, 21–38. [Google Scholar] [CrossRef]
- Alsaedi, A.; Agarwal, R.P.; Ntouyas, S.K.; Ahmad, B. Fractional-Order Integro-Differential Multivalued Problems with Fixed and Nonlocal Anti-Periodic Boundary Conditions. Mathematics 2020, 8, 1774. [Google Scholar] [CrossRef]
- Ahmad, B.; Broom, A.; Alsaedi, A.; Ntouyas, S.K. Nonlinear integro-differential equations involving mixed right and left fractional derivatives and integrals with nonlocal boundary data. Mathematics 2020, 8, 336. [Google Scholar] [CrossRef]
- Amin, R.; Nazir, S.; García-Magariño, I. A Collocation Method for Numerical Solution of Nonlinear Delay Integro-Differential Equations for Wireless Sensor Network and Internet of Things. Sensors 2020, 20, 1962. [Google Scholar] [CrossRef]
- Nemati, S.; Torres, D.F. Application of Bernoulli Polynomials for Solving Variable-Order Fractional Optimal Control-Affine Problems. Axioms 2020, 9, 114. [Google Scholar] [CrossRef]
- Holhos, A.; Rosca, D. Orhonormal wavelet bases on the 3D ball via volume preserving map from the regular octahedron. arXiv 2019, arXiv:1910.08067. [Google Scholar]
- Jäntschi, L. The eigenproblem translated for alignment of molecules. Symmetry 2019, 11, 1027. [Google Scholar] [CrossRef]
- Bazgir, H.; Ghazanfari, B. Existence of Solutions for Fractional Integro-Differential Equations with Non-Local Boundary Conditions. Math. Comput. Appl. 2018, 23, 36. [Google Scholar] [CrossRef]
- Georgieva, A. Double Fuzzy Sumudu Transform to Solve Partial Volterra Fuzzy Integro-Differential Equations. Mathematics 2020, 8, 692. [Google Scholar] [CrossRef]
- Biazar, J.; Asadi, M.A. FD-RBF for partial integro-differential equations with a weakly singular kernel. Appl. Comput. Math. 2015, 4, 445–451. [Google Scholar] [CrossRef]
- Ali, G.; Gómez-Aguilar, J.F. Approximation of partial integro differential equations with a weakly singular kernel using local meshless method. Alex. Eng. J. 2020, 59, 2091–2100. [Google Scholar] [CrossRef]
- Aslefallah, M.; Shivanian, E. A nonlinear partial integro-differential equation arising in population dynamic via radial basis functions and theta-method. J. Math. Comput. Sci. 2014, 13, 14–25. [Google Scholar] [CrossRef]
- Safinejad, M.; Moghaddam, M.M. A local meshless RBF method for solving fractional integro-differential equations with optimal shape parameters. Ital. J. Pure Appl. Math. 2019, 41, 382. [Google Scholar]
- Fu, Z.J.; Chen, W.; Yang, H.T. Boundary particle method for Laplace transformed time fractional diffusion equations. J. Comput. Phys. 2013, 235, 52–66. [Google Scholar] [CrossRef]
- Davies, A.J.; Crann, D.; Mushtaq, J. A parallel implementation of the Laplace transform BEM. WIT Trans. Model. Simul. 1970, 14. [Google Scholar] [CrossRef]
- Gia, Q.T.L.; Mclean, W. Solving the heat equation on the unit sphere via Laplace transforms and radial basis functions. Adv. Comput. Math. 2014, 40, 353–375. [Google Scholar] [CrossRef]
- McLean, W.; Thomee, V. Numerical solution via Laplace transforms of a fractional order evolution equation. J. Integral Equ. Appl. 2010, 22, 57–94. [Google Scholar] [CrossRef]
- Fernandez, M.L.; Palencia, C. On the numerical inversion of the Laplace transform of certain holomorphic mappings. Appl. Numer. Math. 2004, 51, 289–303. [Google Scholar] [CrossRef]
- Jacobs, B.A. High-order compact finite difference and Laplace transform method for the solution of time fractional heat equations with Dirichlet and Neumann boundary conditions. Numer. Methods Partial Differ. Equ. 2016, 32, 1184–1199. [Google Scholar] [CrossRef]
- Li, X.; Haq, A.U.; Zhang, X. Numerical solution of the linear time fractional Klein-Gordon equation using transform based localized RBF method and quadrature. AIMS Math. 2020, 5, 5287–5308. [Google Scholar] [CrossRef]
- Uddin, M.; Ali, A. A localized transform-based meshless method for solving time fractional wave-diffusion equation. Eng. Anal. Bound. Elem. 2018, 92, 108–113. [Google Scholar] [CrossRef]
- Li, J.; Dai, L.; Nazeer, W. Numerical solution of multi-term time fractional wave diffusion equation using transform based local meshless method and quadrature. AIMS Math. 2020, 5, 5813–5838. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, D. Alternating direction implicit difference scheme for the multi-term time-fractional integro-differential equation with a weakly singular kernel. Comput. Math. Appl. 2020, 79, 244–255. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: New York, NY, USA; London, UK, 1974; Volume 111. [Google Scholar]
- Podlubny, I. Fractional Differential Equations. In Mathematics in Science and Engineering; Elsevier: Amsterdam, The Netherlands, 1999; Volume 198. [Google Scholar]
- Popolizio, M. Numerical solution of multiterm fractional differential equations using the matrix Mittag-Leffler functions. Mathematics 2018, 6, 7. [Google Scholar] [CrossRef]
- Schiessel, H.; Metzler, R.; Blumen, A.; Nonnenmacher, T.F. Generalized viscoelastic models: Their fractional equations with solutions. J. Phys. A Math. Gen. 1995, 28, 6567. [Google Scholar] [CrossRef]
- Torvik, P.J.; Bagley, R.L. On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. 1984, 51, 294–298. [Google Scholar] [CrossRef]
- Qin, S.; Liu, F.; Turner, I.; Vegh, V.; Yu, Q.; Yang, Q. Multi-term time-fractional Bloch equations and application in magnetic resonance imaging. J. Comput. Appl. Math. 2017, 319, 308–319. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Šarler, B.; Vertnik, R. Meshfree explicit local radial basis function collocation method for diffusion problems. Comput. Math. Appl. 2006, 51, 1269–1282. [Google Scholar] [CrossRef]
- Talbot, A. The accurate numerical inversion of Laplace transform. J. Inst. Math. Appl. 1979, 23, 97–120. [Google Scholar] [CrossRef]
- Dingfelder, B.; Weideman, J.A.C. An improved Talbot method for numerical Laplace transform inversion. Numer. Algorithms 2015, 68, 167–183. [Google Scholar] [CrossRef]
- Weideman, J.A.C. Optimizing Talbot’s contours for the inversion of the Laplace transform. SIAM J. Numer. Anal. 2006, 44, 2342–2362. [Google Scholar] [CrossRef]
- Sarra, S.A.; Kansa, E.J. Multiquadric radial basis function approximation methods for the numerical solution of partial differential equations. Adv. Comput. Mech. 2009, 2. [Google Scholar]
- Schaback, R. Error estimates and condition numbers for radial basis function interpolation. Adv. Comput. Math. 1995, 3, 251–264. [Google Scholar] [CrossRef]

| N | n | M | Error | Error Estimate | CPU(s) | |||
|---|---|---|---|---|---|---|---|---|
| 1024 | 73 | 10 | 1.90 × | 1.26 × | 4.9 | 1.54 × | 7.395020 | |
| 12 | 1.00 × | 8.37 × | 4.9 | 1.54 × | 7.022358 | |||
| 14 | 9.94 × | 5.53 × | 4.9 | 1.54 × | 7.249688 | |||
| 16 | 9.91 × | 3.66 × | 4.9 | 1.54 × | 7.789044 | |||
| 18 | 9.91 × | 2.42 × | 4.9 | 1.54 × | 8.160190 | |||
| 30 | 20 | 2.20 × | 1.60 × | 3.3 | 1.40 × | 6.398152 | ||
| 40 | 3.70 × | 1.60 × | 4.0 | 1.69 × | 6.328329 | |||
| 50 | 2.0 × | 1.60 × | 4.4 | 1.56 × | 7.150031 | |||
| 60 | 1.60 × | 1.60 × | 4.7 | 1.31 × | 7.898109 | |||
| 70 | 1.60 × | 1.60 × | 4.8 | 2.10 × | 8.372011 | |||
| 729 | 74 | 22 | 1.10 × | 1.05 × | 4.1 | 1.64 × | 5.758024 | |
| 841 | 9.04 × | 1.05 × | 4.5 | 1.16 × | 6.988687 | |||
| 961 | 8.75 × | 1.05 × | 4.8 | 1.26 × | 10.074941 | |||
| 1089 | 1.70 × | 1.05 × | 5.1 | 1.35 × | 10.822728 | |||
| 1225 | 8.47 × | 1.05 × | 5.4 | 1.44 × | 13.236204 | |||
| [40] | 7.16 × |
| N | n | M | Error | Error Estimate | CPU (s) | |||
|---|---|---|---|---|---|---|---|---|
| 1024 | 76 | 10 | 1.30 × | 1.26 × | 4.9 | 1.59 × | 6.665154 | |
| 12 | 2.71 × | 8.37 × | 4.9 | 1.59 × | 7.059290 | |||
| 14 | 2.68 × | 5.53 × | 4.9 | 1.59 × | 7.597790 | |||
| 16 | 2.69 × | 3.66 × | 4.9 | 1.59 × | 8.066648 | |||
| 18 | 2.69 × | 2.42 × | 4.9 | 1.59 × | 8.368624 | |||
| 30 | 20 | 1.13 × | 1.60 × | 3.2 | 8.99 × | 6.499886 | ||
| 40 | 1.90 × | 1.60 × | 3.8 | 5.33 × | 7.088308 | |||
| 50 | 1.30 × | 1.60 × | 4.3 | 2.31 × | 6.949834 | |||
| 60 | 1.70 × | 1.60 × | 4.6 | 1.68 × | 7.556786 | |||
| 74 | 7.44 × | 1.60 × | 4.9 | 1.24 × | 9.184561 | |||
| 973 | 75 | 22 | 5.37 × | 1.05 × | 5.0 | 1.09 × | 8.624205 | |
| 983 | 2.48 × | 1.05 × | 4.9 | 1.76 × | 9.407931 | |||
| 993 | 5.54 × | 1.05 × | 5.0 | 2.12 × | 9.242420 | |||
| 1003 | 5.62 × | 1.05 × | 4.9 | 5.40 × | 9.108576 | |||
| 1013 | 5.39 × | 1.05 × | 4.9 | 1.21 × | 9.380810 | |||
| [40] | 7.16 × |
| N | n | M | Error | Error Estimate | CPU (s) | |||
|---|---|---|---|---|---|---|---|---|
| 1045 | 75 | 10 | 2.00 × | 1.26 × | 5.4 | 4.22 × | 7.879603 | |
| 12 | 9.70 × | 8.37 × | 5.4 | 4.22 × | 8.472794 | |||
| 14 | 9.07 × | 5.53 × | 5.4 | 4.22 × | 8.961569 | |||
| 16 | 9.03 × | 3.66 × | 5.4 | 4.22 × | 9.776831 | |||
| 18 | 9.02 × | 2.42 × | 5.4 | 4.22 × | 9.703955 | |||
| 30 | 20 | 1.20 × | 1.60 × | 3.4 | 6.85 × | 6.230811 | ||
| 40 | 1.70 × | 1.60 × | 4.2 | 8.39 × | 7.051659 | |||
| 50 | 7.94 × | 1.60 × | 4.8 | 4.53 × | 7.786541 | |||
| 60 | 8.99 × | 1.60 × | 5.2 | 3.21 × | 8.323130 | |||
| 72 | 7.80 × | 1.60 × | 5.4 | 3.98 × | 9.694111 | |||
| 736 | 73 | 22 | 7.68 × | 1.05 × | 4.5 | 4.06 × | 5.941242 | |
| 833 | 8.30 × | 1.05 × | 4.8 | 4.06 × | 7.343621 | |||
| 936 | 6.45 × | 1.05 × | 5.1 | 4.06 × | 8.402310 | |||
| 1045 | 7.49 × | 1.05 × | 5.4 | 4.06 × | 10.279795 | |||
| [40] | 7.16 × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamran, K.; Shah, Z.; Kumam, P.; Alreshidi, N.A. A Meshless Method Based on the Laplace Transform for the 2D Multi-Term Time Fractional Partial Integro-Differential Equation. Mathematics 2020, 8, 1972. https://doi.org/10.3390/math8111972
Kamran K, Shah Z, Kumam P, Alreshidi NA. A Meshless Method Based on the Laplace Transform for the 2D Multi-Term Time Fractional Partial Integro-Differential Equation. Mathematics. 2020; 8(11):1972. https://doi.org/10.3390/math8111972
Chicago/Turabian StyleKamran, Kamran, Zahir Shah, Poom Kumam, and Nasser Aedh Alreshidi. 2020. "A Meshless Method Based on the Laplace Transform for the 2D Multi-Term Time Fractional Partial Integro-Differential Equation" Mathematics 8, no. 11: 1972. https://doi.org/10.3390/math8111972
APA StyleKamran, K., Shah, Z., Kumam, P., & Alreshidi, N. A. (2020). A Meshless Method Based on the Laplace Transform for the 2D Multi-Term Time Fractional Partial Integro-Differential Equation. Mathematics, 8(11), 1972. https://doi.org/10.3390/math8111972







