Hydromagnetic Dissipative and Radiative Graphene Maxwell Nanofluid Flow Past a Stretched Sheet-Numerical and Statistical Analysis
Abstract
1. Introduction
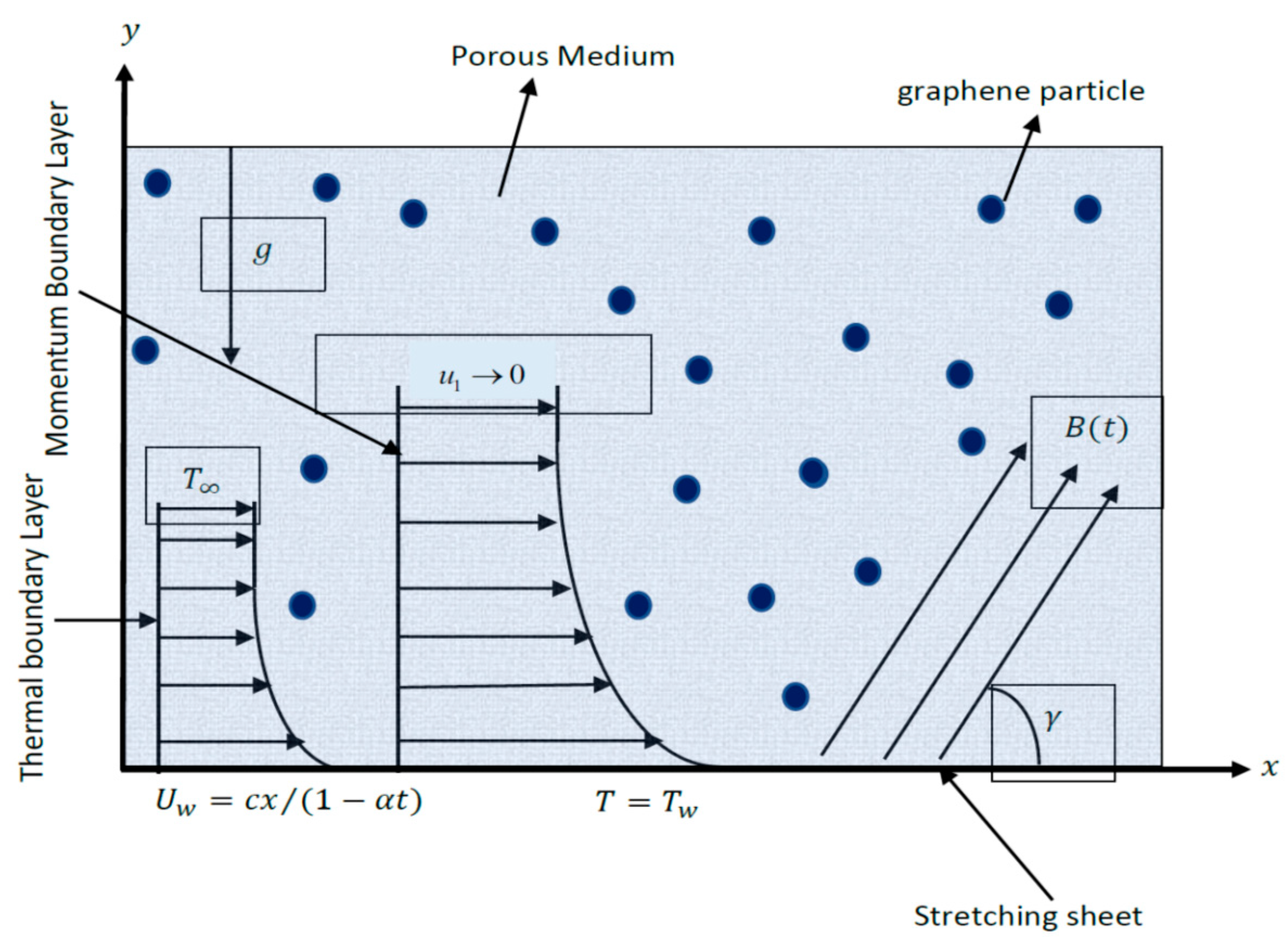
2. Formulation of Problem in Mathematical Form
3. Numerical Solution of Problem
3.1. Implementation of Numerical Method
3.2. Validation of Numerical Solution
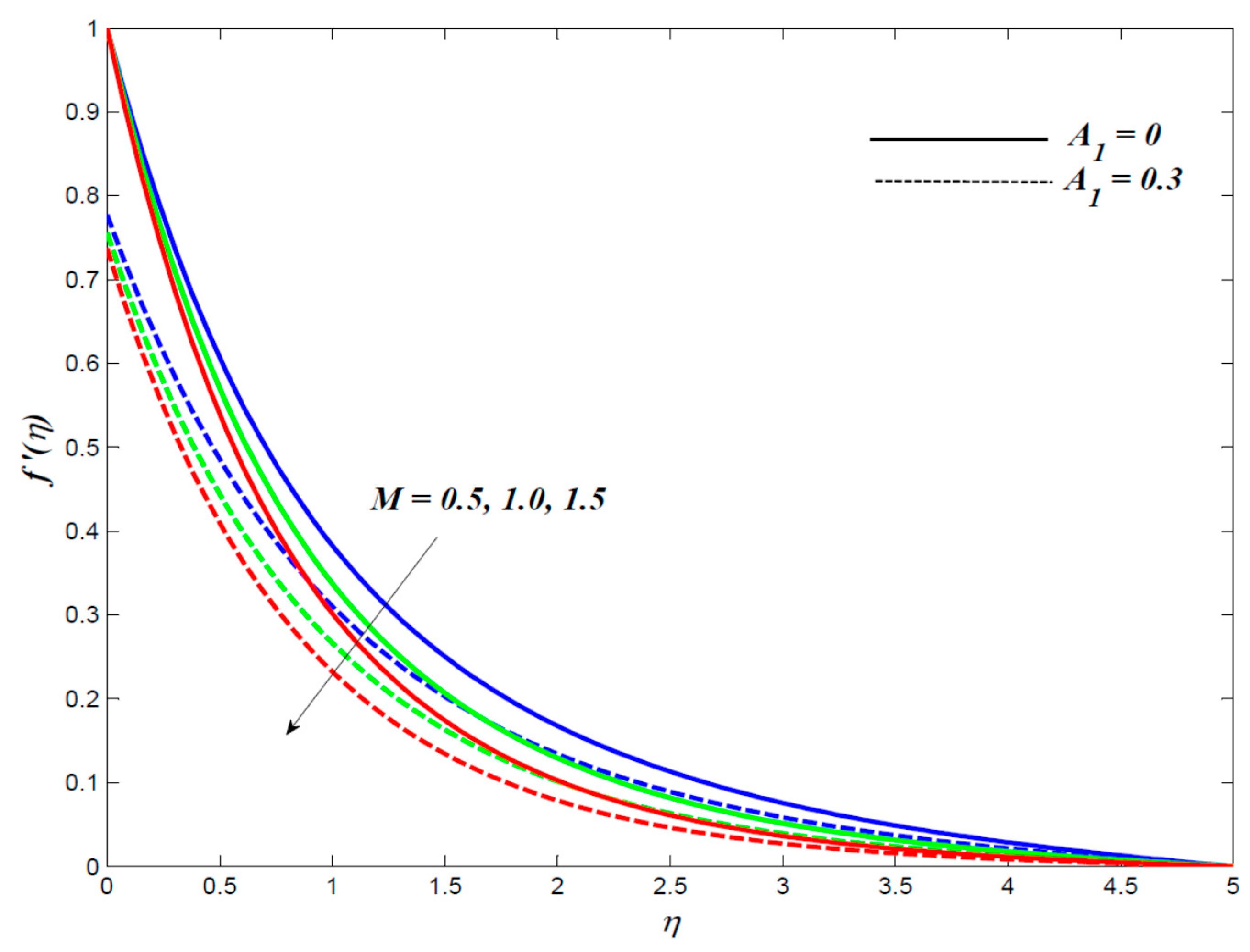
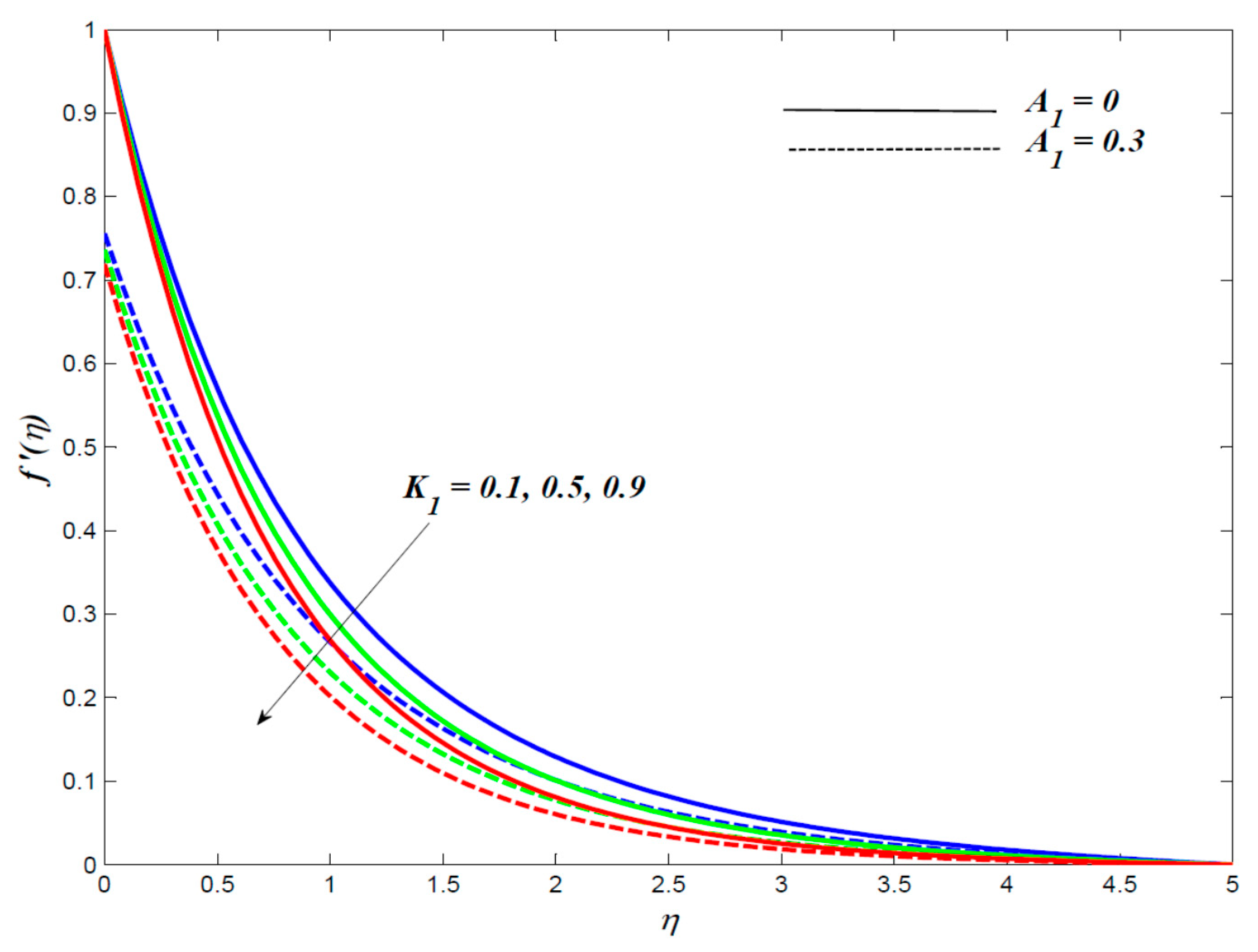
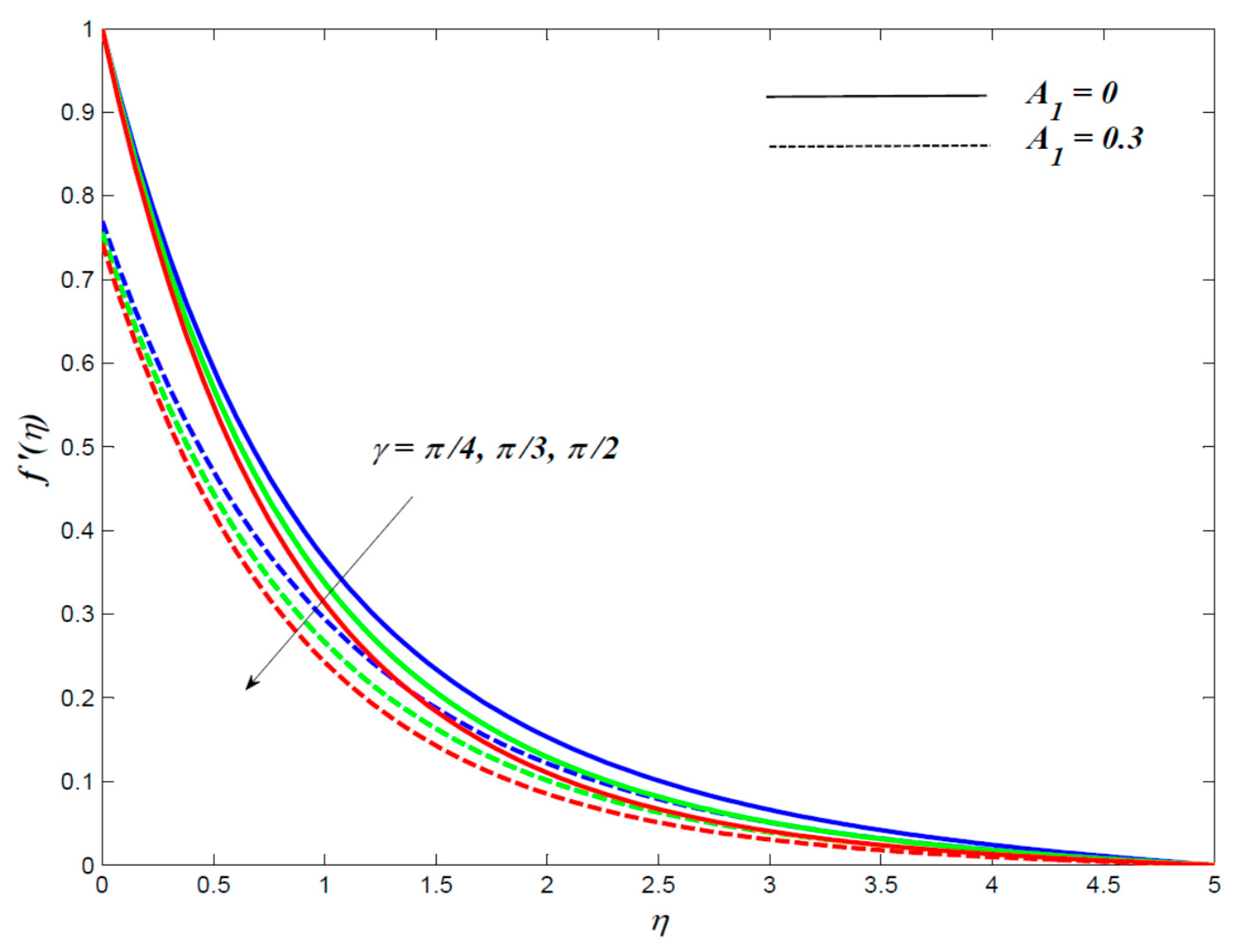
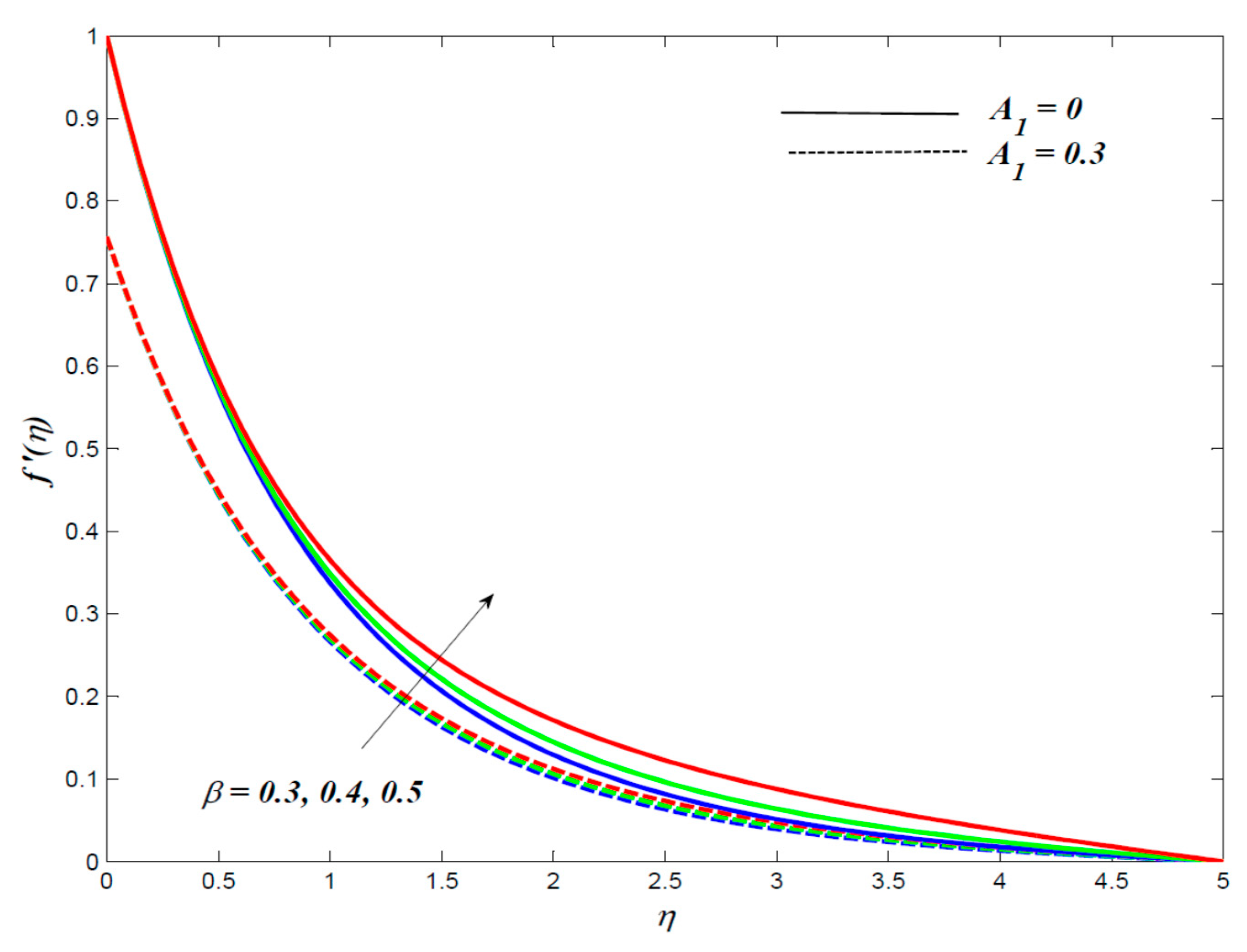
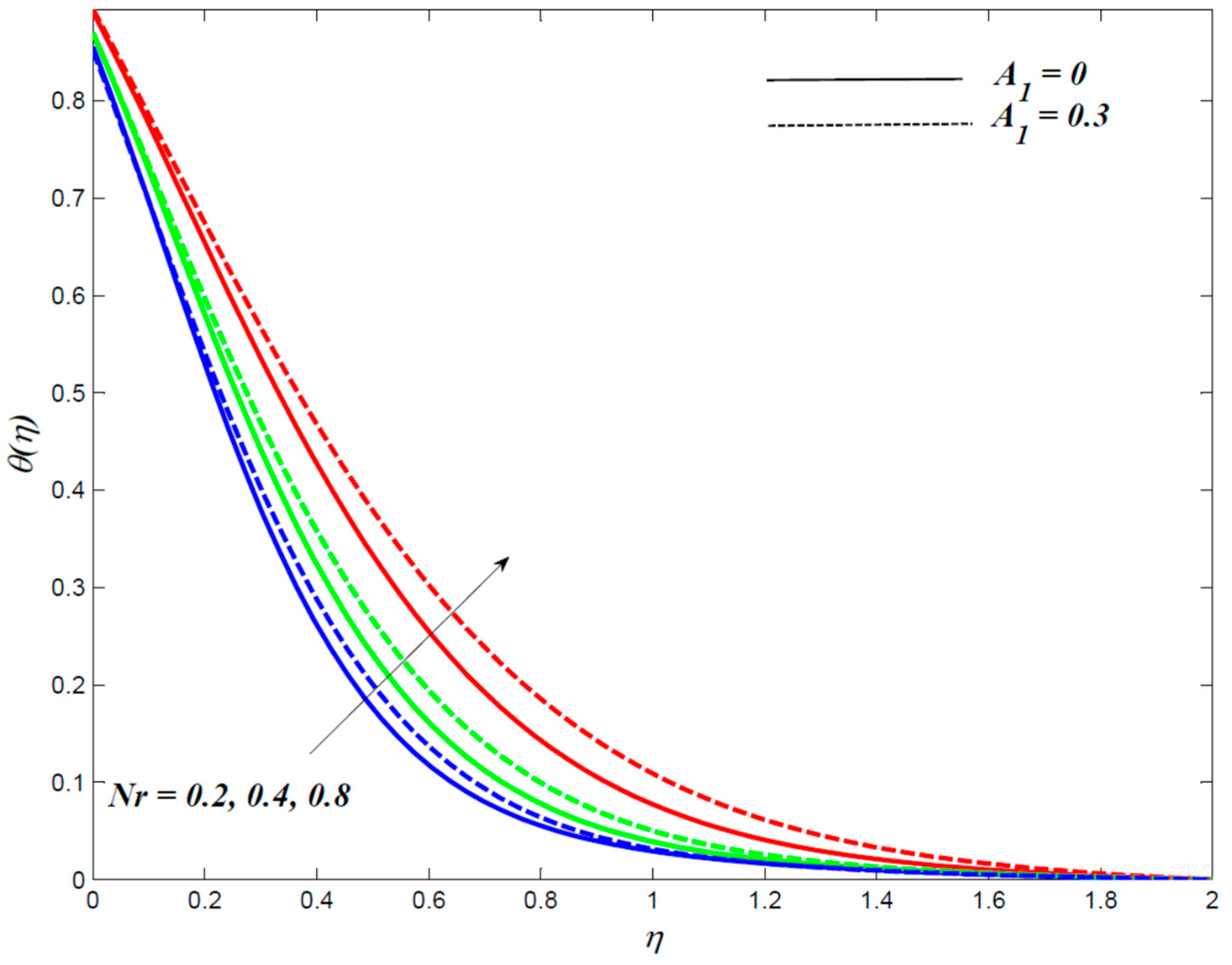
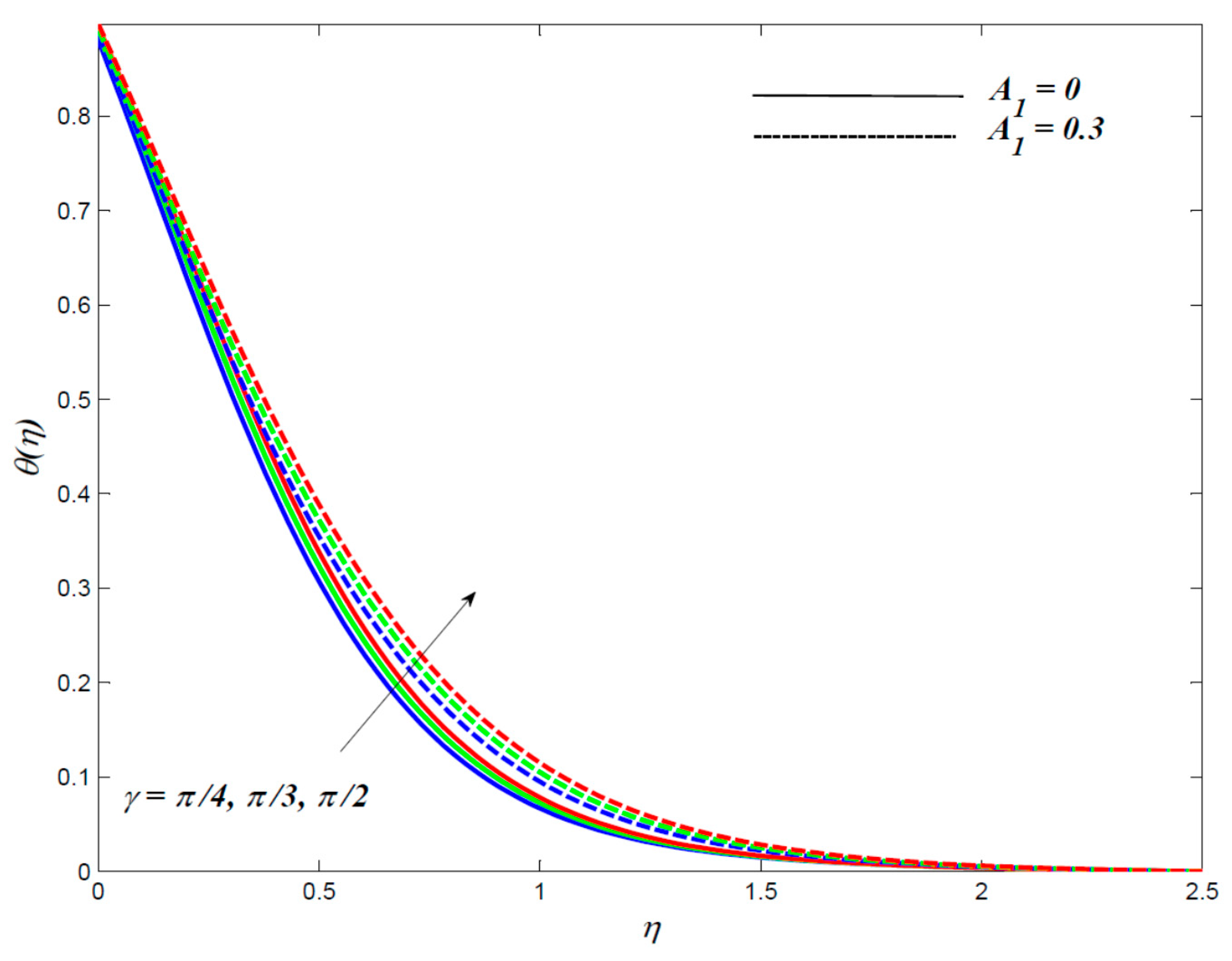
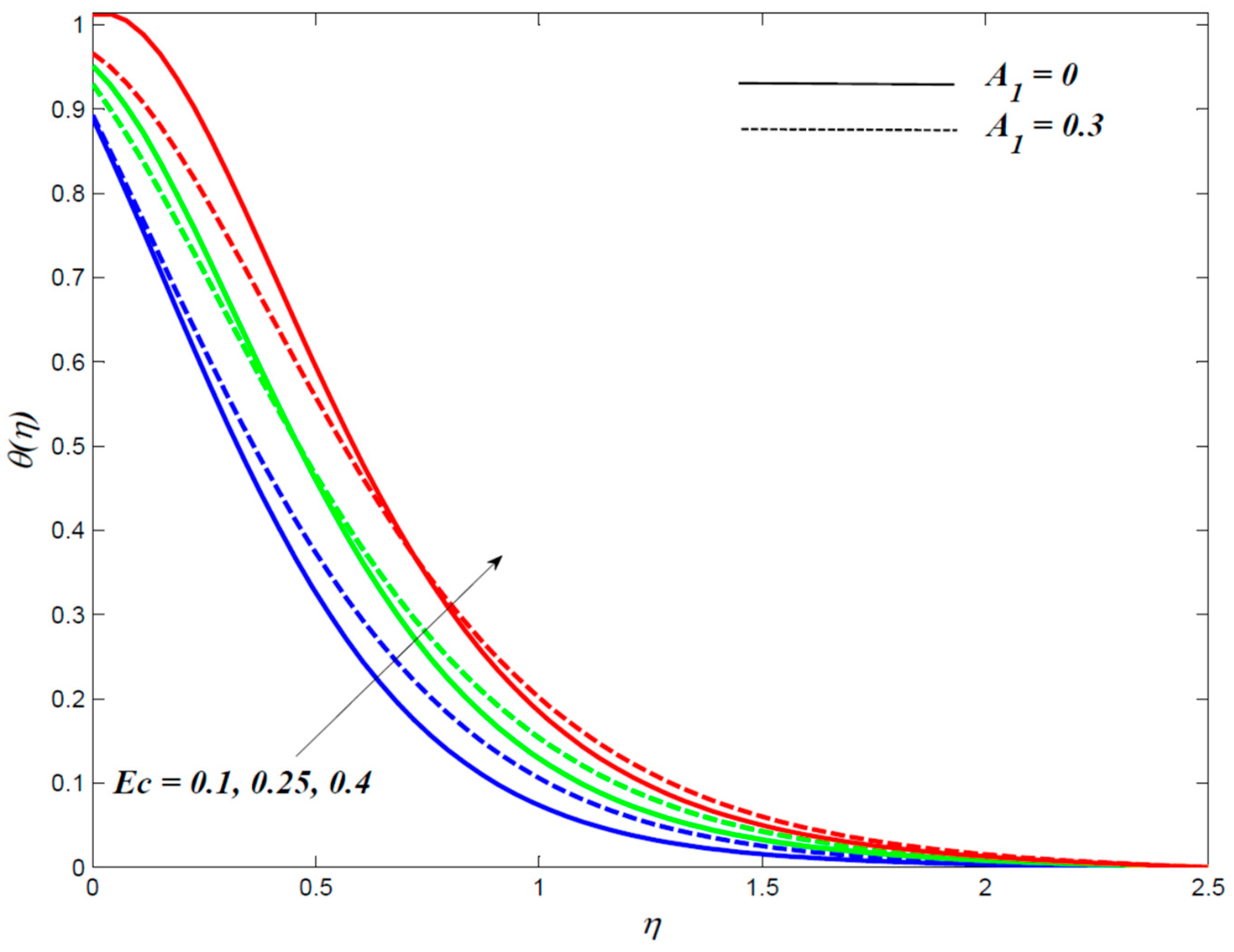
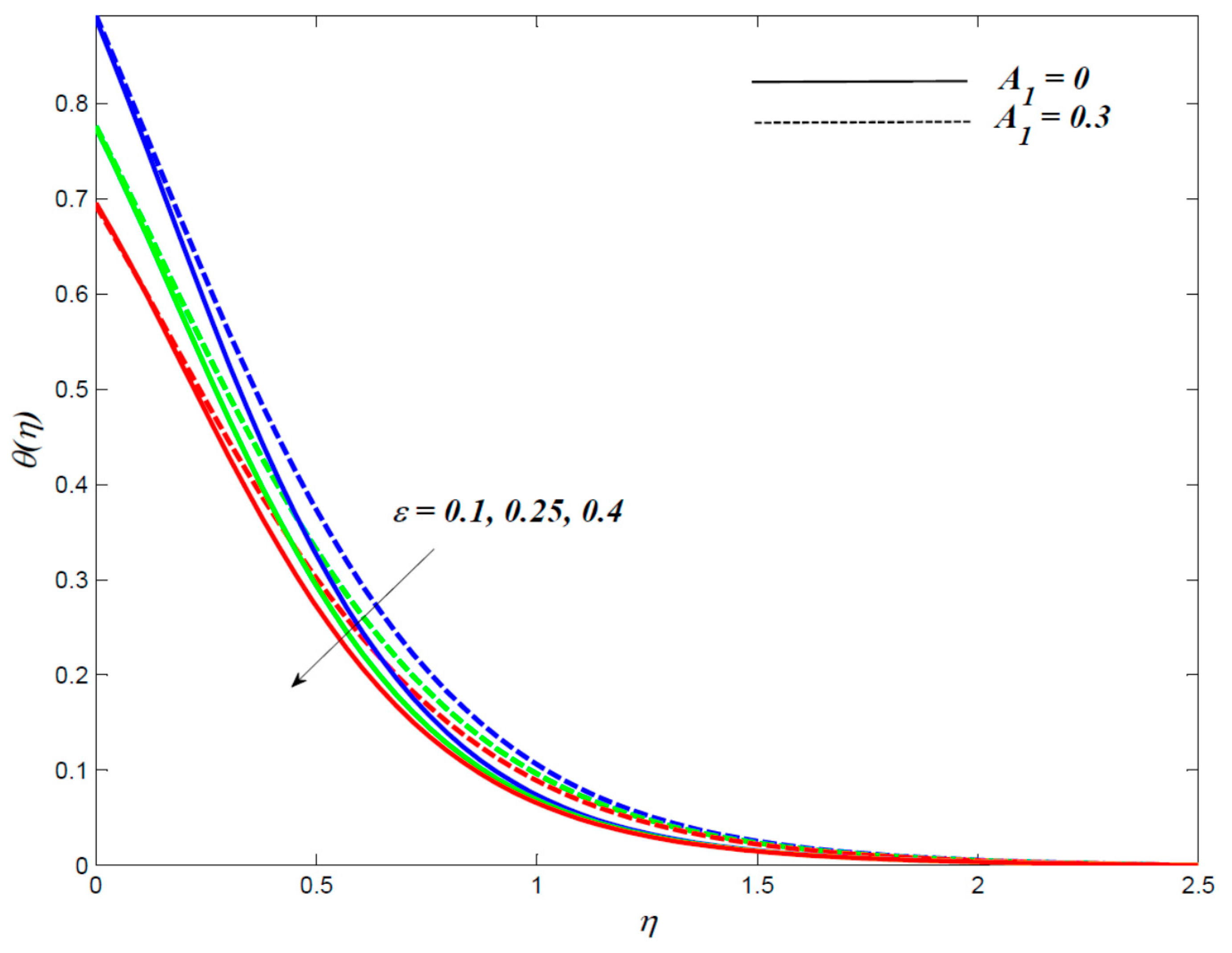
4. Results and Discussion
5. Multiple Regression Analysis: Estimation of Nusselt Number and Skin Friction Coefficients
6. Conclusions
- The graphene Maxwell nanofluid velocity gets reduced owing to enhancement in magnetic field, inclination angle of magnetic field, porosity and unsteadiness parameters whereas behaviour of fluid velocity gets reversed due to Maxwell parameter.
- The slip parameter, thermal radiation and viscous dissipation play a significant role to control the temperature of nanofluid.
- The shear stress at the stretched sheet is more sensitive to permeability of the porous medium as compared to magnetic field effect whereas rate of heat transfer is more prone to thermal radiation parameter as compared to viscous dissipation.
- By controlling the thermal radiation, unsteadiness and thermal slip parameters the heat transfer rate can be maintained, which is very useful in manufacturing industries.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles, developments and applications of non-Newtonian flows. In Proceedings of the 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995; Volume 66, pp. 99–105. [Google Scholar]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Yu, W.; Thompson, L.J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Mahendran, V.; Philip, J. Nanofluid based optical sensor for rapid visual inspection of defects in ferromagnetic materials. Appl. Phys. Lett. 2012, 100, 073104. [Google Scholar] [CrossRef]
- Mahendran, V.; Philip, J. An optical technique for fast and ultrasensitive detection of ammonia using magnetic nanofluids. Appl. Phys. Lett. 2013, 102, 063107. [Google Scholar] [CrossRef]
- Netro, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of grapheme. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Chung, A.; Kim, Y.K.; Shin, D.; Ryoo, S.R.; Hong, B.H.; Min, D.H. Biomedical applications of graphene and graphene oxide. Acc. Chem. Res. 2013, 46, 2211–2224. [Google Scholar] [CrossRef] [PubMed]
- Upadhya, M.S.; Mahesha; Raju, C.S.K. Unsteady flow of Carreau fluid in a suspension of dust and graphene nanoparticles with Cattaneo–Christov heat flux. J. Heat Transf. 2018, 140, 092401. [Google Scholar] [CrossRef]
- Serdar, B.; Dokuz, M.S. Three-dimensional stagnation point flow of a second-grade fluid towards a moving plate. Int. J. Eng. Sci. 2006, 44, 49–58. [Google Scholar]
- Haroun, M.H. Effect of Deborah number and phase difference on peristaltic transport of a third-order fluid in an asymmetric channel. Comm. Nonlinear Sci. Num. Simul. 2007, 12, 464–1480. [Google Scholar] [CrossRef]
- Sajid, M.; Hayat, T.; Asgharm, S. Non-similar analytic solution for MHD flow and heat transfer in a third-order fluid over a stretching sheet. Int. J. Heat Mass Transf. 2007, 50, 1723–1736. [Google Scholar] [CrossRef]
- Hayat, T.; Noreen, S.; Sajid, M. Heat transfer analysis of the steady flow of a fourth-grade fluid. Int. J. Therm. Sci. 2008, 47, 591–599. [Google Scholar] [CrossRef]
- Hayat, T.; Siddiqui, A.M.; Asghar, S. Some simple flows of an Oldroyd-B fluid. Int. J. Eng. Sci. 2001, 39, 135–147. [Google Scholar] [CrossRef]
- Fetecau, C.; Fetecau, C. A new exact solution for the flow of Maxwell fluid past an infinite plate. Int. J. Nonlinear Mech. 2003, 38, 423–427. [Google Scholar] [CrossRef]
- Wang, Y.; Hayat, T. Fluctuating flow of Maxwell fluid past a porous plate with variable suction. Nonlinear Anal. Real World Appl. 2008, 9, 1269–1282. [Google Scholar] [CrossRef]
- Fetecau, C.; Athar, M.; Fetecau, C. Unsteady flow of a generalized Maxwell fluid with fractional derivative due to a constantly accelerating plate. Comp. Math. Appl. 2009, 57, 596–603. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, Z.; Sajid, M. MHD stagnation point flow of an upper-convected Maxwell fluid over a stretching surface. Chaos Solitons Fractals 2009, 39, 840–849. [Google Scholar] [CrossRef]
- Heyhyat, M.; Khabazi, N. Non-isothermal flow of Maxwell fluids above fixed flat plates under the influence of a transverse magnetic field. J. Mech. Eng. Sci. 2011, 225, 909–916. [Google Scholar] [CrossRef]
- Wang, J.; Khan, M.I.; Khan, W.A.; Abbas, S.Z.; Khan, M.I. Transportation of heat generation/absorption and radiative heat flux in homogeneous–heterogeneous catalytic reactions of non-Newtonian fluid (Oldroyd-B model). Comput. Methods Prog. Biomed. 2020, 189, 105310. [Google Scholar] [CrossRef]
- Nayak, M.K.; Shaw, S.; Khan, M.I.; Pandey, V.S.; Nazeer, M. Flow and thermal analysis on Darcy-Forchheimer flow of copper-water nanofluid due to a rotating disk: A static and dynamic approach. J. Mater. Res. Technol. 2020, 9, 7387–7408. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F. Activation energy and binary chemical reaction effect in nonlinear thermal radiative stagnation point flow of Walter-B nanofluid: Numerical computations. Int. J. Mod. Phys. B 2020, 34, 2050132. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Farooq, M.; Alsaedi, A.; Waqas, M.; Yasmeen, T. Impact of Cattaneo–Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int. J. Heat Mass Transf. 2016, 99, 702–710. [Google Scholar] [CrossRef]
- Hussain, S.M.; Jain, J.; Seth, G.S.; Rashidi, M.M. Free convective heat transfer with Hall effects, heat absorption and chemical reaction over an accelerated moving plate in a rotating system. J. Magn. Magn. Mater. 2017, 422, 112–123. [Google Scholar] [CrossRef]
- Hussain, S.M.; Jain, J.; Seth, G.S.; Rashidi, M.M. Effect of thermal radiation on magneto-nanofluids free convective flow over an accelerated moving ramped temperature plate. Sci. Iran. B 2018, 25, 1243–1257. [Google Scholar]
- Kumar, B.; Seth, G.S.; Nandkeolyar, R. Regression model and successive linearization approach to analyse stagnation point micropolar nanofluid flow over a stretching sheet in a porous medium with nonlinear thermal radiation. Phys. Scr. 2019, 94, 115211. [Google Scholar] [CrossRef]
- Ghaffari, A.; Mustafa, I.; Javed, T. Influence of nonlinear radiation on natural convection flow of carbon nanotubes suspended in water-based fluid along a vertical wavy surface. Phys. Scr. 2019, 94, 115214. [Google Scholar] [CrossRef]
- Shahzad, M.; Sun, H.; Sultan, F.; Khan, W.A.; Ali, M.; Irfan, M. Transport of radiative heat transfer in dissipative Cross nanofluid flow with entropy generation and activation energy. Phys. Scr. 2019, 94, 115224. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Imran, M.; Bhatti, M.M. Thermally developed Falkner–Skan bioconvection flow of a magnetized nanofluid in the presence of a motile gyrotactic microorganism: Buongiorno’s nanofluid model. Phys. Scr. 2019, 94, 115304. [Google Scholar] [CrossRef]
- Loghmani, G.B.; Heydari, M.; Hosseini, E.; Rashidi, M.M. A numerical simulation of MHD ow and radiation heat transfer of nano uids through a porous medium with variable surface heat ux and chemical reaction. J. Math. Ext. 2019, 13, 31–67. [Google Scholar]
- Vajravelu, K.; Hadjinicolaou, A. Heat transfer in a viscous fluid over a stretching sheet with viscous dissipation and internal heat generation. Int. Comm. Heat Mass Transf. 1993, 20, 417–430. [Google Scholar] [CrossRef]
- Partha, K.; Murthy, P.V.S.N.; Rajasekhar, G.P. Effect of viscous dissipation on the mixed convection heat transfer from an exponentially stretching surface. Heat Mass Transf. 2005, 41, 360–366. [Google Scholar] [CrossRef]
- Cortell, R. Effects of viscous dissipation and radiation on thermal boundary layer over a nonlinearly stretching sheet. Phys. Lett. 2008, 372, 631–636. [Google Scholar] [CrossRef]
- Aziz, M.A. Viscous dissipation effect on mixed convection flow of a micropolar fluid over an exponentially stretching sheet. Can. J. Phys. 2009, 87, 359–368. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Effects of thermal radiation, viscous and Joule heating on electrical MHD nanofluid with double stratification. Chin. J. Phys. 2017, 55, 630–651. [Google Scholar] [CrossRef]
- Seth, G.S.; Singh, J.K. Mixed convection hydromagnetic flow in a rotating channel with Hall and wall conductance effects. Appl. Math. Mod. 2016, 40, 2783–2803. [Google Scholar] [CrossRef]
- Seth, G.S.; Sarkar, S.; Makinde, O.D. Combined free and forced convection Couette-Hartmann flow in a rotating channel with arbitrary conducting walls and Hall effects. J. Mech. 2016, 32, 613–629. [Google Scholar] [CrossRef]
- Abbas, S.Z.; Khan, W.A.; Kadry, S.; Khan, M.I.; Waqas, M.; Khan, M.I. Entropy optimized Darcy-Forchheimer nanofluid (Silicon dioxide, Molybdenum disulfide) subject to temperature dependent viscosity. Comput. Methods Prog. Biomed. 2020, 190, 105363. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Muhammad, R.; Khan, M.I.; Khan, W.A.; Abbas, S.Z. Entropy optimized MHD nanomaterial flow subject to variable thicked surface. Comput. Methods Prog. Biomed. 2020, 189, 105311. [Google Scholar] [CrossRef] [PubMed]
- Nayak, M.K.; Hakeem, A.K.A.; Ganga, B.; Khan, M.I.; Waqas, M.; Makinde, O.D. Entropy optimized MHD 3D nanomaterial of non-Newtonian fluid: A combined approach to good absorber of solar energy and intensification of heat transport. Comput. Methods Prog. Biomed. 2020, 186, 105131. [Google Scholar] [CrossRef]
- Ibrahim, M.; Khan, M.I. Mathematical modeling and analysis of SWCNT-Water and MWCNT-Water flow over a stretchable sheet. Comput. Methods Prog. Biomed. 2020, 187, 105222. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Gorla, R.S.R. Effects of partial slip on boundary layer flow past a permeable exponential stretching sheet in presence of thermal radiation. Heat Mass Transf. 2012, 48, 1773–1781. [Google Scholar] [CrossRef]
- Singh, G.; Makinde, O.D. Mixed convection slip flow with temperature jump along a moving plate in presence of free stream. Therm. Sci. 2015, 19, 119–128. [Google Scholar] [CrossRef]
- Seth, G.S.; Sharma, R.; Mishra, M.K.; Chamkha, A.J. Analysis of hydromagnetic natural convection radiative flow of a viscoelastic nanofluid over a stretching sheet with Soret and Dufour effects. Eng. Comp. 2017, 34, 603–628. [Google Scholar] [CrossRef]
- Seth, G.S.; Tripathi, R.; Mishra, M.K. Hydromagnetic thin film flow of Casson fluid in non-Darcy porous medium with Joule dissipation and Navier’s partial slip. Appl. Math. Mech. 2017, 38, 1613–1626. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F.; Hobiny, A. Simulation and modeling of second order velocity slip flow of micropolar ferrofluid with Darcy–Forchheimer porous medium. J. Mater. Res. Technol. 2020, 9, 7335–7340. [Google Scholar] [CrossRef]
- Abbas, S.Z.; Khan, M.I.; Kadry, S.; Khan, W.A.; Israr-Ur-Rehman, M.; Waqas, M. Fully developed entropy optimized second order velocity slip MHD nanofluid flow with activation energy. Comput. Methods Prog. Biomed. 2020, 190, 105362. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.I.; Alzahrani, F.; Hobiny, A. Heat transport and nonlinear mixed convective nanomaterial slip flow of Walter-B fluid containing gyrotactic microorganisms. Alex. Eng. J. 2020, 59, 1761–1769. [Google Scholar] [CrossRef]
- Muhammad, R.; Khan, M.I.; Khan, N.B.; Jameel, M. Magnetohydrodynamics (MHD) radiated nanomaterial viscous material flow by a curved surface with second order slip and entropy generation. Comput. Methods Prog. Biomed. 2020, 189, 105294. [Google Scholar] [CrossRef]
- Muhammad, R.; Khan, M.I.; Jameel, M.; Khan, N.B. Fully developed Darcy-Forchheimer mixed convective flow over a curved surface with activation energy and entropy generation. Comput. Methods Prog. Biomed. 2020, 188, 105298. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F.; Hobiny, A.; Ali, Z. Modeling of Cattaneo-Christov double diffusions (CCDD) in Williamson nanomaterial slip flow subject to porous medium. J. Mater. Res. Technol. 2020, 9, 6172–6177. [Google Scholar] [CrossRef]
- Khan, M.I.; Qayyum, S.; Kadry, S.; Khan, W.A.; Abbas, S.Z. Irreversibility analysis and heat transport in squeezing nanoliquid flow of non-Newtonian (second-grade) fluid between infinite plates with activation energy. Arab. J. Sci. Eng. 2020, 45, 4939–4947. [Google Scholar] [CrossRef]
- Aziz, A.; Jamshed, W.; Ali, Y.; Shams, M. Heat transfer and entropy analysis of Maxwell hybrid nanofluid including effects of inclined magnetic field, Joule heating and thermal radiation. Dis. Contin. Dyna. Syst.-S 2020, 13, 2667–2690. [Google Scholar] [CrossRef]
- Babu, M.J.; Sandeep, N. 3D MHD slip flow of a nanofluid over a slendering stretching sheet with thermophoresis and Brownian motion effects. J. Mol. Liquids 2016, 222, 1003–1009. [Google Scholar] [CrossRef]
- Cramer, R.; Pai, S.I. Magneto Fluid Dynamics for Engineers and Applied Physicist; McGraw-Hill Book Company: Washington, DC, USA, 1973. [Google Scholar]
- Mukhopadhyay, S. Heat transfer analysis of the unsteady flow of a Maxwell fluid over a stretching surface in the presence of a heat source/sink. Chin. Phys. Lett. 2012, 29, 054703. [Google Scholar] [CrossRef]
- Brewster, M.Q. Thermal Radiative Transfer and Properties; John Wiley and Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Elbashbeshy, E.M.A.; Bazid, M.A.A. Heat transfer over an unsteady stretching surface with internal heat generation. Appl. Math. Comp. 2003, 138, 239–245. [Google Scholar] [CrossRef]

| Thermo-Physical Properties | ||||
|---|---|---|---|---|
| Ethelene glycol | 0.252 | 2415 | 1114 | 5.5 10−6 |
| Graphene | 2500 | 2100 | 2250 | 1 107 |
| 0.1 | ||
|---|---|---|
| Elbashbeshy and Bzid [56] | Present Result | |
| 0.8 | 1.3321 | 1.3333 |
| 1.2 | 1.4691 | 1.4684 |
| 2 | 1.7087 | 1.7090 |
| 0.5 | 0.1 | 0.5 | 0.1 | 0.787368 | 0.570581 | |
| 1.0 | 0.882124 | 0.625921 | ||||
| 1.5 | 0.967012 | 0.673289 | ||||
| 0.1 | 0.882131 | 0.625924 | ||||
| 0.5 | 0.972382 | 0.676269 | ||||
| 0.9 | 1.054564 | 0.719928 | ||||
| 0.820281 | 0.590109 | |||||
| 0.882134 | 0.625925 | |||||
| 0.939652 | 0.658243 | |||||
| 0.3 | 0.882143 | 0.625921 | ||||
| 0.4 | 0.876278 | 0.624838 | ||||
| 0.5 | 0.866132 | 0.623478 | ||||
| 0.1 | 0.889234 | 0.629462 | ||||
| 0.5 | 0.955132 | 0.666434 | ||||
| 0.9 | 1.017879 | 0.700464 | ||||
| 0.1 | 0.1 | 0.1 | 0.1 | 1.793821 | 1.782463 | |
| 0.3 | 1.609543 | 1.569712 | ||||
| 0.5 | 1.352834 | 1.286441 | ||||
| 1.595722 | 1.519971 | |||||
| 1.493398 | 1.439751 | |||||
| 1.396055 | 1.366131 | |||||
| 0.10 | 1.493372 | 1.439730 | ||||
| 0.25 | 0.680023 | 0.656432 | ||||
| 0.40 | 0.580083 | 0.473145 | ||||
| 0.10 | 1.493371 | 1.439731 | ||||
| 0.25 | 1.215083 | 1.201544 | ||||
| 0.40 | 1.024223 | 1.030946 | ||||
| 0.1 | 1.493362 | 1.439734 | ||||
| 0.4 | 1.341263 | 1.253533 | ||||
| 0.7 | 1.157033 | 0.995855 | ||||
| 0.1 | −0.9221 | −0.2183 | −0.3291 | 0.0072 | 0.0373 | 0.0228 | 0.0057 |
| 0.5 | −0.9154 | −0.2181 | −0.3192 | 0.0069 | 0.0475 | 0.0182 | 0.0062 |
| Pr | ε1 | ||||||
|---|---|---|---|---|---|---|---|
| 5 | −3.0414 | 1.2812 | −2.6633 | −0.1794 | 1.0632 | 1.1211 | 0.000001061 |
| 10 | −4.0872 | 1.9613 | −4.0411 | 0.0701 | 2.0577 | 1.5837 | 0.000026912 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, S.M.; Sharma, R.; Mishra, M.R.; Alrashidy, S.S. Hydromagnetic Dissipative and Radiative Graphene Maxwell Nanofluid Flow Past a Stretched Sheet-Numerical and Statistical Analysis. Mathematics 2020, 8, 1929. https://doi.org/10.3390/math8111929
Hussain SM, Sharma R, Mishra MR, Alrashidy SS. Hydromagnetic Dissipative and Radiative Graphene Maxwell Nanofluid Flow Past a Stretched Sheet-Numerical and Statistical Analysis. Mathematics. 2020; 8(11):1929. https://doi.org/10.3390/math8111929
Chicago/Turabian StyleHussain, Syed M., Rohit Sharma, Manas R. Mishra, and Sattam S. Alrashidy. 2020. "Hydromagnetic Dissipative and Radiative Graphene Maxwell Nanofluid Flow Past a Stretched Sheet-Numerical and Statistical Analysis" Mathematics 8, no. 11: 1929. https://doi.org/10.3390/math8111929
APA StyleHussain, S. M., Sharma, R., Mishra, M. R., & Alrashidy, S. S. (2020). Hydromagnetic Dissipative and Radiative Graphene Maxwell Nanofluid Flow Past a Stretched Sheet-Numerical and Statistical Analysis. Mathematics, 8(11), 1929. https://doi.org/10.3390/math8111929





