1. Introduction
There are a large number of dynamic systems that can be modeled by partial differential equations (PDEs). Many of these systems can be found in the study of mechanical, electrical, or civil engineering as well as in the study of physics and chemistry sciences since all these disciplines deal with the study of fluid flow, heat transfer, electromagnetic field, beam deflection, acoustics, and many other physical phenomena. In the study of health and social sciences, PDEs can also be used to model spread of diseases and viruses as well as population growth. One of the main features of the phenomena mentioned above is that these are listed as distributed parameters systems (DPSs), which are characterized by having two or more independent variables where the combination of one spatial variable with one temporal variable is the most common. Another feature from the DPSs is that these are infinite-dimensional systems. PDEs can be categorized as of parabolic type, elliptic type and hyperbolic type. Each one of these categories describes the behavior of different phenomena, e.g., parabolic PDEs are mainly used to describe heat transfer systems and diffusion systems, elliptic PDEs are used to describe steady state behavior for systems such as electrostatic fields, and hyperbolic PDEs are associated with vibration or wave phenomena. To get the general solution (dynamics) from a PDE system, it is necessary to set not only initial conditions but boundary conditions which can be from three types, namely, the so-called Dirichlet, Neumann, and Robin conditions [
1].
From control theory, the backstepping methodology can be used to force a finite-dimensional nonlinear dynamical system, mainly modeled by ordinary differential equations (ODEs), to behave like a linear system in a new set of coordinates [
2,
3]. The backstepping methodology has been extended from control of finite-dimensional ODEs systems to control of infinite-dimensional PDEs systems. Control of PDEs systems can be performed in two ways, depending on the location of sensors and actuators, either in the domain dimension or at the boundary.
One of the first attempts about backstepping control design for linear parabolic PDEs was reported in [
4]. The backstepping methodology applied to the boundary control of PDEs, from considering Dirichlet and Neumann boundary value problems on the control of an unstable heat equation, was introduced in [
5]. In [
6], from the structure for a class of one-dimensional (1-D) linear parabolic partial integro-differential equations (P(I)DEs), with one Neumann boundary condition and control signal applied through either Dirichlet and Neumann boundary actuation, the backstepping methodology was used to establish an explicit expression for the gain kernel, namely the gain kernel P(I)DE system, of the boundary control law. Furthermore, the backstepping approach was extended to the design of inverse optimal controllers. From the gain kernel, explicit solutions for the boundary state feedback laws to the control of an unstable heat equation, a heat equation with destabilizing boundary condition, a reaction-diffusion (R-D) equation with spatially varying coefficient for the reaction term, and for a solid propellant rocket model, were obtained. In [
7], the backstepping methodology was translated to the design of state observers with boundary sensing. Adaptive boundary controllers for parabolic PDEs were derived in [
8,
9,
10,
11]. The adaptive approaches were extended to reaction-advection-diffusion (R-A-D) systems in higher dimensions (2-D and 3-D) and to systems with spatially varying unknown parameters [
12,
13]. Most of the work cited above was compiled in [
12,
14]. Adaptive control of linear hyperbolic PDEs following the backstepping (Volterra integral transformation) strategy can be found in [
15]. Furthermore, through the use of Volterra and Fredholm integral transformations, the input-to-state stability (ISS) approach has been extended to the control of 1-D PDEs in [
16].
Boundary control design for a R-A-D equation via backstepping approach seems like a challenging task. Because of the inclusion of partial derivatives in its structure, the searching for the solution of the gain kernel PDE represents a tedious work when trying with the solution for an integral equation equivalent to the kernel PDE. In our work, we focus our attention in the design of a Neumann stabilizing controller for a R-A-D equation, namely, a linear parabolic PDE, but with constant coefficients and Neumann boundary conditions, with actuation in one of these latter. A heat equation with Neumann boundary conditions is considered as target system. This work is motivated from [
14], where the Neumann stabilizing controller design to this class of PDE system is left as an exercise to the reader.
The manuscript is summarized as follows. The description of functions spaces is given in
Section 2. In
Section 3, the R-A-D PDE with constant parameters and boundary conditions of the Neumann type is shown. The R-A-D equation is reduced through a proper change of variables to a R-D system in order to implement the backstepping methodology for boundary control. In
Section 4, once that the original system has been reduced to the form of a R-D equation, a target system is proposed in order to, invoking the Lyapunov approach, guarantee exponential stability. In
Section 5, the main idea of the backstepping approach, a Volterra integral transformation in order to map the original PDE system into a reduced one, namely, the target system, is applied. As a result, a new PDE system is obtained in function of the so-called kernel gain. Then, by a change of variables, the solution for the integral equation is obtained. By using the successive approximations method for integral equations, as a result, the value of the kernel gain is obtained at
Section 6. Once the kernel gain value is obtained, in
Section 7 we back to the original variables getting so the stabilizing controller to be implemented on the boundary actuated from the original system. In
Section 8, the numerical algorithm used here, in order to implement and replicate our work, is given. Simulation results are discussed at
Section 9. Conclusions are drawn at the end of the paper.
2. Function Spaces
Let us denote by an open set of with boundary . Let us assume that either is Lipschitz or is of class for . The generic point of is denoted by . The Lebesgue measure on is denoted by .
Let us denote by (resp. or ) the space of real continuous functions on (resp. the space of k times continuously differentiable functions on ), (resp. ) represents the space of real continuous functions on (resp. the space of k times continuously differentiable functions on ). The spaces of real functions on with a compact support in are denoted by .
For
,
is the space of real functions on
which are
for the Lebesgue measure. It is a Banach space for the norm
For
,
is the space of measurable and bounded real functions on
. It is also a Banach space for the norm
For
,
is a Hilbert space for the scalar product
with the corresponding norm denoted by
Let us denote by
,
, the Sobolev space of functions
u in
whose distribution derivatives of order less than or equal to
s are in
. It is a Banach space for the norm
where
,
, is the notation for the partial differential derivatives of a function
u,
,
, and
. For
,
and this is a Hilbert space for the scalar product
Let us consider the Sobolev spaces
which contain
and
. The closure of
in
(resp.
) is denoted by
(resp.
). In particular,
which are Hilbert spaces for the scalar product
For a bounded
, the Poincaré inequality
implies that
is a Hilbert space for the scalar product
and that the corresponding norm
is equivalent to the norm induced by
[
17].
5. Backstepping Transformation
From the backstepping methodology to the bounded control of PDEs [
14], the coordinate transformation, also called the Volterra integral transformation,
is used to transform the system (
20), (
22) and (
23) into the target system (
24)–(26). First of all, the requirement about to find a kernel gain
, that makes that the plant behaves like the target system, must be fulfilled. It is well known that (
42) is invertible, so, the smoothness of the kernels of the direct and inverse transformation in
x and
y establishes the equivalence of norms of
v and
w in both
and
spaces. Thus, from the properties of the heat Equations (
24)–(26) can be concluded that the closed-loop system is exponentially stable in
and
.
Let
be a continuous function such that its partial derivative is continuous in
for
. From the Leibniz differentiation rule [
18]
with
the temporal derivative from (
42) is given as
which, from (
20), can be written as
From this last equation, applying integration by parts twice for the first term into the integral yields
Then, the spatial derivatives from (
42), considering again (
43), result
From (
24), subtracting (
48) and (
49) from (51) yields
By setting, from the integral term in (
52),
it follows that
Furthermore, from (
52), setting equal to zero the term
we have
Moreover, from the first term in (
52), by setting
from (46), it can be written as
Thus, from this last identity, subtracting
and integrating with the differential
it yields
Hence, in order to zeroing the right-hand side from (
52), for all
, the following identities
must be fulfilled.
By inspection of (
60) and (61) we have a hyperbolic PDE system whose solution will be the kernel gain
. We can find the kernel by converting (
60) and (61) into an integral equation. To this end, let us define the following change of variables
and let us denoting
Next, by calculating the derivative with respect to the
x and
y variables from (
64) we have
Substituting (
65)–(68) into (
60) it yields
By applying the change of variables (
63) to the condition (61) we get
Then, by applying (
70) into (62) it results
From all of the above, we arrive to the PDE (
69) with conditions (
70) and (
71).
By integrating (
69) respect to
, with limits from 0 to
, results
Evaluating limits from the integral on the left side of (
72) it yields
From (
70), we calculate the derivative respect to
to then replace it in (
73) yielding
Then, by integrating (
74) with respect to
, for limits from
to
, we have
Evaluating limits of both simple integrals in (
75) yields
Now, we need to express
from this last equation in terms of an integral function. By the identity (
71), we can express
By applying the identity (46) into (
77) results
By integrating (79) respect to
, with limits from 0 to
, we get
Evaluating the limits of the integral on the left side from this last equation we write
and, from (
70), if
then
. By the identity (
71), if
we can say that both map into the same domain. So, we can express (
81) as given by
From (
74), the integral term is given as
So, substituting this last equation in (
82) and then expanding it we get
and evaluating the limits of the first integral on the right side it results
By substituting (
85) into (
76) it yields
and adding similar terms in (
86), this last expression can be written as
Finally, we have arrived to the integral equation (
87) which is equivalent to the PDE (
60) with boundary conditions (61) and (62).
6. Integral Equation Solution
Our next goal is to find the solution for (
87). By using the method of successive approximations, let us begin with the initial guess
Here, we have to set a recursive formula for (
87) that allow us to approximate the step ahead solution
by using the previous solution with the initial guess as the first solution for
. This formula is set up as
Let us denote the difference between two consecutive terms as
so,
Under the assumption that (
89) converges to a limit, the solution
can be written as
or, by using (
90), it can be alternatively written as
Setting
and taking into account (
88)–(
91) we calculate
We have already calculated
, so using (
91) now we get
At this point, it must be clear that we are obtaining the term (
91) for every new value of
n. So, for the case when
we only need to calculate
, this because
must be calculated for
. Hence,
Now, when setting
it yields
Thus, we could still evaluating
n for any time because from (
94)–(
98) the pattern to follow is given as
Then, the solution (
93) can be expressed as
In order to simplify (
100) for software implementation, we use the first-order modified Bessel function of the first kind, i.e.,
By setting
, from (
101) we have
To express (
102) in the form (
100), rearranging terms in (
100) it can be written as
Moreover, separating terms in (
102) it can be written as
Matching the second term from (
103) and (
104), i.e.,
it is easy to see that
By the knowledge of (
105), the Bessel function can be rewritten as
Now, all the terms appearing in (
106) must appear in (
100). So, multiplying (
103) by
then it is possible to express (
102) in the form (
100) as is shown next, i.e.,
Taking into account (
63) we get
so, substituting (
110) and (111) into (109) yields
So, in the manner described above, the kernel gain (
112), key piece in the design of the controller, has been determined. Thus, we have found the solution for
in order to achieve the boundary control of the PDE system (
20), (
22) and (
23).
8. MATLAB Code
In order to validate the dynamic response for the closed-loop system, in what follows it is described how to implement the whole control system through
MATLAB[
19]. To this end, we use the function
pdepe. This function is able to solve initial-boundary value problems for parabolic and elliptic PDEs in the one space variable
x and time
t. This function solves PDEs of the form
By comparing (
13) with (
127), it can be seen that
From
MATLAB, the syntax for the
pdepe function is as follows
sol=pdepe(m,pdefun,icfun,bcfun,xlinspace,tlinspace);
where
m is defined in (131),
pdefun is a function that defines the components of the PDE to be solved,
icfun is a function that defines the initial condition,
bcfun is a function that defines the boundary conditions,
xlinspace is a vector with elements
concerning with
n specific points (defined by the user) for which a solution is required for every value of
tlinspace, also a vector with elements
for
f specific points (also defined by the user).
For all
and
x, the solution components are satisfied for all initial conditions of the form
Furthermore, for all
t and either
or
, where
a represents the left boundary condition and
b represents the right boundary condition, the solution components must satisfy a boundary condition of the form
For the PDE (
13), based on (
128)–(130),
pdefun function is declared as it is shown below.
function[c,f,s]=pdefun(x,t,u,DuDx)
global lambda; global b;
c=1;
f=DuDx;
s=b*f + lambda*u;
For the initial condition, icfun is declared as follows.
function u0=icfun(x)
global initial
global i
u0 = initial(i);
i=i+1;
For the boundary conditions (14)–(15),
bcfun function is declared following the form given by (
133).
cntrllr is for the control law (actuation signal).
function[pl,ql,pr,qr] = bcfun(xl,ul,xr,ur,t)
global cntrllr; global b;
pl=b/2*ul;
ql=1;
pr=-cntrllr;
qr=1;
It should be noticed that the functions declared above are needed when running the pdepe function. The main code that handles these last functions is shown next.
clear all;
global cntrllr; cntrllr=0;
global lambda; lambda=30;
global b; b=10;
global lambda0; lambda0=lambda-b^2/4;
m=0;
The spatial vector x is defined below.
x0=0; xf=1; xn=40;
x=linspace(x0,xf,xn+1);
To define the temporal vector, it must be aware of the next explanation; the solution of a PDE has a mesh where for every spatial value and every temporal value there is a solution value, so we can imagine that for each temporal value there is a spatial vector that we can refer to it as a slice of the solution. We will use two meshes for software implementation: one for a slice of the solution which we call t and the another one for the complete solution of the PDE which we will referring it as T. We need that the slice of the solution has at least three data, so we need to define the step that all slices will have in order to get the solution from the PDE. To this end, the code used is given next.
t0=0; step=0.001; tf=step; tn=3;
zf=20; tt=zf*step; ttn=zf*tn;
t=linspace(t0,tf,tn);
T=linspace(t0,tt,ttn+1);
tt is for the simulation time and ttn is for the total number of simulation data, i.e., the sum of all solution slices. The initial conditions are defined through the following code.
global initial; initial=5*(1-2*sin(3*pi*x/2));
u=initial;
global i; i=1;
pdepe function returns the solution in a 3-D array called sol, where sol(i,j,k) approximates the k-th component of the solution evaluated at and . The size of sol is ttn-by-xn-by-initial and the command to extract the solution of the PDE for the defined size is as follows.
u = sol(:,:,1);
ND=5;
tg=zeros(1,ttn/ND+1);
ug=zeros(ttn/ND+1,xn+1);
ug(1,:)=initial;
A for cycle is implemented to compute the whole solution of the PDE system. The code shown at the bottom is used to plot the solution.
for z=1:zf
sol=pdepe(m,@pdefun,@icfun,@bcfun,x,t);
u=[u; sol(:,:,1)];
root = sqrt(lambda0*(1-x.^2));
bss1 = besseli(1,root);
bss2 = besseli(2,root);
coc1 = (3/2)*bss1./root;
coc2 = bss2./(1-x.^2);
coc1(end) = coc1(end-1)*.89;
coc2(end) = coc2(end-1)*.89;
coc = coc1 + coc2;
int = coc.*exp(b/2*(x-1)).*u(end,:);
integ = trapz(x,int);
u_1 = u(end,end);
cntrllr = -((lambda0+b+1)/2)*u_1 - lambda0*integ;
initial = u(end,:);
i=1;
t0=t0+step;
tf=tf+step;
t=linspace(t0,tf,tn);
end
for h=1:ttn/ND
tg(1,h+1) = T(1,ND*h+1);
ug(h+1,:) = u(ND*h+1,:);
end
figure(1);
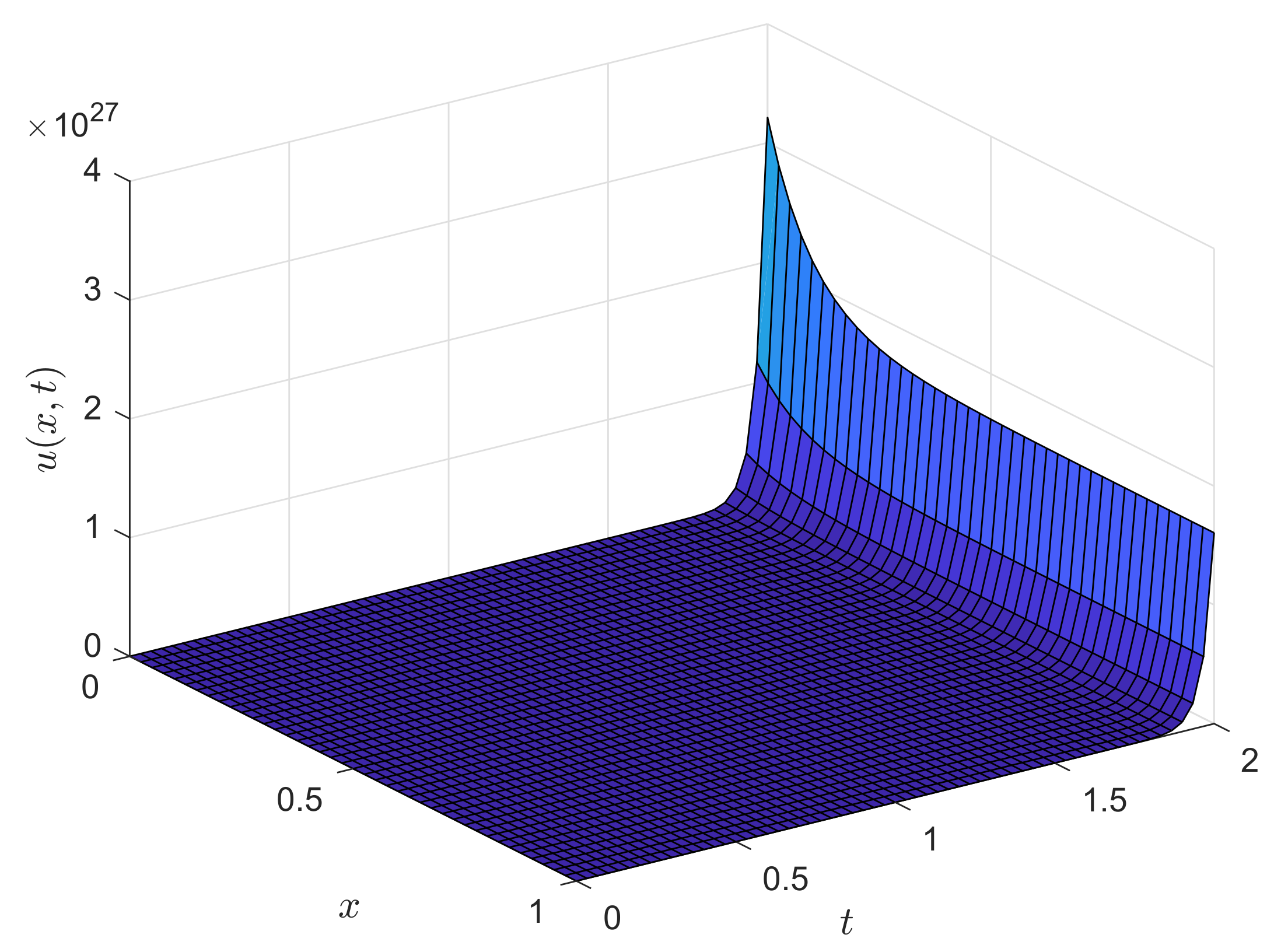
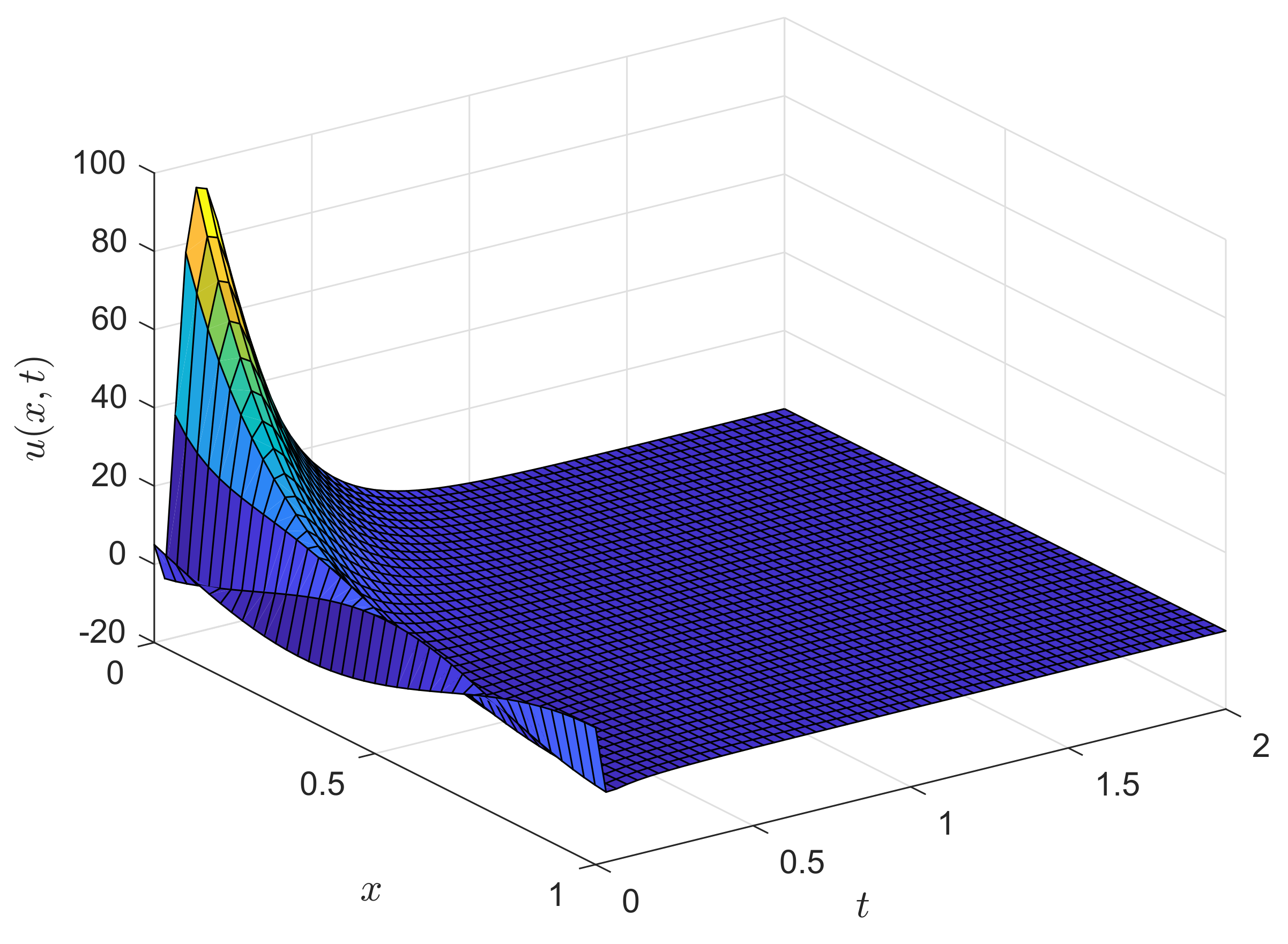
surf(x,tg,ug);
view(45,30);
title(’Reaction-Advection-Diffusion Equation ’,’FontSize’,12’);
xlabel(’Distance $x$’,’Interpreter’,’Latex’,’FontSize’,12’);
ylabel(’Time $t$’,’Interpreter’,’Latex’,’FontSize’,12’);
zlabel(’Solution $u(x,t)$’,’Interpreter’,’Latex’,’FontSize’,12’);
view(55,30)
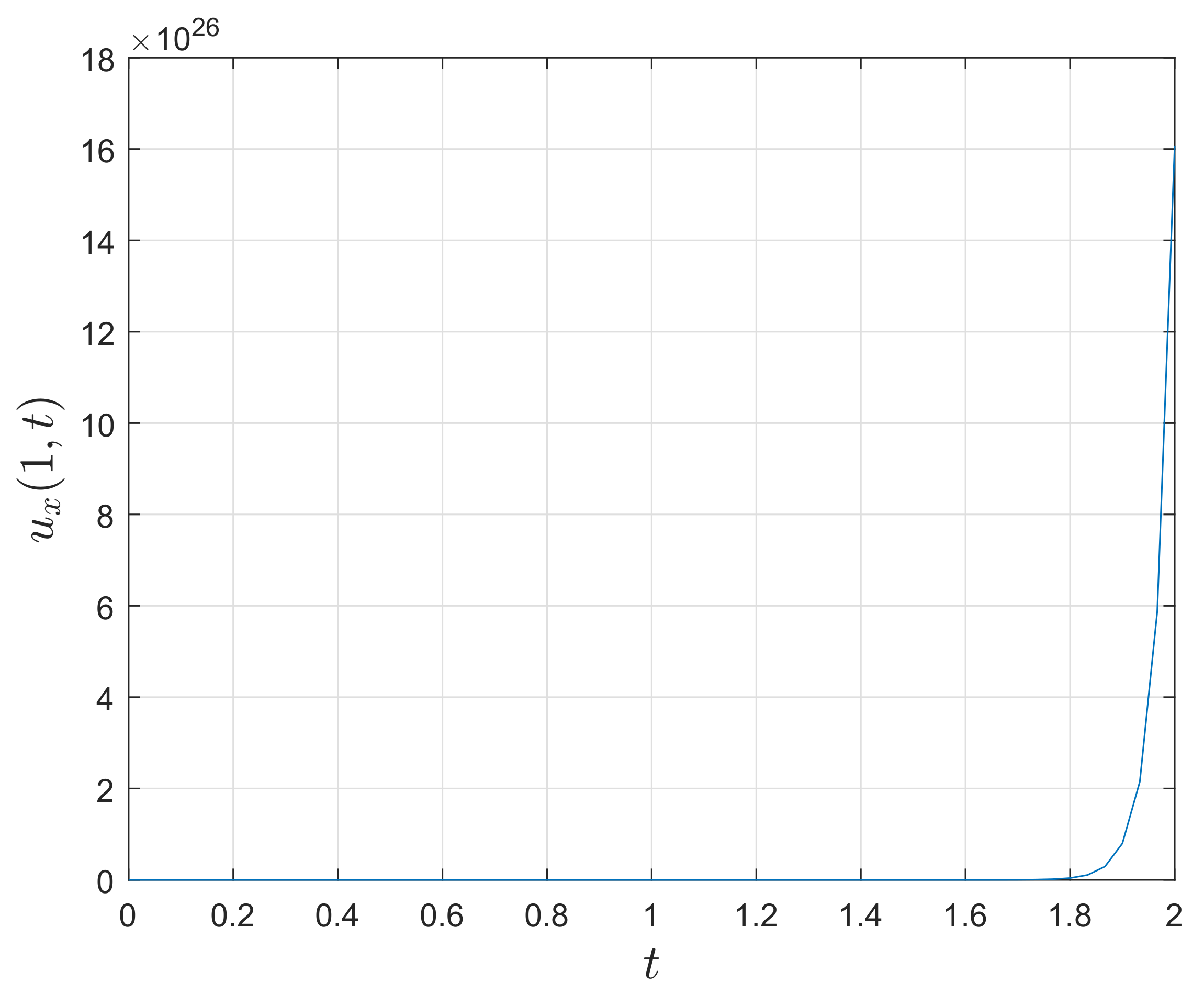
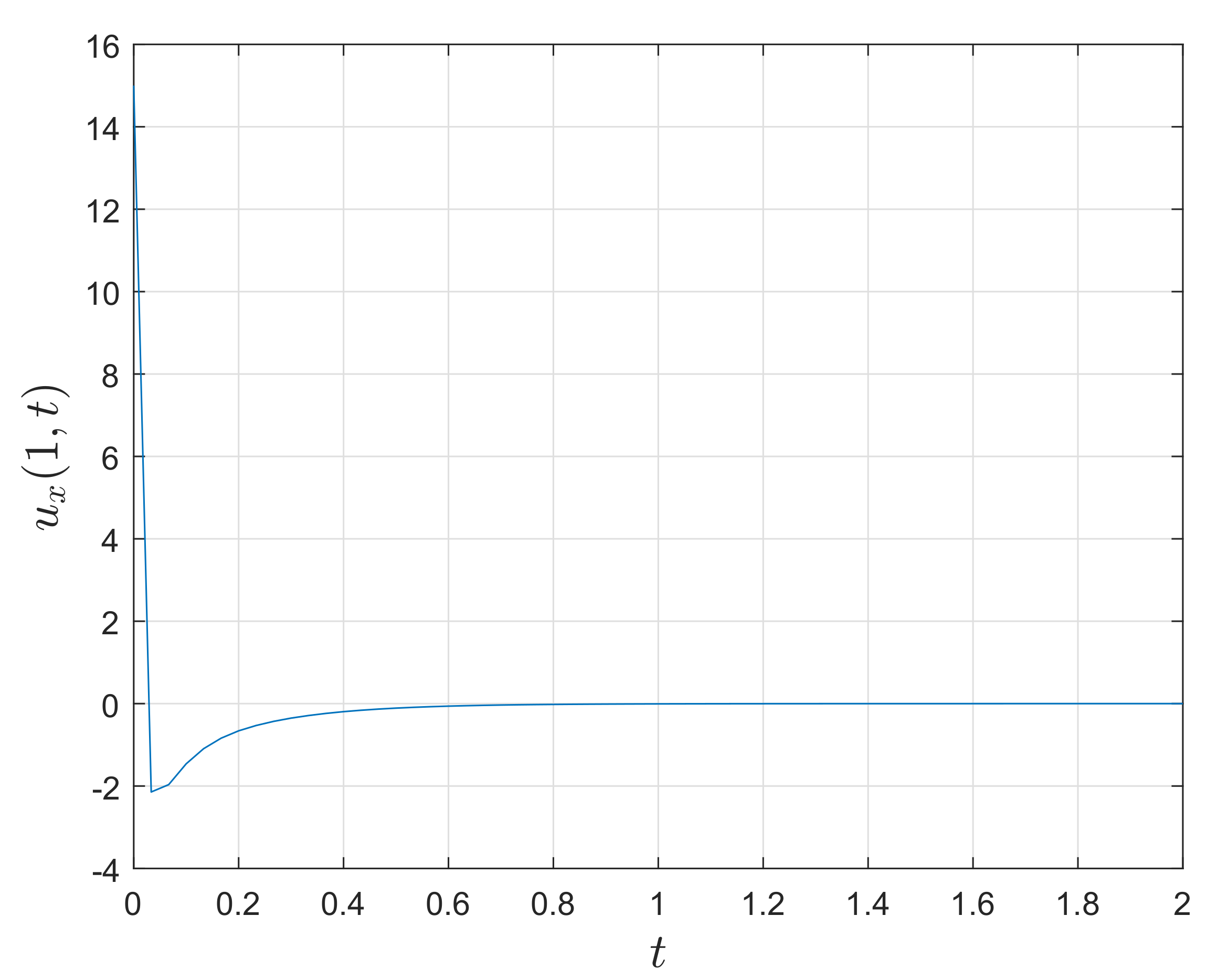
figure(2);
plot(tg,ug(:,end)’);
xlabel(’Time $t$’,’Interpreter’,’Latex’,’FontSize’,15’);
ylabel(’Solution $u(1,t)$’,’Interpreter’,’Latex’,’FontSize’,15’);
grid on;
The MATLAB code shown above is contained in four different M-files. The pdefun.m, icfun.m and bcfun.m files correspond to the pdefun, icfun and bcfun functions, respectively. The main code is saved as BCRAD.m which contains the remaining MATLAB code in the order presented above. The BCRAD.m file must be compiled and then executed to get the numerical solution.