On Tail Dependence and Multifractality
Abstract
1. Introduction
2. Methods
2.1. Multifractality, Its Estimators, and Its Measures
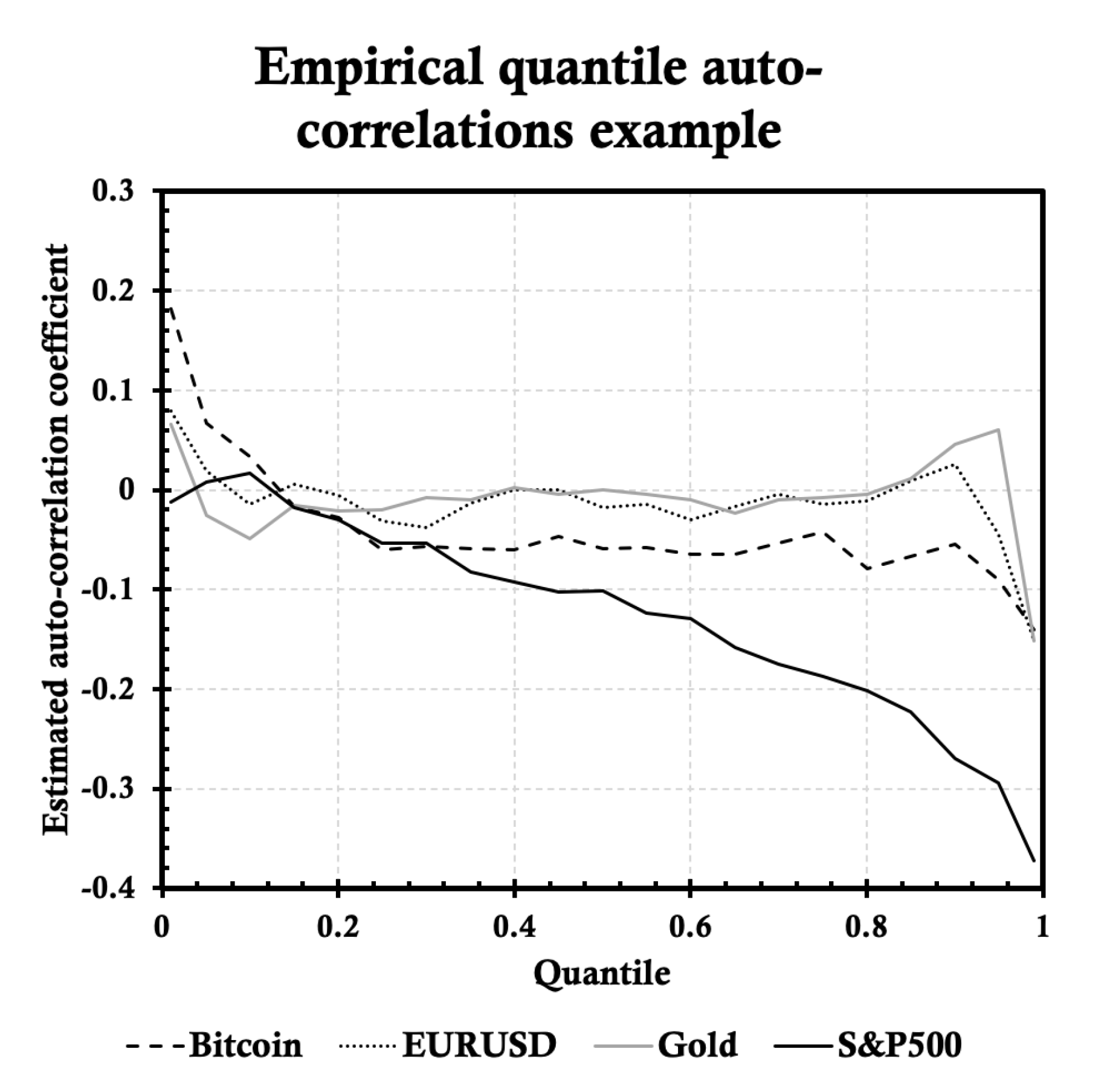
2.2. Quantile Autoregression with Gaussian Copula
3. Simulations Setting
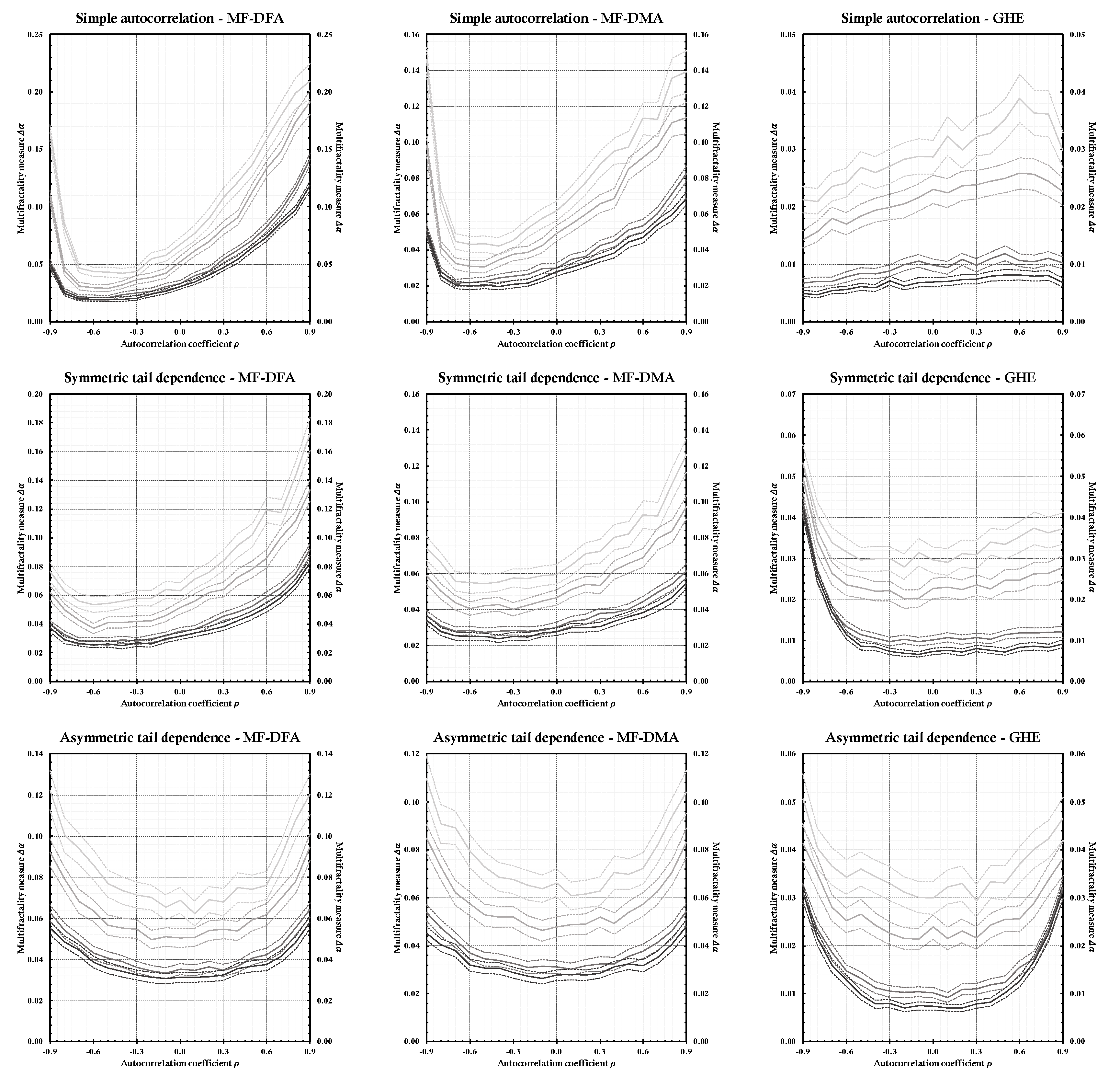
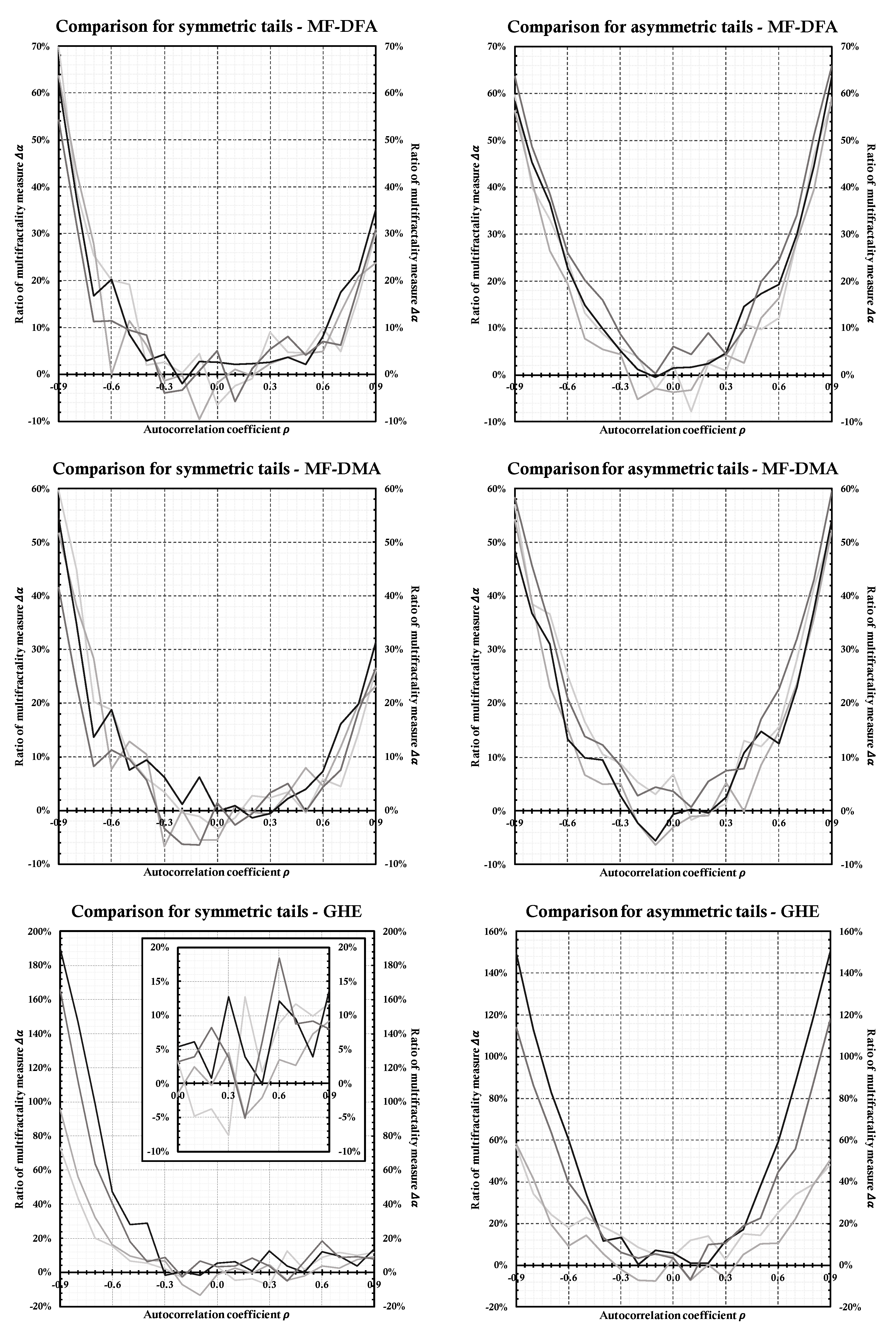
4. Results
4.1. Baseline Settings
4.2. Comparison to the Flat Correlation Structure
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Novikov, E.A. Intermittency and scale similarity in the structure of a turbulent flow. J. Appl. Math. Mech. 1971, 35, 231–241. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Possible refinement of the lognormal hypothesis concerning the distribution of energy dissipation in intermittent turbulence. Stat. Model. Turbul. Lect. Notes Phys. 1972, 12, 333–351. [Google Scholar]
- Mandelbrot, B.B. Intermittent turbulence in self-similar cascades: Divergence of high moments and dimension of the carrier. J. Fluid Mech. 1974, 62, 331–358. [Google Scholar] [CrossRef]
- Grassberger, P. Generalized dimensions of strange attractors. Phys. Lett. 1983, 97, 27–230. [Google Scholar] [CrossRef]
- Grassberger, P. Generalizations of the Hausdorff dimension of fractal measures. Phys. Lett. 1985, 107, 101–105. [Google Scholar] [CrossRef]
- Hentschel, H.G.E.; Procaccia, I. The infinite number of generalized dimensions of fractals and strange attractors. Phys. D 1983, 8, 435–444. [Google Scholar] [CrossRef]
- Müller, U.A.; Dacorogna, M.; Olsen, R.B.; Pictet, O.V.; Schwarz, M.; Morgenegg, C. Statistical study of foreign exchange rates, empirical evidence of a price change scaling law, and intraday analysis. J. Bank. Financ. 1990, 14, 1189–1208. [Google Scholar] [CrossRef]
- Ghashghaie, S.; Breymann, W.; Peinke, J.; Talkner, P.; Dodge, Y. Turbulent cascades in foreign exchange markets. Nature 1996, 381, 767–770. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. A multifractal walk down Wall Street. Sci. Am. 1999, 280, 70–73. [Google Scholar] [CrossRef]
- Jiang, Z.-Q.; Xie, W.-J.; Zhou, W.-X.; Sornette, D. Multifractal analysis of financial markets: A review. Rep. Prog. Phys. 2019, 82, 125901. [Google Scholar] [CrossRef] [PubMed]
- Cont, R. Empirical properties of asset returns: Stylized facts and statistical issues. Quant. Financ. 2001, 1, 223–236. [Google Scholar] [CrossRef]
- Chakraborti, A.; Toke, I.M.; Patriarca, M.; Abergel, F. Econophysics review: I. Empirical facts. Quant. Financ. 2011, 11, 991–1012. [Google Scholar] [CrossRef]
- Chakraborti, A.; Toke, I.M.; Patriarca, M.; Abergel, F. Econophysics review: II. Agent-based models. Quant. Financ. 2011, 11, 1013–1041. [Google Scholar] [CrossRef]
- Kantelhradt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Matteo, T.D.; Aste, T.; Dacorogna, M.M. Long-term memories of developed and emerging markets: Using the scaling analysis to characterize their stage of development. J. Bank. Financ. 2005, 29, 827–851. [Google Scholar] [CrossRef]
- Matteo, T.D. Multi-scaling in finance. Quant. Financ. 2007, 7, 21–36. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Bollerslev, T. Modelling the coherence in short-run nominal exchange rates: A multivariate generalized arch model. Rev. Econ. Stat. 1990, 72, 498–505. [Google Scholar] [CrossRef]
- Muzy, J.-F.; Sornette, D.; Delour, J.; Arneodo, A. Multifractal returns and hierarchical portfolio theory. Quant. Financ. 2001, 1, 131–148. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Fisher, A.J.; Calver, L.E. A multifractal model of asset returns. Cowles Found. Discuss. Pap. 1997, 1164, 1–31. [Google Scholar]
- Mandelbrot, B.B. Scaling in financial prices: III. Cartoon Brownian motions in multifractal time. Quant. Financ. 2001, 1, 427–440. [Google Scholar] [CrossRef]
- Calvet, L.E.; Fisher, A.J. Forecasting multifractal volatility. J. Econom. 2001, 105, 27–58. [Google Scholar] [CrossRef]
- Calvet, L.E.; Fisher, A.J. How to forecast long-run volatility: Regime switching and the estimation of multifractal processes. J. Financ. Econom. 2004, 2, 49–83. [Google Scholar] [CrossRef]
- Bacry, E.; Delour, J.; Muzy, J.F. Multifractal random walk. Phys. Rev. E 2001, 64, 026103. [Google Scholar] [CrossRef] [PubMed]
- Calvet, L.E.; Fisher, A.J. Multifractal Volatility: Theory, Forecasting, and Pricing; Academic Press: Burlington, MA, USA, 2008. [Google Scholar]
- Kukacka, J.; Kristoufek, L. Do ‘complex’ financial models really lead to complex dynamics? agent-based models and multifractality. J. Econ. Dyn. Control 2020, 113, 103855. [Google Scholar] [CrossRef]
- Kukacka, J.; Kristoufek, L. Does Calibration Affect the Complexity of Agent-Based Models? A Multifractal Grid Analysis. Technical Report, SSRN. 2020. Available online: https://ssrn.com/abstract=3654362 (accessed on 13 October 2020).
- Beran, J. Statistics for Long-Memory Processes. In Monographs on Statistics and Applied Probability; Chapman and Hall: New York, NY, USA, 1994. [Google Scholar]
- Calvet, L.E.; Fisher, A.J. Multifractality in asset returns: Theory and evidence. Rev. Econ. Stat. 2002, 84, 381–406. [Google Scholar] [CrossRef]
- Samorodnitsky, G. Long range dependence. Found. Trends Stoch. Syst. 2006, 1, 163–257. [Google Scholar] [CrossRef]
- Kantelhardt, J.W. Encyclopedia of Complexity and Systems Science; Chapter Fractal and multifractal time series; Springer-Veral: New York, NY, USA, 2009; pp. 3754–3779. [Google Scholar]
- Peng, C.; Buldyrev, S.; Goldberger, A.; Havlin, S.; Simons, M.; Stanley, H. Finite-size effects on long-range correlations: Implications for analyzing DNA sequences. Phys. Rev. E 1993, 47, 3730–3733. [Google Scholar] [CrossRef]
- Alessio, E.; Carbone, A.; Castelli, G.; Frappietro, V. Second-order moving average and scaling of stochastic time series. Eur. Phys. J. B 2002, 27, 197–200. [Google Scholar] [CrossRef]
- Vandewalle, N.; Ausloos, M. Crossing of two mobile averages: A method for measuring the roughness exponent. Phys. Rev. E 1998, 58, 6832–6834. [Google Scholar] [CrossRef]
- Matteo, T.D.; Aste, T.; Dacorogna, M. Scaling behaviors in differently developed markets. Phys. A 2003, 324, 183–188. [Google Scholar] [CrossRef]
- Peng, C.; Buldyrev, S.; Havlin, S.; Simons, M.; Stanley, H.; Goldberger, A. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef]
- Roger, K.; Zhijie, X. Quantile autoregression. J. Am. Stat. Assoc. 2006, 101, 980–990. [Google Scholar]
- Sklar, A. Fonctions de répartition à n dimensions et leurs marges. Publications de l’Institut de Statistique de l’Université de Paris 1959, 8, 229–231. [Google Scholar]
- Eric, B.; Mark, S. Dynamic copula quantile regressions and tail area dynamic dependence in forex markets. Eur. J. Financ. 2009, 15, 721–750. [Google Scholar]
- Xiaohong, C.; Roger, K.; Zhijie, X. Copula-based nonlinear quantile autoregression. Econom. J. 2009, 12, S50–S67. [Google Scholar]
- Rak, R.; Grech, D. Quantitative approach to multifractality induced by correlations and broad distribution of data. Phys. A 2018, 508, 48–66. [Google Scholar] [CrossRef]
- Ludescher, J.; Kantelhardt, B.M.I.J.W.; Schumann, A.Y.; Bunde, A. On spurious and corrupted multifractality: The effects of additive noise, short-term memory and periodic trends. Phys. A 2011, 390, 2480–2490. [Google Scholar] [CrossRef]
- Pamula, G.; Grech, D. Influence of the maximal fluctuation moment order q on multifractal records normalized by finite-size effects. Europhys. Lett. 2014, 105, 50004. [Google Scholar] [CrossRef]
- Barunik, J.; Aste, T.; Matteo, T.D.; Liu, R. Understanding the source of multifractality in financial markets. Phys. A 2012, 391, 4234–4251. [Google Scholar] [CrossRef]
- Greenwood-Nimmo, M.J.; Huang, J.; Shin, Y. Risk and return spillovers among the g10 currencies. J. Financ. Mark. 2016, 31, 43–62. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avdulaj, K.; Kristoufek, L. On Tail Dependence and Multifractality. Mathematics 2020, 8, 1767. https://doi.org/10.3390/math8101767
Avdulaj K, Kristoufek L. On Tail Dependence and Multifractality. Mathematics. 2020; 8(10):1767. https://doi.org/10.3390/math8101767
Chicago/Turabian StyleAvdulaj, Krenar, and Ladislav Kristoufek. 2020. "On Tail Dependence and Multifractality" Mathematics 8, no. 10: 1767. https://doi.org/10.3390/math8101767
APA StyleAvdulaj, K., & Kristoufek, L. (2020). On Tail Dependence and Multifractality. Mathematics, 8(10), 1767. https://doi.org/10.3390/math8101767





