Explicit Characterization of Feedback Nash Equilibria for Indefinite, Linear-Quadratic, Mean-Field-Type Stochastic Zero-Sum Differential Games with Jump-Diffusion Models
Abstract
1. Introduction
- (a)
- We extend [6] to the two-player game framework; unlike [6], our cost parameters do not need to be definite matrices. We provide explicit conditions under which the Nash equilibrium can be characterized. Moreover, we provide the numerical example and simulation results to support our theoretical results.
- (b)
- We generalize [14] to the case of jump-diffusion models, where, unlike [14], our paper considers the case of multi-dimensional Brownian motion and Poisson process. Furthermore, the results of this paper were applied to the modified mean-variance stochastic differential game, whereas [14] provided only the simple simulation results.
- (c)
- The problem formulation and the results of this paper are different from those of [11]. Note that [11] considered the LQ nonzero-sum differential game for mean-field-type jump-diffusion models. However, due to the nonzero-sum game structure, reference [11] cannot explain the interaction between two-players captured by a class of nonanticipative strategies and the ordered interchangeability property of multiple Nash equilibria in zero-sum games. Moreover, unlike [11], we consider the general vector-valued jump-diffusion model and the case when the cost parameters are indefinite matrices. In addition, [11] did not provide any theoretical results on the solvability of the Riccati equation, whereas our paper provides an easy-to-check condition of the solvability of the CIRDEs, which leads to the explicit characterization of the Nash equilibrium for the I-LQ-MF-SZSDG-JD. Finally, we provide the extensive simulation results of the modified mean-variance optimization problem, whereas [11] did not provide any simulation results.
2. Problem Formulation
- (i)
- An admissible nonanticipative strategy for Player 1, denoted by , is a mapping defined such that (equivalently, for ) and for any -stopping time and any , with on , it holds that on . The space of admissible nonanticipative strategies for Player 1 is defined by .
- (ii)
- An admissible nonanticipative strategy for Player 2, (equivalently, for ) is defined in a similar way. The space of admissible nonanticipative strategies for Player 2 is defined by .
- (i)
- The control-strategy pair constitutes the Nash equilibrium of the I-LQ-MF-SZSDG-JD if satisfies the following inequalities:The optimal game value of the I-LQ-MF-SZSDG-JD under is .
- (ii)
- The control-strategy pair constitutes the Nash equilibrium of the I-LQ-MF-SZSDG-JD if satisfies the following inequalities:The optimal game value of the I-LQ-MF-SZSDG-JD under is .
- (i)
- In view of Definition 2, if (see (4)) and (see (5)) are Nash equilibria for the I-LQ-MF-SZSDG-JD, then the pair also constitutes a Nash equilibrium of the I-LQ-MF-SZSDG-JD satisfying (3). This follows from the the ordered interchangeability property of multiple Nash equilibria (or saddle-points) in zero-sum games (see ([25], page 302) and ([26], Lemma 2.4)).
- (ii)
- In this case, the optimal game value is given by . This fact can be shown easily. In particular, suppose that and are Nash equilibria of the I-LQ-MF-SZSDG-JD. This implies that . Note also that by Definition 1, the admissible strategy is an -valued mapping for . Then from (4) and (5) it follows that and . This shows that .
3. Main Results
3.1. Coupled Integro-Riccati Differential Equations
- (i)
- Assume that and − are invertible for all . Then in (9) is invertible for all . Moreover, the CIRDE in (6) can be written as the CIRDE in (10).
- (ii)
- Assume that and are invertible for all . Then in (9) is invertible for all . Moreover, the CIRDE in (6) can be written as the CIRDE in (11).
- (i)
- Assume that and are invertible for all . Then in (9) is invertible for all . Moreover, the CIRDE in (7) can be written as the CIRDE in (12).
- (ii)
- Assume that and are invertible for all . Then in (9) is invertible for all . Moreover, the CIRDE in (7) can be written as the CIRDE in (13).
3.2. Characterization of Nash Equilibria
- (i)
- and are (uniformly) negative definite for all ;
- (ii)
- and are (uniformly) positive definite for all .
- (i)
- and are (uniformly) positive definite for all ;
- (ii)
- and are (uniformly) negative definite for all .
- (i)
- and are (uniformly) positive definite for all ;
- (ii)
- and are (uniformly) negative definite for all .
- (i)
- and are (uniformly) positive definite for all ;
- (ii)
- and are (uniformly) negative definite for all .
- (S.1)
- Given the parameters of the MF-SDE with jump diffusions in (1) and the objective functional in (2), check the solvability (existence and uniqueness of the solutions) of the CIRDEs in (6) and (7);
- (S.2)
- If the conditions of (i) and (ii) in Corollary 1 hold, then obtain the Nash equilibrium in given in (18) and (29) by using the parameters in (S.1).
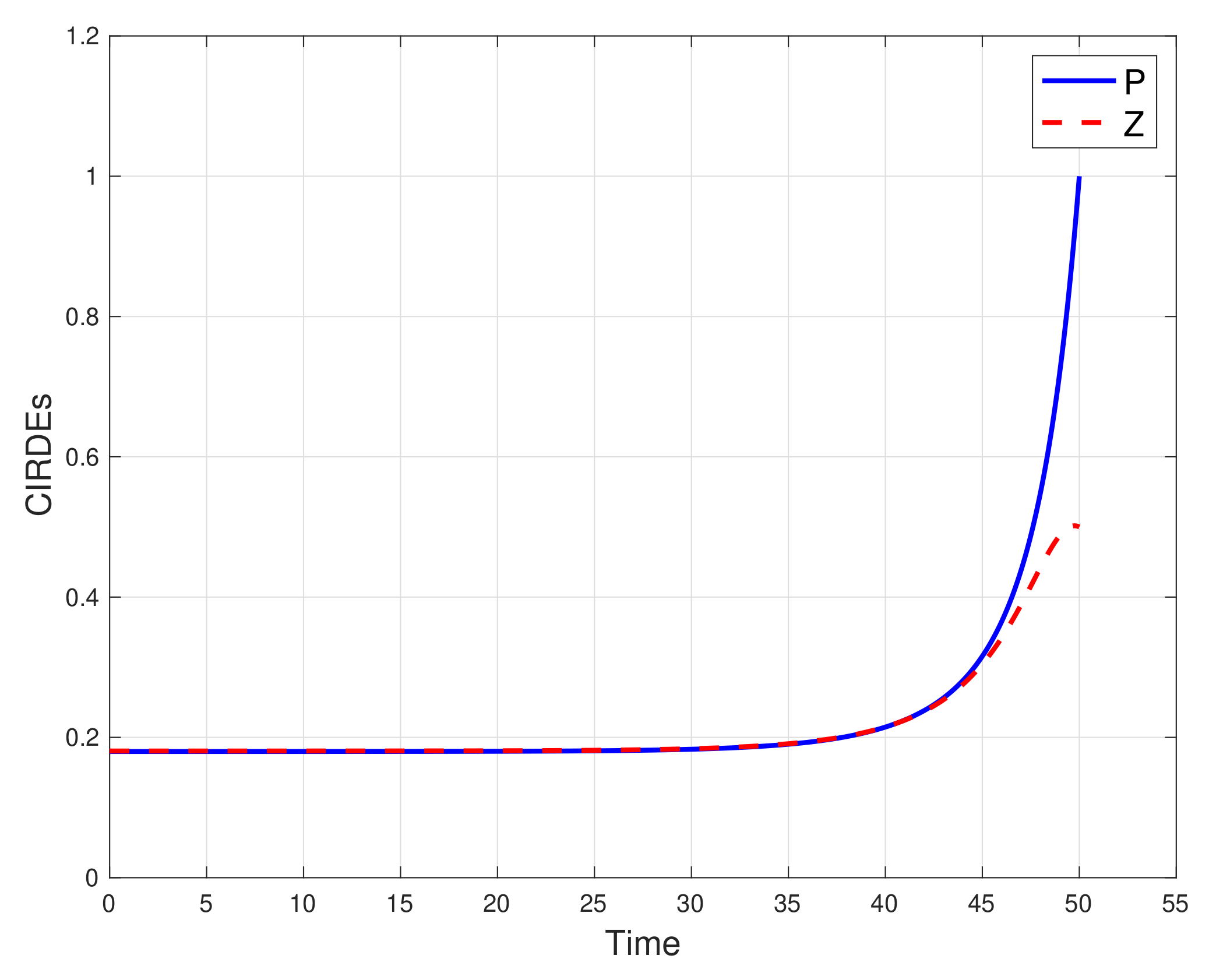
4. Coupled Integro-Riccati Differential Equations: Solvability
- (i)
- Suppose that for and . Let be an symmetric positive definite matrix, and . Assume that there exist and such that and . LetwhereIf (equivalently, is uniformly negative definite for all ), then there exists a unique symmetric bounded solution of the CIRDE in (6) on .
- (ii)
- Suppose that for and . Assume that the IRDE in (6) admits a unique symmetric bounded solution on such that is invertible for all . Let be an symmetric positive definite matrix, and . Assume that there exist and such that and . LetwhereIf (equivalently, is uniformly negative definite for all ), then there exists a unique symmetric bounded solution of the CIRDE in (7) on .
- (i)
- Note that in Theorem 3, and , , are design parameters, which have to be selected to satisfy the conditions of Theorem 3. In particular, we can easily see that Δ is linear in and , and is linear in and . This implies that and in Theorem 3 can be viewed as LMIs. Hence, the conditions in Theorem 3 become equivalent to identifying the feasibility condition of LMIs via various semidefinite programming algorithms [33].
- (ii)
- If the assumptions of Theorem 3 and Corollary 1 hold, then the control-control pair given in (18) and (29) constitutes the Nash equilibrium of the I-LQ-MF-SZSDG-JD in the sense of (3).
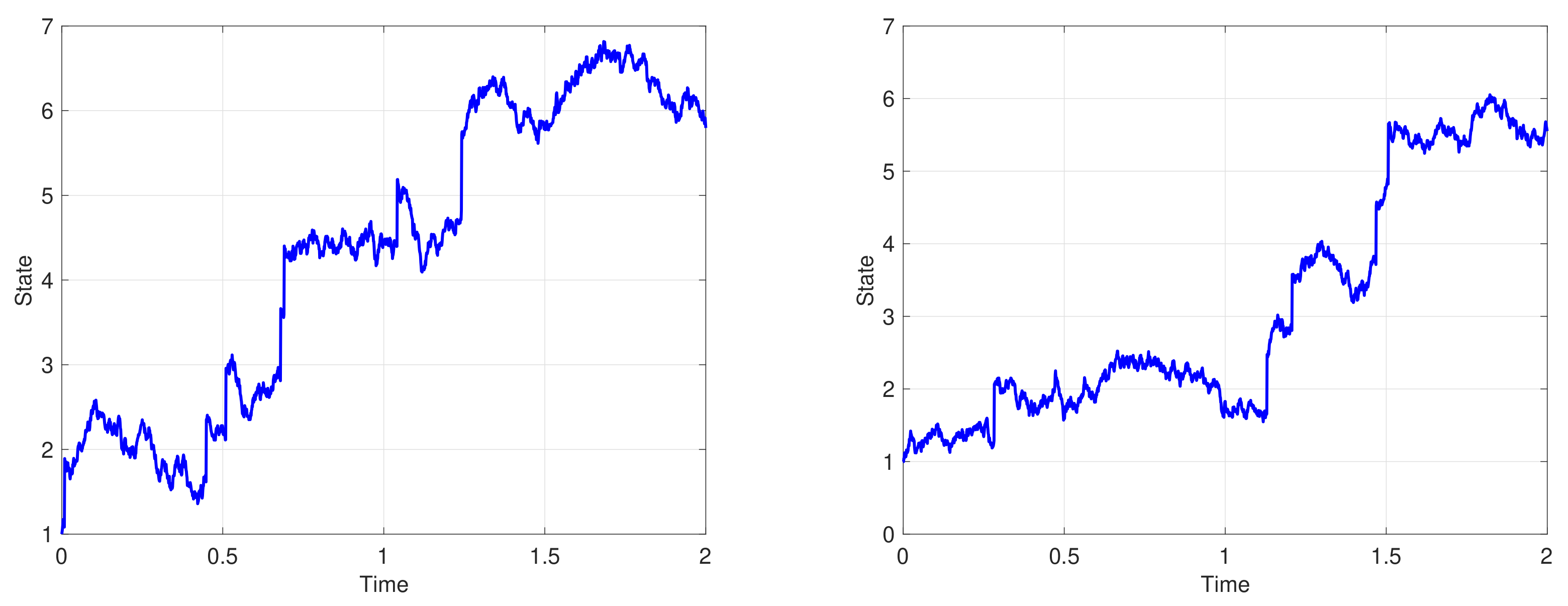
5. Application: Mean-Field-Type Stochastic Mean-Variance Differential Game
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kac, M. Foundation of Kinetic Theory. In Proceedings of the 3rd Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 1 January 1956; Volume 3, pp. 171–197. [Google Scholar]
- McKean, H.P. A class of Markov processes associated with nonlinear parabolic equations. Proc. Natl. Acad. Sci. USA 1966, 56, 1907–1911. [Google Scholar] [CrossRef] [PubMed]
- Chan, T. Dynamics of the McKean-Vlasov equation. Ann. Probab. 1994, 22, 431–441. [Google Scholar] [CrossRef]
- Dawson, D.A. Critical dynamics and fluctuations for a mean-field model of cooperative behavior. J. Stat. Phys. 1983, 31, 29–85. [Google Scholar] [CrossRef]
- Graham, G. McKean-Vlasov Ito-Skorohod Equations, and nonlinear diffusions with discrete jump sets. Stoch. Process. Appl. 1992, 40, 69–82. [Google Scholar] [CrossRef]
- Yong, J. Linear-Quadratic Optimal Control Problems for Mean-Field Stochastic Differential Equations. SIAM J. Control Optim. 2013, 51, 2809–2838. [Google Scholar] [CrossRef]
- Shen, Y.; Siu, T.K. The Maximum Principle for a Jump-Diffusion Mean-Field Model and Its Application to the Mean-Variance Problem. Nonlinear Anal. 2013, 86, 58–73. [Google Scholar] [CrossRef]
- Shen, Y.; Meng, Q.; Shi, P. Maximum Principle for Mean-Field Jump-Diffusion Stochastic Delay Differential Equations and Its Application to Finance. Automatica 2014, 50, 1565–1579. [Google Scholar] [CrossRef]
- Meng, Q.; Shen, Y. Optimal Control of Mean-Field Jump-Diffusion Systems with Delay: A Stochastic Maximum Principle Approach. J. Comput. Appl. Math. 2015, 279, 13–30. [Google Scholar] [CrossRef]
- Tang, M.; Meng, Q. Linear-Quadratic Optimal Control Problems for Mean-Field Type Stochastic Differential Equations with Jumps. Asian J. Control 2019, 21, 809–823. [Google Scholar] [CrossRef]
- Barreiro-Gomez, J.; Duncan, T.E.; Tembine, H. Linear-Quadratic Mean-Field-Type Games: Jump-Diffusion Process With Regime Switching. IEEE Trans. Autom. Control 2019, 64, 4329–4336. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Z.; Xiong, J. A General Stochastic Maximum Principle for a Markov Regime Switching Jump-Diffusion Model of Mean-Field Type. SIAM J. Control Optim. 2018, 56, 2563–2592. [Google Scholar] [CrossRef]
- Benssousan, A.; Djehiche, B.; Tembine, H.; Yam, S.C.P. Mean-Field-Type Games with Jump and Regime Switching. Dyn. Games Appl. 2020, 10, 19–57. [Google Scholar] [CrossRef]
- Moon, J. Linear-quadratic mean field stochastic zero-sum differential games. Automatica 2020, 120. [Google Scholar] [CrossRef]
- Djehiche, B.; Tembine, H.; Tempone, R. A Stochastic Maximum Principle for Risk-Sensitive Mean-Field Type Control. IEEE Trans. Autom. Control 2015, 60, 2640–2649. [Google Scholar] [CrossRef]
- Lasry, J.M.; Lions, P.L. Mean Field Games. Jap. J. Math. 2007, 2, 229–260. [Google Scholar] [CrossRef]
- Tembine, H.; Zhu, Q.; Başar, T. Risk-sensitive Mean Field Games. IEEE Trans. Autom. Control 2014, 59, 835–850. [Google Scholar] [CrossRef]
- Moon, J.; Başar, T. Linear Quadratic Risk-sensitive and Robust Mean Field Games. IEEE Trans. Autom. Control 2017, 62, 1062–1077. [Google Scholar] [CrossRef]
- Duncan, T.E.; Tembine, H. Linear-Quadratic Mean-Field-Type Games: A Direct Method. Games 2018, 9, 7. [Google Scholar] [CrossRef]
- Applebaum, D. Lévy Processes and Stochastic Calculus, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Oksendal, B.; Sulem, A. Applied Stochastic Control of Jump Diffusions, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Buckdahn, R.; Li, J. Stochastic Differential Games and Viscosity Solutions of Hamilton-Jabobi-Bellman-Isaacs Equations. SIAM J. Control Optim. 2008, 47, 444–475. [Google Scholar] [CrossRef]
- Yu, Z. An Optimal Feedback Control-Strategy Pair For Zero-Sum Linear-Quadratic Stochastic Differential Game: The Riccati Equation Approach. SIAM J. Control Optim. 2015, 53, 2141–2167. [Google Scholar] [CrossRef]
- Fleming, W.H.; Souganidis, P.E. On the Existence of Value Functions of Two-Player Zero-Sum Stochastic Differential Game. Indiana Univ. Math. J. 1989, 38, 293–314. [Google Scholar] [CrossRef]
- Başar, T.; Olsder, G.J. Dynamic Noncooperative Game Theory, 2nd ed.; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]
- Buckdahn, R.; Cardaliaguet, P.; Rainer, C. Nash Equilibrium Payoffs for Nonzero-Sum Stochastic Differential Games. SIAM J. Control Optim. 2004, 43, 624–642. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Başar, T.; Bernhard, P. H∞ Optimal Control and Related Minimax Design Problems, 2nd ed.; Birkhäuser: Boston, MA, USA, 1995. [Google Scholar]
- Moon, J.; Kim, Y. Linear Exponential Quadratic Control for Mean Field Stochastic Systems. IEEE Trans. Autom. Control 2019, 64, 5094–5100. [Google Scholar] [CrossRef]
- Zhang, F.; Dong, Y.; Meng, Q. Backward Stochastic Riccati Equation with Jumps Associated with Stochastic Linear Quadratic Optimal Control with Jumps and Random Coefficients. SIAM J. Control Optim. 2020, 58, 393–424. [Google Scholar] [CrossRef]
- Abou-Kandil, H.; Freiling, G.; Ionescu, V.; Jank, G. Matrix Riccati Equations in Control and Systems Theory; Springer: Basel, Switzerland, 2003. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Boyd, S.; Ghaoui, E.; Feron, E.; Balakrishnan, B. Linear Matrix Inequalities in Systems and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Shreve, S. Stochastic Calculus for Finance II: Continuous-Time Models; Springer: New York, NY, USA, 2004. [Google Scholar]
- Touzi, N. Optimal Stochastic Control, Stochastic Target Problems, and Backward SDE; Springer: New York, NY, USA, 2013. [Google Scholar]
- Zhou, X.Y.; Li, D. Continuous-Time Mean-Variance Portfolio Selection: A Stochastic LQ Framework. Appl. Math. Optim. 2000, 42, 19–33. [Google Scholar] [CrossRef]
- Kahaner, D.; Moler, C.; Nash, S. Numerical Methods and Software; Prentice Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Hanson, F.B. Applied Stochastic Processes and Control for Jump-Diffusions; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, J.; Kim, W. Explicit Characterization of Feedback Nash Equilibria for Indefinite, Linear-Quadratic, Mean-Field-Type Stochastic Zero-Sum Differential Games with Jump-Diffusion Models. Mathematics 2020, 8, 1669. https://doi.org/10.3390/math8101669
Moon J, Kim W. Explicit Characterization of Feedback Nash Equilibria for Indefinite, Linear-Quadratic, Mean-Field-Type Stochastic Zero-Sum Differential Games with Jump-Diffusion Models. Mathematics. 2020; 8(10):1669. https://doi.org/10.3390/math8101669
Chicago/Turabian StyleMoon, Jun, and Wonhee Kim. 2020. "Explicit Characterization of Feedback Nash Equilibria for Indefinite, Linear-Quadratic, Mean-Field-Type Stochastic Zero-Sum Differential Games with Jump-Diffusion Models" Mathematics 8, no. 10: 1669. https://doi.org/10.3390/math8101669
APA StyleMoon, J., & Kim, W. (2020). Explicit Characterization of Feedback Nash Equilibria for Indefinite, Linear-Quadratic, Mean-Field-Type Stochastic Zero-Sum Differential Games with Jump-Diffusion Models. Mathematics, 8(10), 1669. https://doi.org/10.3390/math8101669





