Chaos Control and Anti-Control of the Heterogeneous Cournot Oligopoly Model

Abstract

The main aim of this paper focuses on chaos suppression (control) and stimulation (anti-control) of a heterogeneous Cournot oligopoly model. This goal is reached by applying the theory of dynamical systems, namely impulsive control. The main aim was to demonstrate, through massive numerical simulations and estimation of the maximal Lyapunov exponent, the 0-1test for chaos, and bifurcation analysis, that it is possible to control the dynamical behavior of the investigated model by finding injection values under which the desired phenomena are attained. Moreover, it was shown that there are injection values for which the injected system admits a self-excited cycle or chaotic trajectory.

1. Introduction

Not only chaosbut also other types of movement patterns (like period and quasiperiod) that come from experimental data and those generated by simulations of a given model reflect phenomena in mathematics and the sciences (including economics) (for motivation, see, e.g., Reference [1,2]).

Since it seems that chaos is something undesirable, one can try to avoid or prevent it [3]. Conversely, there are numerous situations where having random-looking and irregular patterns is in fact desirable, e.g., the record of EEG. So, it depends on the specific situation whether chaos is desirable or undesirable.

Therefore, many scientists have applied chaos control theory in the hope of achieving suppression (called chaos control) and stimulation (chaos anti-control) for improvement of performance and preservation of stability, which would lead to improved economic efficiency of market models.

Economic dynamics has not been investigated for a long time because of the high mathematical computational requirements. With the recent development of computers, especially ready-made software packages, and the development of mathematical theory, economists can now fairly easily handle complex dynamical systems [4].

For investigative purposes, new methods for controlling the dynamical properties of the impulsive method of dynamical systems theory are used. This changes the systems variable in the form of instantaneous pulses periodically occurring [5,6].

The focus of this paper is on chaos control and anti-control of the heterogeneous Cournot oligopoly model introduced in Reference [7] by investigation of impulsive control (the theory of imperfect competition à la Cournot has been deeply researched for more than the past century (see, e.g., Reference [8,9,10,11]), and influence of demand type functions have been considered: linear in Reference [12], piecewise linear in Reference [11], for duopoly, iso-elastic in Reference [13], for triopoly and other, more sophisticated, types in Reference [14,15]). For this purpose, the impulsed dynamical system is introduced. For chaos and regularity determination, the 0-1 test for chaos, the maximal Lyapunov exponent, and the Power Spectrum Density (PSD) [16] are used, supported by time histories of trajectories, bifurcation diagrams, and basins of attractions.

Using the after-going technique in Equation (2) and application of the previously mentioned methods, it will be shown that there are impulse values for which the impulsed system Equation (11) admits a self-excited cycle or chaotic trajectory (Property 1 and 2). This demonstrates the effectivity of the selected method of chaos suppression and stimulation with its practical importance.

The paper starts with an introduction to the topic in Section 1, followed by the impulsive control system declaration in Section 2, and continuing with the main results in Section 3 and Section 4, where firstly chaos control is researched and secondly chaos anti-control is observed. In the following Section 5, the results of the previous two sections are compared. Next, in Section 6, some alternative approaches to the investigation of impulse control are given to show different possibilities of chaos control and anti-control of the researched system. The paper closes with concluding notes in the last part, Section 7.

2. The Impulsive Control System

Let $(X,F)$ be a discrete dynamical system; usually X is assumed to be a compact metric space and $F:X\to X$ continuous onto (not necessarily into) map. Without loss of generality, we can assume that the dimension of X equals k and the dynamics of $(X,F)$ is given by the difference equation

$$x^{n+1}=F\left(x^n\right),$$

(1)

with $x^n\in X$ for any $n\in \mathbb{N}$, and the underlying initial condition $x\left(1\right)=x^1$.

Following the ideas of Reference [17] (see also references therein), the next impulsive difference equation can be defined for dynamics control of the original difference Equation (1):

$$x^{n+1}=\left\{\begin{array}{cc}F\left(x^n\right)\hfill & \mathrm{if}n\in \mathbb{N}\setminus {\left\{n_i\right\}}_{i\in \mathbb{N}},\hfill \\ x^n+\delta \hfill & \mathrm{if}n=n_i\hfill \end{array}\right.,$$

(2)

where $\left\{n_i\right\}\in \mathbb{N}$ and $n_i=i\Delta =\Delta ,2\Delta ,3\Delta ,\dots$ is an increasing sequence of natural numbers, $\Delta \in \mathbb{N}$ is the step size, and $\delta \in \mathbb{R}$ is the constant injection quantity applied at every $n_i$ step. Note that the above (impulse) difference equation is introduced in a “symmetric” way, meaning that the same valued injection $\delta$ is applied at every $n_i$ step to every variable.

Hence, the impulsed dynamical system can be classified using

$$F\left(x\right)=f^{\Delta }\left(x\right)+y,$$

(3)

since

$$x^n=f^{n-1-\lfloor \frac{n-1}{\Delta }\rfloor \Delta }\left(F^{\lfloor \frac{n-1}{\Delta }\rfloor }\left(x^1\right)\right),n\in \mathbb{N},$$

(4)

where $\lfloor ·\rfloor$ is the floor function, and $f^{\Delta }$ stands for $\Delta$-th iteration of f, that is

$$f^{\Delta }=\underset{\Delta -\mathrm{times}}{\underbrace{f\circ \cdots \circ f.}}.$$

(5)

Using Equation (4), one can easily derive

$$x^{i\Delta +1}=F^i\left(x^1\right),i\in \mathbb{N},$$

(6)

from which it follows that any p-cycle of F generates a $\Delta p$-cycle of Equation (2).

Now, consider the heterogeneous Cournot oligopoly model (HCOM) introduced in Reference [7] (also see Reference [18]), where it is considered a set of identical quantity setting agents $\mathcal{N}=\{1,2,\dots ,N\}$ that compete in the same market for a homogeneous good, in which demand is summarized by a linear inverse-demand function $P\left(Q\right)=max\{a-bQ,0\}$, a and b being its scalar parameters. Let us denote by $q_i^n$ the quantity of goods that is a generic i-th agent, with $i\in \mathcal{N},$ selling in the market at time-period n. All the agents bear the same constant marginal production cost c, so that the generic i-th agent earns the profit

$$\begin{array}{c}\hfill {\pi }_i=P\left(Q\right)q_i-c{q}_i.\end{array}$$

(7)

The oligopoly, in this case, is characterized by introducing heterogeneous decision mechanisms, used to decide what quantity of goods to produce by considering a population structured into two groups of agents of different kinds. The first group, denoted by $q_1$, includes boundedly rational players that use the gradient rule first proposed in Reference [19] and are hence called the gradient players group; $q_2$ includes agents that adopt an imitation-based decision mechanism and are called imitator players.

The collective behavior of the whole heterogeneous population of N players is described by the following 2-dimensional non-linear discrete dynamical system:

$$\mathrm{HCOM}:\left\{\begin{array}{ccc}{q}_1^{n+1}& =& q_1^n+\gamma q_1^n(a-b((N(1-\omega )+1)q_1^n+\omega N{q}_2^n)-c),\hfill \\ q_2^{n+1}& =& {\displaystyle \frac{{\pi }_2^n}{{\pi }_2^n+{\pi }_1^n}{q}_2^n+\frac{{\pi }_1^n}{{\pi }_2^n+{\pi }_1^n}{q}_1^n,}\hfill \end{array}\right.$$

(8)

where

$$\begin{array}{ccc}\hfill {\pi }_1^n& =& (a-c-bN((1-\omega )q_1^n+\omega q_2^n))q_1^n,\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\pi }_2^n& =& (a-c-bN((1-\omega )q_1^n+\omega q_2^n))q_2^n.\hfill \end{array}$$

(10)

The system Equation (8) has two stationary states. The first one (non-zero if $a\ne c$) takes the form $E_N=(q_N,q_N)$, where

$$q_N=\frac{a-c}{b(N+1)},$$

and the second one is located on the positive part of the horizontal axis, that is, $\mathcal{L}=(0,y)$, where $y>0$. Their stability is:

Proposition 1

(Reference [7]).

(i) 

The equilibrium $(q_N,q_N)$ is locally asymptotically stable if

$$\omega \in ({\omega }_f,{\omega }_{ns}),$$

where

$${\omega }_f=\frac{3}{2}\frac{N+1}{N}\left(\frac{1}{2}-\frac{1}{\gamma (a-c)}\right)$$

and

$${\omega }_{ns}=\frac{1}{2}\frac{N+1}{N}\left(\frac{1}{\gamma (a-c)}+1\right).$$

(ii) 

The equilibrium $\mathcal{L}=(0,y)$ is (hyperbolic) stable if

$$y>\frac{a-c}{b\omega N}.$$

Deep analysis of the dynamic properties of the HCOM Equation (8) model was performed in Reference [20] through the investigation of hidden-attractors and multistability.

Finally, by applying impulsive control Equation (2), HCOM Equation (8) becomes an injected heterogeneous Cournot oligopoly model (IHCOM):

$$\mathrm{IHCOM}:(q_1^{n+1},q_2^{n+1})=\left\{\begin{array}{ccc}& & F(q_1^n,q_2^n),ifn\in \mathbb{N}\setminus {\left\{n_i\right\}}_{i\in \mathbb{N}},\hfill \\ & & F(q_1^n,q_2^n)+(\delta ,\delta ),ifn=n_i,\hfill \end{array}\right.$$

(11)

with

$$\begin{array}{c}\hfill F(q_1^n,q_2^n)=(F_1(q_1^n,q_2^n),F_2(q_1^n,q_2^n)),\end{array}$$

(12)

where

$$\begin{array}{ccc}\hfill F_1(q_1^n,q_2^n)& =& q_1^n+\gamma q_1^n(a-b((N(1-\omega )+1)q_1^n+\omega N{q}_2^n)-c),\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill F_2(q_1^n,q_2^n)& =& {\displaystyle \frac{{\left(q_1^n\right)}^2+{\left(q_2^n\right)}^2}{q_1^n+q_2^n}.}\hfill \end{array}$$

(14)

In the following, all simulations were performed with the initial condition located close to the $E_N$ stationary point: $(q^1\left(1\right),q^2\left(1\right))=(q_N+0.25,q_N)=(1.75,1.5)$, and trajectories up to $3\times {10}^3$ were evaluated (K, L, bifurcation diagrams, and PSD), while 20% were skipped to omit the system’s distortions.

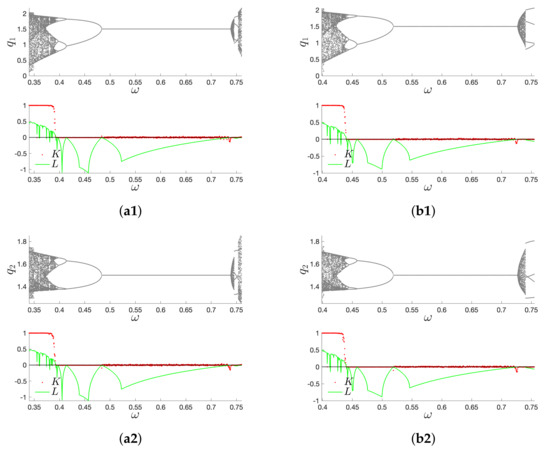
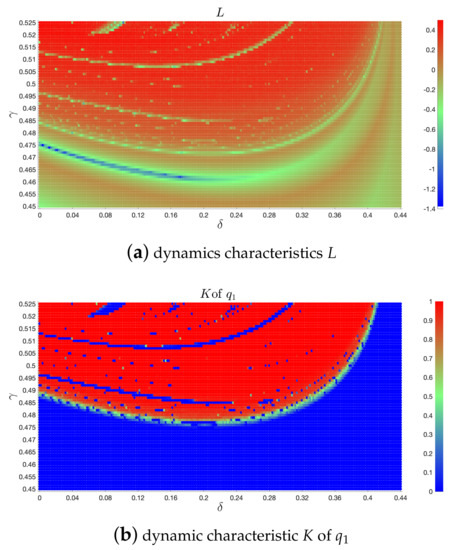
For the further investigation, the system’s IHCOM Equation (11) parameters were set as in Reference [7], summarized in Table 1. The parameter $\gamma$ varies from $0.35$ to $0.525$ to show the original system’s HCOM dynamics. Bifurcations with outputs of the 0-1 test for chaos K (see Reference [21,22,23,24,25]) and maximal Lyapunov exponent L, are given in Figure 1. Hereafter, for the sake of simplicity, we analyze only the first variable $q_1$ since variables $q_1$ and $q_2$ are joined together by the way they are defined. If $\omega$ is a variable parameter, one can easily compare K, L, and bifurcation diagrams of $q_1$ and $q_2$ varying $\omega$ for ${\gamma }_0=0.48$ (Figure 2a) and ${\gamma }_0=0.5244$ (Figure 2b). Their dynamics are identical on $q_1$ and $q_2$ (Figure 2a1 with Figure 2a2 and Figure 2b1 with Figure 2b2, respectively) for both parameters of ${\gamma }_{0,1}$. It is worth noting that $\omega \in [0,1]$, while the results in Figure 2 concentrate on the interval $(0.34,0.76)$ or $(0.399,0.755)$ for ${\gamma }_0=0.48$ or ${\gamma }_1=0.5224$, respectively, since the complement cases are those for which the system HCOM Equation (8) diverges. Consequently, two values, ${\gamma }_0=0.48$ and ${\gamma }_1=0.5224$, are pointed out. HCOM admits a periodic structure for ${\gamma }_0$ and chaos for ${\gamma }_1$ for the parameters given in Table 1. These two values are picked as starting to control and anti-control the chaos (Section 3 and Section 4).

Table 1. Parameters of HCOM Equation (2) and injected HCOM (IHCOM) Equation (11).

a	b	c	N	$\mathit{\omega }$
10	1	1	5	0.4

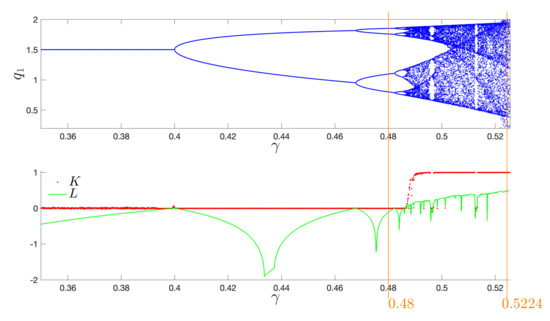
Figure 1. Heterogeneous Cournot oligopoly model (HCOM) Equation (8) system’s (upper) BD${}_{\gamma }$ and (lower) K, L for $q_1$ variable.

Figure 2. HCOM Equation (8) system’s BD${}_{\omega }$, K, and L of $q_1$ (a1,b1) and $q_2$ (a2,b2), for ${\gamma }_0=0.48$ (a1,a2), and ${\gamma }_1=0.5244$ (b1,b2).

3. Chaos Control

In this section, the impulsed system IHCOM Equation (11) is investigated for $\Delta =1$ (i.e., $n_i=i$ for $i=1,2,3,\dots$, that is, the impulse $\delta$ is applied at each step) and $\gamma =0.5244$ corresponding to chaotic behavior (Figure 1) of the original HCOM Equation (8). Hence, the task is to suppress chaotic behaviour of the original HCOM Equation (8) model.

The exploration was done using a bifurcation diagram of the variable $q_1$ versus the impulse $\delta$ (for brevity, DB${}_{\alpha }$ stands for bifurcation diagram varying $\alpha$). The bifurcation analysis is supported by outputs of K and L, computed by the algorithm introduced in Reference [26]. The 0-1 test for chaos, initially designed for testing for the existence of chaos, and later for identifying strange non-chaotic attractors (see, e.g., Reference [17]), returns binary output: values close to 0 which indicate regularity, and values close to 1 which indicate the presence of chaos. This test is applicable to continuous [27] and also to discrete dynamical systems [28], as well as to real data [29].

As Figure 3 reveals, there exist periodic windows among chaotic windows, indicating the possibility to choose impulses $\delta$ for which the IHCOM Equation (11) evolves along some stable cycle. That is visible from bifurcation diagram in Figure 3a-upper and its magnified part in Figure 3d.

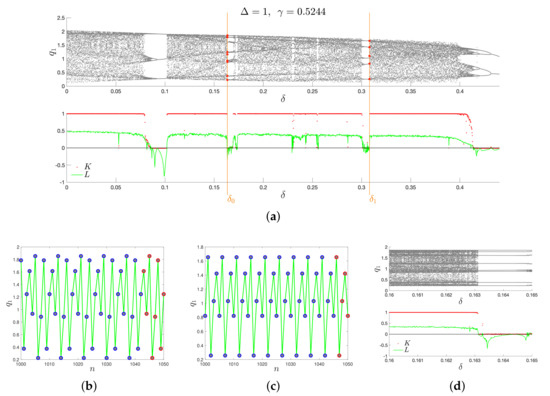
Figure 3. Investigated IHCOM Equation (11) with $\Delta =1$ and $\gamma =0.5244$: (a-upper) BD${}_{\delta }$, (a-lower) chaos characteristics K and L for $q_1$ variable, (b) time history for ${\delta }_0=0.1634$ (8 stable cycle highlighted by the red mark), (c) time history for ${\delta }_1=0.308$ (5 stable cycle highlighted by the red mark), and (d) is magnified part of (a).

In particular, the two parameters ${\delta }_0=0.1634$ and ${\delta }_1=0.308$ are highlighted. In both cases, they correspond to stable cycles ${\delta }_0$, which generates a period–8 stable cycle (highlighted by the red mark), and ${\delta }_1$, which generates a 5–period stable cycle (highlighted by the red mark).

Property 1.

For IHCOM Equation (8) with $\Delta =1$ and $\gamma =0.5244$:

(i)

there is at least one $\delta \in [0,0.442]$ such that IHCOM Equation (11) admits a self-excited cycle,

(ii)

there is at least one $\delta \in [0,0.442]$ such that IHCOM Equation (11) admits chaotic trajectories.

The proof of Property 1 is given by computer graphics analysis studying the basin of attractions and behavior of trajectories of perturbed equilibria as the initial point. Dynamics quantifiers, such as the 0-1 test for chaos, and maximal Lyapunov exponent were applied; see Figure 3a-lower.

The motion of both variables $q_1$ and $q_2$ allows the observation of the full variety of the dynamics character. That is, for a suitable value of $\delta$, one can observe period in Figure 4a1–a3, chaos in Figure 4c1–c3, and also quasiperiod in Figure 4b1–b3. Time histories (Figure 4a1,b1,c1) and PSD (Figure 4a2,b2,c2) are shown together with aggregated density plots for all three cases with a congruent color scheme. The quasiperiodic pattern is clearly visible in Figure 4d, where the numerous full portions (blue marks) indicate that the entire orbit closes and does not repeats itself. The quasiperiodicity is also revealed by the PSD in Figure 4b2, which clearly shows that the periodic orbit in Figure 4a1 presents the first fundamental frequency ${\alpha }_0$ and the harmonic ${\alpha }_1={\alpha }_0+{\beta }_0$. For Figure 4b2, as a consequence of Neimark-Sacker bifurcation, which generally generates quasiperiodicity, a new set of subharmonics are created, e.g., ${\alpha }_{01}$, close to the first frequencies ${\alpha }_0$ and ${\alpha }_1$, at small distance ${\beta }_{01}$.

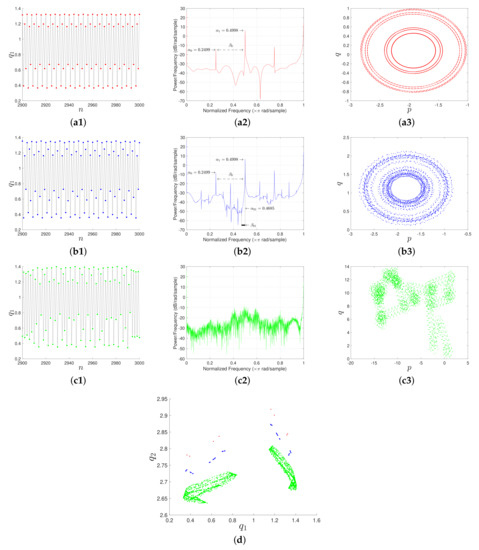
Figure 4. IHCOM Equation (11) with $\Delta =1$: time histories ((a1),(b1),(c1)), PSD ((a2),(b2),(c2)), and translation variables plot in $p-q$ plane ((a3),(b3),(c3)) for periodic (a), quasiperiodic (b), chaotic (c) movement for parameters $\delta$ given in Table 2; (d) aggregated density plots for all three cases with color inherited.

Finally, Figure 4a3,b3,c3 show boundedness or unboundedness of translation variables in the $p-q$ plane of the 0-1 test for chaos, detecting the regularity or irregularity, respectively, of the movement character. Outputs of Figure 4, together with parameters, are aggregated in Table 2.

Table 2. Summarized parameters and outputs of Figure 4.

Movement Type	$\mathit{\delta }$	K	L	Figure 4	Color Marker
periodic	0.426	−0.0025	−0.00625	(a1)–(a2)	red
quasiperiodic	0.4134151	0.0086	0.0034	(b1)–(b2)	blue
chaotic	0.4034	0.9905	0.1478	(c1)–(c2)	green

4. Chaos Anti-Control

Consider the IHCOM Equation (11) for $\Delta =1$ and $\gamma =0.48$. Here, this choice of $\gamma$ corresponds to the periodic behavior of the original HCOM Equation (8) (see Figure 1), and the task is to stimulate chaos in the original HCOM Equation (8).

As in Section 4, bifurcation diagrams together with the 0-1 test for chaos K and L show rich dynamics, see Figure 5a-upper,a-lower,d. The values ${\delta }_2=0.0922$ and ${\delta }_3=0.3078$ were picked to show the non-trivial 12 and 16 stable-cycles, respectively, in Figure 5b,c (highlighted by red marks).

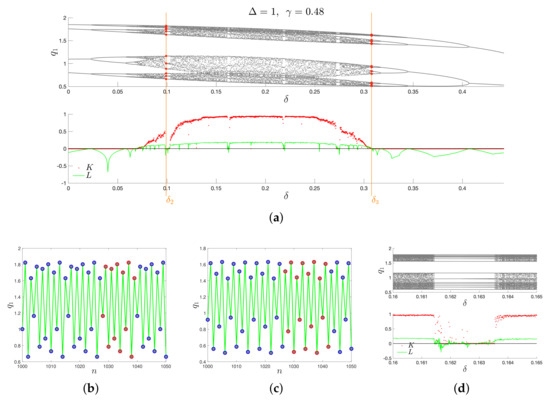
Figure 5. Investigated IHCOM Equation (11), with $\Delta =1$ and $\gamma =0.48$, (a-upper) BD${}_{\delta }$, (a-lower) chaos characteristics K and L for $q_1$ variable, (b) time history for ${\delta }_2=0.0992$ (12 stable cycle highlighted by the red mark), (c) time history for ${\delta }_3=0.3078$ (16 stable cycle highlighted by the red mark), and (d) is magnified part of (a).

Property 2.

For IHCOM Equation (11) with $\Delta =1$ and $\gamma =0.48$:

(i)

there is at least one $\delta \in [0,0.442]$ such that IHCOM Equation (11) admits a self-excited cycle,

(ii)

there is at least one $\delta \in [0,0.442]$ such that IHCOM Equation (11) admits chaotic trajectories.

The proof of Property 2 can be done in an analogous way to the proof of Property 1 using Figure 5.

5. Chaos Control Versus Anti-Control

To see the change of basin of attraction under the influence of the injected value see Figure 6, where the upper part corresponds to the anti-control ($\gamma =0.48$, Section 4) and the lower case to the chaos control ($\gamma =0.5224$, Section 3). The equilibria of both, HCOM and IHCOM Equation (11), are drawn in green circles and a cyan box, respectively. The non-trivial (non-zero) equilibrium $(q_{IN},q_{IN})$ of IHCOM Equation (11) can be computed by direct calculation, where

$$q_{IN}={\displaystyle \frac{a-c+{((\gamma a^2-2\gamma ac+\gamma c^2+4b\delta +4Nb\delta )/\gamma )}^{1/2})}{2b(1+N)}}.$$

(15)

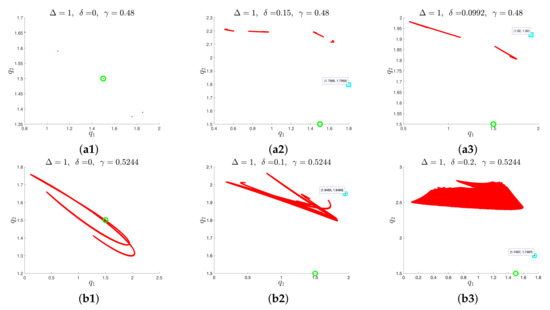
Figure 6. Density plots of IHCOM Equation (11): ((a1)–(a3)) for $\gamma =0.48$ and ((b1)–(b3)) for $\gamma =0.5244$; here, the green circle stands for $(q_N,q_N)$ equilibrium of HCOM, and the cyan box for $(q_{IN},q_{IN})$ equilibrium of IHCOM.

Figure 7 shows the IHCOM Equation (11) system complexity in the parameters plane $\delta \times \gamma =[0,0.44]\times [0.45,0.525]$.

Figure 7. Dynamics detection of IHCOM Equation (11) on $\delta \times \gamma$ with $\Delta =1$: (a) L and (b) K of $q_1$.

6. Alternative Impulse Control Approach

Furthermore, it is possible to control dynamical behavior even if the impulses are applied rarely, e.g., every $\Delta =2$ steps, as shown in Figure 8.

Figure 8. $B{D}_{\delta }$ of IHCOM Equation (11) (upper) and K, L (lower) with $\Delta =2$ and (a) $\gamma =0.5244$: (b) $\gamma =0.48$.

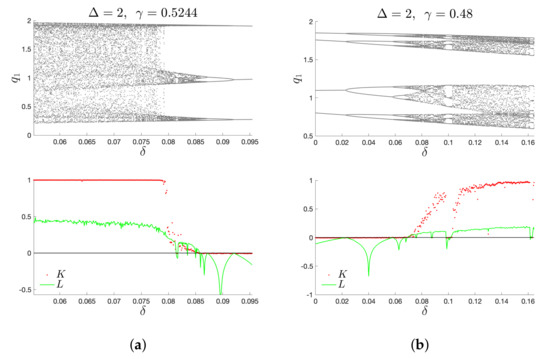
In addition, the IHCOM Equation (11) can be designed as follows:

$$\begin{array}{ccc}\hfill F(q_1^n,q_2^n)+(\delta ,0),& & ifn=n_i,\hfill \end{array}$$

(16)

i.e., only the first variable is impulsed. Note that, for $\gamma =0.5244$ and $\delta >0.014$, the system diverges and chaos is not possible to control; see Figure 9a. And, if $\gamma =0.48$, chaos anti-control is possible if $0<\delta <0.394$; for $\delta \ge 0.394$, the system diverges, see Figure 10a. Modifying the IHCOM Equation (11) by injection only on the second variable:

$$\begin{array}{ccc}\hfill F(q_1^n,q_2^n)+(0,\delta ),& & ifn=n_i,\hfill \end{array}$$

(17)

one can obtain analogous results. In this case, for $\gamma =0.5244$, chaos is possible to control (see Figure 9b), but, for $\gamma =0.48$, anti-control of chaos is not possible (see Figure 10b). This demonstrates the importance of the choice of which variable injection is applied.

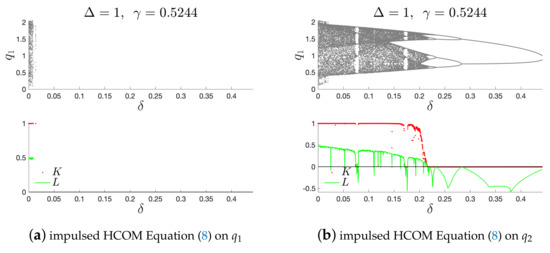
Figure 9. Impulsed HCOM Equation (2) system on $q_1$ (a) and $q_2$ (b): $B{D}_{\delta }$ with $\Delta =1$ and $\gamma =0.5244$.

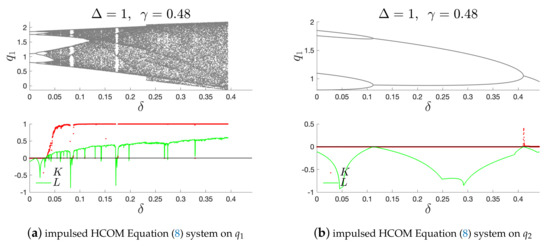
Figure 10. Impulsed HCOM Equation (2) system on $q_1$ (a) and $q_2$ (b): BD${}_{\delta }$ with $\Delta =1$ and $\gamma =0.48$.

7. Conclusions

In this paper, the main focus was on dynamics investigation of a newly introduced injected two-dimensional discrete dynamical system.

Firstly, the original model HCOM Equation (8) is recalled (in Section 2) with a set of the driving parameters (in Table 1), where the system parameter $\gamma$ is used and is crucial for further investigation. For the following research, two of the values were picked (${\gamma }_0=0.48$ and ${\gamma }_1=0.5224$) using bifurcation analysis in Figure 1. The first one, ${\gamma }_0$, corresponds to the regular, and the second one, ${\gamma }_1$, to the chaotic case.

Secondly, the original model is researched under the influence of injection of some additions at every iteration step. Hence, the IHCOM Equation (11) is introduced, and its rich dynamics are extensively studied for two cases through massive numerical simulations:

(i)

in Section 3, for $\gamma =0.5224$ to control chaos, with the main results given in Property 1 and Figure 3,

(ii)

in Section 4, for $\gamma =0.48$ to anti-control chaos, see the main results: Property 2 and Figure 5.

Next, in Section 5, the previous controlling mechanisms were compared by showing selected density plots (Figure 6) and the regularity detection on $\delta \times \gamma$ place (Figure 7).

An alternative approach to impulse control is given in Section 6, where non-symmetric impulses were applied and appropriate analysis was given in Figure 9 and Figure 10.

As a final comment, let us point out that the injected value $\gamma$ was picked as positive number, meaning some addition to the market is given at every time step. It is also possible to anti-control the chaos or to control the model by some tax, that is, the injection value $\gamma$ is negative. This case sometimes causes massive divergences of both values $q_1$ and $q_2$. Hence, this case is left for further research.