Nonlinear Multigrid Implementation for the Two-Dimensional Cahn–Hilliard Equation
Abstract
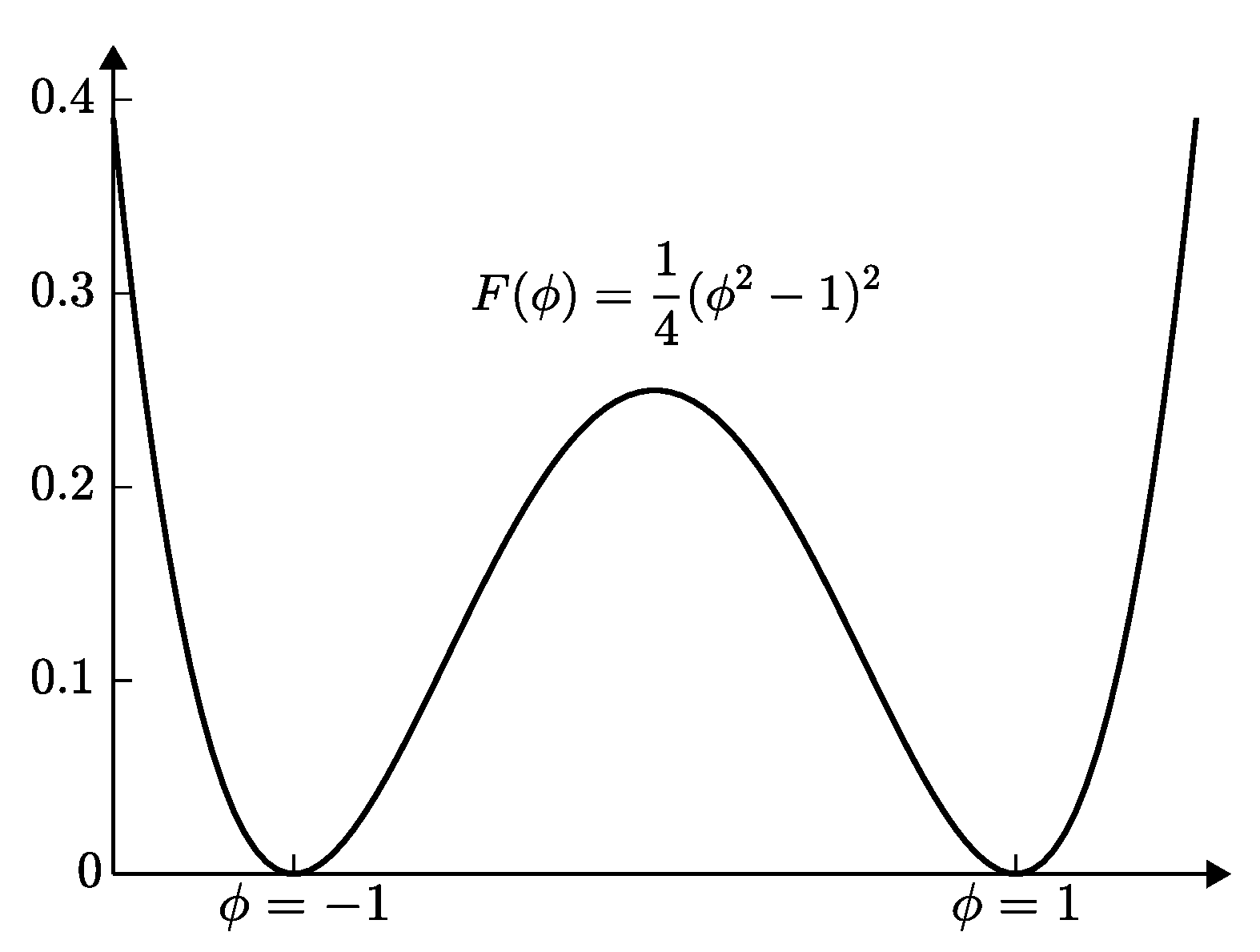
:1. Introduction
2. Numerical Solution
2.1. Discretization
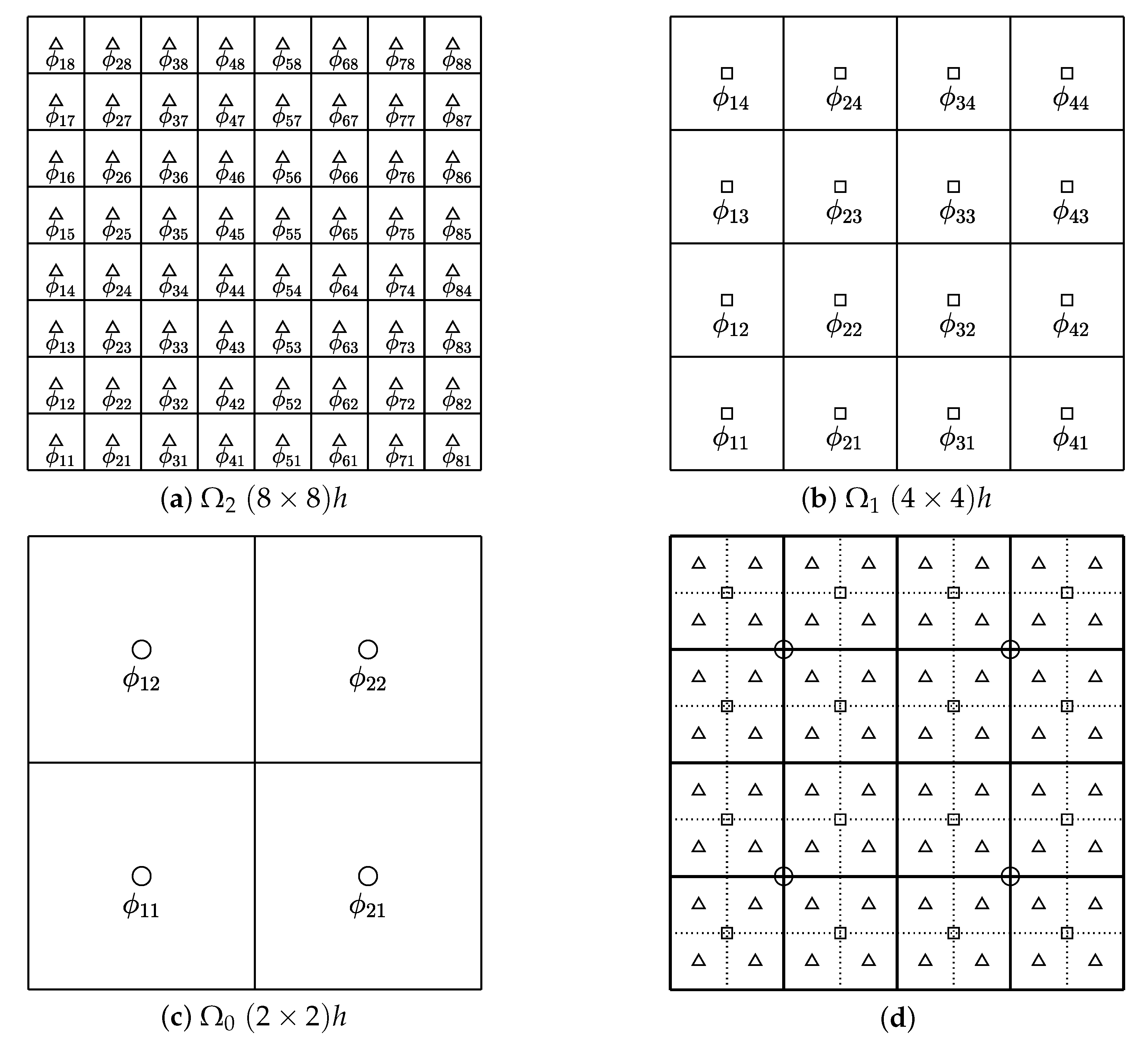
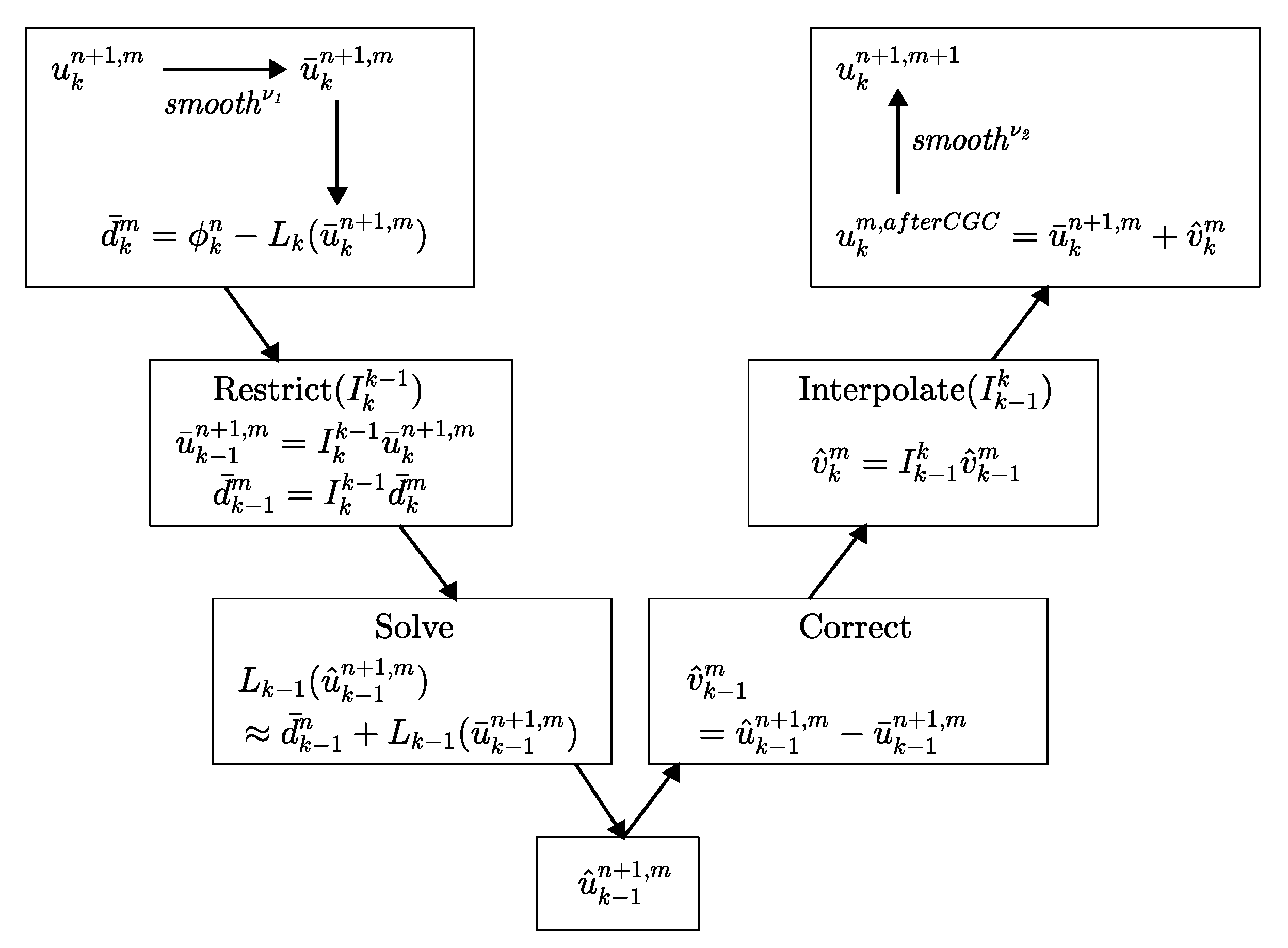
2.2. Multigrid V-Cycle Algorithm
Further Numerical Schemes for the CH Equation
3. Numerical Experiments
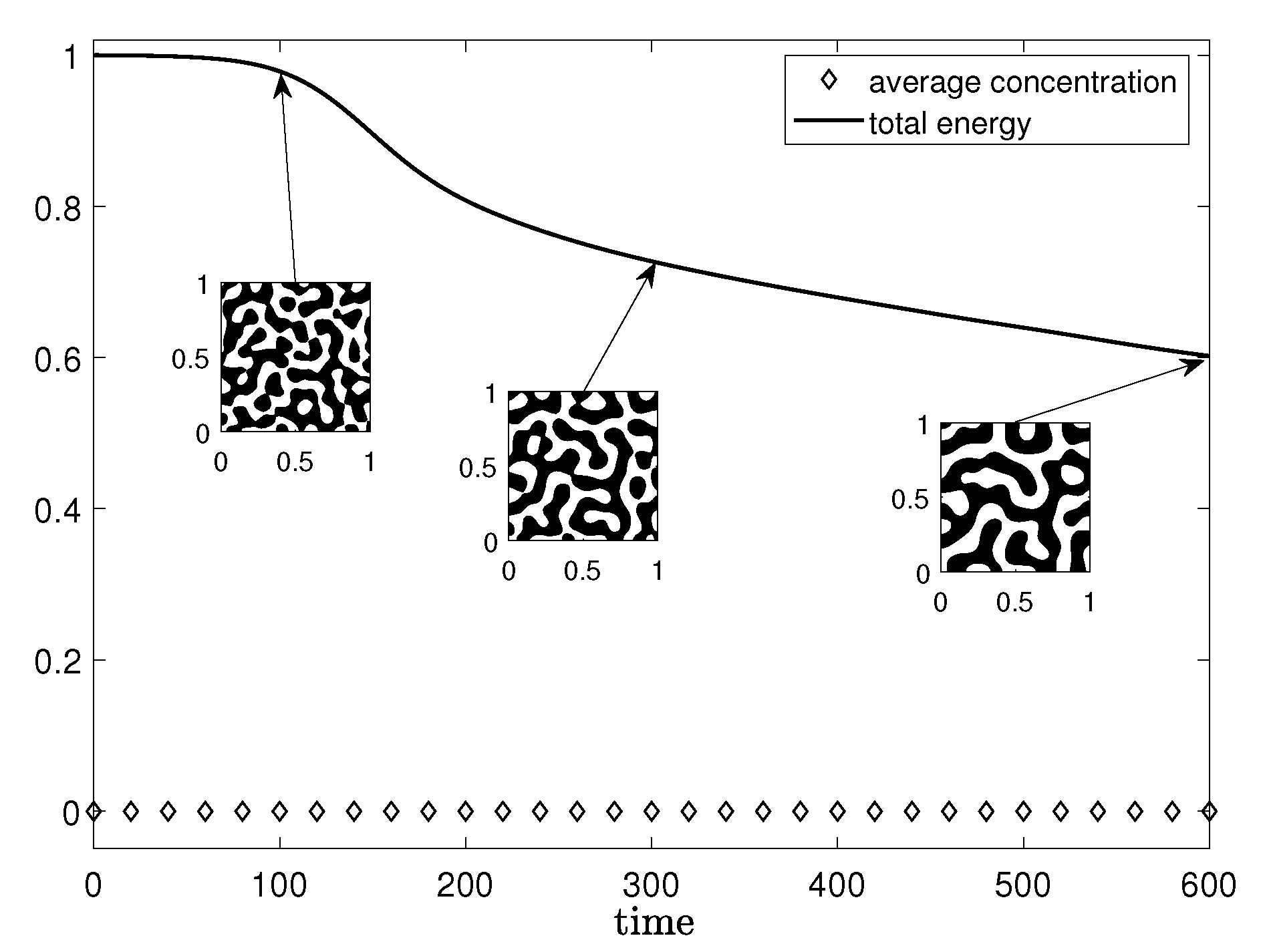
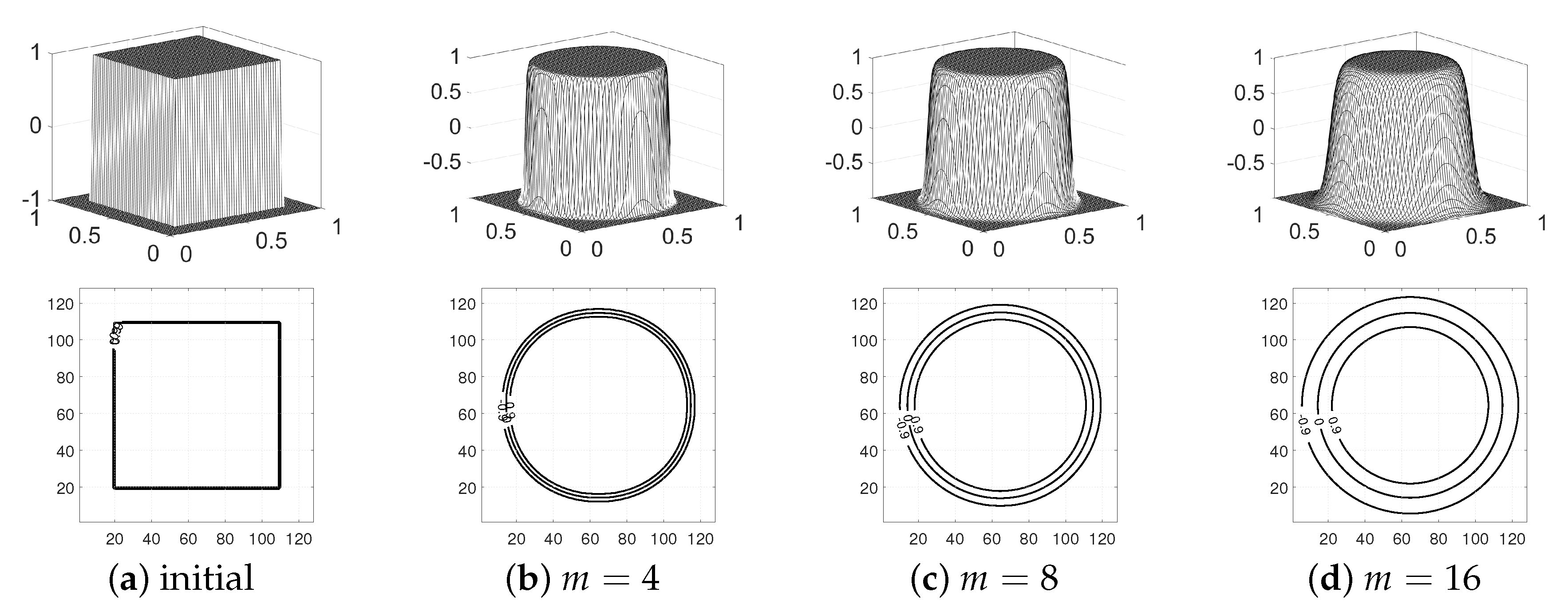
3.1. Phase Separation
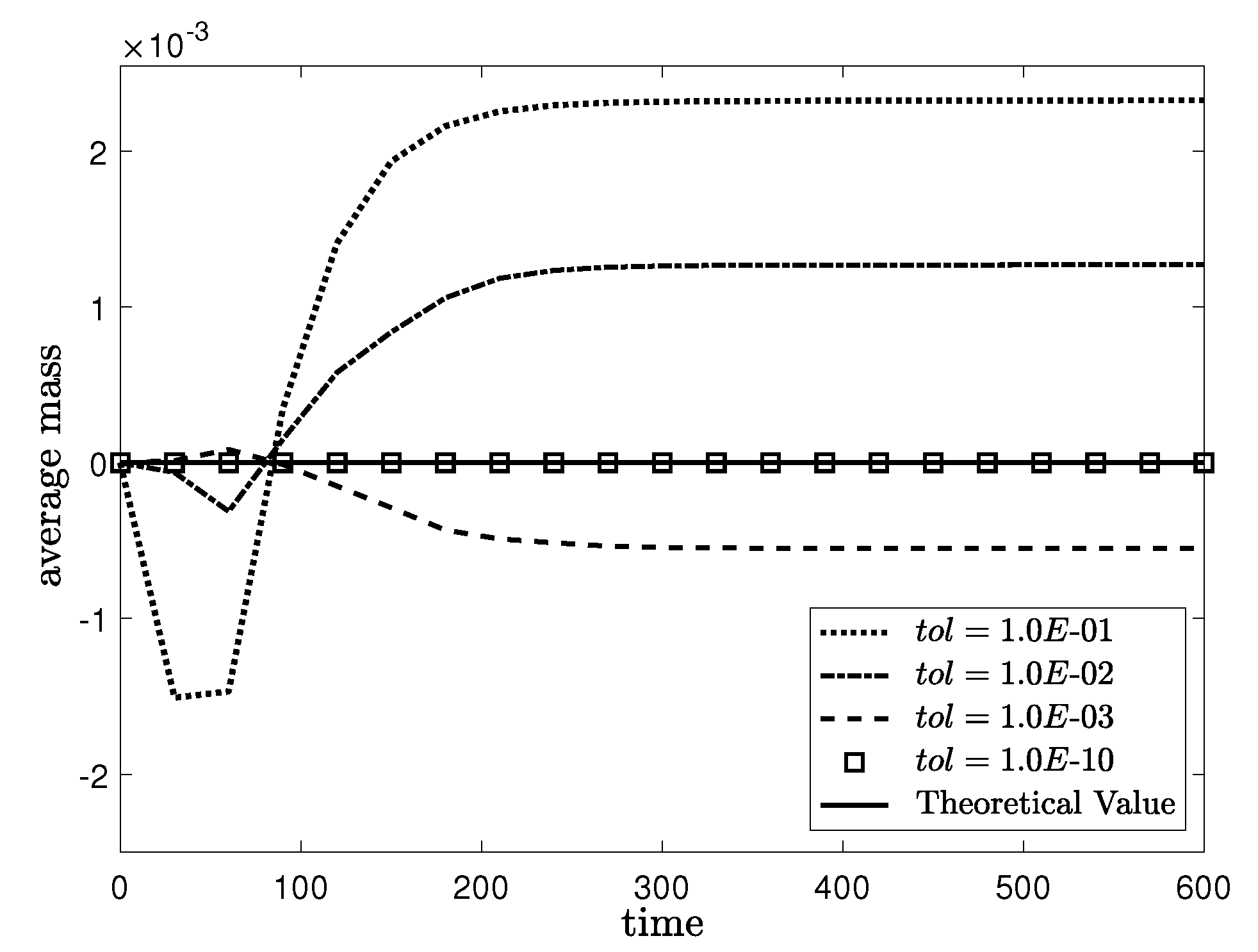
3.2. Non-Increase in Discrete Energy and Mass Conservation
3.3. Convergence Test
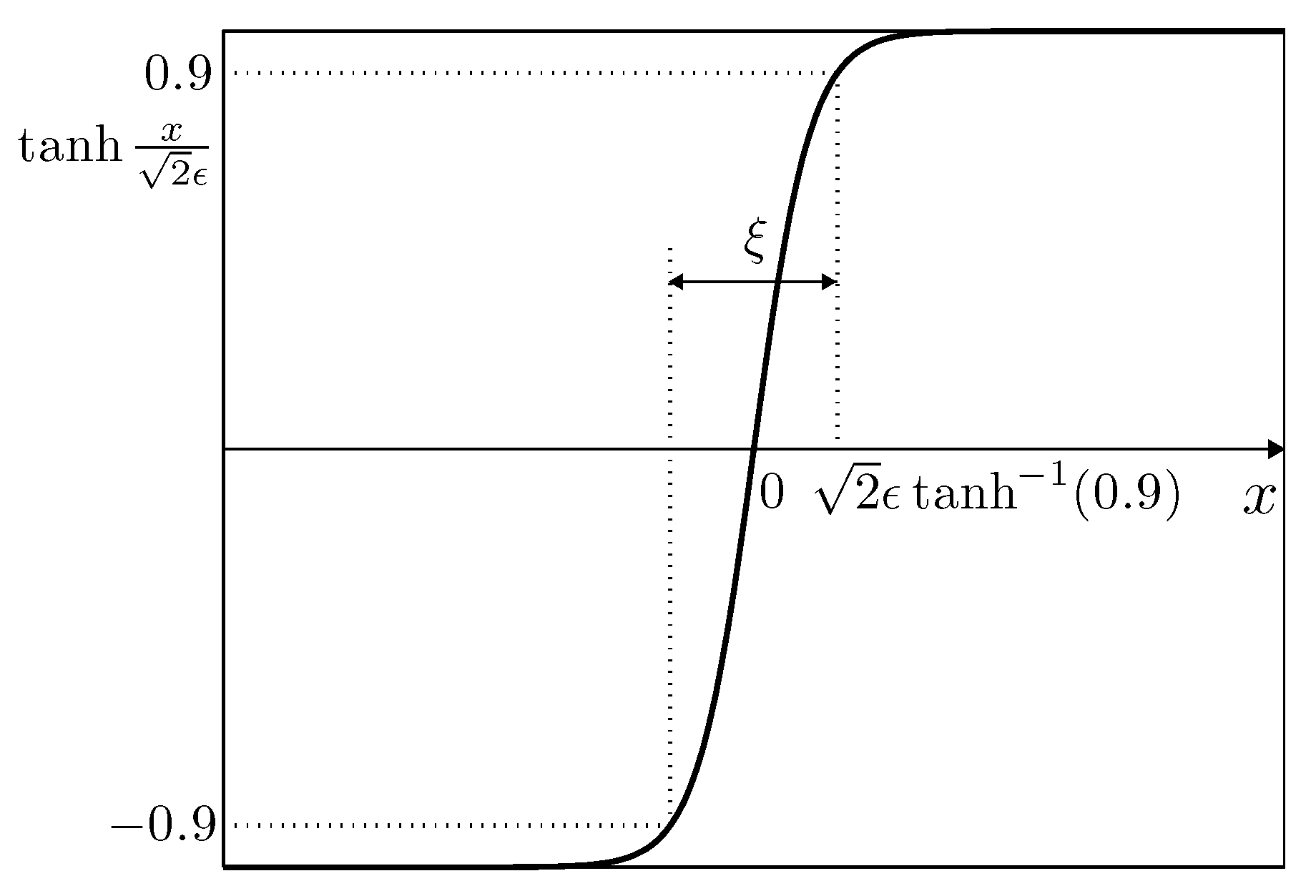
3.4. Effect of Tolerance
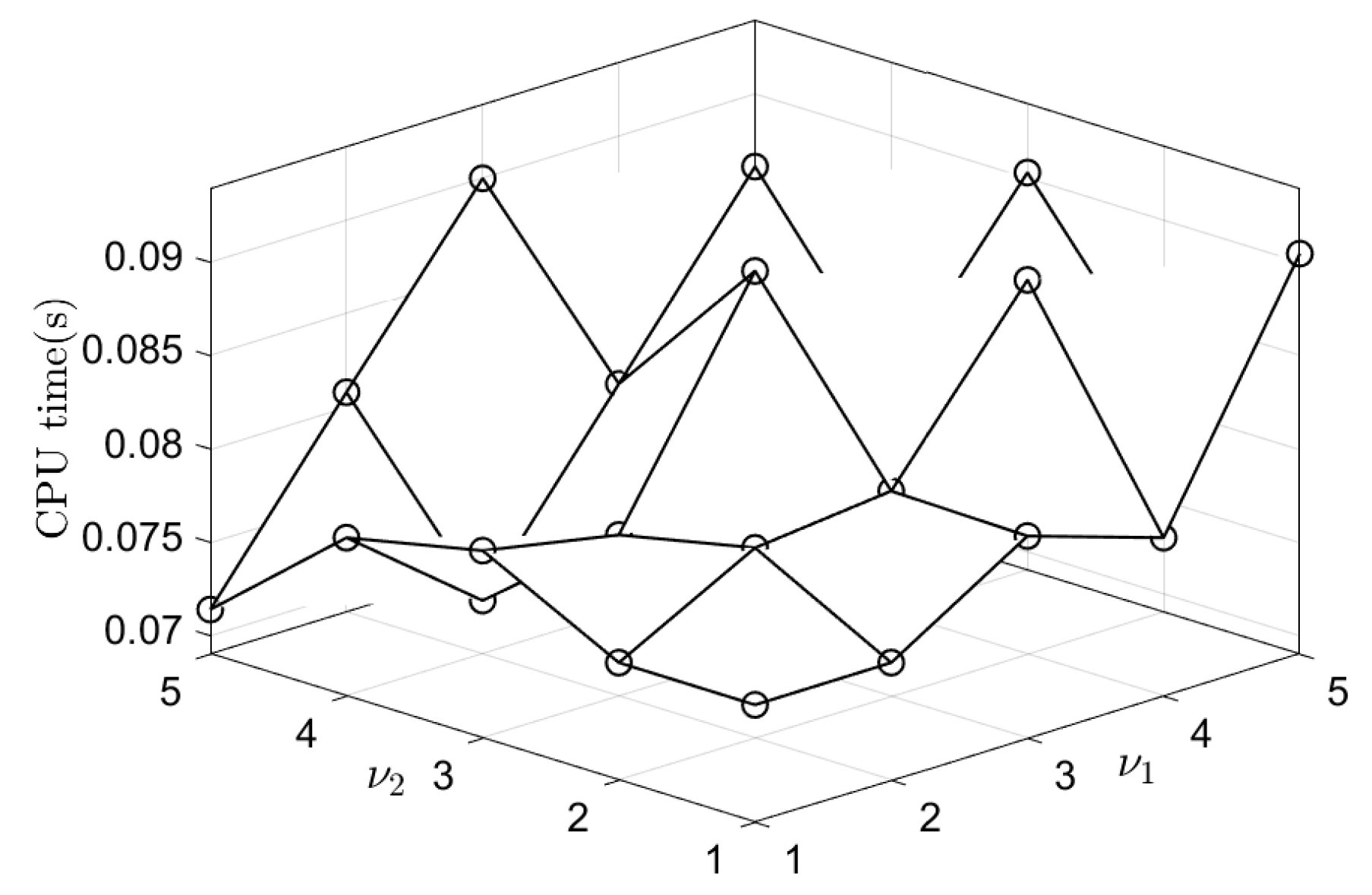
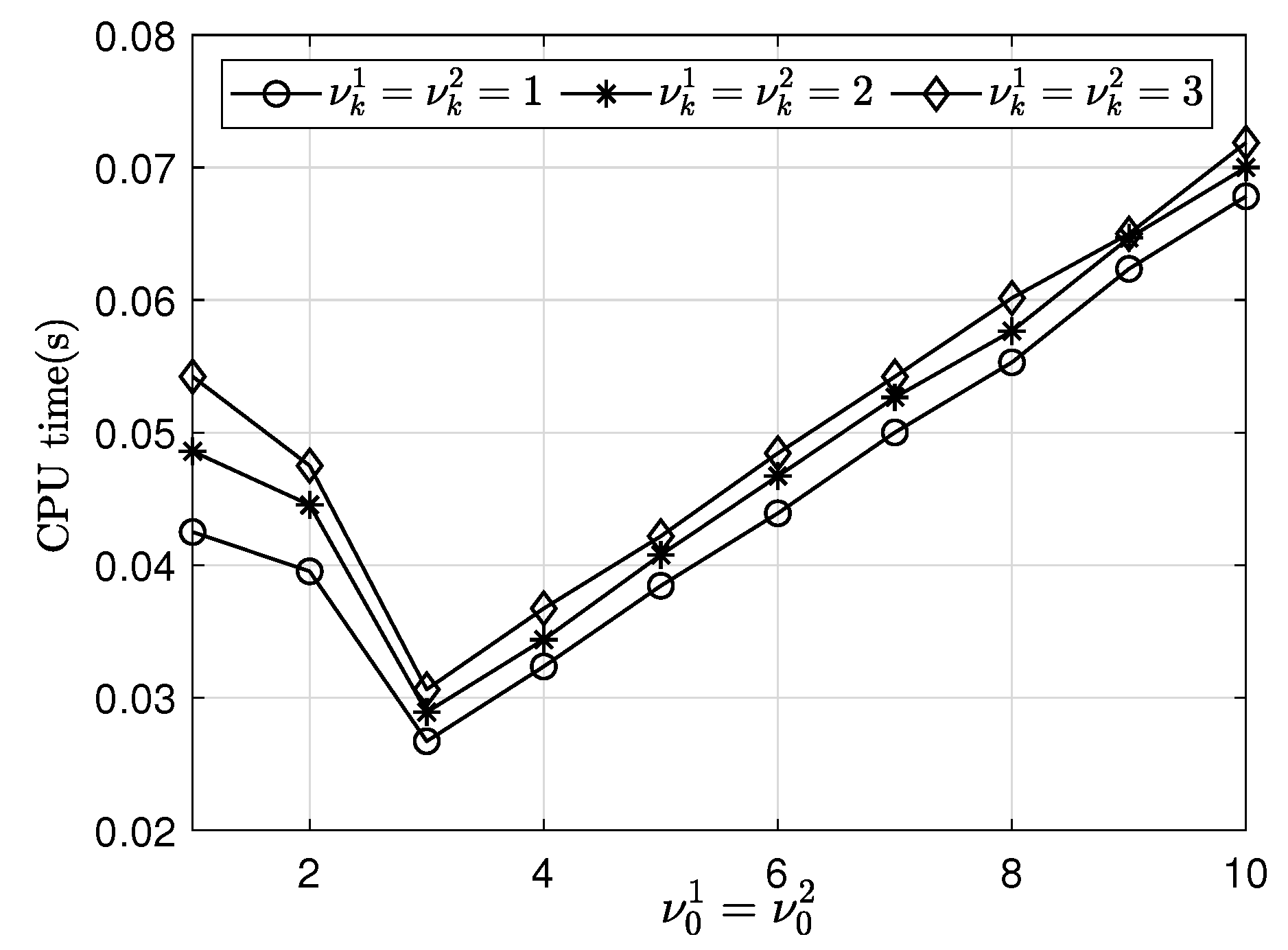
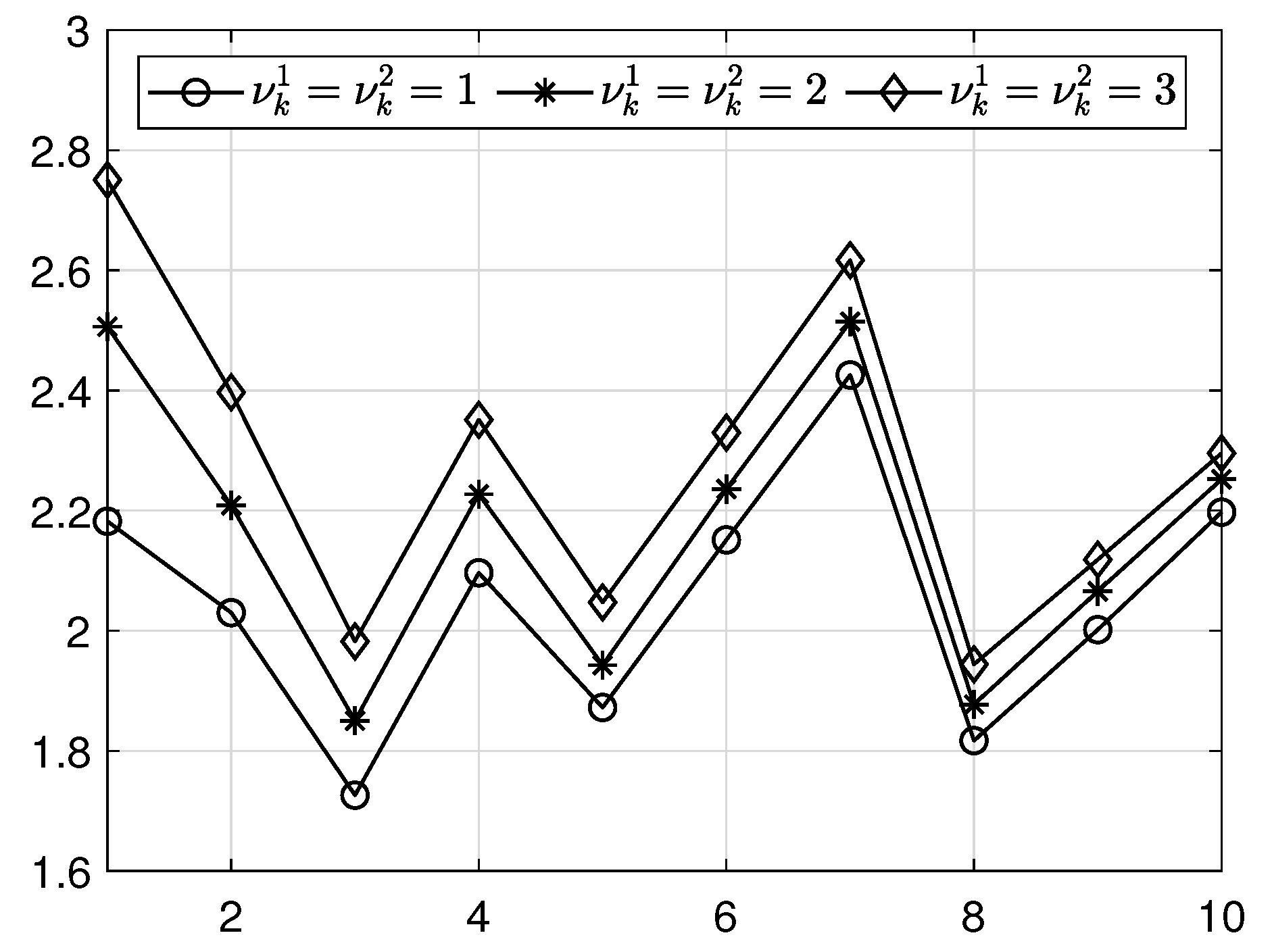
3.5. Effects of the Smooth Relaxation Numbers and
3.6. Effect Of V-Cycle
3.7. Comparison between Gauss–Seidel and Multigrid Algorithms
3.8. Effects of and on the V-Cycle
3.9. Comparison of the Jacobi, Red–Black and Gauss–Seidel
3.10. Effect of
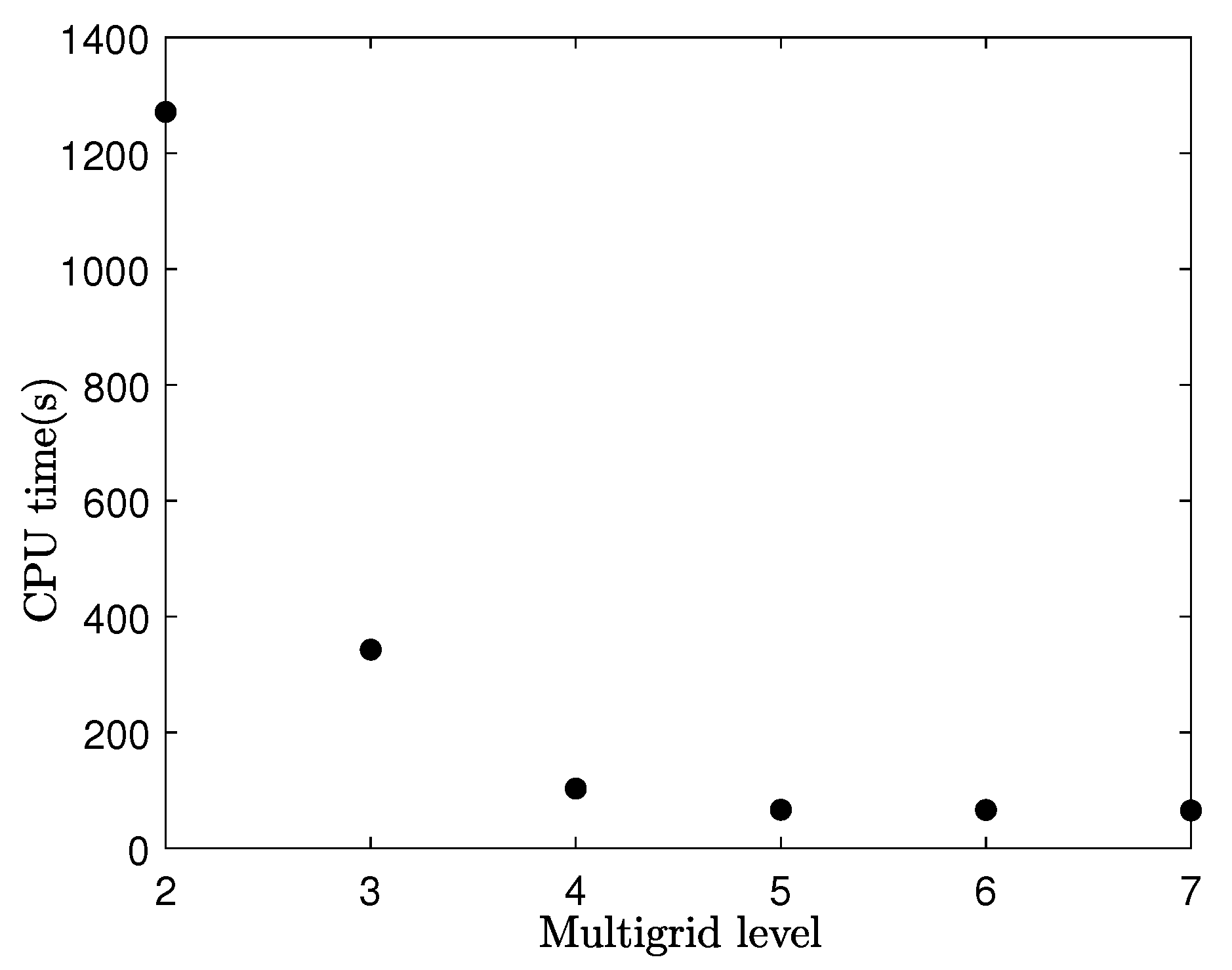
3.11. Effect of mesh size,
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Description |
|---|---|
| nx, ny | maximum number of grid points in the x-, y-direction |
| n_level | number of multigrid level |
| c_relax | number of times being relax |
| dt | |
| xleft, yleft | minimum value on the x-, y-axis |
| xright, yright | maximum value on the x-, y-axis |
| ns | number of print out data |
| max_it | maximum number of iteration |
| max_it_mg | maximum number of multigrid iteration |
| tol_mg | tolerance for multigrid |
| h | space step size |
| h2 | |
| gam | |
| Cahn |
References
- Trottenberg, U.; Schüller, A.; Oosterlee, C.W. Multigrid Methods; Academic Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar]
- Copetti, M.I.M.; Elliott, C.M. Kinetics of phase decomposition processes: Numerical solutions to Cahn–Hilliard equation. Mater. Sci. Technol. 1990, 6, 273–284. [Google Scholar]
- Honjo, M.; Saito, Y. Numerical simulation of phase separation in Fe-Cr binary and Fe-Cr-Mo ternary alloys with use of the Cahn–Hilliard equation. ISIJ Int. 2000, 40, 914–919. [Google Scholar]
- Bertozzi, A.L.; Esedoglu, S.; Gillette, A. Inpainting of binary images using the Cahn–Hilliard equation. IEEE Trans. Image Process. 2007, 16, 285–291. [Google Scholar]
- Bosch, J.; Kay, D.; Stoll, M.; Wathen, A.J. Fast solvers for Cahn–Hilliard inpainting. SIAM J. Imaging Sci. 2014, 7, 67–97. [Google Scholar]
- Choksi, R.; Peletier, M.A.; Williams, J.F. On the phase diagram for microphase separation of diblock copolymers: An approach via a nonlocal Cahn–Hilliard functional. SIAM J. Appl. Math. 2009, 69, 1712–1738. [Google Scholar]
- Tang, P.; Qiu, F.; Zhang, H.; Yang, Y. Phase separation patterns for diblock copolymers on spherical surfaces: A finite volume method. Phys. Rev. E 2005, 72, 016710. [Google Scholar]
- Hu, S.Y.; Chen, L.Q. A phase-field model for evolving microstructures with strong elastic inhomogeneity. Acta Mater. 2001, 49, 1879–1890. [Google Scholar]
- Yu, P.; Hu, S.Y.; Chen, L.Q.; Du, Q. An iterative-perturbation scheme for treating inhomogeneous elasticity in phase-field models. J. Comput. Phys. 2005, 208, 34–50. [Google Scholar]
- Gurtin, M.E.; Polignone, D.; Vinals, J. Two-phase binary fluids and immiscible fluids described by an order parameter. Math. Models Methods Appl. Sci. 1996, 6, 815–831. [Google Scholar]
- Lee, T. Effects of incompressibility on the elimination of parasitic currents in the lattice Boltzmann equation method for binary fluids. Comput. Math. Appl. 2009, 58, 987–994. [Google Scholar]
- Jeong, D.; Kim, J. Phase-field model and its splitting numerical scheme for tissue growth. Appl. Numer. Math. 2017, 117, 22–35. [Google Scholar]
- Kim, J.; Lee, S.; Choi, Y.; Lee, S.M.; Jeong, D. Basic Principles and Practical Applications of the Cahn–Hilliard Equation. Math. Probl. Eng. 2016, 2016, 9532608. [Google Scholar]
- Colli, P.; Gilardi, G.; Sprekels, J. A distributed control problem for a fractional tumor growth model. Mathematics 2019, 7, 792. [Google Scholar]
- Myśliński, A.; Wroblewski, M. Structural optimization of contact problems using Cahn–Hilliard model. Comput. Struct. 2017, 180, 52–59. [Google Scholar]
- Eyre, D.J. Unconditionally gradient stable time marching the Cahn–Hilliard equation. MRS Proc. 1998, 529, 39. [Google Scholar]
- Yang, S.; Lee, H.; Kim, J. A phase-field approach for minimizing the area of triply periodic surfaces with volume constraint. Comput. Phys. Commun. 2010, 181, 1037–1046. [Google Scholar]
- Kim, J. A numerical method for the Cahn–Hilliard equation with a variable mobility. Commun. Nonlinear Sci. Numer. Simul. 2007, 12, 1560–1571. [Google Scholar]
- Shin, J.; Jeong, D.; Kim, J. A conservative numerical method for the Cahn–Hilliard equation in complex domains. J. Comput. Phys. 2011, 230, 7441–7455. [Google Scholar]
- Jeong, D.; Kim, J. A practical numerical scheme for the ternary Cahn–Hilliard system with a logarithmic free energy. Phys. A 2016, 442, 510–522. [Google Scholar]
- Lee, H.; Kim, J. A second-order accurate non-linear difference scheme for the N-component Cahn–Hilliard system. Phys. A 2008, 387, 4787–4799. [Google Scholar]
- Lee, H.G.; Shin, J.; Lee, J.Y. A High-Order Convex Splitting Method for a Non-Additive Cahn–Hilliard Energy Functional. Mathematics 2019, 7, 1242. [Google Scholar]
- Shin, J.; Choi, Y.; Kim, J. An unconditionally stable numerical method for the viscous Cahn–Hilliard equation. Discret. Contin. Dyn. Syst. Ser. B 2014, 19, 1737–1747. [Google Scholar]
- Kim, J. Phase-field models for multi-component fluid flows. Commun. Comput. Phys. 2012, 12, 613–661. [Google Scholar]
- Kim, J.; Bae, H.O. An unconditionally gradient stable adaptive mesh refinement for the Cahn–Hilliard equation. J. Korean Phys. Soc. 2008, 53, 672–679. [Google Scholar]
- Wise, S.; Kim, J.; Lowengrub, J. Solving the regularized, strongly anisotropic Cahn–Hilliard equation by an adaptive nonlinear multigrid method. J. Comput. Phys. 2007, 226, 414–446. [Google Scholar]
- Li, Y.; Jeong, D.; Shin, J.; Kim, J. A conservative numerical method for the Cahn–Hilliard equation with Dirichlet boundary conditions in complex domains. Comput. Math. Appl. 2013, 65, 102–115. [Google Scholar]
- Lee, H.G.; Kim, J. Accurate contact angle boundary conditions for the Cahn–Hilliard equations. Comput. Fluids 2011, 44, 178–186. [Google Scholar]
- Shin, J.; Kim, S.; Lee, D.; Kim, J. A parallel multigrid method of the Cahn–Hilliard equation. Comput. Mater. Sci. 2013, 71, 89–96. [Google Scholar]
- Lee, C.; Jeong, D.; Shin, J.; Li, Y.; Kim, J. A fourth-order spatial accurate and practically stable compact scheme for the Cahn–Hilliard equation. Phys. A 2014, 409, 17–28. [Google Scholar]
- Choi, J.W.; Lee, H.G.; Jeong, D.; Kim, J. An unconditionally gradient stable numerical method for solving the Allen–Cahn equation. Phys. A 2009, 388, 1791–1803. [Google Scholar]
- Baker, A.H.; Falgout, R.D.; Kolev, T.V.; Yang, U.M. Scaling hypre’s multigrid solvers to 100,000 cores. In High-Performance Scientific Computing; Springer: London, UK, 2012; pp. 261–279. [Google Scholar]


| Mesh Size | ||||||
|---|---|---|---|---|---|---|
| V-Cycle | Ratio | Ratio | Ratio | |||
| 1 | ||||||
| 2 | 0.05 | 0.05 | 0.05 | |||
| 3 | 0.05 | 0.05 | 0.05 | |||
| 4 | 0.06 | 0.05 | 0.04 | |||
| 5 | 0.06 | 0.06 | 0.05 | |||
| 6 | 0.07 | 0.06 | 0.06 | |||
| 7 | 0.07 | 0.06 | 0.06 | |||
| 8 | 0.07 | 0.06 | 0.06 | |||
| 9 | 0.07 | 0.07 | 0.07 | |||
| 10 | 0.07 | 0.06 | 0.06 | |||
| 11 | 0.07 | 0.12 | 0.38 | |||
| 12 | ||||||
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0.075(9) | 0.075(7) | 0.081(6) | 0.077(5) | 0.089(5) |
| 2 | 0.075(7) | 0.079(6) | 0.090(5) | 0.089(5) | 0.081(4) |
| 3 | 0.079(6) | 0.082(5) | 0.089(5) | 0.081(4) | 0.090(4) |
| 4 | 0.078(5) | 0.075(4) | 0.081(4) | 0.090(4) | 0.075(3) |
| 5 | 0.072(4) | 0.081(4) | 0.090(4) | 0.075(3) | 0.082(3) |
| 1 | 2 | 3 | |
|---|---|---|---|
| 1 | 0.043 | 0.049 | 0.054 |
| 2 | 0.040 | 0.045 | 0.048 |
| 3 | 0.027 | 0.029 | 0.031 |
| 4 | 0.032 | 0.034 | 0.037 |
| 5 | 0.038 | 0.041 | 0.042 |
| 6 | 0.044 | 0.047 | 0.048 |
| 7 | 0.050 | 0.053 | 0.054 |
| 8 | 0.055 | 0.058 | 0.060 |
| 9 | 0.062 | 0.065 | 0.065 |
| 10 | 0.068 | 0.070 | 0.072 |
| 1 | 2 | 3 | |
|---|---|---|---|
| 1 | 2.182 | 2.506 | 2.750 |
| 2 | 2.030 | 2.208 | 2.397 |
| 3 | 1.726 | 1.850 | 1.982 |
| 4 | 2.096 | 2.227 | 2.351 |
| 5 | 1.872 | 1.943 | 2.047 |
| 6 | 2.151 | 2.236 | 2.330 |
| 7 | 2.426 | 2.514 | 2.617 |
| 8 | 1.817 | 1.877 | 1.944 |
| 9 | 2.002 | 2.066 | 2.118 |
| 10 | 2.197 | 2.252 | 2.295 |
| Level | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| CPU time(s) | 1271.437 | 342.906 | 103.032 | 66.422 | 66.172 | 65.218 |
| Mesh Size | Gauss–Seidel | Multigrid | |
|---|---|---|---|
| 0.468 | 0.046 | ||
| 0.610 | 0.063 | ||
| 0.735 | 0.062 | ||
| 7.046 | 0.203 | ||
| 8.984 | 0.234 | ||
| 11.360 | 0.266 | ||
| 109.093 | 0.844 | ||
| 140.219 | 0.906 | ||
| 174.922 | 1.078 |
| 2 | 2 | 3 | 4 | 6 | 8 | 8 | |
| 10,000 | 2 | 3 | 4 | 7 | 9 | 9 | |
| 10,000 | 10,000 | 3 | 5 | 8 | 10 | 10 | |
| 10,000 | 10,000 | 10,000 | 5 | 9 | 11 | 12 | |
| 10,000 | 10,000 | 10,000 | 10,000 | 10 | 13 | 13 | |
| 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | 14 | 15 | |
| 8 | 7 | 8 | 8 | 9 | 14 | 41 | |
| 9 | 9 | 9 | 9 | 10 | 19 | 91 | |
| 11 | 10 | 10 | 11 | 11 | 24 | 140 | |
| 12 | 12 | 12 | 12 | 13 | 28 | 189 | |
| 14 | 13 | 13 | 13 | 14 | 33 | 238 | |
| 15 | 14 | 15 | 15 | 16 | 38 | 288 |
| Case | Jacobi | Red–Black | Gauss-Seidal |
|---|---|---|---|
| 1 | 32 | 13 | 9 |
| 2 | 16 | 8 | 6 |
| 3 | 11 | 6 | 5 |
| 4 | 8 | 5 | 4 |
| 5 | 7 | 5 | 3 |
| Mesh Size | |||||||
|---|---|---|---|---|---|---|---|
| CPU time(s) | 0.610 | 2.812 | 12.156 | 50.594 | |||
| Ratio | 4.610 | 4.323 | 4.162 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.; Jeong, D.; Yang, J.; Kim, J. Nonlinear Multigrid Implementation for the Two-Dimensional Cahn–Hilliard Equation. Mathematics 2020, 8, 97. https://doi.org/10.3390/math8010097
Lee C, Jeong D, Yang J, Kim J. Nonlinear Multigrid Implementation for the Two-Dimensional Cahn–Hilliard Equation. Mathematics. 2020; 8(1):97. https://doi.org/10.3390/math8010097
Chicago/Turabian StyleLee, Chaeyoung, Darae Jeong, Junxiang Yang, and Junseok Kim. 2020. "Nonlinear Multigrid Implementation for the Two-Dimensional Cahn–Hilliard Equation" Mathematics 8, no. 1: 97. https://doi.org/10.3390/math8010097
APA StyleLee, C., Jeong, D., Yang, J., & Kim, J. (2020). Nonlinear Multigrid Implementation for the Two-Dimensional Cahn–Hilliard Equation. Mathematics, 8(1), 97. https://doi.org/10.3390/math8010097






