1. Introduction
Fractional calculus is an emerging field of mathematics, which is a generalisation of differentiation and integration to non-integer orders. The history of fractional calculus is almost as long as the history of classical calculus, beginning with some speculations of Leibniz (1695, 1697) and Euler (1730). However, fractional calculus and fractional differential equations (FDEs) are increasingly becoming popular in recent years. The progressively developing history of this old and yet novel topic can be found in [
1,
2,
3,
4,
5]. In fact, fractional calculus provides the mathematical modeling of some important phenomena like social and natural in a more powerful way than the classical calculus. During the last few decades, many applications were reported in many branches of science and engineering such as chaotic systems [
6,
7], fluid mechanics [
8], viscoelasticity [
9], optimal control problems [
10,
11], chemical kinetics [
12,
13], electrochemistry [
14], biology [
15], physics [
16], bioengineering [
17], finance [
18], social sciences [
19], economics [
20,
21], optics [
22], chemical reactions [
23], rheology [
24], and so on. Due to the importance of FDEs, the solutions of them are attracting widespread interest. On the other hand, analytical solutions are not always possible for solving them. Therefore, numerical techniques becomes more important for solving such equations.
There are various numerical methods have been developed for solving FDEs in literature such as predictor-corrector method [
25], Laplace transforms [
26], Taylor collocation method [
27], variational iteration method and homotopy perturbation method [
8] (Chapter 6), Adomian decomposition method [
28], Tau method [
29], inverse Laplace transform [
30], Haar wavelet collocation method [
31], generalized block pulse operational matrix [
32], shifted Legendre-tau method [
33], fractional multi-step differential transformed method [
34], q-homotopy analysis transform method [
35], conformable Laplace transform [
36], fractional B-splines collocation method [
37], finite difference method [
38], homotopy analysis method [
39] and so on.
Multi-term fractional differential equations are one of the most important type of FDEs, which is a system of mixed fractional and ordinary differential equations and involving more than one fractional differential operators. Nowadays, they are widely appearing for modelling of many important processes, especially for multirate systems. Their numerical solution is then a strong subject that deserves high attention. In this paper, motivated by the results reported in [
40,
41] for solving a smaller class of problems where the highest order of derivative is an integer and involving at most one noninteger order derivative, we go further and establish a method for numerical solutions for higher order and arbitrary multi-term fractional differential equations which have a general form
where
representing the Caputo fractional derivative of order
and we assume that
where
Multi-term fractional order differential equations also have useful properties and they can describe complex multi-rate physical processes in a various way and can be applied in many fields, see e.g., [
2,
4,
26,
42]. Basset [
43] and Bagley–Torvik [
44] equations can be given as important examples for smaller class of multi-term fractional differential equations. Existence, uniqueness and stability of solution for multi-term fractional differential equations are discussed in [
45,
46,
47,
48,
49]. Because of difficulty of finding the exact solutions for such equations, many new numerical techniques have been developed to investigate the numerical solutions such as Adams method [
50], Haar wavelet method [
51], differential transform method [
52], Adams–Bashforth–Moulton method [
53], collocation method based on shifted Chebyshev polynomials of the first kind [
54], Boubaker polynomials method [
55], matrix Mittag–Leffler functions [
56], differential transform method [
57] and so on.
Our main purpose is to present an effective, reliable method to approximate initial value problem for the Equation (
1). In order to reach this aim, we rewrite and focus the general type of Caputo multi-term fractional differential equation given in Equation (
1) in the following linear form
subject to the
Here, we also state that the highest order need not to be an integer. This equation is important in applications due to the fact it can treat the problems with fractional force, therefore it is suitable for being treated within fractional operators of Caputo type.
In this work, a numerical approach based on fractional Taylor vector is proposed to solve the initial value problem of general type of multi-term fractional differential equations which is given in Equations (
2) and (
3). The core idea of this method is to employ the operational matrix of fractional integration based on fractional Taylor vector to given problem and reduce it to a set of algebraic equations which can be efficiently solved.
The structure of the manuscript is organized as follows. In
Section 2, we briefly introduce some preliminary ideas of fractional calculus and necessary definitions. In
Section 3, an operational matrix of fractional integration based on fractional taylor vector is derived. In
Section 4, we present the numerical algorithm to solve the given equation and a pseudo-code for matlab is also provided in Algorithm 1. In
Section 5, the presented method is applied to six examples to demonstrate the efficiency. A final conclusion is presented in the last section.
4. The Numerical Algorithm
In this section, to solve the given multi-term fractional differential equation in Equations (
2) and (
3), we employ the fractional Taylor method. The algorithm of method is given below.
Firstly, by using the transformation
, we replace the variable
with
. Now, by using Equation (
8) in Equation (
2), we get
where
and
. Similar to Equation (
10) we approximate the
as
such that
is the fractional Taylor vector and the unique coefficients
is given in Equation (
11).
Next, applying the Riemann–Liouville fractional integral on both side of (
14), we get
where
where
Hence, by substituting initial conditions (
3), we get
such that
Now, by using the Equation (
12), we approximate the fractional order integrals in Equation (
17) and we have
Finally, by taking the collocation points
(
) in Equation (
18), we get
linear algebraic equations. This linear system can be solved for the unknown vector
. Consequently,
can be approximated by Equation (
15).
MATLAB Implementation of Method
The pseudocode given in Algorithm 1 below allows us to use proposed method in MATLAB for obtain a numerical solution of given problem [
58].
| Algorithm 1: Fractional Taylor Method |
| [] = (, , , , , R, , m, ) |
% Input % is the highest order of fractional derivative of given equation % is the order of fractional derivatives other than alpha. must be a vector with decending ordered values % is the vector of coefficients % is defining the right hand side of given problem % and R denotes the left and right endpoints % is the initial conditions % m denotes the number of steps % is a real number greater than zero. We usually take or fractional part of
|
| % Output |
| % using , where command is defined by the Equation (18), gives us the linear system which is |
| % algebraic equations with unknown coefficients |
| % Next step is to use matlab function to solve obtained algebraic equation for unknown coefficient vector with dimension . |
| |
| % Output |
% Next step is substituting obtained coefficients to as input, where the command defined by Equation (15), we get the approximate solution of given problem
[] = |
| % Input |
% Output % s is the nodes on in which the approximate solution calculated % y is the numerical solution evaluated in the points of s.
|
5. Illustrative Examples
To illustrate the applicability and effectiveness of the presented method, we give six examples in this section. In each example, we apply the fractional Taylor operational matrix method which is presented in previous section and the approximate results compared with analytical solutions. Obtained results indicate that the proposed technique is very effective for multi-term fractional differential equations. In order to solve the numerical computations, MATLAB version R2015a has been used.
For choosing , we usually take either or , the fractional part of .
5.1. Example 1
Consider the following form of multi-order fractional differential equation [
59]
We let
the coefficients
and
and the function
is
where the exact solution is
We apply the given procedure which is implemented in previous section for solving the Equation (
19) step by step.
Firstly, change variable to by using
Now, we use the Equation (
8) and get
where
.
Next, using Equation (
7) we get
Now, using Equation (
21) and substituting initial conditions
into equation
From Equation (
12), we have
Now, taking
in Equation (
23) and putting the given values for
where
into this equation, we get
Finally, taking the collocation points () generates a linear algebraic system of dimension with unknown vector . In order to solve this system by using presented method and comparing the results, we choose and different values of m.
To show the efficiency, we compared the numerical results with the method given in [
59].
Table 1, compares the obtained results for absolute error with
. We observe from
Table 1 that, the absolute errors for presented method are smaller and the numerical solution is more accurate for the same size of
m.
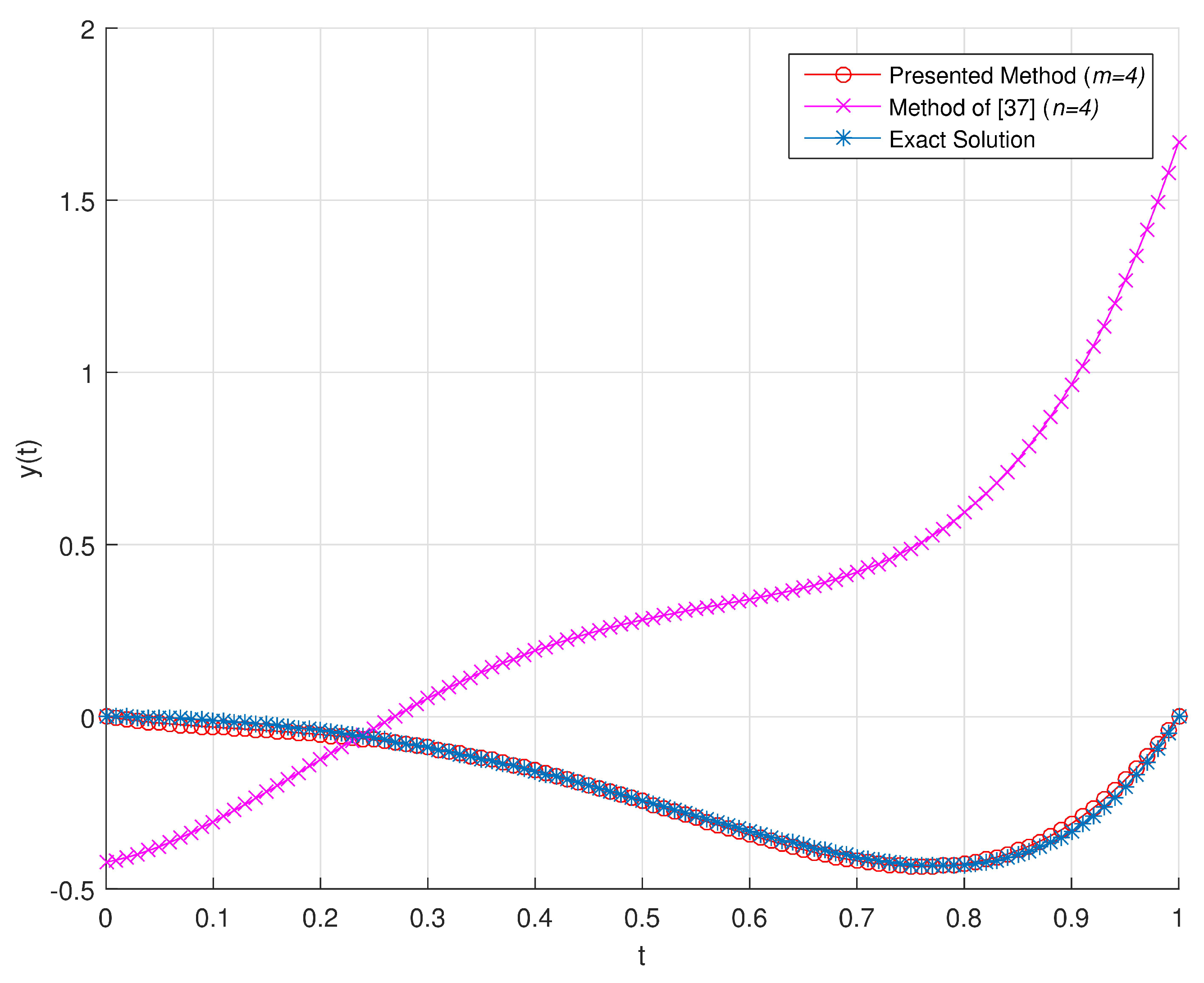
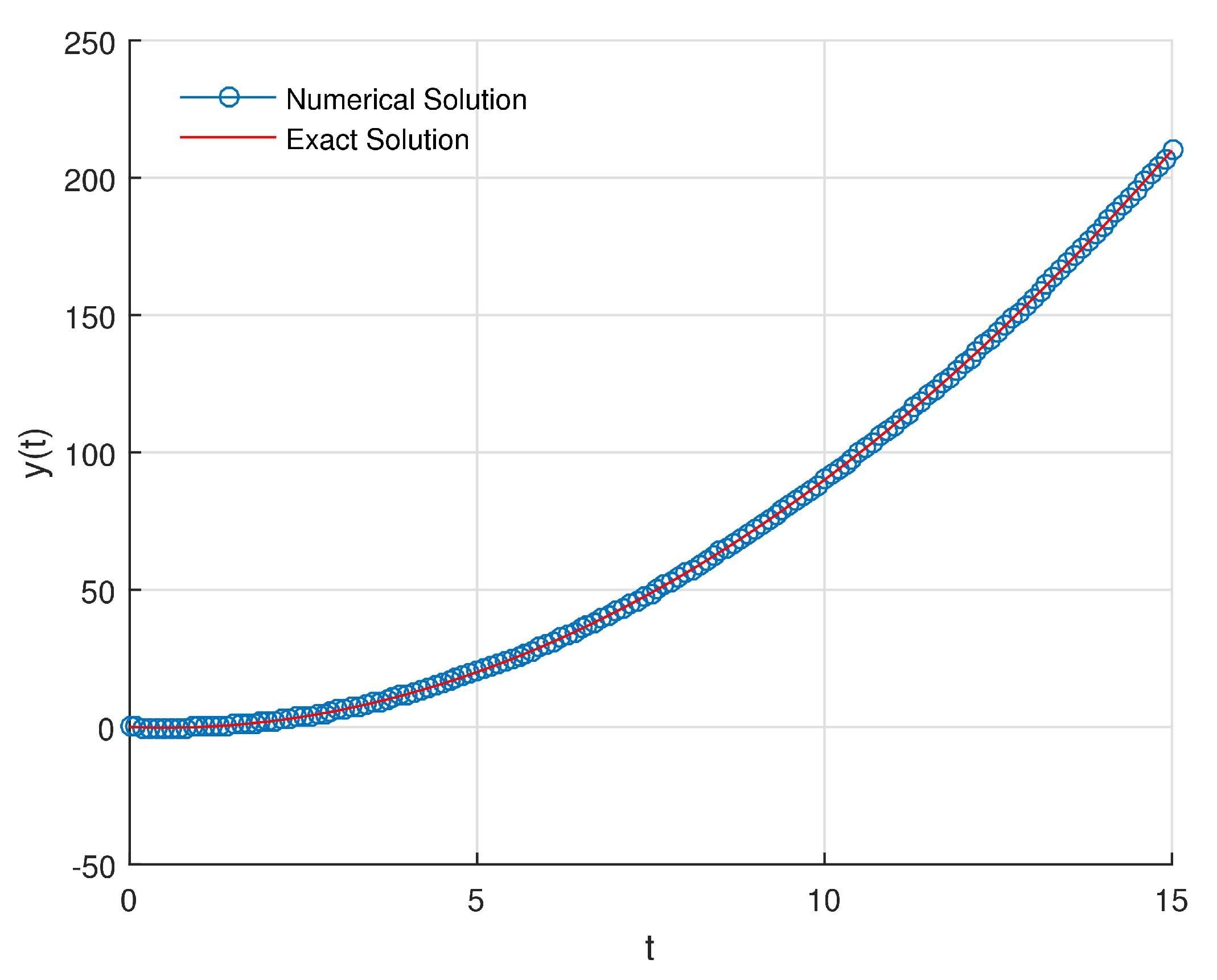
In
Figure 1,
Figure 2 and
Figure 3, we present the graphical representation of comparison between exact solution and the numerical solutions obtained by proposed method and the method of [
59] for the problem (
19) with
respectively. From these results, we can conclude that
and
give larger absolute error, while
gives smaller absolute error (
) and more precise numerical solution. These comparisons also shows that the results obtained by proposed method is closer to the exact solution than the results of [
59].
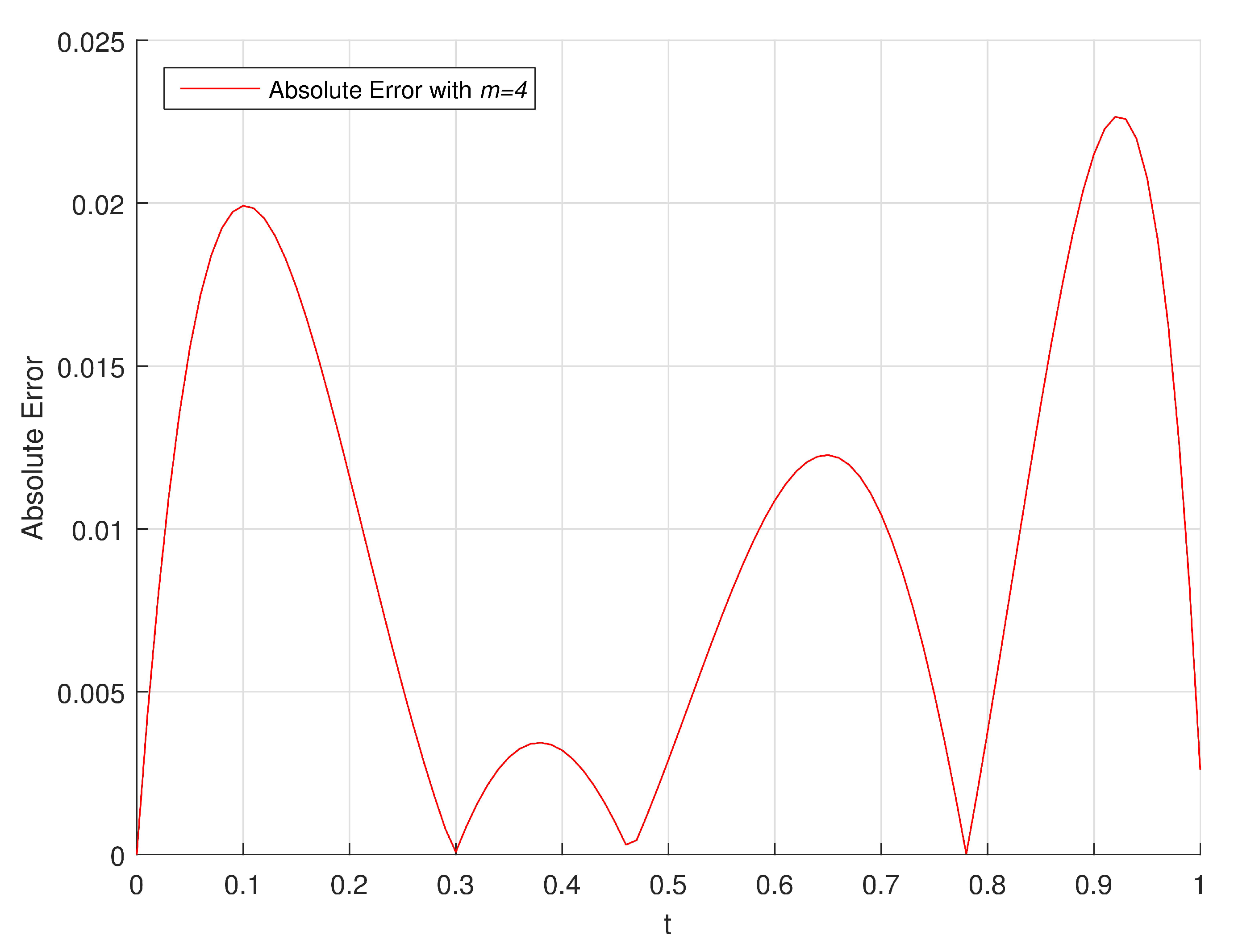
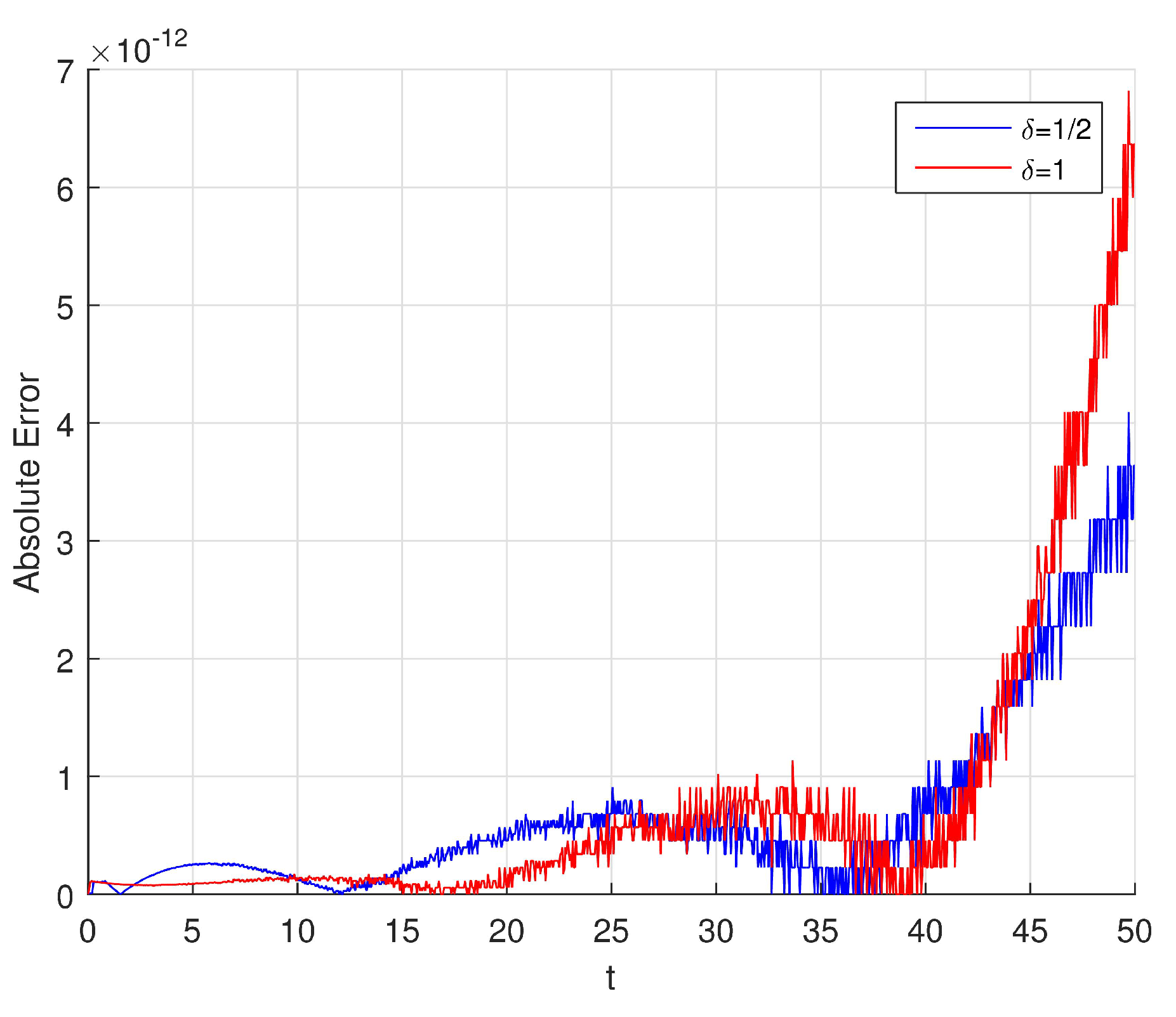
In
Figure 4, we show the graphical representation of absolute errors obtained by using proposed method and the method of [
59] with
.
From
Figure 4, we can conclude that the absolute error obtained by our method is remaining smaller and stable while the absolute error of other method is increasing in the interval
.
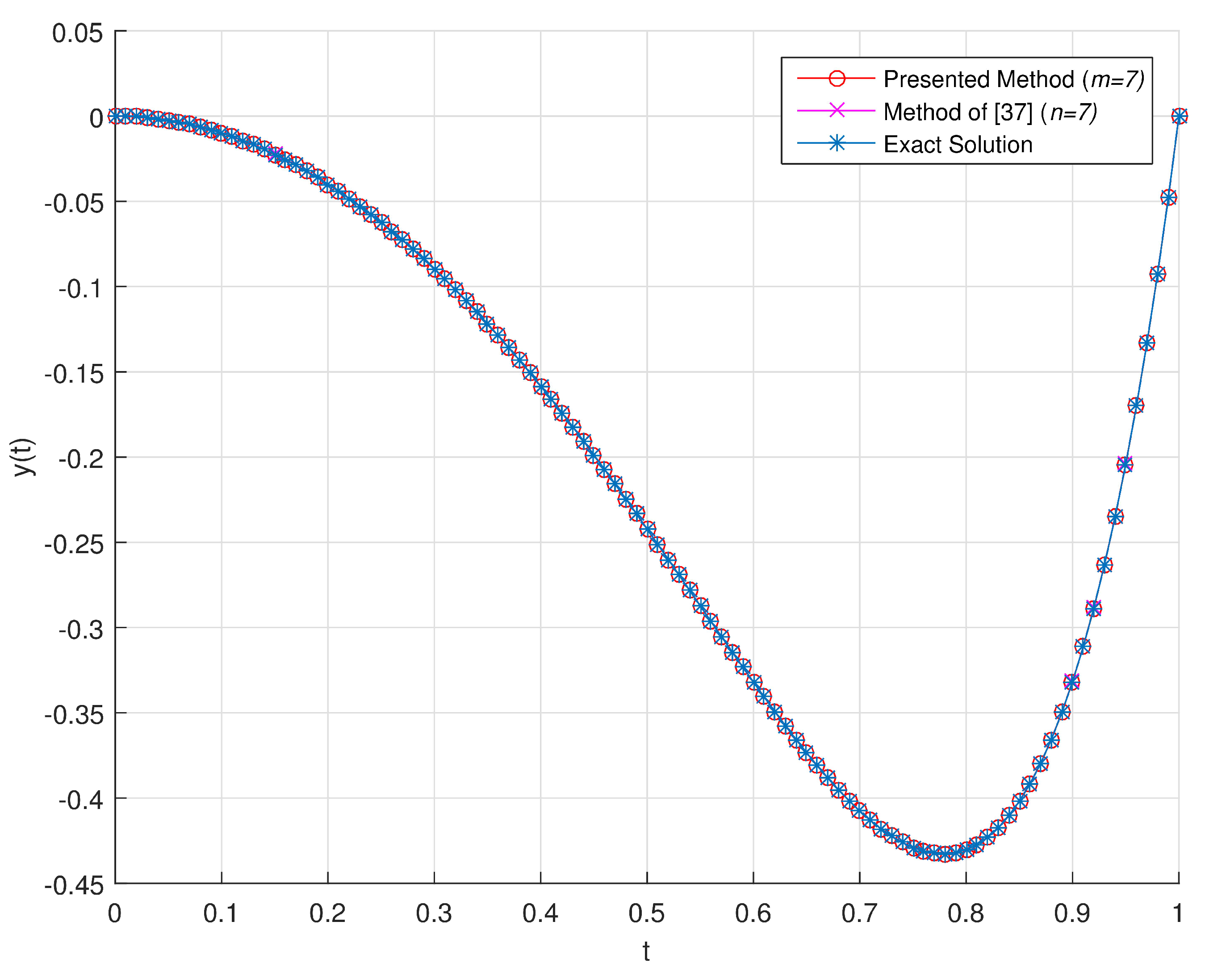
In
Figure 5 and
Figure 6, we give the graphical representation of absolute errors obtained by using proposed method with
respectively.
A pseudo-code for MATLAB implementation of Example 1 is given in Algorithm 2 below:
| Algorithm 2: Fractional Taylor Method |
| ; |
| ; |
| ; |
| @(t) |
| ; |
| ; ; |
| ; |
| ; |
| ; |
| (, , , , , R, , m, ) |
| |
| |
5.2. Example 2
In this example, we consider the Equation (
19) with
the coefficients
and
and the function is
The exact solution of this equation is
[
59].
Applying the same procedure to given problem as presented in Example 1, we get the following equation
As we stated in previous example, collocating this equation at the nodes () generates a system of algebraic equations. In this example, to solve this sysem for , we choose and different values of m.
Table 2 shows the results for obtained absolute errors by using presented method with
. From these results, we can see that, there is satisfactory agreement between the exact solution and numerical solutions. The absolute error is achieved about
. We also note that, the proposed method gives better results for
by taking
.
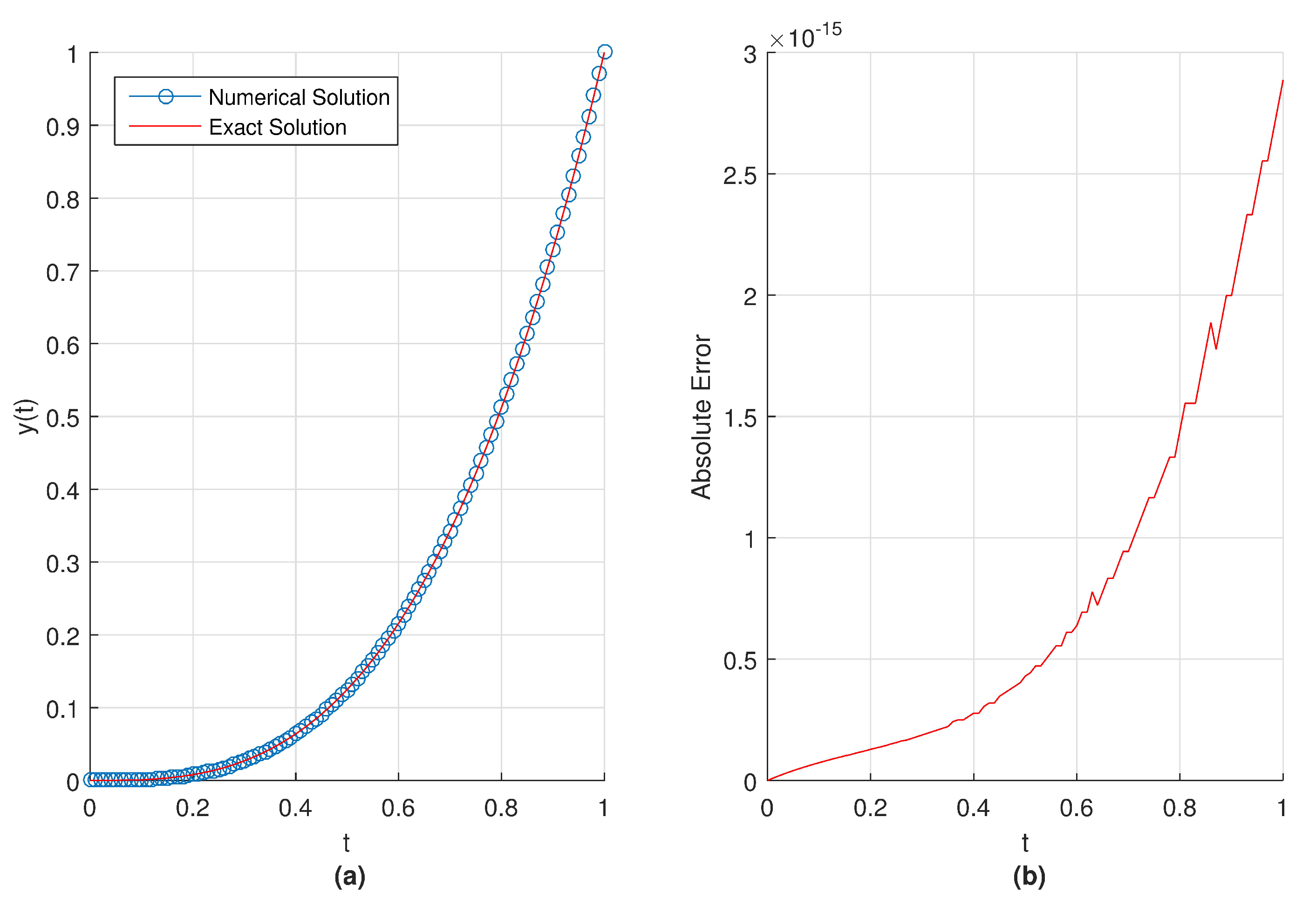
In
Figure 7a, we show the graphical representation of obtained numerical solution and the exact solution of the given problem.
Figure 7b presents the obtained absolute error by using proposed method with
.
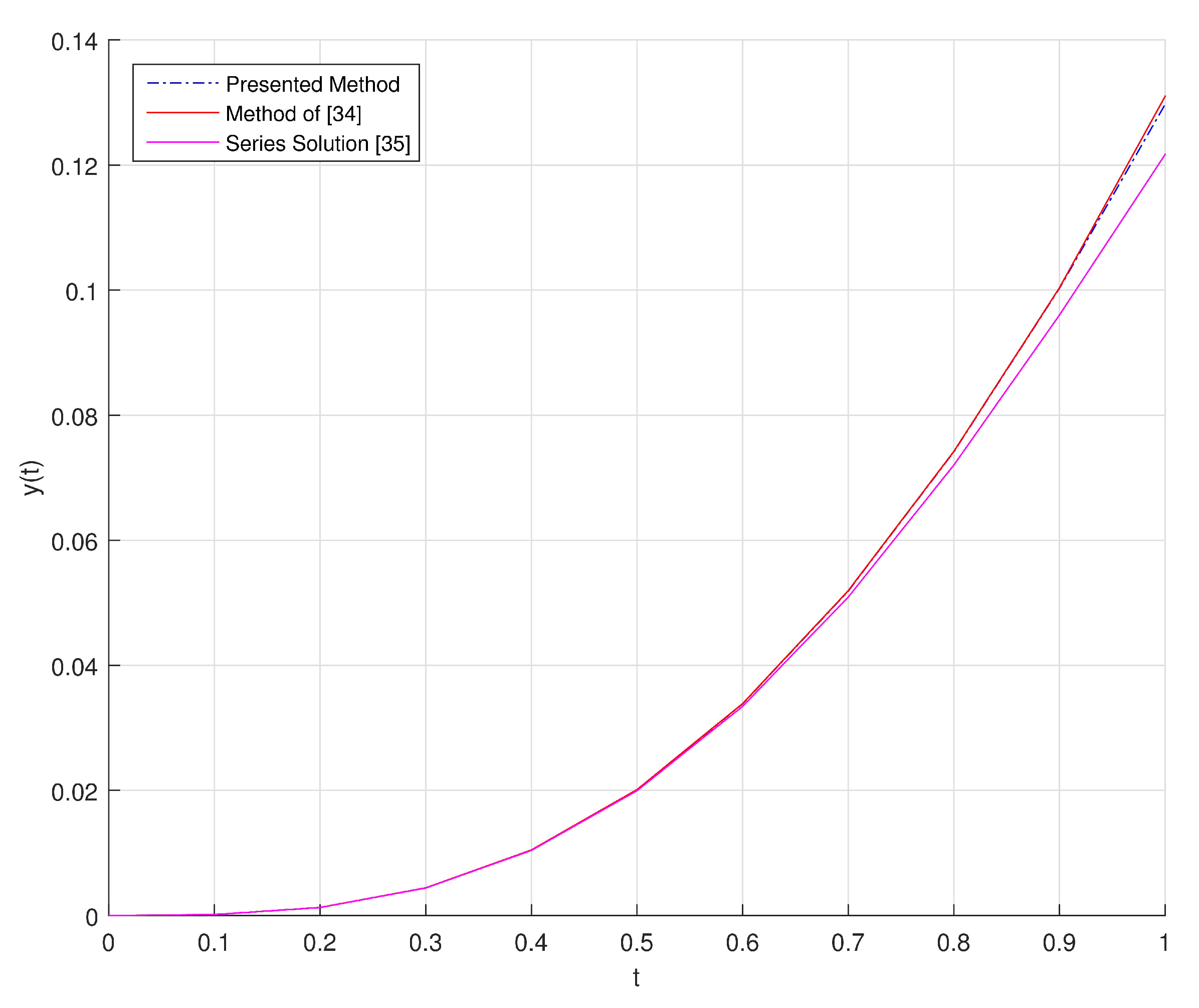
5.3. Example 3
Consider the multi-term fractional order initial value problem [
54]
with initial conditions
where the equation have the series solution given by [
52]
In order to solve this problem, we choose and
We give the comparison of series solution and the numerical solution obtained by presented method in
Table 3.
Table 4 compares the obtained absolute errors by using presented method with the results of [
54]. From this compared results, it can be seen that the approximate solution is very close to series solution for a small number of
m for the given method.
From the compared results of
Table 4, we can conclude that the proposed method has better approach to series solution with a smaller
m.
The graphical representation of comparison between series solution and numerical solutions obtained by presented method and the method of [
54] in the interval
is illustrated in
Figure 8.
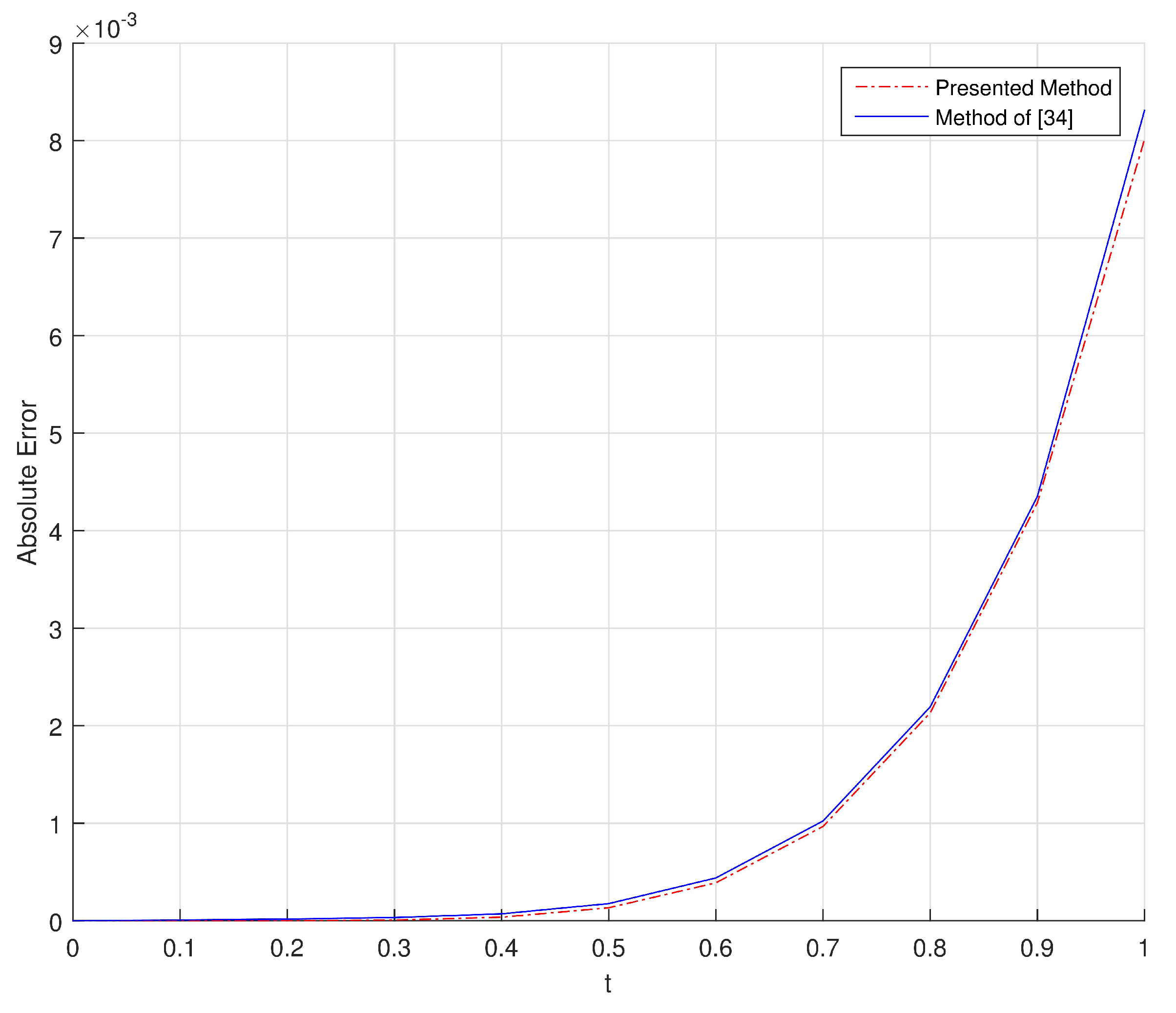
In
Figure 9, we show present graphical representation of absolute errors obtained by using proposed method and the method of [
54] with
.
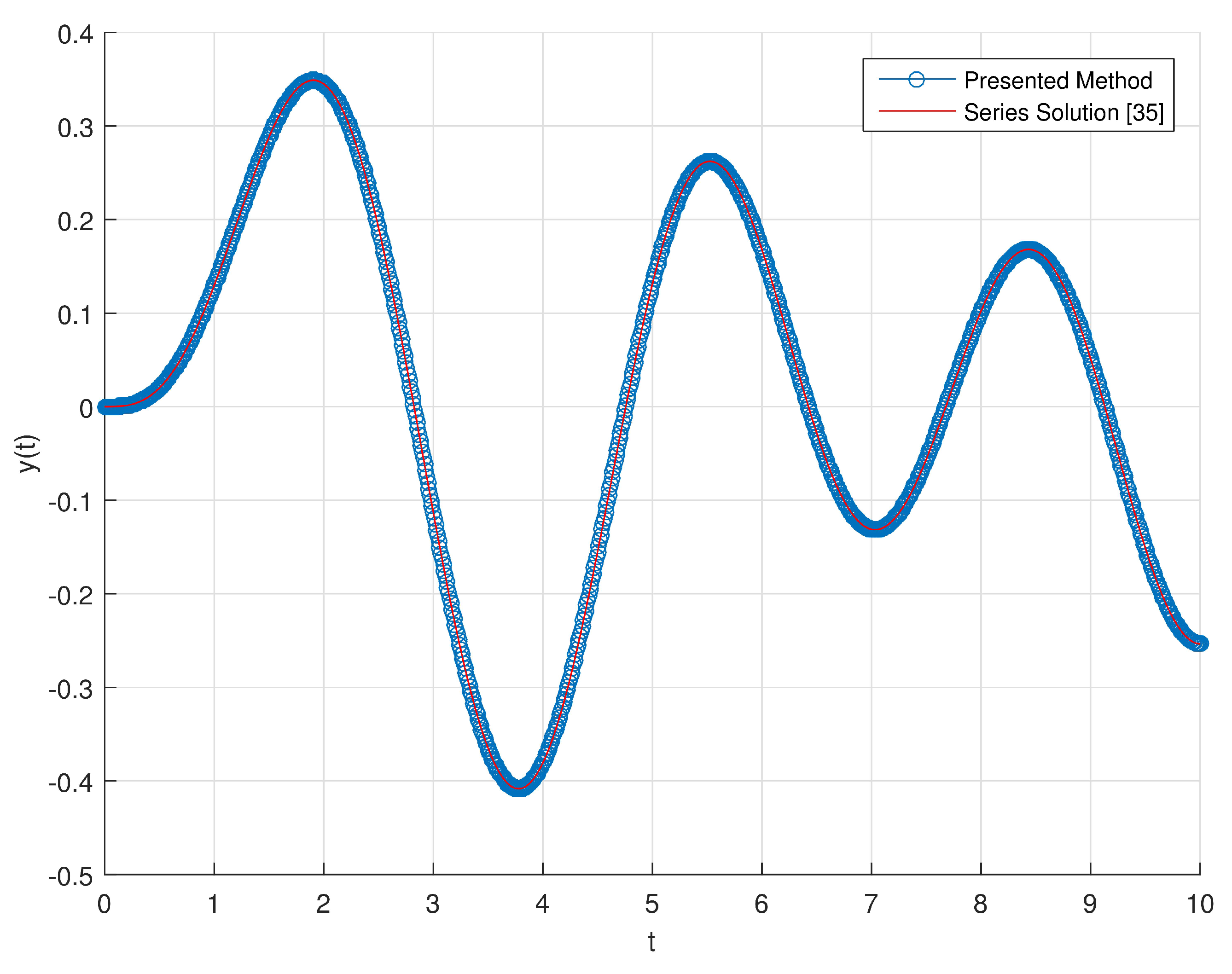
In
Figure 10, we show the graphical representation for series solution and the numerical results of presented method for the interval
. The results plotted in
Figure 10 are in a very good and satisfactory agreement with the series solution given in [
52] and the results of [
60].
5.4. Example 4
Motivated by [
50], we consider the following form of fractional differential equation,
with initial conditions
whose exact solution is
In order to apply the presented method to Equation (
28) and compare the results with methods of [
54,
61,
62], we solve this problem with
and different values for
and
m. The obtained results are presented as below.
In
Table 5, we list the results of obtained absolute errors for
by use of presented method. Also, the results for
are given in
Table 6.
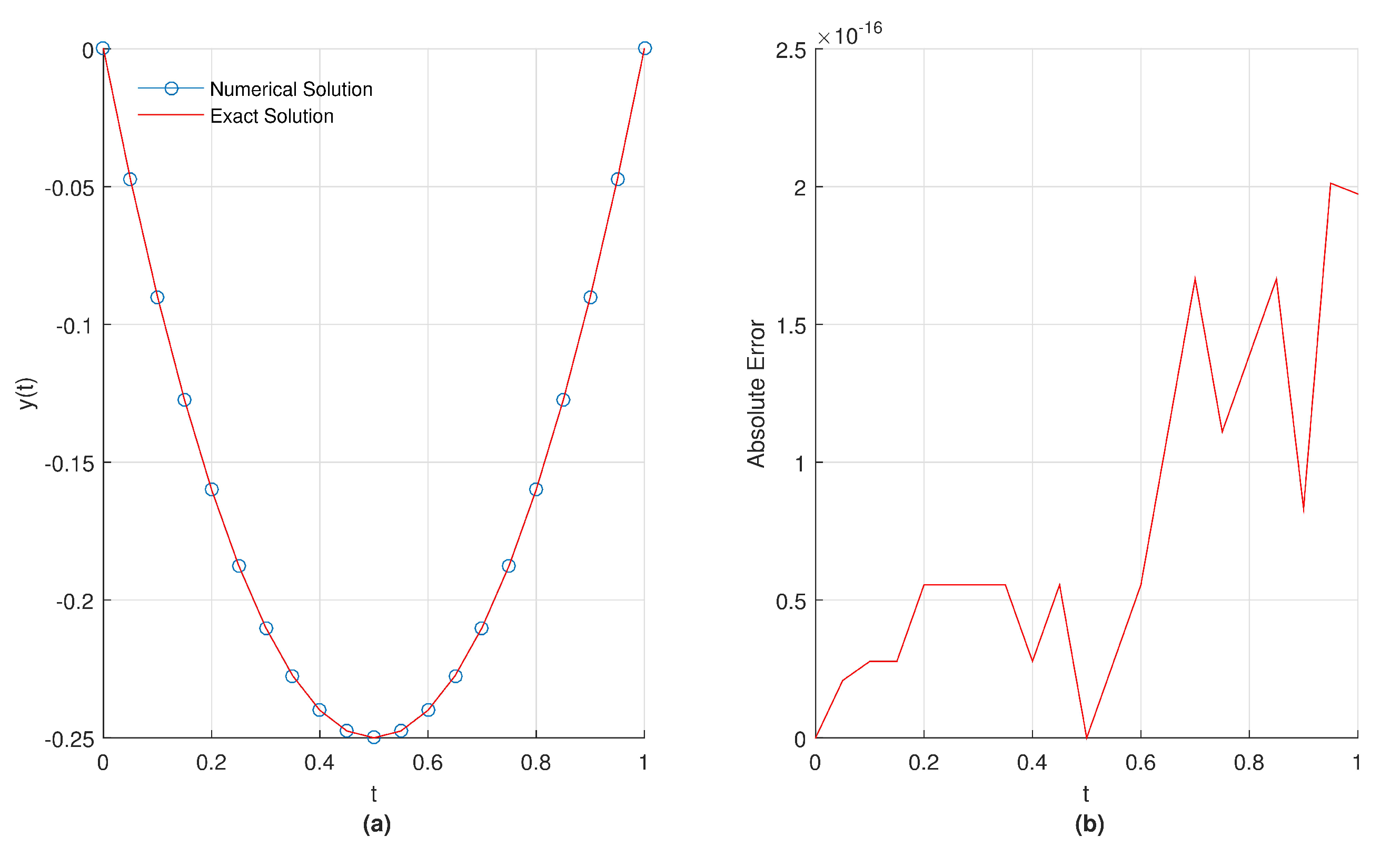
In
Figure 11a,b, we present the graphical representation of obtained results for numerical and exact solution of the given problem and absolute error for
in the interval
.
In
Figure 12, we plot the graphical representation for behavior of the obtained numerical solution by use of the presented method and the exact solution of the given problem for
in the interval
.
Table 7 lists the obtained absolute errors for the given problem (
28) at
and
by use of presented method and some other methods in literature [
54,
61,
62]. From this compared results, we can say that the numerical solution obtained by use of proposed method is in better agreement with the exact solution and obtained absolute error is smaller.
In
Figure 13, the behaviour of absolute error for
with
and
at
is presented. From this graph, it can be seen that we get better results by taking
for this example and the numerical solution is very close to exact solution for a small number of
5.5. Example 5
In this example, we consider the following form of linear multi-term fractional differential equation with variable coefficients [
65]
with,
where
and
whose the exact solution is given by
We give the numerical solution for the given problem by proposed method for with .
In
Table 8, we give the results for maximum errors obtained by use of proposed method and comparison with the results of [
65,
66]. From this compared results, we can see that the numerical solution obtained by use of proposed method is closer to the exact solution.
Figure 14 presents the graphical representation for behaviour of numerical and exact solutions with
. From this representation, we can see that the numerical solution is in a very good agreement with exact solution.
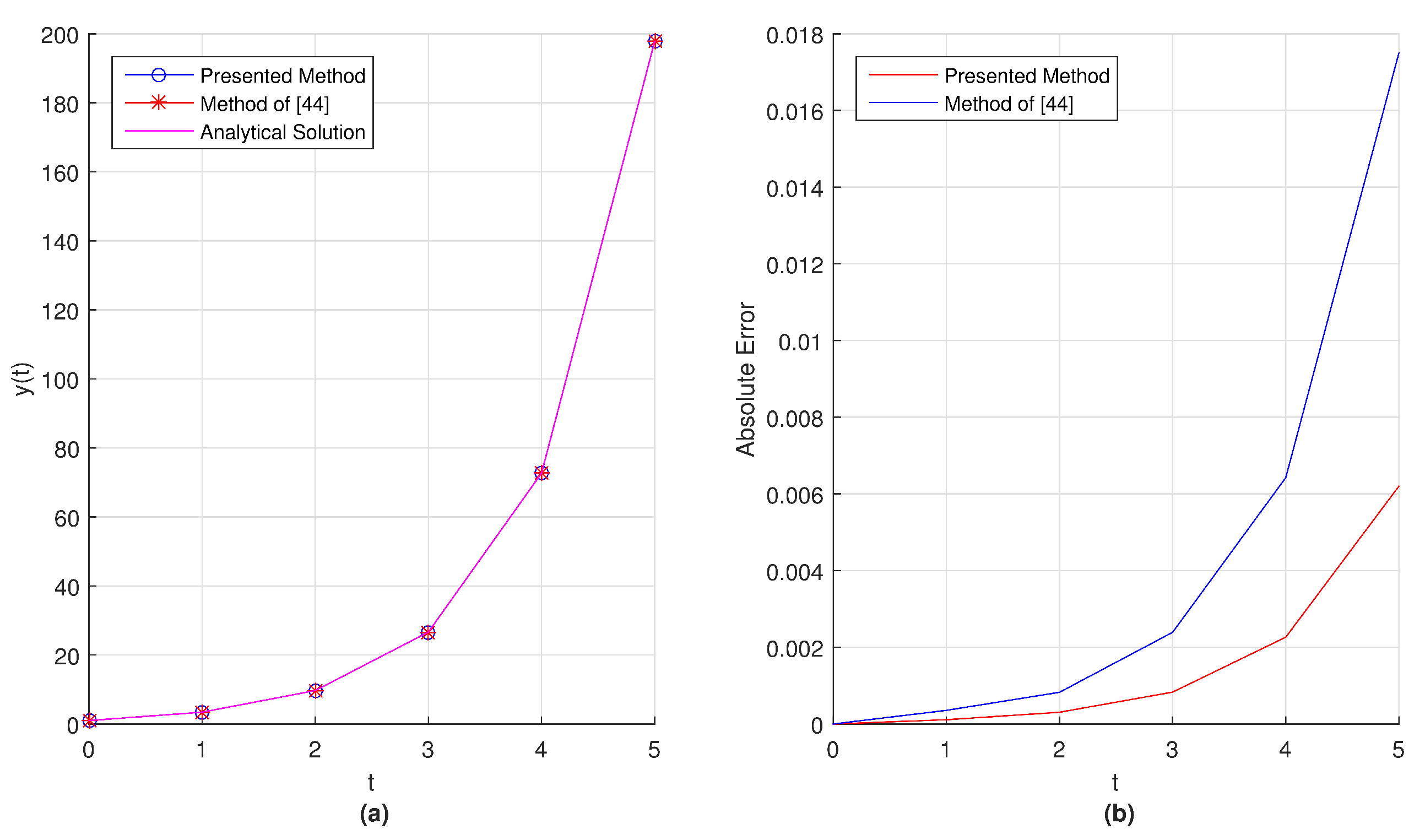
5.6. Example 6
For the last example, let us consider the below fractional differential equation [
63]
which arises, for example, in the study of generalized Basset force occuring when a spherical object sinks in a (relatively dense) incompressible viscous fluid; see [
43,
67]. By use of Laplace transformation of Caputo derivatives, we get the analytical solution as following
where the Mittag–Leffler function
with parameters
is given as
This Mittag–Leffler function and its variations are very significant in fractional calculus and fractional differential equations [
68].
In order to solve given problem by use of proposed method and compare the results, we take and use different values of and m.
Table 9 lists the exact and obtained numerical solutions by use of presented method and method of [
63] for the given problem for
. Comparison of this results shows that, even for small values of
m, the numerical solution obtained by use of presented method is in a better agreement with exact solution.
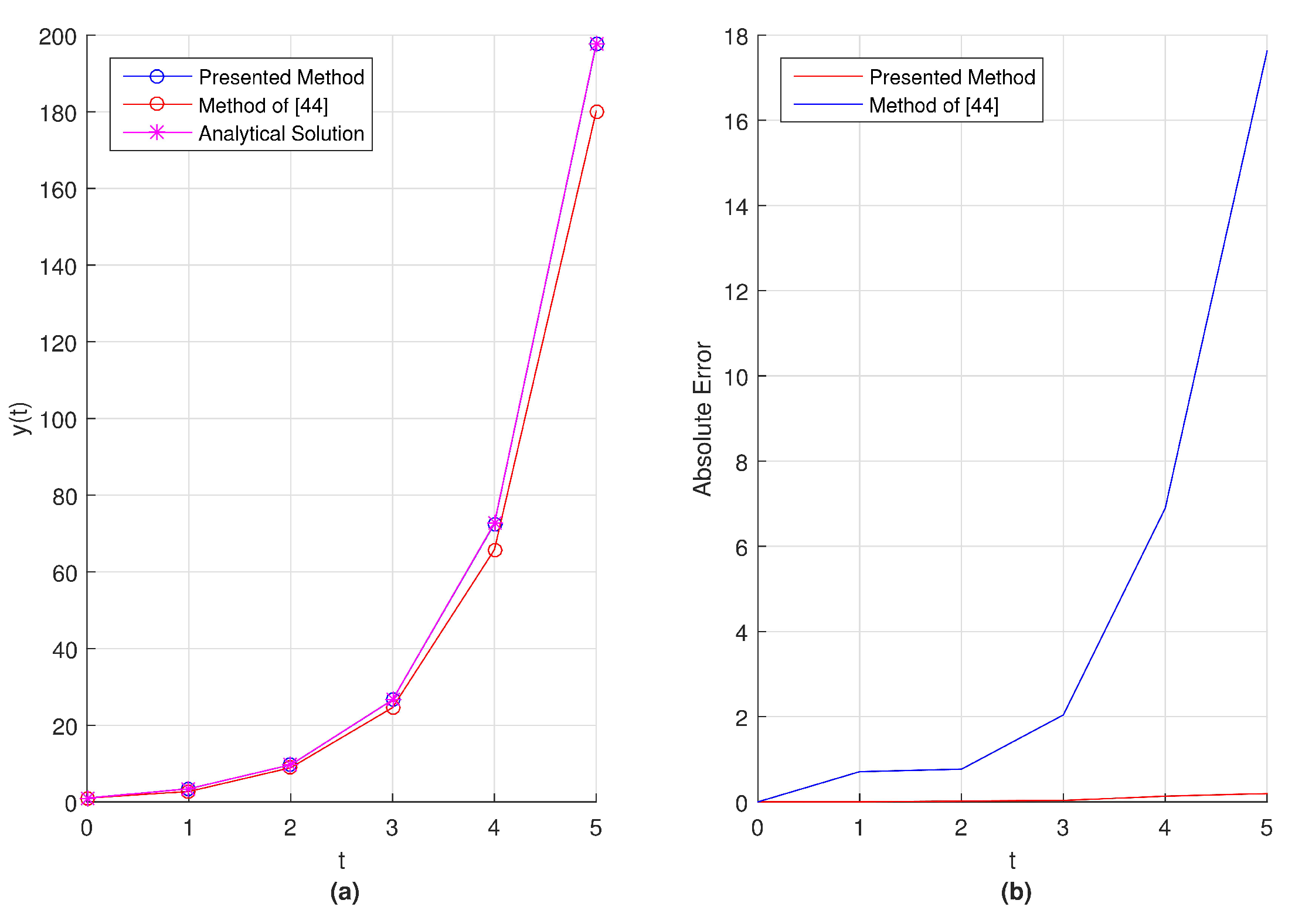
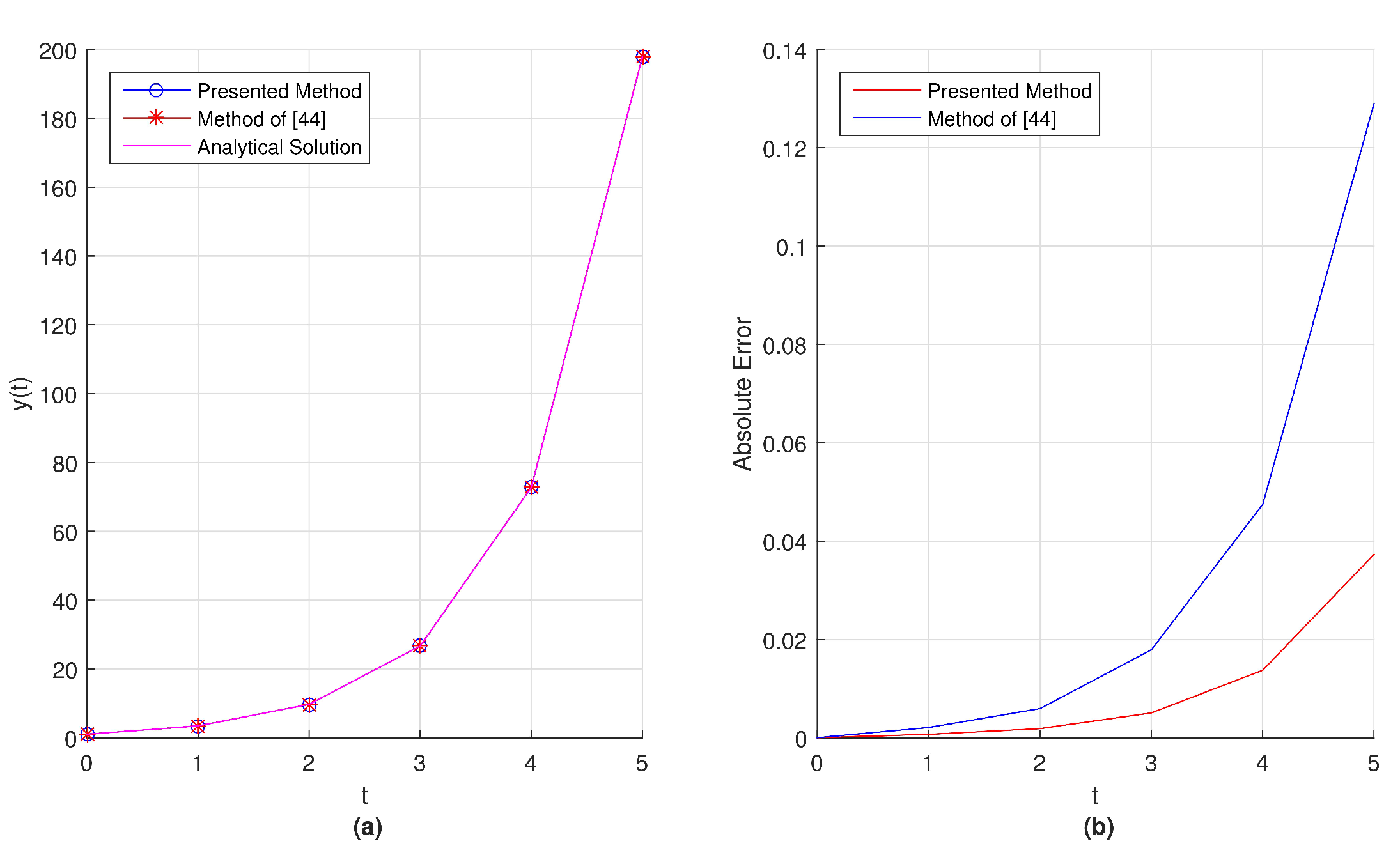
In
Figure 15a,
Figure 16a and
Figure 17a, we present the graphical representation of comparison between exact solution and the numerical solutions obtained by using proposed method and the method of [
63] with taking
respectively. Also in
Figure 15b,
Figure 16b and
Figure 17b we show the behaviour of absolute errors obtained by proposed method and the method of [
63] in the interval
with
.
From these graphical results represented in
Figure 15,
Figure 16 and
Figure 17, we can conclude that the absolute error obtained by our method is remaining smaller when compared the absolute error of method given in Reference [
63].