Some Bounds on Zeroth-Order General Randić Index

Abstract

For a graph G without isolated vertices, the inverse degree of a graph G is defined as $ID(G)={\sum }_{u\in V(G)}d{(u)}^{-1}$ where $d(u)$ is the number of vertices adjacent to the vertex u in G. By replacing $-1$ by any non-zero real number we obtain zeroth-order general Randić index, i.e., ${}^0{R}_{\gamma }(G)={\sum }_{u\in V(G)}d{(u)}^{\gamma }$, where $\gamma \in R-\left\{0\right\}$. Xu et al. investigated some lower and upper bounds on $ID$ for a connected graph G in terms of connectivity, chromatic number, number of cut edges, and clique number. In this paper, we extend their results and investigate if the same results hold for $\gamma <0$. The corresponding extremal graphs have also been identified.

1. Chemical Graph Theory

Chemical graph theory is a branch of mathematics that combines graph theory and chemistry. Graph theory is used to mathematically model molecules in order to gain insight into the physical properties of these chemical compounds. A molecular graph of a chemical compound is a graph in which atoms are represented by vertices and edges are the bonds between them. The molecular graphs of napthalene, pyrene, and coronene are shown in Figure 1. A topological index is a number associated to the molecular graph that can help to predict the various chemical or physical properties of the molecule. Topological indices play vital roles in the field of chemical graph theory.

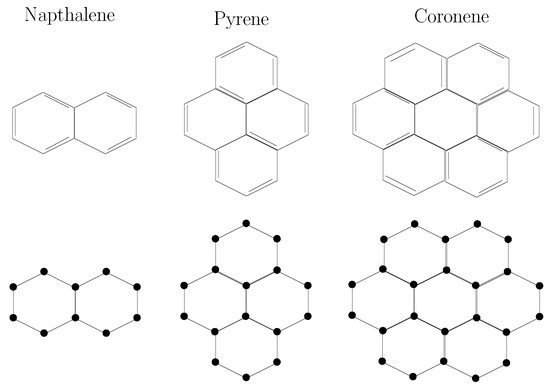
Figure 1. The molecular graphs of some polycyclic aromatic hydrocarbons.

H. Wiener introduced the first topological index when he was working on the boiling points of the paraffin. In [1,2,3], he showed that there are very good correlations between the Wiener index of the molecular graph of organic compounds and different physico-chemical properties of the molecular compounds. After that a lot of research have been done on the applications of graph theory in chemistry [4,5,6,7,8,9,10,11,12,13,14].

Nowadays, study of behavior of topological indices is an important task.

2. Introduction

Throughout this paper, we only consider finite, connected, and simple graphs and for the terminologies on the graph theory not defined here one can see [15]. Let G be a graph with vertex set $V(G)$ and edge set $E(G)$. The number of elements in $V(G)$ and $E(G)$ are called the order and the size of G, respectively. For a vertex u of G, $N_G(u)$ is the set of vertices adjacent to the vertex u in G and the number of elements in $N_G(u)$ is called the degree of the vertex u in G, denoted by $d_G(u)$ or simply $d(u)$. Additionally, $N_G\left[u\right]=N_G(u)\cup \left\{u\right\}$. A vertex u is said to be a pendant vertex if $d(u)=1$ and an edge is said to be a pendant edge if it is incident with a pendant vertex. In a graph G the maximum and minimum degrees are denoted by $▵(G)$ and $\delta (G)$, respectively. For subsets $S\subset V(G)$ and $T\subset E(G)$, $G-S$ and $G-T$ are the subgraphs obtained from G by removing the element of S and T, respectively, from G. For two non-adjacent vertices u and v in a graph G, $G+uv$ is the graph obtained from G by adding an edge between u and v and $G-uv$ is the graph deduced by deleting the edge $uv$.

The minimum number of colors required to color a graph G in such a way that no adjacent vertices have the identical color is called the chromatic number of G and is denoted by $\chi (G)$. A subset of vertices is called a clique if it induces a complete graph. The maximum number of vertices in a clique is called the clique number of G and is denoted by $\omega (G)$. Let $G_1$ and $G_2$ be two vertex disjoint graphs. $G_1\cup G_2$ is the graph which consists of two components $G_1$ and $G_2$. The join of $G_1$ and $G_2$, $G_1+G_2$, is the graph whose vertex set is $V(G_1)\cup V(G_2)$ and the edge set is $E(G_1)\cup E(G_2)\cup \{uv:u\in V(G_1),v\in V(G_2)\}$. A subset of vertices is called an independent set if it induces an empty graph. Two edges in G are said to be independent edges if they are non-adjacent.

A connected graph is called c-connected, for $c\ge 1$, if either G is a $K_{c+1}$ complete graph or else it has at least $c+2$ vertices and has no $(c-1)$-vertex cut. On the same lines, a graph G is c-edge-connected if $\left|G\right|\ge 2$ and it does not have any $(c-1)$-edge cut. The connectivity, $\kappa (G)$, of G is the maximum value of c such that G is c-connected. The edge-connectivity, ${\kappa }^{\prime }(G)$ is defined analogously. Note that for a graph G of order n we have $\kappa (G)\le {\kappa }^{\prime }(G)\le \delta (G)\le n-1$ and $\kappa (G)=n-1,{\kappa }^{\prime }(G)=n-1$ and $G=K_n$ are equivalent.

Throughout this paper, $P_n,S_n,C_n$ and $K_n$ represent the path, star, cycle, and complete graphs with n vertices.

For a graph G without isolated vertices, Kier et al. [16] proposed the zeroth-order Randić index as:

$${}^0{R}_{-\frac{1}{2}}(G)=\sum _{u\in V(G)}d{(u)}^{-1/2}$$

In 2005, Li et al. [17] introduced the zeroth-order general Randić index by replacing the fraction $-\frac{1}{2}$ by any non-zero real number $\gamma$:

$${}^0{R}_{\gamma }(G)=\sum _{u\in V(G)}d{(u)}^{\gamma }$$

In [18], authors investigated some sharp bounds on ${}^0{R}_{\gamma }$ for unicyclic graphs with n vertices and diameter d. Volkmann [19] presented sufficient conditions for digraphs to be maximally edge connected in terms of the zeroth-order general Randić index. In [20] Yamaguchi obtained the trees with first three largest zeroth-order general Randić indices among all the trees with given order, diameter, or radius. Jamil et al. [21] investigated the extremal graphs of k-generalized quasi trees for zeroth-order general Randić index. For further results we refer to [22,23,24,25,26,27,28,29,30,31,32,33,34,35].

For a graph G without isolated vertices, the inverse degree $ID(G)$ of G is defined as:

$$ID(G)=\sum _{u\in V(G)}d{(u)}^{-1}$$

The inverse degree of a graph was initially discussed in [36]. After that a lot of work have been done on inverse degree, for details we refer to [37,38,39,40]. Xu et al. [41] investigated certain bounds on $ID(G)$ for a connected graph G in terms of clique number, chromatic number, connectivity, or number of cut edges. They also characterized the extremal graphs. In this paper, we extended their work and investigated if the corresponding results hold for zeroth-order general Randić index, their results can be viewed as corollaries of the main theorems.

3. Preliminary Results

First we present some lemmas that will be useful in proving main results. From the definition of zeroth-order general Randić index for $\gamma <0$ we have the following lemma.

Lemma 1.

Let G be a graph such that $vw\in E(G)$ and $y,z\in V(G)$ are nonadjacent. Then for $\gamma <0$, we have:

1. 

${}^0{R}_{\gamma }(G-vw)>{}^0{R}_{\gamma }(G)$ if $d(v),d(w)\ge 2$;

2. 

${}^0{R}_{\gamma }(G+xy)<{}^0{R}_{\gamma }(G)$ where x and y are non-isolated vertices in G.

Lemma 2.

For $n>2$, let G be a graph of order n with $v,w\in V(G)$ such that $d(v)\ge d(w)$ and $N_G(w)\setminus N_G\left[v\right]=\{w_1,w_2,\dots ,w_t\}$ where $t>0$. From G we attain a new graph $G^{\ast }=(G-\{w{w}_1,w{w}_2,\dots ,w{w}_t\})+\{v{w}_1,v{w}_2,\dots ,v{w}_t\}$. If $d(w)>t$, for $\gamma <0$ we have ${}^0{R}_{\gamma }(G^{\ast }){>}^0{R}_{\gamma }(G)$.

Proof. 

From the definition of zeroth-order general Randić index, we have ${}^0{R}_{\gamma }(G^{\ast })-{{}^{0}R}_{\gamma }(G)={(d(v)+t)}^{\gamma }-d{(v)}^{\gamma }+{(d(w)-t)}^{\gamma }-d{(w)}^{\gamma }$. We deduce that $f(x)=x^{\gamma }-{(x-t)}^{\gamma }$ is a strictly increasing function for $x>t$ and $\gamma <0$. Since $d(v)\ge d(w)$ we have $d(v)+t>d(w)$ and this implies that ${}^0{R}_{\gamma }(G^{\ast })-{{}^{0}R}_{\gamma }(G)=f(d(v)+t)-f(d(w))>0$.  □

Lemma 3.

For $n\ge x\ge 2$ and $\gamma <0$, the function:

$$\psi (x)=(n-x)x^{\gamma }-(n-x+1){(x-1)}^{\gamma }$$

(1)

is a strictly increasing function.

Proof. 

For given $\psi (x)$, we obtain ${\psi }^{\prime }(x)=\gamma (n-x)x^{\gamma -1}-x^{\gamma }-\gamma (n-x+1){(x-1)}^{\gamma -1}+{(x-1)}^{\gamma }>\gamma ((n-x)x^{\gamma -1}-(n-x+1)x^{\gamma -1})-x^{\gamma }+{(x-1)}^{\gamma }=-\gamma x^{\gamma -1}-x^{\gamma }+{(x-1)}^{\gamma }>0$. Hence, for given $n\ge x\ge 2$ the function $\psi (x)$ is strictly increasing.  □

Lemma 4.

Let $n,c$ be integer numbers, $n\ge 3$ and $1\le c\le n-2$. For $1\le x\le n-c-1$ and $-1\le \gamma <0$, the function $f(x)=x{(x+c-1)}^{\gamma }+(n-c-x){(n-1-x)}^{\gamma }$ is minimum for $x=1$ and $x=n-c-1$. For $c=1$ and $\gamma =-1$ we get $f(x)=2$.

Proof. 

We have $f(x)=f(n-c-x)$, which implies that $x=(n-c)/2$ is a symmetry axis for the graph of this function. Its derivative equals $f^{\prime }(x)={(x+c-1)}^{\gamma -1}(c-1+x(\gamma +1))-{(n-1-x)}^{\gamma -1}(n(\gamma +1)-1-\gamma c-x(\gamma +1))$. By the symmetry of f we can only consider the case when $x\ge (n-c)/2$. We have $f^{\prime }((n-c)/2)=0$ and we shall prove that $f^{\prime }(x)<0$ for $x>(n-c)/2$. This condition is equivalent to:

$${\left(\frac{x+c-1}{n-1-x}\right)}^{\gamma -1}<\frac{(\gamma +1)(n-x)-\gamma c-1}{x(\gamma +1)+c-1}.$$

(2)

Since $x>(n-c)/2$ and $\gamma <0$ it follows that ${\left(\frac{x+c-1}{n-1-x}\right)}^{\gamma -1}<{\left(\frac{x+c-1}{n-1-x}\right)}^{-1}=\frac{n-1-x}{x+c-1}.$ But $\frac{n-1-x}{x+c-1}\le \frac{(\gamma +1)(n-x)-\gamma c-1}{x(\gamma +1)+c-1}$ since this is equivalent to $\gamma (c-1)(2x-n+c)\le 0$ and Equation (2) is proved.  □

Lemma 5.

Every c-chromatic graph has at least c vertices of degree at least $c-1$ [15].

4. Main Results and Discussion

In this section, we will present our main results.

4.1. Extremal Graphs w.r.t. Zeroth-Order General Randić Index in Terms of Chromatic Number and Clique Number

Let $\complement (n,c)$ denote the set of all connected graphs having order n and chromatic number c and $\mho (n,c)$ the set of all connected graphs with order n and clique number c. Hereafter, we always consider that $n_1\ge n_2\ge \dots \ge n_c$ are positive integers with ${\sum }_{i=1}^c{n}_i=n$. A complete c-partite graph of order n whose partite sets are of size $n_1,n_2,\dots ,n_c$, respectively, is denoted by $K_{n_1,n_2,\dots ,n_c}$. $K_{n_1,n_2,\dots ,n_c}$ is called the Turán graph if $|n_i-n_j|\le 1$ for each $1\le i,j\le c$. The Turán graph with n vertices and c-partite sets is denoted by $T_n(c)$ and such a graph is shown in Figure 2. For $c=1$ and $c=n$ we have $\complement (n,c)=\left\{\overline{K_n}\right\}$ and $\complement (n,c)=\left\{K_n\right\}$, respectively. Also, $\mho (n,1)\left\{\overline{K_n}\right\}$, and $\mho (n,n)\left\{K_n\right\}$. Here we will investigate the extremal graphs in $\complement (n,c)$ and $\mho (n,c)$ w.r.t. ${}^0{R}_{\gamma }$.

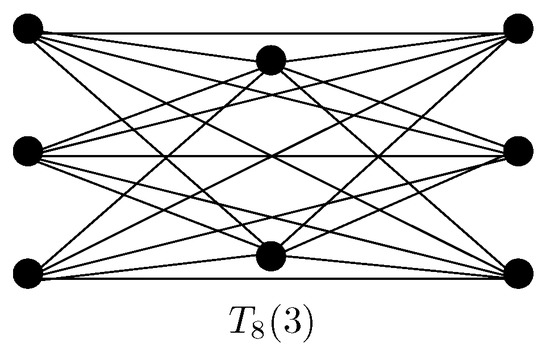
Figure 2. A Turan graph.

Lemma 6.

Suppose that there exist two indices $i,j$ such that $i\ne j$, $1\le i,j\le c$ and $n_j-n_i\ge 2$. Then for $\gamma <0$ we have:

$${}^0{R}_{\gamma }(K_{n_1,\dots ,n_i,\dots ,n_j,\dots ,n_c})>{{}^{0}R}_{\gamma }(K_{n_1,\dots ,n_i+1,\dots ,n_j-1,\dots ,n_c})$$

Proof. 

Suppose that $i<j$. From the definition of zeroth-order general Randić index we have:

$$\begin{array}{cc}\hfill {}^0{R}_{\gamma }(K_{n_1,\dots ,n_i,\dots ,n_j,\dots ,n_c})& -{{}^{0}R}_{\gamma }(K_{n_1,\dots ,n_i+1,\dots ,n_j-1,\dots ,n_c})=n_i{(n-n_i)}^{\gamma }+n_j{(n-n_j)}^{\gamma }\hfill \\ & -(n_i+1){(n-n_i-1)}^{\gamma }-(n_j-1){(n-n_j+1)}^{\gamma }\hfill \\ \hfill & =\psi (x)-\psi (y+1),\hfill \end{array}$$

where $x=n-n_i,y=n-n_j$ and $\psi (x)$ is given by (1). Additionally, we have $n_j-n_i\ge 2$ which implies that $x-y\ge 2$ and $x>y+1$. By Lemma 3$\psi (x)$ is strictly increasing, which yields:

$${}^0{R}_{\gamma }(K_{n_1,\dots ,n_i,\dots ,n_j,\dots ,n_c})-{{}^{0}R}_{\gamma }(K_{n_1,\dots ,n_i+1,\dots ,n_j-1,\dots ,n_c})>0,$$

which completes the proof.  □

For this subsection assume that $1<c<n$ and $n=cq+r$, where $0\le r<c$, i.e., $q=⌊\frac{n}{c}⌋$.

Theorem 1.

For any graph $G\in \complement (n,c)$ and $\gamma <0$, we have:

$${}^0{R}_{\gamma }(G)\ge (c-r)⌊\frac{n}{c}⌋{(n-⌊\frac{n}{c}⌋)}^{\gamma }+r⌈\frac{n}{c}⌉{(n-⌈\frac{n}{c}⌉)}^{\gamma }$$

and lower bound is achieved if and only if $G=T_n(c)$.

Proof. 

Let $G\in \complement (n,c)$ such that G has the minimal zeroth-order general Randić index for $\gamma <0$. From the definition of the chromatic number, G has c color classes and every color class is an independent set. Suppose that each color class contains $n_i$ vertices, where $1\le i\le c$. By Lemma 1 one deduces that G must be a complete c-partite graph $K_{n_1,\dots ,n_c}$ and Lemma 6 guarantees that $G=T_n(c)$. We have:

$${}^0{R}_{\gamma }(T_n(c))=(c-r)⌊\frac{n}{c}⌋{(n-⌊\frac{n}{c}⌋)}^{\gamma }+r⌈\frac{n}{c}⌉{(n-⌈\frac{n}{c}⌉)}^{\gamma },$$

which completes the proof.  □

Further, we shall use some notation introduced in [41]. A graph gained by joining $n-c$ pendant vertices to unique vertex of $K_c$ is called a pineapple graph and is denoted by $P{A}_n(c)$. $S_n(m_1,m_2,\dots ,m_c)$ will denote a connected graph of order n gained by joining $n-c$ pendant vertices to a complete graph $K_c$, such that $m_i$ pendant vertices are attached to the ith vertex of $K_c$ for $1\le i\le c$. A pineapple graph of order 8 is shown in Figure 3. It follows that ${\sum }_{i=1}^c{m}_i=n-c$. We consider that the vertices in the clique are labeled $v_1,v_2,\dots ,v_c$. From the definition of $S_n(m_1,m_2,\dots ,m_c)$ we have $S_n(0,0,\dots ,0)=K_c$ and $S_n(n-c,0,\dots ,0)=P{A}_n(c)$.

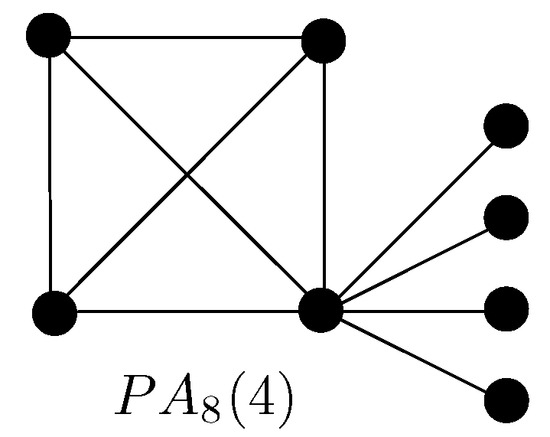
Figure 3. A pineapple graph.

In the following theorem we give the maximum value of ${}^0{R}_{\gamma }(G)$ by using the order n and chromatic numbers c of G.

Theorem 2.

Let $\gamma \le -1$ and $G\in \complement (n,c)$, then,

$${}^0{R}_{\gamma }(G)\le n-c+{(n-1)}^{\gamma }+(c-1){(c-1)}^{\gamma }$$

and the equality holds if and only if $G=P{A}_n(c)$.

Proof. 

Since G is connected it follows that $c\ge 2$. If $c=n$ then $G=K_n$ and the theorem is verified directly. It remains to consider the case when $2\le c\le n-1$. It follows that $n\ge 3$. Clearly, for $c=2$G is a connected bipartite graph. Moreover, if $G=S_n$ (note that the star $S_n$ coincides with $S_n(n-2,0)$ and with $P{A}_n(2))$, then the above equality holds and in this case ${}^0{R}_{\gamma }(G)=n-1+{(n-1)}^{\gamma }$. Otherwise, G has at least two non-pendant vertices. This implies ${}^0{R}_{\gamma }(G)\le 2·2^{\gamma }+n-2<(n-1)+{(n-1)}^{\gamma }$, because $2·2^{\gamma }-1-{(n-1)}^{\gamma }<2·2^{\gamma }-1\le 0$. Hence, G is not maximal if $G\ne S_n$.

Now, we prove the theorem for $3\le c\le n-1$. Assume that $V(G)=\{v_1,v_2,\dots ,v_n\}$. By Lemma 5, we can consider a set of vertices $A(G)=\{v_1,v_2,\dots ,v_c\}$, such that $d(v_i)\ge c-1$ for $1\le i\le c$. Then we have $|V(G)\setminus A(G)|>0$. If there exists $v_k\in V(G)\setminus A(G)$ such that $d(v_k)\ge 2$, then ${}^0{R}_{\gamma }(G)\le c{(c-1)}^{\gamma }+2^{\gamma }+n-c-1<n-c+{(n-1)}^{\gamma }+(c-1){(c-1)}^{\gamma }$ if and only if ${(c-1)}^{\gamma }+2^{\gamma }-1-{(n-1)}^{\gamma }<0$. The last inequality is valid since $c\ge 3$ implies ${(c-1)}^{\gamma }\le 2^{\gamma }$, which yields ${(c-1)}^{\gamma }+2^{\gamma }-1-{(n-1)}^{\gamma }\le 2^{\gamma +1}-1-{(n-1)}^{\gamma }<0$, which holds because $\gamma \le -1$.

This shows that $d(v_k)=1$ for each $v_k\in V(G)\setminus A(G)$, where $c+1\le k\le n$, for a graph having maximum ${}^0{R}_{\gamma }$. Since G has chromatic number c it follows that the subgraph of G induced by $A(G)$ is $K_c$. It follows that G is a complete graph $K_c$ with $n-c$ pendant vertices, that is, $S_n(m_1,m_2,\cdots ,m_c)$ such that ${\sum }_{i=1}^c{m}_i=n-c$. If $S_n(m_1,m_2,\dots ,m_c)=P{A}_n(c)$ we are done. Otherwise, by applying Lemma 2 several times and supposing that $m_1\ge m_2\ge \dots \ge m_c$, we get:

$$\begin{gathered} {}^0{R}_{\gamma }(G)={{}^{0}R}_{\gamma }(S_n(m_1,m_2,\dots ,m_c))<{{}^{0}R}_{\gamma }(S_n(m_1+m_c,m_2,\dots ,m_{c-1},0)) \\ <\dots <{{}^{0}R}_{\gamma }(S_n(n-c-m_2,m_2,0,\dots ,0))<{{}^{0}R}_{\gamma }(S_n(n-c,0,\dots ,0)) \\ ={{}^{0}R}_{\gamma }(P{A}_n(c)), \end{gathered}$$

which completes the proof.  □

The following result gives upper and lower bounds on zeroth-order general Randić index in terms of order n and clique number c.

Theorem 3.

For any graph $G\in \mho (n,c)$ and $\gamma \le -1$ we have:

$$(c-r)⌊\frac{n}{c}⌋{(n-⌊\frac{n}{c}⌋)}^{\gamma }+r⌈\frac{n}{c}⌉{(n-⌈\frac{n}{c}⌉)}^{\gamma }{\le }^0{R}_{\gamma }(G)\le n-c+{(n-1)}^{\gamma }+(c-1){(c-1)}^{\gamma }$$

The lower bound is attained if and only if $G=T_n(c)$ and the upper bound if and only if $G=P{A}_n(c)$.

Proof. 

The main arguments of this proof are similar to those of the proof of Theorem 3.3 from [41].

Upper bound: Let $G^{\prime }\in \mho (n,c)$ having as large as possible zeroth-order general Randić index. Since $G^{\prime }$ has clique number c, we can conclude that $G^{\prime }$ have a clique $\{v_1,v_2,\dots ,v_c\}$. From Lemma 1 (1), we can see that $G^{\prime }$ must be a graph achieved by joining to $v_i$ some tree $T_i$ for $1\le i\le c$. Then the chromatic number of $G^{\prime }$ is c, and the result immediately follows from the proof of Theorem 2.

Lower bound: Let ${\mho }^{\prime }(n,c)$ be the set of all graphs having order n and clique number less than or equal to c. We shall prove the case below first.

Claim 1. For each graph $G\in {\mho }^{\prime }(n,c)$, we have:

$${}^0{R}_{\gamma }(G)\ge {{}^{0}R}_{\gamma }(T_n(c))$$

and equality holds if and only if $G=T_n(c)$.

Proof of Claim 1.

If $G=K_{n_1,\dots ,n_c}$, then by Lemma 6 we have:

$${}^0{R}_{\gamma }(G)={{}^{0}R}_{\gamma }(K_{n_1,\dots ,n_c}){\ge }^0{R}_{\gamma }(T_n(c))$$

and equality holds if and only if $G=T_n(c)$.

Otherwise, G is not a multipatite complete graph of the form $K_{n_1,\dots ,n_c}$. Let $u\in V(G)$ such that u has maximum degree $d(u)=▵(G)$ in G. Let $A=N_G(u)$ and $B=V(G)\setminus A$. The clique number of the induced subgraph of G by A, $G\left[A\right]$, is at most $c-1$ since $\omega (G)\le c$. Now we compose a graph $G^{\ast }$ on $V(G)$ as: $G^{\ast }$ is achieved from the subgraph $G\left[A\right]$ and the subset B by attaching all vertices in A to all vertices of B and removing all possible edges which have both ends in B. One can easily notice that B is an independent set of $G^{\ast }$ and $\omega (G^{\ast })\le c$. Let $w\in V(G^{\ast })=V(G)$; if $w\in A$ we have $d_{G^{\ast }}(w)\ge d_G(w)$ from the construction of $G^{\ast }$ and if $w\in B$ we have $d_{G^{\ast }}(w)\ge d_G(w)$ by the choice of u. This implies that ${}^0{R}_{\gamma }(G^{\ast })\le {{}^{0}R}_{\gamma }(G)$. If $G^{\ast }$ is a complete t-partite graph with n vertices, where $2\le t\le c$, then we have ${}^0{R}_{\gamma }(G){\ge }^0{R}_{\gamma }(G^{\ast }){=}^0{R}_{\gamma }(K_{n_1,\dots ,n_t}){\ge }^0{R}_{\gamma }(T_n(t)){\ge }^0{R}_{\gamma }(T_n(c))$.

The inequality ${}^0{R}_{\gamma }(T_n(t)){\ge }^0{R}_{\gamma }(T_n(c))$ follows since $T_n(t)$ has vertex degrees equal to $n-\lfloor \frac{n}{t}\rfloor$ and $n-\lceil \frac{n}{t}\rceil$, which are less than or equal to the vertex degrees of $T_n(c)$.

Otherwise, repeating the same procedure on $G\left[A\right]$ by at most $c-2$ times (during this process if $G_i$ is a complete t-partite graph with n vertices, we stop the above process), we gain a string of graphs:

$$G=G_0,G_1,\dots ,G_r,G_{r+1},\dots ,G_{p-1},G_p=K_{n_1,\dots ,n_t};t\le c$$

such that ${}^0{R}_{\gamma }(G)={{}^{0}R}_{\gamma }(G_0)\ge {{}^{0}R}_{\gamma }(G_1)\ge \dots \ge {{}^{0}R}_{\gamma }(G_{p-1})\ge {{}^{0}R}_{\gamma }(G_p)$$={{}^{0}R}_{\gamma }(K_{n_1,\dots ,n_t})\ge {{}^{0}R}_{\gamma }(T_n(c)).$

Since G is not a multipatite complete graph of the form $K_{n_1,\dots ,n_c}$, then in the above string of graphs there must occur two successive non-isomorphic graphs $G_r$ and $G_{r+1}$ such that: u being a vertex with maximum degree in $G_r$ and denoting $A=N_{G_r}(u)$ and $B=V(G_r)\setminus A$, when we transform $G_r$ to $G_{r+1}$, there must exist a vertex w in A or B such that $d_{G_r+1}(w)>d_{G_r}(w)$. Hence,

$$\begin{array}{cc}\hfill {}^0{R}_{\gamma }(G)={{}^{0}R}_{\gamma }(G_0)& \ge {{}^{0}R}_{\gamma }(G_1)\ge \cdots {\ge }^0{R}_{\gamma }(G_r){>}^0{R}_{\gamma }(G_{r+1})\ge \dots \hfill \\ & \ge {{}^{0}R}_{\gamma }(G_{p-1})\ge {{}^{0}R}_{\gamma }(G_p)={{}^{0}R}_{\gamma }(K_{n_1,\dots ,n_t})\ge {{}^{0}R}_{\gamma }(T_n(c))\hfill \end{array}$$

and the proof of the claim is complete.  □

Consequently, we have shown that for each graph $G\in {\mho }^{\prime }(n,c)$, ${}^0{R}_{\gamma }(G)$ reaches its minimum in ${\mho }^{\prime }(n,c)$, equal to ${}^0{R}_{\gamma }(T_n(c))=(c-r)⌊\frac{n}{c}⌋{(n-⌊\frac{n}{c}⌋)}^{\gamma }+r⌈\frac{n}{c}⌉{(n-⌈\frac{n}{c}⌉)}^{\gamma }$, only for $T_n(c)$. Note that $\mho (n,c)\subseteq {\mho }^{\prime }(n,c)$ with $T_n(c)\in \mho (n,c)$ and our lower bound was proved.  □

4.2. Extremal Graphs w.r.t. Zeroth-Order General Randić Index in Terms of Number of Cut Edges

In this subsection, we will investigate the bounds on zeroth-order general Randić index in terms of number of cut edges. We shall also characterize the graphs which will provide the extremal values. Let $\Omega (n,c)$ be the set of connected graphs having n vertices and $c>0$ cut edges. Let $C_{n-c}^c$ be a graph gained by joining c pendant vertices to unique vertex of cycle $C_{n-c}$, as illustrated in Figure 4. It is easy to see that $K_n$ and $C_n$ have the minimal and maximal zeroth-order general Randić index among all connected n-vertex graphs without any cut edge, respectively.

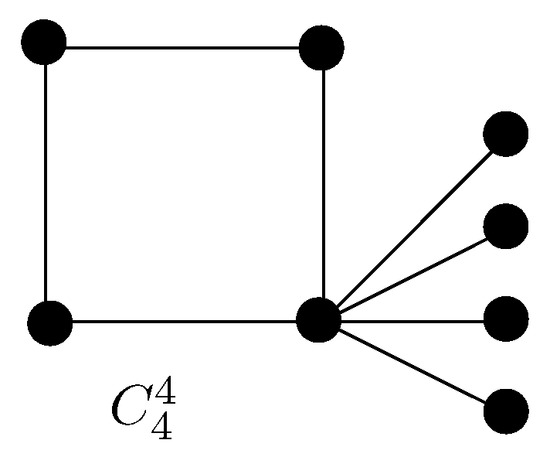
Figure 4. A $C_{n-c}^c$ graph for $n=8$ and $c=4$.

Theorem 4.

Let $G\in \Omega (n,c)$ and $1\le c\le n-3$, then for $\gamma <0$ we have:

$${}^0{R}_{\gamma }(G)\le c+(n-c-1)2^{\gamma }+{(c+2)}^{\gamma }$$

and the equality holds if and only if $G=C_{n-c}^c$.

Proof. 

Suppose that the graph $G\in \Omega (n,c)$ has the maximum zeroth-order general Randić index, for $\gamma <0$, with cut edge set $C=\{e_1,e_2,\dots ,e_c\}$. To prove the main result we first prove two claims.

Claim 1.

Let $e\in C$, then e must be a pendant edge.

Proof of Claim 1.

On contrary suppose that $e_1=u_1{v}_1$ is a non-pendant edge in G such that $d_G(u_1)\ge d_G(v_1)>1$. Suppose that $N_G(v_1)\setminus \left\{u_1\right\}=\{v_{11},v_{12},\dots ,v_{1t}\}$. Now we compose a graph:

$$G^{\ast }=G-\{v_1{v}_{11},v_1{v}_{12},\dots ,v_1{v}_{1t}\}+\{u_1{v}_{11},u_1{v}_{12},\dots ,u_1{v}_{1t}\}.$$

Clearly, $G^{\ast }\in \Omega (n,c)$. Since $e_1$ is a cut edge in G, so $N_G(v_1)\setminus N_G\left[u_1\right]=\{v_{11},v_{21},\dots ,v_{t1}\}$. Then by Lemma 2 and the case when $u_1$ and $v_1$ are adjacent we have ${}^0{R}_{\gamma }(G^{\ast })>{}^0{R}_{\gamma }(G)$, which opposes the maximality of G.  □

Claim 2.

The edges of C have a common vertex.

Proof of Claim 2.

From above all the edges $e_i$, $1\le i\le c$ are pendant. On contrary suppose that $e_1=u_1{v}_1$ and $e_2=u_2{v}_2$ are two distinct edges in G such that $d_G(u_i)=1$ for $i\in \{1,2\}$ and $v_1\ne v_2$. By applying Lemma 2 on $v_1$ and $v_2$, we obtain a new graph $G^{\ast \ast }\in \Omega (n,c)$ such that ${}^0{R}_{\gamma }(G^{\ast \ast })>{{}^{0}R}_{\gamma }(G)$, which is a contradiction.  □

Claim 2 implies that G is a graph attained by joining c pendant vertices to one vertex, say $v_0$ of $G_0$ where $G_0$ is a connected graph without cut edges. Considering that in $G_0$ any vertex has degree greater or equal to 2, we have:

$${}^0{R}_{\gamma }(G)=\sum _{w\in V(G_0)\setminus \left\{v_0\right\}}{(d_{G_0}(w))}^{\gamma }+{(d_{G_0}(v_0)+c)}^{\gamma }+c\le (n-c-1)2^{\gamma }+{(c+2)}^{\gamma }+c$$

and the equality holds if and only if $d_{G_0}(v)=2$ for each $v\in G_0$, i.e., $G_0=C_{n-c}$. Equivalently, $G=C_{n-c}^c$ and we are done.  □

4.3. Extremal Graphs w.r.t. ${{}^{0}R}_{\gamma }$ in Terms of Vertex (Edge) Connectivity

The set of all graphs of order n having connectivity and edge-connectivity equal to $c\le n-1$ is denoted by $V_n^c$ and $E_n^c$, respectively.

Theorem 5.

For any graph $G\in V_n^c$ with $1\le c\le n-1$ and $-1\le \gamma <0$, we have:

$${}^0{R}_{\gamma }(G)\ge c{(n-1)}^{\gamma }+(n-c-1){(n-2)}^{\gamma }+c^{\gamma }$$

with equality holding if and only if $G=K_c+(K_{n_1}\cup K_{n_2})$ with $n_1,n_2\ge 1$ and $n_1+n_2=n-1$ for $c=1$ and $\gamma =-1$ and $G=K_c+(K_1\cup K_{n-c-1})$ for $c=1$ and $-1<\gamma <0$ or $c\ge 2$.

Proof. 

Suppose $G\in V_n^c$ is a graph with minimal ${}^0{R}_{\gamma }(G)$ with c-vertex cut $S=\{v_1,v_2,\dots ,v_c\}$. By Lemma 1 (2), the induced subgraph $G\left[S\right]$ is a complete graph $K_c$.

For $c=n-1$, there is a unique graph $K_n$ in the set $V_n^c$, which can be deal as a special case of $G=K_c+(K_1\cup K_{n-c-1})$ with $c=n-1$. So, in what follows we shall consider $1\le c\le n-2$.

Claim 1.

$G-S$ has exactly two components.

Proof of Claim 1.

On contrary suppose that $G-S$ has at least three components $G_1$, $G_2$, and $G_3$ having $u_i\in V(G_i)$ for $i=1,2$. Then we find $G+u_1{u}_2\in V_n^c$, which implies ${}^0{R}_{\gamma }(G+u_1{u}_2)<{{}^{0}R}_{\gamma }(G)$, which contradicts the choice of G. Now we assume that $G-S=G_1\cup G_2$, where $G_1$ and $G_2$ are the components of $G-S$. From Lemma 1 (2), we conclude that $G_1$ and $G_2$ are cliques and each vertex in S is adjacent to all vertices in $G_1\cup G_2$. Consequently, we get $G=K_c+(K_{n_1}\cup K_{n_2})$ where $n_1+n_2=n-c$.

Without loss of generality, assume that $n_1\le n_2$ in $G=K_c+(K_{n_1}\cup K_{n_2})$. We get:

$${}^0{R}_{\gamma }(G)=c{(n-1)}^{\gamma }+n_1{(n_1+c-1)}^{\gamma }+n_2{(n_2+c-1)}^{\gamma }.$$

For $c=1$ and $\gamma =-1$, we have ${}^0{R}_{\gamma }(G)=\frac{1}{n-1}+2$ for any graph G of the form $G=K_c+(K_{n_1}\cup K_{n_2})$ with $1\le n_1\le n_2\le n-2$ and $n_1+n_2=n-1$. For $c\ge 2$ or $-1<\gamma <0$ we require the least value of the following function:

$$f(n_1,n_2)=n_1{(n_1+c-1)}^{\gamma }+n_2{(n_2+c-1)}^{\gamma },$$

where $1\le n_1\le n_2\le n-c-1$ and $n_1+n_2=n-c$.  □

From Lemma 4 we deduce that the $f(n_1,n_2)$ is minimal when $n_1=1$ and $n_2=n-c-1$ for $n_1+n_2=n-c$. Hence ${}^0{R}_{\gamma }(G)$ attains its minimum value if and only if $G=K_c+(K_1\cup K_{n-c-1})$.  □

Let $\psi (x)=x^{\gamma }+(n-x-1){(n-2)}^{\gamma }+x{(n-1)}^{\gamma }$ for $x>0$ and $\gamma <0$, we have: ${\psi }^{\prime }(x)=\gamma x^{\gamma -1}-{(n-2)}^{\gamma }+{(n-1)}^{\gamma }<0$. This implies that $\psi (x)$ is strictly decreasing for $x>0$. Therefore, we have

$${}^0{R}_{\gamma }(K_i+(K_1\cup K_{n-i-1}))<{{}^{0}R}_{\gamma }(K_{i-1}+(K_1\cup K_{n-i}))$$

(3)

for $2\le i\le c$.

Considering that $V_{n,c}={\cup }_{i=1}^c{V}_n^i$, by Theorem 5 and inequality 3, we have the following result:

Theorem 6.

For any graph $G\in V_{n,c}$ with $1\le c\le n-1$ and $-1\le \gamma <0$, we have:

$${}^0{R}_{\gamma }(G)\ge c^{\gamma }+(n-c-1){(n-2)}^{\gamma }+c{(n-1)}^{\gamma }$$

and equality holds if and only if $G=K_c+(K_{n_1}\cup K_{n_2})$ with $n_1,n_2\ge 1$ and $n_1+n_2=n-1$ for $c=1$ and $\gamma =-1$ and $G=K_c+(K_1\cup K_{n-c-1})$ for $c=1$ and $-1<\gamma <0$ or $c\ge 2$.

As $\kappa (G)\le {\kappa }^{\prime }(G)$ we have $E_n^c\subseteq V_{n,c}$. We get $K_c+(K_1\cup K_{n-c-1})\in E_n^c$ for $c\ge 1$ but $K_1+(K_{n_1}\cup K_{n_2})\notin E_n^1$ if $1<n_1\le n_2$ with $n_1+n_2=n-1$. From Theorem 6 we deduce the following corollary:

Corollary 1.

For any graph $G\in E_n^c$ with $1\le c\le n-1$ and $-1\le \gamma <0$, we have:

$${}^0{R}_{\gamma }(G)\ge c^{\gamma }+(n-c-1){(n-2)}^{\gamma }+c{(n-1)}^{\gamma }$$

and equality holds if and only if $G=K_c+(K_1\cup K_{n-c-1})$.

Again using inequality 3 and the inequalities $\kappa (G)\le {\kappa }^{\prime }(G)\le \delta (G)$, we have the following corollary:

Corollary 2.

Let G be a connected graph of order n and minimum degree $\delta (G)=c$, then for $-1\le \gamma <0$ we have:

$${}^0{R}_{\gamma }(G)\ge c^{\gamma }+(n-c-1){(n-2)}^{\gamma }+c{(n-1)}^{\gamma }$$

and the equality achieved if and only if $G=K_c+(K_1\cup K_{n-c-1})$.

We can see that $E_{n,c}={\cup }_{i=1}^c{E}_n^i$. From Corollary 1 and inequality (3), we can obtain the subsequent result:

Theorem 7.

For any graph $G\in E_{n,c}$ with $1\le c\le n-1$ and $-1\le \gamma <0$, we have:

$${}^0{R}_{\gamma }(G)\ge c^{\gamma }+(n-c-1){(n-2)}^{\gamma }+c{(n-1)}^{\gamma }$$

with equality holding if and only if $G=K_c+(K_1\cup K_{n-c-1})$.

One can notice that for each edge $e\in E(G)$, where $G\in V_{n,c}$ (respectively $E_{n,c}$), $G-e$ also belongs to $V_{n,c}$ (respectively $E_{n,c}$). From [42] we know that $S_n$ has the maximal index ${}^0{R}_{\gamma }$ among all trees of order n for $\gamma <0$ since the function $\phi (x)={(x+1)}^{\gamma }-x^{\gamma }$ is strictly increasing for $x>0$ if $\gamma <0$. So from Lemma 2 (ii) we have the following consequences:

Theorem 8.

For any graph $G\in V_{n,c}$ with $1\le c\le n-1$ and $\gamma <0$, we have:

$${}^0{R}_{\gamma }(G)\le (n-1)+{(n-1)}^{\gamma }$$

and the equality holds if and only if $G=S_n$.

Theorem 9.

For any graph $G\in E_{n,c}$ with $1\le c\le n-1$ and $\gamma <0$, we have:

$${}^0{R}_{\gamma }(G)\le (n-1)+{(n-1)}^{\gamma }$$

and the equality holds if and only if $G=S_n$.

5. Conclusions

Finding bounds on any topological index with respect to different graph parameters is an important task. Authors in [41], investigated the upper and lower bounds on inverse degree index, $ID(G)={\sum }_{u\in V(G)}d{(u)}^{-1}$. They investigated the bounds in terms of connectivtiy, chromatic number, number of cut edges, and clique number. We extend their results for zeroth-order general Randić index, ${}^0{R}_{\gamma }(G)={\sum }_{u\in V(G)}d{(u)}^{\gamma }$, and showed that the same bounds holds when $\gamma <0$. The extremal graphs for each bounds are also investigated. The results in [41] can be found as corollaries of our main results for $\gamma =-1$.