Abstract
We have studied the k-rainbow domination number of for (Gao et al. 2019), in which we present the 3-rainbow domination number of , which should be bounded above by the four-rainbow domination number of . Therefore, we give a rough bound on the 3-rainbow domination number of . In this paper, we focus on the 3-rainbow domination number of the Cartesian product of cycles, . A 3-rainbow dominating function (3RDF) f on a given graph G is a mapping from the vertex set to the power set of three colors in such a way that every vertex that is assigned to the empty set has all three colors in its neighborhood. The weight of a 3RDF on G is the value . The 3-rainbow domination number, , is the minimum weight among all weights of 3RDFs on G. In this paper, we determine exact values of the 3-rainbow domination number of and and present a tighter bound on the 3-rainbow domination number of for .
1. Introduction
In a graph G with vertex set and edge set , the open neighborhood of a vertex is a set , denoted by . The degree of a vertex is . The minimum degree of G is denoted by and the maximum degree by . If for each vertex , there is a such that , then S is a dominating set. The domination number is the minimum cardinality among all dominating sets in G and it is denoted by .
Domination in graphs originates from location problems in operations research. As a variation of domination in graphs, rainbow domination was introduced by Brešar et al. [1]. The essence of the rainbow domination is to study how to dispatch many types of “guards” to dominate a graph. It is required that each vertex in a graph that is not settled by a “guard” has all types of “guards” in its adjacent vertices.
A function f is called a k-rainbow dominating function (kRDF) on a graph G satisfying the condition that for each vertex v such that , . The weight of kRDF on G is the value . The minimum weight among all weights of kRDFs on G is called the k-rainbow domination number, denoted by . Let f be a kRDF function on G; if , then f is called the -function.
The k-rainbow domination has many practical applications, such as storage hierarchy optimization, in information transfer or people allocation between company departments, channel assignment, network security, logistics scheduling, and so on. Therefore, it has been extensively studied by scholars. There are numerous studies on two-rainbow domination [2,3,4,5,6,7,8,9,10].
For , it is more difficult to determine the k-rainbow domination number of a graph. Chang et al. [11] proved that the k-rainbow domination is NP-complete, and they studied the k-rainbow domination problem on trees. Shao et al. [12] gave bounds for the k-rainbow domination number on an arbitrary graph, and they investigated the 3-rainbow domination numbers of cycles, paths, and generalized Petersen graphs. They determined the 3-rainbow domination number of and the upper bounds for and . Fujita et al. [13] proved sharp upper bounds on the k-rainbow domination number for all values of k. Hao et al. [14] studied the k-rainbow domination number of directed graphs and presented the exact values of the k-rainbow domination number on the Cartesian product graph of two directed cycles. Wang et al. [15] determined the k-rainbow domination number of for . Brezovnik et al. [16] studied the complexity of k-rainbow independent domination and presented sharp bounds for the k-rainbow independent domination number of the lexicographic product and the exact formula for . Kang et al. [17] initiated the study of outer-independent k-rainbow domination and presented sharp lower and upper bounds on the outer-independent two-rainbow domination number. There are also some references related to k-coloring of a graph [18,19].
, the Cartesian product of and , is the graph with the vertex set , and if either and or and . Figure 1 shows the graph of .

Figure 1.
Graph .
Vizing initiated the problem of domination on Cartesian product graphs [20]. Since then, various domination numbers of were extensively studied [21,22,23,24].
In this paper, we focus on the study of the 3-rainbow domination number of Cartesian products of two undirected cycles, . Here, we recall some important results.
Theorem 1.
([12]) Let G be a connected graph. Then, .
Theorem 2.
([25]) Let G be a connected graph of order with . Then, .
In , , , by Theorems 1 and 2, we can get:
We studied the k-rainbow domination number of for [26], in which we presented that the 3-rainbow domination number of is bounded above by the four-rainbow domination number of , i.e.:
Since for , by Equations (1) and (2), we can get a rough bound of as described in the following Lemma 1.
Lemma 1.
For , .
It is very difficult to determine the k-rainbow domination number of a graph for , since the problem is NP-complete. Only with some effective methods, one can present a sharp bound on the k-rainbow domination number, or make the known bound tighter, or determine the exact k-rainbow domination number for a given family of graphs. In this paper, we lower the upper bound in Lemma 1 by constructing some good enough 3RDFs; upon these functions, we can get a sharp upper bound of . Furthermore, we promote the lower bound in Lemma 1 for and by providing proofs for the new lower bounds. Thus, we determine the exact values of and . For and any integer m, we present a tighter bound of than in Lemma 1.
2. Upper Bounds on the 3-rainbow Domination Number of
In this section, we construct some 3-rainbow dominating functions according to the characteristics of ; upon these functions, we can get upper bounds of . Figure 2a shows a 3RDF on . We use 0, 1, 2, 3 to represent the color sets ∅, , , , respectively, and use to encode the color set . In this way, we could use Figure 2b to show a function in the following sections.

Figure 2.
A 3RDF on . (a) Vertex labeled with color sets. (b) Vertex labeled with codes.
By symmetry of , we can only discuss the cases of .
Lemma 2.
For and , .
Proof.

We define a 3RDF f as follows.
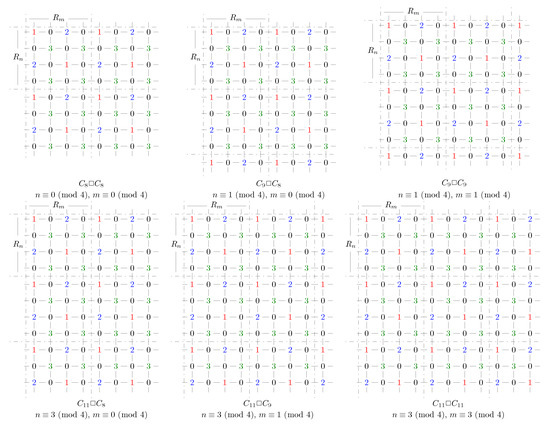
Figure 3 shows f on , , , , , and , where means we repeat the four columns with m becoming bigger and means we repeat the four rows with n becoming bigger.

Figure 3.
f on some for .
One can check that f is a 3RDF, and its weight is shown in Table 1.

Table 1.
The weight of f on .
Hence, for and . □
Lemma 3.
For , , .
Proof.

We first define a 3RDF g on .
Then, for , , , we define a 3RDF f as follows.
where h is a function defined on ,
Figure 4 shows f on , where means we repeat the four columns with m becoming bigger and means we repeat the four rows with n becoming bigger.

Figure 4.
f on .
One can check that f is a 3RDF, and the weight of f is .
Hence, for , . □
Lemma 4.
For , , .
Proof.



Case 1..
Case 1.1. For , we first define a 3RDF on ,
Then, we construct a 3RDF f on ,
where h is a function defined on ,
Case 1.2. For , define .
Case 1.3. For , we first define on ,
Then, we define f as follows.
where h is a function defined on ,

Figure 5.
f on some for .
One can check that f is a 3RDF, and its weight is shown in Table 2.

Table 2.
The weight of f on .
Case 2. For , we first define a function g on .
Then, we define f as follows.
where , , are defined as follows.
Figure 6 shows f on , where means we repeat the four columns with m becoming bigger and means we repeat the four rows with n becoming bigger.

Figure 6.
f on .
One can check that f is a 3RDF, and the weight of f is .
Hence, for , . □
Lemma 5.
For , , .
Proof.
We first define a function g on .
Then, for , , we define a 3RDF f on as follows.
where , , are defined as follows.
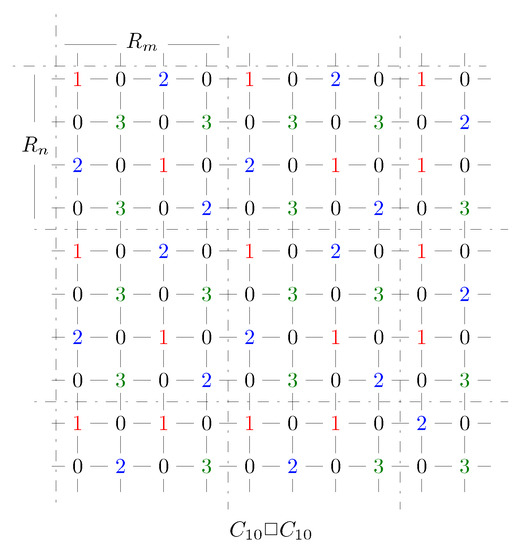
Figure 7 shows f on , where means we repeat the four columns with m becoming bigger and means we repeat the four rows with n becoming bigger.

Figure 7.
f on .
One can check that f is a 3RDF, and the weight of f is .
Hence, for , . □
Lemma 6.
For , ,
Proof.

Case 1. For , we define f in two subcases.
Case 1.1..
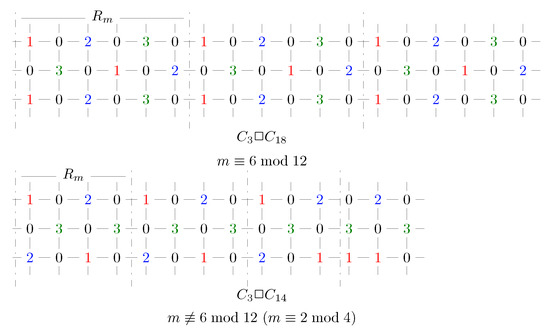
Figure 8 (above) shows f on , where means we repeat the six columns with m becoming bigger. One can check that f is a 3RDF. The weight of f is . Hence, for .

Figure 8.
3RDFs on and .
Case 1.2.. We first define a function g on .
Then, we define f as follows.
where h is a function defined on ,
Figure 8 (below) shows f on , where means we repeat the four columns with m becoming bigger. One can check that f is a 3RDF. The weight of f is f is . Hence, for .
Hence, for ,
Case 2. For , we define f in two subcases.
Case 2.1..
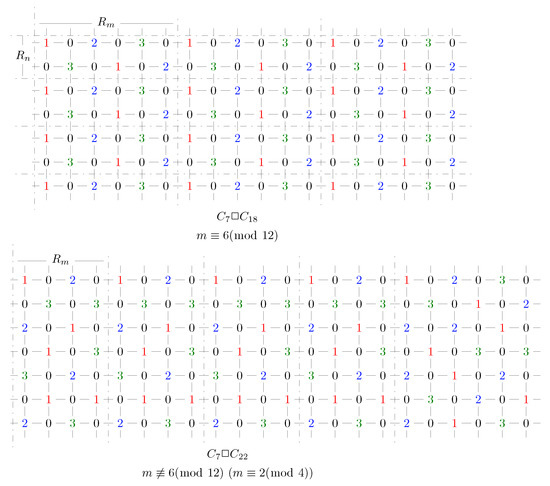
Figure 9 (above) shows f on , where means that we repeat the six columns with m becoming bigger and means we repeat the two rows with n becoming bigger. One can check that f is a 3RDF, and the weight of f is .

Figure 9.
3RDFs on and .
Case 2.2.. We first define a function g on .
Then, we define f as follows.
where h is a function defined on ,
Figure 9 (below) shows f on , where means we repeat the four columns with m becoming bigger. One can check that f is a 3RDF, and the weight of f is .
Hence, , .
Case 3..
We first define a function g on .
Then, we define f as follows.
where , , are defined as follows.
Figure 10 shows f on , where means we repeat the four columns with m becoming bigger and means we repeat the four rows with n becoming bigger.

Figure 10.
f on .
One can check that f is a 3RDF, and the weight of f is .
Hence, for , . □
By Lemmas 2–6, we have:
Theorem 3.
3. The 3-rainbow Domination Number of
Let f be an arbitrary 3RDF on ; we denote .
Lemma 7.
Let f be a 3-rainbow dominating function on . Then:
- (1)
- if , then ;
- (2)
- if , then .
Proof.
(1) Since , then . It follows that .
(2) Since , without loss of generality, let , then . It follows that . □
Theorem 4.
For , .
Proof.
By Theorem 2, .
If there exists , by Lemma 7 (1), it follows that .
If for , and if there exists , then by Lemma 7 (2), for , and for .
If for , then . Thus, for . □
Lemma 8.
Let f be a -function , then for .
Proof.
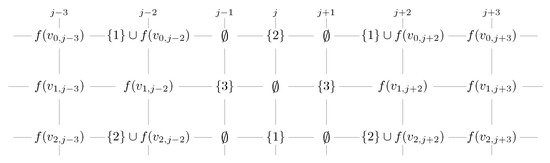
By contrast, suppose f is an arbitrary -function and there exists a j with ; by Lemma 7 (1), we have .
We construct a function as follows, and Figure 11 shows the sketch of .

Figure 11.
The sketch of in Lemma 8.
Thus, , a contradiction with that f being a -function. □
Theorem 5.
For ,
Proof.



First, we prove for .
Let f be a -function. By Lemma 8, for .
For , by Lemma 7 (2), .
For , .
For , .
Hence,
Thus, .
Then, we prove for that the lower bounds of can be improved to instead of .
If there exists , or ∧, or ∧, then the inequality in (1) is strictly true, that is , i.e., .
Excluding the above cases, we will prove that the remaining cases ∧ and ∧ cannot exist in for .
By contrast, without loss of generality, let and , then . By the definition of 3RDF, or .
Case 1.. In this case, by the definition of 3RDF, , , , , . Continuing in this way, we have:
where .
If we let , then . For , i.e., , f on is shown in Figure 12. Then, and ; this is a contradiction to the definition of 3RDF.

Figure 12.
f on for .
Case 2.. In this case, we have , . Continuing in this way, we have:
where .
If we let , , then we have .
Case 2.1.. It follows that , , . Continuing in this way, we have:
where .
For , i.e., , f on is shown in Figure 13. Then, and , a contradiction.

Figure 13.
Graph of f in Case 4.2.1.
Case 2.2.. It follows the and . Continuing in this way, we have:
where .
For , i.e., , f on is shown in Figure 14. Then, and , a contradiction.

Figure 14.
Graph of f in Case 4.2.2.
Thus, for . □
By Theorems 3–5, we have:
Theorem 6.
For ,
4. The 3-rainbow Domination Number of
Let f be an arbitrary 3RDF on ; we denote .
Lemma 9.
Let f be a 3-rainbow dominating function on . Then:
- (1)
- if , then ;
- (2)
- if , then .
Proof.
(1) Since , then . It follows that .
(2) Since , we can let , then , and . It follows that . □
Theorem 7.
.
Proof.
By Theorem 2, .
If there exists , by Lemma 9 (1), it follows that .
If for , and if there exists , then by Lemma 9 (2), it follows that .
If for , then .
Thus, , together with , and we have . □
Lemma 10.
Let f be a -function , then for .
Proof.

By contrast, suppose f is an arbitrary -function and there exists a j with . By Lemma 9 (1), we have .
We construct a function as follows, and Figure 15 shows the sketch of .

Figure 15.
The sketch of in Lemma 10.
Then, , a contradiction with f being a -function. □
Lemma 11.
Let f be a -function. If = |, then .
Proof.
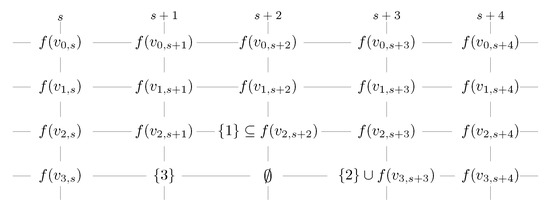
By contrast, suppose . Without loss of generality, we may assume that ; it follows that , and .
We can construct a function such that . Figure 16 shows the sketch of .
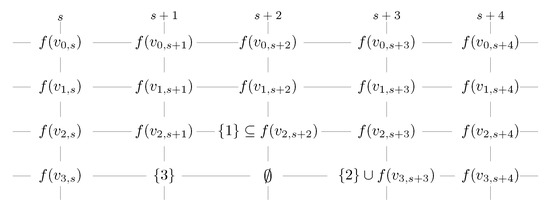
Figure 16.
The sketch of in Lemma 11.
Then, , a contradiction with f being a -function. □
Lemma 12.
There is a -function f such that , where = |.
Proof.
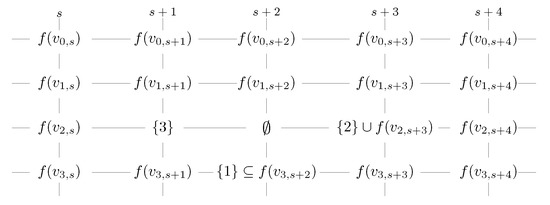
By contrast, suppose for all -functions, that is the minimum is one. Let f be a -function such that ; we denote . Let s be the smallest positive integer such that . Without loss of generality, we may assume that ; it follows that , , and .
We can construct a function as follows satisfying and (see Figure 17 for the sketch of ). Thus, there is a contradiction with the minimum being one.
□
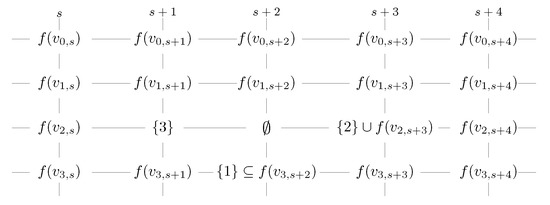
Figure 17.
The sketch of in Lemma 12.
Lemma 13.
Let f be a -function with , then , where and are defined as in Lemmas 11 and 12.
Proof.
By Lemma 10, for .
Case 1. If , by Lemma 9 (2),
Case 2. If , then there are three subcases.
Case 2.1. There is one vertex v with . Let , then . It follows that , , . Hence, .
Case 2.2. There are two vertices with a weight of one, and they are neighbors. Let , then . It follows that , . Hence, .
Case 2.3. There are two vertices with a weight of one, and they are not neighbors. Let . By Lemmas 11 and 12, we can get and . Hence, .
Case 3. If ,
Thus,
That is, . □
Theorem 8.
For , .
Proof.
By Theorem 3 and Lemma 13, it has ; together with Theorem 7, we have . □
5. Conclusions
In this paper, we investigate the 3-rainbow domination number of Cartesian products of cycles . We determine the exact values of the 3-rainbow domination number of and , i.e., , for , and for , . For , by Lemma 1 and Theorem 3, we present a better bound on the 3-rainbow domination number of , that is .
Author Contributions
H.G. contributes for supervision, methodology, validation, project administration and formal analysis. C.X. contributes for resource, some computations and wrote the initial draft of the paper. Y.Y. writes the final draft. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Fundamental Research Funds for the Central University, Grant No. 3132019323.
Acknowledgments
The authors gratefully acknowledge the reviewers for taking time out of their busy schedules to review this paper. The comments and suggestions certainly improved the presentation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brešar, B.; Henning, M.A.; Rall, D.F. Rainbow domination in graphs. Taiwan. J. Math. 2008, 12, 213–225. [Google Scholar] [CrossRef]
- Wu, Y.J.; Rad, N.J. Bounds on the 2-rainbow domination number of graphs. Graphs Combin. 2013, 29, 1125–1133. [Google Scholar] [CrossRef]
- Chellali, M.; Haynes, T.W.; Hedetniemi, S.T. Bounds on weak roman and 2-rainbow domination numbers. Discrete Appl. Math. 2014, 178, 27–32. [Google Scholar] [CrossRef]
- Furuya, M. A note on total domination and 2-rainbow domination in graphs. Discrete Appl. Math. 2015, 184, 229–230. [Google Scholar] [CrossRef]
- Stepień, Z.; Zwierzchowski, M. 2-Rainbow domination number of Cartesian products: Cn□C3 and Cn□C5. J. Comb. Optim. 2014, 28, 748–755. [Google Scholar] [CrossRef][Green Version]
- Stepień, Z.; Szymaszkiewicz, A.; Szymaszkiewicz, L.; Zwierzchowski, M. 2-Rainbow domination number of Cn□C5. Discrete Appl. Math. 2014, 170, 113–116. [Google Scholar] [CrossRef]
- Stepień, Z.; Szymaszkiewicz, L.; Zwierzchowski, M. The Cartesian product of cycles with small 2-rainbow domination number. J. Comb. Optim. 2015, 30, 668–674. [Google Scholar] [CrossRef]
- Li, Z.P.; Shao, Z.H.; Wu, P.; Zhao, T.Y. On the 2-rainbow domination stable graphs. J. Comb. Optim. 2019, 37, 1327–1341. [Google Scholar] [CrossRef]
- Tong, C.L.; Lin, X.H.; Yang, Y.S.; Luo, M.Q. 2-rainbow domination of generalized Petersen graphs P(n,2). Discrete Appl. Math. 2009, 157, 1932–1937. [Google Scholar] [CrossRef]
- Shao, Z.H.; Jiang, H.Q.; Wu, P.; Wang, S.H.; Žerovnik, J.; Zhang, X.S.; Liu, J.B. On 2-rainbow domination of generalized Petersen graphs. Discrete Appl. Math. 2019, 257, 370–384. [Google Scholar] [CrossRef]
- Chang, G.J.; Wu, J.J.; Zhu, X.D. Rainbow domination on trees. Discrete Appl. Math. 2010, 158, 8–12. [Google Scholar] [CrossRef]
- Shao, Z.H.; Liang, M.L.; Yin, C.; Xu, X.D.; Pavlič, P.; Žerovnik, J. On rainbow domination numbers of graphs. Inform. Sci. 2014, 254, 225–234. [Google Scholar] [CrossRef]
- Fujita, S.; Furuya, M.; Magnant, C. General bounds on rainbow domination numbers. Graphs Combin. 2015, 31, 601–613. [Google Scholar] [CrossRef]
- Hao, G.L.; Qian, J.G. On the rainbow domiantion number of digraphs. Graphs Combin. 2016, 32, 1903–1913. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, X.L.; Dehgardi, N.; Amjadi, J.; Khoeilar, R.; Liu, J.B. k-rainbow domination number of P3□Pn. Mathematics 2019, 7, 203. [Google Scholar] [CrossRef]
- Brezovnik, S.; Šumenjak, T.K. Complexity of k-rainbow independent domination and some results on the lexicographic product of graphs. Appl. Math. Comput. 2019, 349, 214–220. [Google Scholar] [CrossRef]
- Kang, Q.; Samodivkin, V.; Shao, Z.; Sheikholeslami, S.M.; Soroudi, M. Outer-independent k-rainbow domination. J. Taibah Univ. Sci. 2019, 1, 883–891. [Google Scholar] [CrossRef]
- Furmańczyk, H.; Kubale, M. Tight bounds on the complexity of semi-equitable coloring of cubic and subcubic graphs. Appl. Math. Lett. 2018, 237, 116–122. [Google Scholar] [CrossRef]
- Pikies, T.; Kubale, M. Better polynomial algorithms for scheduling unit-length jobs with bipartite incompatibility graphs on uniform machines. Bull. Pol. Acad. Sci.-Tech. Sci. 2019, 1, 31–36. [Google Scholar]
- Vizing, V.G. Some unsolved problems in graph theory. Uspehi Mater. Nauk. 1968, 23, 117–134. [Google Scholar] [CrossRef]
- Wang, H.C.; Kim, H.K.; Deng, Y.P. On signed domination number of Cartesian product of directed paths. Util. Math. 2018, 109, 45–61. [Google Scholar]
- Ye, A.S.; Miao, F.; Shao, Z.H.; Liu, J.B.; Žerovnik, J.; Repolusk, P. More results on the domination number of Cartesian product of two directed cycles. Mathematics 2019, 7, 210. [Google Scholar] [CrossRef]
- Mollard, M. The domination number of Cartesian product of two directed paths. J. Comb. Optim. 2014, 27, 144–151. [Google Scholar] [CrossRef]
- Li, Z.P.; Shao, Z.H.; Xu, J. Weak 2-domination number of Cartesian products of cycles. J. Comb. Optim. 2018, 35, 75–85. [Google Scholar] [CrossRef]
- Furuya, M.; Koyanagi, M.; Yokota, M. Upper bound on 3-rainbow domination in graphs with minimum degree 2. Discrete Optim. 2018, 29, 45–76. [Google Scholar] [CrossRef]
- Gao, H.; Li, K.; Yang, Y.S. The k-rainbow domination number of Cn□Cm. Mathematics 2019, 7, 1153. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).